时间序列分析报告——ARMA模型实验
时间序列中的ARMA模型

c u=
1 (1 2 ... p)
旳无条
7
ARIMA模型旳概念
Yt-u=1(Yt-1-u)+ 2(Yt-2-u)+...+p(Yt-p-u)+vt
0=1 1+ 2 2+...+p p+ 2 1=1 0+ 2 1+...+ p p-1
……
p=1 p-1+ 2 p-2+...+ p 0
(1
2
1
1≤j≤22q ... q2 )
0 j>q
j>q时,ACF(j)=0,此现象为截尾,是MA(q)过程旳一种特征
如下图:
18
ARMA模型旳辨认
MA(2)过程
yt =0.5ut-1 0.3ut2 ut
19
ARMA模型旳辨认
⑵ AR(p)过程旳偏自有关函数
j p 时,偏自有关函数旳取值不为0 j>q 时,偏自有关函数旳取值为0 AR(p)过程旳偏自有关函数p阶截尾 如下图:
32
ARMA模型旳预测
二. 基于MA过程旳预测
过程 结论:
MA (2) 过程仅有2期旳记忆力
33
ARMA模型旳预测
三. 基于ARMA过程旳预测
结合对AR过程和MA过程进行预测 ARMA模型一般用于短期预测
34
五、实例:ARMA模型在金融数 据中旳应用
数据: 1991年1月到2023年1月旳我国货币供
3
ARIMA模型旳概念
2.MA(q)过程旳特征
1. E(Yt)=u
2.
var(Yt)
(1
2
ARMA模型时间分析分析

ARMA 模型分析我国工业总产值华北科技学院基础部计算B091班刘建红摘要:本文摘录了从1990年1月至1997年12月我国工业总产值的月度资料(1990年不变价格),共有96个观测值。
在我国工业总产值逐年增长的同时,随季节、月份的改变,总产值也会出现轻微波动情况。
研究工业总产值随时间的变化,将有利于我们更细致地了解一年内每个季度,每个月份工业产值的变化规律。
本文运用数据分析功能强大的数据分析软件EVIEWS 进行分析,通过时间序列自相关系数分析,得到我国总产值的发展趋势图,以及该时间序列的自相关与偏自相关分析图;由自相关分析图来很难看出序列是有季节性,并对原序列进行逐期差分,以消除趋势;对新序列进行季节差分,消除序列的趋势,得到该序列的自相关与偏自相关分析图,表明序列可以直接进行ARMA 模型;又运用序列均值检验,均值与0无显著差异,进一步表明序列可以直接进行ARMA 模型。
然后运用ARIMA (3,1,1)模型对我国1997年工业总产值进行试预测,得到模型预测值与实际观测值的对比折线图,并且模型预测值与实际观测值很接近,说明预测精度较高,进一步说明了ARIMA 模型的拟合效果很好。
同时运用ARIMA (3,1,1)模型对我国1998年工业总产值进行试预测,得到1998年各月工业总产值预测折线图。
关键字:EVIEWS 软件 自相关分析 ARMA 模型 季节性 预测1、 研究背景随着我国经济的迅速发展,工业总产值也逐年增加。
在我国工业总产值逐年增长的同时,随季节的改变,总产值也会出现轻微波动情况。
研究工业总产值随时间的变化,将有利于我们更细致地了解一年内每个季度,甚至每个月份大致变化规律,通过这些规律我们可以对未来我国工业总产值的变化,做很好的预测。
因此,研究我国工业总产值的变化规律就显得非常必要了。
本文运用分析功能强大的数据分析软件EVIEWS 进行数据分析,建立ARMA 模型,并进行简单预测,节约了手工计算时间,简化了手工计算过程,更精确地反映我国工业总产值的变化规律。
时间序列上机实验ARMA模型的建立

实验一ARMA模型建模一、实验目的学会检验序列平稳性、随机性。
学会分析时序图与自相关图。
学会利用最小二乘法等方法对ARMA模型进行估计,以及掌握利用ARMA模型进行预测的方法。
学会运用Eviews软件进行ARMA模型的识别、诊断、估计和预测和相关具体操作。
二、基本概念宽平稳:序列的统计性质不随时间发生改变,只与时间间隔有关。
AR模型:AR模型也称为自回归模型。
它的预测方式是通过过去的观测值和现在的干扰值的线性组合预测,自回归模型的数学公式为:乂2『t2 川p y t p t式中:p为自回归模型的阶数i(i=1,2,,p)为模型的待定系数,t为误差,yt 为一个平稳时间序列。
MA模型:MA模型也称为滑动平均模型。
它的预测方式是通过过去的干扰值和现在的干扰值的线性组合预测。
滑动平均模型的数学公式为:y t t 1 t 1 2 t 2 川q t q式中:q为模型的阶数;j(j=1,2,,q)为模型的待定系数;t为误差;yt为平稳时间序列。
ARMA模型:自回归模型和滑动平均模型的组合,便构成了用于描述平稳随机过程的自回归滑动平均模型ARMA,数学公式为:y t 1 y t 1 2 y t 2 p y t p t 1 t 1 2 t 2 q t q三、实验内容(1)通过时序图判断序列平稳性;(2)根据相关图,初步确定移动平均阶数q 和自回归阶数p;(3)对时间序列进行建模四、实验要求学会通过各种手段检验序列的平稳性;学会根据自相关系数和偏自相关系数来初步判断ARMA模型的阶数p和q,学会利用最小二乘法等方法对ARMA 模型进行估计,学会利用信息准则对估计的ARMA 模型进行诊断,以及掌握利用ARMA 模型进行预测。
五、实验步骤1.模型识别(1)绘制时序图在Eviews 软件中,建立一个新的工作文件, 500个数据。
通过Eviews 生成随机序列“ e,再根据“ x=*x(-1)*x(-2)+e ”生成AR(2)模型序列“ x” 默认x(1)=1, x(2)=2,得到下列数据,由于篇幅有限。
时序实验ARMA建立预测

实验二 ARMA 模型建模与预测指导一、实验目的学会通过各种手段检验序列的平稳性;学会根据自相关系数和偏自相关系数来初步判断ARMA 模型的阶数p 和q ,学会利用最小二乘法等方法对ARMA 模型进行估计,学会利用信息准则对估计的ARMA 模型进行诊断,以及掌握利用ARMA 模型进行预测。
掌握在实证研究中如何运用Eviews 软件进行ARMA 模型的识别、诊断、估计和预测和相关具体操作。
二、基本概念宽平稳:序列的统计性质不随时间发生改变,只与时间间隔有关。
AR 模型:AR 模型也称为自回归模型。
它的预测方式是通过过去的观测值和现在的干扰值的线性组合预测, 自回归模型的数学公式为:1122t t t p t p t y y y y φφφε---=++++式中: p 为自回归模型的阶数i φ(i=1,2, ,p )为模型的待定系数,t ε为误差, t y 为一个平稳时间序列。
MA 模型:MA 模型也称为滑动平均模型。
它的预测方式是通过过去的干扰值和现在的干扰值的线性组合预测。
滑动平均模型的数学公式为:1122t t t t q t q y εθεθεθε---=----式中: q 为模型的阶数; j θ(j=1,2, ,q )为模型的待定系数;t ε为误差; t y 为平稳时间序列。
ARMA 模型:自回归模型和滑动平均模型的组合, 便构成了用于描述平稳随机过程的自回归滑动平均模型ARMA , 数学公式为:11221122t t t p t p t t t q t q y y y y φφφεθεθεθε------=++++----三、实验内容及要求1、实验内容:(1)根据时序图判断序列的平稳性;(2)观察相关图,初步确定移动平均阶数q 和自回归阶数p ;(3)运用经典B-J 方法对某企业201个连续生产数据建立合适的ARMA (,p q )模型,并能够利用此模型进行短期预测。
2、实验要求:(1)深刻理解平稳性的要求以及ARMA 模型的建模思想;(2)如何通过观察自相关,偏自相关系数及其图形,利用最小二乘法,以及信息准则建立合适的ARMA 模型;如何利用ARMA 模型进行预测; (3)熟练掌握相关Eviews 操作,读懂模型参数估计结果。
金融时序分析ARMA模型实验报告
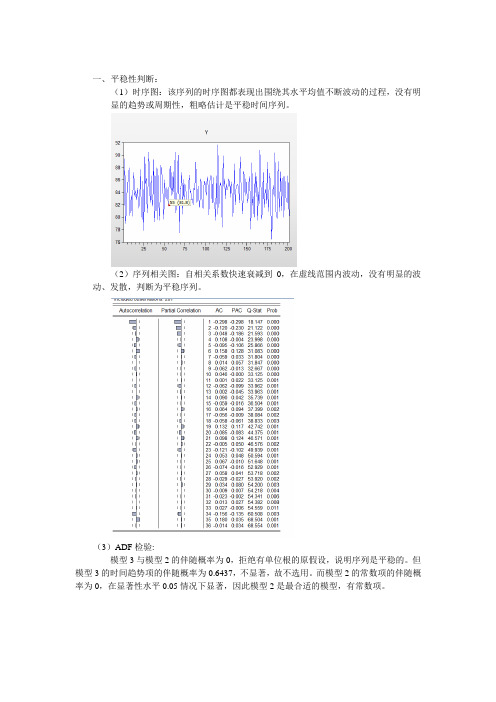
一、平稳性判断:(1)时序图:该序列的时序图都表现出围绕其水平均值不断波动的过程,没有明显的趋势或周期性,粗略估计是平稳时间序列。
(2)序列相关图:自相关系数快速衰减到0,在虚线范围内波动,没有明显的波动、发散,判断为平稳序列。
(3)ADF检验:模型3与模型2的伴随概率为0,拒绝有单位根的原假设,说明序列是平稳的。
但模型3的时间趋势项的伴随概率为0.6437,不显著,故不选用。
而模型2的常数项的伴随概率为0,在显著性水平0.05情况下显著,因此模型2是最合适的模型,有常数项。
模型1的t检验的伴随概率为0.6128,不能拒绝有单位根的原假设,不选用。
综上所述,该序列是平稳的。
二、随机性检验观察自相关图最后两列可以看到,Q检验的伴随概率均小于0.05,拒绝没有自相关性的原假设,因此该序列不是白噪声序列,没有把信息都提取出来。
观察其AC,虽落入虚线内后没有再到虚线外,但不是由非0骤降到0,判断为拖尾。
观察PAC,结果与AC类似,因此AC、PAC都是拖尾,初步判断使用ARMA模型。
接下来将尝试使用AR(1)、AR(2)、MA(1)、MA(2)、ARMA(1,3)、ARMA(1,2)模型进行拟合。
三、模型估计与白噪声检验(1)AR(1):该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,拒绝没有自相关性的原假设,不是白噪声序列。
(2)AR(2):该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,阶数较小时拒绝没有自相关性的原假设,不是白噪声序列。
(3)MA(1):该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,接受没有自相关性的原假设,是白噪声序列。
(4)MA(2):该模型MA(2)项不显著,不选用。
(5)ARMA(1,3):该模型各项显著,故对其进行残差项白噪声检验,观察Q检验及其伴随概率,在显著性水平为0.05时,接受没有自相关性的原假设,是白噪声序列。
时间序列实验报告(ARMA模型的参数估计)

时间序列分析实验报告实验课程名称时间序列分析
实验项目名称 ARMA,ARIMA模型的参数估计年级
专业
学生姓名
成绩
理学院
实验时间:2015 年11月20日
学生所在学院:理学院专业:金融学班级:数学班
1、判断该序列的稳定性和纯随机性
该序列的时序图如下:
从图中可以看出具有很明显的下降趋势和周期性,所以通常是非平稳的。
在做它的自相关图。
由该时序图我们基本可以认为其是平稳的,再做DX自相关图和偏自相关图
自相关图显示延迟12阶自相关系数显著大于2倍标准差范围。
说明差分后序列中仍蕴含着非常显著的季节效应。
3、模型参数估计和建模
普通最小二乘法下,输入D(X,1,12) AR(1) MA(1) SAR(12) SMA(12) ,得到下图,其中,所有的参数估计量的
于0.05,均显著。
AIC为1.896653,SC为1.964273 。
普通最小二乘法,输入D(X,1,12)AR(1 )MA(1)SAR(12)SAR(24)SMA(12),
值小于0.05,均显著。
AIC为1.640316,SC为1.728672 。
4、参数估计结果
比较这两个模型,因为第二个模型的SC值小于第一个模型的SC值,所以相对而言,第二个模型是最优模型。
模型结果为:。
ARMAARIMA模型介绍及案例分析

ARMAARIMA模型介绍及案例分析ARMAARIMA模型是一种时间序列分析方法,用于对具有自回归和移动平均特性的数据进行建模和预测。
这个模型是由自回归(AR)和移动平均(MA)两个组成部分构成的,对于非平稳的数据还需要加入差分(I)的过程,所以称为ARMAARIMA模型。
ARMA模型是根据时间序列的自相关和滑动平均性质来进行建模的。
自回归是指当前数据与历史数据之间的相关关系,移动平均则关注当前数据与滞后差分误差之间的关系。
ARMA模型的一般形式可以表示为:Y(t)=c+φ₁Y(t-1)+...+φₚY(t-p)+ε(t)-θ₁ε(t-1)-...-θₚε(t-q)其中,Y(t)表示当前的观测值,c是常数,φ₁...φₚ是自回归系数,ε(t)是白噪声误差项,θ₁...θₚ是滑动平均系数,p和q分别表示AR和MA的阶数。
对于非平稳的时间序列数据,需要进行差分操作,即I(积分)的过程,来将数据变为平稳的。
差分阶数常用d表示。
而ARIMA(自回归移动平均积分模型)则是对ARMA模型进行补充,主要针对非平稳时间序列数据。
ARIMA模型的一般形式可以表示为:ΔY(t)=c+φ₁ΔY(t-1)+...+φₚΔY(t-p)+ε(t)-θ₁ε(t-1)-...-θₚε(t-q)其中ΔY(t)表示差分后的序列,其他参数与ARMA模型类似。
下面以一个股票价格的时间序列数据为例进行ARMAARIMA模型的案例分析。
假设我们有一段时间内的股票价格数据,要通过ARMAARIMA模型对未来的股票价格进行预测。
首先,我们需要对数据进行平稳性检验,可以使用单位根检验(如ADF检验)来确定是否需要进行差分。
接下来,需要确定ARMA模型的阶数,可以通过观察自相关图(ACF)和偏自相关图(PACF)来确定。
根据图形的截尾和拖尾情况,可以估计出AR和MA的阶数。
然后,可以利用最大似然估计方法来估计模型参数,这可以通过软件来实现。
在估计参数之后,需要对模型进行检验,主要包括检查残差序列是否为白噪声,可以通过自相关图和偏自相关图进行检查。
平稳时间序列分析-ARMA模型

1 0 1 2
所以,平稳AR(2)模型的协方差函数递推公式为
0
1 2 (1 2 )(1 1 2 )(1 1
2
)
2
1
1 0 1 2
k
1 k1 2 k2,k
2
4、自相关系数
(1)自相关系数的定义:
k
k 0
特别
0 1
(2)平稳AR(P)模型的自相关系数递推公式:
k 1k 1 2 k 2 p k p
例3.5:— (3)xt xt1 0.5xt2 t
自相关系数呈现出“伪周期”性
例3.5:— (4)xt xt1 0.5xt2 t
自相关系数不规则衰减
6、偏自相关函数
自相关函数ACF(k)给出了Xt与Xt-k的总体 相关性,但总体相关性可能掩盖了变量间完全 不同的相关关系。
例如,在AR(1) 中,Xt与Xt-2间有相关性可 能主要是由于它们各自与Xt-1间的相关性带来 的:
对于非中心化序列
xt 0 1xt1 2 xt2
p xt p t
作变换
1 1
0
p
yt xt
则原序列即化为中心化序列
yt 1 yt1 2 yt2 p yt p t
所以,以后我们重点讨论中心化时间序列。
AR模型的算子表示
令 (B) 11B 2B2 p B p
则 AR( p) 模型可表示为
平稳AR(1)模型的传递形式为
xt
t 1 1B
i0
(1B)i t
1i ti
i0
Green函数为 Gj 1 j , j 0,1,
平稳AR(1)模型的方差为
Var(xt )
G2jVar(t )
j0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于ARMA模型的社会融资规模增长分析————ARMA模型实验第一部分实验分析目的及方法一般说来,若时间序列满足平稳随机过程的性质,则可用经典的ARMA模型进行建模和预则。
但是, 由于金融时间序列随机波动较大,很少满足ARMA模型的适用条件,无法直接采用该模型进行处理。
通过对数化及差分处理后,将原本非平稳的序列处理为近似平稳的序列,可以采用ARMA模型进行建模和分析。
第二部分实验数据2.1数据来源数据来源于中经网统计数据库。
具体数据见附录表5.1 。
2.2所选数据变量社会融资规模指一定时期内(每月、每季或每年)实体经济从金融体系获得的全部资金总额,为一增量概念,即期末余额减去期初余额的差额,或当期发行或发生额扣除当期兑付或偿还额的差额。
社会融资规模作为重要的宏观监测指标,由实体经济需求所决定,反映金融体系对实体经济的资金量支持。
本实验拟选取2005年11月到2014年9月我国以月为单位的社会融资规模的数据来构建ARMA模型,并利用该模型进行分析预测。
第三部分 ARMA模型构建3.1判断序列的平稳性首先绘制出M的折线图,结果如下图:图3.1 社会融资规模M曲线图从图中可以看出,社会融资规模M序列具有一定的趋势性,由此可以初步判断该序列是非平稳的。
此外,m在每年同时期出现相同的变动趋势,表明m还存在季节特征。
下面对m的平稳性和季节性·进行进一步检验。
为了减少m的变动趋势以及异方差性,先对m进行对数化处理,记为lm,其时序图如下:图3.2 lm曲线图对数化后的趋势性减弱,但仍存在一定的趋势性,下面观察lm的自相关图表3.1 lm的自相关图上表可以看出,该lm序列的PACF只在滞后一期、二期和三期是显著的,ACF随着滞后结束的增加慢慢衰减至0,由此可以看出该序列表现出一定的平稳性。
进一步进行单位根检验,由于存在较弱的趋势性且均值不为零,选择存在趋势项的形式,并根据AIC自动选择之后结束,单位根检验结果如下:表3.2 单位根输出结果Null Hypothesis: LM has a unit rootExogenous: Constant, Linear TrendLag Length: 0 (Automatic - based on SIC, maxlag=12)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -8.674646 0.0000Test critical values: 1% level -4.0469255% level -3.45276410% level -3.151911*MacKinnon (1996) one-sided p-values.单位根统计量ADF=-8.674646小于临界值,且P为0.0000,因此该序列不存在单位根,即该序列是平稳序列。
由于趋势性会掩盖季节性,从lm图中可以看出,该序列有一定的季节性,为了分析季节性,对lm进行差分处理,进一步观察季节性:图3.3 dlm曲线图观察dlm 的自相关表:表3.3 dlm的自相关图Date: 11/02/14 Time: 22:35Sample: 2005M11 2014M09Included observations: 106Autocorrelation Partial Correlation AC PAC Q-Stat Prob****|. |****|.| 1 -0.566 -0.566 34.934 0.000.|* | **|.| 2 0.113 -0.305 36.341 0.000.|. | *|.| 3 0.032 -0.093 36.455 0.000*|. | *|.| 4 -0.084 -0.114 37.244 0.000.|* | .|.| 5 0.105 0.015 38.494 0.000*|. | *|.| 6 -0.182 -0.182 42.296 0.000.|* | *|.| 7 0.105 -0.156 43.563 0.000.|. | *|.| 8 -0.058 -0.171 43.954 0.000.|. | *|.| 9 -0.019 -0.196 43.996 0.000.|* | .|.| 10 0.110 -0.045 45.429 0.000**|. | **|.| 11 -0.242 -0.329 52.501 0.000.|*** | .|.| 12 0.363 0.023 68.516 0.000*|. | .|.| 13 -0.202 0.032 73.534 0.000.|* | .|*| 14 0.101 0.125 74.815 0.000.|. | .|*| 15 0.004 0.141 74.817 0.000*|. | *|.| 16 -0.161 -0.089 78.110 0.000.|** | .|.| 17 0.219 0.037 84.252 0.000**|. | .|.| 18 -0.221 -0.036 90.623 0.000.|* | .|.| 19 0.089 -0.046 91.662 0.000*|. | *|.| 20 -0.080 -0.158 92.516 0.000.|. | .|.| 21 0.067 -0.039 93.115 0.000.|. | .|.| 22 0.068 0.056 93.749 0.000**|. | *|.| 23 -0.231 -0.130 101.08 0.000.|*** | .|*| 24 0.359 0.116 119.04 0.000| | 25 -0.189 0.123 124.09 0.000.|. | .|.| 26 0.032 0.034 124.23 0.000.|. | .|.| 27 0.059 0.037 124.74 0.000*|. | .|.| 28 -0.126 0.044 127.08 0.000.|* | *|.| 29 0.087 -0.079 128.21 0.000.|. | .|*| 30 -0.050 0.092 128.58 0.000.|. | .|.| 31 -0.037 -0.019 128.79 0.000.|. | *|.| 32 -0.035 -0.113 128.97 0.000.|. | .|.| 33 0.041 -0.056 129.24 0.000.|* | .|.| 34 0.078 -0.027 130.21 0.000**|. | *|.| 35 -0.215 -0.197 137.64 0.000.|*** | .|*| 36 0.380 0.130 161.26 0.000 由dlm的自相关图可知,dlm在滞后期为12、24、36等差的自相关系数均显著异于零。
因此该序列为以12为周期呈现季节性,而且季节自相关系数并没有衰减至零,因此为了考虑这种季节性,进行季节性差分,得新变量sdlm:观察sdlm的自相关图:表3.4 sdlm的自相关图Date: 11/02/14 Time: 22:40Sample: 2005M11 2014M09Included observations: 94Autocorrelation Partial Correlation AC PAC Q-Stat Prob****|. |****|.| 1 -0.505 -0.505 24.767 0.000. |. | ***|.| 2 -0.057 -0.419 25.082 0.000. |. | **|.| 3 0.073 -0.292 25.609 0.000| | 4 0.160 0.067 28.169 0.000**|. | .*|.| 5 -0.264 -0.125 35.252 0.000. |* | .*|.| 6 0.098 -0.110 36.244 0.000. |* | . |.| 7 0.098 0.019 37.243 0.000. |. | . |*| 8 -0.041 0.082 37.419 0.000.*|. | . |.| 9 -0.132 -0.038 39.275 0.000. |* | .*|.| 10 0.076 -0.139 39.902 0.000. |** | . |**| 11 0.227 0.247 45.485 0.000***|. | **|.| 12 -0.459 -0.259 68.647 0.000. |* | **|.| 13 0.193 -0.251 72.777 0.000. |* | .*|.| 14 0.132 -0.101 74.753 0.000.*|. | .*|.| 15 -0.142 -0.189 77.056 0.000. |. | . |.| 16 -0.053 -0.056 77.378 0.000. |** | . |*| 17 0.233 0.091 83.751 0.000**|. | .*|.| 18 -0.234 -0.179 90.258 0.000. |* | . |.| 19 0.102 0.054 91.505 0.000. |. | . |.| 20 -0.052 -0.035 91.841 0.000. |* | . |.| 21 0.123 -0.009 93.714 0.000. |. | . |*| 22 -0.059 0.120 94.150 0.000. |. | . |**| 23 -0.011 0.215 94.166 0.000. |. | .*|.| 24 -0.032 -0.170 94.301 0.000. |* | .*|.| 25 0.088 -0.137 95.303 0.000| | 26 -0.105 -0.034 96.760 0.000. |* | .*|.| 27 0.077 -0.116 97.562 0.000. |. | .*|.| 28 -0.054 -0.178 97.967 0.000. |. | . |.| 29 0.010 0.032 97.982 0.000. |* | . |.| 30 0.102 0.039 99.457 0.000.*|. | .*|.| 31 -0.179 -0.099 104.06 0.000. |. | . |.| 32 0.071 -0.058 104.79 0.000. |. | .*|.| 33 0.031 -0.066 104.93 0.000.*|. | .*|.| 34 -0.089 -0.144 106.13 0.000. |. | . |*| 35 0.036 0.082 106.32 0.000. |* | .*|.| 36 0.105 -0.102 108.05 0.000 Sdlm在滞后期24之后的季节ACF和PACF已衰减至零,下面对sdlm建立SARMA模型。
