截长补短法例题
截长补短经典例题

截长补短经典例题
1.问题:一个长方形的长是宽的2倍,如果长减少4厘米,宽增加6厘米,那么面积就会增加18平方厘米。
请问原来的长方形的长和宽各是多少厘米?
解:设原来的长方形的宽为X厘米,那么长为2x厘米。
根据题意,我们可以得到一个方程:
(x+6)*(2x-4)=2x^2+18
解这个方程,我们得到:
2x2-4x+12x-24=2x2+18
IOx=42
X=4.2
所以原来长方形的宽为4.2厘米,长为4.2*2=8.4厘米。
2.问题:一个圆的半径是另一个圆半径的2倍,如果大圆的面积比小圆的面积大16兀平方厘米,那么大圆和小圆的半径各是多少厘米?(兀取
3.14)
解:设小圆的半径为r厘米,那么大圆的半径为2r厘米。
根据题意,我们可以得到一个方程:
π*(2r)^2一n*r^2=16π
解这个方程,我们得到:
3.14*(4r^2-r^2)=16π
3.14*3/2=16π
3/2=16
r^2=5.3333(保留四位小数)
所以小圆的半径约为2.3厘米,大圆的半径约为4.6厘米。
专题02 辅助线之截长补短

几何专题02 辅助线之截长补短一、 知识导航截长:在长边截取一条与某一短边相等的线段,再证明剩下的线段长度与另一短边相等。
例:如图,在AB 上截取AD AC=补短:通过延长或是旋转等方式使两短边拼接在一起,然后证明与长边相等。
例:延长AC 至点D ,使得AD AB=D CB A二、 典型例题题型一 截长补短证明线段(角)和差关系例1 已知:如图,在△ABC 中,∠1=∠2,∠B =2∠C .求证:AB BD AC +=.变式训练1 已知:在ABC △中,AB CD BD =-,AD BC ⊥,求证:2B C∠=∠例2 在四边形ABCD 中,AB =AD ,∠ABC+∠ADC =180°,E 、F 分别是边BC ,CD 上的两点,且∠EAF=G F E C B D A A DBCE FG FE C B D A A D B C EF 12∠BAD ,求证:BE+DF =EF .变式训练2 正方形ABCD 中,点E 在CD 延长线上,点F 在BC 延长线上,45EAF ∠=︒,求证:EF BF DE=-题型二 截长补短探究线段长度关系例3 如图,Rt △ABC 中,∠BAC =90°,AB =AC .点D 是边BC 下方一点,∠BDC =90°,探索三条线段DA 、DB 、DC 之间的等量关系,并证明你的结论.变式训练3 在四边形ABDC 中,180B C ∠+∠=︒,DB DC =,120BDC ∠=︒,以D 为顶点作EDF ∠为60︒角,角的两边分别交AB ,AC 于E ,F 两点,连接EF ,请直接写出线段BE ,CF ,EF 之间的数量关系.GAB DC E F FEC D BA三、 巩固练习1. 正方形ABCD 中,已知AB=3,点E ,F 分别在BC 、CD 上,且∠BAE=30°,∠DAF=15°,求△AEF 的面积.2. 如图,在ΔABC 中,AB >AC ,∠1=∠2,P 为AD 上任意一点.求证:AB AC PB PC ->-.截长补短方法归纳总结:线段间的和差倍分,就把几条线段间的数量关系转为两条线段的等量关系.但凡出现了线段的和差关系时,一定要尝试一下用截长补短的方法来进行处理,但不是每一个和差关系的题目都可以同时使用截长法和补短法,有时截长法能更加便捷的解决问题,而有时补短法又优于截长法,这都是需要根据具体的题目取选择具体的方法的。
截长补短法经典例题

1.在解决几何问题时,截长补短法常用于:A.证明线段相等B.证明角度相等(答案)C.计算面积D.求解体积2.下列哪个图形问题最适合使用截长补短法来解决?A.求解圆的半径B.证明两个三角形全等(答案)C.计算长方体的表面积D.求解一次方程的根3.使用截长补短法时,通常需要:A.添加辅助线来构造相似图形B.延长或截取线段来构造等长线段(答案)C.使用勾股定理D.计算图形的周长4.在三角形ABC中,AB > AC,为了证明某条线段与AB相等,可以使用截长补短法,下列哪个步骤是正确的?A.延长AC至D,使得CD = ABB.截取AB的一部分,使其与AC相等(答案)C.在三角形外部构造一个与三角形ABC全等的三角形D.计算三角形ABC的面积5.截长补短法在解决哪类问题时特别有用?A.代数方程求解B.图形面积计算C.线段长度比较和证明(答案)D.体积计算6.下列哪个不是截长补短法的常见应用?A.证明线段和差关系B.构造平行线来证明角度相等C.通过截取和延长来构造等边三角形(答案,这更多是等边三角形的性质或构造法,不是截长补短法的直接应用)D.利用线段的相等关系来证明三角形的全等7.在使用截长补短法时,如果延长了某条线段,通常是为了:A.增加图形的面积B.构造一个与已知线段相等的线段(答案)C.改变图形的形状D.计算图形的周长8.下列哪个步骤是使用截长补短法证明线段相等时的常见策略?A.延长较短的线段至与较长线段相等B.计算两条线段的长度差C.通过截取较长线段的一部分来构造与较短线段相等的线段(答案)D.使用三角形的相似性质。
三角形全等例题+练习(常用方法)
B
DE C
7
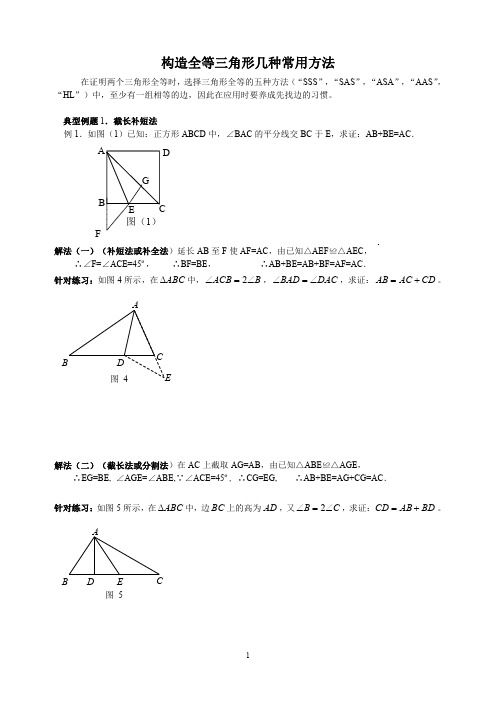
典型例题 5.翻折法 若题设中含有垂线、角的平分线等条件的,可以试用轴对称性质,沿轴翻转图形来构造全等三角形.
例 5.如图(8)已知:在△ABC 中,∠A=45º, AD⊥BC,若 BD=3,DC=2, 求:△ABC 的面积.
A
E
F
B DC
G
针对练习 1:如图2所示,已知 ABC 中, AC BC , ACB 90 , BD 平分 ABC , 求证: AB BC CD 。
0
60
,
C
400
,P,Q
分别在
BC,CA
上,并且
AP
、BQ 分别是 BAC , ABC 的角平分线。求证:BQ+AQ=AB+BP
A
B Q
P
C
截长补短 4、如图,在四边形 ABCD 中,BC>BA,AD=CD,BD 平分 ABC , 求证: A C 1800
A D
B
C
截长补短 5、如图在△ABC 中,AB>AC,∠1=∠2,P 为 AD 上任意一点,求证;AB-AC>PB-PC
∠MBN 60 ,∠MBN 绕 B 点旋转,它的两边分别交 AD,DC (或它们的延长线)于
E,F . 当∠MBN 绕 B 点旋转到 AE CF 时(如图 1),易证 AE CF EF . 当∠MBN 绕 B 点旋转到 AE CF 时,在图 2 和图 3 这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,线段 AE,CF , EF 又有怎样的数量关系?请写出你的 猜想,不需证明.
A
B
EM
A
B
EM
A B
CF
截长补短法例题完整

截长补短法例题(可以直接使用,可编辑优秀版资料,欢迎下载)截长补短法例1. 已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC .求证:∠BAD +∠BCD =180°.分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现.证明:过点D 作DE 垂直BA 的延长线于点E ,作DF ⊥BC 于点F ,如图1-2∵BD 平分∠ABC ,∴DE =DF ,在Rt △ADE 与Rt △CDF 中,⎩⎨⎧==CD AD DF DE ∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF .又∠BAD +∠DAE =180°,∴∠BAD +∠DCF =180°,即∠BAD +∠BCD =180°F E D C B A 图1-2 A B C D图1-1例2. 已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD .求证:∠BAP +∠BCP =180°.分析:与例1相类似,证两个角的和是180°,可把它们移到一起,让它们是邻补角,即证明∠BCP =∠EAP ,因而此题适用“补短”进行全等三角形的构造.证明:过点P 作PE 垂直BA 的延长线于点E ,如图3-2∵∠1=∠2,且PD ⊥BC ,∴PE =PD ,在Rt △BPE 与Rt △BPD 中,⎩⎨⎧==BP BP PD PE ∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD .∵AB +BC =2BD ,∴AB +BD +DC =BD +BE ,∴AB +DC =BE即DC =BE -AB =AE .在Rt △APE 与Rt △CPD 中,⎪⎩⎪⎨⎧=∠=∠=DC AE PDC PEA PD PEA B C D P 12N图3-1P 12NA B C D E 图3-2AD B CE 图2-1 ∴Rt △APE ≌Rt △CPD (SAS),∴∠PAE =∠PCD又∵∠BAP +∠PAE =180°,∴∠BAP +∠BCP =180°例3. 如图2-1,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB .求证:CD =AD +BC .分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在CD 上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的.证明:在CD 上截取CF =BC ,如图2-2在△FCE 与△BCE 中,⎪⎩⎪⎨⎧=∠=∠=CE CE BCE FCE CB CF∴△FCE ≌△BCE (SAS ),∴∠2=∠1.又∵AD ∥BC ,∴∠ADC +∠BCD =180°,∴∠DCE +∠CDE =90°,∴∠2+∠3=90°,∠1+∠4=90°,∴∠3=∠4. 在△FDE 与△ADE 中,⎪⎩⎪⎨⎧∠=∠=∠=∠43DEDE ADE FDE ∴△FDE ≌△ADE (ASA ),∴DF =DA ,∵CD =DF +CF ,∴CD =AD +BC .例4. 已知:如图4-1,在△ABC 中,∠C =2∠B ,∠1=∠2. 求证:AB =AC +CD .分析:从结论分析,“截长”或“补短”都可实现问题的转化,即延长AC 至E 使CE =CD ,或在AB 上截取AF =AC .证明:方法一(补短法)延长AC 到E ,使DC =CE ,则∠CDE =∠CED ,如图4-2 AD B CEF 1234图2-2D C B A 12图4-1 ED CB A 12图4-2∴∠ACB =2∠E ,∵∠ACB =2∠B ,∴∠B =∠E ,在△ABD 与△AED 中,⎪⎩⎪⎨⎧=∠=∠∠=∠AD AD E B 21∴△ABD ≌△AED (AAS ),∴AB =AE .又AE =AC+CE =AC +DC ,∴AB =AC +DC .方法二(截长法)在AB 上截取AF =AC ,如图4-3在△AFD 与△ACD 中,⎪⎩⎪⎨⎧=∠=∠=AD AD AC AF 21∴△AFD ≌△ACD (SAS ),∴DF =DC ,∠AFD =∠ACD . 又∵∠ACB =2∠B ,∴∠FDB =∠B ,∴FD =FB .∵AB =AF +FB =AC +FD ,∴AB =AC +CD .F D C B A 12图4-3超重和失重 问题超重和失重是两个很重要的物理现象。
微专题 截长补短法

(1)BC=2; (2)证明:如解图,在AM上截取AN=DF,连接DN. ∵F为边BC的中点, ∴BC=2CF. ∵CD=2CE, ∴CE=CF, ∵∠MCF=∠MCE,CM=CM, ∴△MCF ≌△MCE(SAS). ∴∠CFM=∠CEM=90°,MF=ME.
第4题解图
∵DC=AD,∠CDF=∠DAN,DF=AN, ∴△CDF ≌△DAN(SAS). ∴∠CFD=∠DNA=90°=∠DNM. ∵∠CFM=∠DNM=90°,∠CMF=∠DMN,CM=DM ∴△CMF ≌△DMN(AAS). ∴MF=MN=ME. ∵AM=AN+MN, ∴AM=DF+ME.
∴∠ACB=2∠E,
∵∠ACB=2∠B,
B E
∴∠B=∠E,在△ABD与△AED中,1 2
∴△ABD ≌△AED(AAS),
AD AD
∴AB=AE.
又∵AE=AC+CE=AC+DC,
∴AB=AC+CD.
例题解图②
针对训练
1. 在正方形ABCD中,E为BC上的一点,F为CD上的一点,BE+DF= EF,则∠EAF的度数为( C ) A.30° B.37.5° C.45° D.60°
∴CM=BN,∠ACM=∠B=45°,
∴∠MCE=45°,
CM BN
∴∠B=∠MCE,在△MCE和△NBE中,MCB B
∴EN,
∴AE=AM+EM=CN+EN.
4. 已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过 M作ME⊥CD于点E,∠BAC=∠CDF. (1)若CE=1,求BC的长; (2)求证:AM=DF+ME.
第3题图
证明:如解图,在AE上截取AM=CN,连接CM, ∵∠CAB=∠CBA=45°, ∴∠BCA=180°-∠CAB-∠CBA=90°,即∠1+∠NCA=90°, ∵CN⊥AE ∴∠2+∠NCA=90° ∴∠1=∠2.
数学中考截长补短法例题

截长补短法例1.已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC .求证:∠BAD +∠BCD =180°.分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现.证明:过点D 作DE 垂直BA 的延长线于点E ,作DF ⊥BC 于点F ,如图1-2∵BD 平分∠ABC ,∴DE =DF ,在Rt △ADE 与Rt △CDF 中,⎩⎨⎧==CDAD DFDE ∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF .又∠BAD +∠DAE =180°,∴∠BAD +∠DCF =180°,即∠BAD +∠BCD =180°例2.已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD .求证:∠BAP +∠BCP =180°.分析:与例1相类似,证两个角的和是180°,可把它们移到一起,让它们是邻补角,即证明∠BCP =∠EAP ,因而此题适用“补短”进行全等三角形的构造.证明:过点P 作PE 垂直BA 的延长线于点E ,如图3-2∵∠1=∠2,且PD ⊥BC ,∴PE =PD ,在Rt △BPE 与Rt △BPD 中,⎩⎨⎧==BPBP PD PE ∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD .∵AB +BC =2BD ,∴AB +BD +DC =BD +BE ,∴AB +DC =BE 即DC =BE -AB =AE .FEDCBA图1-2ABCDP12N图3-1P12NABCD E 图3-2ABC D图1-1ADBCE图2-1在Rt △APE 与Rt △CPD 中,⎪⎩⎪⎨⎧=∠=∠=DC AE PDC PEA PD PE ∴Rt △APE ≌Rt △CPD (SAS),∴∠PAE =∠PCD 又∵∠BAP +∠PAE =180°,∴∠BAP +∠BCP =180°例3.如图2-1,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB .求证:CD =AD +BC .分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在CD 上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的.证明:在CD 上截取CF =BC ,如图2-2在△FCE 与△BCE 中,⎪⎩⎪⎨⎧=∠=∠=CE CE BCE FCE CB CF ∴△FCE ≌△BCE (SAS ),∴∠2=∠1.又∵AD ∥BC ,∴∠ADC +∠BCD =180°,∴∠DCE +∠CDE =90°,∴∠2+∠3=90°,∠1+∠4=90°,∴∠3=∠4.在△FDE 与△ADE 中,⎪⎩⎪⎨⎧∠=∠=∠=∠43DE DE ADE FDE ∴△FDE ≌△ADE (ASA ),∴DF =DA ,∵CD =DF +CF ,∴CD =AD +BC .ADB CE F1234图2-2例4.已知:如图4-1,在△ABC 中,∠C =2∠B ,∠1=∠2.求证:AB =AC +CD .分析:从结论分析,“截长”或“补短”都可实现问题的转化,即延长AC 至E 使CE =CD ,或在AB 上截取AF =AC .证明:方法一(补短法)延长AC 到E ,使DC =CE ,则∠CDE =∠CED ,如图4-2∴∠ACB =2∠E ,∵∠ACB =2∠B ,∴∠B =∠E ,在△ABD 与△AED 中,⎪⎩⎪⎨⎧=∠=∠∠=∠AD AD E B 21∴△ABD ≌△AED (AAS ),∴AB =AE .又AE =AC+CE =AC +DC ,∴AB =AC +DC .方法二(截长法)在AB 上截取AF =AC ,如图4-3在△AFD 与△ACD 中,⎪⎩⎪⎨⎧=∠=∠=AD AD AC AF 21∴△AFD ≌△ACD (SAS ),∴DF =DC ,∠AFD =∠ACD .又∵∠ACB =2∠B ,∴∠FDB =∠B ,∴FD =FB .∵AB =AF +FB =AC +FD ,∴AB =AC +CD .DCB A 12图4-1EDCBA12图4-2FDCBA 12图4-3。
专题5——截长补短法

1、如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°, AC=10cm,P为BC的中点,动点Q从点P出发,沿射线PC 方向以 3cm/s的速度运动,以P为圆心,PQ长为半径作
圆.设点Q运动的时间为ts.
(1)当t=2.5s时,判断直线AB与⊙P的位置关系,并说明
理由.
(2)已知⊙O为Rt△ABC的外接圆,若⊙P与⊙O相切, 求t的值.
2、如图①,△ABC是边长为3的等边三角形,△BDC是 等腰三角形,且∠BDC=120°,以D为顶点,做一个 60°角使其两边分别交AB于点M,交AC于点N,连接
MN,请求出△AMN的周长。
3、如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的
等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC
G A D A D(G) F A D F
G B
F C E B C E B C E
图①
图②
图③
5、 如图,正方形ABCD的边长为2,点E在AB边上.四边形EFGB
也为正方形,设△AFC的面积为S,则 (
A.S=2 B.S=2.4 C.S=4
)
D.S与BE长度有关
6、正方形 ABCD 、正方形 BEFG 和正方形 RKPF 的位置如图所
示,点G在线段DK上,正方形 BEFG 的边长为4,则 △DEK
的面积为:
(A)10
(B)12
(C)14
(D)16
D
C G F P
R
K
A
B
E
7、如图,矩形 ABCD 中,AB=3cm,AD=6cm,点 E为AB边上的任意一点,四边形 EFGB 也是矩
EF 2 BE ,则 S△ AFC 形,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
截长补短法
例1. 已知,如图1-1,在四边形ABCDK BC>AB, AD=DC BD平分/ ABC
求证:/ BAD +/ BCD180° .
分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现.
证明:过点D作DE垂直BA的延长线于点E作DF丄BC于点F,如图1-2
•/ BD平分/ ABC:DE=DF
在Rt A ADE与Rt A CDF中,
DE DF
AD CD
••• Rt△ ADE^ Rt A CDF HD,/-Z DAE/ DCF
又/ BAD Z DAE180°,/.Z BAB Z DCI=180
即Z BAD Z BCD180°
例2. 已知,如图3-1 , Z仁Z 2 , P为BN上一点,且POL BC于点D, AB^BC=2BD 求证:Z BAF+ Z BCP180° .
分析:与例1相类似,证两个角的和是180°,可把它们移到一起,让它们是邻补角, 即证明Z BCP Z EAP因而此题适用“补短”进行全等三角形的构造
证明:过点P作PE垂直BA的延长线于点E,如图3-2
•••Z 仁Z 2,且P[丄BC, •/ PE=PD
在Rt A BPE与Rt A BPD中 ,
PE PD
BP BP
• Rt△ BPE^ Rt A BPD HD,• BE=BD
•/ AB F BC=2BD•/ AB F B&DCB&BE•/ AB F D(=BE即DC=BEAB=AE 图3-1
E
图3-2
D C
在Rt A APE与Rt A CPD
中,
PE PD
PEA PDC
AE DC
••• Rt△ APE^Rt A CPD SAS), •••/ PAE Z PCD
又•••/ BAF+Z PAE180 ° ,•••/ BAF+Z BCP=180°
例3. 如图2-1 , AD// BC 点E在线段AB上, Z ADE Z CDE Z DCE Z ECB
求证:COABBC
分析:结论是COAD^BC可考虑用“截长补短法”中的“截长”,即在CDh截取CF=CB 只要再证D巨DA即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的.
证明:在CD上截取CF=BC如图2-2
在厶FCE^ BCE中,
CF CB
FCE BCE
CE CE
• △ FCE^A BCE(SAS , •Z 2=Z 1.
又••• AD/ BC •••/ ADGZ BCD180°,「
• Z 2+Z 3=90 ° ,Z 1 + Z 4=90 °,「・
Z
在厶FDE与△ ADE
中,
FDE ADE
DE DE
• △ FDE^A ADE( ASA , • DF=DA
•/ CD F DF+CF,• CDA[>BC
例4. 已知:如图4-1,在△ ABC中,/ C= 2/ B,/ 1 = Z 2.
求证:A&AGCD
分析:从结论分析,“截长”或“补短”都可实现问题的转化,即延长AC至E使CE=CD或在AB上截取AF=AC
证明:方法一(补短法)
延长AC到E,使DGCE 则/ CDE=Z CED 如图4-2
•••/ ACB= 2/ E
•••/ ACB= 2/ B •/ B=Z E,
在厶ABD W^ AED中,
1 2
B E
AD AD
•••△ ABD^ AED( AAS,二AB=AE 又AEAC+CEAGDC •- AB=A(+DC 方法二(截长法)
在AB上截取AF=AC如图4-3
在厶AFD与△ ACD中,
AF AC
1 2
AD AD
• △ AFD^A ACD( SAS , • DF=DC / AFD=Z ACD 又•••/ACB= 2 / B, •••/ FDB=Z B, • FD=FB
•/ AB=AF+FB=A(+FD, • AB=AGCD E
图4-1 图4-2。
