三角形中的几个特殊点：旁心、费马点和欧拉线-高中数学知识点讲解

高中数学《三角形“五心”的完美统一》

三角形“五心”的完美统一数学的诱惑力就在于对一个问题的研究，越研究越觉得有味道，越琢磨越觉得数学美的存在，就拿三角形“五心”来说吧，有不少人如文[1],[2],[3]做过类似研究.现在伴随新课程的改革和教学理念的更新,结合本人先前做过的一些粗浅的研究，对其又有了新的收获，它们完全可以达到数和形的完美统一，而这些都来自于课堂上学生对问题的积极思考和发问，让我不得不放弃原来的教学计划和学生一起探究与发现.也正如一位大家所说“教学是一门奇缺的艺术，数学美的东西就在你身边，关键看你有没有发现美的眼睛”.下面就把我的教学片段展示出来，与大家共勉.“问题是数学的心脏”，笔者在复习平面向量这部分内容时，只想简单的涉及一道有关三角形中常见的“心”的高考题目让学生见识一下，但谁知学生课上突然发问，三角形的其它心——垂心、外心、重心、旁心，应该有怎样的向量表达式，学生也曾通过我推荐阅读的文[1]了解了三角形的重心、内心、垂心、外心的坐标形式，使我不得不在新课程的一个基本理念“倡导积极主动、勇于探索的学习方式——学生的数学学习不应只限于接受、记忆、模仿和练习，高中数学课程还应倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式，这些方式有助于发挥学生的主动性，使学生的学习过程成为在教师引导下的“再创造”过程同时，高中数学课程应设立“数学探究”、“数学建模”等学习活动，为学生形成积极主动的、多样的学习方式创造有利的条件，以激发学生的数学学习兴趣，鼓励学生在学习过程中，养成独立思考、积极探索的习惯，高中数学课程应力求通过各种不同形式的自主学习、探究活动，让学生体验数学发现和创造的历程，发展他们的创新意识”,问题提出（2003年新课程高考理4）：点O 是平面上一定点，A ，B ，C 是平面上不共线的三点，动点P 满足[),0,AB AC OP OA AB AC λλ⎛⎫ ⎪=++∈+∞ ⎪⎝⎭，则点P 的轨迹一定通过ABC ∆的( ) A 外心 B 内心 C 重心 D 垂心问题解决：学生利用向量加法的几何意义及单位向量的概念不难得出正确答案B.本打算再让学生看下面的题目若将上题中的条件“[),0,AB AC OP OA AB AC λλ⎛⎫ ⎪=++∈+∞ ⎪”改为“()[),0,OP OA AB AC λλ=++∈+∞”则点P 的轨迹一定通过ABC ∆的( )A 外心B 重心C 垂心D 内心答案B谁知一学生突然站起来提出以下问题S1：老师,若点G 是ABC ∆的重心，则有=++，从而有()13OG OA OB OC =++，可知点G 的坐标为)3,3(C B A C B A y y y x x x ++++，那么根据ABC ∆的重心G 的坐标形式与向量表示的这种关系，由△ABC 内心I 的坐标为),(c b a cy by ay c b a cx bx ax C B A C B A ++++++++，（,,a b c 为三角形的三边长），于是我猜想出ABC ∆的内心I 的向量形式是aOA bOB cOC OI a b c++=++，这种猜想对吗?我们能证明吗？ T:你的想法太好了，猜想是正确的,我们能证明,我们是否下课再证呢?这时有的同学喊道还是当堂证一下吧，也包括刚才站起来的那位同学，我只好和学生一块证明起来（也许有些学生故意要将老师的军，看你临场反应如何？）命题1 若点I是ABC ∆的内心，则0aOA bOB cOC aIA bIB cIC OI a b c ++++=⇔=++. 反之，也成立.证明：如图1 设,AI u AD BI BE λ==因为AD 是角平分线所以bAB c AC AD b c +=+ 同理 aBA cBC BE a c +=+ a AB cBC BI a c λλ+∴=+ ()(1)a c AB cAC AB BI AI a c λλ+-+∴+==+ 又ubAB uc AC AI b c +=+ 1ub b c c uc a c b c λλ-=+=++⎧∴⎨⎩()1u a c ub b c b c +∴-=++ ()b c u a b c ∴+=++ B 图1b c u a b c +∴=++ 1()AI bAB cAC a b c∴=+++ ()()a b c IA bAB cAC O ∴++++=aIA bIB cIC O ∴++=，从而 aOA bOB cOC OI a b c ++=++ 反之，也成立，因为以上证明的后三步是可逆的.T:我们可以到此收兵了吗？S2:老师，其它心——垂心,外心,旁心的向量形式是什么呢?那只好再研究下去.T:现在我给你们时间自己证一下，看谁能快速证出.不料5分钟过后，有的学生就有了下面的答案.命题2 若点H 是ABC ∆的垂心，则0cos cos cos a b c HA HB HC A B C ++=. 反之，也成立. 证明:如图2,设,AH u AD BH BE λ==,因为AD 是BC 边上的高线,所以:BD DC =cos :cos c B b C 所以cos cos cos cos b cAB AC b C AD b c B C +=+ 同理 cos cos cos cos a c BA BC A C BE a c A C +=+ 同命题1的证明方法可证得 0cos cos cos a b c HA HB HC A B C++=. 同理可证明以下命题(由学生课下完成)命题3点O 是ABC ∆的外心02sin 2sin 2sin =⋅+⋅+⋅⇔OC C OB B OA A命题4点I '是ABC ∆的旁心0'''=++⇔C I c B I b A I a (C ∠作为一内角)通过以上的探究锻炼了学生发现问题和解决问题的能力.也由此得到了三角形的“五心”数和形结合的完美统一.由以上可知三角形各心的坐标如下：（1）若BE 、CF 为△ABC 边的中线,则△ABC 重心G 的坐标为)3,3(CB AC B A y y y x x x ++++ C 图2（2）若BE 、CF 为△ABC 的内角平分线,则△ABC 内心I 的坐标为),(cb a cy by ayc b a cx bx ax C B A C B A ++++++++ （3）若BE 、CF 为△ABC 的高,则△ABC 垂心H 的坐标为)cos cos cos cos cos cos ,cos cos cos cos cos cos (C c B b A a y C c y B b y Aa C c Bb A a x Cc x B b x A a CB AC B A ++++++++ （4）若BE 、CF 的交点为△ABC 的外心,则△ABC 外心O 的坐标为)2sin 2sin 2sin 2sin 2sin 2sin ,2sin 2sin 2sin 2sin 2sin 2sin (CB AC y B y A y C B A C x B x A x C B A C B A ++++++++ （5）若BE 、AF 为△ABC 的外角平分线,则△ABC 旁心I '的坐标为(,)A B C A B C ax bx cx ay by cy a b c a b c+-+-+-+-(C ∠作为一内角) 由此顺藤摸瓜将“五心”推广到一般形式：（证法由学生提供）命题5在ABC ∆内任取一点O ，用,,A B C S S S 分别表示,,BOC COA AOB ∆∆∆的面积，求证:0A B C S OA S OB S OC ⋅+⋅+⋅=.证法1:如图3以,,αβγ分别表示,,BOC COA AOB ∠∠∠,以123,,e e e 分别表示,,OA OB OC 单位向量,则111sin sin 22A S OA OB OC OA OB OC OA e αα⋅=⋅⋅⋅=⋅⋅⋅⋅ 同理可得, 21sin 2B S OB OA OB OC e β⋅=⋅⋅⋅⋅ 31sin 2C S OC OA OB OC e γ⋅=⋅⋅⋅⋅, 即证:123sin sin sin 0e e e αβγ⋅+⋅+⋅=. 如上图, 在OA 上取点D,使1sin OD e α=⋅,作//DE OB 交CO 的延长线于E点,在EOD ∆中,由正弦定理可知sin DE β=,即2sin DE e β=⋅,3sin EO e γ=⋅,由于,,OD DE EO 构成三角形,所以123sin sin sin 0e e e αβγ⋅+⋅+⋅=证法2: 设点()()()112233,,,,,A x y B x y C x y ,则()()()()33221132321131213231213201110,,,222001A x y S OA x y x y x y y x x y x x y x y x x y y y y x ⋅=⋅=-⋅=-- 同理: ()()1133221232311231230110,,B x y S OB x y x y x x y x x y x y y y y x ⋅=⋅=--图3()2313122132311,2C S OC x x y x x y x y y y y x ⋅=--, 所以0A B C S OA S OB S OC ⋅+⋅+⋅=证法3 实际上我们知道若点G 是ABC ∆的重心，则0GA GB GC ++=，且GAB GAC GBC S S S ∆∆∆==，于是根据这个知识点可以如下证明.证明:设,,A B C S S S 分别为,,x y z ，'xOA OA =,'yOB OB =,'zOC OC =,则'''0OA OB OC ++=,所以O 是'''A B C ∆的重心如图4,且OA B OA C OB C S S S ''''''∆∆∆==, 由此得到:1sin 121sin 2OBC OB C OB OC BPC OB OC S S yz OB OC OB OC BPC ∆''∆∠===''''∠, 所以1OBC OB C S S yz ''∆∆=, 同理: 1OAC OA C S S xz ''∆∆=,1OAB OA B S S xy ''∆∆=.所以111::::::OBC OAC OAB S S S x y z yz xz xy ∆∆∆== 从而 0A B C S OA S OB S OC ⋅+⋅+⋅=. 证法3显然优美简洁，这是学生课下研究出来的.配套练习题.⒈(2005年全国卷Ⅰ文) 点O 是ABC ∆所在平面内的一点，满足OA OB ⋅=OB OC OC OA ⋅=⋅,则点O 是ABC ∆的( )A.三个内角的角平分线的交点B.三条边的垂直平分线的交点C.三条中线的交点D.三条高的交点答案D⒉已知O 是ABC ∆所在平面上一点，若0aOA bOB cOC ++=，则点O 是ABC ∆( )A ．外心B ．内心C ．重心D 垂心答案B⒊已知O 是ABC ∆所在平面上一点，满足222222OA BC OB CA OC AB +=+=+，则点O 是ABC ∆的( )图4A.外心B.内心C.重心D.垂心答案D⒋已知点O 是ABC ∆所在平面上一点，若222OA OB OC ==，则点O 是ABC ∆的（）A.外心B.内心C.重心D.垂心答案A⒌(2005年高考湖南理科第10题) 设P 是ABC ∆内任意一点，ABC S ∆表示ABC ∆的面积，123,,PBC PCA PAB ABC ABC ABC S S S S S S λλλ∆∆∆∆∆∆===,定义()()123,,f P λλλ=,若G 是ABC ∆的重心，()111,,236f Q ⎛⎫= ⎪⎝⎭,则 A ．点Q 在GAB ∆内 B ．点Q 在GBC ∆内 C ．点Q 在GCA ∆内 D ．点Q 与G 重合答案A⒍(2005全国卷Ⅰ理15) ABC ∆的外接圆圆心为O ，两条边上的高交点为H ，()m ++=，则实数m =___________. 法1因在三角形中，外心、重心、垂心三点共线，这条线为欧拉线，重心G 分外心O 和垂心H 的比为1:2，()13OG OA OB OC =++ 又1,2:1:==m 故法2或者特殊值验证,或者证明OH ++=⒎（2004年全国数学联赛）设O 是ABC ∆内一点，且有230OA OB OC ++=，则ABC ∆的面积与AOC ∆的面积的比为A.2B.32C. 3D.53答案C⒏若点O 是在ABC ∆内部一点，且有()0(,0)mOA nOB m n OC m n +++=>，则::()::AOB BOC AOC S S S m n m n ∆∆∆=+思考：⒈题目形式由特殊到一般，给学生提供了一种解决问题的思路和方法，从而教师变成了学生数学活动的激励者、合作者，使学生和教师均能获益匪浅，增强了对教材的处理能力.⒉虽说没有按教学计划完成任务，但满足了学生的求知欲望，使他们的思路得到了极大的开阔，培养了学生的钻研精神，配套练习训练了学生灵活运用知识解决问题的能力，激发了学生学习数学的极大兴趣.⒊探究由学生发现，并当堂和学生一起解决，教师敢于暴露自己的解法和思路，使学生领略了教师的解题过程，从而也锻炼了学生的解题思维.⒋教师一定要有足够的知识灵活应变学生突然反问的能力，以及灵活驾驭课堂的能力，一定要相信自己的学生，只要正确引导，他们的潜力是巨大的，命题5的三种证法就足够说明这一点.这也论证了新课程的教学理念.。

数学竞赛辅导(三角形五心)

锐角三角形的垂心是以三个垂足为顶点的三角形的内心。锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆
半径之和的2倍。
等价于证明
三、内心的性质
三角形的三条内角平分线交于一点,这点称为三角形的内心三角形的内心到三边的距离相等,都等于三角形内切圆半径设三角形面积为S，设I为ΔABC的内心，则∠BIC = 90 °+∠A/2,类似地还有两式。B
数学竞赛辅导
三角形的五心
Preview one
一、外心的性质
A
O
B
C
三角形的外心到三角形的三个顶点距离相等．都等于三角形的外接圆半径． ∠BOC=2∠BAC 三角形的三条边的垂直平分线交于一点,这点称为三角形的外心(外接圆圆心) 欧拉线
Example one
二、垂心的性质
斜三角形的三个顶点与垂心这四个点中，任何三个为顶点的三角形的垂心就是第四个点．所以把这样的四个点称为一个“垂心组”．
（3）三角形的外心是它的中点三角形的垂心；（4）三角形的重心也是它的中点三角形的重心；（5）三角形的中点三角形的外心也是其垂足三角形的外心．（6）鸡爪定理（7）鸭爪定理
Example six
△ABC的外心为O，AB=AC，D是AB中点，E是△ACD的重心. 证明OE丄CD.
Example seven
A
M
F
E
K I
DH
C
四、重心的性质
Байду номын сангаас
三角形的三条中线交于一点,这点称为三角形的重心
三角形的重心到边的中点与到相应顶点的距离之比为 1∶ 2
空间直角坐标系：
横坐标：(X1+X2+X3)/3

平面几何竞赛讲座(三)三角形的“五心”

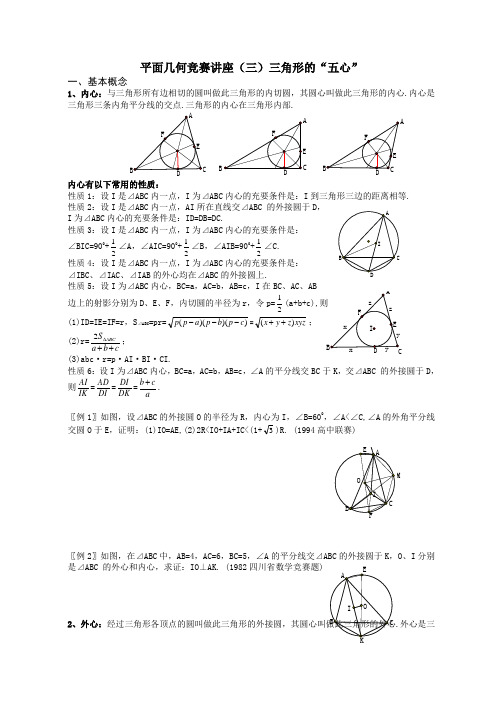
M平面几何竞赛讲座（三）三角形的“五心”一、基本概念1、内心：与三角形所有边相切的圆叫做此三角形的内切圆，其圆心叫做此三角形的内心.内心是三角形三条内角平分线的交点.三角形的内心在三角形内部.内心有以下常用的性质：性质1：设I是⊿ABC内一点，I为⊿ABC内心的充要条件是：I到三角形三边的距离相等.性质2：设I是⊿ABC内一点，AI所在直线交⊿ABC 的外接圆于D，I为⊿ABC内心的充要条件是：ID=DB=DC.性质3：设I是⊿ABC内一点，I为⊿ABC内心的充要条件是：∠BIC=900+21∠A，∠AIC=900+21∠B，∠AIB=900+21∠C.性质4：设I是⊿ABC内一点，I为⊿ABC内心的充要条件是：⊿IBC、⊿IAC、⊿IAB的外心均在⊿ABC的外接圆上.性质5：设I为⊿ABC内心，BC=a，AC=b，AB=c，I在BC、AC、AB边上的射影分别为D、E、F，内切圆的半径为r，令p=21(a+b+c),则(1)ID=IE=IF=r，S⊿ABC=pr=))()((cpbpapp---=xyzzyx)(++；(2)r=cbaSABC++∆2；(3)abc·r=p·AI·BI·CI.性质6：设I为⊿ABC内心，BC=a，AC=b，AB=c，∠A的平分线交BC于K，交⊿ABC 的外接圆于D，则IKAI=DIAD=DKDI=acb+.〖例1〗如图，设⊿ABC的外接圆O的半径为R，内心为I，∠B=600，∠A<∠C,∠A的外角平分线交圆O于E，证明：(1)IO=AE,(2)2R<IO+IA+IC<(1+3)R. (1994高中联赛)〖例2〗如图，在⊿ABC中，AB=4，AC=6，BC=5，∠A的平分线交⊿ABC的外接圆于K，O、I分别是⊿ABC 的外心和内心，求证：IO⊥AK. (1982四川省数学竞赛题)2、外心：.外心是三角形三条边的垂直平分线的交点. 锐角三角形的外心在三角形内部，直角三角形的外心在斜边中点，钝角三角形的外心在三角形外部.性质1：⊿ABC所在平面上一点是其外心的充要条件是：该点到三角形三顶点的距离相等.性质2：设O是⊿ABC所在平面内一点，则O为⊿ABC的外心的充要条件是：(1)∠BOC=2∠A，∠ACC=2∠B，∠AOB=2∠C.(2)OB=OC, 且∠BOC=2∠A.性质3：R=ABCSabc4或S⊿ABC=Rabc4.〖例3〗如图，设AD是⊿ABC的∠BAC的平分线，O是⊿ABC的外心，01是⊿ABD的外接圆的圆心，02是⊿ADC的外接圆的圆心.求证：OO1=OO2. (1990高中联赛)3、重心：三角形三条边中线的交点叫做此三角形的重心.重心在三角形内部.重心到顶点的距离等于它到对边中点距离的2倍（即：重心将每条中线分成1:2两部分）.重心有以下常用的性质：性质1：设G是⊿ABC的重心，连AG并延长交BC于D，则D为BC的中点，AD2=21(AB2+AC2)-BC2,且AG:GD=2:1.性质2：设G是⊿ABC的重心，P为⊿ABC内任意一点，则(1)AP2+BP2+CP2=AG2+BG2+CG2+3PG2；(2)AG2+BG2+CG2=31(AB2+BC2+CA2).性质3：设G是⊿ABC内一点，G是⊿ABC的重心的充要条件是下列条件之一：(1)S⊿GBC=S⊿GCA=S⊿GAB=31S⊿ABC；(2)当AG、BG、CG的延长线交三边于D、E、F时，S⊿AFG=S⊿BDG=S⊿CEG.(3)当点G在三边BC、CA、AB上的射影分别为D、E、F时，GD·GE·GF值最大；H (4)过G 的直线交AB 于P ，交AC 于Q 时，AP AB +AQAC=3； (5)BC 2+3AG 2=CA 2+3GB 2=AB 2+3GC 2.4、垂心：三角形三条边高线的交点叫做此三角形的垂心。

三角形的五心一次看个够

三角形的五心一次看个够三角形中有许多重要的特殊点，特别是三角形的“五心”，在解题时有很多应用，在这里分别给予介绍．一、三角形外心的性质外心定理的证明：如图，设AB 、BC 的中垂线交于点O ，则有OA =OB =OC ，故O 也在A 的中垂线上，因为O 到三顶点的距离相等，故点O 是ΔABC 外接圆的圆心．因而称为外心．设⊿ABC 的外接圆为☉G(R)，角A 、B 、C 的对边分别为a 、b 、c ，p=(a+b+c)/2．1：（1）锐角三角形的外心在三角形内；（2）直角三角形的外心在斜边上，与斜边中点重合；（3）钝角三角形的外心在三角形外. 2：∠BGC=2∠A ，（或∠BGC=2(180°-∠A).3：点G 是平面ABC 上一点，那么点G 是⊿ABC 外心的充要条件是：点G 是ABC ∆的外心⇔GA GB GC == (或GA 2=GB 2=GC 2)(点G 到三顶点距离相等)⇔(GA +GB )·AB =(GB +GC )·BC =(GC +GA )·CA =0(G 为三边垂直平分线的交点)4：点G 是平面ABC 上一点，点P 是平面ABC 上任意一点，那么点G 是⊿ABC 外心的充要条件是：PG =((tanB+tanC) PA +(tanC+tanA) PB +(tanA+tanB) PC )/2(tanA+tanB+tanC).或PG =(cosA/2sinBsinC)PA +(cosB/2sinCsinA)PB +(cosC/2sinAsinB)PC . 5：R=abc/4S ⊿ABC.正弦定理：2R=a/sinA=b/sinB=c/sinC 。

6.外心坐标：给定112233(,),(,),(,)A x y B x y C x y 求外接圆心坐标O （x ，y ）①. 首先，外接圆的圆心是三角形三条边的垂直平分线的交点，我们根据圆心到顶点的距离相等，可以列出以下方程：22221122()()()()x x y y x x y y ---=--- 22223322()()()()x x y y x x y y ---=--- ②.化简得到：2222212122112()2()x x x y y y x y x y -+-=+--2222232322332()2()x x x y y y x y x y -+-=+--令1212()A x x =-；1212()B y y =-;222212211C x y x y =+-- 2232()A x x =-；2232()B y y =-;222222233C x y x y =+--A B C O7.若O 是△ABC 的外心，则S △BOC ：S △AOC ：S △AOB =sin ∠BOC ：sin ∠AOC ：sin ∠AOB=sin∠2A ：sin ∠2B ：sin ∠2C 故sin ∠2A ·OA +sin ∠2B ·OB +sin ∠2C ·OC =0 证明：设O 点在ABC ∆内部，由向量基本定理，有()+∈=++R r n m OC r OB n OA m ,,0，则r n m S S S AOB COA BOC ::::=∆∆设：r n m ===,,，则点O 为△DEF 的重心，又EOF BOC S nr S ∆∆=1，DOF AOC S mr S ∆∆=1，DOE AOB S mnS ∆∆=1，∴r n m S S S AOB COA BOC ::::=∆∆若O 是△ABC 的外心，则S △BOC ：S △AOC ：S △AOB =sin ∠BOC ：sin ∠AOC ：sin ∠AOB =sin∠2A ：sin ∠2B ：sin ∠2C故si n ∠2A ·OA +si n ∠2B ·OB +si n ∠2C ·OC =0二、三角形的内心内心定理的证明：如图，设∠A 、∠C 的平分线相交于I 、过I 作ID ⊥BC ，IE ⊥AC ，IF ⊥AB 则有IE=IF =ID ．因此I 也在∠C 的平分线上，即三角形三0aOA bOB cOC ++=。

高中数学竞赛讲义(全套)

高中数学竞赛资料一、高中数学竞赛大纲全国高中数学联赛全国高中数学联赛（一试）所涉及的知识范围不超出教育部2000年《全日制普通高级中学数学教学大纲》中所规定的教学要求和内容，但在方法的要求上有所提高。

全国高中数学联赛加试全国高中数学联赛加试（二试）与国际数学奥林匹克接轨，在知识方面有所扩展；适当增加一些教学大纲之外的内容，所增加的内容是：1.平面几何几个重要定理：梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理。

三角形中的几个特殊点：旁心、费马点，欧拉线。

几何不等式。

几何极值问题。

几何中的变换：对称、平移、旋转。

圆的幂和根轴。

面积方法，复数方法，向量方法，解析几何方法。

2.代数周期函数，带绝对值的函数。

三角公式，三角恒等式，三角方程，三角不等式，反三角函数。

递归，递归数列及其性质，一阶、二阶线性常系数递归数列的通项公式。

第二数学归纳法。

平均值不等式，柯西不等式，排序不等式，切比雪夫不等式，一元凸函数。

复数及其指数形式、三角形式，欧拉公式，棣莫弗定理，单位根。

多项式的除法定理、因式分解定理，多项式的相等，整系数多项式的有理根*，多项式的插值公式*。

n次多项式根的个数，根与系数的关系，实系数多项式虚根成对定理。

函数迭代，简单的函数方程*3. 初等数论同余，欧几里得除法，裴蜀定理，完全剩余类，二次剩余，不定方程和方程组，高斯函数[x]，费马小定理，格点及其性质，无穷递降法，欧拉定理*，孙子定理*。

4.组合问题圆排列，有重复元素的排列与组合，组合恒等式。

组合计数，组合几何。

抽屉原理。

容斥原理。

极端原理。

图论问题。

集合的划分。

覆盖。

平面凸集、凸包及应用*。

注：有*号的内容加试中暂不考，但在冬令营中可能考。

二、初中数学竞赛大纲1、数整数及进位制表示法，整除性及其判定；素数和合数，最大公约数与最小公倍数；奇数和偶数，奇偶性分析；带余除法和利用余数分类；完全平方数；因数分解的表示法，约数个数的计算；有理数的概念及表示法，无理数，实数，有理数和实数四则运算的封闭性。

高中数学竞赛讲义

高中数学竞赛资料一、高中数学竞赛大纲全国高中数学联赛全国高中数学联赛〔一试〕所涉及的知识范围不超出教育部2000年【全日制普通高级中学数学教学大纲】中所规定的教学要求和内容，但在方法的要求上有所提高。

全国高中数学联赛加试全国高中数学联赛加试〔二试〕与国际数学奥林匹克接轨，在知识方面有所扩展；适当增加一些教学大纲之外的内容，所增加的内容是：1.平面几何几个重要定理：梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理。

三角形中的几个特殊点：旁心、费马点，欧拉线。

几何不等式。

几何极值问题。

几何中的变换：对称、平移、旋转。

圆的幂和根轴。

面积方法，复数方法，向量方法，解析几何方法。

2.代数周期函数，带绝对值的函数。

三角公式，三角恒等式，三角方程，三角不等式，反三角函数。

递归，递归数列及其性质，一阶、二阶线性常系数递归数列的通项公式。

第二数学归纳法。

平均值不等式，柯西不等式，排序不等式，切比雪夫不等式，一元凸函数。

复数及其指数形式、三角形式，欧拉公式，棣莫弗定理，单位根。

多项式的除法定理、因式分解定理，多项式的相等，整系数多项式的有理根*，多项式的插值公式*。

n 次多项式根的个数，根与系数的关系，实系数多项式虚根成对定理。

函数迭代，简单的函数方程*3. 初等数论同余，欧几里得除法，裴蜀定理，完全剩余类，二次剩余，不定方程和方程组，高斯函数[x]，费马小定理，格点及其性质，无穷递降法，欧拉定理*，孙子定理*。

4.组合问题圆排列，有重复元素的排列与组合，组合恒等式。

组合计数，组合几何。

抽屉原理。

容斥原理。

极端原理。

图论问题。

集合的划分。

覆盖。

平面凸集、凸包及应用*。

注：有*号的内容加试中暂不考，但在冬令营中可能考。

三、高中数学竞赛根底知识第一章集合与简易逻辑一、根底知识定义1 一般地，一组确定的、互异的、无序的对象的全体构成集合，简称集，用大写字母来表示；集合中的各个对象称为元素，用小写字母来表示，元素x 在集合A 中，称x 属于A ，记为A x ∈，否那么称x 不属于A ，记作A x ∉。

高中数学竞赛讲义(免费)(完整资料).doc

【最新整理，下载后即可编辑】高中数学竞赛资料一、高中数学竞赛大纲全国高中数学联赛全国高中数学联赛（一试）所涉及的知识范围不超出教育部2000年《全日制普通高级中学数学教学大纲》中所规定的教学要求和内容，但在方法的要求上有所提高。

全国高中数学联赛加试全国高中数学联赛加试（二试）与国际数学奥林匹克接轨，在知识方面有所扩展；适当增加一些教学大纲之外的内容，所增加的内容是：1.平面几何几个重要定理：梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理。

三角形中的几个特殊点：旁心、费马点，欧拉线。

几何不等式。

几何极值问题。

几何中的变换：对称、平移、旋转。

圆的幂和根轴。

面积方法，复数方法，向量方法，解析几何方法。

2.代数周期函数，带绝对值的函数。

三角公式，三角恒等式，三角方程，三角不等式，反三角函数。

递归，递归数列及其性质，一阶、二阶线性常系数递归数列的通项公式。

第二数学归纳法。

平均值不等式，柯西不等式，排序不等式，切比雪夫不等式，一元凸函数。

复数及其指数形式、三角形式，欧拉公式，棣莫弗定理，单位根。

多项式的除法定理、因式分解定理，多项式的相等，整系数多项式的有理根*，多项式的插值公式*。

n次多项式根的个数，根与系数的关系，实系数多项式虚根成对定理。

函数迭代，简单的函数方程*3. 初等数论同余，欧几里得除法，裴蜀定理，完全剩余类，二次剩余，不定方程和方程组，高斯函数[x]，费马小定理，格点及其性质，无穷递降法，欧拉定理*，孙子定理*。

4.组合问题圆排列，有重复元素的排列与组合，组合恒等式。

组合计数，组合几何。

抽屉原理。

容斥原理。

极端原理。

图论问题。

集合的划分。

覆盖。

平面凸集、凸包及应用*。

注：有*号的内容加试中暂不考，但在冬令营中可能考。

三、高中数学竞赛基础知识第一章集合与简易逻辑一、基础知识定义1 一般地，一组确定的、互异的、无序的对象的全体构成集合，简称集，用大写字母来表示；集合中的各个对象称为元素，用小写字母来表示，元素x 在集合A 中，称x 属于A ，记为A x ∈，否则称x 不属于A ，记作A x ∉。

高中数学竞赛讲义(全套)

高中数学竞赛资料一、高中数学竞赛大纲全国高中数学联赛全国高中数学联赛（一试）所涉及的知识范围不超出教育部2000年《全日制普通高级中学数学教学大纲》中所规定的教学要求和内容，但在方法的要求上有所提高。

全国高中数学联赛加试全国高中数学联赛加试（二试）与国际数学奥林匹克接轨，在知识方面有所扩展；适当增加一些教学大纲之外的内容，所增加的内容是：1.平面几何几个重要定理：梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理。

三角形中的几个特殊点：旁心、费马点，欧拉线。

几何不等式。

几何极值问题。

几何中的变换：对称、平移、旋转。

圆的幂和根轴。

面积方法，复数方法，向量方法，解析几何方法。

2.代数周期函数，带绝对值的函数。

三角公式，三角恒等式，三角方程，三角不等式，反三角函数。

递归，递归数列及其性质，一阶、二阶线性常系数递归数列的通项公式。

第二数学归纳法。

平均值不等式，柯西不等式，排序不等式，切比雪夫不等式，一元凸函数。

复数及其指数形式、三角形式，欧拉公式，棣莫弗定理，单位根。

多项式的除法定理、因式分解定理，多项式的相等，整系数多项式的有理根*，多项式的插值公式*。

n次多项式根的个数，根与系数的关系，实系数多项式虚根成对定理。

函数迭代，简单的函数方程*3.初等数论同余，欧几里得除法，裴蜀定理，完全剩余类，二次剩余，不定方程和方程组，高斯函数[x]，费马小定理，格点及其性质，无穷递降法，欧拉定理*，孙子定理*。

4.组合问题圆排列，有重复元素的排列与组合，组合恒等式。

组合计数，组合几何。

抽屉原理。

容斥原理。

极端原理。

图论问题。

集合的划分。

覆盖。

平面凸集、凸包及应用*。

注：有*号的内容加试中暂不考，但在冬令营中可能考。

二、初中数学竞赛大纲1、数整数及进位制表示法，整除性及其判定；素数和合数，最大公约数与最小公倍数；奇数和偶数，奇偶性分析；带余除法和利用余数分类；完全平方数；因数分解的表示法，约数个数的计算；有理数的概念及表示法，无理数，实数，有理数和实数四则运算的封闭性。

三角形各个心的有关向量结论

三角形各个心的有关向量结论三角形是初中数学的重点之一，它们在几何的许多领域都有应用。

除了三条边之外，三角形还有很多其他有趣的属性和结论。

今天，我们将重点关注与三角形各个心的有关向量结论。

首先，让我们来介绍一下三角形的“心”。

一个三角形的“心”是它的重心、外心、内心、垂心和费马点。

这五个点都具有特殊的几何意义，它们与三角形的性质密切相关。

现在，我们来看一些关于这五个“心”的向量结论。

这些结论包括：1. 重心：三角形的三条中线的交点是三角形的重心。

向量表示为$$\overrightarrow{G}=\frac{1}{3}(\overrightarrow{A}+\overrigh tarrow{B}+\overrightarrow{C})$$其中，A、B、C分别是三角形的三个顶点的向量表示。

2. 外心：三角形外接圆的圆心是三角形的外心。

向量表示为$$\overrightarrow{O}=\frac{\overrightarrow{a}\times\overright arrow{b}+\overrightarrow{a}\times\overrightarrow{c}+\overrigh tarrow{b}\times\overrightarrow{c}}{2\overrightarrow{a}\cdot\o verrightarrow{b}\times\overrightarrow{c}}$$其中，a、b、c分别是三角形的三个边的向量表示。

3. 内心：三角形内切圆的圆心是三角形的内心。

向量表示为$$\overrightarrow{I}=\frac{a\overrightarrow{A}+b\overrightarr ow{B}+c\overrightarrow{C}}{a+b+c}$$其中，a、b、c分别是三角形的三个边的长度；A、B、C分别是三角形的三个顶点的向量表示。

4. 垂心：三角形的三条高线交于垂心，它与对应的顶点相连的线段垂直。

三角形的五心问题(le)

三角形的五心问题三角形的“五心”指的是三角形的外心，内心，重心，垂心和旁心．一、重心(G)：三角形三条中线交点. 性质：1.重心到顶点的距离与重心到对边中点的距离之比为2：1。

即：:2:1AG GD =2.重心和三角形任意两个顶点组成的3个三角形面积相等。

即重心到三条边的距离与三条边的长成反比。

即：ABC GACGAB GBC S S S S ∆∆∆∆===313.以重心为起点，以三角形三定点为终点的三条向量之和等于零向量。

即：0=++GC GB GA4.在平面直角坐标系中，重心的坐标是顶点坐标的算术平均数. 即:重心坐标为)3y ,3(C B A c B A y y x x x ++++5.中线与三边的关系式：2222412121BC AC AB AD -+=推广：(1)2222221()3GA GB GC AB AC BC ++=++（2)2222222222333()3BC GA CA GB AB GC AB AC BC +=+=+=++6.重心到三角形3个顶点距离的平方和最小。

即： 222GA GB GC ++最小。

性质证明：1.过点G 做GD 的延长线DH,使得DH=GD,连接BH=CHG DF EABCAGGD GHGD GHAG AH G AC E CH GE BGCH CDBD 2121//=∴==∴∴∴= 又中点。

即为中点为又为平行四边形四边形又2.ABC AGC AGC CGD AGC ABC ACD CGD AGC S S S S S S S S S DG AG ∆∆∆∆∆∆∆∆∆=∴=+===∴=31232122 3.()()()031313132),(21=++∴+=+=+=∴=+=C G B G A G BC A C G C CB A B G B CA B A G A DA AG C AB A D A同理：由 4.)3,3(0=------∴=++c B A G c B A G y y y y x x x x C G B G A G∴)3y ,3CB A G c B A G y y y x x x x ++=++=5.()()22222222222222412121)21((241)))((2(4124121CB C A B A D A C B D A C A B A B D D A C D D A C A B A B A C A C A B A C A B A D A-+=∴⎪⎭⎫ ⎝⎛-++=++++=∙++=⎪⎭⎫ ⎝⎛+= 2222412121BC AC AB AD -+=∴推广：.222222222222222222222222222222223911142242219992219992219991()32333()3GA AD AG AB AC BC AG AB AC BC AB BC AC CG AC BC AB AG BG CG AB BC CA BC GA CA GB AB GC AB BC CA =∴=+-∴=+-=+-=+-∴++=++∴+=+=+=++同理BG6.设三角形三个顶点为112233(,),(,),(,)x y x y x y 平面上任意一点为(),x y 则该点到三顶点距离平方和为：()()()()()()()()()()22222211223322222222123123123123222222221231231231232212312332()32()1133331133x x y y x x y y x x y y x x x x x y y y y y x x x y y y x x x x y y y y x x x y y y x x x y y y -+-+-+-+-+-=-+++-++++++++⎛⎫⎛⎫=-+++-++++++++ ⎪ ⎪⎝⎭⎝⎭-++-++显然当123123y ,)33x x x y y x y ++++==重心坐标）时上式取得最小值。

高中数学竞赛讲义(全套)

高中数学竞赛资料一、高中数学竞赛大纲全国高中数学联赛全国高中数学联赛（一试）所涉及的知识范围不超出教育部2000年《全日制普通高级中学数学教学大纲》中所规定的教学要求和内容，但在方法的要求上有所提高。

全国高中数学联赛加试全国高中数学联赛加试（二试）与国际数学奥林匹克接轨，在知识方面有所扩展；适当增加一些教学大纲之外的内容，所增加的内容是：1.平面几何几个重要定理：梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理。

三角形中的几个特殊点：旁心、费马点，欧拉线。

几何不等式。

几何极值问题。

几何中的变换：对称、平移、旋转。

圆的幂和根轴。

面积方法，复数方法，向量方法，解析几何方法。

2.代数周期函数，带绝对值的函数。

三角公式，三角恒等式，三角方程，三角不等式，反三角函数。

递归，递归数列及其性质，一阶、二阶线性常系数递归数列的通项公式。

第二数学归纳法。

平均值不等式，柯西不等式，排序不等式，切比雪夫不等式，一元凸函数。

复数及其指数形式、三角形式，欧拉公式，棣莫弗定理，单位根。

多项式的除法定理、因式分解定理，多项式的相等，整系数多项式的有理根*，多项式的插值公式*。

n次多项式根的个数，根与系数的关系，实系数多项式虚根成对定理。

函数迭代，简单的函数方程*3.初等数论同余，欧几里得除法，裴蜀定理，完全剩余类，二次剩余，不定方程和方程组，高斯函数[x]，费马小定理，格点及其性质，无穷递降法，欧拉定理*，孙子定理*。

4.组合问题圆排列，有重复元素的排列与组合，组合恒等式。

组合计数，组合几何。

抽屉原理。

容斥原理。

极端原理。

图论问题。

集合的划分。

覆盖。

平面凸集、凸包及应用*。

注：有*号的内容加试中暂不考，但在冬令营中可能考。

二、初中数学竞赛大纲1、数整数及进位制表示法，整除性及其判定；素数和合数，最大公约数与最小公倍数；奇数和偶数，奇偶性分析；带余除法和利用余数分类；完全平方数；因数分解的表示法，约数个数的计算；有理数的概念及表示法，无理数，实数，有理数和实数四则运算的封闭性。

三角形五心及其性质

三角形五心及其性质三角形的三条高的交点叫做三角形的垂心。

三角形垂心的性质设△ABC的三条高为AD、BE、CF，其中D、E、F为垂足，垂心为H，角A、B、C的对边分别为a、b、c，p=(a+b+c)/2．1、锐角三角形的垂心在三角形内；直角三角形的垂心在直角顶点上；钝角三角形的垂心在三角形外.2、三角形的垂心是它垂足三角形的内心；或者说，三角形的内心是它旁心三角形的垂心；3、垂心H关于三边的对称点，均在△ABC的外接圆上。

4、△ABC中，有六组四点共圆，有三组(每组四个)相似的直角三角形，且AH?HD=BH?HE=CH?HF。

5、 H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。

6、△ABC，△ABH，△BCH，△ACH的外接圆是等圆。

7、在非直角三角形中，过H的直线交AB、AC所在直线分别于P、Q，则 AB/AP?tanB+AC/AQ?tanC=tanA+tanB+tanC。

8、三角形任一顶点到垂心的距离，等于外心到对边的距离的2倍。

9、设O，H分别为△ABC的外心和垂心，则∠BAO=∠HAC，∠ABH=∠OBC，∠BCO=∠HCA。

10、锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。

11、锐角三角形的垂心是垂足三角形的内心；锐角三角形的内接三角形(顶点在原三角形的边上)中，以垂足三角形的周长最短。

12、西姆松定理（西姆松线）：从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。

13、设锐角△ABC内有一点T，那么T是垂心的充分必要条件是PB*PC*BC+PB*PA*AB+PA*PC*AC=AB*BC*CA。

垂心的向径定义设点H为锐角三角形ABC的垂心，向量OH=h，向量OA=a，向量OB=b，向量OC=c，则h=(tanA a +tanB b +tanC c)/(tanA+tanB+tanC).垂心坐标的解析解：设三个顶点的坐标分别为(a1，b1)(a2，b2)(a3，b3)，那么垂心坐标x=Δx/2/Δ，y=-Δy/2/Δ。

三角形五心的总结与归纳

性质：
性质1 ：三角形的一条内角平分线与其他两个角的外角平分线交于一点，该点即为三角形的旁心。
性质2：旁心到三角形三边的距离相等。
性质3：三角形有三个旁切圆，三个旁心。旁心一定在三角形外。
性质角形旁切圆的圆心简称为三角形旁心它是三角形一个内角的平分线和其他两个内角的外角平分线的交点
三角形的内心、外心、重心、垂心、旁心称为三角形的五心.它们都是三角形的重要相关点.（注：没有中心）
三角形内心
定义：三角形内接圆的圆心叫做三角形的内心，三角形的内心也就是三角形三个内角的三条角平分线交点。
图形：
性质：
1、内心是三角形三个内角角平分线的交点；
2、内心到三角形三边的距离都相等，都等于内切圆半径r；
3、内心是内切园的园心。
做法：
1.做出△ABC的两个内角的平分线，交于一点，该点即为三角形内心。
三角形外心
定义：三角形外接圆的圆心叫做三角形的外心。三角形外接圆的圆心也就是三角形三边垂直平分线的交点。
图形：
性质：
1、外心是三角形三条边垂直平分线的交点；
2、外心到三角行三个顶点的距离相等，都等于外切圆半径R；
3、外心是外切圆的圆心。
作法：
分别作三角形两边的中垂线交点计作O
以O为圆心OA为半径画圆
圆O即为所求
其他：（1）锐角三角形的外心在三角形内；
（2）直角三角形的外心在斜边上，与斜边中点重合；
（3）钝角三角形的外心在三角形外.
3、重心和三角形3个顶点组成的3个三角形面积相等。
三角形的垂心
定义：
垂心：三角形的三条高或其延长线相交于一点，这点称为三角形的垂心。
图形：
性质：
1、三角形的三条高或其延长线的交点；

三角形各种心的性质归纳

三角形各种心的性质研究一、基础知识三角形的心是指重心、外心、垂心、旁心和界心．三角形的心是三角形的重要几何点．在数学竞赛中，有关三角形的心的几何问题是竞赛的热点问题，因此，我们对三角形的心的几何性质做概括归纳，对有关的证明方法和解题技巧做深入探讨．1．重心：设G 是ABC ∆的重心，AG 的延长线交BC 于D ，则，DC BD =)1(，（ 2）3:2:=AD AG ；（3）4222222BC AC AB AD -+=，（4）3ABCGBCS S ∆∆=．2.外心：设⊙O （R ）是ABC ∆的外接圆，BC OD ⊥于D 交⊙O 于E ，则（1）R OC OB OA ===；（2）A BOC ∠=∠2或)180(20A ∠-；（3）DC BD =⌒BE =⌒EC ；（4）C B A R Rabc S ABCsin sin sin 24==∆（正弦定理）3.内心：设ABC ∆的内心圆⊙I （)r 切边AB 于P ，AI 的延长线交外接圆于D ，则（1）A BIC ∠+︒=∠2190; (2)a c b a a c b A r AP -++=-+=∠=)(21221cot ；(3)DC DI DB ==；(4)2)(c b a r SABC++=∆; 4.垂心：设H G O ,,分别是ABC ∆的外心，重心，垂心，BC OD ⊥于D ，AH 的延长线交外接圆于1H ，则，（1）OD AH 2=；（2）H 与1H 关于BC 成轴对称；（3）⊙=BCH ⊙ABC ；（4）,,,H G O 三点共线，且2:1:=GH OG ；5．旁心：设ABC ∆在A ∠内的旁切圆⊙1I （)1r 与AB 的延长线切于1P ，则，（1）A C BI ∠-=∠219001；（2）2211c b a A ctg r AP ++=∠=；（3）21c b a BP -+=；（4）21CB AI ∠=∠；（5）2)(1a c b r S ABC -+=∆ 6．三角形中内切圆、旁切圆和外圆半径的几个关系在△ABC 中，内切圆⊙O 分别与三边相切于点K M ,L ，BC 边上的帝切圆⊙a O 与BC 边切于点H ，且分别与AB 边和AC 这的延长线相切于点Q 、点P ．设三边BC 、CA 、AB 分别为c b a ,,，C B A ∠∠∠,,分别为γβα,,，)(21c b a p ++=，内切圆半径为r ，旁切圆半径分别为c b a r r r ,,，外接圆半径为R ，三角形面积为∆S ，则有如下关系式：（1）p AP =，a p AK -=，c b LH -=；（2）Ma p rp r a -=；（3）直角三角形斜边上的旁切圆的半径等于三角形周长的一半；（4）))((1c p b p rr a --=；（5）cb a r r r r 1111--=；（6）2tan2tanγβ⋅=r r a7．界心如果三角形一边上的一点和这边对的顶点把三角形的周界分割为两条等长的折线，那么就称这一点为三角形的周界中点．其中三角形的周界是指由三角形的三边所组成的围．由于三角形的任意两边之和大于第三边，可知三角形任一边上的周界中点必介于这边两端点之间．三角形的顶点与其对边的周界中点的连线，叫三角形的周界中线（有时也称周界中线所在直线为三角形的周界中线）．三角形的周界中线交于一点．定义：称三角形的周界中线的交点为三角形的界心．二、例题分析例1．设△ABC 的外接圆O 的半径为R ，内心为I ，︒=∠60B ，C A ∠<∠，A ∠的外角平分线交圆O 于E ，证明：（1）AE IO =；（2）R IC IA IO R )31(2+<++<．【证明】（1）延长BI 交外接圆于M ，连结Am OM OA ,,，易知︒=∠=∠60B AOM ，故△AOM 为正三角形，∴CM AM OA OM ===．易证MAI MIA ∠=∠，∴MI MA =．同理，MI MC =，即C I O A ,,,在以M 为圆心，R 为半径的圆上，设AI 的延长线交⌒BC 于F ，则AF 、AE 分别为A ∠的内、外角平分线，︒=∠90EAF ，即EF 为⊙O 的直径，∴AOE OFI OAI ∠=∠=∠21．又在⊙M 中，OMI OAI ∠=∠21，∴OMI AOE ∠=∠，但⊙M 与⊙O 为等圆，故OI AE =．（2）连接FC ，同上易证FC IF =，又︒=∠=∠60ABC IFC ，∴△IFC 为等边三角形，IF IC =∵)60(21)(212121︒-∠=∠-∠=∠=∠=∠C AMO AMI OMI AOE AFE ，记AFE ∠为θ∴AF AE AF IA AE IC IA IO +=++=++)cos (sin 2cos 2sin 2θθθθ+=+=R R R)152sin(22)45sin(22︒+=︒+=CR R θ 由C A ∠<∠知，︒<∠<︒12060C ，从而有︒<∠<︒602130C ，即︒<︒+∠<︒75152145C∴︒<++<︒75sin 2245sin 22R IC IA IO R ，又46275sin +=︒，故R IC IA IO R )31(2+<++<．例2．锐角△ABC 的外心为O ，线段BC OA ,的中点分别为M 、N ．，OMN ABC ∠=∠4OMN ACB ∠=∠6．求OMN ∠．【解】设θ=∠OMN ，则θ4=∠ABC ，θ6=∠ACB ，θ10180)(180-︒=∠+∠-︒=∠ACB ABC BAC又θ1018021-︒=∠=∠=∠BAC BOC NOC ；θ82=∠=∠=∠ABC AOC MOC从而θθθ2180)10180(8-︒=-︒+=∠MONOMN OMN MON ONM ∠==+-︒-︒=∠+∠-︒=∠θθθ)2180(180)(180即OMN ∆为等腰三角形，OC OA OM ON 2121=== ∵︒=∠90ONC ，∴︒=∠60NOC ，又∵θ10180-︒=∠NOC ，∴︒==∠12θOMN 例3．如图I O ,分别为△ABC 的外心和内心，AD 是BC 边上的高。

中考必备：三角形的五个“心”及一些平面几何的著名定理

中考必备：三角形的五个“心”及一些平面几何的著名定理三角形的五个“心” 一、重心：（又叫中心） 1这点就是三角形的重心。

2. 重心定理：（1）一个三角形三条边上的中线必交一点；证明：找AB 中点F ，AC 中点E ，连接这两条中线交于点O ，连接AO 并延长，交BC 于点D ，可得S三角形ABE =S 三角形ACF =1/2×S 三角形ABC （同底同高），得S 三角形BOF =S 三角形COE （两三角形同减S四边形AEOF ），得S 三角形AOB =S 三角形AOC （都为上面两三角形面积的两倍），得B 到AD 和C 到AD 的距离h 相等（面积相等，底相等），所以S 三角形BOD =S 三角形COD （同底OD ，等高h ），所以BD=CD （面积相等，高相等），即D 为BC 中点，所以三角形三条中线交于一点。

（2）三角形的三条中线交于一点，这点到顶点的距离是它到对边中点距离的2倍。

证明：方法一△ABC ，AB 、BC 、CA 中点分别为D 、E 、F ，交于一点G 。

∴DF//BC ，DF=BC/2 ①（中位线定理）。

∴△ADF ∽△ABC, E 为BC 中点，∴H 为DF 中点（可证AH ／AE=DH ／BE=HF ／EC, BE=EC, ∴DH=HF) ∴HF=DF ／2 , BE=BC ／2，又可由①知HF=BE ／2 ∴HF//BE. 又∵∠BGE=∠FGH 。

∴△BGE ∽△FGH ∴BG/GF=BE/HF=2。

∴BG=（2/3）BF方法二：（简单）AA连结AO、BO、CO形成了三个三角形，S三角形ABC = S三角形ABO+ S三角形BCO + S三角形ACO= 1/2*（a+b+c）* r = s*r据海伦公式：S三角形ABC =√[s(s-a)(s-b)(s-c)] 所以r=S三角形ABC/s三、垂心：1．定义：三角形的三条高交于一点。

该点叫做三角形的垂心。

三角形的五心欧拉线的相关知识及证明

三角形的五心欧拉点：三个顶点到垂心连线的中点，又称费尔巴哈点。

欧拉圆：又称“九点圆”，即3个欧拉点、三边中点和三高垂足九点共圆。

欧拉线：三角形的外心、重心、九点圆圆心、垂心，依次位于同一直线上，这条直线就叫三角形的欧拉线。

证明：作△ABC的外接圆，连结并延长BO，交外接圆于点D。

连结AD、CD、AH、CH、OH。

作中线AM，设AM交OH于点G’∵ BD是直径∴ ∠BAD、∠BCD是直角∴ AD⊥AB，DC⊥BC∵ CH⊥AB，AH⊥BC∴ DA‖CH，DC‖AH∴ 四边形ADCH是平行四边形∴ AH=DC∵ M是BC的中点，O是BD的中点∴ OM= 1/2DC∴ OM= 1/2AH∵ OM‖AH∴ △OMG’ ∽△HAG’∴AG’/MG’=AH/MO=2/1∴ G’是△ABC的重心∴ G与G’重合∴ O、G、H三点在同一条直线上垂心：已知：ΔABC中，AD、BE是两条高，AD、BE交于点O，连接CO并延长交AB于点F求证：CF⊥AB证明：连接DE∵∠ADB=∠AEB=90度∴A、B、C、D到AB中点距离相等∴A、B、D、E四点共圆（以AB为直径的圆）同理C、D、O、E到OC中点距离相等∴C、D、O、E四点共圆（以OC为直径的圆）∴∠ACF=∠ADE=∠ABE又∵∠ABE+∠BAC=90度∴∠ACF+∠BAC=90度∴CF⊥AB重心：已知：△ABC中，D为BC中点，E为AC中点，AD与BE交于O，CO延长线交AB于F。

求证：F为AB中点。

证明：根据燕尾定理，S△AOB=S△AOC，又S△AOB=S△BOC，∴S△AOC=S△BOC，再应用燕尾定理即得AF=BF外心：已知：有一△ABC，F是AB中点，E是AC中点 FO垂直AB，EO垂直AC。

证明:AO=BO=CO解：在△AFO与△BFO中AF=BFFO=FO∠AFO=∠BFO=90°(垂直平分线)∴△AOF全等于△FOB(SAS)∴AO=BO(两个三角形全等,三边对应等)在△AOE与△ECO中AE=ECEO=EO∠AEO=∠CEO(垂直平分线)∴△AOE全等于△COE(SAS)∴AO=CO(两个三角形全等,三边对应等)∵AO=BO(两个三角形全等,三边对应等)又∵AO=CO(两个三角形全等,三边对应等)∴AO=BO=CO即O为△ABC的外接圆的圆心内心有一△ABC，AO,BO为角平分线，求证OC为角平分线。

高中数学平面几何--三角形的五心的重要结论及经典例题

三角形“五心”的重要结论及经典例题1．重心(中线交点)①G 是△ABC 的重心⇔0GA GB GC ++= 证明作图如右，图中GB GC GE +=连结BE 和CE ，则CE=GB ，BE=GC ⇔BGCE 为平行四边形⇒D 是BC 的中点，AD 为BC 边上的中线.将GB GC GE +=代入GA GB GC ++=0，得GA EG +=0⇒2GA GE GD =-=-，故G 是△ABC 的重心.(反之亦然(证略))②1()3PG PA PB PC =++⇔G 为△ABC 的重心(P 是平面上的点).证明 PG PA AG PB BG PC CG =+=+=+⇒3()()PG AG BG CG PA PB PC =+++++ ∵G 是△ABC 的重心∴GA GB GC ++=0⇒AG BG CG ++=0，即3PG PA PB PC =++由此可得1()3PG PA PB PC =++.(反之亦然(证略)例、已知向量1OP ，2OP ，3OP 满足条件1OP +2OP +3OP =0，|1OP |=|2OP |=|3OP |=1，求证 △P 1P 2P 3是正三角形.(《数学》第一册(下)，复习参考题五B 组第6题)证明由已知1OP +2OP =-3OP ，两边平方得1OP ·2OP =12-，同理2OP ·3OP =3OP ·1OP =12-， ∴|12P P |=|23P P |=|31P P△P 1P 2P 3是正三角形.反之，若点O 是正三角形△P 1P 2P 3的中心，则显然有1OP +2OP +3OP =0且|1OP |=|2OP |=|3OP |.即O 是△ABC 所在平面内一点，1OP +2OP +3OP =0且|1OP |=|2OP |=|3OP |⇔点O 是正 △P 1P 2P 3的中心.三角形三条中线的交点，叫做三角形的重心.掌握重心将每条中线都分成定比2:1及中线长度公式，便于解题.例．AD ，BE ，CF 是△ABC 的三条中线，P 是任意一点.证明：在△PAD ，△PBE ，△PCF 中，其中一个面积等于另外两个面积的和. (第26届莫斯科数学奥林匹克)分析：设G 为△ABC 重心，直线PG 与AB，BC 相交.从A ，C ，D ，E ，F 分别作该直线的垂线，垂足为A ′，C ′， D ′，E ′，F ′. 易证AA ′=2DD ′，CC ′=2FF ′，2EE ′=AA ′+CC ′，∴EE ′=DD ′+FF ′. 有S △PGE =S △PGD +S △PGF .两边各扩大3倍，有S △PBE =S △PAD +S △PCF . 例．如果三角形三边的平方成等差数列，那么该三角形和由它的三条中线围成的新三角形相似.其逆亦真.分析：将△ABC 简记为△，由三中线AD ，BE ，CF 围成的三角形简记为△′.G 为重心，连DE 到H ，使EH =DE ，连HC ，HF ，则△′就是△HCF . (1)a 2，b 2，c 2成等差数列⇒△∽△′. 若△ABC 为正三角形，易证△∽△′.AA 'F F 'GE E 'D 'C 'P C B D不妨设a ≥b ≥c ，有CF =2222221c b a -+， BE =2222221b ac -+，AD =2222221a cb -+.将a 2+c 2=2b 2，分别代入以上三式，得 CF =a 23，BE =b 23，AD =c 23. ∴CF :BE :AD =a 23:b 23:c 23=a :b :c .故有△∽△′.(2)△∽△′⇒a 2，b 2，c 2成等差数列. 当△中a ≥b ≥c 时， △′中CF ≥BE ≥AD . ∵△∽△′， ∴∆∆S S '＝(aCF )2. 据“三角形的三条中线围成的新三角形面积等于原三角形面积的43”，有∆∆S S '=43.∴22aCF =43⇒3a 2=4CF 2=2a 2+b 2-c 2⇒a 2+c 2=2b 2.2．垂心(高线交点)三角形三条高的交战，称为三角形的垂心.由三角形的垂心造成的四个等(外接)圆三角形，给我们解题提供了极大的便利.H 是△ABC 的垂心⇔HA HB HB HC HC HA •=•=• 由()00HA HB HB HC HB HC HA HB AC HB AC ⋅=⋅⇔⋅-=⇔⋅=⇔⊥, 同理HC AB ⊥，HA BC ⊥.故H 是△ABC 的垂心.(反之亦然(证略))若H 是△ABC (非直角三角形)的垂心，则 S △BHC ：S △AHC ：S △AHB =tanA ：tanB ：tanC 故tanA ·HA +tanB ·HB +tanC ·HC =0 例、设A 1A 2A 3A 4为⊙O 内接四边形，H 1，H 2，H 3，H 4依次为△A 2A 3A 4，△A 3A 4A 1，△A 4A 1A 2，△A 1A 2A 3的垂心.求证：H 1，H 2，H 3，H 4四点共圆，并确定出该圆的圆心位置. (1992，全国高中联赛) ABC DH ABCDO A A 12分析：连接A 2H 1，A 1H 2，H 1H 2，记圆半径为R .由△A 2A 3A 4知13212sin H A A H A ∠=2R ⇒A 2H 1=2R cos ∠A 3A 2A 4；由△A 1A 3A 4得A 1H 2=2R cos ∠A 3A 1A 4.但∠A 3A 2A 4=∠A 3A 1A 4，故A 2H 1=A 1H 2. 易证A 2H 1∥A 1A 2，于是，A 2H 1 A 1H 2，故得H 1H 2 A 2A 1.设H 1A 1与H 2A 2的交点为M ，故H 1H 2与A 1A 2关于M 点成中心对称. 同理，H 2H 3与A 2A 3，H 3H 4与A 3A 4，H 4H 1与A 4A 1都关于M 点成中心对称.故四边形H 1H 2H 3H 4与四边形A 1A 2A 3A 4关于M 点成中心对称，两者是全等四边形，H 1，H 2，H 3，H 4在同一个圆上.后者的圆心设为Q ，Q 与O 也关于M 成中心对称.由O ，M 两点，Q 点就不难确定了.例、H 为△ABC 的垂心，D ，E ，F 分别是BC ，CA ，AB 的中心.一个以H 为圆心的⊙H 交直线EF ，FD ，DE 于A 1，A 2，B 1，B 2，C 1，C 2. 求证：AA 1=AA 2=BB 1=BB 2=CC 1=CC 2.(1989，加拿大数学奥林匹克训练题) 分析：只须证明AA 1=BB 1=CC 1即可.设 BC =a ， CA =b ，AB =c ，△ABC 外接圆半径为R ，⊙H 的半径为r . 连HA 1，AH 交EF 于M . A 21A =AM 2+A 1M 2=AM 2+r 2-MH 2=r 2+(AM 2-MH 2)， ①又AM 2-HM 2=(21AH 1)2-(AH -21AH 1)2 =AH ·AH 1-AH 2=AH 2·AB -AH 2=cos A ·bc -AH 2， ② 而ABH AH∠sin =2R ⇒AH 2=4R 2cos 2A ,Aasin =2R ⇒a 2=4R 2sin 2A . ∴AH 2+a 2=4R 2，AH 2=4R 2-a 2. ③ 由①、②、③有 A 21A=r 2+bca cb 2222-+·bc -(4R 2-a 2)=21(a 2+b 2+c 2)-4R 2+r 2. 同理，21BB =21(a 2+b 2+c 2)-4R 2+r 2，21CC =21(a 2+b 2+c 2)-4R 2+r 2.∥=∥=H H HM AB B A A BC CC F12111222D E故有AA 1=BB 1=CC 1.3．外心(边垂直平分线交点，外接圆圆心)三角形外接圆的圆心，简称外心.与外心关系密切的有圆心角定理和圆周角定理. O 是△ABC 的外心⇔|OA |=|OB |=|OC |(或OA 2=OB 2=OC 2)(点O 到三边距离相等) ⇔(OA +OB )·AB =(OB +OC )·BC =(OC +OA )·CA =0(O 为三边垂直平分线) 若O 是△ABC 的外心，则S △BOC ：S △AOC ：S △AOB =sinBOC ：sinAOC ：sinAOB =sin 2A ：sin 2B ：sin 2C故sin 2A ·OA 2sin 2B ·OB +sin 2C ·OC =0 例1．过等腰△ABC 底边BC 上一点P 引PM ∥CA 交AB 于M ；引PN ∥BA 交AC 于N .作点P 关于MN 的对称点P ′.试证：P ′点在△ABC 外接圆上. (杭州大学《中学数学竞赛习题》)分析：由已知可得MP ′=MP =MB ，NP ′=NP=NC ，故点M 是△P ′BP 的外心，点N 是△P ′PC 的外心.有∠BP ′P =21∠BMP =21∠BAC ，∠PP ′C =21∠PNC =21∠BAC .∴∠BP ′C =∠BP ′P +∠P ′PC =∠BAC .从而，P ′点与A ，B ，C 共圆、即P ′在△ABC 外接圆上. 由于P ′P 平分∠BP ′C ，显然还有 P ′B :P ′C =BP :PC .例2．在△ABC 的边AB ，BC ，CA 上分别取点P ，Q ，S .证明以△APS ，△BQP ，△CSQ 的外心为顶点的三角形与△ABC 相似. (B ·波拉索洛夫《中学数学奥林匹克》)分析：设O 1，O 2，O 3是△APS ，△BQP ，△CSQ 的外心，作出六边形O 1PO 2QO 3S 后再由外心性质可知 ∠PO 1S =2∠A ， ∠QO 2P =2∠B ， ∠SO 3Q =2∠C .∴∠PO 1S +∠QO 2P +∠SO 3Q =360°.从而又知∠O 1PO 2+∠O 2QO 3+∠O 3SO 1=360°将△O 2QO 3绕着O 3点旋转到△KSO 3，易判断△KSO 1≌△O 2PO 1，同时可得△O 1O 2O 3≌△O 1KO 3. ∴∠O 2O 1O 3=∠KO 1O 3=21∠O 2O 1K =21(∠O 2O 1S +∠SO 1K ) =21(∠O 2O 1S +∠PO 1O 2)=21∠PO 1S =∠A ；A B C PP MN 'A B C QK P O O O ....S 123同理有∠O 1O 2O 3=∠B .故△O 1O 2O 3∽△ABC .4．内心(角平分线交点，内切圆圆心)三角形内切圆的圆心，简称为内心. O 是△ABC 的内心充要条件是()()()0||||||||||||AB ACBA BCCA CBOA OB OC AB AC BA BC CA CB •-=•-=•-=引进单位向量，使条件变得更简洁。

1-三角形中的特殊点和四点共圆

人人（智启）教育个性化教案教学过程三角形中有非常多的特殊点，比如重心，垂心，旁心，内心，外心，奈格尔点，格尔纲点，布洛卡尔点，spieker点，Baven点，九点圆圆心，陪位重心等等，也有很多特殊的直线，比如欧拉线，西姆松线，等等.经过无数人研究，它们已经成为几何的基本工具，用以研究其余问题，掌握这些传统知识，能使我们更好的理解和掌握平面几何的更深刻的问题.下面我们就从给最基本的开始，即四个心：重心G，垂心H，外心O，内心I.(以下如果没有特别说明，a,b,c表示三角形ABC的顶点A,B,C的对边长度,S表示三角形ABC的面积,p表示三角形的周长的一半.R表示外接圆半径,r表示内切圆半径.)1,重心：三角形三条中心的交点,G.众所周知，重心把每条中线都分为2:1的两部分.下面我们来证明三条重线的确交于一点，为了给出一个统一的判断方法，我们先来证明下面的塞瓦定理和四点共圆的判定方法：塞瓦定理：三角形ABC 三边上分别有D,E,F 三点（如图），若直线AD,BE,CF 三线共点，则有：1=FBAFEA CE DC BD另外，塞瓦定理的逆定理也成立，这就是判定三线共点的一种方法.也就是：若上面的式子成立，则有AD,BE,CF 共点.注意，上式中的线段都是有向线段. 塞瓦定理的角元形式：三角形ABC 三边上分别有D,E,F 三点（如图），直线AD,BE,CF 三线共点的等价条件为：16sin 5sin 4sin 3sin 2sin 1sin =∠∠∠∠∠∠那么，利用塞瓦定理逆定理，我们很容易证明三角形三条中线交于一点.甚至之后很多特殊点也可以用塞瓦定理逆定理来判定. 四点共圆:即四个点(ABCD)在同一个圆上.圆内接四边形ABCD 的基本性质: (1)对角互补,即∠BAD+∠BCD=180° (2)一边在同侧的张角相等,即∠DAC=∠DBC. 四点共圆的判定方法:(1)若∠BAD+∠BCD=180°,即对角互补,则ABCD 四点共圆. (2)若∠DAC=∠DBC,即一边在同侧的张角相等,则ABCD 四点共圆.以上性质和判定都很容易用圆周角的性质来证明.请自己完成,其中判定方法是非常重要的. 另外,我们可以证明三角形ADP 相似于三角形BCP.这样便得到下面的相交弦定理:DP BP CP AP ⋅=⋅(有向线段)这同时也是四点共圆的一种判定方法.由此可见, CP AP ⋅的值只与P 的位置有关,与如何过P 作圆的弦无关.这个值,我们把它叫做P 点关于圆O 的幂,简称P 的幂.特别地,我们作直线PO,与圆O 交于X,Y ,则我们有YP XP CP AP ⋅=⋅我们定义P 关于圆O 的幂为22r OP -,r 为圆O 的半径,可以看出:YP XP r OP r OP r OP ⋅=+-=-))((22当P 在圆内时,幂为负,在圆外时,幂为正,圆周上幂为0.如图:由圆外一点P作两条射线,与圆O分别交于A,D和B,C,求证:=PA⋅⋅DPCPBP由此,也给出一个四点共圆的判定方法.请自己考虑极限情况:当BC两点重合的情形.我们来看下面的证明题：三角形ABC的外接圆与另一圆D交于H，I，AB，AC分别与直线HI交于F，G，过D作BC 的垂线与圆D交于E点，若FEC，GEB都三点共线，证明：AE平分∠BAC.托勒密定理：圆内接四边形ABCD中，两组对边的乘积的和等于两条对角线的乘积.即：+⋅AB=⋅BDACBCCD⋅AD我们用相似三角形给出托勒密定理的一种证明，一定要重视证明的方法.将来我们还要给出托勒密定理的推广.米库尔定理：如图，四边形ABCD的两组对边延长后分别交于E，F（通常称之为完全四线形），则以下四个三角形的外接圆共点M：△ABF，△BCE，△CDF，△ADE.事实上我们假设△ABF，△BCE的外接圆交于B，M，然后证明FMCD四点共圆即可，这很容易用对角互补来判定.2,垂心：三角形三条高线所在直线的交点,H.请用塞瓦定理逆定理四点共圆两种方法证明：三条高的确交于一点.另外我们以后将要证明，锐角三角形的垂足三角形（即三角形DEF ）的内心就是H ，以及，锐角三角形ABC 的垂足三角形是所有内接三角形中周长最小者. 请根据垂心的定义,找出上图中相等的角:请给出线段EF 和HD 的计算方法,用a,b,c,A,B,C 来表示.3,外心:三角形三边中垂线的交点,O.我们用中垂线的定义和基本性质就能证明它们交于一点O,另外,O 点到三个顶点的距离相等,所以可以以O 为圆心作圆同时经过三个顶点,这个圆叫做三角形ABC 的外接圆. 由正弦定理我们知道外接圆半径R 的计算方法,以及和面积的关系: SabcR 4 . 请由圆周角和圆心角的关系,给出线段OD 的长度计算公式:请问:直角三角形的外心在哪里?请计算一个三边长分别是4,5,6的三角形的外接圆半径.3,内心:三角形三条角平分线的交点,I.我们用角平分线的定义和基本性质就能证明它们交于一点I,另外,I点到三条边的距离相等,所以可以以I为圆心作圆同时与三条边相切,这个圆叫做三角形ABC的内切圆.请用面积法给出内切圆的半径r的计算方法.用面积法给出角平分线AD长的计算公式.用角平分线定理给出AI和ID的比值.如图三角形ABC的内切圆与三边的切点分别是D,E,F,证明:三角形DEF是锐角三角形.例题:1,锐角三角形ABC的垂心为H,三高垂足分别是D,E,F,证明:H是三角形DEF的内心.且三角形DEF是ABC的内接三角形中周长最小的.2,三角形ABC的垂心为H,外心为O,D是BC中点,求证:AH=2OD.这是一个重要关系,我们用两种方法加以证明,一种用纯几何方式,另一种用计算法.另外,由此关系,请证明下面这个重要的向量关系:+OH+=OBOAOC3,三角形ABC中,H,G,O分别时垂心,重心,外心,证明:H,G,O三点共线,且HG=2GO4,三角形ABC 的外心为O,内心为I,外接圆半径为R,内切圆半径为r,设IO 长度为d,则Rr d R 222=-(欧拉定理)这个关系非常重要,事实上,它的逆定理仍然成立,即,若两个半径为R,r 的圆的圆心距d 满足上式,则任何一个内接于大圆的三角形必外切于小圆,而任何一个外切于小圆的三角形必定内接于大圆.另外,由此公式,我们可以用a,b,c 表示内心I 在外接圆中的幂.。

三角形的费马点

三角形的费马点
费马点是指在平面上给定一些点，费马点是这些点到达的其他点距离之和最短的点。

对于一个三角形来说，费马点就是使得三个顶点与费马点的距离之和最小的点。

在一个三角形中，费马点即为三条角平分线的交点，它也被称为费马点、斯坦纳点，或者直角三角形中的乌尔什拉斯点。

以一个三角形ABC为例，设费马点为P。

费马点满足三个角度相等的条件，即∠APB = ∠BPC = ∠CPA = θ。

在三角形ABC中，任意取一点P，可以得到AP、BP、CP与∠APB、∠BPC、∠CPA的关系：
1.根据三角形内角和定理，有∠APB + ∠BPC + ∠CPA = 180°。

2.根据正弦定理，有AP/sin(∠APB) = BP/sin(∠BPC) =
CP/sin(∠CPA)。

由于AP + BP + CP是常数，求解使得AB + BC + CA最小的点P，等价于求解使得AP + BP + CP最小的点P。

因此可以通过构造三个角等于θ的角平分线，找到这个最小值。

通过计算三个角度相等的角平分线的交点，即可确定费马点的位置。

这个点既可以在三角形内部，也可以在三角形外部，它到三角形的各个顶点的距离之和是最小的。