投入产出数学模型
投入产出模型

投入产出模型投入产出模型是指对于经济系统(这一经济系统可以是一个国家,一个地区,一个行业或一个企业的经济活动)的多部门的投入与产出进行研究,编制投入产出表,并建立其数学模型,称作投入产出模型。
这种将经济系统的投入产出关系编制成投入产出表,建立投入产出模型进行研究的方法叫做投入产出法。
投入产出法是由美国著名经济学家瓦西里·列昂节夫20世纪30年代首先提出的。
最初是由研究一国的国民经济各个产业部门间的联系发展起来的,因此被人们称作部门联系平衡法,又叫产业关联法。
利用投入产出模型对经济活动进行分析和进行经济预测,这是一种重要的经济数量分析,叫做投入产出分析。
投入产出分析的理论基础是第七章我们所介绍的一般均衡理论,主要是对一个国家或一个地区宏观经济的研究。
但随着这一方法的广泛应用,它也可以研究一个部门(行业)的经济活动,一个公司或企业的生产经营活动。
本章将在介绍投入产出模型的基础上,着重介绍投入产出模型在国民经济预测和企业经济预测方面的应用。
第一节投入产出模型的基本形式一、投入产出表所谓投入,是指产品生产所需原材料、辅助材料、燃料、动力、固定资产折旧和劳动力的投入;所谓产出,是指产品生产的总量及其分配使用的方向和数量,包括生产消费(中间产品)、生活消费、积累和净出口等。
生产过程就是投入与产出关系的客观反映,一定时期内产品的产出受投入的影响。
投入与产出的数量关系可以编制成一种矩形的表格表示,即投入产出表。
投入产出表可以按实物形态编制,也可以按价值形态编制。
按实物形态编制的投入产出表叫实物表,按价值形态编制的投入产出表叫价值表,两者基本结构形式是相同的,它们之间只差一个价格因素。
投入产出表按编制的范围不同,可以分作世界投入产出表、国家投入产出表、地区投入产出表、部门投入产出表和企业投入产出表。
这里仅以价值形态的全国表为例介绍投入产出表的结构。
假设把国民经济划分为n 个部分,用1,2,…,n 等号码表示。
第四章-投入产出系数和模型

农业 轻工业 重工业
其它
农业 1. 109 0. 0464 0. 4114
0.0904
轻工业 × × × ×
重工业 × × × ×
其它 × × × ×
上表的第一列表明:要保证农业部门能提供一亿元的 最终产品,则农业部门的生产量要达到1·109亿元, 轻 工 业 部 门 要 达 到 0·0464 亿 元 , 重 工 业 部 门 要 达 到 0·4114亿元,其它部门要达到0·0904亿元。其中农业 部门生产总量只超过最终产品的部分(0·0904亿元) 以及引起其它各部门生产的数量,都是因为农业生产
Bv Av (B I )或者是Bv Av (I A)1
(2·7)
其中, Bv ——完全劳动消耗系数行向量, Bv (bv1, bv2 ,, bvn ) ;
Av ——直接劳动消耗系数行向量, Av (a01, a02 ,, a0n ) 。
二、实物型投入产出表的特点
1、实物型投入产出表的实物量作为计量单位,各类 产品的计量单位并不相同,表的纵列不能相加。
产品投入与产出的关系。若用“负”号表示投入,用 “正”号表示产出,则矩阵中每一列的含义说明,为生 产一个单位各种产品,需要消耗(投入)其它产品(包 括自身)的数量。而主对角线上各元素,则表示各种产 品扣除自身消耗后的净产出比重。同时,也可看到,此 矩阵的“行”则没有经济含义,因为每一行的元素不能 运算。
2、实物形态投入产出模型
(1) 实物形态投入产出模型的表式
在实物投入产出表中,是以产品来进行分类的,其计量 单位则是以实物单位来计量的。简化的实物形态投入产 出表如下所示:
上表的简要解释:
从行向看,反映的是各类产品的分配使用情况,其
中一部分作为中间产品供其它产品生产中使用(消 耗),另一部分则作为最终产品供投资和消费使用, 两部分相加就是一定时期内各类产品的生产总量。从 列向看,反映了各类产品生产中要消耗其它产品(包 括自身)的数量。但应指出的是,由于列向各类产品 的计量单位不一致,故不能进行运算,因此,实物投 入产出模型只有行模型没有列模型。
线性代数6.1 投入产出模型简介

6.1 投入产出模型简介
6.2 线性规划
6.3 单纯形法
《线性代数》精品课程
1.1 n阶行列式的定义
• 一、投入产出模型 • 二、直接消耗系数
• 三、平衡方程组的解 • 四、完全消耗系数 • 五、应用举例
一、投入产出模型
• 假设一个经济系统是由n个产业部门组成的,将这n个产
《线性代数》精品课程
直接消耗系数矩阵A具有以下性质: • 性质1 所有元素均非负,且
0 aij 1(i, j 1,2, , n)
性质2 各列元素的绝对值之和均小于1,即
n
a ij 1 ( j 1,2, , n)
i1
根据这两条性质,可证明以下结论: 投入产出模型中的矩阵(E-A)和(E-C)都是可逆矩阵。
x11 x12 x13 0 0.2 0.31256.49
0
0
x21 x22 x23 0.1 0 0.4 0 1448.16 0
x31 x32 x33 0.3 0.4 0 0
0 1556.20
0 289.63 466.86 125.65 0 622.48
376.95 579.26 0
《线性代数》精品课程
四、完全消耗系数
定义2 第j部门生产单位产品时对第i部门产品 量的直接消耗和间接消耗之和,称为第j部门 对第i部门的完全消耗系数,记作bij,即
n
bij aij bik akj k 1
(i, j 1,2, , n)
间接消耗的总和
矩阵表示为B=A+BA
完全消耗系数矩阵的计算公
60 y 70
60
试求该系统的总产出
矩阵X .
解:因为 X (E - A)-1Y (B E)Y
关于农业投入产出的线性回归模型

关于农业投入产出的线性回归模型农业投入产出的线性回归模型是利用数学方法来描述农业生产中投入与产出之间的关系,通过建立数学模型对农业投入产出关系作出预测和评估。
线性回归模型指的是将一个或多个自变量与一个因变量之间的关系建立为线性方程形式,并进行拟合。
对于农业投入产出的分析,可以将农业生产的投入因素作为自变量,将农产品产出作为因变量,建立起农业投入产出模型。
Y = α + β1X1 + β2X2 + β3X3 + ... + βkXk其中Y表示农产品产量,X1、X2、X3...Xk表示农业生产中的各项投入因素,如劳动力、农作物种植面积、施肥量、农药使用量等等,α是截距,β1、β2、β3...βk是回归系数,它们表示各项投入因素对产出的影响程度。
在模型中,回归系数βi表示在其他因素不变的情况下,投入因素X1、X2、X3...Xk 每变化一个单位,农产品产量Y会发生的变化量。
比如,如果β1的值为2,表示每增加1个劳动力,农产品产量会增加2个单位。
线性回归模型的建立需要依据已有的数据进行拟合。
为了得到准确的拟合结果,需要采集农业生产的相关数据,进行数据处理和分析,或者通过调查问卷等方式获取数据。
在数据采集和处理时,需要注意采集的数据必须是质量可信的、齐全、准确,并且各项指标间不存在显著的相关性,否则会影响模型的准确性和可靠性。
建立出的线性回归模型可以通过计算农业生产各项投入的系数和截距来确定各项投入因素对农产品产出的影响程度,在实际应用中可以预测未来的生产情况和进行相应的决策。
总之,农业投入产出的线性回归模型是一种定量分析的工具,适用于农业经济领域的生产分析、投资分析、政策制定等方面,它可以帮助我们更准确地理解农业生产中各项投入因素对产出的影响程度,为制定科学的农业生产计划和决策提供参考依据。
投入产出数学模型练习题 数学建模
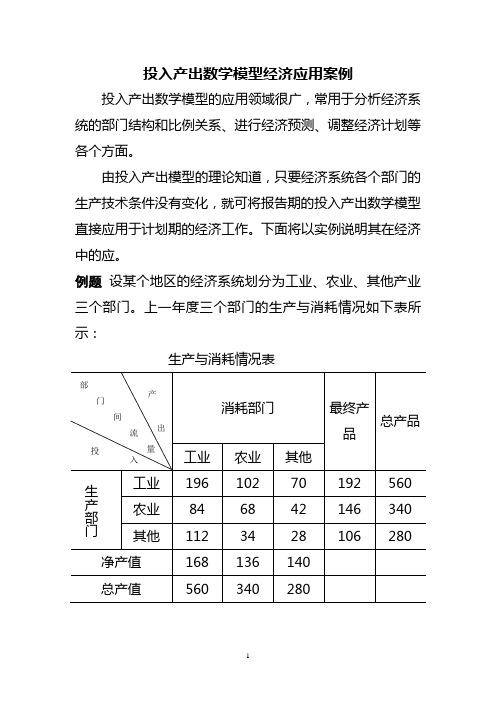
投入产出数学模型经济应用案例投入产出数学模型的应用领域很广,常用于分析经济系统的部门结构和比例关系、进行经济预测、调整经济计划等各个方面。
由投入产出模型的理论知道,只要经济系统各个部门的生产技术条件没有变化,就可将报告期的投入产出数学模型直接应用于计划期的经济工作。
下面将以实例说明其在经济中的应。
例题设某个地区的经济系统划分为工业、农业、其他产业三个部门。
上一年度三个部门的生产与消耗情况如下表所示:生产与消耗情况表假定该系统三个部门的生产技术条件都没有变化,从而该系统的直接消耗系数矩阵不变,由此建立的产品分配方程组和产值构成方程组也不变。
在此基础上,分别分析该系统的报告期投入产出数学模型在计划期经济计划工作方面的下列应用。
(1)在经济预测中的应用假定根据上例所示经济系统的生产发展情况,预计该系统工业、农业、其他产业三个部门的计划期总产品将在报告期总产品的基础上分别增长9%、7%、6%。
由于在生产过程中系统内部存在着复杂的产品消耗关系,故一般说来,各个部门最终产品的增长幅度与总产品的增长幅度并不一致。
试预测该系统最终产品的增长情况。
(2)在制订计划中的应用投入产出数学模型为合理制订经济系统的生产计划提供了一个科学的方法。
根据社会需要确定社会产品的原则,先通过对计划期需要量的预测,确定系统各个部门的最终产品,再利用投入产出数学模型推算出各个部门的总产品,在此基础上编制经济系统计划期的投入产出表,作为安排各个部门计划期生产活动的依据。
现假定通过预测,引例所示经济系统三个部门的计划期最终产品需要量分别为工业部门:1216y=亿元,农业部门:2716y=亿元,其他产业部门:3120y=亿元。
试确定计划期总产品、部门间流量及计划期各部门净产值。
(3)在调整计划中的应用以上介绍了如何根据对最终产品的需求,制订经济系统的生产计划。
但是在执行计划时,可能由于不可预测的原因,导致系统某些部门的最终产品出现缺口(计划产量小于需要量),或者某些部门的最终产品出现余量(计划产量大于需求量),从而破坏了经济系统原计划的平衡性。
投入产出模型

证明 由定理3知,
n
bij aij bik akj
k 1
将 n2个等式用矩阵表示为
i, j 1,2,,n
B A BA或BE A A
由定理1知(E-A)可逆,故
B AE A1
E E AE A1 E A1 E 16
例3 假设某公司三个生产部门间的报告价值型投入产出表如表4,
投入产出数学模型
1
一、投入产出数学模型(基础) 二、区域间投入产出模型基础知识
2
一、投入产出数学模型(基础)
在经济活动中分析投入多少财力、物力、人力,产出多 少社会财富是衡量经济效益高低的主要标志。
投入产出技术正是研究一个经济系统各部门间的“投入” 与“产出”关系的数学模型.
该方法最早由美国著名的经济学家瓦.列昂捷夫 (W.Leontief)提出,是目前比较成熟的经济分析方法。
4
表1:投入产出表
流量 产出 消耗部门
最终需求
投入
生1
产2
部
门
n
新 工资
创 纯收入
价 值
合计
总投入
1 2 n 消费 累计 出口
x11 x12 x1n x21 x22 x2n
xn1 xn2
xnn
v1 v2 vn m1 m2 mn z1 z2 zn
x1 x2 xn
合计
y1 y2 yn
3
(一)投入产出数学模型的概念
投入:从事一项经济活动的消耗; 产出:从事经济活动的结果; 投入产出数学模型:通过编制投入产出表,运用线性代数工具
建立数学模型,从而揭示国民经济各部门、再生产各环节之 间的内在联系,并据此进行经济分析、预测和安排预算计划。
按计量单位不同,该模型可分为价值型和实物型。 首先,必须清楚投入产出表。见下:
投入产出模型

线性代数 在经济管理中的应用
经济与管理学院 黄丽娟
西安电子科技大学 Xi Dian
University
目录
1 模型简介 投入产出模型是什么? 2 模型思路 投入产出模型如何建? 3 应用举例 投入产出模型怎么用?
西安电子科技大学 Xi Dian
University
1 投入产出模型简介
0.15 1
0.35
0.1 2
0.15
0.3 3
西安电子科技大学 Xi Dian
University
经济与管理学院 黄丽娟 - 8 -
3 投入产出模型应用举例
【国民经济宏观模型】设国民经济由制造业、农业
和服务业三部门组成。各部门的单位消耗列向量如
下表所示。
向下列部门 购买
制造业
每单位输出的输入消耗
向下列部门
每单位输出的输入消耗
购买 制造业 农业 服务业
制造业
农 业0.5 服 5务0业
v 0.5
1000v.12
100 00..3405 .2
002..1205
0.15 1 0.01 .15 10.35
西安电子科技大学 Xi Dian
University
经济与管理学院 黄丽娟 - 10 -
University
2 投入产出模型思路
基本假设:
对于每个部门,存在一个在 n 维单位消耗列向
量 vi ,它表示第 i 个部门每产出一个单位(比如
100万美金)产品,需消耗其他部门产出的数量。
把这 n 个 vi 并列起来,就可以构成一个 n n
的系数矩阵,成为内部需求矩阵V。由于要向外 部提供产品,V 矩阵各列向量元素之和必小于1。
1-投入产出表与模型

引入直接消耗系数
• 直接消耗系数是投入产出分析中的基本概念之一, 其含义是生产某种单位产品对另一种产品的消耗 量。 • 公式形式为:
aij xij / x j
– 分子为价值表第I象限的元素,表示j部门生产中对i产 品所消耗的价值量,分母xj是价值表列向总计,为j部门 的总投入量。 – aij的含义则是j部门每单位产值中对i产品消耗的价值量。
棉花100 80 纱200 180 布300 200 服装500
20消费
20出口
100消费
500消费
• 初始投入:(70+30)+(50+70)+( 60+60)+(120+180)=640 • 最终产品与初始投入在价值量上是相等的
投入产出表与模型
• 表与模型
– 投入产出模型有两种表现形式,即投入产出表和与其 对应的投入产出数学模型。
• 问题:投入产出表与GDP核算?
– 生产法 – 收入法 – 支出法
按行建立的数学模型
行向投入产出数学模型
• 依据实物表和价值表上的同行元素的关系 得到 •
• 采用求和符号与矩阵形式记为:
X
i 1
n
ij
yi xi
Zi y x
(I=1,2 ,……, n)
– 产品平衡关系式表现了各产品的生产、分配关 系 – 但各式之间的联系不够紧凑,它未形成一个有 机联系的整体,所反映的数量关系简单化、表 面化,有待进一步深化其关系 – 引入直接消耗系数
引入A系数的意义
– 把行与列联结起来,使平衡数量关系得以深化
• 引入该系数后,即可将物质生产中的技术联系置入 模型中,从而使模型不再局限于行向元素数量关系 上,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总投入
x1
x2 xn
4
投入产出表描述了各经济部门在某个时期
的投入产出情况。它的行表示某部门的产出;
列表示某部门的投入。如表7.1中第一行x1表 示部门1的总产出水平,x11为本部门的使用 量,x1 j (j=1,2,…,n)为部门1提供给部门j的使用 量,各部门的供给最终需求(包括居民消耗、 政府使用、出口和社会储备等)为 y j (j=1,2,…,n)。这几个方面投入的总和代表了这 个时期的总产出水平。
令 X x1
(7-18)
x2 xn , Y y1
y2 yn ,
(7-19)
12
(7-18)式可表示为 AX Y X ,或
E A X Y
称矩阵E-A为列昂捷夫矩阵。
类似地把 xij aij x j 代入平衡方程(7-14)得到
a11 x1 a21 x2 an1 xn z1 x1 a x a x a x z x 12 1 22 2 n2 n 2 2 a1n x1 a2 n x2 ann xn zn xn
9
例1 已知某经济系统在一个生产周期内投入
产出情况如表7.2,试求直接消耗系数矩阵。
表7.2
产出 投入 中 1 间 2 投 3 入 净产值 总投入 中间消耗 1 2 3 100 25 30 80 50 30 40 25 60
最终需求
总产出
400 250 300
400 250 300
10
xij 解 由直接消耗系数的定义 aij x ,得直接 j
(7-14)
xij z j x j j 1,2,, n
i 1
n
(7-15)7Fra bibliotek由(7-11)和(7-14),可得
y z
i 1 i j 1
n
n
j
(7-16)
这表明就整个国民经济来讲,用于非生 产的消费、积累、储备和出口等方面产品的 总价值与整个国民经济净产值的总和相等。
投入产出数学模型
1
在经济活动中分析投入多少财力、物力、
人力,产出多少社会财富是衡量经济效益高
低的主要标志。投入产出技术正是研究一个
经济系统各部门间的“投入”与“产出”关 系的 数学模型,该方法最早由美国著名的经济学
家瓦.列昂捷夫(W.Leontief)提出,是目前
比较成熟的经济分析方法。
2
一、投入产出数学模型的概念
a
i 1
n
ij
1 j 1,2,, n
11
由直接消耗系数的定义 xij aij x j,代入(7-17),得
a11 x1 a12 x2 a1n xn y1 x1 a x a x a x y x 21 1 22 2 2n n 2 2 an1 x1 an 2 x2 ann xn yn xn
消耗部门
1 2 n
x11 x21 xn1 x12 x1n x22 x2 n xn 2 xnn
最终需求 消费 累计 出口 合计
y1 y2 yn
总 产出
x1 x2 xn
生 产 部 门
1 2 n
新 工 资 v1 v2 vn 创 纯收入 m1 m2 mn 价 z1 z2 zn 合 计 值
8
二、直接消耗系数
定义7.2.1 第j部门生产单位价值所消耗第i部
门的价值称为第j部门对第i部门的直接消耗
系数,记作aij i, j 1,2,, n 。
xij 由定义得 aij i, j 1,2,, n xj
(7-17)
把投入产出表中的各个中间需求 xij 换成相应 的 aij 后得到的数表称为直接消耗系数表,并 称n阶矩阵 A aij 为直接消耗系数矩阵。
(7-11)
x
j 1
n
ij yi xi i 1,2,, n
(7-12)
6
需求平衡方程组:
xi xij yi i 1,2,, n
j 1
n
(7-13)
投入平衡方程组(也称消耗平衡方程组):
x11 x21 xn1 z1 x1 x x x z x 12 22 n2 2 2 x1n x2 n xnn zn xn
5
投入产出的基本平衡关系
从左到右: 中间需求+最终需求=总产出 从上到下: 中间消耗+净产值=总投入 (7-9) (7-10)
由此得产出平衡方程组(也称分配平衡方程组):
x11 x12 x1n y1 x1 x x x y x 21 22 2n 2 2 xn1 xn 2 xnn yn xn
投入~从事一项经济活动的消耗; 产出~从事经济活动的结果; 投入产出数学模型~通过编制投入产出表,运 用线性代数工具建立数学模型,从而揭示 国民经济各部门、再生产各环节之间的内 在联系,并据此进行经济分析、预测和安 排预算计划。按计量单位不同,该模型可 分为价值型和实物型。
3
表7.1:投入产出表
流量 投入 产出
写成矩阵形式为
(7-20)
X DX Z 或 E D X Z
其中
n D diag ai1 i 1 Z z1
(7-21)
ai 2
i 1
n
a in , i 1
n
13
z2 zn
定理7.2.1 列昂捷夫矩阵E-A是可逆的。
如果各部门的最终需求Y y1
y2 yn
已知,则由定理7.2.1知,方程(7-19)存在惟一 解 X x1 x2 xn 。
消耗系数矩阵
0.25 0.10 0.10 A 0.20 0.20 0.10 0.10 0.10 0.20 直接消耗系数 aij i, j 1,2,, n 具有下面重
要性质:
性质7.2.1 0 aij 1 i, j 1,2,, n 性质7.2.2
