专题训练(四) 与三角形有关的角度计算的四种方法
三角形中的角度计算

三角形中的角度计算三角形是一个由三个线段构成的图形,其中三个线段相交的点称为顶点,而线段则称为边。
三角形中的角是指由两条边所构成的角,三角形共有三个内角。
在三角形中,角度的大小是由其对应的边的长度所决定的。
根据三角形内角和定理,三角形的三个内角之和总是等于180度。
在计算三角形中的角度时,我们可以利用不同的方法,如正弦定理、余弦定理和正弦定理等。
一、正弦定理正弦定理是用来计算任意一个三角形中的一个角度的方法,其基本公式为:\[\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}\]其中,a、b、c是三角形的边长,A、B、C是对应的角度。
例如,已知一个三角形的边长分别为a=6,b=8,c=10,我们可以利用正弦定理来计算三角形中的一个角度:\[\frac{6}{sinA}=\frac{8}{sinB}=\frac{10}{sinC}\]我们可以先计算角度A的大小,通过移项得到:利用反正弦函数我们可以求得角度A的大小。
二、余弦定理余弦定理是用来计算三角形中的一个角度的方法,其基本公式为:\(c^2=a^2+b^2-2ab*cosC\)通过这个定理,我们可以计算出三角形中的一个角度。
例如,已知一个三角形的边长分别为a=6,b=8,c=10,我们可以利用余弦定理来计算三角形中的一个角度:通过移项我们可以得到:利用反余弦函数我们可以求得角度C的大小。
三、正弦定理正弦定理是用来计算三角形中的一个角度的方法,其基本公式为:\(\frac{sinA}{a}=\frac{sinB}{b}=\frac{sinC}{c}\)例如,已知一个三角形的边长分别为a=6,b=8,c=10,我们可以利用正弦定理来计算三角形中的一个角度:\(\frac{sinA}{6}=\frac{sinB}{8}=\frac{sinC}{10}\)我们可以先计算角度A的大小,通过移项得到:利用反正弦函数我们可以求得角度A的大小。
三角形的角度计算

三角形的角度计算三角形是几何学中最基本的形状之一,它由三条边和三个内角组成。
在解决与三角形相关的问题时,计算各个角度的大小是十分重要的。
本文将介绍常见的计算三角形角度的方法,包括正弦定理、余弦定理和基本角度关系。
1. 使用正弦定理计算角度正弦定理是指在任意三角形ABC中,边长与角度之间存在关系:a/sin(A) = b/sin(B) = c/sin(C)。
其中,a、b、c分别表示三角形的边长,A、B、C为对应的角度。
根据这一定理,我们可以通过已知两边和一个角度,来求解其他角度。
例如,已知三角形ABC的边长分别为a=3,b=4,c=5,我们需要计算角度A所对应的角度。
根据正弦定理:a/sin(A) = b/sin(B) = c/sin(C)我们可以得到:3/sin(A) = 4/sin(B) = 5/sin(C)将已知数据代入:3/sin(A) = 4/sin(B) = 5/sin(C)通过求解,我们可以得到:sin(A) ≈ 0.6,此时的角度A约等于36.87°2. 使用余弦定理计算角度余弦定理是指在任意三角形ABC中,边长与角度之间存在关系:c^2 = a^2 + b^2 - 2ab*cos(C)。
其中,a、b、c分别表示三角形的边长,C表示对应的角度。
例如,已知三角形ABC的边长分别为a=4,b=5,c=6,我们需要计算角度C所对应的角度。
根据余弦定理:c^2 = a^2 + b^2 - 2ab*cos(C)将已知数据代入:6^2 = 4^2 + 5^2 - 2 * 4 * 5*cos(C)通过求解,我们可以得到:cos(C) ≈ 0.7,此时的角度C约等于45.57°3. 基本角度关系在某些情况下,我们可以通过已知角度关系直接计算三角形的角度。
例如,对于直角三角形,我们知道其中一个角度为90度,而其他两个角度之和为90度;对于等边三角形,每个角度都是60度。
此外,对于一个普通的三角形ABC,根据角度和的关系,我们可以得知:角度A + 角度B + 角度C = 180度。
三角形中的角度计算

三角形中的角度计算要进行三角形的角度计算,首先要搞清楚三角形角度之间的关系变化。
1、内角和定理在△ABC中,∠A+∠B+∠C=180?/SPAN>2、外角定理三角形的一个外角等于和它不相邻的两个内角的和3、直角三角形的两锐角直角三角形的两个锐角之和等于90?/SPAN>4、等腰三角形的三角的关系已知等腰三角形的顶角为n埃 蛄降捉俏?/SPAN>(180埃?/SPAN>n?/SPAN>);已知等腰三角形的一个底角为n埃 蛄硪桓龅捉且彩?/SPAN>n?/SPAN>,顶角为180埃?/SPAN>2n?/SPAN>.三角形中的角度计算主要分以下三种形式:1、方程法,2、推理代换法,3、特殊值法1、方程法例1、在△ABC中,AB=AC,CD平分∠C,∠ADC=150埃 蟆?/SPAN>B[分析] (1)所求的∠B在△DBC内,已知的∠ADC是△DBC的外角,所以有∠ADC=∠B+∠BCD。
∠B是等腰△ABC的顶角,∠BCD是底角的一半,可以用∠B表示,所以可利用方程式求∠B。
(2)因为∠A是底角,∠ACD是底角的一半,∠ADC是已知角,所以可以先求出∠A。
解法1、设∠B=x,则∠ACB=(180埃?/SPAN>x),∠BCD=(180埃?/SPAN>x),由三角形的内角和定理,可得∠B+∠BCD=∠ADC,即x+(180埃?/SPAN>x)=150?/SPAN>所以x=140?/SPAN>解法2、设∠A=x,则∠ACB=x,∠ACD=x。
因为∠A+∠ACD+∠ADC=180埃?/SPAN>所以 x+x+150?/SPAN>=180?/SPAN>解得x=20?/SPAN>,即∠A=20?/SPAN>∴∠B=180埃?/SPAN>2×20?/SPAN>=140?/SPAN>例2、在△ABC中,∠A:∠B=5:7,∠C比∠A大10埃 蟆?/SPAN>C解:设∠C=x,则∠A=x-10?/SPAN>,∠B=(x-10?/SPAN>),所以有x+(x-10?/SPAN>)+(x-10?/SPAN>)=180?/SPAN>解得x=60?/SPAN>,即∠C=60?/SPAN>例3、D是△ABC的BC边上一点,AD=BD,AB=AC=CD,求∠BAC[分析]因为AD=BD,AB=AC=CD,所以有∠B=∠BAD=∠C,∠DAC=∠ADC,且∠BAC+∠B+∠C=180埃 庋 颐强梢陨琛?/SPAN>B=x,列出方程即可求。
11.2利用三角形内外角定理求角度的常见类型人教版2024—2025学年八年级上册
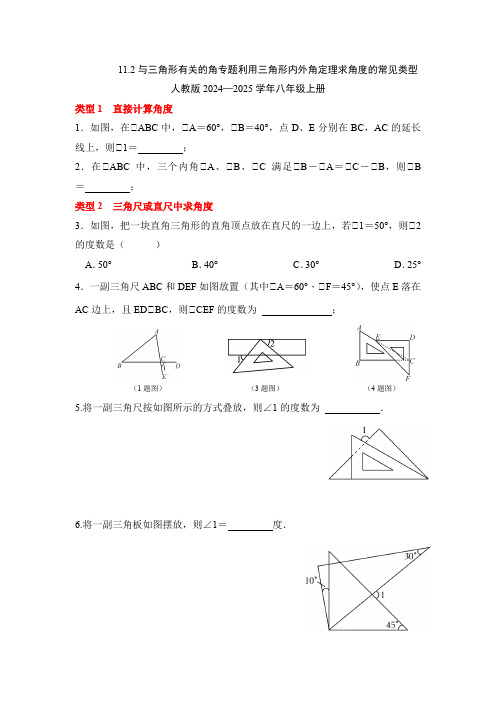
11.2与三角形有关的角专题利用三角形内外角定理求角度的常见类型人教版2024—2025学年八年级上册类型1 直接计算角度1.如图,在△ABC 中,△A =60°,△B =40°,点D 、E 分别在BC ,AC 的延长线上,则△1= ;2.在△ABC 中,三个内角△A 、△B 、△C 满足△B -△A =△C -△B ,则△B = ;类型2 三角尺或直尺中求角度3.如图,把一块直角三角形的直角顶点放在直尺的一边上,若△1=50°,则△2的度数是( )A .50°B .40°C .30°D .25°4.一副三角尺ABC 和DEF 如图放置(其中△A =60°,△F =45°),使点E 落在AC 边上,且ED△BC ,则△CEF 的度数为 ;5.将一副三角尺按如图所示的方式叠放,则∠1的度数为 .6.将一副三角板如图摆放,则∠1= 度.(3题图) (4题图)(1题图)7.如图,将一副直角三角尺按图中所示放置,则图中的∠α=°.8.一副三角尺如图所示摆放,以AC为一边,在△ABC外作△CAF=△DCE,边AF交DC的延长线于点F,求△F的度数.类型3与平行线的性质综合求角度9.如图,AB△CD,△ABE=60°,△D=50°,求△E的度数;类型4截角和折叠综合求角度10.如图,在△ABC中,△C=70°,若沿图中虚线截去△C,则△1+△2等于()A.360° B.250° C.180° D.140°11.如图,将△ABC沿着DE翻折,使B点与B′点重合,若△1+△2=80°,求△B 的度数;13.已知△ABC中,∠A=65°,将∠B、∠C按照如图所示折叠,若∠ADB′=35°,则∠1+∠2+∠3=°.14.如图,把一张Rt△ABC纸片沿DE折叠,若∠1=70°,∠C=90°,则∠2的度数为.15.如图,在△ABC中,∠A=50°,若剪去∠A得到四边形BCDE,则∠1+∠2=.类型5利用内角和的关系求角度16.如图,在△ABC中,△A=60°,△ABC和△ACD的平分线交于点O,求△O 的度数;17.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P=°.18.如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点F,则∠AFC的度数是.19.如图,在△ABC中,∠ABC,∠ACB的平分线BO,CO交于点O,CE为△ABC的外角∠ACD的平分线,BO的延长线交CE于点E,∠1=60°,则∠2的大小为.课后能力提升1.如图,在△ABC中,∠C=90°,BE平分∠ABC,AF平分外角∠BAD,BE与F A交于点E,则∠E的度数为.2.如图,在△ABC中,∠A=α,∠ABC的平分线与∠ACD的平分线交于点A1得∠A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A5BC 的平分线与∠A5CD的平分线交于点A6,得∠A6,则∠A6=.3.将纸片△ABC沿DE折叠使点A落在点A'处【感知】如图①,点A落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是;【探究】如图②,若点A落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由.【拓展】如图③,点A落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为.。
三角形角度公式大全

三角形角度公式大全
在平面几何中,三角形是指由三条线段所构成的图形。
三角形具有一些特殊的属性和角度公式,下面列出了一些常见的三角形角度公式大全:
1. 内角和公式:三角形的三个内角之和总是等于180°,表示为:A + B + C = 180°,其中A、B、C分别表示三角形的三个内角。
2. 外角和公式:三角形的一个外角等于其不相邻两个内角的和,表示为:D = A + B 或 D = B +
C 或
D = A + C,其中D表示一个外角。
3. 直角三角形的角度公式:直角三角形的两个小角相加等于直角,表示为:A + B = 90°或 A +
C = 90°或 B + C = 90°,其中A、B、C分别表示三角形的三个内角。
4. 等边三角形的角度公式:等边三角形的三个内角都等于60°。
5. 等腰三角形的角度公式:等腰三角形的两个底角相等,表示为:A = B 或 A = C 或 B = C,
其中A、B、C分别表示三角形的三个内角。
6. 锐角三角形的角度公式:锐角三角形的三个内角都小于90°。
7. 钝角三角形的角度公式:钝角三角形的一个内角大于90°。
这些是一些常见的三角形角度公式大全,根据具体的三角形形状和条件,可以应用不同的公式进行角度计算。
三角形的角度求解

三角形的角度求解三角形是几何学中的基本形状之一,由三条边和三个角组成。
在解决三角形相关问题时,经常需要求解三角形的角度。
本文将介绍三种常见的方法来求解三角形的角度:正弦定理、余弦定理和正切定理。
1. 正弦定理(Sine Rule)正弦定理是一种常用的三角形角度求解方法,适用于任意三角形,其表达式为:a/sinA = b/sinB = c/sinC其中,a、b、c 分别为三角形的边长,A、B、C 分别为与相应边相对的角度。
2. 余弦定理(Cosine Rule)余弦定理也是常见的三角形角度求解方法,可以用于不等边三角形,其表达式为:c^2 = a^2 + b^2 - 2abcosC其中,c 为三角形的斜边,a、b 为与此斜边相关的两条边,C 为斜边相对的角度。
3. 正切定理(Tangent Rule)正切定理适用于直角三角形,其表达式为:tanA = a/b, tanB = b/a其中,a、b 分别为直角三角形的两条边,A、B 分别为与相应边相对的角度。
这些定理可以帮助我们在已知三角形边长或角度时求解未知角度。
下面通过具体例子演示这些定理的使用方法。
例1:已知三角形的两条边长 a = 5cm,b = 7cm,以及它们夹角的正弦值 sinC = 0.8,求解三角形的角度。
解:根据正弦定理,我们可以得到:a/sinA = b/sinB = c/sinC5/sinA = 7/sinB = c/0.8根据已知信息可得:sinA = 5/7sinB,c = 0.8c由此可得:sinA = 5/7(0.8)通过反正弦函数,我们可以求得角度 A 的值。
例2:已知三角形的两条边长 a = 3cm,b = 4cm,以及夹角 C = 60°,求解第三边 c 和角度 A、B。
解:根据余弦定理,我们可以得到:c^2 = a^2 + b^2 - 2abcosCc^2 = 3^2 + 4^2 - 2(3)(4)cos60°根据已知信息可得:c^2 = 9 + 16 - 24cos60°通过开方运算,我们可以求得第三边 c 的长度。
专题训练(四) 与三角形有关的角度计算的四种方法-学习文档

专题训练(四)与三角形有关的角度计算的四种方法►方法一根据三角形的内角和定理及其推论直接计算角度1.如图4-ZT-1,在△ABC中,∠C=90°,∠B=40°,AD是角平分线,则∠ADC 的度数为()图4-ZT-1A.25°B.50°C.65°D.70°2.如图4-ZT-2,已知∠A=32°,∠B=45°,∠C=38°,则∠DFE的度数为()图4-ZT-2A.120°B.115°C.110°D.105°3.2019·枣庄如图4-ZT-3,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D等于()图4-ZT-3A.15°B.17.5°C.20°D.22.5°4.2019·岳西期中如图4-ZT-4,AB∥CD,∠C=65°,CE⊥BE,垂足为E,则∠B 的度数为________.图4-ZT-45.2019·安徽绩溪期中如图4-ZT-5,已知a∥b,∠1=70°,∠2=40°,则∠3=________°.图4-ZT-56.2019·安徽舒城月考如图4-ZT-6,直线l1∥l2,AB⊥CD,∠1=34°,那么∠2=________°.图4-ZT-67.2019·淅川县期末如图4-ZT-7,在△ABC中,D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.(1)填空:∠AFC=________°;(2)求∠EDF的度数.8.探索与发现:在△ABC中,AD是BC边上的高,AE是∠BAC的平分线.(1)在图4-ZT-8①中,若∠B=20°,∠C=50°,求∠EAD的度数;(2)在图②中,当∠ACB为钝角时,设∠B=α,∠ACB=β,请用含α,β的式子表示∠EAD,并说明理由.图4-ZT-8►方法二三角尺或直尺的组合放置中的角度计算9.将一副三角尺如图4-ZT-9放置,若∠AOD=20°,则∠BOC的度数为()A.140°B.160°C.170°D.150°图4-ZT-910.2019·营口如图4-ZT-10,将一副三角尺叠放在一起,使直角顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为()图4-ZT-10A.85°B.70°C.75°D.60°11.将一把直尺与一块三角尺如图4-ZT-11放置.若∠1=40°,则∠2的度数为()图4-ZT-11A.125°B.120°C.140°D.130°12.2019·枣庄将一副三角尺和一张对边平行的纸条按图4-ZT-12所示方式摆放,两个三角尺的一直角边重合,含30°角的三角尺的斜边与纸条一边重合,含45°角的三角尺的一个顶点在纸条的另一边上,则∠1的度数是()图4-ZT-12A.15°B.22.5°C.30°D.45°►方法三与截取或折叠有关的角度计算13.如图4-ZT-13,小明将一张三角形纸片(△ABC)沿着DE折叠(点D,E分别在边AB,AC上),并使点A与点A′重合,若∠A=70°,则∠1+∠2的度数为()A .140°B .130°C .110°D .70°► 方法四 与平行线的性质或判定综合的角度计算14.如图4-ZT -14所示,已知AB ∥CD ,直线EF 交AB 于点E ,交CD 于点F ,且EG 平分∠FEB ,∠1=50°,则∠2等于( )图4-ZT -14A .50°B .60°C .70°D .80°15.2019·金华如图4-ZT -15,已知AB ∥CD ,BC ∥DE.若∠A =20°,∠C =120°,则∠AED 的度数是________.图4-ZT -1516.如图4-ZT -16,在△ABC 中,∠A =90°,点D 在AC 边上,DE ∥BC ,若∠ADE =155°,求∠B 的度数.图4-ZT -1617.已知:如图4-ZT -17,AB ∥CD ,∠1=∠2,求证:∠BEF =∠EFC.图4-ZT -17详解详析1.[解析] C ∵∠C =90°,∠B =40°,∴∠BAC =90°-∠B =90°-40°=50°.∵AD 是∠BAC 的平分线,∴∠BAD =12∠BAC =25°,∴∠ADC =∠B +∠BAD =40°+25°=65°.故选C.2.[解析] B ∠DFE =∠A +∠ADF =∠A +∠B +∠C =32°+45°+38°=115°.故选B.3.[解析] A ∵∠ABC 与∠ACE 的平分线相交于点D ,∴∠DBE =12∠ABC ,∠DCE =12∠ACE .又∵∠DCE -∠DBE =∠D ,∠ACE -∠ABC =∠A ,∴∠D =12∠A =12×30°=15°.故选A.4.25° 5.70 6.567.解:(1)∵△ABD 沿AD 折叠得到△AED ,∴∠BAD =∠DAF .∵∠B =50°,∠BAD =30°,∴∠AFC =∠B +∠BAD +∠DAF =110°.故答案为110.(2)∵∠B =50°,∠BAD =30°,∴∠ADB =180°-50°-30°=100°.∵△ABD 沿AD 折叠得到△AED ,∴∠ADE =∠ADB =100°,∴∠EDF =∠EDA +∠BDA -∠BDF =100°+100°-180°=20°.8.解:(1)∵∠B =20°,∠C =50°,∴∠BAC =180°-∠B -∠C =180°-20°-50°=110°.∵AE 平分∠BAC ,∴∠BAE =55°.又∵AD ⊥BC ,∴∠BAD =90°-∠B =90°-20°=70°.∴∠EAD =∠BAD -∠BAE =70°-55°=15°.(2)∠EAD =12β-12α.理由如下: ∵∠BAC =180°-α-β,AE 是∠BAC 的平分线,∴∠BAE =12(180°-α-β). ∵∠BAD =90°-α,∴∠EAD =∠BAD -∠BAE =(90°-α)-12(180°-α-β),即∠EAD =12β-12α. 9.[解析] B ∠BOC =∠AOB +∠COD -∠AOD =90°+90°-20°=160°.10.C11.[解析] D在Rt△ABC中,∵∠A=90°,∠1=40°,(已知)∴∠3=90°-∠1=50°,(三角形的内角和定理)∴∠4=180°-∠3=130°.(平角定义)∵EF∥MN,(已知)∴∠2=∠4=130°.(两直线平行,同位角相等)故选D.12.[解析] A如图,过点A作AB∥a,∴∠1=∠2,∵a∥b,∴AB∥b,∴∠3=∠4=30°.∵∠2+∠3=45°,∴∠2=15°,∴∠1=15°.故选A.13.[解析] A∵△A′DE是由△ADE翻折而得,∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′=70°,∴∠AED+∠ADE=∠A′ED+∠A′DE=180°-70°=110°,∴∠1+∠2=360°-2×110°=140°.故选A.14.[解析] D∵EG平分∠FEB,∴∠FEB=2∠1=2×50°=100°.∵AB∥CD,∴∠2+∠FEB=180°,∴∠2=180°-∠FEB=180°-100°=80°.故选D.15.[答案] 80°[解析] 延长DE交AB于点F,∵AB∥CD,BC∥DE,∴∠AFE=∠B,∠B+∠C=180°. ∴∠AFE+∠C=180°. 又∵∠C=120°,∠A=20°,∴∠AFE=60°,∴∠AED=∠A+∠AFE =80°.16.解:∵∠ADE=155°,∴∠EDC=25°.∵DE∥BC,∴∠C=∠EDC=25°.在△ABC中,∠A=90°,∴∠B+∠C=90°,∴∠B=65°.17.证明:连接BC,如图.∵AB∥CD,∴∠ABC=∠DCB,(两直线平行,内错角相等)即∠1+∠EBC=∠2+∠FCB. 又∵∠1=∠2,∴∠EBC=∠FCB,∴BE∥FC,(内错角相等,两直线平行)∴∠BEF=∠EFC.(两直线平行,内错角相等)。
初中数学求角的度数四法学法指导

初中数学求角的度数四法在学习与三角形有关的角时,同学们会遇到许多求角的大小的问题,其中有些题目看似简单,却很难入手,有些题目因思考不全面而造成漏解。
怎么办?要知道,数学思想方法是数学的灵魂,是解决数学问题的金钥匙。
本文就谈谈数学思想方法在求解角的度数问题中的运用,希望对同学们解题有所帮助。
1、整体法例1 如图1,若点P 为△ABC 中∠ABC 、∠ACB 的角平分线的交点,求∠BPC 21-∠A 的度数。
图1分析:解本题的关键在于从整体着眼,利用∠PBC+∠PCB 建立∠A 和∠BPC 的联系。
解:∵∠PBC=21∠ABC ∠PCB=21∠ACB ∠BPC=180°-(∠PBC+∠PCB )∴∠BPC -21∠A ︒=︒⨯-︒=⎪⎭⎫ ⎝⎛∠+∠+∠-︒=9018021180A 21ACB 21ABC 21180 2、方程法例2 如图2,在△ABC 中,∠A :∠ABC :∠ACB=3:4:5,BD 、CE 分别是AC 、AB 边上的高,BD 、CE 相交于点H ,求∠BHC 的度数。
图2分析:根据三角形的内角和定理,结合已知条件可先求出∠A 、∠ABC 、∠ACB 的度数。
在△BHC 中,还需求出∠DBC 和∠ECB 的度数。
解:设∠A=3x 度,则∠ABC=4x 度,∠ACB=5x 度。
所以180x 5x 4x 3=++。
解得x=15,即∠A=45°,∠ABC=60°,∠ACB=75°在△DBC 中,由∠BDC=90°,可知△DBC 是直角三角形。
所以∠DBC=90°-75°=15°在△ECB 中,由∠CEB=90°,可知△ECB 是直角三角形。
所以∠ECB=90°-60°=30°在△BHC 中,∠BHC=180°-15°-30°=135°点评:由于∠A :∠ABC :∠ACB=3:4:5,设∠A=3x 度,则∠ABC=4x 度,∠ACB=5x 度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题训练(四)与三角形有关的角度计算的四种方法►方法一根据三角形的内角和定理及其推论直接计算角度1.如图4-ZT-1,在△ABC中,∠C=90°,∠B=40°,AD是角平分线,则∠ADC 的度数为()图4-ZT-1A.25° B.50° C.65° D.70°2.如图4-ZT-2,已知∠A=32°,∠B=45°,∠C=38°,则∠DFE的度数为()图4-ZT-2A.120° B.115° C.110° D.105°3.2019·枣庄如图4-ZT-3,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D等于()图4-ZT-3A.15° B.17.5°C.20° D.22.5°4.2019·岳西期中如图4-ZT-4,AB∥CD,∠C=65°,CE⊥BE,垂足为E,则∠B 的度数为________.图4-ZT-45.2019·安徽绩溪期中如图4-ZT-5,已知a∥b,∠1=70°,∠2=40°,则∠3=________°.图4-ZT-56.2019·安徽舒城月考如图4-ZT-6,直线l1∥l2,AB⊥CD,∠1=34°,那么∠2=________°.图4-ZT-67.2019·淅川县期末如图4-ZT-7,在△ABC中,D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.(1)填空:∠AFC=________°;(2)求∠EDF的度数.8.探索与发现:在△ABC中,AD是BC边上的高,AE是∠BAC的平分线.(1)在图4-ZT-8①中,若∠B=20°,∠C=50°,求∠EAD的度数;(2)在图②中,当∠ACB为钝角时,设∠B=α,∠ACB=β,请用含α,β的式子表示∠EAD,并说明理由.图4-ZT-8►方法二三角尺或直尺的组合放置中的角度计算9.将一副三角尺如图4-ZT-9放置,若∠AOD=20°,则∠BOC的度数为()A.140° B.160°C.170° D.150°图4-ZT-910.2019·营口如图4-ZT-10,将一副三角尺叠放在一起,使直角顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为()图4-ZT-10A.85° B.70° C.75° D.60°11.将一把直尺与一块三角尺如图4-ZT-11放置.若∠1=40°,则∠2的度数为()图4-ZT-11A.125° B.120° C.140° D.130°12.2019·枣庄将一副三角尺和一张对边平行的纸条按图4-ZT-12所示方式摆放,两个三角尺的一直角边重合,含30°角的三角尺的斜边与纸条一边重合,含45°角的三角尺的一个顶点在纸条的另一边上,则∠1的度数是()图4-ZT-12A.15° B.22.5° C.30° D.45°►方法三与截取或折叠有关的角度计算13.如图4-ZT-13,小明将一张三角形纸片(△ABC)沿着DE折叠(点D,E分别在边AB,AC上),并使点A与点A′重合,若∠A=70°,则∠1+∠2的度数为()A .140°B .130°C .110°D .70°► 方法四 与平行线的性质或判定综合的角度计算14.如图4-ZT -14所示,已知AB ∥CD ,直线EF 交AB 于点E ,交CD 于点F ,且EG 平分∠FEB ,∠1=50°,则∠2等于( )图4-ZT -14A .50°B .60°C .70°D .80°15.2019·金华如图4-ZT -15,已知AB ∥CD ,BC ∥DE.若∠A =20°,∠C =120°,则∠AED 的度数是________.图4-ZT -1516.如图4-ZT -16,在△ABC 中,∠A =90°,点D 在AC 边上,DE ∥BC ,若∠ADE =155°,求∠B 的度数.图4-ZT -1617.已知:如图4-ZT -17,AB ∥CD ,∠1=∠2,求证:∠BEF =∠EFC.图4-ZT -17详解详析1.[解析] C ∵∠C =90°,∠B =40°,∴∠BAC =90°-∠B =90°-40°=50°.∵AD 是∠BAC 的平分线,∴∠BAD =12∠BAC =25°,∴∠ADC =∠B +∠BAD =40°+25°=65°.故选C.2.[解析] B ∠DFE =∠A +∠ADF =∠A +∠B +∠C =32°+45°+38°=115°.故选B.3.[解析] A ∵∠ABC 与∠ACE 的平分线相交于点D ,∴∠DBE =12∠ABC ,∠DCE =12∠ACE .又∵∠DCE -∠DBE =∠D ,∠ACE -∠ABC =∠A ,∴∠D =12∠A =12×30°=15°.故选A.4.25° 5.70 6.567.解:(1)∵△ABD 沿AD 折叠得到△AED ,∴∠BAD =∠DAF .∵∠B =50°,∠BAD =30°,∴∠AFC =∠B +∠BAD +∠DAF =110°.故答案为110.(2)∵∠B =50°,∠BAD =30°,∴∠ADB =180°-50°-30°=100°.∵△ABD 沿AD 折叠得到△AED ,∴∠ADE =∠ADB =100°,∴∠EDF =∠EDA +∠BDA -∠BDF =100°+100°-180°=20°.8.解:(1)∵∠B =20°,∠C =50°,∴∠BAC =180°-∠B -∠C =180°-20°-50°=110°.∵AE 平分∠BAC ,∴∠BAE =55°.又∵AD ⊥BC ,∴∠BAD =90°-∠B =90°-20°=70°.∴∠EAD =∠BAD -∠BAE =70°-55°=15°.(2)∠EAD =12β-12α.理由如下: ∵∠BAC =180°-α-β,AE 是∠BAC 的平分线,∴∠BAE =12(180°-α-β). ∵∠BAD =90°-α,∴∠EAD =∠BAD -∠BAE =(90°-α)-12(180°-α-β),即∠EAD =12β-12α. 9.[解析] B ∠BOC =∠AOB +∠COD -∠AOD =90°+90°-20°=160°.10.C11.[解析] D在Rt△ABC中,∵∠A=90°,∠1=40°,(已知)∴∠3=90°-∠1=50°,(三角形的内角和定理)∴∠4=180°-∠3=130°.(平角定义)∵EF∥MN,(已知)∴∠2=∠4=130°.(两直线平行,同位角相等)故选D.12.[解析] A如图,过点A作AB∥a,∴∠1=∠2,∵a∥b,∴AB∥b,∴∠3=∠4=30°.∵∠2+∠3=45°,∴∠2=15°,∴∠1=15°.故选A.13.[解析] A∵△A′DE是由△ADE翻折而得,∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′=70°,∴∠AED+∠ADE=∠A′ED+∠A′DE=180°-70°=110°,∴∠1+∠2=360°-2×110°=140°.故选A.14.[解析] D∵EG平分∠FEB,∴∠FEB=2∠1=2×50°=100°.∵AB∥CD,∴∠2+∠FEB=180°,∴∠2=180°-∠FEB=180°-100°=80°.故选D.15.[答案] 80°[解析] 延长DE交AB于点F,∵AB∥CD,BC∥DE,∴∠AFE=∠B,∠B+∠C=180°. ∴∠AFE+∠C=180°. 又∵∠C=120°,∠A=20°,∴∠AFE=60°,∴∠AED=∠A+∠AFE =80°.16.解:∵∠ADE=155°,∴∠EDC=25°.∵DE∥BC,∴∠C=∠EDC=25°.在△ABC中,∠A=90°,∴∠B+∠C=90°,∴∠B=65°.17.证明:连接BC,如图.∵AB∥CD,∴∠ABC=∠DCB,(两直线平行,内错角相等)即∠1+∠EBC=∠2+∠FCB.又∵∠1=∠2,∴∠EBC=∠FCB,∴BE∥FC,(内错角相等,两直线平行)∴∠BEF=∠EFC.(两直线平行,内错角相等)。
