初一数学有理数加减乘除混合运算及一元一次方程习题
初一数学有理数加减乘除混合运算练习题

初一数学有理数加减乘除混合运算练习题有理数加减乘除混合运算练习题37734(-1620512)×(-15×4)187(-2.4)341121 2÷(-7)×7÷(-51]÷(-117)[152-(14÷15+32)8)1531121×(-5)÷(-1 5)×5-(3-21+14-7)÷(-42)521-13×23-0.34×7+3×(-13)-7×0.348-(-25)÷(-5)11111(-13)×(-134)×13×(-67)(-478)-(-52)+(-44)-3821(-16-50+35)÷(-2)(-0.5)-(-314)+6.75-522178-87.21+4321+531921-12.79(-6)×(-4)+(-32)÷(-8)-321-7-(-12)+|-12|(-9)×(-4)+(-60)÷12[(-149)-157+218]÷(-421)-34×(8-213-0.04)(213-312+11718)÷(-116)×(-7)|-3|÷10-(-15)×13-1315×(327-165)÷22-有理数加减乘除混合运算练习题(-167337420512)×(-15×4)187(-2.4)2÷(-7)×7÷(-57)[152-(14÷15+32)]÷(-18)2113111×(-5)÷(-)×5-(-+-)÷(-)5-13×3-0.34×7+3×(-13)-7×0.34 8-(-25)÷(-5)(-13)×(-134)×(-16-50+35)÷(-2)(-0.5)-(-34)+6.75-5 ×(-1677111)(-48)-(-52)+(-44)-381178-87.21+4321+5321-12.79(-6)×(-4)+(-32)÷(-8)-3-7-(-2)+|-12|(-9)×(-4)+(-60)÷1219158 [(-14)-17+21]÷(-42)-|-3|÷10-(-15)×3 22191131-4×(8-23-0.04)3157-15×(32-16)÷22(23-32+118)÷(-16)×(-7)每日一练(一)一、计算。
7年级有理数的加减乘除混合运算

七年级有理数的加减乘除混合运算题题目一:(-3)×2 + 5解析:先算乘法,(-3)×2 = -6,再算加法,-6 + 5 = -1。
题目二:4 - 2×(-3)解析:先算乘法,2×(-3) = -6,再算减法,4 - (-6) = 4 + 6 = 10。
题目三:(-2)×3÷(-6)解析:先算乘法,(-2)×3 = -6,再算除法,-6÷(-6) = 1。
题目四:5 + (-3)×4解析:先算乘法,(-3)×4 = -12,再算加法,5 + (-12) = -7。
题目五:(-4)÷2 + 3解析:先算除法,(-4)÷2 = -2,再算加法,-2 + 3 = 1。
题目六:2×(-3) - 4解析:先算乘法,2×(-3) = -6,再算减法,-6 - 4 = -10。
题目七:(-5)×2÷(-10)解析:先算乘法,(-5)×2 = -10,再算除法,-10÷(-10) = 1。
题目八:3 + (-2)×(-4)解析:先算乘法,(-2)×(-4) = 8,再算加法,3 + 8 = 11。
题目九:(-6)÷3 + 2解析:先算除法,(-6)÷3 = -2,再算加法,-2 + 2 = 0。
题目十:4×(-2) + 6解析:先算乘法,4×(-2) = -8,再算加法,-8 + 6 = -2。
题目十一:(-3)×(-3) - 5解析:先算乘法,(-3)×(-3) = 9,再算减法,9 - 5 = 4。
题目十二:5÷(-5) + 4解析:先算除法,5÷(-5) = -1,再算加法,-1 + 4 = 3。
题目十三:(-2)×4÷(-8)解析:先算乘法,(-2)×4 = -8,再算除法,-8÷(-8) = 1。
初一数学专项练习题

初一数学专项练习题一、有理数及其运算1. 计算下列各题:(3) + 7 24 (5) + 63 × 5 ÷ (2)8 ÷ (4) × (2)2. 简化下列各题:5 3 + 2 42 × (3) ÷ 67 ÷ (7) × (7)二、整式及其运算1. 计算下列各题:(3x 5) + (2x + 7)(4x + 6) (5x 2)2(x 3) + 3(2x + 1)5(2x 3) 2(3x + 4)2. 化简下列各题:3x^2 2x^2 + 5x 4x4a^2b 3ab^2 + 2a^2b 5ab^2(x + 3)(x 2) (x 1)(x + 4)三、一元一次方程1. 解下列方程:3x 7 = 2x + 55(x 2) = 3(2x + 1)4 2(x + 3) = 3x 12. 解决实际问题:某数的3倍减去5等于这个数的2倍加7,求这个数。
四、平面几何1. 计算下列图形的周长和面积:一个长为8cm,宽为6cm的长方形。
一个边长为5cm的正方形。
一个半径为4cm的圆。
2. 判断下列说法是否正确:对角线互相垂直的四边形是矩形。
有一组对边平行的四边形是平行四边形。
三个角都是直角的三角形是等边三角形。
五、数据初步认识1. 下列数据中,哪个是众数?哪个是中位数?2, 3, 3, 4, 5, 5, 5, 6, 72. 计算下列各题的平均数:8, 10, 12, 14, 1615, 18, 21, 24, 27六、二元一次方程组1. 解下列方程组:\(\begin{cases} 2x + 3y = 8 \\ x y = 1 \end{cases}\)\(\begin{cases} 4x 5y = 12 \\ 3x + 2y = 9\end{cases}\)\(\begin{cases} 7x + y = 21 \\ 2x 3y = 6\end{cases}\)七、不等式与不等式组1. 解下列不等式:\(3x 5 > 2x + 1\)\(4 2(x 1) \geq 3x 3\)\(5(x 2) < 2(x + 4)\)2. 解下列不等式组:\(\begin{cases} x + 2y > 6 \\ 2x y \leq 4\end{cases}\)\(\begin{cases} 3x y < 3 \\ x + 4y \geq 8\end{cases}\)八、分式及其运算1. 计算下列各题:\(\frac{3}{4} + \frac{1}{6} \frac{2}{3}\)\(\frac{5}{8} \times \frac{2}{3} \div \frac{1}{4}\) \(\frac{2}{5} \frac{1}{3} + \frac{3}{10}\)2. 化简下列各题:\(\frac{4x}{6} \frac{2x}{3}\)\(\frac{3a}{5} + \frac{2a}{3} \frac{a}{15}\)九、图形的性质1. 判断下列图形是否为轴对称图形:一个等边三角形一个矩形一个任意四边形2. 下列图形中,哪个是中心对称图形?一个正方形一个等腰三角形一个圆十、概率初步1. 计算下列事件的概率:从一副去掉大小王的普通扑克牌中随机抽取一张牌,抽到红桃的概率。
有理数的加减乘除乘方混合运算专题训练(带答案)
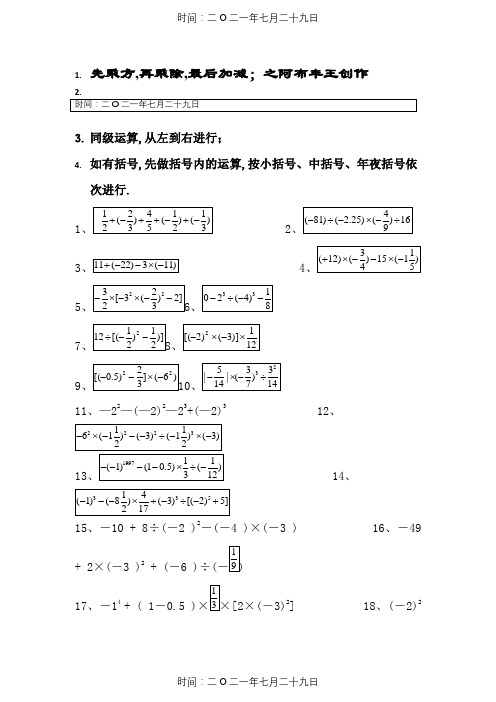
1.先乘方,再乘除,最后加减;之阿布丰王创作3.同级运算,从左到右进行;4.如有括号,先做括号内的运算,按小括号、中括号、年夜括号依次进行.1357911、—22—(—2)2—23+(—2)3 12、13、15、-10 + 8÷(-2 )2-(-4 )×(-3 ) 16、-49+ 2×(-3 )2 + (-6 )÷(17、-14 + ( 1-0.5 )[2×(-3)2] 18、(-2)2-2×[(2-3192123、 24、25、6-(-12、(-48)÷ 8 -(-5)27、420.25 2829、(-5)×6+(-125) ÷(-5)3311、【基础题】计算:(1÷(2)(3(4(1(2(3(4(1(34(5(6(7(8;(9)10(1)11+(-22)-3×(-11);(2)(34;(5(6(7)(-6)(8)(1(2(34(5(6)-10+84×3;(7(81-0.5)(1)(-8)×5-40;(2)()÷(-(-2);(3)-20÷5×(-3)÷15;(4)-3[-5+(÷-2)];(5)-23÷2÷(2;(6×(-2.4)参考谜底1、-1/52、-13、224、95、96、 07、-48 8、-1 9、-15 10、-15/34311、-24 12、-89 13、3 14、215、-2016、23 17、2 18、24 19、-2820、9/1621、1 22、10 23、-1/12 24、104/325、926、1427、-3128、-81又1/81 29、-9 30、-2931、-1/5 32、91、【谜底】(1)17;(2(3)31;(4)-112、【谜底】(1)-10;(2)22;(3)-16;(4)3、【谜底】(1)1;(2)0;(3)42;(4(5)18;(6)0;(7)-4.64;(8(9)8;(104、【谜底】(1)22;(2)0;(3)-17;(4(5(6)-95;(7)-85;(8)6 .5、【谜底】(1)3;(2)1;(3)-54;(4)0;(5)(6)-20;(7)-2;(86、【谜底】(1)-80;(2)5.6;(3)-2;(4)16;(5)-复习有理数的乘除、乘方运算测试题一、填空题(每小题3分,共30分)1.3×(-2)=________,(-6=________.2.(-3)2的底数是________,;-32的底数是________,结果是________.3=________=________;(+8)÷(-=________.4.233=________2=________.5________=1________=-162.4=________.7.-32×(-5)23=________.83600平方公里,________.9.________;________10①23________222________3③32________22)3________)2二、判断题(每小题1分,共5分)11.零除以任何数都得零()12.互为相反数的两个数的积为负数()13.如果ab>0,则a>0且b>0()14.1除以一个非零数的商叫做这个数的倒数()15.(-3)5暗示5个-3相乘()三、选择题(每小题3分,共21分)16.下列说法,其中毛病的有①一个数与1相乘得原数;②一个数乘以-1得原数的相反数;③0乘以任何数得0;④同号两数相乘,符号不变.A.1个B.2个C.3个D.4个17.下列各对数:①1与1;②-1与1;③a-b与b-a;④-1与-1;⑤-5与|6|,其中互为倒数的是A.①②③B.①③⑤C.①③④D.①④18.下列各题中两个式子的值相等的是A.-23与(-2)3 B.32与23C.(-2)2与-22 D.|-2|与-|-2|19.下列结论中,其中正确的个数为①0的倒数是0;②一个不即是0的数的倒数的相反数与这个数的相反数的倒数相等;③其倒数即是自身的数是±1;④若a,b互为倒数,则-ab=-1.A.4 B.3C.2 D.120.下列各式中结果年夜于0的是A.1-910×3 B.(1-910)×3C.1-(9×3)10 D.(1-9)10×3 21.下列说法中正确的是A.一个数的平方必为正数B.一个数的平方必小于这个数的绝对值C.一个数的平方必年夜于这个数D.一个数的平方不成能为负数22.用科学记数法暗示的数2.89×104,原来是A.2890 B.2890000 C.28900 D.289000四、计算题(共35分)23.(3分)(-3)×(-5)×(+1224.(3分)-6÷(+3)÷(-4)×(+2)25.(3分)-5-626.(3分)(-81)÷16)27.(3分)-22×(-328.(3分)(-1)2000200120021)200329.(3分)(-2)×(-20011-200230.(331.(332.(3分)(-2.53)33.(5分)30五、解答题(934.已知A=a+a2+a3+……+a2000(1)若a=1,求A的值.(2)若a=-1,求A的值.一、1.-6 2 2.-3 9 3 -9 3-3245103平方公里9.>>><13.×14.√15.√三、16.A 17.D 18.A 19.B 21.D 22.C四、23.-90 24.1 25.-3 2627.15 28.1 29.-200230.1 31.30 3233.-4五、34.(1)2000 (2)0。
初一上册数学课堂练习题

初一上册数学课堂练习题一、有理数及其运算1. 计算下列各题:(1) (3) + 7(2) 5 (2)(3) (4) × 25(4) 120 ÷ (30)(5) (8) ÷ (2)2. 简化下列各题:(1) 5 + (3) + 2 7(2) (4) × 9 ÷ (3)(3) (5) + 15 (10)二、整式的加减1. 计算下列各题:(1) 3x 2x + 5x(2) 4a 7a + 2a(3) 5xy 2xy + 8xy2. 简化下列各题:(1) 2x^2 3x^2 + 4x^2(2) 5ab 3ab + 6ab 2ab(3) 7m^2n 4m^2n + 9m^2n 5m^2n三、一元一次方程1. 解下列方程:(1) 3x 7 = 11(2) 5 2x = 3(3) 4x + 9 = 2x 32. 解决实际问题:(1) 某数的3倍减去5等于这个数的2倍加上7,求这个数。
(2) 甲、乙两人年龄之和为50岁,甲的年龄是乙的2倍,求甲、乙的年龄。
四、几何图形初步认识1. 判断下列说法是否正确:(1) 平行线永不相交。
(2) 长度相等的两条线段是全等线段。
(3) 角的度数越大,角的边越长。
2. 填空题:(1) 一个直角三角形的两个锐角之和是______度。
(2) 两条平行线之间的距离是______。
五、数据的初步认识1. 填空题:(1) 1千克等于______克。
(2) 1米等于______厘米。
2. 选择题:(1) 下列哪个单位是长度单位?A. 千克B. 米C. 秒(2) 下列哪个单位是质量单位?A. 米B. 克C. 分钟六、平面图形的认识1. 填空题:(1) 一个正方形的对角线将其分成了两个______三角形。
(2) 一个等腰三角形的底角相等,底边两侧的边称为______。
2. 判断题:(1) 所有四边形都有四个直角。
()(2) 对角线互相垂直的四边形一定是矩形。
七年级有理数的加减乘除乘方计算训练(80小题)-有解析

有理数的加减乘除乘方计算(80小题)1.计算:(1)(−37)−(−47);(2)(−53)−16;(3)(−210)−87;(4)1.3−(−2.7).【答案】解:(1)(−37)−(−47)=−37+47=10;(2)(−53)−16=−69;(3)(−210)−87=−297;(4)1.3−(−2.7)=1.3+2.7=4.【解析】此题主要考查有理数的减法,解题关键是掌握有理数的减法法则,据此求解即可.(1)根据有理数的减法法则计算即可;(2)根据有理数的减法法则计算即可;(3)根据有理数的减法法则计算即可;(4)根据有理数的减法法则计算即可.2.计算:(1)−7+3−5+20;(2)223+(−223)+513−(−512);(3)4.25+(−2.18)−(−2.75)+5.18;(4)43−(−87)−2−13−17【答案】解:(1)原式=−12+23=11;(2)原式=0+163+112=326+336=656=1056;(3)原式=(4.25+2.75)+(5.18−2.18)=7+3=10;(4)原式=(43−13)−2+(87−17)=1−2+1=0.【解析】此题考查有理数的加减混合运算,熟练掌握有理数的加减混合运算法则和运算律是解题关键.(1)根据结合律和交换律先同号相加,再异号相加即可求解;(2)根据结合律和相反数的定义算223+(−223)并将513和512化成假分数,然后通分后算加法得出结果再化成带分数即可;(3)根据结合律和交换律先算4.25−(−2.75)和(−2.18)+5.18,再算加法即可求解;(4)根据结合律和交换律先算43−13和87−17,再算加减即可求解.3. 计算:(1)|−7|+|−9715|; (2)(+4.85)+(−3.25);(3)(−3.1)+6.9;(4)−(−15)+(−645); (5)(−3.125)+(+318).【答案】解:(1)原式=7+9715=16715;(2)原式=4.85−3.25=1.6;(3)原式=−(6.9−3.1)=−3.8;(4)原式=15−645=−635;(5)原式=−3.125+3.125=0.【解析】本题考查有理数的加法,以及绝对值,掌握运算法则是解题关键.(1)先化简绝对值,再计算加法即可;(2)先化简括号,再计算即可;(3)根据异号两数相加,取绝对值较大的符号,再用较大的绝对值减较小的绝对值即可;(4)先化简括号,再计算即可;(5)将分数化为小数,再计算即可.4. 用简便方法计算:(1)−13×23−0.34×27+13×(−13)−57×0.34;(2)(−13−14+15−715)×(−60).【答案】解:(1)原式=(−13)×(23+13)+0.34×(−17−57)=−13×1+0.34×(−1)=−13−0.34=−13.34;(2)原式=−13×(−60)−14×(−60)+15×(−60)−715×(−60)=20+15−12+28=51【解析】本题主要考查了有理数的混合运算,关键是熟练掌握乘法运算律.(1)运用乘法分配律进行计算可得结果;(2)利用乘法分配律进行计算,最后计算加减可得结果.5. 计算:(1)(−8)×9×(−1.25)×(−19);(2)−113×214÷(−112);(3)(−132)÷(134−58+12);(4)(−3)÷134×0.75×|−213|÷9.【答案】解:(1)原式=(−8)×(−1.25)×[9×(−19)]=10×(−1)=−10;(2)原式=−43×94×(−23) =2;(3)原式=(−132)÷(148−58+48)=(−132)÷138 =−132×813=−152;(4)原式=−3×47×34×73×19=−13.【解析】本题主要考查的是有理数的乘法,有理数的混合运算的有关知识.(1)利用有理数的乘法的计算法则进行计算即可;(2)利用混合运算的运算法则进行计算即可;(3)利用混合运算的运算法则进行计算即可;(4)利用混合运算的运算法则进行计算即可.6.计算:(1)−2.2+(−4.3)(2)−(−334)+(−15.5)(3)−(−5)−|−4|(4)−21−12+33+12−67.【答案】解:(1)−2.2+(−4.3)=−(2.2+4.3)=−6.5(2)−(−334)+(−15.5)=3.75−15.5=−(15.5−3.75)=−11.75(3)−(−5)−|−4|=5−4=1(4)−21−12+33+12−67=−100+45=−55.【解析】此题主要考查有理数的加减及混合运算(1)根据同号两数相加,取相同的符号,并把绝对值相加求解(2)先求出相反数,根据异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值求解(3)先求出相反数和绝对值,再相减(4)利用分组法,符号相同的加在一起,再根据异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值求解7.计算:(1)(−99)+(−103);(2)(−16)+9;(3)3+(−8)+(−1).(4)|−18|+|−6|;(5)|−36|+|+24|.【答案】解:(1)(−99)+(−103)=−(99+103)=−202(2)(−16)+9=−(16−9)=−7;(3)3+(−8)+(−1)=3+(−9)=−(9−3)=−6.(4)|−18|+|−6|=18+6=24;(5)|−36|+|+24|=36+24=60.【解析】此题主要考查有理数的加法,根据同号两数相加,取相同的符号,并把绝对值相加,异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值求解(1)根据同号两数相加,取相同的符号,并把绝对值相加求解(2)根据异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值求解(3)先同号相加,再异号相加求解较简便(4)先求个数的绝对值,再相加(5)先求个数的绝对值,再相加8.计算题(1)−(−8)+(−32)+(−|−16|)+(+28)(2)0.36+(−7.4)+0.3+(−0.6)+0.64;(3)(−3.5)+(−43)+(−34)+(+72)+0.75+(−73)(4)(+1734)+(−9511)+(−2.25)+(−17.5)+(−10611)(5)1+(−2)+3+(−4)…+2009+(−2010)+2011+(−2012)【答案】解:(1)−(−8)+(−32)+(−|−16|)+(+28)=8−32−16+28=36−48=−12;(2)0.36+(−7.4)+0.3+(−0.6)+0.64=(0.36+0.64)+(−7.4−0.6)+0.3=1−8+0.3=−6.7;(3)(−3.5)+(−4)+(−3)+(+7)+0.75+(−7)=(−3.5+72)+(−43−73)+(−34+0.75)=0−323+0=−323;(4)(+1734)+(−9511)+(−2.25)+(−17.5)+(−10611)=(+1734−2.25−17.5)+(−9511−10611)=−2−20=−22;(5)1+(−2)+3+(−4)…+2009+(−2010)+2011+(−2012)=(1−2)+(3−4)…+(2009−2010)+(2011−2012)=−1×1006=−1006.【解析】本题考查了有理数的加法,在进行有理数加法运算时,首先判断两个加数的符号:是同号还是异号,是否有0,从而确定用那一条法则.在应用过程中,要牢记“先符号,后绝对值”.(1)先化简,再算加减法即可求解;(2)根据减法交换律和结合律即可求解;(3)、(4)先算同分母分数,再算加减法即可求解;(5)两个一组计算即可求解.9. (1) (−0.9)+1.51(2)13+(−25)(3)(−213)+(−116) (4)314–(–134)(5)0–(–7)(6)(–8)–(–8)(7)(–1.76)+(–19.15)+ (–8.24)(8)(+ 314)+(–235)+ 534+(–825) (9)23−(+17)+6− (+3)(10)214−(+113)−(+0.25)+13(11)(−478)−(−512)+(−414)−(+318)(12)−14+56+23−12(13)(−23)+|0−516|+|−456|−(+913)(14)已知|a|=7,|b|=3,且a <b ,求a +b 的值.【答案】解:(1) (−0.9)+1.51=1.51−0.9=0.61;;(3)(−213)+(−116)=−146−76=−216=−72; (4)314–(–134)=134+74=204=5;(5)0–(–7)=0+7=7;(6)(–8)–(–8)=−8+8=0;(7)(–1.76)+(–19.15)+ (–8.24)=−(1.76+8.24) −19.15=−10−19.15=−29.15;(8)(+ 314)+(–235)+ 534+(–825)=(134+234)−(135+425)=9−11=−2;(9)23−(+17)+6−(+3) =23−17+6−3=23−3−17+6=3+6=9;(10)214−(+113)−(+0.25)+13=94−14−43+13=2−1 =1;(11)(−478)−(−512)+(−414)−(+318)=−398−258+224−174=−8+5 4=−634;(12)−14+56+23−12=−1−2+5+4=−34+96=−34+32=−34+64=34;(13)(−23)+|0−516|+|−456|−(+913)=−46+316+296−566=−46−566+(316+296)=−10+10 =0;(14)已知|a|=7,|b|=3,且a <b ,求a +b 的值.根据|a|=7,|b|=3,且a <b ,可得:a =7时,b 值不存在,a =−7时,b 值为3或−3,所以a +b 的值为−4或−10.【解析】本题考查了理数加法或减法运算,绝对值数,代数式求值,有理数的加减混合运算.(1)到(12)分别利用有理数加法或减法运算法则,以及有理数的加减混合运算法则,分别计算即可;(13)先计算绝对值,再通分结合,即可求得答案;(14)根据|a|=7,|b|=3,且a <b ,可得a =7时,b 值不存在,a =−7时,b 值为3或−3,再分别计算a +b 的值.10. 计算(1)4.25+(−2.18)−(−2.75)+5.18;(2)(−205)+40034+(−20423)+(−112);(3)|−0.75|+(−9)−(−0.25)+|−18|+78;(4)43−(−87)−2−(13)−17; (5)(−418)−|−1+0.125|−|−313|−(−617)+(−517); (6)比较−821和−37大小.【答案】解:(1)原式=(4.25+2.75)+(5.18−2.18)=7+3=10.(2)原式=−205+40034−20423−112=40034−124−20423−205 =39914−205−20423=19414−20423=194312−204812=−10512.(3)原式=34−9+14+18+78=34+14+18+78−9=2−9 =−7.(4)原式=43+87−2−13−17=43−13+87−17−2=1+1−2 =0.(5)原式=−418−1+18−313+617−517=−4−1−313+1=−713.(6)∵|−821|=821,|−37|=37=921,而821<921,即|−821|<|−37|,∴−821>−37.【解析】本题考查的是有理数的加减混合运算有关知识,绝对值以及有理数比较大小.熟练掌握法则是解题的关键.(1)首先对该式变形,然后再进行计算即可;(2)首先对该式变形,然后再进行计算即可;(3)首先对该式去掉绝对值,然后再计算即可;(4)首先对该式变形,然后再进行计算即可.(5)先对该式去掉绝对值,然后再计算即可;(6)根据两个负数比较大小的方法比较即可.11.计算下列各题:(1)(−0.6)+1.7+(+0.6)+(−1.7)+(−9)(2)(+0.25)+(−318)+(−14)+(−514) 【答案】解:(1)原式=[(−0.6)+(+0.6)]+[1.7+(−1.7)]+(−9),=−9;(2)原式=[(+0.25)+(−14)]+[(−318)+(−514)], =−(318+514),=−838.【解析】本题主要考查有理数的加法.(1)互为相反数的两个数相加得零;(2)互为相反数的两个数相加得零,同号两数相加,取相同的符号,并把绝对值相加.12. 计算:(1)(+27)+(−16)−(−18)−(+5);(2)(−23)+(−12)+(−45)−(−16);(3)36+(−8)−(−2.5)−(−6)+(+1.5);(4)−|−35−(−25)|+(−14)+(−12).【答案】解:(1)原式=27+(−16)+18+(−5)=27+18+[(−16)+(−5)]=45+(−21)=24;(2)原式=(−23)+(−12)+(−45)+(+16)=[(−23)+(−12)+(+16)]+(−45) =−1+(−45) =−1.8;(3)原式=36+(−8)+2.5+6+1.5=28+10=38;(4)原式=−|−35+25|+(−34)=−15+(−34)=−1920.【解析】本题主要考查了有理数的加减混合运算,关键是熟练掌握有理数的加减混合运算的顺序和法则.(1)先将减法转化为加法,然后利用加法运算律计算可得结果;(2)先将减法转化为加法,然后利用加法运算律计算可得结果;(3)先将减法转化为加法,然后利用加法运算律计算可得结果;(4)先计算绝对值中的减法,然后再计算加法可得结果.13.计算.(1)(−8.37)−(−2.43);(2)−378−(−634);(3)−712+(−5.12)+712;(4)23−23−(+34);(5)0−14−(+13)−(−32)−(+56);(6)|−312|−(−2.5)−|2−313|;(7)178−87.21−(−432)+15319−12.79;(8)1734−(+6.25)−(−812)−(+0.75)−(+2214).【答案】解:(1)(−8.37)−(−2.43)=2.43−8.37=−5.94;(2)−378−(−634)=−378+634=278;(3)−712+(−5.12)+712=712−712+(−5.12)=−5.12;(4)23−23−(+34)=0−34=−34;(5)0−14−(+13)−(−32)−(+56)=−13+32−14−56=112;(6)|−312|−(−2.5)−|2−313|=312+2.5−313+2=423;(7)178−87.21−(−43221)+1531921−12.79=178−87.21+43221+1531921−12.79=178−(87.21+12.79)+(43221+1531921)=275;(8)1734−(+6.25)−(−812)−(+0.75)−(+2214)=1734−6.25+812−0.75−2214=(173−0.75)−(6.25+221)+81=−3.【解析】本题主要考查有理数的减法,有理数的加减混合运算和绝对值的性质;掌握有理数的减法,有理数的加减混合运算和绝对值的性质;(1)根据有理数的减法法则计算即可;(2)根据有理数的减法法则计算即可;(3)利用交换律后再用有理数加减法法则运算即可;(4)根据有理数的减法法则计算即可;(5)根据有理数加减法法则运算即可;(6)先去绝对值符号,再用加减法法则运算即可;(7)根据有理数加减法法则运算即可;(8)根据有理数加减法法则运算即可;14.计算:(1)−4.2+5.7−8.4+10;(2)−14+56+23−12;(3)12−(−18)+(−7)−15;(4)4.7−(−8.9)−7.5+(−6);(5)(−478)−(−512)+(−414)−(+318); (6)(−23)+|0−516|+|−456|+(−913).【答案】解:(1)−4.2+5.7−8.4+10=(−4.2−8.4)+(5.7+10)=−12.6+15.7=3.1;(2)−14+56+23−12=−312+1012+812−612 =34;(3)12−(−18)+(−7)−15=12+18−7−15=30−22=8;(4)4.7−(−8.9)−7.5+(−6)=4.7+8.9−7.5−6=13.6−13.5=0.1;(5)(−478)−(−512)+(−414)−(+318) =(−478−318)+(512−414) =−8+114=−634;(6)(−23)+|0−516|+|−456| +(−913) ==(−23−913)+(516+456) =−10+10=0.【解析】本题考查了有理数的加减及绝对值,熟练掌握计算法则是解决本题的关键。
初一数学计算(有理数加减、合并同类项、解一元一次方程)
1.化简求值,其中.2.计算与化简:(1)4﹣|﹣6|﹣3× ;(2)﹣32+(﹣1)2001÷ +(﹣5)2;(3)2x2y﹣2(3xy﹣x2y)﹣xy;(4)6a2b﹣[2ab2﹣3(a2b﹣2ab2)].3.先化简再求值:,其中.4.计算(1)(2)(3)(4)5.解方程:(1)3x-7(x-1)=5-2(x+ 3);(2)x- =2-6.先化简,再求值:3x2y-[2x2y-3(2xy-x2y)-xy],其中x=-1,y=-2。
7.先化简,再求值:-2a2+(-4a+5a2)-(3a2+2a-1),其中a=8.计算:3m4·m5+m10÷m-(2m3)39.列式计算:如果减去某个多项式的差是,求这个多项式.10.先化简再求值:,其中x=-1,y =2.11.化简:(1)(2)12.(1)合并同类项:(2)先化简,再求值:,其中,13.解下列方程.(1).(2).14.解方程:.15.解方程:16.解方程(1)x=8- (20-x) (2)17.解方程:18.解方程(1)(2)答案解析部分一、计算题1.【答案】解:将代入原式中原式【解析】【分析】根据整式的运算:去括号法则:括号外是正数,括号内的各项符号不变,括号的数是负数,括号内的各项符号相反;按小括号、中括号、大括号的顺序即可化简,代入a、b的值即可。
2.【答案】(1)解:原式=4﹣6+1=﹣1;(2)解:原式=﹣9﹣1×6+25=﹣9﹣6+25=10;(3)解:原式=2x2y﹣6xy+2x2y﹣xy=4x2y﹣7xy;(4)解:原式=6a2b﹣2ab2+3a2b﹣6ab2=9a2b﹣8ab2.【解析】【分析】(1)(2)根据有理数的混合运算法则“先乘方,再乘除,后加减,若有括号先计算括号里面的”计算即可求解;(3)(4)根据去括号法则'括号前面是“+”号,去掉括号不变号;括号前面是“-”号,去掉括号全变号"可去括号,再根据合并同类项法则“把同类项的系数相加,字母和字母的指数不变”可求解.3.【答案】解:原式= ,当,时,原式=(-2)2×(-3)=-12.【解析】【分析】根据去括号法则"括号前面是“+”号,去掉括号不变号;括号前面是“-”号,去掉括号全变号"计算可去括号,再根据合并同类项法则“合并同类项法则:把同类项的系数相加,字母和字母的指数不变”计算可将原式化简;再把x、y的值代入化简后的代数式计算即可求解.4.【答案】(1)解:=;(2)解:=-4+20÷4=;(3)解:== ;(4)解:=.【解析】【分析】(1)根据减去一个数等于加上这个数的相反数将减法转化为加法,再根据有理数的加法法则计算即可求解;(2)根据有理数的混合运算法则“先乘方,再乘除,后加减,若有括号先计算括号里面的”计算即可求解;(3)根据去括号法则"括号前面是“+”号,去掉括号不变号;括号前面是“-”号,去掉括号全变号"计算可去括号,再根据合并同类项法则“合并同类项法则:把同类项的系数相加,字母和字母的指数不变”计算即可求解;(4)根据去括号法则"括号前面是“+”号,去掉括号不变号;括号前面是“-”号,去掉括号全变号"计算可去括号,再根据合并同类项法则“合并同类项法则:把同类项的系数相加,字母和字母的指数不变”计算即可求解.5.【答案】(1)解:去括号得:3x-7x+7=5-2x-6,移项合并得:-2x=-8,解得:x=4;(2)解:去分母得:10x-5x+5=20- 2x-36,移项合并得:7x=-21,解得:x=-3【解析】【分析】(1)根据等式的基本性质,求出方程的解即可;(2)同理,利用那个等式的基本性质,解出方程的解即可。
初一数学课后练习题
初一数学课后练习题一、有理数及其运算1. 计算下列各题:(1) (3) + 7(2) 5 (2)(3) (4) × 25(4) 18 ÷ 3(5) (5 3) × 22. 化简下列各题:(1) 2 + 3 5(2) 4 (3) + 7(3) 4 × (3) ÷ 2(4) (8 5) × (2)二、整式的加减1. 计算下列各题:(1) 3a 2a(2) 4b + 5b 2b(3) 7x 3x + 2x(4) 5m 4n + 2m n2. 化简下列各题:(1) 2a 3a + 4a(2) 5b 2b 3b(3) 6x 4x + 7x(4) 8m 5m 2m三、一元一次方程1. 解下列方程:(1) 3x 7 = 11(2) 5 2y = 1(3) 4a + 9 = 7a(4) 6b 3 = 3b + 122. 求下列方程的解:(1) 2(x 3) = 8(2) 3(y + 4) 7 = 2y(3) 5(a 2) + 3 = 2(a + 1)四、几何图形初步1. 判断下列说法是否正确:(1) 对顶角相等。
(2) 平行线的同旁内角互补。
(3) 钝角大于直角。
2. 画出下列图形:(1) 一个等边三角形。
(2) 一个直角边长分别为3cm和4cm的直角三角形。
(3) 一个边长为5cm的正方形。
五、数据初步认识1. 计算下列各题:(1) 众数:2,3,3,4,5,5,5,6(2) 中位数:7,8,9,10,11,12,13(3) 平均数:15,18,21,22,25,28,302. 下列数据中,哪个是极差?(1) 10,12,14,16,18(2) 5,7,9,11,13,15,17六、平面图形的对称性1. 判断下列图形是否是轴对称图形:(1) 等腰三角形(2) 长方形(3) 正五边形2. 找出下列图形的对称轴:(1) 正方形(2) 等边三角形(3) 半圆七、概率初步1. 计算下列事件的概率:(1) 从一副去掉大小王的扑克牌中随机抽取一张红桃。
有理数加减乘除混合运算50题
有理数加减乘除混合运算题50题一、加法与乘法混合运算1. 2 + 3×4-解析:先算乘法3×4 = 12,再算加法2 + 12 = 14。
2. 5 + (-2)×3-解析:先算乘法(-2)×3 = -6,再算加法5 + (-6)= -1。
3.(-3)+4×2-解析:先算乘法4×2 = 8,再算加法(-3)+8 = 5。
4. 6 + (-1)×(-2)-解析:先算乘法(-1)×(-2)=2,再算加法6 + 2 = 8。
4.(-4)+3×(-2)-解析:先算乘法3×(-2)= -6,再算加法(-4)+(-6)= -10。
二、减法与乘法混合运算1. 8 - 2×3-解析:先算乘法2×3 = 6,再算减法8 - 6 = 2。
2. 7 - (-3)×2-解析:先算乘法(-3)×2 = -6,再算减法7 - (-6)= 13。
-解析:先算乘法4×2 = 8,再算减法(-5)-8 = -13。
4. 9 - (-1)×3-解析:先算乘法(-1)×3 = -3,再算减法9 - (-3)= 12。
4.(-6)-3×(-2)-解析:先算乘法3×(-2)= -6,再算减法(-6)-(-6)= 0。
三、加法与除法混合运算1. 4 + 8÷2-解析:先算除法8÷2 = 4,再算加法4 + 4 = 8。
2. 5 + (-6)÷3-解析:先算除法(-6)÷3 = -2,再算加法5 + (-2)= 3。
3.(-3)+12÷4-解析:先算除法12÷4 = 3,再算加法(-3)+3 = 0。
4. 6 + (-8)÷4-解析:先算除法(-8)÷4 = -2,再算加法6 + (-2)= 4。
七年级上册数学混合计算题
七年级上册数学混合计算题一、有理数混合运算1. 计算:(-2)+3 (-5)解析:根据有理数减法法则,减去一个数等于加上这个数的相反数。
所以-(-5)= + 5。
则原式变为(-2)+3 + 5。
按照从左到右的顺序计算,(-2)+3=1,然后1 + 5=6。
2. 计算:-3×(-4)+(-28)÷7解析:先计算乘除运算。
根据有理数乘法法则,两数相乘,同号得正,异号得负,所以-3×(-4)=12。
根据有理数除法法则,(-28)÷7=4。
最后计算加法:12+(-4)=12 4 = 8。
二、整式加减混合运算1. 化简:3a + 2b 5a b解析:将同类项找出来。
在这个式子中,3a和-5a是同类项,2b和-b是同类项。
合并同类项,3a-5a=(3 5)a=-2a,2b b=(2 1)b = b。
所以化简后的结果为-2a + b。
2. 计算:(2x^2-3x + 1)-(x^2+2x 3)解析:去括号,括号前是正号,去掉括号后各项不变号;括号前是负号,去掉括号后各项变号。
所以原式变为2x^2-3x + 1-x^2-2x + 3。
然后合并同类项,(2x^2-x^2)+(-3x-2x)+(1 + 3)=x^2-5x + 4。
三、一元一次方程与有理数、整式的混合计算1. 已知方程2x+3 = 5x 9,求x的值,并计算x^2-2x + 1的值。
解析:首先解方程2x+3 = 5x 9。
移项,将含有x的项移到等号一边,常数项移到等号另一边,得到2x-5x=-9 3。
合并同类项,-3x=-12。
系数化为1,x = 4。
然后将x = 4代入x^2-2x + 1。
原式=4^2-2×4 + 1先计算指数运算,4^2=16。
再计算乘法运算,2×4 = 8。
最后计算16-8 + 1=9。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
每日一练(一)
姓名_____________
一、计算。
180-(-10)= (-10)+(-1)= (-25)+(-7)= (-13)+5= (45)+(-45)= (-8)+(-9)= 3-5= 3-(-5)= (-3)-5= (-3)-(-5)= 9-(-11)= 0-(-7)= 33-(-27)=
=--)31(21 =+-4
125.2 =-+)43
(41 (-4)×5= (-5)×(-7)= =⨯-)38(-)83( =⨯-421)8( =-⨯)4
5(32 (-15)÷(-3)= (-0.75)÷0.25= 5÷(-51
)=
=-43 =--3)3( =2)54
(
二、计算。
1、)31328()43(-+-⨯-
2、)4()81
()2(163-⨯---÷
3、(-378)÷(-7)÷(-9)
4、(-4)×(-5)×0.25
5、36)18
1
6191(⨯-- 6、4.7-3.4-(-8.5)
7、5.1)21
(7+--
姓名____________
一、计算。
-7+28= 31+( )=-85 ( )-(-21)=37 (-17)+21= (-12)+25= (-28)+37=
-2.5+(51-)= =-5271 =--)3
1
(21
(-8)×1.25= =-⨯-)98()163( =⨯-7
5
314
=-÷)71(215 (-1)÷(-1.5)= =-÷)12(74
二、计算。
1、(-25)+34+156+(-65); 2、(-64)+17+(-23)+68; 3、(-72)-(-37)-(-22)-17; 4、33.1-(-22.9)+(-10.5)
5、(-2.1)×(-2.3)×253;
6、(-0.75)÷45
÷(-0.3);
6、)]4()2[(233---÷
三、1、在下列式子(1)m+5,(2)ab ;(3)a=1,(4)0,(5)π, (6)3(m+n ),(7)3x>5中,是代数式的有__________________。
2、一间教室有2扇门和12扇铝合金窗,已知每扇门的价格为800元,每扇窗的价格为200元。
问:(1)n 间这样的教室的门窗一共需要多少钱? (2)学校有24间教室,那么门窗共需要多少钱?
姓名____________
一、计算(直接写得数)。
1、(–3)+(–9) 2、85+(+15)
3、(–361)+(–33
2) 4、(–3.5)+(–532
)
5、(–45) +(+23)
6、(–1.35)+6.35
7、4
1
2+(–2.25) 8、(–9)+7
9、(–3)–(–5) 10、341–(–14
3
)
11、0–(–7) 12、(–4)×(–9)
13、(–52)×81
14、(–6)×0
15、(–253)×13
5
16、(–18)÷(–9)
17、(–63)÷(7) 18、0÷(–105)
二、计算。
19、3×(–9)+7×(–9) 20、 20–15÷(–5)
21、 [65÷(–21–31)+281
]÷(–18
1)
22、-49 + 2×( -3 )2+ ( -6 ) ÷ ( -9
1
)
23、100×(0.7–103–254+ 0.03) 24、(–11)×52+(–11)×95
3
25、–99 + 100–97 + 98–95 + 96–……+2 26、–1–2–3–4–……–100
姓名______________
1、化简:
(1)(2x-3y)+(5x+4y); (2)(8a-7b)-(4a-5b);
(3)a-(2a+b)+2(a-2b); (4)3(5x+4)-(3x-5);
(5)(8x-3y)-(4x+3y-z)+2z ; (6)-5x 2+(5x-8x 2)-(-12x 2+4x)+2;
(7)2-(1+x)+(1+x+x 2-x 2); (8)3a 2+a 2-(2a 2-2a)+(3a-a 2)。
2、去括号:
(1)a+3(2b+c-d); (2)3x-2(3y+2z).
(3)3a+4b-(2b+4a); (4)(2x-3y)-3(4x-2y).
3、根据去括号法则,在___上填上“+”号或“-”号:
(1) a___(-b+c)=a-b+c ; (2)a___(b-c-d)=a-b+c+d ; (3) ___(a-b)___(c+d)=c+d-a+b 4、已知x+y=2,则x+y+3= ,5-x-y= . 5、 已知:1-x +2-x =3,求{x-[x 2-(1-x)]}-1的值.
姓名___________
1、 化简下列各式:
(1)1310354
2
2
4
-+--+x y x y x x (2)pq p pq p +-++2
2
863
(3))58()37(z y z y --- (4))37()6(5
b b a +----
(5))45(3)92(22
2
b a b a --++ (6))6(4)2(32
2
-++--xy x xy x
2、先化简,再求值: (1))3
2(3692
2
x x x x --+,其中2-=x ; (2))121()824(412---+-x x x ,其中2
1=x ;
(3))35()()35(2
2
2
2
2
2
b a b a b a +-++-;其中1,1=-=b a ;
(4)22)1(2)(22
2
2
2
----+ab b a ab b a ;其中2,2=-=b a .
3、一个窗户的上部是由4个扇形组成的半圆形,下部分是由边长相同的4个小正方形
姓名___________
一、解方程
(1)512=+-x (2)132
1
-=x x
(3)4
5
4346+=+x x (4))35(2)57(15x x x -+=-- (5)612144+=--x x (6)3
8
316.036.13.02+=
--x x x (7)2
1
434121-=-x x (8))3(3)1(2)12(3++-=-y y y (9)
83457=-y (10)16
1
5312=--+x x
二、小芬买15份礼物,共花了900元,已知每份礼物内都有1包饼干及每支售价20元的棒棒糖2支,求每包饼干的售价为多少元?
姓名___________
(1)、2x :3=5:6 (2)、2(x-2)-3(4x-1)=5(1-x) (3)、151423=+--x x (4)、4
1
32131--
=-+x x (5)6.12.045.03=+--x x (6)103
.031.031.02.0=--x x (7)
2
5
03.002.003.05.09.04.0-=
+-+x x x
(8)3(2y-1)=2(1-y)+3(y+3)
(9)8
3
457=-y (10)-7x+2=2x-4
(11)231318=+++x x (12)16
1
5312=--+x x。
