高三数学第六次月考试题及答案理科
2020届湖南省浏阳市第一中学高三上学期第六次月考数学(理)试题含答案
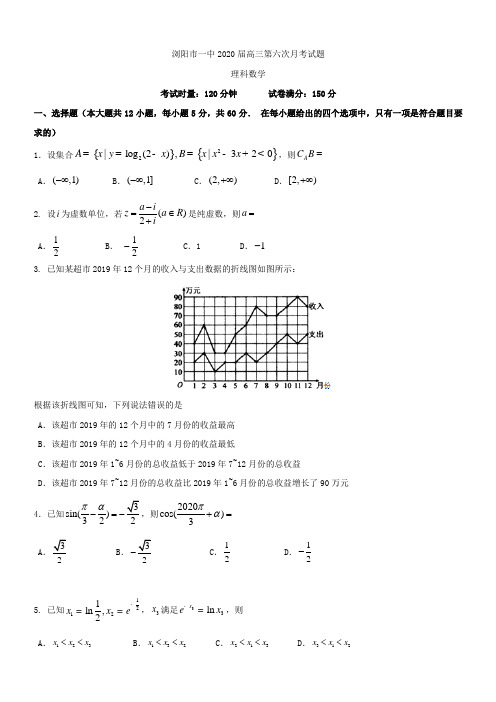
浏阳市一中2020届高三第六次月考试题理科数学考试时量:120分钟 试卷满分:150分一、选择题(本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的) 1.设集合{}{}22|log (2),|320A x y x B x x x ==-=-+<,则A C B =A .(,1)-∞B .(,1]-∞C .(2,)+∞D .[2,)+∞2. 设i 为虚数单位,若()2a iz a R i-=∈+是纯虚数,则a = A .12 B . 12- C .1 D .1- 3. 已知某超市2019年12个月的收入与支出数据的折线图如图所示:根据该折线图可知,下列说法错误的是A .该超市2019年的12个月中的7月份的收益最高B .该超市2019年的12个月中的4月份的收益最低C .该超市2019年1~6月份的总收益低于2019年7~12月份的总收益D .该超市2019年7~12月份的总收益比2019年1~6月份的总收益增长了90万元 4.已知3sin()322πα-=-,则2020cos()3πα+= A .23B .23-C .12D .12-5. 已知12121ln ,2x x e -==,3x 满足33ln x e x -=,则A .123x x x <<B .132x x x <<C .213x x x <<D .312x x x <<6. 函数2()1sin 1xf x x e ⎛⎫=-⎪+⎝⎭图象的大致形状是A B C D7.公元前5世纪,古希腊哲学家芝诺发表了著名的阿基里斯悖论:他提出让乌龟在阿基里斯前面1000米处开始与阿基里斯赛跑,并且假定阿基里斯的速度是乌龟的10倍.当比赛开始后,若阿基里斯跑了1000米,此时乌龟便领先他100米,当阿基里斯跑完下一个100米时,乌龟先他10米,当阿基里斯跑完下一个10米时,乌龟先他1米,……所以,阿基里斯永远追不上乌龟.按照这样的规律,若阿基里斯和乌龟的距离恰好为210-米时,乌龟爬行的总距离为A .410190-米B .5101900-米C .510990-米D .4109900-米8.已知函数()2sin()(0,0),()2,()082f x x f f ππωϕωϕπ=+><<==,且()f x 在(0,)π上单调.则下列说法正确的是 A .12ω=B .62()8f π--=C .函数()f x 在[,]2ππ--上单调递增 D .函数()f x 的图象关于点3(,0)4π对称 9.在AOB ∆中,OA a OB b ==u u u r r u u u r r ,,满足||2a b a b ⋅=-=r r r r,则AOB ∆的面积的最大值为3 B. 2C. 23210.已知双曲线C :22221(0,0)x y a b a b-=>>,12,F F 分别为其左、右焦点,O 为坐标原点,若点2F 关于渐近线的对称点恰好落在以1F 为圆心,1OF 为半径的圆上,则C 的离心率是 A 2B 3C .2D .311. 在正方体1111ABCD A B C D -中,P ,Q 分别为1AD ,1B C 上的动点,且满足1AP B Q =,则下列4个命题中: ①存在P ,Q某一位置,使AB PQ ∥; ②BPQ V 的面积为定值;③当0PA >时,直线1PB 与直线AQ 一定异面;④无论P ,Q 运动到何位置,均有BC PQ ⊥. 其中所有正确命题的序号是A. ①②④B. ①③④C. ①③D. ②④12.若函数12()2log (0)x x f x e x a a -=+->在区间(0,2)内有两个不同的零点,则实数a的取值范围是A. 22,2)eB. (0,2]C. 222,2)e + D. 3424(2,2)e +二、填空题(本大题共4小题,每小题5分,共20分. 把答案填在答题卡中的横线上)13.若25(ax x的展开式中5x 的系数为80-,则实数a =__ __. 14.在菱形ABCD 中,060DAB ∠=,将这个菱形沿对角线BD 折起,使得平面DAB ⊥平 面BDC ,若此时三棱锥A BCD -的外接球的表面积为5π,则AB 的长为 . 15.已知数列{}n a 满足11a =,135n n a a n ++=+,*n N ∈,则(1)21n a -= , (2)2111(1)i i ni i a a +=+-=∑ .16.如图,衡阳市有相交于点O 的一条东西走向的公路l 与一条南北走向的公路m ,有一商城A 的部分边界是椭圆的四分之一,这两条公路为椭圆的对称轴,椭圆的长半轴长为2,短半轴长为1(单位:千米). 根据市民建议,欲新建一条公路PQ ,点,P Q 分别在公路,l m 上,且要求PQ 与椭圆形商城A 相切,当公路PQ 长最短时,OQ 的长为________千米.lm QO三、解答题(本大题共6小题,共70分. 解答应写出文字说明,证明过程或演算步骤) (一)必考题:60分.17.(本小题满分12分) 已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且tan (sin 2cos )cos 2222A C A Ca b a +=. (1)求角B 的值;(2)若△ABC 的面积为33D 为边AC 的中点,求线段BD 长的最小值.18.(本小题满分12分) 已知正方形ABCD ,E ,F 分别为AB ,CD 的中点,将△ADE 沿DE 折起,使△ACD 为等边三角形,如图所示,记二面角A-DE-C 的大小为(0)θθπ<<. (1)证明:点A 在平面BCDE 内的射影G 在直线EF 上; (2)求角θ的正弦值.C BEFE19.(本小题满分12分) 如图,已知椭圆2222:1(0)x y C a b a b+=>>的长轴12A A 长为4,过椭圆的右焦点为F作斜率为(0)k k ¹的直线交椭圆于B ,C 两点,直线12,BA BA 的斜率之积为34-. (1)求椭圆C 的方程;(2)已知直线:4l x =,直线11,A B A C 分别与l 相交于,M N 两点,设E 为线段MN 的中点,求证:BC EF ^20.(本小题满分12分)已知函数()e sin )(2()2xf x x a R ax π=--∈+.(1)当1a =时,求函数()f x 在区间[,]ππ-上的值域; (2)对于任意120x x π<<<,都有2121()()22x x f x f x a e e π->---,求实数a 的取值范围.21. (本小题满分12分) 随着科学技术的飞速发展,网络也已经逐渐融入了人们的日常生活,网购作为一种新的消费方式,因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可.某网购公司统计了近五年在本公司网购的人数,得到如下的相关数据(其中“x =1”表示2015年,“x =2”表示2016年,依次类推; y 表示人数):x 1 2 3 4 5 y (万人)2050100150180(1)试根据表中的数据,求出y 关于x 的线性回归方程,并预测到哪一年该公司的网购人数能超过300万人; (2)该公司为了吸引网购者,特别推出“玩网络游戏,送免费购物券”活动,网购者可根据抛掷骰子的结果,操控微型遥控车在方格图上行进. 若遥控车最终停在“胜利大本营”,则网购者可获得免费购物券500元;若遥控车OMNlCA 2A 1EyxFB最终停在“失败大本营”,则网购者可获得免费购物券200元. 已知骰子出现奇数与偶数的概率都是12,方格图上标有第0格、第1格、第2格、…、第20格。
四川省绵阳市三台县芦溪中学高三数学上学期第六次月考试题 理

芦溪中学2012届高三上学期第六次月考数学理科试题班级:高2012级 班 姓名: 得分: 命题:陈新宇本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.全卷满分为150分,完成时间120分钟. 参考公式:如果事件A 、B 互斥,那么P A B P A P B ++()=()() 如果事件A 、B 独立,那么P A B P A P B ⋅⋅()=()()如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k 次的概率-1k k n kn nP k C P P -()=() 第I 卷(选择题,共60分) 一、选择题:本大题共12小题,每小题5分,共60分. 1.计算212sin8π-的值为A .lB .12CD2.已知a 、b ∈R,i 为虚数单位,若bi a ii+=+12,则a +b 的值为A .0B .1C .2D .33.设}{|01A x x =<<,}{|1B x x =<,则“x A ∈”是“x B ∈”的 A .充分而不必要的条件 B .必要而不充分条件C .充要条件D .既不充分也不必要的条件 4.)(212lim *1N n nn n ∈++∞→的结果为A .1B .2C .3D .不存在5.设等比数列{}n a 的公比2q =,前n 项和为n S ,则42S a =( ) A. 2 B. 4 C.152D.1726.若非零向量||||=+满足与,则△ABC 的形状是A .等边三角形B .等腰三角形C .直角三角形D .等腰直角三角形7.若函数y g =(x )与21y x =+0x ≤()互为反函数,则函数y g x =(-)大致图象为8.已知a ,b 是非零向量,且,3a b π<>=,则向量||||a bp a b =+的模为 A.2 D .39.已知变量x 、y 满足条件1,0,290,x x y x y ≥⎧⎪-≤⎨⎪+-≤⎩则x+y 的最大值是A.2B.5C.6D.810.已知定义在R 上的函数)(),(x g x f 分别满足:)()(,0)1()1(x g x g x f x f =-=-++,则下列函数中,一定为奇函数的是 A .)()(x g x f y ⋅= B .)()1(x g x f y ⋅+=C .)()1(x g x f y ⋅-=D .)1()(-⋅=x g x f y11.为了得到函数y =sin(2x -6π)的图像,可以将函数y =cos2x 的图像 A .向右平移6π个单位长度 B .向左平移3π个单位长度C .向左平移6π个单位长度D .向右平移3π个单位长度12.设在四次独立重复试验中,事件A 至少发生一次的概率为8180,则在一次试验中事件A 发生的概率是A . 56B . 12C . 13D .32第Ⅱ卷(非选择题,共90分)二、填空题:(本大题共4小题,每小题4分,共16分)把答案填在题中横线上.13.已知数列{}n a 的通项公式为211n a n =-+,其前n 项的和为n S ()n N *∈,则当n S 取最大值时,n = .14.设直线30ax y -+=与圆22(1)(2)4x y -+-=相交于A 、B 两点,且弦AB的长为a =___________.15.设向量a 与b 的夹角为θ,且)3,3(=a,)1,1(2-=-a b ,则=θcos .16.已知a R ∈,且2k παπ≠+,k Z ∈设直线:tan l y x m α=+,其中0m ≠,给出下列结论:①l 的倾斜角为arctan(tan )α;②l 的方向向量与向量(cos ,sin )a αα=共线;③l与直线sin cos 0x y n αα-+=()n m ≠一定平行;④若04a π<<,则l 与y x =直线的夹角为4πα-;⑤若4k παπ≠+,k Z ∈,与l 关于直线y x =对称的直线l '与l 互相垂直.其中真命题的编号是 (写出所有真命题的编号)三、解答题:(本大题共6小题,共74分)解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知点A 、B 、C 的坐标分别为A (3,0),B (0,3),C (cos α,sin α),α∈(23,2ππ).(1)若||||AC CB =,求角α的值; (2)若AC CB ⋅=-1,求a aa tan 12sin sin 22++的值.18.(本小题满分12分)设平面直角坐标系xoy 中,设二次函数)(2)(2R x b x x x f ∈++=的图像与两坐标轴有三个交点,经过这三个交点的圆记为C .求: (1)求实数b 的取值范围; (2)求圆C 的方程;(3)问圆C 是否经过某定点(其坐标与b 无关)?请证明你的结论.19.(本小题满分12分)设函数23)(3++-=x x x f 分别在1x 、2x 处取得极小值、极大值.xoy 平面上点A 、B 的坐标分别为))(,(11x f x 、))(,(22x f x ,该平面上动点P 满足4=∙,点Q 是点P 关于直线)4(2-=x y 的对称点.求:(Ⅰ)点A 、B 的坐标 ;(Ⅱ)动点Q 的轨迹方程.20.(本小题满分12分)某单位有三辆汽车参加某种事故保险,单位年初向保险公司缴纳每辆900元的保险金.对在一年内发生此种事故的每辆汽车,单位获9000元的赔偿(假设每辆车最多只赔偿一次).设这三辆车在一年内发生此种事故的概率分别为111,,,91011且各车是否发生事故相互独立,求一年内该单位在此保险中: (1)获赔的概率;(4分)(2)获赔金额ξ的分别列与期望.(8分)21.(本小题满分12分)已知定义在R 上的奇函数24()1x bf x ax +=+的导函数为()f x ',且()f x '在点1x =处取得极值. (1)求函数()f x 的解析式;(2)若函数()f x 在区间(,2)m m +上是增函数,求实数m 所有取值的集合; (3)当12,x x R ∈时,求12()()f x f x ''-的最大值.22.(本小题满分14分)已知各项均为正数的数列{}n a 满足:12323(1),3n n na a a na a a n N n *+++++=∈,(1)求1a 、2a 、3a ,猜测n a 的表达式并证明;(2)求证:sin n a π≥2na ;(3)设数列1sin n n a a π+⎧⎫⎨⎬⎩⎭的前n 项和为n S ,求证:132n S π<<.四川省绵阳市三台县芦溪中学2012级高三上期末考试数学(理)模拟试题综合练习参考答案一、选择题:1—5DCABC 6—10CDBCB 11—12CD 二、填空题: 13.5;14.0;15; 16.②④ 三、解答题:17.解:.(1)∵AC =(cos α-3, sin α), BC =(cos α, sin α-3).∴∣AC ∣=a a a sin 610sin )3(cos 22-=+-.∣BC ∣=a a a sin 610)3sin (cos 22-=-+.由∣AC ∣=∣BC ∣得sin α=cos α.又∵α)23,2(ππ∈,∴α=45π. (2)由AC ·BC =-1,得(cos α-3)cos α+sin α (sin α-3)=-1∵sin α+cos α=32.①又a a aaa a aa a cos sin 2cos 1cos sin 2sin 2tan 12sin sin 222=++=++. 由①式两边平方得1+2sin αcos α=94 , ∴2sin αcos α=95-,∴95tan 12sin sin 22-=++a a a 18.解:(Ⅰ)令x =0,得抛物线与y 轴交点是(0,b );令()220f x x x b =++=,由题意b ≠0 且Δ>0,解得b <1 且b ≠0. (Ⅱ)设所求圆的一般方程为2x 20y Dx Ey F ++++=,令y =0 得20x Dx F ++=这与22x x b ++=0 是同一个方程,故D =2,F =b . 令x =0 得2y Ey +=0,此方程有一个根为b ,代入得出E =―b ―1. 所以圆C 的方程为222(1)0x y x b y b ++-++=.(Ⅲ)圆C 必过定点(0,1)和(-2,1).证明如下:将(0,1)代入圆C 的方程,得左边=02+12+2×0-(b +1)+b =0,右边=0, 所以圆C 必过定点(0,1).同理可证圆C 必过定点(-2,1).19.解: (Ⅰ)令033)23()(23=+-='++-='x x x x f 解得11-==x x 或 当1-<x 时,0)(<'x f , 当11<<-x 时,0)(>'x f ,当1>x 时,0)(<'x f 所以,函数在1-=x 处取得极小值,在1=x 取得极大值,故 1,121=-=x x ,4)1(,0)1(==-f f 所以, 点A 、B 的坐标为)4,1(),0,1(B A -.(Ⅱ) 设),(n m p ,),(y x Q ,()()4414,1,122=-+-=--∙---=∙n n m n m n m21-=PQ k ,所以21-=--m x n y ,又PQ 的中点在)4(2-=x y 上,所以⎪⎭⎫⎝⎛-+=+4222n x m y消去n m ,得()()92822=++-y x20.解:设k A 表示第k 辆车在一年内发生此种事故,123k =,,.由题意知1A ,2A ,3A 独立,且11()9P A =,21()10P A =,31()11P A =. (Ⅰ)该单位一年内获赔的概率为123123891031()1()()()19101111P A A A P A P A P A -=-=-⨯⨯=.(Ⅱ)ξ的所有可能值为0,9000,18000,27000.12312389108(0)()()()()9101111P P A A A P A P A P A ξ====⨯⨯=,123123123(9000)()()()P P A A A P A A A P A A A ξ==++ 123123123()()()()()()()()()P A P A P A P A P A P A P A P A P A =++19108110891910119101191011=⨯⨯+⨯⨯+⨯⨯2421199045==, 123123123(18000)()()()P P A A A P A A A P A A A ξ==++ 123123123()()()()()()()()()P A P A P A P A P A P A P A P A P A =++1110191811910119101191011=⨯⨯+⨯⨯+⨯⨯273990110==, 123123(27000)()()()()P P A A A P A P A P A ξ===111191011990=⨯⨯=. 综上知,ξ的分布列为求ξ的期望有两种解法:解法一:由ξ的分布列得811310900018000270001145110990E ξ=⨯+⨯+⨯+⨯ 299002718.1811=≈(元). 解法二:设k ξ表示第k 辆车一年内的获赔金额,123k =,,,则1ξ有分布列故1900010009E ξ=⨯=. 同理得21900090010E ξ=⨯=,319000818.1811E ξ=⨯≈. 综上有1231000900818.182718.18E E E E ξξξξ=++≈++=(元).21.解:(1)14)(2++=ax bx x f 是奇函数,易求得b =0.又)(,)1(24)1(4)(222x f ax axx ax x f 且+⋅-+='在点x =1处取得极值, 24()0. 1.().1xf x a f x x '∴===+可得故 (2).110)(,)1()1)(1(4)(22<<-⇒>'++--='x x f x x x x f 由 )(x f ∴的单调递增区间为(-1,1).若)(x f 在区间(m ,m +2)上是增函数,则有m =-1.即m 取值的集合为{-1}.(3)]11)1(2[4)1()1)(1(4)(22222+-+=++--='x x x x x x f ,令].1,0(,21)41(8)2(4)()(,11222∈--=-=='+=t t t t t g x f x t 则12119()[,4].()()4().222f x f x f x '''∴∈-∴-≤--=)()(21x f x f '-'∴的最大值为29.22.解:(1).4,3,2321===a a a 猜测:.1+=n a n①当n =1时,a 1=1+1=2,猜想成立.②假设当n =k 时成立,即a k =k +1.).(2)1()1(0)2(23)1(3)1)(1()1(,1.3)1)(1(3)1(,),2(3)1)(1()1(32.3)1(323)1(321122112111111111321321321舍去时则当得两式相减k a k a k a k k a a a a k a a k a k k n a a n a a n na n a a n a n a a a a a n na a a a a a n na a a a k k k k k k k k k k n n n n n n n n nn n n n n -=+=⇒+=-⇒=+--⇒+-++=++=+--+=≥+-=-++++∴+=++++∴+=++++++++++++-----即当n =k +1时,猜想成立.故对一切1,*+=∈n a N n n 成立.(2)设)20(2sin )(ππ≤<-=x x x x f ,由.2arccos ,02cos )(ππ==-='x x x f 得由]2,0()(,cos π在知的单调性x f x y =内有且只有一个极大值点,且.0)2()0(==πf f 因此在]2,0(π内,).20(2sin ,0)(ππ≤<>>x x x x f 即22,(0,],sin.1,,sin .22nnnn n n nx n a a a a a a a πππππππ=∈∴>==∴=令又当时.2.sinnna a ≥∴π(3)).2,0(,611ππ∈∴≥++n n n n a a a a 由(2)可知.2sin11++>n n n n a a a a π.31)2121()211141313121(2)2()1(sin43sin32sin≥+-=+-+++-+->+⋅+++⋅+⋅=∴n n n n n S n πππ.31,*>∈n S N n 即对一切 同理可证).20(sin π<<<x x x.2)2121()211141313121()2()1(sin43sin32sinππππππ<+-=+-+++-+-<+⋅+++⋅+⋅=∴n n n n n S n.2,*π<∈n S N n 即对一切 .231π<<∴n S。
贵州师大附中2010届高三第六次月考数学试题(理科)答案

3cos 05B =>20tan 3a B =3cos 5B =4sin 5B =4tan 3B =1sin 2S acB =贵州师大附中2009——2010学年第一学期期末考试高三数学 理科参考答案13、3 14、6 15、32316、a17、【解】(I )由sin 4b A =得4sin =B a ,由320tan =B a 与4sin =B a 两式相除,有: , 又通过 知:0tan >B ,………………….3分则由 , ,得 则5a =.……………………….5分 (II )由 ,得到5c =.C A =∴…………………………….7分 由2571)53(21cos 21)(cos 212cos 24cos 2222-=-⨯=-=-+=-=B C A C C …0分18、【解】(I )证明:在PBC V 中,1,BC PC PB ===222BC PC PB \+=90PCB\?o,即PC BC^, ---------------------------1分,AB PC AB BC B^=Q I ,PC \^平面ABCD . ---------------------------4分(II )解:设点B 到平面P AD 的距离为h ,A B B C^Q ,AC \=PC ^Q 平面ABCD ,PC AC\^,PA \=在直角梯形ABCD 中,1,1,2AB BC CD ===, AD \=在PAD V 中,AD =QPA PD ==\222A D P A P D+=, 90PAD\?o,PAD \V 的面积122P A D S A D P A=?V ----------------8分Q 三棱锥B -P AD 的体积B PADP ABDV V --=,13PAD S h \鬃V 13ABD S PC=鬃V ,-------------10分即1(11)122h创 ,解得6h =, \点B 到平面P AD 的距离为6.---------12分19、【解】(I ))2(2,2)1(11≥=-+=--++n a a n a a n na n n n n nn a a a a s a a n n 2}{,2,2,212121==-∴+==等差所以………………………6分 (II )121223221,2222--++++===n n n nnn n T n n a112224,21)2(221221222121--+-=+-=+-+++=n n nn nn n n T n T n n T …………………………………12分20、【解】(I )从10道不同的题目中不放回的随机抽取三次,每次只抽取1道题,抽法总数为1819110C C C ,只有第一次抽到艺术类题目的抽法总数为131416C C C 1116431111098110C C C P C C C ∴==…………………………………………………………………(4分)(II )抽到体育类题目数的可能取值为0,1,2则157)0(1819110161718===CC C C C C P ξ157)1(181911017181213===C C C C C C C P ξ 151)2(1819110121318===C C C C C C P ξ…………………(8分)所以ξ的分布列为:…………………………………………………………(10分)从而有53151215711570=⨯+⨯+⨯=ξE ………………………………………(12分)21、【解】(I )()02≥-='x a x x f 在(]2,1∈x 恒成立,所以22x a ≤,2≤∴a .又()021≤-='xa x g 在()1,0∈x 恒成立,所以 x a 2≥,2≥∴a .……………4分从而有2=a .故()x x x f ln 22-=,()x x x g 2-=. …………………………6分 (II )令2)()()(--=x g x f x F ,则xx x x F 1122)('+--=xx x x x x )222)(1(+++-=所以()x F 在()1,0上是减函数,在()+∞,1上是增函数,……………………………9分 从而当0>x 时,()()01min ==F x F ,所以方程2)()(+=x g x f 在()+∞,0只有一个解1=x . ……………………12分22、【解】(I )设C :y 2a 2+x 2b 2=1(a >b >0),设c >0,c 2=a 2-b 2,由条件知a-c =22,ca =22,∴a =1,b =c =22,故C 的方程为:y 2+x 212=1 …………………………4分(II )由AP =λPB 得OP -OA =λ(OB -OP ),(1+λ)OP =OA +λOB , ∴λ+1=4,λ=3 ………………………………………………6分 设l 与椭圆C 交点为A (x 1,y 1),B (x 2,y 2) ⎩⎨⎧y =kx +m 2x 2+y 2=1得(k 2+2)x 2+2kmx +(m 2-1)=0 Δ=(2km )2-4(k 2+2)(m 2-1)=4(k 2-2m 2+2)>0 (*)x 1+x 2=-2km k 2+2, x 1x 2=m 2-1k 2+2 ………………………………………………8分∵AP =3PB ∴-x 1=3x 2 ∴⎩⎨⎧x 1+x 2=-2x 2x 1x 2=-3x 22消去x 2,得3(x 1+x 2)2+4x 1x 2=0,∴3(-2km k 2+2)2+4m 2-1k 2+2=0整理得4k 2m 2+2m 2-k 2-2=0 ………………………………………………10分 m 2=14时,上式不成立;m 2≠14时,k 2=2-2m 24m 2-1,因λ=3 ∴k ≠0 ∴k 2=2-2m 24m 2-1>0,∴-1<m <-12 或 12<m <1容易验证k 2>2m 2-2成立,所以(*)成立即所求m 的取值范围为(-1,-12)∪(12,1) ………………………12分.。
河北省重点中学2024年高三第6次月考数学试题

河北省重点中学2024年高三第6次月考数学试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置. 3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效. 5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设等差数列{}n a 的前n 项和为n S ,若495,81a S ==,则10a =( ) A .23B .25C .28D .292.已知双曲线()2222:10,0x y C a b a b-=>>的左,右焦点分别为12,F F ,O 为坐标原点,P 为双曲线在第一象限上的点,直线PO ,2PF 分别交双曲线C 的左,右支于另一点12,,3M N PF PF =若,且260MF N ∠=,则双曲线的离心率为( ) A .52B .3C .2D .723. “幻方”最早记载于我国公元前500年的春秋时期《大戴礼》中.“n 阶幻方()*3,n n ≥∈N ”是由前2n 个正整数组成的—个n 阶方阵,其各行各列及两条对角线所含的n 个数之和(简称幻和)相等,例如“3阶幻方”的幻和为15(如图所示).则“5阶幻方”的幻和为( )A .75B .65C .55D .454.将函数()32cos 2f x x x =-向左平移6π个单位,得到()g x 的图象,则()g x 满足( )A .图象关于点,012π⎛⎫⎪⎝⎭对称,在区间0,4π⎛⎫ ⎪⎝⎭上为增函数 B .函数最大值为2,图象关于点,03π⎛⎫⎪⎝⎭对称C .图象关于直线6x π=对称,在,123ππ⎡⎤⎢⎥⎣⎦上的最小值为1 D .最小正周期为π,()1g x =在0,4⎡⎤⎢⎥⎣⎦π有两个根 5.已知定点1(4,0)F -,2(4,0)F ,N 是圆22:4O x y +=上的任意一点,点1F 关于点N 的对称点为M ,线段1F M 的垂直平分线与直线2F M 相交于点P ,则点P 的轨迹是( ) A .椭圆B .双曲线C .抛物线D .圆6.函数cos 1ln(),1,(),1x x x f x xex π⎧->⎪=⎨⎪≤⎩的图象大致是( ) A . B .C .D .7.根据党中央关于“精准”脱贫的要求,我市某农业经济部门派四位专家对三个县区进行调研,每个县区至少派一位专家,则甲,乙两位专家派遣至同一县区的概率为( ) A .16B .14C .13D .128.若函数()2xf x e mx =-有且只有4个不同的零点,则实数m 的取值范围是( )A .2,4e ⎡⎫+∞⎪⎢⎣⎭B .2,4e ⎛⎫+∞ ⎪⎝⎭C .2,4e ⎛⎫-∞ ⎪⎝⎭D .2,4e ⎛⎤-∞ ⎥⎝⎦9.已知复数()11z ai a R =+∈,212z i =+(i 为虚数单位),若12z z 为纯虚数,则a =( )A .2-B .2C .12-D .1210.若0,0ab >>,则“4a b +≤”是 “4ab ≤”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件11.已知函数()()sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭,1,03A ⎛⎫ ⎪⎝⎭为()f x 图象的对称中心,若图象上相邻两个极值点1x ,2x 满足121x x -=,则下列区间中存在极值点的是( ) A .,06π⎛⎫-⎪⎝⎭B .10,2⎛⎫ ⎪⎝⎭C .1,3π⎛⎫⎪⎝⎭D .,32ππ⎛⎫ ⎪⎝⎭12.已知双曲线22221(0,0)x y a b a b-=>>的左右焦点分别为1(,0)F c -,2(,0)F c ,以线段12F F 为直径的圆与双曲线在第二象限的交点为P ,若直线2PF 与圆222:216⎛⎫-+= ⎪⎝⎭c b E x y 相切,则双曲线的渐近线方程是( )A .y x =±B .2y x =±C . 3y x =±D .2y x =±二、填空题:本题共4小题,每小题5分,共20分。
2019-2020学年云南师大附中高三(下)月考数学试卷(理科)(含答案)

2019-2020学年云南师大附中高三(下)月考数学试卷(理科)(六)一、选择题.1.(5分)已知集合2{|log 1}A x x =<,集合{|||2}B x N x =∈<,则(A B = )A .{|01}x x <<B .{|02}x x <C .{|22}x x -<<D .{0,1}2.(5分)已知i 为虚数单位,则复数3(1)(1)(i i --= )A .2iB .2i -C .2D .2-3.(5分)已知平面向量a ,b 的夹角为30︒,||1a =,1()2a a b -=-,则||(b = )AB .2C .3D .44.(5分)已知实数x ,y 满足约束条件()1221x y x y y +⎧⎪-⎨⎪⎩,则yx 的最大值为( )A .2B .32C .1D .235.(5分)在区间(0,3)上随机地取一个数k ,则事件“直线y kx =与双曲线22:1C x y -=有两个不同的交点“发生的概率为( ) A .13B .12C .23D .16.(5分)已知3(21)()x x a -+展开式中各项系数之和为27,则其展开式中2x 项的系数为( )A .24B .18C .12D .47.(5分)ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c,若sin A =,a =,c a >,则角C 的大小为( )A .3πB .2πC .23πD .34π8.(5分)在下面四个三棱柱中,A ,B 为三棱柱的两个顶点,E ,F ,G 为所在棱的中点,则在这四个三棱柱中,直线AB 与平面EFG 不平行的是( )A .B .C .D .9.(5分)已知椭圆2222:1(0)x y C a b a b +=>>与抛物线2:2(0)E y px p =>有公共焦点F ,椭圆C 与抛物线E 交于A ,B 两点,且A ,B ,F 三点共线,则椭圆C 的离心率为( )A 21B .22C .3D .51-10.(5分)已知数列{}n a 满足:对*n N ∀∈,1log (2)n n a n +=+,设n T 为数列{}n a 的前n 项之积,则下列说法错误的是( ) A .12a a >B .17a a >C .63T =D .76T T <11.(5分)数学家托勒密从公元127年到151年在亚历山大城从事天文观测,在编制三角函数表过程中发现了很多重要的定理和结论,如图便是托勒密推导倍角公式“2cos212sin αα=-”所用的几何图形。
贵州师大附中2010届高三第六次月考数学(理科)试题

贵州师大附中2009—2010学年第一学期期末考试试卷高 三 数 学 (理科) 2010-01-29考生注意:1.本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分;2.请将答案填(涂)在答题卡的相应位置上,在试卷上作答一律无效;3.考试时间120分钟,满分150分.第Ⅰ卷(选择题 共60分)一、单项选择题(每小题5分,共60分) 1.52i i+=A .2i +B .12i +C .2i -+D .12i -+2.设集合{|32}M m m =∈-<<Z ,{|13}N n n M N =∈-=Z 则,≤≤A .{}01,B .{}101-,, C .{}012,, D .{}1012-,,, 3.()2tan cot cos x x x +=A .tan xB .sin xC .cos xD .cot x 4.若曲线4y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为 A .430x y -+= B .450x y +-= C .430x y --= D .430x y ++=5.对于不重合的两个平面βα,,给定下列条件: ①存在直线l ,使得βα⊥⊥l l ,; ②存在 平面γ,使γβγα⊥⊥,; ③α内有不共线三点到β的距离相等; ④存在异面直线βαβα//,//,//,//,,m m l l m l 使.其中可以确定βα//的有A .4个B .3个C .2个D .1个6.若13(1)ln 2ln ln x e a x b x c x -∈===,,,,,则 A .a <b <c B .c <a <b C .b <a <c D .b <c <a7.已知向量a =,b是不平行于x 轴的单位向量,且3=⋅b a,则b =A .(122) B .(1,22C .(13,44) D .(1,0)8.若将函数()tan 04y x πωω⎛⎫=+> ⎪⎝⎭的图像向右平移6π个单位长度后,与函数tan 6y x πω⎛⎫=+ ⎪⎝⎭的图像重合,则ω的最小值为A .12B .13C .14D .169.若动圆222()()1x a y b b -+-=+始终平分定圆222270x y x y +++-=的周长,则动点 P (a ,b )的轨迹曲线是 A .圆B .椭圆C .双曲线D .抛物线10.在某次数学测验中,学号)4,3,2,1(=i i 的四位同学的考试成绩}98,96,93,92,90{)(∈i f ,且满足)4()3()2()1(f f f f <<<,则这四位同学的考试成绩的所有可能情况的种数为A .5种B .9种C .10种D .15种11.双曲线122=-y x 的左右焦点分别是21,F F ,点()() ,3,2,1,=n y x P n n n 在其右支上,且满足2121121,F F F P F P F P n n ⊥=+,则2010x 的值是A .B .2009C .D .201012.某种游戏中,黑、黄两个“电子狗”从棱长为1的正方体ABCD -A 1B 1C 1D 1的顶点A 出发沿棱向前爬行,每爬完一条棱称为“爬完一段”. 黑“电子狗”爬行的路线是111AA A D →→,黄“电子狗”爬行的路线是1AB BB →→ ,它们都遵循如下规则:所爬行的第i +2段与第i 段所在直线必须是异面直线(其中i 是正整数). 设黑“电子狗”爬完2010段、黄“电子狗”爬完2009段后各自停止在正方体的某个顶点处,这时黑、黄“电子狗”间的距离是A . 0B .1C .D .第Ⅱ卷(非选择题 共90分)二、填空题:(每小题5分,共20分) 13.在等差数列}{n a 中,2365-==a a ,,则=+++843a a a __________.14.(4-的展开式中33x y 的系数为 .15.一个球的球心到过球面上A 、B 、C 三点的截面的距离等于球半径的一半,若AB =BC =CA =3,则球的体积为 . 16.已知AB 是椭圆)0(12222>>=+b a by ax 的长轴,若把该长轴n 等分,过每个等分点作AB 的垂线,依次交椭圆的上半部分于点121,,,n P P P - ,设左焦点为1F ,则1111111()lim n n F A F P F P F B n-→∞++++ =.三、解答题:(解答应写出文字说明、证明过程或演算步骤). 17.设A B C △的内角A B C ,,所对的边长分别为a b c ,,,且320tan =B a ,sin 4b A =.(I )求B cos 和边长a ;(II )若A B C △的面积10S =,求C 4cos 的值.18.如图,在四棱锥P-ABCD 中,底面ABCD 是直角梯形,90,//,B C D A B C D ?o又1,2,AB BC PC PB CD AB PC =====^.(I )求证:P C ^平面A B C D ; (II )求点B 到平面PAD 的距离.A BD CP19.已知数列{a n }的前n 项和为S n ,并且满足a 1=2,n a n +1=S n +n(n +1). (I )求数列{a n }的通项公式a n ; (II )设n T 为数列2n n a ⎧⎫⎨⎬⎩⎭的前n 项和,求n T .20.某次演唱比赛,需要加试综合素质测试,每位参赛选手需回答三个问题,组委会为每位选手都备有10道不同的题目可供选择,其中有6道艺术类题目,2道文学类题目,2道体育类题目.测试时,每位选手从给定的10道题中不放回地随机抽取三次,每次抽取一道题,回答完该题后,再抽取下一道题目作答.(I )求某选手在三次抽取中,只有第一次抽到的是艺术类题目的概率; (II )求某选手抽到体育类题目数ξ的分布列和数学期望ξE .21.已知函数()2ln f x x a x =-在区间(1,2 ]上是增函数,()g x x =-在区间(0,1)上为减函数.(I )试求函数()(),f x g x 的解析式;(II )当 x >0时,讨论方程()()2f x g x =+解的个数.22.椭圆C 的中心为坐标原点O ,焦点在y 轴上,离心率e =22,椭圆上的点到焦点的最短距离为1-e , 直线l 与y 轴交于点P (0,m ),与椭圆C 交于相异两点A 、B ,且AP PB λ=.(I )求椭圆方程;(II )若4OA OB OP λ+=,求m 的取值范围.。
届高三理科数学六大专题训练题含详解

届高三理科数学六大专题训练题含详解IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】高三数学(理科)专题训练一《三角函数、三角恒等变换与解三角形》一、选择题1.α为三角形的一个内角,,125tan -=α则=αcos ()A .1312-B .135-C .135D .13122.函数x y sin =和函数x y cos =都是增函数的区间是()A .)](22,232[Z k k k ∈++ππππB.)](232,2[Z k k k ∈++ππππC .)](22,2[Z k k k ∈+πππD .)](2,22[Z k k k ∈++ππππ3.已知,51)25sin(=+απ那么=αcos ()A .52-B .51-C .51D .524.在图中,A 、B 是单位圆O 上的点,C 是圆与x 轴正半轴的交点,A点的坐标为),54,53(且AOB ∆是正三角形.则COB ∠cos 的值为()A .10334+B .10334- C .10343+D .10343-5.将函数)(sin cos 3R x x x y ∈+=的图象向左平移)0(>m m 个长度单位后,所得到的图象关于y 轴对称,则m 的最小值是() A .12πB .6πC .3πD .65π6.下列关系式中正确的是() A .︒<︒<︒168sin 10cos 11sin B .︒<︒<︒10cos 11sin 168sinC .︒<︒<︒10cos 168sin 11sinD .︒<︒<︒11sin 10cos 168sin7.在锐角ABC ∆中,角A ,B 所对的边长分别为b a ,.若,3sin 2b B a =则角A 等于()A .3πB .4πC .6πD .12π8.已知函数),,0,0)(cos()(R A x A x f ∈>>+=ϕωϕω则“)(x f 是奇函数”是“=ϕ2π”的()A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 二、填空题9.已知扇形AOB 的周长是6cm ,该扇形中心角是1弧度,则该扇形面积是____.10.设,sin 2sin αα-=),,2(ππα∈则α2tan 的值是________. 11.在锐角ABC ∆中,,1=BC ,2A B ∠=∠则AACcos 的值等于___,AC 的取值范围为___. 12.函数)cos(sin 2)2sin()(ϕϕϕ+-+=x x x f 的最大值为________. 三、解答题 13.已知函数)22,0)(sin(3)(πϕπωϕω<≤->+=x x f 的图象关于直线3π=x 对称,且图象上相邻两个最高点的距离为.π(1)求ω和ϕ的值;(2)若),326(43)2(παπα<<=f 求)23cos(πα+的值.14.已知向量),21,(cos -=x a ),2cos ,sin 3(x x b =,R x ∈设函数.)(b a x f ⋅=(1)求)(x f 的最小正周期; (2)求)(x f 在]2,0[π上的最大值和最小值.15.已知函数,),4sin()(R x x A x f ∈+=π且.23)125(=πf (1)求A 的值;(2)若),2,0(,23)()(πθθθ∈=-+f f 求).43(θπ-f16.已知函数,2cos 21cos sin 3)(x x x x f ωωω-=,0>ω,R x ∈且函数)(x f 的最小正周期为.π(1)求ω的值和函数)(x f 的单调增区间;(2)在ABC ∆中,角C B A ,,所对的边分别是,,,c b a 又,54)32(=+πA f ,2=b ABC ∆的面积等于3,求边长a 的值. 17.已知函数⋅+=2cos 34cos 4sin 2)(xx x x f(1)求函数)(x f 的最小正周期及最值;(2)令),3()(π+=x f x g 判断函数)(x g 的奇偶性,并说明理由. 18.在ABC ∆中,内角C B A 、、所对的边分别为.c b a 、、已知,3,==/c b a(1)求角C 的大小;(2)若,54sin =A 求ABC ∆的面积.高三数学(理科)专题训练二数列一、选择题1.数列,,11,22,5,2 的一个通项公式是()A .33-=n a nB .13-=n a n C .13+=n a n D .33+=n a n 2.已知等差数列}{n a 中,,1,16497==+a a a 则12a 的值是() A .15B .30C .31D .64 3.等比数列}{n a 中,,20,647391=+=a a a a 则11a 的值是()A .1B .64C .1或64D .1或324.ABC ∆的三边c b a ,,既成等差数列又成等比数列,则此三角形是()A .等腰三角形B .直角三角形C .等腰直角三角形D .等边三角形 5.已知数列}{n a 满足),2(11≥-=-+n a a a n n n ,3,121==a a 记,321n n a a a a S ++++= 则下列结论正确的是()A .2,120142014=-=S aB .5,320142014=-=S aC .2,320142014=-=S aD .5,120142014=-=S a6.如果在等差数列}{n a 中,,12543=++a a a 那么=+++721a a a ()A .14B .21C .28D .357.数列}{n a 中,,,10987,654,32,14321 +++=++=+==a a a a 那么=10a ()A .495B .505C .550D .5958.各项均为实数的等比数列}{n a 的前n 项和为,n S 若,1010=S ,7030=S 则=40S ()A .150B .200-C .150或200-D .400或50- 二、填空题9.在等差数列}{n a 中,,8,12543531=-=++a a a a a a 则通项=n a ________.10.设等比数列}{n a 的前n 项和为,n S 若,336=S S 则=69S S________.11.设平面内有n 条直线),2(≥n 其中任意两条直线都相交且交点不同;若用)(n f 表示这n 条直线把平面分成的区域个数,则=)2(f ______,=)3(f ______,=)4(f ______.当4>n 时,=)(n f ________. 12.已知数列}{n a 的通项公式为*).(21log 2N n n n a n ∈++=设其前n 项和为,n S 则使5-<n S 成立的最小自然数n 是________. 三、解答题13.等差数列}{n a 的前n 项和为,23,1=a S n 公差d 为整数,且第6项为正,从第7项起变为负. (1)求d 的值;(2)求n S 的最大值;(3)当n S 是正数时,求n 的最大值.14.设d a ,1为实数,首项为、1a 公差为d 的等差数列}{n a 的前n 项和为n S ,满足.01565=+S S(1)若,55=S 求6S 及;1a(2)求d 的取值范围.15.已知数列}{n a 的首项n S a a ,1=是数列}{n a 的前n 项和,且满足,0,32122=/+=-n n n n a S a n S (1)若数列}{n a 是等差数列,求a的值;(2)确定a 的取值集合M ,使M a 时,数列}{n a 是递增数列.16.已知}{n a 为递增的等比数列,且}.16,4,3,1,0,2,6,10{},,{531---⊆a a a(1)求数列}{n a 的通项公式; (2)是否存在等差数列},{n b 使得221123121--=+++++--n b a b a b a b a n n n n n 对一切*N n ∈都成立?若存在,求出n b ;若不存在,说明理由. 17.等差数列}{n a 各项均为正整数,,31=a 前n 项和为n S ,等比数列}{n b 中,,11=b 且,6422=S b }{n a b 是公比为64的等比数列. (1)求n a 与;n b(2)证明:⋅<+++4311121n S S S 18.已知数列},{n a n S 为其前n 项的和,,9+-=n n a n S .*N n ∈(1)证明数列}{n a 不是等比数列;(2)令,1-=n n a b 求数列}{n b 的通项公式n b ;(3)已知用数列}{n b 可以构造新数列.例如:},3{n b },12{+n b },{2nb },1{nb },2{n b },{sin n b …,请写出用数列}{n b 构造出的新数列}{n p 的通项公式,使数列}{n p 满足以下两个条件,并说明理由.①数列}{n p 为等差数列;②数列}{n p 的前n 项和有最大值.高三数学(理科)专题训练三<概率>一、选择题1.对满足B A ⊆的非空集合B A 、有下列四个命题:其中正确命题的个数为()①若任取,A x ∈则B x ∈是必然事件②若,A x ∉则B x ∈是不可能事件③若任取,B x ∈则A x ∈是随机事件④若,B x ∉则A x ∉是必然事件 A .4B .3C .2D .12.从1,2,…,9中任取两个数,其中在下列事件中,是对立事件的是()①恰有一个是偶数和恰有一个是奇数②至少有一个是奇数和两个都是奇数③至少有一个是奇数和两个都是偶数④至少有一个奇数和至少有一个偶数A .①B .②④C .③D .①③ 3.如图所示,设D 是图中边长为4的正方形区域,E 是D 内函数2x y =图象下方的点构成的区域,向D 中随机投一点,则该点落入E 中的概率为() A .21B .31C .41D .51 4.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A ,“骰子向上的点数是3”为事件B ,则事件A 、B 中至少有一件发生的概率是() A .125B .21C .127D .43 5.如图所示,圆C 内切于扇形,3,π=∠AOB AOB 若在扇形AOB内任取一点,则该点在圆C 内的概率为() A .21B .31C .32D .43 6.已知随机变量ξ服从正态分布),,0(2σN 若,023.0)2(=>ξP 则)22(≤≤-ξP 的值为()A ....7.把半径为2的圆分成相等的四弧,再将四弧围成星形放在半径为2的圆内,现在往该圆内任投一点,此点落在星形内的概率为() A .14-πB .π2C .214-πD .218.某市组织一次高三调研考试,考试后统计的数学成绩服从正态分布)10,80(~2N ξ,则下列命题中不正确的是()A .该市这次考试的数学平均成绩为80分B .分数在120分以上的人数与分数在60分以下的人数相同C .分数在110分以上的人数与分数在50分以下的人数相同D .该市这次考试的数学成绩标准差为10 二、填空题9.盒子里共有大小相同的三只白球、一只黑球,若从中随机摸出两只球,则它们颜色不同的概率是__________. 10.在集合}10,,3,2,1,6|{ ==n n x x π中任取1个元素,所取元素恰好满足方程21cos =x 的概率是__________.11.在区间]3,3[-上随机取一个数x ,使得1|2||1|≤--+x x 成立的概率为______.12.在一次教师联欢会上,到会的女教师比男教师多12人,从这些教师中随机挑选一人表演节目,若选到男教师的概率为,209则参加联欢会的教师共有____人. 13.已知,4|),{(},0,0,6|),{(≤=≥≥≤+=Ωx y x A y x y x y x 若向区域Ω上随机投一点P ,则P 落入区域A 的概率是________. 三、解答题14.袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,已知得到红球的概率是,31得到黑球或黄球的概率是,125得到黄球或绿球的概率也是,125试求得到黑球、黄球、绿球的概率分别是多少?15.某企业有甲、乙两个研发小组,他们研发新产品成功的概率分别是32和53.现安排甲组研发新产品A ,乙组研发新产品B.设甲、乙两组的研发相互独立.(1)求至少有一种新产品研发成功的概率;(2)若新产品A 研发成功,预计企业可获利润120万元;若新产品B 研发成功,预计企业可获得利润100万元.求该企业可获利润的分布列和数学期望. 16.一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示:将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立. (1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另一天的日销售量低于50个的概率; (2)用X 表示在未来3天里日销售量不低于100个的天数,求随机变量X 的分布列,期望()E X 及方差()D X . 17设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.60.50.50.4、、、,各人是否需使用设备相互独立.(1)求同一工作日至少3人需使用设备的概率;(2)X 表示同一工作日需使用设备的人数,求X 的数学期望. 18乒乓球台面被球网分成甲、乙两部分.如图,甲上有两个不相交的区域,A B ,乙被划分为两个不相交的区域,C D .某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C 上记3分,落点在D 上记1分,其它情况记0分,落点在C 上的概率为15,在D 上的概率为35.假设共有两次来球且落在,A B 上各一次,小明的两次回球互不影响.求:(I )小明两次回球的落点中恰有一次的落点在乙上的概率;(II )两次回球结束后,小明得分之和 的分布列与数学期望.高三数学(理科)专题训练四《立体几何初步》一、选择题1.已知ABC ∆的三个顶点为、、)7,3,4()2,3,3(-B A ),1,5,0(C 则BC 边上的中线长为() A .5B .4C .3D .22.如图所示,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A .6B .9C .12D .183.一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可能是()A .球B .三棱锥C .正方体D .圆柱4.已知n m 、表示两条不同直线,α表示平面,下列说法中正确的是()A .若αα//,//n m ,则n m //B .若,,//n m m ⊥α,则α⊥nC .若,,n m m ⊥⊥α,则α//nD .若,,αα⊂⊥n m ,则n m ⊥ 5.已知一个几何体的三视图如图所示(单位:cm ),则该几何体的体积为() A .310cm πB .320cm πC .3310cm πD .3320cm π6.已知过球面上C B A ,,三点的截面和球心的距离等于球半径的一半,且,2===CA BC AB 则球的半径是()A .32B .34C .36D .17.用c b a ,,表示三条不同的直线,α表示平面,给出下列命题:其中正确的命题是()①若,//,//c b b a 则;//c a ②若,,c b b a ⊥⊥则;c a ⊥③若,//,//ααb a 则;//b a ④若,,αα⊥⊥b a 则.//b aA .①②B .②③C .①④D .③④ 8.一个圆锥和一个半球有公共底面,如果圆锥的体积恰好与半球的体积相等,那么这个圆锥的轴截面顶角的余弦值是() A .43B .54C .53D .53-二、填空题9.已知三棱柱111C B A ABC -的6个顶点都在球O 的球面上,若,4,3==AC AB,AC AB ⊥,121=AA 则球O 的半径为_______.10.在三棱锥ABC P -中,,1====BC PC PB PA 且,2π=∠BAC 则PA 与底面ABC 所成角为______.11.在长方体1111D C B A ABCD -中,,2,31cm AA cm AD AB ===则四棱锥D D BB A 11-的体积为____cm 3. 三、解答题12.如图所示,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,求切削掉部分的体积与原来毛坯体积的比值.ABCD P -与ABCD Q -的高都是2,.4=AB(1)求证:⊥PQ 平面;ABCD (2)求四面体QAD P -的体积. 14.如图所示,在直三棱柱111C B A ABC -中,,,901CC BC AC ACB o ===∠点M 为AB 的中点,点D 在11B A 上,且.311DB D A =(1)求证:平面⊥CMD 平面;11A ABB(2)求二面角M BD C --的余弦值.中,底面ABCD 为矩形,,ABCD PA 平面⊥E 为PD 的中点. (1)证明:AEC PB 平面//;(2)设二面角C AE D --为60°,,3,1==AD AP求三棱锥ACD E -的体积.16.如图所示,直二面角E AB D --中,四边形ABCD 是边长为2的正方形,,EB AE =点F 为CE 上的点,且⊥BF 平面.ACE (1)求证:⊥AE 平面;BCE (2)求二面角E AC B --的余弦值;(3)求点D 到平面ACE 的距离. 17.如图所示,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上的点.(1)求证:平面PAC ⊥平面PBC . (2)若,1,1,2===PA AC AB 求二面角A PB C --的余弦值.18.如图所示,平行四边形ABCD中,.4,2,60===∠AD AB DAB 将CBD ∆沿BD 折起到EBD ∆的位置,使平面⊥EDB 平面ABD. (1)求证:⊥AB 平面;EBD (2)求三棱锥ABD E -的侧面积.高三数学(理科)专题训练五《圆锥曲线方程》一、选择题 1.已知双曲线)0,0(1:2222>>=-b a by a x C 的离心率为,25则C 的渐近线方程为()A .x y 41±=B .x y 31±=C .x y 21±=D .x y ±=2.已知,40πθ<<则双曲线1cos sin :22221=-θθy x C 与1sin cos :22222=-θθx y C ()A .实轴长相等B .虚轴长相等C .离心率相等D .焦距相等 3.椭圆1422=+y x的两个焦点为,,21F F 过1F 作垂直于x 轴的直线与椭圆相交,一个交点为P ,则=||2PF ()A .23B .3C .27D .4 4.已知双曲线14222=-b y x 的右焦点与抛物线x y 122=的焦点重合,则该双曲线的焦点到其渐近线的距离等于() A .5B .24C .3D .5 5.设1F 和2F 为双曲线)0,0(12222>>=-b a b y a x 的两个焦点,若)2,0(,,21b P F F 是正三角形的三个顶点,则双曲线的离心率为() A .23B .2C .25D .36.已知双曲线1222=-y x 的焦点为,,21F F 点M 在双曲线上,且,021=⋅则点M 到x 轴的距离为() A .34B .35C .332D .37.设双曲线的左焦点为F ,虚轴的一个端点为B ,右顶点为A ,如果直线FB 与BA 垂直,那么此双曲线的离心率为()A .2B .3C .213+D .215+ 8.已知F 是抛物线x y =2的焦点,点A 、B 在该抛物线上,且位于x 轴的两侧,2=⋅(其中O 为坐标原点),则ABO ∆与AFO ∆面积之和的最小值是() A .2B .3C .8217D .10 二、填空题9.已知抛物线x y 82=的准线过双曲线)0,0(12222>>=-b a by a x 的一个焦点,双曲线的离心率为2,则该双曲线的方程为_________. 10.已知21,F F 是椭圆)0(1:2222>>=+b a by a x C 的两个焦点,P 为椭圆C 上一点,且.21PF ⊥若21F PF ∆的面积为9,则=b _________.11.抛物线)0(22>=p py x 的焦点为F ,其准线与双曲线13322=-y x 相交于A ,B 两点,若ABF ∆为等边三角形,则=p _________. 12.椭圆12222=+by a x 的四个顶点为,,,,D C B A 若菱形ABCD 的内切圆恰好经过它的焦点,则此椭圆的离心率是____. 三、解答题13.如图所示,动圆)31(:2221<<=+t t y x C 与椭圆19:222=+y x C 相交于DC B A ,,,四点,点21,A A 分别为2C 的左、右顶点,当t 为何值时,矩形ABCD 的面积取得最大值?并求出其最大面积.14.已知双曲线)0,0(12222>>=-b a b y a x 的两条渐近线方程为,33x y ±=若顶点到渐近线的距离为1,求双曲线方程.15.如图,在平面直角坐标系xOy中,21,F F 分别是椭圆)0(12222>>=+b a b y a x 的左右焦点,顶点B 的坐标是),,0(b 连结2BF 并延长交椭圆于点A ,过点A 作x 轴的垂线交椭圆于另一点C ,连结.1C F(1)若点C 的坐标为),31,34(且,2||2=BF 求椭圆的方程;(2)若,1AB C F ⊥求椭圆离心率e 的值.16.椭圆)0(1:2222>>=+b a by a x C 的两个焦点分别为,,21F F 点P 在椭圆C 上,且,211F F PF ⊥ (1)求椭圆C 的方程;(2)若直线l 过圆02422=-++y x y x 的圆心M ,交椭圆C 于A ,B 两点,且A ,B 关于点M 对称,求直线l 的方程.17.若点O 和点F 分别为椭圆13422=+y x 的中心和左焦点,点P 为椭圆上的任意一点,求FP OP ⋅的最大值.18.已知抛物线C 的顶点为原点,其焦点)0)(,0(>c c F 到直线02:=--y x l 的距离为.223设P 为直线l 上的点,过点P 作抛物线C 的两条切线PA ,PB ,其中A ,B 为切点. (1)求抛物线C 的方程;(2)当点),(00y x P 为直线l 上的定点时,求直线AB 的方程;(3)当点P 在直线l 上移动时,求||||BF AF ⋅的最小值.高三数学(理科)专题训练六《导数及其应用》一、选择题1.若,)(3x x f =,6)('0=x f 则=0x () A .2B .2-C .2±D .1± 2.函数133+-=x x y 的单调递减区间是()A .)2,1(B .)1,1(-C .)1,(--∞D .),1(+∞3.与直线052=+-y x 平行的抛物线2x y =的切线方程是()A .032=+-y xB .032=--y x C .012=+-y x D .012=--y x4.已知曲线x x y ln 342-=的一条切线的斜率为,21则切点的横坐标为()A .3B .2C .1D .215.曲线x y cos =与x 轴在区间]23,2[ππ-上所围成的图形的面积是()A .1B .2C .3D .46.设)(),(x g x f 是定义域为R 的恒大于零的可导函数,且,0)(')()()('<-x g x f x g x f 则当x a <b <时,有()A .)()()()(b g b f x g x f >B .)()()()(x g a f a g x f >C .)()()()(x g b f b g x f >D .)()()()(a g a f x g x f >7.若)2ln(21)(2++-=x b x x f 在区间),1(+∞-内是减函数,则实数b 的取值范围是()A .),1[+∞-B .),1(+∞-C .]1,(--∞D .)1,(--∞8.如图,某飞行器在4千米高空水平飞行,从距着陆点A 的水平距离10千米处下降,已知下降飞行轨迹为某三次函数图象的一部分,则函数的解析式为()A .x x y 5312513-=B .x x y 5412523-= C .x x y -=31253D .x x y 5112533+-=二、填空题9.若曲线)1ln(+-=x ax y 在点)0,0(处的切线方程为,2x y =则=a ______. 10.若曲线xbax y +=2(a 、b 为常数)过点),5,2(-P 且该曲线在点P 处的切线与直线++y x 2703=平行,则=+b a ______. 11.若,)(2)(12dx x f x x f ⎰+=则=⎰dx x f )(1______.12.设,R a ∈若函数)(3R x x e y ax ∈+=有大于零的极值点,则a 的取值范围是______. 三、解答题13.设函数)0()(=/=k xe x f kx .(1)求曲线)(x f y =在点))0(,0(f 处的切线方程;(2)求函数)(x f 的单调区间.14.已知函数x=xxxf-+ln.1()1)(+(1)若,1xxf求实数ax)('2++≤ax的取值范围;(2)证明:.0f-xx)()1(≥15.设,12321ln )(+++=x x x a x f 其中,R a ∈曲线)(x f y =在点))1(,1(f 处的切线垂直于y 轴. (1)求a 的值;(2)求函数)(x f 的极值.16.如图所示,已知曲线21:x y C =与曲线)1(2:22>+-=a ax x y C 交于点O 、A ,直线)10(≤<=t t x 与曲线21C C 、分别相交于点D 、B ,联结.AB DA OD 、、(1)写出曲边四边形ABOD (阴影部分)的面积S 与t 的函数关系式);(t f S =(2)求函数)(t f S =在区间]1,0(上的最大值.17.某村庄拟修建一个无盖圆柱形蓄水池(不计厚度),设该蓄水池的底面半径为r 米,高为h 米,体积为V 立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为π12000(π为圆周率).(1)将V 表示成r 的函数V (r ),并求该函数的定义域;(2)讨论函数V (r )的单调性,并确定r 和h 为何值时该蓄水池的体积最大.18.已知函数.)2(ln )(2x a ax x x f -+-=(1)讨论)(x f 的单调性;(2)设,0>a 证明:当ax 10<<时,);1()1(x ax a f ->+(3)若函数)(x f y =的图象与x 轴交于A 、B 两点,线段AB 中点的横坐标为,0x证明:.0)('0<x f高三数学(理科)专题训练一《三角函数、三角恒等变换与解三角形》参考答案9.2cm 210.311.2,)3,2(12.1 三、解答题13.(1)因)(x f 的图象上相邻两个最高点的距离为,π所以)(x f 的最小正周期,π=T 从而.22==Tπω又因)(x f 的图象关于直线3π=x 对称,所以,,2,1,0,232 ±±=+=+⋅k k ππϕπ因≤-2π2πϕ≤得,0=k 所以⋅-=-=6322πππϕ(2)由(1)得=-⋅=)622sin(3)2(πααf ,43所以⋅=-41)6sin(πα由326παπ<<得,260ππα<-< 所以=--=-)6(sin 1)6cos(2παπα⋅=-415)41(12 因此+-==+)6sin[(sin )23cos(πααπα6sin )6cos(6cos )6sin(]6ππαππαπ-+-= 14.(1)π=T (2)21)(,1)(min max -==x f x f15.(1)==+=32sin )4125sin()125(ππππA A f ,23233sin )3sin(===-A A A πππ所以=A ,3所以).4sin(3)(π+=x x f(2))()(θθ-+f f )4sin(3)4sin(3πθπθ+-++=,23cos 6==θ所以,46cos =θ因为,0sin ),2,0(>∈θπθ则=θsin ,410)46(1cos 122=-=-θ 故=+-=-]4)43sin[(3)43(πθπθπf ⋅=⨯==-4304103sin 3)sin(3θθπ16.(1)1=ω)](3,6[Z k k k ∈+-ππππ(2)13=a17.(1)因),32sin(22cos 32sin)(π+=+=x x x x f 故)(x f 的最小正周期.4212ππ==T当1)32sin(-=+πx 时,)(x f 取得最小值;2-当1)32sin(=+πx 时,)(x f 取得最大值2.(2)由(1)知⋅+=)32sin(2)(πx x f 又⋅+=)3()(πx f x g故]3)3(21sin[2)(ππ++=x x g ⋅=+=2cos 2)22sin(2xx π故).(2cos 2)2cos(2)(x g xx x g ==-=-所以函数)(x g 是偶函数. 18.(1)由题意得,=+-+22cos 122cos 1BA ,2sin 232sin 23B A - 即=-A A 2cos 212sin 23-=--B A B B 2sin()62sin(,2cos 212sin 23π),6π 由b a =/得,,B A =/又),,0(π∈+B A 得,6262πππ=-+-B A 即,32π=+B A 所以⋅=3πC(2)由,3=c Cc A a A sin sin ,54sin ==得58=a ,由,c a <得,C A <从而,53cos =A故=+=+=C A C A C A B sin cos cos sin )sin(sin ,10334+ 所以ABC ∆的面积为==B ac S sin 21⋅+251838高三数学(理科)专题训练二《数列》参考答案9.133-n 10.3711.4;7;11;222++n n 12.63 三、解答题13.(1)由已知,0076⎩⎨⎧<>a a 得,06230523⎩⎨⎧<+>+d d 解得,623523-<<-d 又d 为整数,故.4-=d (2)nn n n n S n 252)4(2)1(232+-=-⨯-+=,8625)425(22+--=n当6=n 时,;78=n S 当7=n 时,.77=n S 取最大值为78. (3)令,0>n S 得,02522>+-n n 解得<<n 0*),(225N n ∈ 故n 的最大值为12. 14.(1)由题意知:.31556-=-=S S .8566-=-=S S a所以,85510511⎩⎨⎧-=+=+d a d a 解得,71=a 所以.7,316=-=a S(2)因为,01565=+S S 所以,015)156)(105(11=+++d a d a即.0110922121=+++d da a 故.8)94(221-=+d d a 所以.82≥d故d 的取值范围为22-≤d 或.22≥d15.(1)在21223-+=n n n S a n S 中分别令,2=n 3=n 及,1a a =得++=+a a a a a (,12)(2222.)(27)223232a a a a a ++=+因为,0=/n a 所以2a ,212a -=.233a a +=因为数列}{n a 是等差数列,所以+1a ,223a a =即,23)212(2a a a ++=-解得.3=a经检验3=a 时,,2)1(3,3+==n n S n a n n ,2)1(31-=-n n S n 满足.32122-+=n n n S a n S(2)由,32122-+=n n n S a n S 得,32212n n n a n S S =--即,3))((211n n n n n a n S S S S =-+--因为,0=/n a ,2≥n 所以,321n S S n n =+-①所以,)1(321+=++n S S n n ② ②-①得,361+=++n a a n n 所以=+-1n n a a ,3)1(6+-n两式相减得:).2(611≥=--+n a a n n即数列 642,,a a a 及数列 ,,,753a a a 都是公差为6的等差数列,因为,23,21232a a a a +=-=所以⎪⎩⎪⎨⎧+-≥-+==.,623,3,623,1,为偶数为奇数且n a n n n a n n a a n要使数列}{n a 是递增数列,须有,21a a <且当n 为大于或等于3的奇数时,1+<n n a a且当n 为偶数时,1+<n n a a 即⎪⎩⎪⎨⎧-++<+-≥+-+<-+-<为偶数为奇数且n a n a n n n a n a n a a ,62)1(36233,62)1(3623,212 解得⋅<<41549a所以M 为),415,49(当Ma ∈时,数列}{n a 是递增数列.16.(1)12-n (2)存在17.(1)设}{n a 公差为d ,由题意易知,0>d 且∈d *,N则,)1(3d n a n -+=.2)1(3d n n n S n -+=设}{n b 公比为q ,则.1-=n n q b 由,6422=S b 可得64)6(=+d q …①又}{n a b 是公比为64的等比数列,所以6411111====---+++d a a a a a a q q qq b b n n n n n n …② 由①②,且*,N d >,0>d 可解得.2,8==d q所以,12+=n a n .*,81N n b n n ∈=- (2)由(1)知),2(22)1(3+=⨯-+=n n n n n S n .*N n ∈所以),211(21)2(11+-=+=n n n n S n 所以+-=+++)311[(2111121n S S S )]211()5131()4121(+-++-+-n n 18.(1)略(2)1)21(4-=n n b (3)=n p )1(log >a b n a高三数学(理科)专题训练三《概率》参考答案一、选择题BCBCCCAB 二、填空题9.2110.5111.3212.120人13.278三、解答题14.设得到黑球、黄球的概率分别为,y x 、由题意得⎪⎪⎩⎪⎪⎨⎧=---+=+,125)311(,125y x y y x 解得⎪⎪⎩⎪⎪⎨⎧==,61,41y x 故41)6141311(=---,所以得到黑球、黄球、绿球的概率分别是⋅416141、、15解:记E ={甲组研发新产品成功},F ={乙组研发新产品成功},由题可知32)(=E P ,31)(=E P ,53)(=F P ,52)(=F P .且事件E 与F ,E 与F ,E 与F ,E 与F 都相互独立.(1)记H ={至少有一种新产品研发成功},则F E H =,于是1525231)()()(=⨯==F P E P H P ,故所求概率为15131521)(1)(=-=-=H P H P .(2)设企业可获利润为X (万元),则X 的可能取值为0,100,120,220.又因1525231)()0(=⨯===F E P X P ,1535331)()100(=⨯===F E P X P ,1545232)()120(=⨯===F E P X P ,1565332)()220(=⨯===EF P X P .11521001562201541201531001520)(==⨯+⨯+⨯+⨯=X E .16(Ⅰ)设1A 表示事件“日销售量不低于100个”,2A 表示事件“日销售量低于50个”,B 表示事件“在未来连续3天里有连续2天日销售量不低于100个且另一天的日销售量低于50个”.因此1()(0.0060.0040.002)500.6P A =++⨯=.2()0.003500.15P A =⨯=.()0.60.60.1520.108P B =⨯⨯⨯=. (Ⅱ)X 的可能取值为0,1,2,3.相应的概率为033(0)(10.6)0.064P X C ==⋅-=,123(1)0.6(10.6)0.288P X C ==⋅-=,223(2)0.6(10.6)0.432P X C ==⋅-=,333(3)0.60.216P X C ==⋅=,=,方差D (X )=3××()= 17解:记i A 表示事件:同一工作日乙、丙中恰有i 人需使用设备,0,1,2i =B 表示事件:甲需使用设备C 表示事件:丁需使用设备D 表示事件:同一工作日至少3人需使用设备(1)122D A B C A B A B C =⋅⋅+⋅+⋅⋅ 所以122()()P D P A B C A B A B C =⋅⋅+⋅+⋅⋅122()()()P A B C P A B P A B C =⋅⋅+⋅+⋅⋅ (2)X 的可能取值为0,1,2,3,40(0)()P X P B C A ==⋅⋅0()()()P B P C P A =2(10.6)(10.4)0.50.06=-⨯-⨯=. 0.25=,2(4)()P X P B C A ==⋅⋅2()()()P B P C P A =20.50.60.40.06=⨯⨯=,(3)()(4)0.25P X P D P X ==-==, 所以(X)(2)0(0)1(1)2(3)3(3)4(4)E P X P X P X P X P X P X ===⨯=+⨯=+⨯=+⨯=+⨯=0.2520.3830.2540.06=+⨯+⨯+⨯2=.18解:(I )设恰有一次的落点在乙上这一事件为A高三数学(理科)专题训练四《立体几何初步》参考答案9.21310.3π11.6三、解答题12.底面半径为3cm ,高为6cm 的圆柱体的体积为:1211h R V ⋅=π632⋅⋅=π.54π=从某零件的三视图可知:该几何体为左边是一个底面半径为2cm 、高为4cm 的圆柱体,右边是一个底面半径为3cm 、高为2cm 的圆柱体.其中左边的圆柱体的体积为:所以切削掉部分的体积为:.204322ππ=-⋅⋅=V V因此切削掉部分的体积与原来毛坯体积的比值为:⋅==271054201ππV V 13.(1)如图所示,取AD 的中点M ,连接.,QM PM因为ABCD P -与ABCDQ -都是正四棱锥,所以,,QM AD PM AD ⊥⊥ 从而.PQM AD 平面⊥又,PQM PQ 平面⊂所以.AD PQ ⊥同理,AB PQ ⊥所以.ABCD PQ 平面⊥(2)连接OM ,则,21221PQ AB OM ===所以,90o PMQ =∠即⋅⊥MQ PM由(1)知,PM AD ⊥所以,QAD PM 平面⊥从而PM 就是四面体QAD P -的高,在直角PMO ∆中,.22222222=+=+=OM PO PM又,242242121=⋅⋅=⋅=∆QM AD S QAD故⋅=⋅⋅=⋅=∆-31622243131PM S V QAD QAD P14.(1)在ABC ∆中,,BC AC =点M 为AB 的中点,故.AB CM ⊥又因三棱柱111C B A ABC -是直三棱柱,故,11ABC A ABB 平面平面⊥又,ABC CM 平面⊂故11A ABB CM 平面⊥,而,CMD CM 平面⊂故11A ABB CMD 平面平面⊥ (2)以点C 为原点,分别以1,,CC CB CA 所在直线为z y x ,,轴,建立如图所示的空间直角坐标系,令,11===CC BC AC则),0,0,0(C ),0,0,1(A ),1,0,1(1A ),0,1,0(B ),1,1,0(1B故),0,1,0(=CB )1,43,41(=CD设平面CBD 的法向量为),,,(z y x n =则⎪⎩⎪⎨⎧=⋅=⋅00CD n CB n ⇒⎪⎩⎪⎨⎧=++=043410z y x y ⇒⎩⎨⎧=+=040z x y ,取,1-=z 则,4=x ,0=y 故)1,0,4(-=n ,而平面MBD 的法向量是),0,21,21(=CM故>=<n ,cos 1722)1,0,4()0,21,21(⨯-⋅⋅=17342 即二面角M BD C --的余弦值为⋅17342 15.(1)连结BD 交AC 于点O ,连结EO .因为ABCD 为矩形,所以O 为BD 的中点.又E 为PD 的中点,所以.//PB EO又,AEC EO 平面⊂,AEC PB 平面⊂/所以.//AEC PB 平面(2)因为,ABCD PA 平面⊥ABCD 为矩形,所以AP AD AB ,,两两垂直.如图所示,以A 为坐标原点,的方向为x 轴的正方向,||AP 为单位长,建立空间直角坐标系,xyz A -则),21,23,0(),0,3,0(E D ⋅=)21,23,0( 设),0)(0,0,(>m m B 则),0,3,(m C ).0,3,(m =设),,(1z y x n =为平面ACE 的法向量,则⎪⎩⎪⎨⎧=⋅=⋅011n n ,即⎪⎩⎪⎨⎧=+=+.02123,03z y y mx 可取),3,1,3(1-=m n 又)0,0,1(2=n 为平面DAE 的法向量,由题设,21|,cos |21=><n n 即=+2433m ,21解得⋅=23m因为E 为PD 的中点,所以三棱锥ACD E -的高为⋅21所以三棱锥ACD E -的体积为:⋅=⨯⨯⨯⨯=83212332131V16.(1)因⊥BF 平面.ACE 故.AE BF ⊥又因二面角E AB D --为直二面角,且,AB CB ⊥故⊥CB 平面.ABE故.AE CB ⊥⊥AE 平面.BCE (2)以点A 为原点,建立如图所示的空间直角坐标系.因⊥AE 面,BCE ⊂BE 面,BCE故.BE AE ⊥则),0,0,0(A ),0,1,1(E ,2,0(C ).2),0,1,1(=AE ⋅=)2,2,0(AC设平面AEC 的法向量为),,,(z y x n =则⎪⎩⎪⎨⎧=⋅=⋅00AC n AE n ,即,0220⎩⎨⎧=+=+z y y x 解得⋅⎩⎨⎧=-=xz x y令,1=x 得=n )1,1,1(-是平面AEC 的一个法向量,又平面BAC 的一个法向量为),0,0,1(=m且n m ,所成的角就是二面角E AC B --的平面角,因>=<n m ,cos ||||n m n m ⋅⋅,3331==故二面角E AC B --的余弦值为⋅33 (3)因),2,0,0(=AD 故点D 到平面ACE 的距离=d .33232||||==⋅n n 17.(1)略(2)4618.(1)证明:如图所示,在ABD ∆中,因,60,4,2o DAB AD AB =∠==故=∠⋅-+=DAB AD AB AD AB BD cos 2222,32故,222AD BD AB =+故.BD AB ⊥又因,ABD EBD 平面平面⊥,BD ABD EBD =平面平面,ABD AB 平面⊂故.EBD AB 平面⊥(2)解:由(1)知,//,AB CD BD AB ⊥故,BD CD ⊥从而.DB DE ⊥在DBE Rt ∆中, 因,2,32====AB DC DE DB 故.3221=⋅=∆DE DB s BDE又因,EBD AB 平面⊥,EBD BE 平面⊂故.BE AB ⊥因,4===AD BC BE 故.421=⋅=∆BE AB S ABE 因,BD DE ⊥平面EBD ⊥平面ABD ,故.ABD ED 平面⊥而,ABD AD 平面⊂故,AD ED ⊥故.421=⋅=∆DE AD S ADE 综上得三棱锥ABDE -的侧面积为.328+=S高三数学(理科)专题训练五《圆锥曲线方程》参考答案9.1322=-y x 10.3=b 11.612.215-三、解答题13.设),,(00y x A 则矩形ABCD 的面积||40x S =.||0y由192020=+y x 得,,912020x y -=故202020x y x =,49)29(91)91(22020---=-x x当21,292020==y x 时,,6max =S故当5=t 时,矩形ABCD 的面积最大,最大面积为6.14.根据几何性质有.1=cab又因,33=a b 解得⎪⎩⎪⎨⎧==34422b a 故双曲线的方程为.143422=-y x15.(1)由题意,),,0(),0,(2b B c F =||2BF ,222==+a c b又)31,34(C 在椭圆上,所以,1)31(2)34(222=+b 解得.1=b 所以椭圆方程为.1222=+y x(2)直线2BF 方程为,1=+byc x 与椭圆方程12222=+by a x 联立方程组,解得A 点坐标为),,2(223222c a b c a c a +-+则C 点坐标为,2(222c a c a +),223ca b + 又,c bk AB -=由AB C F ⊥1得⋅+3233c c a b ,1)(-=-cb 即,34224c c a b += 所以=-222)(c a ,3422c c a +化简得.55==ac e 16.(1)由于点P 在椭圆上,故.3,6||||221==+=a PF PF a 在21F PF Rt ∆中,.52||||||212221=-=PF PF F F 解得,5=c 从而.4222=-=c a b因此椭圆C 的方程为.14922=+y x (2)设A ,B 的坐标分别为).,(),,(22]1y x y x已知圆的方程为,5)1()2(22=-++y x 圆心).1,2(-设直线l 方程为,1)2(++=x k y代入椭圆C 的方程得273636)1836()94(2222-+++++k k x k k x k 0=由于A ,B 关于点M 对称,所以,29491822221-=++-=+k kk x x 解得98=k因此直线l 的方程为,1)2(98++=x y 即.02598=+-y x 17.由题意,),0,1(-F 设点),,(00y x P 则有,1342020=+y x 解得)41(32020x y -=因为),,1(00y x +=),,(00y x =所以200)1(y x x ++=⋅,34)41(3)1(0202000++=-++=x x x x x此二次函数对应的抛物线的对称轴为.20-=x因为,220≤≤-x 所以当20=x 时,⋅取得最大值.632422=++ 18.(1)y x 42=(2)02200=--y y x x (3)29高三数学(理科)专题训练六《导数及其应用》参考答案9.310.-311.31-12.)3,(--∞三、解答题13.(1),)1()('kx e kx x f +=,1)0('=f ,0)0(=f故曲线)(x f y =在点))0(,0(f 处的切线方程为.x y =(2)由0)1()('=+=kx e kx x f 得).0(1=/-=k kx ①若,0>k 则当)1,(kx --∞∈时,,0)('<x f 函数)(x f 单调递减;当),1(+∞-∈kx 时,,0)('>x f 函数)(x f 单调递增,②若,0<k 则当)1,(kx --∞∈时,,0)('>x f 函数)(x f 单调递增;当),1(+∞-∈kx 时,,0)('<x f 函数)(x f 单调递减.14.(1)因为),0(1ln 1ln 1)('>+=-++=x xx x x x x f 所以.1ln )('+=x x x xf 由,1)('2++≤ax x x xf 得.ln x x a -≥令,ln )(x x x g -=则11)('-=xx g 当10<<x 时,;0)('>x g 当1>x 时,.0)('<x g所以1=x 是最大值点,.1)1()(max -==g x g 故,1-≥a即a 的取值范围是).,1[+∞- (2)由(1)知,1)1(ln )(-=≤-=g x x x g 故.01ln ≤+-x x当10<<x 时,x x x x x x f ln 1ln )1()(=+-+=;01ln ≤+-+x x当1≥x 时,+=+-+=x x x x x f ln 1ln )1()(.0)111(ln ln 1ln ≥-+-=+-xx x x x x x综上,.0)()1(≥-x f x15.(1)因为,12321ln )(+++=x x x a x f 故⋅+-=2321)('2x x a x f由于曲线)(x f y =在点))1(,1(f 处的切线垂直于y 轴,故该切线斜率为0,即,0)1('=f 从而,02321=+-a 解得.1-=a(2)由(1)知)0(12321ln )(>+++-=x x x x x f 令,0)('=x f 解得,11=x 312-=x (因312-=x 不在定义域内,舍去).当)1,0(∈x 时,,0)('<x f 故)(x f 在)1,0(上为减函数;当),1(+∞∈x 时,,0)('>x f 故)(x f 在,1()∞+上为增函数.故)(x f 在1=x 处取得极小值.3)1(=f16.(1)由⎩⎨⎧+-==axx y x y 222得点).,(),0,0(2a a A O又由已知得).,(),2,(22t t D at t t B +-故)(t f S =+⋅⋅-+-=⎰2221)2(t t dx ax x t)()2(2122t a t at t -⋅-+-(2).221)('22a at t t f +-=令,0)('=t f即,022122=+-a at t 解得a t )22(-=或.)22(a t +=因为,10≤<t ,1>a 所以a t )22(+=舍去.若,1)22(≥-a 即222221+=-≥a 时,对,10≤<t 有.0)('≥t f故)(t f 在区间]1,0(上单调递增,S 的最大值是⋅+-=61)1(2a a f若,1)22(<-a 即2221+<<a 时,对,)22(0a t -<<有;0)('>t f当t a <+)22(1≤时,有.0)('<t f 故)(t f 在))22(,0(a -上单调递增,在]1,)22((a +上单调递减,)(t f 的最大值是.3222))22((3a a f -=- 综上所述,=max)]([t f ⎪⎪⎩⎪⎪⎨⎧+<<-+≥+-222132222226132a a a a a 17.(1)),4300(5)(3r r r V -=π定义域为);35,0((2))(r V 在区间)5,0(上单调递增,在区间)35,5(上单调递减;当,5=r 8=h 时,蓄水池的体积最大18.(1))(x f 的定义域为-=+∞xx f 1)('),,0(⋅-+-=-+xax x a ax )1)(12()2(2若,0≤a 则,0)('>x f 所以)(x f 在),0(+∞单调递增.若,0>a 则由0)('=x f 得,1ax =且当∈x )1,0(a时,,0)('>x f 当ax 1>时,.0)('<x f 所以)(x f 在)1,0(a单调递增,在),1(+∞a单调递减.(2)设函数),1()1()(x af x a f xg --+=则,2)1ln()1ln()(ax ax ax x g ---+=.12211)('2223x a x a a axa ax a x g -=--++=当ax 10<<时,,0)('>x g 而,0)0(=g 所以.0)(>x g故当ax 10<<时,⋅->+)1()1(x af x a f (3)由(1)可得,当0≤a 时,函数)(x f y =的图象与x 轴至多有一个交点,故,0>a 从而)(x f 的最大值为),1(a f 且.0)1(>af 不妨设,0),0,(),0,(2121x x x B x A <<则⋅<<<2110x ax 由(2)得=>-+=-)()11()2(111x f x a a f x a f ).(02x f =又,1,1221ax a x a >>-从而,212x ax ->于是⋅>+=ax x x 12210由(1)知,.0)('0<x f。
重庆市西南大学附属中学校2022届高三第六次月考数学试题及答案

西南大学附属中学校高2022届第六次月考数 学 试 题(满分:150分;考试时间:120分钟)2022年2月注意事项:1.答题前,考生先将自己的姓名、班级、考场/座位号、准考证号填写在答题卡上.2.答选择题时,必须使用2B 铅笔填涂;答非选择题时,必须使用0.5毫米的黑色签字笔书写;必须在题号对应的答题区域内作答,超出答题区域书写无效;保持答卷清洁、完整.3.考试结束后,将答题卡交回(试题卷学生保存,以备评讲).一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合2{230}A x x x =−−≤,{26}B x Z x =∈<<,则AB =( )A .{25}x x <≤B .{23}x x <≤C .{345},,D .{3}2. 圆锥的母线长是4,侧面积是4π,则该圆锥的高为( )A B .4C .3D .23. 若复数z 满足(1i)|2|2i z +=−+,则z 的共轭复数z 对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限4. 若2()4x a −<成立的一个充分不必要条件是1102x+≤−,则实数a 的取值范围为( ) A .(4]−∞,B .[14],C .(1,4)D .(1]4,5. 已知()f x 是定义在R 上的偶函数,且在(−∞,0)上单调递减,若3log 10a =−,12log 8b =,4512c −⎛⎫= ⎪⎝⎭,则()f a ,()f b ,()f c 的大小关系为( ) A .()()()f a f c f b >> B .()()()f a f b f c >> C .()()()f b f a f c >>D .()()()f c f a f b >>6. 已知(0)απ∈,,且2cos2cos 1αα+=,则tan α=( )A B .53C D7. 设O 为坐标原点,P 是以F 为焦点的抛物线220y px p =>()上任意一点,且点P 在第一象限,M 是线段PF 上的点,若3PM MF =,则直线OM 的斜率的最大值为( )A .2B C .12D 8. 已知函数()ln 0a f x x a x a =−>(),()e x g x x =−,若2(1e )x ∈,时,()()f x g x ≤成立,则实数a 的最大值是( ) A .1B .eC .2e 2D .2e二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分. 9. 下列说法正确的是( )A .市教委为了解附中高中生对参加某项社会实践活动的意向,拟采用分层抽样的方法从我校三个年级的学生中抽取一个容量为60的样本,已知我校高一、高二,高三年级学生之比为6∶5∶4,则应从高三年级中抽取20名学生B .方差描述了一组数据围绕平均数波动的大小,方差越大,数据的离散程度越大,方差越小,数据的离散程度越小C .命题“0x ∀>,2lg(1)0x +≥”的否定是“0x ∃>,2lg(1)0x +<”D .线性回归方程ˆˆˆyb x a =+对应的直线至少经过其样本数据点中的一个点 10. 下列关于多项式5122x x ⎛⎫⎪⎝⎭−−的展开式的结论中,正确的是( )A .各项系数之和为1−B .各项系数的绝对值之和为1C .不存在4x 项D .常数项为4811. 正方体1111ABCD A BC D −的棱长为6,M 、N 为底面1111D C B A 内两点,11111AM AA A B A D λλ=++,[01]λ∈,,异面直线BN 与1CC 所成角为30°,则正确的是( )A .CM BD ⊥B .直线MN 与1DD 为异面直线C .线段MN 长度最小值为D .三棱锥1B AMN −的体积可能取值为1212. 设函数()y f x =的定义域为R ,如果存在常数(0)T T ≠,对于任意x ∈R ,都有()()f x T T f x +=⋅,则称函数()y f x =是“类周期函数”,T 为函数()y f x =的“类周期”.现有下面四个命题,正确的是( ) A .函数()x f x −=3是“类周期函数” B .函数3()f x x =是“类周期函数”C .如果函数c (s )o x f x ω=是“类周期函数”,那么“k ωπ=,Z k ∈”D .如果“类周期函数”()y f x =的“类周期”为1−,那么它是周期为2的周期函数 三、填空题:本大题共4小题,每小题5分,共20分.13. 已知a ,b 为单位向量,a ,b 的夹角为60°,向量c 满足0a c ⋅=,且c a b λ=+,则实数λ= .14. 已知随机变量X 的概率分布为()12310(1)aP X n n n n ===⋅⋅⋅+(,,,,),则实数a = . 15. 安排高三年级一、二两个班一天的数、语、外、物、体,一班的化学及二班的政治各六节课.要求体育课两个班一起上,但不能排在第一节;由于选课之故,一班的化学和二班的政治要安排在同一节;其他语、数、外、物四科由同一任课教师分班上课,则不同的排课表方法共有 种. 16. 已知实数x ,y 满足||||14x x y y +=,则|24|x y +−的取值范围是 . 四、解答题:本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.17. (10分) 已知数列{}n a 的前n 项和为n S ,12a =,且1221n n S S n +=+≥(),{}n b 是公差不为0的等差数列,且124b b b ,,成等比数列,2104a b a ,,成等差数列. (1) 求{}n a ,{}n b 的通项公式;(2) 若1221(1)(1)log n n n nn c b a ++=−+,求{}n c 的前2n 项和2n T .18. (12分) 乒乓球被称为我国的国球,是一种深受人们喜爱的球类体育项目.为减轻高三学子学习压力,提高学习效率,年级打算开学后举办乒乓球比赛,规则如下:比赛以11分为一局,采取七局四胜制.在一局比赛中,先得11分的选手为胜方;如果比赛一旦出现10平,先连续多得2分的选手为胜方.(1) 假设甲选手在每一分争夺中得分的概率为23.在一局比赛中,若现在甲、乙两名选手的得分为8比8平,求这局比赛甲以先得11分获胜的概率;(2) 假设甲选手每局获胜的概率为34,在前三局甲获胜的前提下,记X 表示到比赛结束时还需要比赛的局数,求X 的分布列及数学期望.19. 如图,△ABC 中,AC = 4,BC =,AC BC ⊥,点M ,N 是线段AB 上两点(包括端点),30MCN ∠=︒. (1) 当2AM =时,求△MNC 的周长;(2) 设ACM θ∠=,当△MNC 的面积为1)时,求θ的值.20. 如图,三棱柱111ABC A B C −中,侧面11BB C C 是菱形,其对角线的交点为O ,且1AB AC =,1AB B C ⊥. (1) 求证: AO ⊥平面11BB C C ;(2) 设160B BC ∠=︒,若直线11A B 与平面11BB C C 所成的角为45︒ ,求二面角111A B C B −−的余弦值.21. 已知椭圆2222:10x y C a b a b+=>>()的离心率与等轴双曲线的离心率互为倒数关系,直线:0l x y −+=与以原点为圆心,以椭圆C 的短半轴长为半径的圆相切.(1) 求椭圆C 的方程;(2) 设M 是椭圆的上顶点,过点M 分别作直线MA ,MB 交椭圆于A ,B 两点,设两直线的斜率分别为1k ,2k ,且125k k +=,求证:直线AB 过定点.22. 已知函数2()ln 22(1)0f x x ax a x a =+++≠().(1) 讨论函数()f x 的极值;(2) 当0a <时,证明:[()2]1a f x +≥−恒成立.高2022届第六次月考数学参考答案题号123456789101112答案D AA D CDBBBCADACDACD13.12-14.111015.540016.)44⎡-⎣17.(1)∵当2n ≥,112222n nnn S S S S +-=+⎧⎨=+⎩,两式相减可得()122n n a a n +=≥由112S a ==,代入122n n S S +=+可得226,4S a ==,满足212a a =,所以{}*12,,n n n a a n N a +=∈为等比数列,∴2n n a =,不妨设等差数列{}n b 公差为d ,由条件可得22141024,2b b b b a a ==+,即()()()21111329416b d b b d b d ⎧+=+⎪⎨+=+⎪⎩,解得11,1b d ==,所以()111n b n n=+-⨯=(2)由(1)可知()()()1121111111n n n n c n n n n +++⎛⎫=-⨯=-⨯+ ⎪++⎝⎭∴21232n n T c c c c =++++ 1111111122334221n n ⎛⎫⎛⎫⎛⎫⎛⎫=+-++++-+ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭ 1212121nn n =-=++.18.(1)设这局比赛甲以先得11分获胜为事件A ,则事件A 中包含事件B 和事件C ,事件B :甲乙再打3个球,甲先得11分获胜,事件C :甲乙再打4个球,甲先得11分获胜.事件B :甲乙再打3个球,这三个球均为甲赢,则()33328327p B C ⎛⎫== ⎪⎝⎭,事件C :甲乙再打4个球,则前三个球甲赢两个,最后一个球甲赢,则()223212833327p C C ⎛⎫=⨯⨯= ⎪⎝⎭;则()()()8816272727p A P B P C =+=+=(2)X 的可能取值为1,2,3,4.()314p X ==,()13324416p X ==⨯=,()1133344464p X ==⨯⨯=,()1111444464p X ==⨯=,所以X 的分布列为:X 1234p34316364164其中()3331851234416646464E X =⨯+⨯+⨯+⨯=.即数学期望为8564.19.(1)∵4AC =,B C =,AC BC ⊥,∴30B =︒,则60A=︒,在△ACM 中,由余弦定理得:2222cos CM AC AM AC AM A =+-⋅⋅1164242122=+-⨯⨯⨯=,则CM =222ACAM CM =+,即CM AB ⊥,又30MCN ∠=︒,∴tan 302MN CM =︒=,而24CN MN ==,∴△MNC 的周长为246++=+;(2)在△ACN 中,90ANC θ∠=︒-,由()sin 60sin 90CN CA θ=︒︒-得:CN =在△ACM 中,由()sin 60sin 60CM CA θ=︒︒+,得CM =()13sin 302sin 60cosCMN S CN θθ=⋅⋅︒==+︒222,)61=得:()1sin 2602θ+︒=,又060θ︒≤≤︒,所以60260180θ︒≤+︒≤︒,则260150θ+︒=︒,所以45θ=︒.20.(1)∵四边形11BB C C 是菱形,∴11B C BC ⊥.∵1B C AB ⊥,1AB BC B =I ,∴1B C ⊥平面1ABC ,又AO ⊂平面1ABC ,∴1B C AO ⊥.∵1AC AB =,O 是1BC 的中点,∴1AO BC ⊥,又11B C BC O = ,∴AO ⊥平面11BB C C .(2)法一:∵11//AB A B ,∴直线11A B 与平面11BB C C 所成的角等于直线AB 与平面11BB C C 所成的角,∵AO ⊥平面11BB C C ,∴直线AB 与平面11BB C C 所成的角即ABO ∠,∴45ABO ∠= ,不妨设菱形11BB C C 的边长为2,则在等边三角形1BB C 中,3BO =,11CO B O ==,在Rt ABO △中,3AO BO ==.如图,以O 为坐标原点,分别以1,,OB OB OA 所在的直线为,,x y z 轴建立空间直角坐标系,则111(0,1,0),(0,1,0),(3,0,0),(0,0,3),(3,1,3)B C C A A ---,则1111(3,0,3),(3,1,0),(0,0,3)A B B C OA =-=--=.设平面111A B C 的法向量为1(,,)n x y z =,则111111·330·30n A B x z n B C x y ⎧=-=⎪⎨=--=⎪⎩ ,得1(1,3,1)n =- .易知平面11BB C C 的一个法向量为(0,0,3)OA =,则11135cos ,535n OA n OA n OA⋅===⨯,由图可知二面角111A B C B --为钝二面角,∴二面角111A B C B --的余弦值为55-.法二:几何法21.(1)∵等轴双曲线的离心率为2,∴椭圆的离心率22,又∵直线:20l x y -+=与以原点为圆心,以椭圆C 的短半轴长为半径的圆相切,∴222|1|1b +=,即1b =,可得22222112c b e a a ==-=,即22a =,则椭圆的方程为:2212x y +=;(2)①若直线AB 的斜率不存在,设方程为0x x =,则点0(A x ,0)y ,0(B x ,0)y -,由125k k +=,即0000115y y x x ---+=,解得025x =-,此时直线AB 的方程为25x =-;②若直线AB 的斜率存在,设AB 的方程为y kx m =+,由题意可得1m ≠±,设1(A x ,1)y ,2(B x ,2)y ,则22220y kx mx y =+⎧⎨+-=⎩,整理可得:222(12)4220k x kmx m +++-=,()()222222168121210k m k m k m ∆=-+-=+->,且122412km x x k +=-+,21222212m x x k -=+,由125k k +=,可得1212115y y x x --+=,即1212115kx m kx m x x +-+-+=,即12122(1)5x x k m x x ++-⋅=,2251km k m -=+,521k m =-,故直线AB 的方程为21()1255k y kx k x =+-=+-,即直线AB 过定点(125,)--,综上所述:直线AB 过定点(125,)--.22.(1)显然()f x 的定义域为(0,)+∞,因为2()ln 22(1)f x x ax a x =+++,所以()1(21)(21)422ax x f x ax a x x++'=+++=,若0a <,则当10,2x a ⎛⎫∈- ⎪⎝⎭时,()0f x '>,当1,2x a ⎛⎫∈-+∞ ⎪⎝⎭时,()0f x '<,故函数()f x 在10,2a ⎛⎫- ⎪⎝⎭上单调递增,在1,2a ⎛⎫-+∞ ⎪⎝⎭上单调递减;故()f x 在12x a =-处取得唯一的极大值,且极大值为111ln 222f a a a⎛⎫⎛⎫-=--- ⎪ ⎪⎝⎭⎝⎭ 1.若0a >,则当,()0x ∈+∞时()0f x '>恒成立,故函数()f x 在(0,)+∞上单调递增,无极值.综上,当0a <时,()f x 的极大值为11ln 122a a⎛⎫--- ⎪⎝⎭,无极小值;当0a >时,()f x 无极值.(2)当0a <时,若证[()2]1a f x +≥-恒成立,只需证1()2f x a≤--恒成立,即证max 1()2f x a≤--,由(1)知()f x 在12x a =-处取得最大值,最大值为111ln 1222f a a a ⎛⎫⎛⎫-=--- ⎪ ⎪⎝⎭⎝⎭,所以即证111ln 1222a a a ⎛⎫---≤-- ⎪⎝⎭,即证11ln 1022a a⎛⎫-++≤ ⎪⎝⎭.令12t a=-,因为0a <,所以0t >,则只需证明ln 10t t -+≤,令()ln 1g t t t =-+,0t >,则11()1tg t t t-'=-=,当(0,1)t ∈时,()0g t '>,当(1,)t ∈+∞时,()0g t '<.故()g t 在(0,1)上单调递增,在(1,)+∞上单调递减,故()(1)0g t g ≤=,故()0g t ≤,即ln 10t t -+≤.因此当0a <时,[()2]1a f x +≥-恒成立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六安中学第六次月考数学试题(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合=⋂-==<--=P M x y y P x x x M 那么},1|{},032|{2( )A .(0,3)B .)3,0[C .)3,1[D .),1[+∞-2.设函数⎩⎨⎧≥-<=)0(12)0(||lg )(x x x x f x,若0)(0>x f ,则0x 的取值范围是( )A.),1()1,(+∞--∞YB. ),0()1,(+∞--∞YC. )1,0()0,1(Y -D. ),0()0,1(+∞-Y3.直线022:2)2(:22=--++-=y x y x C x k y l 与圆相切,则直线l 的一个方向量=( )A .(2,-2)B .(1,1)C .(-3,2)D .(1,21) 4.函数32()f x x bx cx d =+++图象如图,则函数 2233cy x bx =++的单调递增区间为( ) A .]2,(--∞B .),3[+∞C .]3,2[-D .),21[+∞5.在AC AB S AC AB ABC ABC ⋅===∆∆则已知中,3,1||,4||,的值为( )A .—2B .2C .4±D .2±6.若第一象限内的点),(y x A 落在经过点(6,—2)且方向向量为)2,3(-=a 的直线l 上,则3223log log t y x =-有( )A .最大值23 B .最大值1 C .最小值23 D .最小值17.设M 是ABC ∆内任一点,且,30,320=∠=•BAC AC AB 设MAB MAC MBC ∆∆∆,,的面积分别为z y x ,,,且21=z ,则在平面直角中坐标系中,以,x y 为坐标的点),(y x 的轨迹图形是 ( )ACBD8.已知)4()5(),1()2)(1(:*,,35-⨯-=-+++=∈∈-M n x x x x M N n R x n x 例如定义ΛΛx COS M x f x 20062005)(,60)3(73⋅=-=-⨯-则函数 ( )A .是偶函数不是奇函数B .是奇函数不是偶函数C .既是奇函数、又是偶函数D .既不是奇函数又不是偶函数9、下列命题:①若)(x f 是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,)2,4(ππθ∈,则(sin )(cos ).f f θθ>②在ABC ∆中,A B >是cos cos A B <的充要条件. ③若,,a b c r r r为非零向量,且a b a c ⋅=⋅r r r r ,则b c =r r .④要得到函数sin2x y =的图像,只需将函数sin()24x y π=-的图像向右平移2π个单位.其中真命题的个数有( )A .1B .2C . 3D .410.若直线1x ya b+=通过点(cos sin )M αα,,则( ) A .221a b +≤ B .221a b +≥ C .22111a b+≤D .22111a b+≥ 11.在等比数列{}n a 中,若1234158a a a a +++=,2398a a =-,则12341111a a a a +++=( ) A .53B .35 C .53-D .35-12.已知F 1、F 2为椭圆E 的左右两个焦点,抛物线C 以F 1为顶点,F 2为焦点,设P 为椭圆与抛物线的一个交点,如果椭圆离心率为e ,且||||21PF e PF =则e 的值为 ( )A .22 B .32-C .33 D .22-二、填空题:本大题共4小题,每小题4分,共16分. 把答案填在题中横线上13、若命题04,:2>++∈∀c cx x R x p 对为真命题,则实数c 的取值范围是 . 14.函数x x x f cos 2)(+=在⎥⎦⎤⎢⎣⎡π2,0上的最大值为15. 有4张分别标有数字1,2,3,4的红色卡片和4张分别标有数字1,2,3,4的蓝色卡片,从这8张卡片中取出4张卡片排成一行.如果取出的4张卡片所标数字之和等于10,则不同的排法共有 种(用数字作答).16.已知某算法的流程图如图所示,若将输出的(,)x y 值依次记为11(,)x y 、22(,)x y 、…、(,)n n x y 、….(1)若程序运行中输出的一个数组是(,8)t -,则t = (2)程序结束时,共输出(,)x y 的组数为 .三.解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)已知向量a (cos ,2cos )x x =,向量b ()(2cos ,sin )x x π=-,若()f x =a ·b +1 .(I )求函数)(x f 的解析式和最小正周期;(II) 若⎥⎦⎤⎢⎣⎡∈2,0πx ,求)(x f 的最大值和最小值.18.已知函数f (x )=264xx -+,g (x )=x 2-3ax +2a 2(a <0),若不存在...实数x 使得f (x )>1和g (x )<0同时成立,试求a 的范围.19.已知过点A (0,1),且方向向量为22(1,):(2)(3)1a k l C x y =-+-=r 的直线与圆,相交于M 、N 两点.(1)求实数k 的取值范围;(2)若O 为坐标原点,且12,OM ON k ⋅=u u u u r u u u r求的值.20.(本小题满分12分)已知数列}{n a 的前n 项和为n S ,且有n n S n 211212+=,数列}{n b 满足0212=+-++n n n b b b)(*N n ∈,且113=b ,前9项和为153.(1)求数列}{n a 、}{n b 的通项公式; (2)设)12)(112(3--=n n n b a c ,数列}{n c 的前n 项和为n T ,求使不等式57k T n >对一切*N n ∈都成立的最大正整数k 的值.21. (本小题满分12分)在直角坐标系中,已知一个圆心在坐标原点,半径为2的圆,从这个圆上任意一点P 向y 轴作垂线段PP ′,P ′为垂足. (1)求线段PP ′中点M 的轨迹C 的方程;(2)过点Q (-2,0)作直线l 与曲线C 交于A 、B 两点,设N 是过点)0,174(-,且以)1,0(=为方向向量的直线上一动点,满足+=(O 为坐标原点),问是否存在这样的直线l ,使得四边形OANB 为矩形?若存在,求出直线l 的方程;若不存在,说明理由.22.(本小题满分14分) 设函数2132()x f x x eax bx -=++,已知2x =-和1x =为()f x 的极值点.(Ⅰ)求a 和b 的值;(Ⅱ)讨论函数()f x 的单调性; (Ⅲ)设322()3g x x x =-,比较()f x 与()g x 的大小.六安中学第六次月考数学试题(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1..B 2. B. 3. A 4. D 5. D 6. B7. A8. B 9、A10. D11. C12. C二、填空题:本大题共4小题,每小题4分,共16分. 把答案填在题中横线上 13、()1,0(,)4-∞⋃+∞14.6π+15. 432 16..81,1004三.解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分) 解:(I )∵a (cos ,2cos )x x =, b ()(2cos ,sin )x x π=-,∴()f x =a ·b +122cos 2cos sin()1x x x π=+-+- ------------------------------2分1cos sin 22cos 1+++=x x x - -------------------------------------------4分22sin 2cos ++=x x --------------------------------------------------------6分2)42sin(2++=πx . ------------------------------------------------------7分∴函数()f x 的最小正周期ππ==22T . -----------------------------8分 (II) ⎥⎦⎤⎢⎣⎡∈2,0πx Θ, ∴52,444x πππ⎡⎤+∈⎢⎥⎣⎦. ---------------------------------------------------------------------9分∴时即当8,242πππ==+x x ,()2f x 有最大值 -------------------10分时即当2,4542πππ==+x x ,()f x 有最小值1. ------------------------12分18.解:由f (x )>1,得264x x -+>1,化简整理得)2)(3()1)(2(+-+-x x x x <0.解得-2<x <-1或2<x <3.即f (x )>1的解集为A ={x |-2<x <-1或2<x <3}. 由g (x )<0得x 2-3ax +2a 2<0,即(x -a )(x -2a )<0(a <0). 则g (x )<0的解集为B ={x |2a <x <a ,a <0}.根据题意,有A ∩B =∅.因此,a ≤-2或-1≤2a <0.故a 的范围是{a |a ≤-2或-21≤a <0}.19.解:(1)(1,),l a k =rQ 直线过点(0,1)且方向向量 1l y kx ∴=+直线的方程为……………………2分1,<得4433k -<<……………………5分 1122(2)(,),(,)M x y N x y 设1y kx x =+22将代入方程(-2)+(y-3)=1得k x k x 22(1+)-4(1+)+7=0……………………11分212227,11k x x x x k k ∴=++124(1+)+=……………………12 2121212122(1)()18121k k OM ON x x y y k x x k x x k ∴⋅=+=++++=+=+u u u u r u u u r 4(1+)24,11k k k k∴==+4(1+)解得1,0,1k k =∆>∴=又当时……………………12分20.(本小题满分12分) 解:(1)因为n n S n 211212+=;故 当2≥n 时;51+=-=-n S S a n n n ;当1=n 时,611==S a ;满足上式; 所以5+=n a n ;又因为0212=+-++n n n b b b ,所以数列}{n b 为等差数列; 由1532)(9739=+=b b S ,113=b ,故237=b ;所以公差3371123=--=d ; 所以:23)3(3+=-+=n d n b b n ; …………5分 (2)由(1)知:)12)(12(1)12)(112(3+-=--=n n b a c n n n而)121121(21)12)(12(1)12)(112(3+--=+-=--=n n n n b a c n n n ;所以:n n c c c T +++=Λ21)]121121()5131()311[(21+--++-+-=n n Λ 12)1211(21+=+-=n nn ;又因为0)12)(32(1123211>++=+-++=-+n n n n n n T T n n ;所以}{n T 是单调递增,故31)(1min ==T T n ; 由题意可知5731k >;得:19<k ,所以k 的最大正整数为18; …………12分 21. (本小题满分12分) 解:(1)设M (x ,y )是所求曲线上的任意一点,P (x 1,y 1)是方程x 2 +y 2 =4的圆上的任意一点,则).,0(1y P '则有:44,2,222211111=+⎩⎨⎧==⎪⎪⎩⎪⎪⎨⎧+==y x y y x x y y y x x 代入即得, 轨迹C 的方程为.1422=+y x (1)当直线l 的斜率不存在时,与椭圆无交点.所以设直线l 的方程为y = k (x +2),与椭圆交于A (x 1,y 1)、B (x 2,y 2)两点,N 点所在直线方程为.0174=+x 由.0444)4()2(14222222=-+++⎪⎩⎪⎨⎧+==+k x k x k x k y y x 得 由△= .34,0)44)(4(4162224≤∴≥-+-k k k k 即.332332≤≤-k (4)1(4,4422212221k k x x k k x x +-=+-=+ ,+=Θ即OB AN =,∴四边形OANB 为平行四边形 假设存在矩形OANB ,则0=⋅OB OA ,即02121=+y y x x , 即04)(2)1(2212212=++++k x x k x x k ,于是有0441622=+-k k 得.21±=k … 设17444),,(2221000-=+-=+=+=k k x x x y x N 得由,即点N 在直线174-=x 上. ∴存在直线l 使四边形OANB 为矩形,直线l 的方程为).2(21+±=x y22(本小题满分14分)【解:】(Ⅰ)因为122()e (2)32x f x x x ax bx -'=+++1e (2)(32)x x x x ax b -=+++,又2x =-和1x =为()f x 的极值点,所以(2)(1)0f f ''-==,因此620,3320,a b a b -+=⎧⎨++=⎩解该方程组得13a =-,1b =-.(Ⅱ)因为13a =-,1b =-,所以1()(2)(e 1)x f x x x -'=+-,令()0f x '=,解得12x =-,20x =,31x =. 因为当(,2)x ∈-∞-(0,1)U 时,()0f x '<; 当(2,0)(1,)x ∈-+∞U 时,()0f x '>.所以()f x 在(2,0)-和(1,)+∞上是单调递增的;在(,2)-∞-和(0,1)上是单调递减的.(Ⅲ)由(Ⅰ)可知21321()e3x f x x x x -=--, 故21321()()e (e )x x f x g x x x x x ---=-=-,令1()e x h x x -=-,则1()e 1x h x -'=-. 令()0h x '=,得1x =,因为(,1)x ∈-∞时,()0h x '<,所以()h x 在(,1)x ∈-∞上单调递减.故(,1)x ∈-∞时,()(1)0h x h >=; 因为(1,)x ∈+∞时,()0h x '>,所以()h x 在(1,)x ∈+∞上单调递增. 故(1,)x ∈+∞时,()(1)0h x h >=.所以对任意(,1)(1,)x ∈-∞+∞U ,恒有()0h x >,又0x ≠时,20x >, 因此0x ≠且1x ≠时()()0f x g x ->,1x =或0x =时()()0f x g x -=, 所以, (1)0x ≠且1x ≠时()()f x g x >(2) 1x =或0x =时,()()f x g x =【注:】按以下做法不扣分(以下是高考命题人给的原解)这种解法不太严谨,但也被大部分人所接受(Ⅲ)由(Ⅰ)可知21321()e3x f x x x x -=--, 故21321()()e (e )x x f x g x x x x x ---=-=-,令1()e x h x x -=-,则1()e 1x h x -'=-. 令()0h x '=,得1x =,因为(,1]x ∈-∞时,()0h x '≤,所以()h x 在(,1]x ∈-∞上单调递减.故(,1]x ∈-∞时,()(1)0h x h ≥=; 因为[1,)x ∈+∞时,()0h x '≥,所以()h x 在[1,)x ∈+∞上单调递增. 故[1,)x ∈+∞时,()(1)0h x h ≥=.所以对任意(,)x ∈-∞+∞,恒有()0h x ≥,又20x ≥,因此()()0f x g x -≥, 故对任意(,)x ∈-∞+∞,恒有()()f x g x ≥.六安中学第六次月考数学试题(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合=⋂-==<--=P M x y y P x x x M 那么},1|{},032|{2(.B )A .(0,3)B .)3,0[C .)3,1[D .),1[+∞-2.设函数⎩⎨⎧≥-<=)0(12)0(||lg )(x x x x f x,若0)(0>x f ,则0x 的取值范围是(B. )A.),1()1,(+∞--∞YB. ),0()1,(+∞--∞YC. )1,0()0,1(Y -D. ),0()0,1(+∞-Y3.直线022:2)2(:22=--++-=y x y x C x k y l 与圆相切,则直线l 的一个方向量=( A )A .(2,-2)B .(1,1)C .(-3,2)D .(1,21) 4.函数32()f x x bx cx d =+++图象如图,则函数 2233cy x bx =++的单调递增区间为( D ) A .]2,(--∞B .),3[+∞C .]3,2[-D .),21[+∞5.在S ABC ABC ⋅===∆∆则已知中,3,1||,4||,的值为( D )A .—2B .2C .4±D .2±6.若第一象限内的点),(y x A 落在经过点(6,—2)且方向向量为)2,3(-=a 的直线l 上,则3223log log t y x =-有(B )A .最大值23 B .最大值1 C .最小值23 D .最小值1 7.设M 是ABC ∆内任一点,且,30,320=∠=•BAC 设MABMAC MBC ∆∆∆,,的面积分别为z y x ,,,且21=z ,则在平面直角中坐标系中,以,x y 为坐标的点),(y x 的轨迹图形是 (A )8.已知)4()5(),1()2)(1(:*,,35-⨯-=-+++=∈∈-M n x x x x M N n R x n x 例如定义ΛΛx COS M x f x 20062005)(,60)3(73⋅=-=-⨯-则函数 ( B )A .是偶函数不是奇函数B .是奇函数不是偶函数C .既是奇函数、又是偶函数D .既不是奇函数又不是偶函数9、下列命题:①若)(x f 是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,)2,4(ππθ∈,则(sin )(cos ).f f θθ>②在ABC ∆中,A B >是cos cos A B <的充要条件. ③若,,a b c r r r为非零向量,且a b a c ⋅=⋅r r r r ,则b c =r r .④要得到函数sin2x y =的图像,只需将函数sin()24x y π=-的图像向右平移2π个单位.其中真命题的个数有(A )A .1B .2C . 3D .410.若直线1x ya b+=通过点(cos sin )M αα,,则(D ) A .221a b +≤ B .221a b +≥ C .22111a b+≤D .22111a b+≥ 11.在等比数列{}n a 中,若1234158a a a a +++=,2398a a =-,则12341111a a a a +++=( C )A .53B .35C .53-D .35-12.已知F 1、F 2为椭圆E 的左右两个焦点,抛物线C 以F 1为顶点,F 2为焦点,设P 为椭圆与抛物线的一个交点,如果椭圆离心率为e ,且||||21PF e PF =则e 的值为(C )ACBDA .22 B .32-C .33 D .22-二、填空题:本大题共4小题,每小题4分,共16分. 把答案填在题中横线上13、若命题04,:2>++∈∀c cx x R x p 对为真命题,则实数c 的取值范围是 .()1,0(,)4-∞⋃+∞ 14.函数x x x f cos 2)(+=在⎥⎦⎤⎢⎣⎡π2,0上的最大值为 36π+15. 有4张分别标有数字1,2,3,4的红色卡片和4张分别标有数字1,2,3,4的蓝色卡片,从这8张卡片中取出4张卡片排成一行.如果取出的4张卡片所标数字之和等于10,则不同的排法共有 种(用数字作答).43216.已知某算法的流程图如图所示,若将输出的(,)x y 值依次记为11(,)x y 、22(,)x y 、…、(,)n n x y 、….(1)若程序运行中输出的一个数组是(,8)t -,则t = ; (2)程序结束时,共输出(,)x y 的组数为 .81,1004三.解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)已知向量a (cos ,2cos )x x =,向量b ()(2cos ,sin )x x π=-,若()f x =a ·b +1 .(I )求函数)(x f 的解析式和最小正周期;(II) 若⎥⎦⎤⎢⎣⎡∈2,0πx ,求)(x f 的最大值和最小值. 17.(本小题满分12分)解:(I )∵a (cos ,2cos )x x =, b ()(2cos ,sin )x x π=-,∴()f x =a ·b +122cos 2cos sin()1x x x π=+-+- ------------------------------2分1cos sin 22cos 1+++=x x x - -------------------------------------------4分22sin 2cos ++=x x --------------------------------------------------------6分2)42sin(2++=πx . ------------------------------------------------------7分∴函数()f x 的最小正周期ππ==22T . -----------------------------8分 (II) ⎥⎦⎤⎢⎣⎡∈2,0πx Θ, ∴52,444x πππ⎡⎤+∈⎢⎥⎣⎦. ---------------------------------------------------------------------9分∴时即当8,242πππ==+x x ,()2f x 有最大值 -------------------10分时即当2,4542πππ==+x x ,()f x 有最小值1. ------------------------12分 18.已知函数f (x )=264xx -+,g (x )=x 2-3ax +2a 2(a <0),若不存在...实数x 使得f (x )>1和g (x )<0同时成立,试求a 的范围.18.解:由f (x )>1,得264x x -+>1,化简整理得)2)(3()1)(2(+-+-x x x x <0.解得-2<x <-1或2<x <3.即f (x )>1的解集为A ={x |-2<x <-1或2<x <3}. 由g (x )<0得x 2-3ax +2a 2<0,即(x -a )(x -2a )<0(a <0). 则g (x )<0的解集为B ={x |2a <x <a ,a <0}.根据题意,有A ∩B =∅.因此,a ≤-2或-1≤2a <0.故a 的范围是{a |a ≤-2或-21≤a <0}.19.已知过点A (0,1),且方向向量为22(1,):(2)(3)1a k l C x y =-+-=r 的直线与圆,相交于M 、N 两点.(1)求实数k 的取值范围;(2)若O 为坐标原点,且12,OM ON k ⋅=u u u u r u u u r求的值.19.解:(1)(1,),l a k =rQ 直线过点(0,1)且方向向量 1l y kx ∴=+直线的方程为……………………2分1,<得4433k -<<……………………5分 1122(2)(,),(,)M x y N x y 设1y kx x =+22将代入方程(-2)+(y-3)=1得k x k x 22(1+)-4(1+)+7=0……………………11分212227,11k x x x x k k ∴=++124(1+)+=……………………12 2121212122(1)()18121k k OM ON x x y y k x x k x x k ∴⋅=+=++++=+=+u u u u r u u u r 4(1+)24,11k k k k∴==+4(1+)解得1,0,1k k =∆>∴=又当时……………………12分20.(本小题满分12分)已知数列}{n a 的前n 项和为n S ,且有n n S n 211212+=,数列}{n b 满足0212=+-++n n n b b b)(*N n ∈,且113=b ,前9项和为153.(2)求数列}{n a 、}{n b 的通项公式; (2)设)12)(112(3--=n n n b a c ,数列}{n c 的前n 项和为n T ,求使不等式57k T n >对一切*N n ∈都成立的最大正整数k 的值.解:(1)因为n n S n 211212+=;故当2≥n 时;51+=-=-n S S a n n n ;当1=n 时,611==S a ;满足上式; 所以5+=n a n ;又因为0212=+-++n n n b b b ,所以数列}{n b 为等差数列; 由1532)(9739=+=b b S ,113=b ,故237=b ;所以公差3371123=--=d ; 所以:23)3(3+=-+=n d n b b n ; …………5分 (2)由(1)知:)12)(12(1)12)(112(3+-=--=n n b a c n n n而)121121(21)12)(12(1)12)(112(3+--=+-=--=n n n n b a c n n n ;所以:n n c c c T +++=Λ21)]121121()5131()311[(21+--++-+-=n n Λ 12)1211(21+=+-=n nn ; 又因为0)12)(32(1123211>++=+-++=-+n n n n n n T T n n ;所以}{n T 是单调递增,故31)(1min ==T T n ; 由题意可知5731k >;得:19<k ,所以k 的最大正整数为18; …………12分 21. (本小题满分12分)在直角坐标系中,已知一个圆心在坐标原点,半径为2的圆,从这个圆上任意一点P 向y 轴作垂线段PP ′,P ′为垂足. (1)求线段PP ′中点M 的轨迹C 的方程;(2)过点Q (-2,0)作直线l 与曲线C 交于A 、B 两点,设N 是过点)0,174(-,且以)1,0(=a 为方向向量的直线上一动点,满足+=(O 为坐标原点),问是否存在这样的直线l ,使得四边形OANB 为矩形?若存在,求出直线l 的方程;若不存在,说明理由. 解:(1)设M (x ,y )是所求曲线上的任意一点,P (x 1,y 1)是方程x 2 +y 2 =4的圆上的任意一点,则).,0(1y P '则有:44,2,222211111=+⎩⎨⎧==⎪⎪⎩⎪⎪⎨⎧+==y x y y x x y y y x x 代入即得, 轨迹C 的方程为.1422=+y x (1)当直线l 的斜率不存在时,与椭圆无交点.所以设直线l 的方程为y = k (x +2),与椭圆交于A (x 1,y 1)、B (x 2,y 2)两点,N 点所在直线方程为.0174=+x 由.0444)4()2(14222222=-+++⎪⎩⎪⎨⎧+==+k x k x k x k y y x 得 由△= .34,0)44)(4(4162224≤∴≥-+-k k k k 即.332332≤≤-k (4)1(4,4422212221k k x x k k x x +-=+-=+,+=Θ即=,∴四边形OANB 为平行四边形 假设存在矩形OANB ,则0=⋅OB OA ,即02121=+y y x x , 即04)(2)1(2212212=++++k x x k x x k ,于是有0441622=+-k k 得.21±=k … 设17444),,(2221000-=+-=+=+=k k x x x OB OA ON y x N 得由,即点N 在直线174-=x 上. ∴存在直线l 使四边形OANB 为矩形,直线l 的方程为).2(21+±=x y 22.(本小题满分14分) 设函数2132()x f x x eax bx -=++,已知2x =-和1x =为()f x 的极值点.(Ⅰ)求a 和b 的值;(Ⅱ)讨论函数()f x 的单调性; (Ⅲ)设322()3g x x x =-,比较()f x 与()g x 的大小.22(本小题满分14分)【解:】(Ⅰ)因为122()e (2)32x f x x x ax bx -'=+++1e (2)(32)x x x x ax b -=+++,又2x =-和1x =为()f x 的极值点,所以(2)(1)0f f ''-==,因此620,3320,a b a b -+=⎧⎨++=⎩解该方程组得13a =-,1b =-.(Ⅱ)因为13a =-,1b =-,所以1()(2)(e 1)x f x x x -'=+-,令()0f x '=,解得12x =-,20x =,31x =. 因为当(,2)x ∈-∞-(0,1)U 时,()0f x '<; 当(2,0)(1,)x ∈-+∞U 时,()0f x '>.所以()f x 在(2,0)-和(1,)+∞上是单调递增的;在(,2)-∞-和(0,1)上是单调递减的.(Ⅲ)由(Ⅰ)可知21321()e3x f x x x x -=--, 故21321()()e (e )x x f x g x x x x x ---=-=-,令1()e x h x x -=-,则1()e 1x h x -'=-. 令()0h x '=,得1x =,因为(,1)x ∈-∞时,()0h x '<,所以()h x 在(,1)x ∈-∞上单调递减.故(,1)x ∈-∞时,()(1)0h x h >=; 因为(1,)x ∈+∞时,()0h x '>,所以()h x 在(1,)x ∈+∞上单调递增. 故(1,)x ∈+∞时,()(1)0h x h >=.所以对任意(,1)(1,)x ∈-∞+∞U ,恒有()0h x >,又0x ≠时,20x >, 因此0x ≠且1x ≠时()()0f x g x ->,1x =或0x =时()()0f x g x -=, 所以, (1)0x ≠且1x ≠时()()f x g x >(2) 1x =或0x =时,()()f x g x =【注:】按以下做法不扣分(以下是高考命题人给的原解)这种解法不太严谨,但也被大部分人所接受(Ⅲ)由(Ⅰ)可知21321()e3x f x x x x -=--, 故21321()()e (e )x x f x g x x x x x ---=-=-,令1()e x h x x -=-,则1()e 1x h x -'=-. 令()0h x '=,得1x =,因为(,1]x ∈-∞时,()0h x '≤,所以()h x 在(,1]x ∈-∞上单调递减.故(,1]x ∈-∞时,()(1)0h x h ≥=; 因为[1,)x ∈+∞时,()0h x '≥,所以()h x 在[1,)x ∈+∞上单调递增. 故[1,)x ∈+∞时,()(1)0h x h ≥=.所以对任意(,)x ∈-∞+∞,恒有()0h x ≥,又20x ≥,因此()()0f x g x -≥, 故对任意(,)x ∈-∞+∞,恒有()()f x g x ≥.。
