《电路原理导论》第六章习题解答
电子电路基础第六章习题答案

第六章习题6. 1求习题图6・1所示的电路的传递函数H(a)) = V o/V t•习题图6. 1•• RH ——解:(%-匕)-MC 八V jwLjcoL - 3、RLCR + jcoL-cerRLCjcoCR一ja)CR — e f CL6・2对于习题图6. 2所示的电路,求传递函数二丿6. 3串联RLC网络有R二5G, L二10川H, C二1 “F,求该电路的谐振角频率.特征阻抗和品质因数。
当外加电压有效值为24V时,求谐振电流、电感和电容上的电压值。
解:电路的谐振角频率卧忌一皿特征阻抗0二姑= 100。
品质因数0二二20谐振电流人吕十A电感和电容上的电压值U L = U c = U a Q = 480V 6・4设计一个串联RLC电路,使其谐振频率q 二50m〃/“品质因数为80,且谐振时的阻抗为10Q,并求英带宽。
解:B 二色=0. 625rad / 56. 5对于习题图6. 5所示的电路,求和,(/)为同相时的频率解••阶S叫+盏血5将厶二1乩厶二\H、C =一"+ y(w_ ♦W 1 + M rIQ F卜I w谐振时虚部为零,沙——+——二0W 1 +讥厂得出,W二0・7861 6. 6并联RLC网络有R二50G, L二4〃M・C二160 “八求并联电路谐振频率和品质因数。
若外接电流源有效值为2A,求谐振时电阻、电感及电容上的电流值。
解:电路的谐振角频率%二二I・25xl0rad/s4LC品质因数Q二毬CR ==10谐振时电阻、电感及电容上的电流值h二2AJ L二Ic二I K・Q = 2OA6. 7并联谐振电路,其品质因数为120,谐振频率是6x10%/ 〃/ “计算其带宽。
6・8计算习题图6. 8所示的电路的谐振角频率叫,品质因数Q和带宽Bo3好20m H 冒2jfcQ i6“戸〒习题图6・81 1 1 c C 1解:y 二 >・(5//C2)+一+— = 一+7 (=_)谐振时Y的虚部为0沙• g-一丄=0 C] + C、wL得出w =Q = qRC = CD O R(C( //CJ 二20B二八二2^0rad/.y 6. 9习题图6. 9所示的电路,已知电容值C为固圧,欲使电路在© 时发生并联谐振,而在©时发生串联谐振,求厶、乙的值。
电子电路第六章习题及参考答案

习题六6-1 什么是本征半导体?什么是杂质半导体?各有什么特征?答:所谓本征半导体就是指完全纯净的、结构完整的半导体。
在本征半导体中掺入杂质后的半导体称为杂质半导体。
本征的半导体中的自由电子数量和空穴的数量是相等的,而杂质半导体中根据掺杂的元素不同可分为N 型半导体和P 型半导体,在N 型半导体中电子的浓度远远大于空穴的浓度,而P 型半导体恰恰相反。
6-2 掺杂半导体中多数载流子和少数载流子是如何产生的?答:在本征半导体中,由于半导体最外层有四个电子,它与周边原子的外层电子组成共价键结构,价电子不仅受到本身原子核的约束,而且受到相邻原子核的约束,不易摆脱形成自由电子。
但是,在掺杂的半导体中,杂质与周边的半导体的外层电子组成共价键,由于杂质半导体的外层电子或多(5价元素)或少(3价元素),必然有除形成共价键外多余的电子或不足的空穴,这些电子或空穴,或者由于受到原子核的约束较少容易摆脱,或者容易被其它的电子填充,就形成了容易导电的多数载流子。
而少数载流子是相对于多数载流子而言的另一种载流子,它是由于温度、电场等因素的影响,获得更多的能量而摆脱约束形成的。
6-3,黑表笔插入COM ,红表笔插入V/Ω(红笔的极性为“+”),将表笔连接在二极管,其读数为二极管正向压降的近似值。
用模拟万用表测量二极管时,万用表内的电池正极与黑色表笔相连;负极与红表笔相连。
测试二极管时,将万用表拨至R ×1k 档,将两表笔连接在二极管两端,然后再调换方向,若一个是高阻,一个是低阻,则证明二极管是好的。
当确定了二极管是好的以后就非常容易确定极性,在低阻时,与黑表笔连接的就是二极管正极。
6-4 什么是PN 结的击穿现象,击穿有哪两种。
击穿是否意味着PN 结坏了?为什么? 答:当PN 结加反向电压(P 极接电源负极,N 极接电源正极)超过一定的时候,反向电流突然急剧增加,这种现象叫做PN 结的反向击穿。
击穿分为齐纳击穿和雪崩击穿两种,齐纳击穿是由于PN 结中的掺杂浓度过高引起的,而雪崩击穿则是由于强电场引起的。
电路理论习题答案 第六章

第六章习题答案6.1---6.12 : B 、A 、E 、B 、B 、A 、C 、C 、D 、E 、C 、C6.13、(1)012()()()30)()i t i t i t t A ω=+=+∴)I A == (2)12()()()1)()i t i t i t t A ω=+=+ ∴I ==(3)012()()()60))i t i t i t t t ωω=+=++6.14、∵ 0001()ab Y j j c R j L ωωω=++∴ 2220001Re[()]Re[]2()ab ab R L Z j R Y j R ωωω+=== 故得:0R L ω=,012C R ω=6.15、02()0.67cos(2130)i t t =- 6.16、将02()sin 2cos(290)i t t t ==-,因为两个电流为同频率同一函数形式,可以得到其相量模型,列回路方程即可求得:01143.1()U V =<,故01()cos(2143.1)()U t t V =+。
6.17、激励 ()s i t 和 ()s u t 不同频率,只能在时域使用迭加定理:()s u t 单独作用,用相量法及.00011.8()10.2cos(511.8)i t t I ∴=+' A()s i t 单独作用,用相量法得.00015() 2.06cos(415)I i t t ''''∴=+ A 即有: 000()()()i t i t i t '''=+6.18、因为回转器输出端口的阻抗可求得为:'''22221211221121[()]ab ab ab R L Z j R jX n n c n n n n ωω=+-++=+所以2'2'2''2'2'2'2()()()()ab ab ab ab ab ab ab ab r R r X r Z j Z R X R X ==-++ab ab R jX =-(设ab X >0) 6.19、0()56.3)()U t t V =-6.20、(1)0123//861036.9()Z Z Z Z j =+=-=∠-Ω .0136.9()s U A Z I ∴==∠(2) 2Re 8P I Z W ==26(var)Q I lmZ ==-S = 0.8P S λ∴==6.21、* 1.8580.564()Ls Z Z j ==+Ωm a x 8.107()L P w = 6.22、由并联电路图6-47可知:L= 310-H(1) 710210()()1010()Z j j ωωω=Ω+- (2)2010(/)rad s ω=(3)210(/)BW rad s = (4) 310Q =6.23、∵方波的傅立叶级数为:11140011()100[sin 3sin 5sin 5]()35s U t t t t V ωωωπ=++++ΛΛ 基频 312210/rad s T πωπ==⨯∵ ()()()j L L H j R j L s U j U j ωωωωω∙==+ ∴ ()()()()L s s j L U j H j U j U j R j L ωωωωωω==+ 故:000()()()(0)(0)0L s s U j H j U j H j U j ωωω===,0U ∞=(直流分量) 00101400()()00.95517.66L s U H j U j ωωπ==∠⨯∠,0011121.28cos(17.66)()U t V ω=+ 000340000.993 6.0542.1173.953L U π=+∠⨯∠=∠,0031()42.1cos(3173.95)()U t t V ω=- 000540000.998 3.6625.35 3.665L U π=+∠⨯∠=∠,0051()25.35cos(5 3.66)()U t t V ω=- ………………∴ 0135()()()()()L L L L L U t U t U t U t U t =++++ΛΛ6.24、(1) 00111222cos cos P U I U I U I =+Φ+Φ+(2) 111222sin sin Q U I U I =Φ+Φ+0104sin45sin 040(var)2Q O π=⨯++⨯= (3)因S UI ++则有25146.4()S V A == (4)∵奇变功率T = ∴139.4T W== (5)20cos 0.137146.4P S λ=Φ===6.25、∵ C 对直流等效成开路, ∴ ()103cos s U t t =+中只有交流信号才提供输出功率,因此端口的戴维宁等效电路参数为:..001301msm R R j L jz U U ω==⨯∠++ (采用最大值相量)21.20.61.8()0.6g j t -=-=- 10.80.6()s R j l Z j j c R j l ωωω=+=-Ω+故*0.80.6()L s Z Z j ==+Ω时负载获得max L P ∴22m a x 8)0.28880.8om L U P w RS ===⨯6.26、∵ 由理想变压器的性质可知21 2.5n n n ==,2s u nu =-,1b a i i n =, ∴ 2 2.5s u u =-, 0.4b a i i =∵ 由KCL 定理可知:2b a u i i R -=+ , 2.50.4s a a u i i R -=+ 02.140a i =∠,00.8560b i =∠即为所求6.27、(1)设R1,.1s U 组合支路的端点为ab ,因为.1s U ,.2s U 为同频率相量,可以在ω域使用迭加定理。
《电路理论基础》(第三版 陈希有)习题答案第六章

答案6.22解:对图(a)电路做戴维南等效,如图(b)所示。
OC U inZ (b)i j 1/(j )Z L C ωω=+ (1)SOC j I U Cω=(2) 由图(b)可知,当i 0Z =时,电阻两端电压U 与电阻R 无关,始终等于OC (0)U R ≠。
由式(1)解得1/100rad/s ω== 将式(3)代入式(2)得OC 1100A 1090V j100rad/s 0.01FU U ==∠︒⨯=∠-︒⨯90V u t ω=-()答案6.23解:先对图(a)电路ab 端左侧电路作戴维南等效,如图(b)所示。
U iZ (b)令32000rad/s 210H 4L X L ω-==⨯⨯=Ω得等效阻抗i 4j48//8//j42(1j)4j4Z Ω⨯Ω=ΩΩΩ==+ΩΩ+Ω由OCi 1j U i Z R Cω=++知,欲使电流i 有效值为最大,电容的量值须使回路阻抗虚部为零,即:012]j 1Im[=-=++CC R Z i ωω 等效后电路如图(b)所示。
解得1250μF 2C ω==答案6.24解:应用分压公式,输出电压o U 可表示为o n1n 2U U U =-i i 1j 12j U C U R Cωω=-⨯+ i i i j 121j 2(j 1)U U CR U CR CR ωωω-=-=++ 当 0=R , o U 超前于i U 180;当 1R Cω=,o U 超前于i U ︒90;当 ∞→R , o U 与i U 同相位。
即当R 由零变到无穷时,o U 超前于i U 相位差从180到0变化。
答案6.25解:图示电路负载等效导纳为22221j j()j ()()R LY C C R L R L R L ωωωωωω=+=+-+++ (1) 22222222222)()(21)()(C L R LC L R L C L R R Yωωωωωωω++-=⎥⎥⎦⎤⎢⎢⎣⎡+-+⎥⎥⎦⎤⎢⎢⎣⎡+= (2) 由式(2)可见:当)2/(12LC =ω时,Y C ω=与R 无关,电流有效值CU U Y I ω==不随R 改变。
电路理论基础第三版陈希有第六章答案

第六章答案6.1解:将2i 和3i 改写为余弦函数的标准形式,即234cos(190)A 4cos(190180)A 4cos(10)A5sin(10)A 5cos(1090)A 5cos(80)Ai t t t i t t t ωωωωωω=-+︒=+︒-︒=+︒=+︒=+︒-︒=-︒电压、电流的有效值为12370.7V, 1.414A 2.828A, 3.54A U I I I ======== 初相位12310,100,10,80u i i i ψψψψ====-相位差111010090u i ϕψψ=-=-=- 11u i u i 与正交,滞后于; 2210100u i ϕψψ=-=︒-︒= u 与2i 同相; 3310(80)90u i ϕψψ=-=︒--︒= u 与3i 正交,u 超前于3i答案6.2()()()().a 10cos(10)V-8b arctg 10233.1V,233.1)V -6-20.8c arctg 20.889.4A,20.8cos(89.4)A 0.2d 30180A,180)A m u t U u t I i t I i t ωωωω=-︒==∠︒=+︒==∠-︒=-︒=∠︒=+︒答案6.3解:(a)利用正弦量的相量表示法的线性性质得:11221,U I n U I n ==- (b)磁通相量通常用最大值表示,利用正弦量的相量表示法的微分性质得:mj m U N ω=Φ (c) 利用正弦量的相量表示法的线性性质与微分性质得:j URI LI ω=+答案6.4解:由KCL 得电流i 的振幅相量m 1m 2m 3mI I I I =++ (2100410580)A =∠︒+∠︒+∠-︒(0.347j 1.97 3.939j0.6950.868j4.924)A =-++++-A 86.265︒-∠=电流i 的瞬时值为5cos(26.86)A i t ω=-︒答案6.5解:电压表和电流表读数为有效值,其比值为阻抗模,即/U I =将已知条件代入,得100V 15A 100V10⎧=⎪⎪=Ω 联立方程,解得13.7mH, 5.08L R ==Ω答案6.6解:(a) RC 串联电路中电阻电压与电容电压相位正交,各电压有效值关系为30V U ===电流i 的有效值为30V 3A 10C C U I I X ====Ω(b)302A 60V C C U X I ==Ω⨯=60V 1.2A 50R U I R ===ΩRC 并联电路中电阻电流与电容电流相位正交,总电流有效值为2.33I A === (c)30130C C C U X I A V ==Ω⨯=由30215C L C L L L U V U U X I I A X ==⇒===Ω并联电容、电感上电流相位相反,总电流为1L C I I I A =-= 电阻电压与电容电压相位正交,总电压为:50U V ===答案6.7解:感抗()3210rad/s 0.1H 200L X L ω==⨯⨯=Ω容抗()()3611100210rad/s 510FC X C ω--=-==-Ω⨯⨯⨯ 图(a)电路的相量模型如图(b)所示。
《电路原理导论》第六章习题解答

习题六6-1某三相变压器其绕组作星形联接,额定相电压为230V ,在一次检修后测得相电压V 230===C B A U U U ,但测得线电压V 400;V 230===BC CA AB U U U ,试用相量图分析,这种现象是怎么造成得,如何纠正。
解:A 相首末端倒反以后会出现这种情况,如图示6-2某三相供电电路,其每相阻抗Ω=8L Z ,那么此电路一定是对称三相电路吗? 6-3在三相四线制供电线路中中线电流等于0,那么此时三相负载一定是对称负载吗? 试用相量图分析说明在什么条件下,不对称负载也可能出现中线电流等于0。
解:不对称的三相电流有可能合成中线电流等于0。
其条件是0sin sin sin 0cos cos cos =++=++C CC B B B A A A C CC B B BA A A Z U Z UZ U Z U Z U Z U ψψψψψψ式中ψ是电流的初相角,不是阻抗角φ,图6—3′为一例。
6-4在三相Y ˿Y 供电系统中,对称负载Ω+=66.85j Z L ,负载相电压等于220V ,试求线电流,每相有功功率和无功功率以及功率因数。
答:A 022 ∠=A I ;5.0cos =φ; VA j S P56.41912420604840+=∠= 解:设 0220∠=AU 6-5在三相四线制供电系统中,电源侧线电压等于400V ,对称负载Ω+=66.85j Z L 线路阻抗Ω+=11j Z l ,Ω+=12j Z n ,试求线电流及负载端的线电压。
解:V 2313==l SP U U ,设V 0231∠=AU ,则 6-6在三相Y ˿Y 供电系统中,电源侧线电压等于400V ,不对称负载,Ω=5A Z ,Ω+=55j Z B ,Ω-=86j Z C ,试求中线断开时负载端的中性点位移及各相电压。
解:设 0230∠=SAU ,用弥尔曼定理求中性点位移 (a )(b )图6—3′()()()()()()()()()V 172232.14281.2718.336.05.14501.1002.036.067.525.808.006.01.01.02.075.283.2242.842.314613.531.0451414.02.013.1732316553.324613.531014507.715113.53101202304507.712023050230j j j j j j j U NN --=-∠=-∠-∠=---=++-++-+--+=∠+-∠+∠+-∠+=-∠+∠+-∠∠+∠-∠+∠='各相负载电压 6-7在三相Y ˿Y 供电系统中,电源侧线电压等于400V ,线路阻抗Ω+=11j Z l ,Ω+=12j Z n ,不对称负载,Ω=5A Z ,Ω+=55j Z B ,Ω-=86j Z C ,试求中性点位移及各相电压。
电路理论课后答案,带步骤
解:(1)该电路有三个网孔。设网孔电流分别为 、 ,
参考方向如图3-4所示。并设受控源两端电压为U。
(2)列写网孔方程:
辅助方程为:
联立求解得:
U= V
所以: mW
3-5电路如题图3-5所示,试用网孔分析法求电流 和电压 。
题图3-5题图3-5(b)
解:(1)将原图中20A电流源与2 电阻并联部分等效为40V电压源与2 电阻串联,如图3-5(b)所示。
(2)列写节点方程:
整理得:
求解得: V
V
所以: V
3-7电路如题图3-7所示,①试用节点分析法列写电路的节点方程;②该电路能否用网孔分析法分析?为什么?
题图3-7题图3-7(b)
①解:
(1)将原图中的 电压源与 串联部分等效为 电流源与 并联。
且 。如图3-7(b)所示。
(2)该电路有5个节点,以节点5为参考点,节点电压分别设为: 、 、 ,
Ua=10-3I=4V
Ub=2I=4V
Uab=Ua–Ub=0V
题图1-2
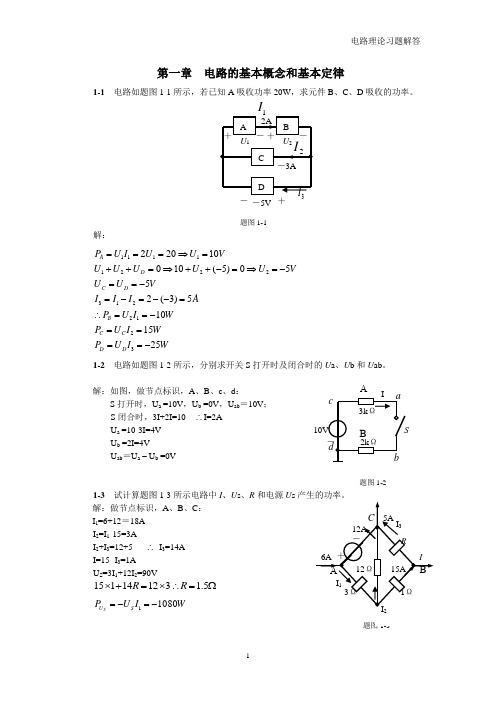
1-3试计算题图1-3所示电路中I、Us、R和电源Us产生的功率。
解:做节点标识,A、B、C:
I1=6+12=18A
I2=I1-15=3A
I2+I3=12+5 I3=14A
I=15- I3=1A
US=3I1+12I2=90V
题图1-3
2-15题图2-15所示电路,试问当电阻R等于何值时,可获得最大功率,最大功率等于多少?
题图2-15图2-15(b)
解:先将a,b与R断开,则
得:
所以:共戴维南等效电路为图(a)所示
所以:当 时,获得最大功率
电子电路基础第六章习题答案

第六章习题6.1 求习题图6.1所示的电路的传递函数()/o i H V V ω=gg。
习题图6.1解:1//()i o oR V V jwCjwLV -=g gg22()oi V j L RLCH R j L RLCV ωωωωω-==+-gg 6.2 对于习题图6.2所示的电路,求传递函数()o iI H I ω=gg。
习题图6.2解:2()11o iI R j CRH j CR CL I jwL R jwCωωωω===-+++gg6.3 串联RLC 网络有R=5Ω,L=10mH ,C=1F μ,求该电路的谐振角频率、特征阻抗和品质因数。
当外加电压有效值为24V 时,求谐振电流、电感和电容上的电压值。
解:电路的谐振角频率4010/rad s LCω== 特征阻抗100LCρ==Ω 品质因数020LQ Rω==谐振电流0 4.8mU I A R== 电感和电容上的电压值L 480V C m U U U Q ===6.4 设计一个串联RLC 电路,使其谐振频率050/rad s ω=,品质因数为80,且谐振时的阻抗为10Ω,并求其带宽。
解:00.625rad /B s Qω==6.5 对于习题图6.5所示的电路,求()v t 和()i t 为同相时的频率ω。
习题图6.5解:12()1Z (//)()v t jwL R L i t jwC==++ 121,1,1,1L H L H C F R ====Ω将代入2221Z ()11w w j w w w w-=+-+++谐振时虚部为零,2101w w w w -+=+ 0.7861w =得出,6.6 并联RLC 网络有R=50Ω,L 4mH =,C=160F μ,求并联电路谐振频率和品质因数。
若外接电流源有效值为2A ,求谐振时电阻、电感及电容上的电流值。
解:电路的谐振角频率30 1.2510rad /s LCω==⨯ 品质因数010LQ CR RCω=== 谐振时电阻、电感及电容上的电流值2A,20A R L C R I I I I Q ====g6.7 并联谐振电路,其品质因数为120,谐振频率是6610/rad s ⨯,计算其带宽。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题六
6-1某三相变压器其绕组作星形联接,额定相电压为230V ,在一次检修后测得相电压
V 230===C B A U U U ,但测得线电压V 400;V 230===BC CA AB U U U ,试用相量图分析,这
种现象是怎么造成得,如何纠正。
解:A 相首末端倒反以后会出现这种情况,如图示
6-2某三相供电电路,其每相阻抗Ω=8L Z ,那么此电路一定是对称三相电路吗? 6-3在三相四线制供电线路中中线电流等于0,那么此时三相负载一定是对称负载吗? 试用相量图分析说明在什么条件下,不对称负载也可能出现中线电流等于0。
解:不对称的三相电流有可能合成中线电流等于0。
其条件是
0sin sin sin 0cos cos cos =++=++C C
C B B B A A A C C
C B B B
A A A Z U Z U
Z U Z U Z U Z U ψψψψψψ
式中ψ是电流的初相角,不是阻抗角φ,图6—3′为一例。
6-4在三相Y ˿Y 供电系统中,对称负载Ω+=66.85j Z L ,负载相电压等于220V ,试求线电流,每相有功功率和无功功率以及功率因数。
答:A 022 ∠=A I ;5.0cos =φ; VA j S P
56.41912420604840+=∠= 解:设 0220∠=A
U 6-5在三相四线制供电系统中,电源侧线电压等于400V ,对称负载Ω+=66.85j Z L 线路阻抗Ω+=11j Z l ,Ω+=12j Z n ,试求线电流及负载端的线电压。
解:V 2313
==
l SP U U ,设V 0231∠=A
U ,则 6-6在三相Y ˿Y 供电系统中,电源侧线电压等于400V ,不对称负载,Ω=5A Z ,
Ω+=55j Z B ,Ω-=86j Z C ,试求中线断开时负载端的中性点位移及各相电压。
解:设 0230∠=SA
U ,用弥尔曼定理求中性点位移 (a )
(b )
图6—3′
(
)()()()
()()()()()V 172232.14281.2718
.336.05.14501.1002
.036.067
.525.808.006.01.01.02.075.283.2242.842.314613.531.0451414.02.013.1732316553.324613.531014507.715113.53101202304507.712023050230j j j j j j j U N
N --=-∠=-∠-∠=---=
++-++-+--+=∠+-∠+∠+-∠+=
-∠+
∠+-∠∠+
∠-∠+∠='
各相负载电压 6-7在三相Y ˿Y 供电系统中,电源侧线电压等于400V ,线路阻抗Ω+=11j Z l ,
Ω+=12j Z n ,不对称负载,Ω=5A Z ,Ω+=55j Z B ,Ω-=86j Z C ,试求中性点位移及各相
电压。
解:设 0230∠=SA
U ,用弥尔曼定理求中性点位移
各相负载电流 各相负载电压
6-8在图
Ω6,Ω+=552j Z ,Ω=103Z ,
试求各线电流。
(1(26-9图2A ,设
出相量图。
0 ∠=U U A 所以相量图如次
6-10图6-10所示对称三相电路中,已知电源线
电压l U =380V ,
图6-9 习题6-9题图
负载功率因数等于0.8(感性),三相负载总功率P =3000W ,求负载阻抗Z L 。
解: A 7.58
.038033000cos 3=⨯⨯=
⨯⨯=
φ
l l U P I
6-11三相负载端线电压等于380V ,对称负载,Ω+=66.85j Z L ,三角形联接,试求相电流和线电流,三相总功率,并画出相量图。
欲把功率因数提高到0.9应并多大电容器?
解:设V 0380 ∠=AB
U ,顺序 A 60
100380
6038-∠=∠∠==L AB AB
Z U I ;A 18038-∠=BC I ; A 6038∠=CA I A 90338-∠=A I ;A 150338∠=B I ;A 30338∠=C
I 605
66
.8tan 1
==-ϕ ; 5.0cos =ϕ 每相功率 KW 22.7=p P 提高功率因数后 84.259.0cos 1==-ϕ 电容器组F 36.198μ⨯
6-12三相形星对称负载,Ω+=55j Z L ,V 380=l U ,欲把功率因数提高到0.9,应接入多大的电容器(采用三角形联接)。
解:设V 0220 ∠=A
U ,顺序 等效成三角形连接
功率因数提高到0.9每相电容
电容器组 F 388.54μ⨯
6-13三相感应电动机额定功率40KW (输出的有效机械功),额定电压380V (Δ)效率0.9,满载时的功率因数为0.85试求
①当线电压为380V 时电动机应如何联接,试计算满载线电流和相电流。
②若接成星形联接时线电流、相电流和功率有何变化?试算之。
解:当线电压为380V 时三角形连接
A 9
.085.0380310403
79.44=⨯⨯⨯⨯=
∆l I ; A 45.87=∆p I
每相阻抗模 Ω==24.887.45380
Z 接成星形 A 24
.822026.7==Y l I 线电流和功率变化为
37.2644.79==Y ∆l l I I ; 333
==Y
∆P
p p p l l Z U Z U I I
6-14三相电动机额定功率4KW (输出的有效机械功),额定电压V 220380(∆Y )效率0.9,满载时的功率因数为0.8试求在电源电压为380V 和220V 条件下满载运行时的线电流。
解:线电压为380V 时正确的连接方式是星形连接 线电压为220V 时正确的连接方式是三角形连接
3-15对称三相电路中,已知三角形联接负载阻抗()j2418+=Z Ω,三相负载功率
P =3000W ,试求线电流及线电压。
解:每相功率1000W
A 18
1000
7.45===
R P I ; A 12.9=l I 6-16图6-16电路中已知V 380=l U ,对称负载阻抗Ω+=126j Z ,试计算两功率表的读数和三相总功率。
解:此电路为两瓦特计法测量三相总功率的电路
设V 0220 ∠=A
U ,则 V 30380 -∠=AC U ;V 90380 -∠=BC
U 按图示的连接关系有下图的相量关系
A 43.634.1643
.6342.1302201260220
-∠=∠∠=+∠=j I A 图6-16 习题6-16题图
6-17图示电路已知负载对称,仪表读数分别为:KW 41=P ;KW 22=P .试求:①三相对称负载的功率因数;② 三相负载的无功功率;③第三个功率表的读数.
解:此题中W 1和W 2为两瓦特计法测量三相总功率的
电路,通过相量图分析来求解最为直观
①设电压相量为
0∠=P
A U U ; 30∠=l A
B U U 设负载为感性画相量图如图2,由相量图可知,
()
W
400030cos cos 1=-==ϕ
α A AC A AC I U I U P
因为212P P =,负载对称
所以 ()()ϕϕ+=- 30cos 230cos 根据三角公式 ()βαβαβαsin sin cos cos cos =± ∴
30577.0arctg ==ϕ
故三相负载的功率因数为 866.030cos =
②三相负载的总功率为 W 600030cos 321==+= l l I U P P P ∴视在功率 VA 20.692830
cos 6000
3==
l l I U 无功功率 Var 30sin 33464.1== l l I U Q
③第三只瓦特表用了电流B I 和电压CA U ,因为B
U 与CA U 的相位差是 90,所以B I 与CA U 的相位差是 6090=-=φγ 故第三只瓦特表的读数是
从第二部知 40003
2.6928==l l I U
所
以
W 20005.0400060cos 3=⨯== l l I U P
6-18 试证明图6-18所示电路中功率表的读数正
图6-17 习题6-17题图
比于三相对称负载电路的总无功功率。
比例系数是多少?
解:设三相负载星形连接,根据连接关系画出图示相量图,该测量线路中应用了线电流I A 和γ ,
所以瓦特表的读数为 根据三角公式 ()βαβαβαsin sin cos cos cos =± 有 所以
可见瓦特表示数正比于无功因数sin φ 。
因为三相总无功功率 ϕsin 3l l I U Q = 所以三相总无功功率与瓦特表示数的比例系数为3
前习题中瓦特表3即为检测无功功率的线路,其读数为2000W ,所以无功功率为 其结果相吻合。
图6-18 习题6-18题图
C
B
A。
