北京化工大学《化工传递过程导论》课程第六次作业参考答案
《化工传递过程导论》课程作业参考答案分析

《传递过程原理》课程第三次作业参考答案1. 不可压缩流体绕一圆柱体作二维流动,其流场可用下式表示θθθsin ;cos 22⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛-=D r C u D r C u r其中C ,D 为常数,说明此时是否满足连续方程。
解:由题意,柱坐标下的连续性方程一般表达式为: ()()11()0r z u ru u t r r r z θρρρρθ∂∂∂∂+++=∂∂∂∂ 不可压缩流体:0tρ∂=∂且上式后三项可去除密度ρ 二维流动:()0z u zρ∂=∂则连续性方程简化为:()110r u ru r r r θθ∂∂+=∂∂22()111(cos )cos r ru C C r D D r r r r r r r θθ∂∂⎛⎫⎛⎫=-=-- ⎪ ⎪∂∂⎝⎭⎝⎭22111(sin )cos u C C D D r r r r r θθθθθ∂∂⎛⎫⎛⎫=+=+ ⎪ ⎪∂∂⎝⎭⎝⎭故:22()()1111cos cos 0r u ru C C D D r r r r r r r θθθθ∂∂⎛⎫⎛⎫+=--++= ⎪ ⎪∂∂⎝⎭⎝⎭ 由题意,显然此流动满足连续方程。
2. 判断以下流动是否可能是不可压缩流动(1)⎪⎩⎪⎨⎧-+=--=++=zx t u zy t u y x t u z y x 222 (2)()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-==-=22221211ttz u xy u x y u z y x ρρρρ解:不可压缩流动满足如下条件:0y x zu u u x y z∂∂∂++=∂∂∂ (1)2110y x zu u u x y z∂∂∂++=--=∂∂∂故可能为不可压缩流动 (2)122(222)0y x z u u u t x x t x y z tρρ∂∂∂++=-+-=-=-≠∂∂∂2t ρ=且。
显然不可能是不可压缩流动。
3. 对于下述各种运动情况,试采用适当坐标系的一般化连续性方程描述,并结合下述具体条件将一般化连续性方程加以简化,指出简化过程的依据。
北京化工大学《化工传递过程导论》课程第三次作业参考答案

31. 不可压缩流体绕一圆柱体作二维流动,其流场可用下式表示θθθsin ;cos 22⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛-=D r C u D r C u r ,其中C ,D 为常数,说明此时是否满足连续方程。
解:由题意,柱坐标下的连续性方程一般表达式为:()()11()0r z u ru u t r r r z θρρρρθ∂∂∂∂+++=∂∂∂∂不可压缩流体:0t ρ∂=∂且上式后三项可去除密度ρ 二维流动:()0z u z ρ∂=∂,则连续性方程简化为:()110r u ru r r r θθ∂∂+=∂∂ 22()111(cos )cos r ru C C r D D r r r r r r r θθ∂∂⎛⎫⎛⎫=-=-- ⎪ ⎪∂∂⎝⎭⎝⎭ 111(sin )cos u C C D D r r r r r θθθθθ∂∂⎛⎫⎛⎫=+=+ ⎪ ⎪∂∂⎝⎭⎝⎭故:22()()1111cos cos 0r u ru C C D D r r r r r r r θθθθ∂∂⎛⎫⎛⎫+=--++= ⎪ ⎪∂∂⎝⎭⎝⎭,满足 2. 判断以下流动是否可能是不可压缩流动(1) ⎪⎩⎪⎨⎧-+=--=++=z x t u z y t u y x t u z y x 222 (2)()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-==-=22221211t tz u xy u xy u z y x ρρρρ 解:不可压缩流动满足如下条件:0y x z u u u x y z∂∂∂++=∂∂∂ (1)2110y x z u u u x y z∂∂∂++=--=∂∂∂故可能为不可压缩流动(2)122(222)0y x z u u u t x x t x y z t ρρ∂∂∂++=-+-=-=-≠∂∂∂2t ρ=且。
显然不可能是不可压缩流动。
3. 对于下述各种运动情况,试采用适当坐标系的一般化连续性方程描述,并结合下述具体条件将一般化连续性方程加以简化,指出简化过程的依据。
北京化工大学化工原理实验思考题答案汇编 DHX

一、流体阻力实验思考题1、不锈钢管、镀锌钢管实验测量的只是Re改变后的λ值,为什么判断λ受Re和ε/d共同影响答:分析实验结果,不锈钢管与镀锌钢管的摩擦阻力系数均随雷诺数的增大而减小,在Re相同的情况下,、镀锌钢管的摩擦阻力系数λ要高于不锈钢管的,由此说明λ受Re和ε/d共同影响。
2、在不同设备(包括相对粗糙度相同而管径不同)、不同温度下测定的λ-Re数据能否关联在一条曲线上为什么答:只要ε/d相同,λ-Re数据就能关联在一条曲线上。
3、以水作工作流体所测得的λ-Re关系能否适用于其它种类的牛顿型流体为什么答:对于其他牛顿型流体也适用。
Re反应了流体的性质,其他的流体的密度和黏度都可以在Re上面反应出来。
所以仍然适用。
4、以下测出的直管摩擦阻力与设备的放置状态有关吗它们分别是多少(管径、管长一样,管内走水,且R=R=R)312uuu-gzgz?2211??h????+=() ,压差计高度差R 答:无关,21222u??pup?Plu-gzgz21?,因为R=()+即反映了两个测压点截面位能和压强能综合变化f??2d2p?p值,21?R=R=R,u=u,所以三种状态下的hf不变,推出λ不变。
232115、柏努利方程的适用条件是什么该条件与本实验有什么联系答:不可压缩的理想流体在稳定状态下恒温流动。
本实验的流体满足柏努利方程,推导水平无变径直管道摩擦阻力系数λ的时候就采用了柏努利方程,满足柏努利方程是该实验的理论基础。
6、在测量前,为什么要将设备中的空气排净怎样才能迅速排净答:本实验所研究的对象为单一连续流体,排净气体是为了使流体连续流动,以达使流体迅速流过各直迅速排净的方法:主管路:开大流量调节阀,到实验的条件要求。
.管,将气泡冲出;引压管:打开引压管控制阀,流体流过引压管,气泡被带出。
排净标志为流量为零时,传感器示数为零。
二、离心泵实验思考题1,根据离心泵的工作原理,分析为什么离心泵启动前要灌泵在启动前为何要关闭调节阀离心泵是靠叶轮旋转产生的离心力把水排出,泵内的水排出后形成真空,又把水吸进泵中,依次循环工作。
化工传递过程过程性考核(一) - 答案

化工传递Array过程过程性考核试卷(一)一.填空题(每空1分,本大题共41分)1. 流体静力学基本方程的应用包括压力压差的测量、液位的测量和液封高度的计算。
2. 甲地大气压为100 kPa,乙地大气压为80 kPa。
某刚性设备在甲地,其内部的真空度为25 kpa,则其内部的绝对压强为75 kpa;若将其移至乙地,则其内部的表压强为-0.5 mH2O。
3. 流体流动有两种基本形态,即层流和湍流。
判断流体流动形态的无量纲数群为雷诺数,其表达形式为Re=duρ/μ,物理意义为表示流体惯性力与与黏性力比值。
4. 复杂管路分为分支管路和并联管路。
5. 常用的流量计中,孔板流量计和文丘里属于差压流量计;转子流量计属于截面流量计;测速管可测量点速度。
6. 流体在圆形直管内做层流流动,若流量不变,将管径变为原来的两倍,则平均流速变为原来的1/4 ,流动摩擦系数变为原来的2倍,直管阻力损失变为原来的1/16 。
7. 流体在一套管环隙内流动,若外管内径为50 mm,内管外径为25 mm,则其流动当量直径为25 mm.8. 流体在圆形直管内做稳态层流流动,若管截面上平均流速为0.05 m/s ,则最大流速为 1.0 m/s 。
9. 联系各单元操作的两条主线为 传递过程 和 研究工程问题的方法论 。
10. 湍流边界层可以分为 层流底层 、 过渡层 和 湍流主体 ,其中传热、传质阻力主要集中在层流底层 。
11. 随体导数的表达形式为zu y u x u θzy x ∂∂+∂∂+∂∂+∂∂=θD D 。
12. 不可压缩流体连续性方程的一般表达形式为0=•∇u。
13. 量纲分析的基础是 量纲一致性原则 和 π 定理。
14. 在研究流体的运动时,常采用两种观点,即 欧拉 观点和 拉格朗日 观点。
15. 牛顿黏性定律的表达形式为yu xd d μτ-=。
16. 流体质点的运动轨迹称为 迹线;在某一时刻,在流线上任一点的切线方向与流体在该点的速度方向相同 。
北京化工大学《化工传递过程导论》课程第六次作业参考答案精选全文完整版

可编辑修改精选全文完整版61. 有一黏性流体沿一无限宽的垂直壁面下流,其运动黏度ν=2⨯10-4m 2/s ,密度ρ=0.8×103kg/m 3,液膜厚度δ=2.5mm ,假如液膜内流体的流动为匀速定态,且流动仅受重力的影响,流动方向上无压强降,试计算此流体沿壁面垂直下流时,通道单位宽度液膜时的质量流率。
解:由题意可知,流体流动可看成平壁面上的降膜流动,故液膜内流体的主体流速223249.81(2.510)m 0.102s 333210b g g u v ρδδμ--⨯⨯====⨯⨯流体垂直下流,通过单位宽度液膜的质量流率为33kg(1)(0.810)0.102(2.510)10.204sb b w u A u ρρδ-===⨯⨯⨯⨯⨯=以上计算结果仅当液膜内流动为层流时才是正确的。
液膜雷诺数为3444(2.510)0.102Re 5.130210e bb d u u v ρδμ--⨯⨯⨯====<⨯,成立2. 直径为1.5mm ,质量为13.7mg 的钢珠在—个盛有油的直管中垂直等速下落。
测得在56s 内下落500mm ,油的密度为950kg/m 3,管子直径及长度足够大,可以忽略端部及壁面效应。
求油的黏度μ值,并验算Re 数,以验证计算过程所作的假定是否合理。
解:由题意,根据力的衡算可确定液体的黏度。
定态下,作用在小球上的重力与浮力之差必等于小球所受阻力,即006ball liquid ball m g u r gV πμρ=+ 得到油的黏度μ的计算式如下:006ball liquid ballm g gV u r ρμπ-=故,油的黏度计算如下:3333300(13.710)9.819509.81(1.510)60.935Pa s50010 1.51066562ball liquid ballm g gV u r πρμππ----⨯⨯-⨯⨯⨯⨯-===⋅⨯⨯⨯⨯校验Re :33050010(1.510)95056Re 0.013610.935d u ρμ--⨯⨯⨯⨯===< 属于爬流,计算合理。
化工传递过程答案

中国海洋大学继续教育学院命题专用纸试题名称 :化工传递过程 学年学期: 2019学年第一学期 站点名称:层次: 专业: 年级: 学号: 姓名: 分数:一、选择题(共10小题,每小题4分,共40分)1.粘性是指流体受到剪切作用时抵抗变形的能力,其原因是( B )。
a 组成流体的质点实质是离散的b 流体分子间存在吸引力c 流体质点存在漩涡与脉动 2. 连续方程矢量式中哈密顿算符“k zj y i x ∂∂+∂∂+∂∂=∇”的物理意义可以理解为计算质量通量的( C )。
a 梯度 b 旋度 c 散度 3.描述流体运功的随体导数中局部导数项θ∂∂表示出了流场的( B )性。
a 不可压缩 b 不确定 c 不均匀4.分析流体微元运动时,在直角坐标x-y 平面中,微元围绕z 轴的旋转角速度z ω正比于特征量( A )。
ay u xu xy ∂∂-∂∂ b y u x u x y ∂∂+∂∂ c xu y u x y ∂∂-∂∂5.流体爬流流过球形固体时,流动阻力中形体阻力与表面阻力之比应为( C )。
a 1:1 b 1:2 c 2:16.推导雷诺方程时,i 方向的法向湍流附加应力应表示为( B )。
a i r ii u '-=ρτb 2ιρτu rii '-= c j i r iiu u ''-=ρτ 7.固体内发生非稳态导时,若固体内部存在明显温度梯度,则可断定传热毕渥准数Bi 的数值( A )0.1。
a 大于等于 b 等于 c 小于等于8.依据普兰特混合长理论,湍流传热时,涡流热扩散系数h α可表示为( C )。
a dy du l h =αb 2⎪⎪⎭⎫ ⎝⎛=dy du l h α c dy du l h 2=α 9.流体流入溶解扩散管后形成稳定的湍流边界层,溶质溶解扩散进入流体,则沿管长方向对流传质系数的变化规律应是( B )。
a 始终不变 b 先下降,后上升,最终趋于稳定 c 先上升,后下降,最终趋于稳定 10.利用雷诺类似求解湍流传质问题的前提是假定( C )。
《化工传递过程导论》课程作业参考答案

《传递过程原理》课程第三次作业参考答案1. 不可压缩流体绕一圆柱体作二维流动,其流场可用下式表示θθθsin ;cos 22⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛-=D r C u D r C u r其中C ,D 为常数,说明此时是否满足连续方程。
解:由题意,柱坐标下的连续性方程一般表达式为: ()()11()0r z u ru u t r r r z θρρρρθ∂∂∂∂+++=∂∂∂∂ 不可压缩流体:0tρ∂=∂且上式后三项可去除密度ρ 二维流动:()0z u zρ∂=∂则连续性方程简化为:()110r u ru r r r θθ∂∂+=∂∂22()111(cos )cos r ru C C r D D r r r r r r r θθ∂∂⎛⎫⎛⎫=-=-- ⎪ ⎪∂∂⎝⎭⎝⎭22111(sin )cos u C C D D r r r r r θθθθθ∂∂⎛⎫⎛⎫=+=+ ⎪ ⎪∂∂⎝⎭⎝⎭故:22()()1111cos cos 0r u ru C C D D r r r r r r r θθθθ∂∂⎛⎫⎛⎫+=--++= ⎪ ⎪∂∂⎝⎭⎝⎭ 由题意,显然此流动满足连续方程。
2. 判断以下流动是否可能是不可压缩流动(1)⎪⎩⎪⎨⎧-+=--=++=zx t u zy t u y x t u z y x 222 (2)()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-==-=22221211ttz u xy u x y u z y x ρρρρ解:不可压缩流动满足如下条件:0y x zu u u x y z∂∂∂++=∂∂∂ (1)2110y x zu u u x y z∂∂∂++=--=∂∂∂故可能为不可压缩流动 (2)122(222)0y x z u u u t x x t x y z tρρ∂∂∂++=-+-=-=-≠∂∂∂2t ρ=且。
显然不可能是不可压缩流动。
3. 对于下述各种运动情况,试采用适当坐标系的一般化连续性方程描述,并结合下述具体条件将一般化连续性方程加以简化,指出简化过程的依据。
化工反应工程答案 第六章
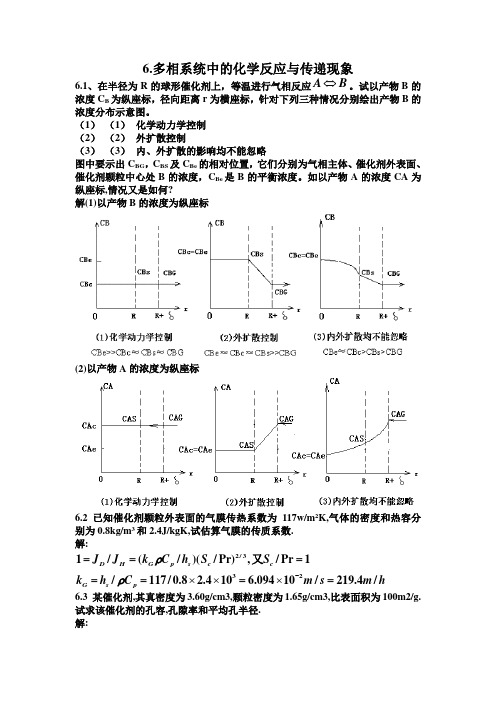
6.多相系统中的化学反应与传递现象6.1、在半径为R 的球形催化剂上,等温进行气相反应⇔A B 。
试以产物B 的浓度C B 为纵座标,径向距离r 为横座标,针对下列三种情况分别绘出产物B 的浓度分布示意图。
(1) (1) 化学动力学控制 (2) (2) 外扩散控制(3) (3) 内、外扩散的影响均不能忽略图中要示出C BG ,C BS 及C Be 的相对位置,它们分别为气相主体、催化剂外表面、催化剂颗粒中心处B 的浓度,C Be 是B 的平衡浓度。
如以产物A 的浓度CA 为纵座标,情况又是如何?解(1)以产物B 的浓度为纵座标(2)以产物A 的浓度为纵座标6.2 已知催化剂颗粒外表面的气膜传热系数为117w/m 2K,气体的密度和热容分别为0.8kg/m 3和2.4J/kgK,试估算气膜的传质系数. 解:-=====⨯⨯=⨯=2/3321/(/)(/P r),/P r 1/117/0.8 2.410 6.09410/219.4/D H G p s c c G s p J J k C h S S k h C m s m hρρ又6.3 某催化剂,其真密度为3.60g/cm3,颗粒密度为1.65g/cm3,比表面积为100m2/g.试求该催化剂的孔容,孔隙率和平均孔半径. 解:=-=<>=<>====3(1),0.5422/,65.6/0.542/1.650.328/ p t p p a p r p a g p p r S r AV cm g ρρεεερερ由得由得由催化剂6.4 已知铁催化剂的堆密度为 2.7g/cm 3, 颗粒密度为 3.8 g/cm 3,比表面积为16m 2/g,试求每毫升颗粒和每毫升床层的催化剂表面积. 解:==2260.8/43.2/p g g S m m lS m m lρρb 每毫升颗粒的表面积=每毫升床层的表面积=6.5 试推导二级反应和半级反应的扩散有效因子表达式(6.23)和(6.24). 解:(1)二级反应,()()(()=-=-==-±=⎡⎤=-±⎣⎦=-2222222,,/2/1/21,/A w A S G m A G A S w A SG m ww A S w A G G m w A G w A G G m R k C k a C C k C k a k k C k C k a k C k C k a αηA Sx 由上解得:C按定义此即(6.23)式式中D a=(2)半级反应()(=-=-==-±==-+⎛=-+=+- ⎝⎭1/21/21/21/21/21/21/221/2,(),/2/(/2122A w A S G m A G A S w A SA S w G mw A S w A G w G m A GR k C k a C C k C C k k a k C k C k k a C D a D a D αηx 由上解得:按定义:-⎡+⎢=-⎢⎢⎣⎦⎡⎤⎛+⎢⎥ =-⎢⎥ ⎢⎥⎝⎣⎦=1/221/221/222212(6.24),:/w A G G mD a D a D a k C k a 此即式式中6.6 在充填ZnO-Fe2O3催化剂的固床反应器中,进行乙炔水合反应:+→++2223322232C H H O C H C O C H C O H已知床层某处的压力和温度分别为0.10Mpa,400℃,气相中C 2H 2含量为3%(mol),该反应速率方程为r=kC A ,式中C A 为C 2H 2的浓度,速率常数k=7.06×107exp(-61570/RT),h -1,试求该处的外扩散有效因子.数据:催化剂颗粒直径0.5cm,颗粒密度1.6g/cm 3,C 2H 2扩散系数7.3×10-5m 2/s,气体粘度2.35×10-5Pa ﹒s,床层中气体的质量流速0.2kg/m 2s. 解:由已知条件可得()()---=⋅=⨯⨯=⨯+⨯=+===⨯⨯⨯===-=⨯⨯2530.359552/370.24/R e 0.0050.24/2.351051.06260.03180.972730.3303/22.44002730.357/(R e )0.24852.3510/(0.33037.310)0.97460.1837/()615707.0610exp 8.314673D b c G Dc G kg m skg mj S Gk j m sS k ρερ()-⎡⎤= = ⎢⎥⎣⎦==⨯ ⋅⎡⎤=⨯=⎢⎥⎣⎦332221174.6/0.3263//0.203910/10.005/(0.005)16000.756w p m l h l s k k m kg s a m ρππ====+/0.0014810.99851w G m D a k k a D aπη6.7实验室管式反应器的内径2.1cm,长80cm ,内装直径6.35mm 的银催化剂进行乙烯氧化反应,原料气为含乙烯 2.25%(mol)的空气,在反应器内某处测得P=1.06×105Pa,T G =470K,乙烯转化率35.7%,环氧乙烷收率23.2%,已知+→ =-⨯ +→+ =-⨯ 42422412462422222419.6110/232 1.2510/C H O C H O H J m olC H C H O C O H O H J m olC H ∆∆颗粒外表面对气相主体的传热系数为58.3w/m 2K,颗粒密度为 1.89g/cm 3.设乙烯氧化的反应速率为 1.02×10-2kmol/kg ﹒h,试求该处催化剂外表面与气流主体间的温度差. 解:()-= ⋅⎛⎫-=-+--=⨯ ⎪⎝⎭= ⋅=⨯⋅⋅=== -=--= 512252223()10.2/23.223.2()()1 5.00110/35.735.758.3/ 2.09910/0.50/16()()/48.59A r s p pm p pp pg G A r s m R m ol kg h H H H J m ol h w m k J m K h S d a m kgV d T T R H h a Kπρπρ∆∆∆∆6.8 一级连串反应:−−→−−→12A B C在0.1Mpa 及360℃下进行,已知k 1=4.368 s -1,k 2=0.417 s -1,催化剂颗粒密度为1.3g/cm 3,(k G a m )A 和(k G a m )B 均为20cm 3/g ﹒s.试求当C BG /C AG =0.4时目的产物B 的瞬时选择性和外扩散不发生影响时的瞬时选择性.解:外扩散无影响时,由(6.35)式得:⨯'=-=0.41730.410.96184.368S外扩散有影响时,由(6.34)式得:⨯=-=+10.41730.4(1.168)0.940310.01605 4.368(1.01605)S上式中所用的 ====1122/0.168/0.01605a G m a G mk D k a k D k a ρρ6.9 在Pt/Al 2O 3催化剂上于200℃用空气进行微量一氧化碳反应,已知催化剂的孔容为0.3cm 3/g,比表面积为200m 2/g,颗粒密度为1.2g/cm 3,曲节因子为3.7.CO-空气二元系统中CO 的正常扩散系数为0.192cm 2/s.试求CO 在该催化剂颗粒中的有效扩散系数.(----=== ===≥=⨯⨯=⨯ ==⨯ 53822322/30,10,0.36/216.610,,:9.7103010 1.19610// 1.16410/ g g p g pa k k p V S A cm V r D cm sD e D cm sλερλετa 解:r 为努森扩散故有6.10 试推导球形催化剂的内扩散有效因子表达式(6.60). 解:==-=-+2222223,:1122A A AC u dC du u dr r drrd C d uduudr r dr r dr r 令可得用以上各式对教材中(6.55)式进行变量置换得:= =2222p d u b udrb k D e式中 (A)(A) (A) 式为二阶常系数齐次微分方程,边界条件:r=0 du/dr=0; r=R p u=C AS R p (B) 结合边界条件(B)式解(A)得:= sinh()()sinh()p A AS p R br C C C r bR有内扩散影响时的反应速率为:()=-= 24()pA A pr R dC R D e R D drπ()=⎛⎫-=- ⎪⎝⎭(),():114tanh pA r R A p s A S s s dC C D drR R C D e πφφφ由式求出代入式得 按内扩散有效因子的定义:⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭3411311()3tanh tanh 4p s A S s s s s s p p A S R C D e E R k C πφηφφφφφπ==s p pbR R φ式中==⎛⎫=- ⎪⎝⎭/3():111()tanh(3)3s E F φφηφφφ若令则式可改写为(F)即为教材(6.60)式,(E)式是(6.60)的又一形式.6.11 在球形催化剂上进行气体A 的分解反应,该反应为一级不可逆放热反应.已知颗粒直径为0.3cm,气体在颗粒 中有效扩散系数为 4.5×10-5m 2/h,颗粒外表面气膜传热系数为44.72w/m 2﹒K,气膜传质系数为310m/h,反应热效应为-162kJ/mol,气相主体A 的浓度为0.20mol/l,实验测得A 的表观反应速率为1.67mol/minl, 试估算:(1) (1) 外扩散阻力对反应速率的影响; (2) (2) 内扩散阻力对反应速率的影响; (3) (3) 外表面与气相主体间的温度差. 解:--=⋅=⨯⋅⨯⨯==⨯<*53331.67/m in 1.00210/(1)31.671060.8081100.150.2(310/60),.A A G GR m ol l m ol m h LC k *A判别外扩散阻力的影响用(6.79)式:R故仅从传质考虑外扩散影响可不计==*2(2)(6.82),:2.783s A s A GR LD eC φφ判别内扩散阻力的影响用式先求出====2,2.783,(6.60)3.1,0.288,s s φηφφφη因有从可借助式估算出由此可知内扩散阻力影响严重.(3)计算外表面与气相主体间温度差⊿Tm :=-=⋅⋅⋅*)/m G s A s T T T R h ∆∆r 颗粒体积(H 颗粒外表面积=50.4K6.12 在固体催化剂上进行一级不可逆反应→ ()A B A已知反应速率常数k,催化剂外表面积对气相的传质系数为k G a m ,内扩散有效因子η.C AG 为气相主体中组分A 的浓度. (1)试推导:()()-= +11A G A G mCR B k k a η(2)若反应式(A)改为一级可逆反应则相应的(B)式如何?解:(1)一级不可逆反应A B:()()()()-=-==+==+/1A G A GA S m G m A G G mA G G mR k C C a k k a C k k a C k k a kηηηηA SA SAA SC由上可解得:C 解得:-RC(2)一级可逆反应:A B()()()()()()()()-=-=+-+=+--=+-=++:11 A G m A G A S A SA e G m A G A eG m A G A S A A S A e G m R k a C C k kCC k a C kC k a k C C R k kC C k a k kηηηηηA S由解得:C则有6.13 在150℃,用半径100μm 的镍催化剂进行气相苯加氢反应,由于原料中氢大量过剩,可将该反应按一级(对苯)反应处理,在内,外扩散影响已消除的情况下,测得反应速率常数k p =5min -1, 苯在催化剂颗粒中有效扩散系数为0.2cm 2/s,试问:(1) (1) 在0.1Mpa 下,要使η=0.8,催化剂颗粒的最大直径是多少?(2) (2) 改在 2.02Mpa 下操作,并假定苯的有效扩散系数与压力成反比,重复上问的计算.(3) (3) 改为液相苯加氢反应,液态苯在催化剂颗粒中的有效扩散系数10-5cm 2/s.而反应速率常数保持不变,要使η=0.8,求催化剂颗粒的最大直径. 解:()==⎛⎫- ⎪ ⎪⎝⎭(1)0.107611tanh 33pd φηφφφ1由(6.60)式=用试差法从上二式可解得当η=0.8时,需d p <6.36cm(2)2.02Mpa 时,De ≈0.2×0.101/2.02=0.01 cm 2/s,与此相对应:==0.418pd φ同上法可求得当η=0.8时,需d p <1.42cm(3)液相反应时,De=1×10-6cm 2/s,与此相应的φ为21.51dp,同上法可求得当η=0.8时,需d p <0.0142cm.6.14 一级不可逆反应A B,在装有球形催化剂的微分固定床反应器中进行温度为400℃等温,测得反应物浓度为0.05kmol/m 3时的反应速率为 2.5 kmol/m 3床层﹒min ,该温度下以单位体积床层计的本征速率常数为k v =50s -1 ,床层孔隙率为0.3,A 的有效扩散系数为0.03cm 2/s,假定外扩散阻力可不计,试求:(1) (1) 反应条件下催化剂的内扩散有效因子 (2) (2) 反应器中所装催化剂颗粒的半径()===== --==-==⨯⨯ ⋅3171.43/18.13500.05/p v B B B vvvpB pA v A SV k V V V k k k l sV V V d R k C km ol s m εεφηηp p 解:k k 床层实验测得(-R A )=0.0417 kmol/s ﹒m 3床层, 解上二式得η=0.0167,可见内扩散影响严重.由η=1/φ=1/8.13dp=0.0167,可解出dp=7.38cm,即反应器所装催化剂的颗粒 半径为3.69cm.6.15 在0.10Mpa,530℃进行丁烷脱氢反应,采用直径5mm 的球形铬铝催化剂,此催化剂的物理性质为:比表面积120m 2/g,孔容0.35cm 3/g,颗粒密度1.2g/cm 3,曲节因子 3.4.在上述反应条件下该反应可按一级不可逆反应处理,本征反应速率常数为0.94cm 3/gs,外扩散阻力可忽略,试求内扩散有效因子.解:丁烷分子量为58,λ=10-5cm,<ra>=2Vg/Sg=58.3×10-8cm, λ/2<ra>=8.576,此值与10接近,故可近似扩散是以奴森扩散为主:--=⨯⨯=⨯22970058.3102.10410/k D cm s-==⨯==32/ 2.610/1.736k p m D e D cm sετφ由(6.60)式算得η=0.465.6.16 在固定床反应器中等温进行一级不可逆反应,床内填充直径为6mm 的球形催化剂,反应组分在其中的扩散系数为0.02cm 2/s,在操作温度下,反应式速率常数等于0.01min -1,有人建议改有3mm 的球形催化剂以提高产量,你认为采用此建议能否增产?增产幅度有多大?假定催化剂的物理性质及化学性质均不随颗粒大小而改变,并且改换粒度后仍保持同一温度操作.解:=======0.6,0.02887,0.9995,0.3,0.01444,0.9998p p d cm d cm φηφη故采用此建议产量的增加是很有限的.6.17 在V 2O 5/SiO 2催化剂上进行萘氧化制苯酐的反应,反应在 1.013×105Pa 和350℃下进行,萘-空气混合气体中萘的含量为0.10%(mol),反应速率式为:⎛⎫=⨯-⋅ ⎪⎝⎭50.381353603.82110exp ,/A Ar p km ol kg hR T式中PA 为萘的分压,Pa.已知催化剂颗粒密度为1.3g/cm 3,颗粒直径为0.5cm,试计算萘氧化率为80%时萘的转化速率(假定外扩散阻力可忽略),有效扩散系数等于3×10-3cm 2/s.解:因外扩散阻力可不计,故C AS ≈C AG ,()-= ⋅0.38/A p AGR k C km ol kg h η式中η由教材(6.66)式计算,为此先计算以下数据:--==⨯⎛⎫=⨯-⋅ ⎪⎝⎭⎛⎫ =⨯-⋅ ⎪⎝⎭13250.3850.383/12,310/,1353603.8210exp /1353603.8210exp /p p p A G p A Ga V cmD e cm s k p km ol kg hR T p km ol m h R T ρA 的值由:r 颗粒 将此P AG =C AG RT,ρp =1300kg/m 3颗粒,T=(350+273)K 代入上式,并将小时换为秒计则得:-=⨯⋅40.3832.19610/A AG r C km ol m s 颗粒 由上式得 k p =2.196×10-4又:C AS =C AG =P AG /RT=105×0.1%(1-0.8)/(8314×623)=3.861×10-6 kmol/m 3 将有关数值代入(6.66)式得:()()()()--=====⨯==⨯⎰⎰⎰1/20.3831/20.381/24]1.12:8.76910[][]1.566310A S A CA S A CA S C A A C C A S A G A GA A C C A A a f C dC f C f C C f C dC C dC η式中最后得萘氧化率为80%时的萘的转化速率为:()--==⨯⋅0.38632.15710/A p AGR k C km ol m sη颗粒6.18 乙苯脱氢反应在直径为0.4cm 的球形催化剂上进行,反应条件是0.10Mpa,600℃,原料气为乙苯和水蒸汽的混合物,二者摩尔比为1:9,假定该反应可按拟一级反应处理.⎛⎫''= =-⋅⋅ ⎪⎝⎭913000.1244exp ,/wE B w r k p k km ol kg h Pa R T 苯乙烯(1)当催化剂的孔径足够大,孔内扩散属于正常扩散,扩散系数D’=1.5×10-5m 2/s, 试计算内扩散有效因子.(2)当催化剂的平均孔径为100Å时,重新计算内扩散有效因子. 已知:催化剂颗粒密度为1.45g/cm 3,孔率为0.35,曲节因子为3.0. 解:为计算内扩散有效因子,先求取K p := ⋅= ⋅3//EB p EB r kp km ol kg h k p km ol m hρ由颗粒将 P E B =RTC E B ,T=(600+273)代入上式得:=⨯ ⋅= ⋅3334.50810/ 1.252/BE EB r C km ol m h C km ol m s 颗粒颗粒 由此得K p =1.252 s -1(1) (1) 孔径足够大,属正常扩散时,-==⨯ 62/ 1.7510/p m De D m sετ由此求得Φ=0.564,由(6.60)式算得η=0.85(2) (2) 孔半径为100Å时:λ/2<ra>=10-5/200×10-8=5,属于过渡区扩散,由教材(6.36)式可算得乙苯的Dk=2.784×10-2cm 2/s.--==⨯+⨯2221 2.34810/112.784100.15D cm s--==⨯=⨯32722.73910/ 2.73910/pmD D e cm s m sετ由上数据可算得φ=1.425,由教材(6.60)式算得η=0.5286.19 苯(B)在钒催化剂上部分氧化成顺酐(MA),反应为:这三个反应均为一级反应.实验测得反应器内某处气相中苯和顺酐的浓度分别为 1.27%和0.55%(均为mol%),催化剂外表面温度为623K,此温度下,k1=0.0196 s -1,k2=0.0158 s -1,k3=1.98×10-3 s -1,苯与顺酐的k G a m 均为 1.0×10-4m 3/skg.催化剂的颗粒密度为1500kg/m 3,试计算反应的瞬间选择性并与外扩散无影响时的瞬时选择性相比较.解:()()---==⨯=⨯=⨯⋅====-=+ 55512332312/ 1.30710, 1.05310,0.13210/./0.1307,0.1053,0.0132),w p w w w w G m a a m B G B S w w B S k k k k k m kg s D a k k a D D A a C C k k C ρa12G 由可算出单位均为由可算得D为简化起见以表示顺酐,C 表示(C O +C O 由教材(6.18)式可写出:k ()()(A )-= - (B )-= - (1223)m A S A G w B S w A S m C S C G w A S w B S a C C k C k C a C C k C k C C G G k k=++=+++++1221121(1)/(1)(2)/(1)/[(1)(1)]B S B G a a A s A G a a B G a a a C C D D C C D D C D D D 由得由得 有外扩散影响时的瞬时选择性:()()()()()=-+⎡⎤⎡⎤++=-+⎢⎥⎢⎥++++++⎣⎦⎣⎦⎡⎤++=-+⎢⎥++++⎣⎦=1213121131313213212131131322/1111(1)110.4742w B S w A S w w B Sw w A G a B G a a w w w w a a a a B G w w a a A G a w w w w a B G a S k C k C k k C k k C D C D D k k k k D D D D C k k D D C D k k k k D C D 无外扩散影响时的瞬时选择性:'=-=++1213130.5726w w C G w w w w B G k k C S k k k k C6.20 原题见教材,今补充如下:实验测得A 的气相浓度为1.68×10-5mol/cm 3时的反应速率为1.04×10-5(mol/cm 3床层﹒s).解:已知 ()---=⨯-=⨯ ⋅*5531.0410/(10.4) 1.73310/AR m ol cm s 颗粒若不计外扩散阻力,则C AS =C AG =1.68×10-5mol/cm 3 由教材312页: ()=-*2/s A AG R L DeC φL=dp/6=0.04cm,可算得s φ=0.1375,由(6.82)式=2sφφη,将此式与(6.60)式用试差法联立求解可得:φ=0.387 η=0.92。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6
1. 有一黏性流体沿一无限宽的垂直壁面下流,其运动黏度ν=2⨯10-4m 2/s ,密度
ρ=0.8×103kg/m 3,液膜厚度δ=2.5mm ,假如液膜内流体的流动为匀速定态,且流动仅受重力的影响,流动方向上无压强降,试计算此流体沿壁面垂直下流时,通道单位宽度液膜时的质量流率。
解:由题意可知,流体流动可看成平壁面上的降膜流动,故液膜内流体的主体流速
2232
49.81(2.510)m 0.102s 333210
b g g u v ρδδμ--⨯⨯====⨯⨯
流体垂直下流,通过单位宽度液膜的质量流率为
33kg (1)(0.810)0.102(2.510)10.204s
b b w u A u ρρδ-===⨯⨯⨯⨯⨯=
以上计算结果仅当液膜内流动为层流时才是正确的。
液膜雷诺数为
34
44(2.510)0.102Re 5.130210e b
b d u u v ρδμ
--⨯⨯⨯=
===<⨯,成立
2. 直径为1.5mm ,质量为1
3.7mg 的钢珠在—个盛有油的直管中垂直等速下落。
测得在
56s 内下落500mm ,油的密度为950kg/m 3,管子直径及长度足够大,可以忽略端部及壁面效应。
求油的黏度μ值,并验算Re 数,以验证计算过程所作的假定是否合理。
解:由题意,根据力的衡算可确定液体的黏度。
定态下,作用在小球上的重力与浮力之差必
等于小球所受阻力,即006ball liquid ball m g u r gV πμρ=+ 得到油的黏度μ的计算式如下:00
6ball liquid ball
m g gV u r ρμπ-=
故,油的黏度计算如下:
333
3
3
00
(13.710)9.819509.81(1.510)6
0.935Pa s
50010 1.51066562
ball liquid ball
m g gV u r π
ρμππ----⨯⨯-⨯⨯⨯⨯-=
=
=⋅⨯⨯⨯⨯
校验Re :
3
3
050010(1.510)95056Re 0.013610.935
d u ρμ--⨯⨯⨯⨯
===< 属于爬流,计算合理。
3. 有一球形固体颗粒,其直径为0.1mm 。
在常压和30℃的静止空气中沉降,已知沉降速
度为0.01mm/s ,试求算
(1)距颗粒中心,r =0.3mm 、θ=π/4处空气与球体之间的相对速度; (2)颗粒表面出现最大剪应力处的θ值(弧度)和最大剪应力值; (3)空气对球体施加的形体阻力、摩擦阻力和总阻力。
解:常压,0
30C 条件下的空气黏度为6
1.8610Pa s -⨯⋅,3
300.1100.05102
r m --⨯=
=⨯,300.0110u m -=⨯
(1) 由题意有,0.3,4
r mm π
θ==
时
300031cos [1()()]22r r r
u u r r
θ=-+
33
630.0510.050.0110cos [1()()] 5.31910420.320.3
r m u s π--⇒=⨯-+=⨯
300031sin [1()()]44r r
u u r r
θθ=---
33
630.0510.050.0110sin [1()()] 6.17810440.340.3
m u s θπ--⇒=-⨯--=-⨯
故求得此题意条件下空气与球体之间的相对速度为(空气静止):
65.31910r m u s -=⨯,66.17810m u s
θ-=-⨯
(2) 颗粒表面处(3
00.0510r r m -==⨯)的剪应力表达式如下:
00
3(
)sin 2r u u u
r r r θθθτμμθ∂=-=-∂ 其中0θπ≤≤
显然当sin 12
π
θθ=⇒=
时,颗粒表面出现最大剪应力。
0max
2
3()2r r r u r θπ
θτμ==
=-
3660max
3
0330.0110()(18.610) 5.5810Pa 220.0510
r u r θτμ----⨯⇒=-=-⨯⨯⨯=-⨯⨯ (3) 由题意可知形体阻力002ds F r u πμ=
3
6
3140.1102(18.610)(0.0110) 5.84102
ds F N π----⨯⇒=⨯⨯⨯⨯⨯=⨯
摩擦阻力004df F r u πμ=
3
6
3140.1104(18.610)(0.0110)11.68102
df F N π----⨯⇒=⨯⨯⨯⨯⨯=⨯
总阻力d ds df F F F =+
1417.5210N d ds df F F F -⇒=+=⨯。
