电阻的星形连接与三角形连接的等效变换
电阻星形连接与三角形连接的等效变换

公正处法人授权委托书范本一、前言为了明确公正处法人的授权范围和内容,确保代理人能够合法、合规地代表法人行事,特制定本授权委托书。
本授权委托书旨在规范法人授权行为,保障法人及其代理人的合法权益,维护社会经济秩序。
二、授权主体1. 授权单位:×××公正处2. 法定代表人:×××3. 授权人:×××三、授权范围1. 代理人代表公正处参加各类法律诉讼活动,包括但不限于起诉、应诉、举证、质证、调解、和解等。
2. 代理人代表公正处与各类当事人进行法律事务谈判、协商,并签署相关法律文件。
3. 代理人代表公正处处理各类法律事务,包括但不限于合同审查、起草、签订、变更、解除等。
4. 代理人代表公正处参加各类行政复议、行政诉讼活动,维护公正处的合法权益。
5. 代理人代表公正处处理各类法律咨询、法律培训、法律宣传等活动。
6. 代理人代表公正处与各类政府部门、企事业单位、社会团体等进行法律事务往来。
7. 代理人代表公正处处理其他各类法律事务,包括但不限于知识产权、劳动关系、交通事故等。
四、授权期限本授权委托书的有效期为自授权人之签名或盖章之日起至法定代表人书面声明本授权作废之日止。
五、授权方式1. 法定代表人签字或盖章。
2. 公正处盖章。
六、注意事项1. 代理人应当在授权范围内行事,不得超出授权范围进行任何活动。
2. 代理人不得转委托授权,不得将授权事项转让给他人。
3. 代理人不得以公正处名义从事任何非法活动,不得损害公正处的合法权益。
4. 代理人应当严格遵守国家法律法规,合规行事。
5. 代理人应当保持与当事人的良好沟通,确保授权事项的顺利进行。
6. 代理人应当及时向法定代表人报告授权事项的进展情况。
七、法律后果1. 代理人依据本授权委托书行事,其法律后果由公正处承担。
2. 代理人超出授权范围行事,其法律后果由代理人自行承担。
3. 代理人违反国家法律法规、本授权委托书约定,给公正处造成损失的,应当承担赔偿责任。
电阻三角形和星形变换公式

电阻三角形和星形变换公式
电阻三角形和星形变换公式是在电路中常用的一种计算方法,特别是在进行串联和并联电路计算时,可以大大简化计算的复杂度。
电阻三角形和星形变换公式是根据电路的基本原理推导出来的,通过将电路进行转换可以得到等效的电路形式,从而简化计算。
电阻三角形变换公式是指将三个电阻串联的电路转换为三个电阻并联的等效电路的方法。
具体的转换方法是:将三个电阻分别连接成一个三角形,然后将三角形中的任意一个角连接到电路的两端,从而形成一个并联电路。
这样得到的等效电路中,三个电阻的并联等效电阻就是原始电路中三个电阻的串联等效电阻。
星形变换公式是指将三个电阻并联的电路转换为三个电阻串联的等效电路的方法。
具体的转换方法是:将三个电阻分别连接成一个星形,然后将星形的中心点连接到电路的两端,从而形成一个串联电路。
这样得到的等效电路中,三个电阻的串联等效电阻就是原始电路中三个电阻的并联等效电阻。
这两种变换公式在电路的设计和分析中都有着广泛的应用,可以帮助工程师们更加高效地进行电路设计和计算。
在实际应用中,需要根据电路特点选择合适的变换公式,从而得到更加准确和简化的计算结果。
- 1 -。
电阻网络中的三角形星形等效变换解析实例

电阻网络中的三角形星形等效变换解析实例电阻网络中的三角形-星形等效变换解析实例在电路分析中,等效变换是一种将复杂电路简化成简单电路的方法。
其中,三角形-星形等效变换是常用的一种方法,可以将电阻网络中的三角形形式转换为星形形式,使得电路的计算更加简便。
本文将通过几个实例来解析电阻网络中的三角形-星形等效变换,以展示这一方法的应用。
实例一:在如下电阻网络中,我们希望将三角形形式转换为星形形式:R1 R2 R3o--------o-----------o-----------o| | |RL R5 R6| | |o--------o-----------o-----------oR4 R7 R8首先,我们按照以下步骤进行等效变换:1. 将RL与R1进行并联,得到RL1;2. 将RL1与R7进行并联,得到RL2;3. 将R4与RL2进行并联,得到RL3;4. 将R5与RL3进行并联,得到RL4。
经过以上等效变换后,得到如下的星形形式电路:RL4 RL3 RL2o--------o-----------o-----------o| | |R2 R3 R8| | |o--------o-----------o-----------oR1 R5 R6通过以上变换,我们成功将电阻网络转换为了星形形式,从而简化了电路的计算。
实例二:现在考虑一个稍为复杂的电阻网络,其中包含多个三角形形式的电阻网络。
我们希望将整个电路转换为星形形式。
R2 R3o--------o----------------------o|R1 L|o|RL R4 RL|R5 L|o|R6 R7o ----------------------o----------------o为实现等效变换,我们按照以下步骤进行处理:1. 将RL与R1进行并联,得到RL1;2. 将RL1与R4进行并联,得到RL2;3. 将RL2与R5进行并联,得到RL3;4. 将R6与RL3进行并联,得到RL4;5. 将RL4与R3进行并联,得到RL5;6. 将RL5与R7进行并联,得到RL6。
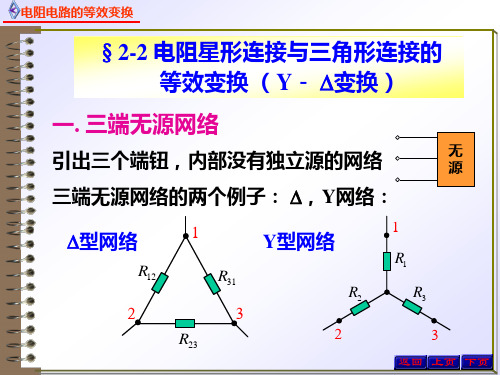
电阻星形连接与三角形连接的等效变换
i1
u12 R12
u31 R31
i2
u23 R23
u12 R12
(1)
i3
u31 R31
u23 R23
由等效条件,比较式(3)与式(1),得由Y接接的变换结果
R12
R1 R2
R2 R3 R3
R3 R1
R23
R1 R2
R2 R3 R1
R3
R1
或
R31
R1 R2
R2 R3 R2
R3
R1
d
h
b
f
a
e
c
g
b
f
返回 上页 下页
电阻电路的等效变换
d
将等电位点短接,
a
e
画出等效电路:
h
c
g
b
f
b de a
cf h
Rag
R 3
R 6
R 3
g
5
R
6
返回 上页 下页
电阻电路的等效变换
(2)求Rab
d
由电路对称性,
h
找出等电位点:
a c
b
a
e
d、e等电位
c、f等电位
g
7
f
Rab 12 R
hg
1.5 (0.6 1.4)(1 1) 2.5 0.6 1.4 1 1
求得: i 10 10 4 R 2.5
返回 上页 下页
电阻电路的等效变换
+
10V -
i1
3 2
2
1.4
3
图(a)
5 Y→△ +
4
10V
-
1
i1
3
2
知识点: 电阻的星形、三角形联结及其等效变换-教学文稿

三个联结点再分别与外电路联结于三个点a、b、c(此三点电位不同)。 3.在电路分析时,有时为了分析和计算的方便,需要将星形联接的电阻和三 角形联接的电阻进行等效变换。等效的原则依然是等效前后对外部电路不发 生任何影响。
若星形联结的三个电阻阻值相等,则变换后的三角形联结的三个电阻也相等, 它们之间的关系为 RΔ 3RY
三、知识深化
例10 如图1-55(a)所示桥式电路,试求电流I。
解:图1-55(a)所示桥式电路中的电阻并非串联或并联,而是由两个三角形 网络组成,我们可以将图1-55(a)中的一个三角形网络(abc)变换为星形 联结形式,这样电路就可以简化为如图1-55(b)所示的串并联形式。
三角形联结是把三个电阻Rab、Rca、Rbc依次联成一个闭合回路,然后三
个联结点再分别与外电路联结于三个点a、b、c(此三点电位不同),如图154(a)和(b)。三角形联结也可写成Δ形联结或π形联结。
图1-54 电阻星型联结和三角形联结的等效变换
二、知识准备
(三)三角形与星形连结之间的等效变换
在电路分析时,有时为了分析和计算的方便,需要将星形联接的电阻和三 角形联接的电阻进行等效变换。等效的原则依然是等效前后对外部电路不发生 任何影响;将这一原则用于Y、Δ电路之间的等效变换时,具体的内容应当是, 在两种不同的联结方式中对应一个端子悬空的情况下,若剩余两个端子间的电 阻值相等,则它们就等效。根据以上原则,我们可以推导出等效变换的公式。
图1-55 例10图
将图1-55(a)中的6Ω、10Ω、4Ω三个电阻组
成的三角形网络等效变换为星形网络,其等效电阻
为
6 10 R1 6 4 10 3 (Ω)
电路与电工基础项目2.2 电阻星形连接和三角形连接的等效变换

Rbc
c
(a)
(b)
图2-14电阻的星形连接与三角形连接
2.2.1电阻的星形连接和三角形连接
• 在图2-14 (a)中,三个电阻元件Ra、Rb、Rc的 一端O连在一起,另一端分别连接到电路的三 个节点,这种连接方式叫做星形连接,也叫Y 连接。在图2-14(b)中,三个电阻元件Rab、Rbc 、Rca首尾相连,接成一个三角形,这种连接 方式叫做三角形连接,也叫△连接。
1 3
R
2.2.2电阻星形连接和三角形连接的等 效变换
• 星形变换到三角形的等效关系式 :
Rab
ra rb
rb rc rc
rc ra
Rbc
ra rb
rbrc ra
rc ra
Rca
ra rb
rb rc rb
rc ra
若ra=rb=rc= rY,则Rab=Rbc=Rca=R△,且
2.2.2电阻星形连接和三角形连接的等效变换
• 三角形变换到星形的等效关系式 :
ra
Rab
Rab Rca Rbc
Rca
rb
Rab
Rbc Rab Rbc Rca
rc
Rab
Rbc Rca Rbc
Rca
若Rab=Rbc=Rca=R△,则ra= rb= rc= rY,且
rY
模块二 电路元件和电路的等效变换
项目2.1 电阻元件及其串、并联的等效变换 项目2.2 电阻星形连接和三角形连接的等效变换 项目2.3 电容元件和电感元件 项目2.4 有源元件及实际电源的等效变换
1
模块二 电路元件和电路的等效变换
电路原理2.2.1电阻的星形联结和三角形联结的等效变换 - 电阻星形连接与三角形连接的等效变换
返回 上页 下页
电阻电路的等效变换
由式(2)解得:
i1Y
u12Y R3 u31Y R2 R1R2 R2 R3 R3 R1
i2Y
u23Y R 1 u12Y R1R2 R2 R3
R3 R3
R1
(3)
i3Y
u31Y R2 u23Y R1 R1R2 R2 R3 R3 R1
G12
G1
G1G2 G2 G3
G23
G1
G2G3 G2 G3
G31
G1
G3G1 G2
G3返回
上页
下页
电阻电路的等效变换
由Y接 接的变换结果:
R12
R1 R2
R2 R3 R3
R3 R1
R23
R1 R2
R2 R3 R1
R3
R1
或
R31
R1 R2
R2 R3 R2
R3
R1
4
35 R1 3 2 5 1.5
32 R2 3 2 5 0.6
R3
3
2 2
5
5
1
返回 上页 下页
电阻电路的等效变换
+
10V -
i1
1.5
0.6 1
2
3
1.4
1
再用电阻串联和 并联公式,求出连接 到电压源两端单口的 等效电阻:
4
R 1.5 (0.6 1.4)//(1 1)
5 )
17
R23
(5
2+2 1+1 5
5 )
3.4;
R31
(
5
2+2 1+1 2
5 )
8.5
电阻的星形和三角形连接的等效变换

电阻的星形和三角形连接的等效变换之马矢奏春创作1、电阻的星形和三角形连接三个电阻元件首尾相连接,连成一个封闭的三角形,三角形的三个顶点接到外部电路的三个节点,称为电阻元件的三角形连接简称△连接,如图 2.7(a )所示。
三个电阻元件的一端连接在一起,另一端分别连接到外部电路的三个节点,称为电阻元件的星形连接,简称Y 形连接,如图2.7(b )所示。
三角形连接和星形连接都是通过三个节点与外部电路相连,它们之间的等效变换是要求它们的外部特性相同,也就是当它们的对应节点间有相同的电压12U 、23U 、31U 时,从外电路流入对应节点的电流1I 、2I 、3I 也必须分别相等,即Y-△变换的等效条件。
一种简单的推导等效变换方法是:在一个对应端钮悬空的同等条件下,分别计算出其余两端钮间的电阻,要求计算出的电阻相等。
悬空端钮3时,可得:12233112122331()R R R R R R R R ++=++ 悬空端钮2时,可得:31122331122331()R R R R R R R R ++=++悬空端钮1时,可得:23123123122331()R R R R R R R R ++=++ 联立以上三式可得:123111223311223212233131233122331R R R R R R R R R R R R R R R R R R =++=++=++ (2-2)式(2-2)是已知三角形连接的三个电阻求等效星形连接的三个电阻的公式。
从式(2-2)可解的:121212323232313131312R R R R R R R R R R R R R R R R R R =++=++=++ (2-3)以上互换公式可归纳为:当Y 形连接的三个电阻相等时,即123Y R R R R ===,则等效△形连接的三个电阻也相等,它们等于1223313Y R R R R R ∆==== 或 1=3Y R R ∆ (2-4)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章 直流电阻电路的分析计算
例 2.5(四)
图2.10(b)是电阻混联网络, 串联的Rc、R2的 等效电阻Rc2=40Ω, 串联的Rd、R4的等效电阻 Rd4=60Ω, 二者并联的等效电阻
第2章 直流电阻电路的分析计算
例 2.5(三)
解 将△形连接的R1, R3, R5等效变换为Y形连接的 Ra, Rc、Rd, 如图2.10(b)所示, 代入式(2.8)求得
R3 R1 50 40 Ra 20 R5 R3 R1 10 50 40 R1R5 40 10 Rc 4 R5 R3 R1 10 50 40 R5 R3 10 50 Rd 5 R5 R3 R1 10 50 40
桥式电阻的端口电流
Us 225 I 5A R0 Ri 1 44
R2、R4的电流各为 Rd 4 60 I2 I 5 3A Rc 2 Rd 4 40 60
Rc 2 40 I4 I 5 1A Rc 2 Rd 4 40 60
电子发烧友 电子技术论
电子发烧友 电子技术论
第2章 直流电阻电路的分析计算
教学方法
在得到星—三转换公式时,启发学生自己找 到记忆公式的规律。
电子发烧友 电子技术论
第2章 直流电阻电路的分析计算
2.2 电阻的星形连接与 三角形连接的等效变换
电子发烧友 电子技术论
第2章 直流电阻电路的分析计算
目的与要求
会进行星形连接与三角形连接间的等效变换
电子发烧友 电子技术论
40 60 Rab 24 40 60
Ra与Rob串联, a、b间桥式电阻的等效电阻
Ri 20 24 44
电子发烧友 电子技术论
第2章 直流电阻电路的分析计算
例 2.5(五)
第2章 直流电阻电路的分析计算
例 2.5(二)
I2 R1 I1 R2 Ra Rc I4 I Rd R0 + Us R4 - I2 R2
I3
R3 R0
R5
I4
I
R4
+ Us -
(a )
(b )
图 2.10 例 2阻电路的分析计算
思考题
求下图所示网络的等效电阻 Rab
a 10 20 10 5
b
5
电子发烧友 电子技术论
I1 I1 R31 3 I3 R23 I23 I 2 1 I31 1 I12 R12 2 R3 I3 3 R2 2 I2 R1
(a )
电子发烧友 (b ) 电子技术论
第2章 直流电阻电路的分析计算
⒉ 三角形、星形等效的条件
电子技术论
第2章 直流电阻电路的分析计算
4.已知星形连接电阻求三角形连接电阻
R1R2 R2 R3 R3 R1 R1R2 R12 R1 R2 R3 R3 R1R2 R2 R3 R3 R1 R2 R3 R23 R2 R3 R1 R1 R1R2 R2 R3 R3 R1 R3 R1 R31 R3 R1 电子发烧友 R2 R2 电子技术论
端口电压U12、U23、U31 和电流I1、I2 、I3都 分别相等,则三角形星形等效。
电子发烧友 电子技术论
第2章 直流电阻电路的分析计算
3.已知三角形连接电阻求星形连接电阻
R12 R31 R1 R12 R23 R31 R23 R12 R2 R12 R23 R31 R31 R23 R3 R12 R23 R31 电子发烧友
例 2.5(一)
图2.10(a)所示电路中, 已知Us=225V, R0=1Ω, R1=40Ω, R2=36Ω, R3=50Ω, R4=55Ω, R5=10Ω, 试求 各电阻的电流。
电子发烧友 电子技术论
第2章 直流电阻电路的分析计算
5.特殊情况
设三角形电阻R12=R23=R32= R ,则
R
R =R1=R2=R3= 3
反之, R =R12=R23=R31=3 R
电子发烧友 电子技术论
第2章 直流电阻电路的分析计算
第2章 直流电阻电路的分析计算
例 2.5(六)
为了求得R1、R3、R5的电流, 从图2.10(b)求得 回到图2.10(a)电路, 得
Uac Ra I Rc I 2 20 5 4 3 112 V
U ac 112 I1 2.8 A R1 40
并由KCL得
I 3 I I1 5 2.8 2.2 A I 5 I 3 I 4 2.2 2 0.2 A
第2章 直流电阻电路的分析计算
重点与难点
重点: 星形连接与三角形连接的等效变换
难点: 星形与三角形等效变换的公式
电子发烧友 电子技术论
第2章 直流电阻电路的分析计算
⒈三角形连接和星形连接
三角形连接:三个电阻元件首尾相接构成一 个三角形。如下图a所示。 星形连接:三个电阻元件的一端连接在一起, 另一端分别连接到电路的三个节点。如上图b所 示。
