电阻的星形联结与三角形联结
星型连接和三角形连接的相电压和线电压的关系

星型连接和三角形连接的相电压和线电压的关系
星形连接是线电压是相电压的根号3倍,而三角形连接是相电压是等于线电压的。
每相负载中流过的电流为相电流,流过每条电源线中的电流为线电流。
线电流与相电流的关系也与三相负载的接法有关。
当三相负载为三角形联结时,每一线电流都分成两路,其中一路为一相,另一路由两相串联组成,所以线电流要大于相电流,即线电流是相电流的√3倍;当三相负载为星形联结时,线电流和相电流相等。
三相电路特点:
对称三相电源和对称三相负载相连接,称为对称三相电路(一般情况下,电源总是对称的)。
三相电源与负载之间的连接方式有y-y,△-y,△-△,y-△连接方式。
三相电路实际是正弦交流电路的一种特殊类型。
在三相电路中,三相功率的相连接方式同意于功率每相的额定电压和电源的线电压。
由于等距三相电路中每组的积极响应都就是与鞭策同相序的对秤。
所以,每二者不但接法有效值成正比,相电流有效值也成正比。
而且每接法与电流的相位差也成正比。
从而每相的军功功率成正比。
知识点: 电阻的星形、三角形联结及其等效变换-教学文稿

三个联结点再分别与外电路联结于三个点a、b、c(此三点电位不同)。 3.在电路分析时,有时为了分析和计算的方便,需要将星形联接的电阻和三 角形联接的电阻进行等效变换。等效的原则依然是等效前后对外部电路不发 生任何影响。
若星形联结的三个电阻阻值相等,则变换后的三角形联结的三个电阻也相等, 它们之间的关系为 RΔ 3RY
三、知识深化
例10 如图1-55(a)所示桥式电路,试求电流I。
解:图1-55(a)所示桥式电路中的电阻并非串联或并联,而是由两个三角形 网络组成,我们可以将图1-55(a)中的一个三角形网络(abc)变换为星形 联结形式,这样电路就可以简化为如图1-55(b)所示的串并联形式。
三角形联结是把三个电阻Rab、Rca、Rbc依次联成一个闭合回路,然后三
个联结点再分别与外电路联结于三个点a、b、c(此三点电位不同),如图154(a)和(b)。三角形联结也可写成Δ形联结或π形联结。
图1-54 电阻星型联结和三角形联结的等效变换
二、知识准备
(三)三角形与星形连结之间的等效变换
在电路分析时,有时为了分析和计算的方便,需要将星形联接的电阻和三 角形联接的电阻进行等效变换。等效的原则依然是等效前后对外部电路不发生 任何影响;将这一原则用于Y、Δ电路之间的等效变换时,具体的内容应当是, 在两种不同的联结方式中对应一个端子悬空的情况下,若剩余两个端子间的电 阻值相等,则它们就等效。根据以上原则,我们可以推导出等效变换的公式。
图1-55 例10图
将图1-55(a)中的6Ω、10Ω、4Ω三个电阻组
成的三角形网络等效变换为星形网络,其等效电阻
为
6 10 R1 6 4 10 3 (Ω)
§2-3电阻的星形联结与三角形联结

星形联结与三角形联结特点
星形联结
三个电阻器的一端连接在一起,另一 端分别接到电路的三个节点上,形如 “Y”或“星”形。星形联结具有总 电阻小、分压作用等特点。
三角形联结
三个电阻器首尾相连形成一个闭合的 三角形,每个电阻器都承担一部分电 压和电流。三角形联结具有总电阻大 、电流分布均匀等特点。
功率计算与分配原则
星形联结中,总功率等于各相功率之 和。
通过功率计算公式可得出各相功率及 总功率。
各相功率分配原则:按照电阻大小成 反比分配。
实际应用案例分享
星形联结在三相四线制供电系 统中广泛应用。
例如:家庭用电、照明电路等 均采用星形联结方式。
通过实际案例分享,了解星形 联结在实际应用中的优点和注 意事项。
通过电流、电压的相互关系,推 导三角形联结的总电阻和总电流。
功率计算与分配原则
根据功率公式,计算三角形联结中各电 阻的功率消形联结与三角形联结在功率计算
探讨不同电阻值对功率分配的影响。
和分配方面的异同点。
实际应用案例分享
分享一些实际工程中采用三角形联结的案例,如电力系统、电子设备等。
测量数据
按照实验步骤,分别测量 星形联结和三角形联结电 路中的电压、电流和功率 等参数。
数据记录
将测量得到的数据及时记 录下来,以便后续的分析 和处理。
实验结果分析与讨论
数据处理
01
对测量得到的数据进行整理、计算和分析,得出电阻星形联结
和三角形联结的电路特性。
结果分析
02
根据数据分析结果,比较两种联结方式的优缺点,并解释产生
转换过程中注意事项
复杂电路中的电阻计算口诀
复杂电路中的电阻计算口诀1、口诀复杂电路变简单,可将星角来变换。
变时一点要牢记,外接三点不能变。
星变角时求某边,两两积和除对面。
角变星时求某枝,两臂之积除和三。
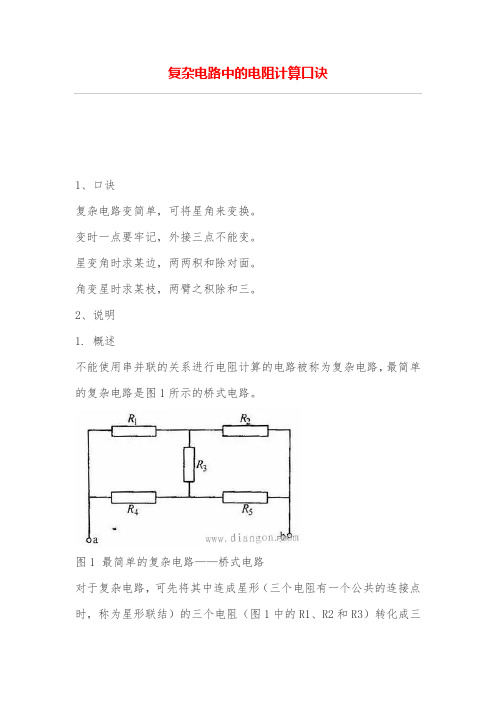
2、说明1. 概述不能使用串并联的关系进行电阻计算的电路被称为复杂电路,最简单的复杂电路是图1所示的桥式电路。
图1 最简单的复杂电路——桥式电路对于复杂电路,可先将其中连成星形(三个电阻有一个公共的连接点时,称为星形联结)的三个电阻(图1中的R1、R2和R3)转化成三角形电路(三个电阻依次连接成为一个闭合回路时,称为三角形联结),或将其中连成三角形的三个电阻(图1中的R1、R3和R4)转化成星形电路,这就是所谓的电阻星-三角变换问题。
进行上述变换后,原有的复杂电路就会转变为简单电路,就可以用串并联的计算方法求出总电阻值。
电阻星-三角变换的理论推导相对较复杂,在此不准备给出。
下面只给出转换方法口诀和使用方法举例。
2. 口诀说明设星形联结的三个电阻分别是R1、R2和R3,三角形联结的三个电阻分别是R12(对应星形连接的R1和R2)、R23(对应星形连接的R2和R3)和R31(对应星形连接的R3和R1),参照图2说明转换口诀的使用方法。
图2 电阻的星-三角变换电路(1)当由星形联结转换成三角形联结时,口诀为“星变角时求某边,两两积和除对面”。
这里的“两两”是指星形联结时的每两个电阻,“两两积和”即为(R1R2+ R2R3+ R3R1);“对面”是指与转换成三角形联结后的一个电阻相对的原星形联结的那个电阻,如图2中R12的“对面”应是R3。
由此可得到由星形联结转换成三角形联结时的三个电阻计算公式为R12=(R1R2+ R2R3+ R3R1)/R3R23=(R1R2+ R2R3+ R3R1)/R1R31=(R1R2+ R2R3+ R3R1)/R2(2)当由三角形联结转换成星形联结时,口诀为“角变星时求某枝,两臂之积除和三”。
这里的“两臂”是指与转换成星形联结的一个电阻(后面称为“一枝”,例如R1)同一个顶点的三角形联结时的两个电阻(例如对应R1的两臂是R12和R31),“和三”即为三角形联结时三个电阻之和,即(R12+ R23+ R31)。
电路原理2.2.1电阻的星形联结和三角形联结的等效变换 - 电阻星形连接与三角形连接的等效变换
返回 上页 下页
电阻电路的等效变换
由式(2)解得:
i1Y
u12Y R3 u31Y R2 R1R2 R2 R3 R3 R1
i2Y
u23Y R 1 u12Y R1R2 R2 R3
R3 R3
R1
(3)
i3Y
u31Y R2 u23Y R1 R1R2 R2 R3 R3 R1
G12
G1
G1G2 G2 G3
G23
G1
G2G3 G2 G3
G31
G1
G3G1 G2
G3返回
上页
下页
电阻电路的等效变换
由Y接 接的变换结果:
R12
R1 R2
R2 R3 R3
R3 R1
R23
R1 R2
R2 R3 R1
R3
R1
或
R31
R1 R2
R2 R3 R2
R3
R1
4
35 R1 3 2 5 1.5
32 R2 3 2 5 0.6
R3
3
2 2
5
5
1
返回 上页 下页
电阻电路的等效变换
+
10V -
i1
1.5
0.6 1
2
3
1.4
1
再用电阻串联和 并联公式,求出连接 到电压源两端单口的 等效电阻:
4
R 1.5 (0.6 1.4)//(1 1)
5 )
17
R23
(5
2+2 1+1 5
5 )
3.4;
R31
(
5
2+2 1+1 2
5 )
8.5
电阻的星形联结与三角形联结

2-1 电阻分压和分流电路(自学) 2-2 电阻单口网络(重点) 2-3 电阻的星形联结与三角形联结(公式) 2-4 简单非线性电阻电路分析(自学)
2-5 电路设计,电路实验实例 (自学)
第二章 用网络等效简化电路分析
2b法的缺点是需要联立求解的方程数目 太多,给求解带来困难。
u u1 u2
列出电路元件的VCR方程
u uS u1 R1i1
u2 R2i2
将电阻元件的欧姆定律代入KVL方程,得到电流i的计算公式
uS u1 u2=R1i1 R2i2 (R1 R2 )i i uS
R1 R2
将它代入电阻元件的欧姆定律,得到计算电阻电压的分压公式
u1
R1 R1 R2
a
6Ω
12Ω
Rab
18Ω 9Ω
b 图3
2、图示电路,求I 。
I
6Ω 3A
3Ω
图1
历年考题:
1、图示电路,a、b两 端等效电阻Rab=? 6 Ω
a
6Ω
12Ω
Rab
18Ω 9Ω
b 图3
2、图示电路,求I 。2A
I
6Ω 3A
3Ω
图1
历年考题:
3、图示电路,求i 。
i 3Ω
8V
8Ω 3Ω
6Ω
3Ω
4、图示电路,求u 。
§2-2 电阻单口网络
VCR相同
N1
等效
N2
单口网络:只有两个端钮与其它电路相连接的网 络,称为二端网络。当强调二端网络的端口特性,而 不关心网络内部的情况时,称二端网络为单口网络, 简称为单口(One-port)。
§2-2 电阻单口网络
电阻的Y-△等效变换
等效变换的条件是:三端的电流与任何两 点之间的电压在变换前后保持相同,对外电路 的作用是完全一样的。
Y 联结转换为△联结的变换公式:
R12
R1
R2
R1 R2 R3
R23
R2
R3
R2 R3 R1
§3-8 电阻的Y-△等效变换
学习目标
掌握电阻Y-△等效变换的方法。
一、星形(Y)联结和三角形(△)联结
星形联结——把3个电 阻R1、R2、R3的一端联结 在一起,成为一个节点, 电阻的另外三端分别与电 路的不同部分联结的连接 方式,简称Y联结。
三角形联结——把3 个电阻R12、R23、R31联成 一个闭合的三角形,三角 形的三个顶点分别与电路 的不同部位相联结的联结 方式,简称△联结。
对称的Y联结和△联结的等效变换公式为:
1
RY = 3 RV
或
RV 3RY
[例3-12]
计算下图a所示电桥电路中的总电流I以及通 过桥上的电流IP。
解:由于图a所示电桥电路没有处于平衡状态,
故属于复杂直流电路,若按照一般的复杂直流电路
的解法求解非常复杂,更不能用电阻串并联的方法
求解。仔细观察不难发现,图中的三个电阻R2、R3、 R5正好构成对称的三角形接法,根据Y-△等效变 换原则,可把它们等效为星形接法,接成图b所示
的电路。其中
RY
1 3
RV
9 3
(3 )
这时原来的复杂直流电路已经等效成为简单
直流电路,此时的总电阻为:
Rcd = 15 3 / / 6 3 3=( 9 )
复杂电路的计算整合
电磁学论文班级:13物理(1)班姓名:李建民学号:20131040212复杂电路的计算天水师范学院,13物理(1)班,李建民摘要解决复杂电路计算的基本公式是基尔霍夫方程组,原则上它可以用来计算任何复杂电路中每一支电路中的电流,可是实际的电路计算常常并不需要计算每一支电路的电流,而只计算某一支路的电流,或某部分电路的等效电阻等。
在解决这样的问题中,可运用基尔霍夫方程组导出的定理,可以简化计算。
这些定理有等效电源定理、叠加定理、Y—△等效代换定理。
关键词复杂电路基尔霍夫方程组等效电源定理、叠加定理、Y—△等效代换定理一、定理的表述在此部分,我将所要引用的几个定理作以详细表述。
(一)基尔霍夫方程组。
1、基尔霍夫第一方程组。
基尔霍夫第一方程组又称节点电流方程组,它的理论基础是恒定条件。
我们规定:流向节点的电流前写负号,反之,流出节点的电流前写正号,则此节点处的代数和为0。
.0321=+--I I I2、 基尔霍夫第二方程组。
基尔霍夫第二方程组又称回路电压方程组,它的理论基础是恒定电场的环路定理。
我们规定:在一个回路中预先确定一绕行方向,电势从高到低降落为正,从低到高降落为负,则沿回路环绕一周,电势降落代数和为0。
即:.0)(14323222111=-+++++-R I R r I R I r I εε(二) 电压源与电流源 等效电源定理。
1、电压源与电流源。
一个实际电源可以看成是电动势为ε内阻为0的理想电压源与内阻r 的串联。
当电源两端接上外电阻R 时,其上就有电流和电压。
在理想情况下,r=0,不管外电阻如何,电源提供的电压总是恒定值ε,我们把这种电源叫恒压源(即理想电压源)。
在非理想情况下,0≠r ,这样的电源叫电压源,它相当于内阻r 与恒压电源串联,如图a我们也可以设想有一种理想电源,不管外电阻如何变化,它总是提供不变的电流0I ,0I 相当于恒压源中的电动势。
这种理想的电源叫做恒流源。
一个电池串联很大的电阻,就近似于一个恒流源,因为它对外电阻所提供的电流基本上由电动势和所串联的大电阻决定,几乎于外电阻无关。
简谈电阻电路常用分析和计算方法
<)
-
+
-
0 图4
^
Ri _ 尺2 + 尺 3 Ul0
只2只3
R 3l
R xR 2 + R 2R 3 +^3^!
'
R2
-R3+ Rx
■
r2
已 知 星 形 联 结 电 阻 只 2、尽 求 等 效 三 角 形 联 结 电 阻
只12、只23、屯 的 公 式 如 上 。当 星 形 联 结 的 三 个 电 阻 '相 等
时 ,其 等 效 三 角 形 联 结 的 三 个 电 阻 也 相 等 即 :
丄 +丄+丄+丄
R2 + G礼 G, + G2 + G3 + G4
( 3 ) 根据欧姆定律求出各支路电流。 总结节点电压法对于两个以上节点,列写方程通式为: 自电导x 本节点的电压值+ Z 互 电 导 x 相邻结点电压=
Z 本节点上所有流人电流源的大小 注意:所有的自电导均为+ , 互电导均为五 、结语 等 效 变 换 可 以 将 电 路 简 化 后 再 进 行 计 算 ,电 路 节 点 少 ,
( 1 ) 以网孔为基础,假设网孔的电流参考方向。
(2)
列出各网孔的回路电压方程。列 方 程 时 ,凡参考方
向与网孔绕行方向一致的电源电压取负号,反 之 取 正 号 ; 二^ + i ?2、i ?22 + i ?3 分 别 是 网 孔 1 与 网 孔 2 的电阻之和,
电阻星形连接与三角形连接的等效变换公式
电阻星形连接与三角形连接的等效变换公式一、电阻星形连接的等效变换公式在电路中,星形连接是指将三个电阻分别连接在一个共节点上,形成一个星形的连接方式。
在星形连接中,我们可以通过等效变换将星形连接转换为三角形连接。
设电阻A、B、C分别为星形连接中的三个电阻,它们与共节点的连线分别为AB、AC、BC。
根据星形连接的特性,我们可以得到以下关系式:1/RA = 1/AB + 1/AC1/RB = 1/AB + 1/BC1/RC = 1/AC + 1/BC根据以上关系式,我们可以推导出电阻星形连接的等效变换公式:1/RA = 1/R1 + 1/R2 + 1/R31/RB = 1/R1 + 1/R2 + 1/R31/RC = 1/R1 + 1/R2 + 1/R3其中,R1、R2、R3分别为星形连接中的三个电阻。
二、电阻三角形连接的等效变换公式与电阻星形连接相反,电阻三角形连接是指将三个电阻分别两两相连,形成一个三角形的连接方式。
在三角形连接中,我们可以通过等效变换将三角形连接转换为星形连接。
设电阻X、Y、Z分别为三角形连接中的三个电阻,它们之间的连线分别为XY、XZ、YZ。
根据三角形连接的特性,我们可以得到以下关系式:1/RX = 1/XY + 1/XZ1/RY = 1/XY + 1/YZ1/RZ = 1/XZ + 1/YZ根据以上关系式,我们可以推导出电阻三角形连接的等效变换公式:1/RX = 1/RA + 1/RB + 1/RC1/RY = 1/RA + 1/RB + 1/RC1/RZ = 1/RA + 1/RB + 1/RC其中,RA、RB、RC分别为三角形连接中的三个电阻。
三、电阻星形连接与三角形连接的等效性通过对电阻星形连接和三角形连接的等效变换公式的分析,我们可以得出结论:电阻星形连接与三角形连接是等效的。
在电路分析中,等效电路可以简化复杂的电路结构,使计算更加方便。
通过等效变换,我们可以将电阻星形连接转换为三角形连接,或将三角形连接转换为星形连接,从而简化电路的计算过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i2
(2 14)
如果要求电阻星形联结和三角形联结等效,则要 求以上两
个VCR方程的对应系数分别相等,即:
R1
R3
R31 R12
( R12 R23 ) R23 R31
R1
R12
R31 R12 R23
R31
R3
R12
R23 R31 R23
§2-3 电阻的星形联结与三角形联结
电阻的星形联结:将三个电阻的一端连在一起,另一端 分别与外电路的三个结点相连,就构成星形联结,又称为 Y形联结,如图2-24(a)所示。
电阻的三角形联结:将三个电阻首尾相连,形成一个三 角形,三角形的三个顶点分别与外电路的三个结点相连, 就构成三角形联结,又称为Δ形联结,如图(b)所示。
R31
(2
15)
由此
解得
R2
R12
R12 R23 R23
R31
(2 16)
R2
R3
R23( R12
R31 )
R12 R23 R31 Βιβλιοθήκη R3R12
R23 R31 R23
R31
R1
R31 R12 R12 R23
R31
(2 13)
图2-26
对电阻三角形联结的三端网络,外加两个电流源i1和i2, 将电流源与电阻的并联单口等效变换为一个电压源与电阻 的串联单口,得到图(b)电路,由此得到
i12
R31i1 R23i2 R12 R23 R31
u1 R31i1 R31i12 R31(i1 i12 ) u2 R23i12 R23i2 R23(i2 i12 )
i12
R31i1 R23i2 R12 R23 R31
uu12
R31i1 R31i12 R23i12 R23i2
R31(i1 i12 ) R23(i2 i12 )
将i12表达式代入上两式,得到
u1
R31( R12 R23 ) R12 R23 R31
一、电阻的星形联结与三角形联结的电压电流关系
电阻的星形联结或三角形联结构成一个电阻三端网络,它 有两个独立的端口电流和两个独立的端口电压。电阻三端网 络的端口特性,可用联系这些电压和电流的两个代数方程来 表征。用外加两个电流源,计算端口电压表达式的方法,推 导出电阻星形联结和三角形联结网络的端口 VCR方程。
i1
R12
R23 R31 R23
R31
i2
u2
R12
R23 R31 R23
R31
i1
R23( R12 R31 ) R12 R23 R31
i2
(2 14)
式(2-13)和(2-14)分别表示电阻星形联结和三角形联 结网络的 VCR方程。
u1 (R1 R3 )i1 R3i2
由式(2-15)可解得:
R12
R1 R2
R2 R3 R3
R3
R1
R23
R1 R2
R2 R3 R1
R3
R1
R31
R1 R2
R2 R3 R2
R3 R1
(2 19)
电阻星形联结等效变换为电阻三角形联结的公式为
形电阻两两乘积之和 Rmn 不与mn端相连的电阻
(2 20)
当R1= R2= R3= RY时,有
R12 R23 R31 R 3R (2 21)
在复杂的电阻网络中,利用电阻星形联结与电阻三角 形联结网络的等效变换,可以简化电路分析。
例2-13 求图2-27(a)电路中电流 i。
图2-27
解:将3、5和2三个电阻构成的三角形网络等效变换 为星形网络[图(b)],其电阻值由式(2-16)求得
u2
R3i1
(R2
R3
)i2
(2 13)
u1
R31( R12 R23 ) R12 R23 R31
i1
R12
R23 R31 R23
R31
i2
u2
R12
R23 R31 R23
R31
i1
R23( R12 R31 ) R12 R23 R31
35
32
25
R1 3 2 5 1.5 R2 3 2 5 0.6 R3 3 2 5 1
图2-27
再用电阻串联和并联公式,求出连接到电压源两端单 口的等效电阻
R 1.5 (0.6 1.4)(1 1) 2.5 0.6 1.4 1 1
R2
R12
R12 R23 R23
R31
R3
R12
R23 R31 R23
R31
(2 16)
电阻三角形联结等效变换为电阻星形联结的公式为
接于i端两电阻之乘积 Ri 形三电阻之和
当R12= R23= R31= R时,有
1 R1 R2 R3 R 3 R
7 非线性电阻器件VCR曲线
3:59 8 线性与非线性分压电路
9 非线性电阻单口网络VCR曲线 2:30 10 半波整流电路实验
11 全波整流电路实验
2:54 12 整流电路波形
13 万用表测量电阻
2:41 14 稳压电路实验
15 理想二极管实验
3:00 16 电阻单口网络VCR曲线
17 白炽灯的特性
3:23 18 白炽灯电路实验1
19 白炽灯电路实验2
3:45
时间 1:26 3:30 2:25 2:49 2:15 3:22 2:50 2:50 3:44
郁 金 香
电阻的星形联结和电阻的三角形联结是一种电阻三端网 络,电阻三端网络的特性是由端口电压电流关系来表征的, 当两个电阻三端网络的电压电流关系完全相同时,称它们 为等效的电阻三端网络。将电路中某个电阻三端网络用它 的等效电阻三端网络代替时,不会影响端口和电路其余部 分的电压和电流。
一、电阻的星形联结与三角形联结的电压电流关系
对于电阻星形联结的三端网络,外加两个电流源i1和i2。 用2b方程求出端口电压u1和u2的表达式为:
u1 R1i1 R3 (i1 i2 ) u2 R2i2 R3 (i1 i2 )
整理得到
u1 (R1 R3 )i1 R3i2
u2
R3i1
( R2
R3
)i2
最后求得
i 10V 10V 4A R 2.5
在幻灯片放映时,请用鼠标单击图片放映录像。
根据教学需要,用鼠标点击名称的方法放映相关录像。
名称
时间
名称
1 电阻分压电路实验
3:11 2 双电源电阻分压电路
3 负电阻分压电路
2:12 4 可变电压源
5 电阻三角形和星形联结
3:06 6 普通万用表的VCR曲线
