第08章习题解答
金融学习题答案第08章货币供给

第八章货币供给参考答案一、单项选择题(在每小题列出的四个备选项中只有一个是最符合题目要求的,请将其代码写在题后的括弧内。
错选、多选或未选均无分。
)1. C2. B3. B4. D5. C6. D7. B8. D9. C 10.D二、多项选择题(在小题列出的五个备选项中,至少有二个是符合题目要求的,请将其代码写在题后的括弧内。
错选、多选、少选或未选均无分)1.ABCD2. ABC3.AB4. ABC5. ABCD6.BD7.ABCDE8.ADE9. CD 10.ACDE11.ABC 12.ABC 13.ACE三、计算题(要求写出计算过程和计算公式)(一)1.M0=1252.影响因素:对国有商业银行贷款. 财政透支借款. 金银外汇占款国有商业银行存款. 财政性存款. 自有资金和当年结益.3.增加10亿货币投放(二)1.存款乘数派生存款=原始存款×(K-1)=100×(3.06-1)=206万元2.M1=m×B=3.09×980=3028亿元四、简述题(回答要点并加以解释或说明)1.银行自身具有创造资金来源的能力,为了便于说明,将银行的资产负债表汇总并简化如下表根据资金平衡表原理,有如下公式:123412345(1)资金运用(资产)不增加,资金来源(负债)不会增加。
在资金运用不增加的情况下,以上A1、A2、A3、A4各项的增加,都是在信贷资金来源一方的各项目之间此增彼减,并不影响资金来源总量的变化。
(2)资金运用(资产)发生变动,资金来源(负债)会相应变动。
资金运用减少,在一般情况下,一是企业用销货收入提前归还贷款,则表现为A1和L1相应减少同一额度;二是银行按期收回贷款,则A1或A3与L1相应减少同一额度。
若资金运用增加,如某企业向银行贷款,则表现为L1和A1相应增加;企业贷款中部分要提取现金,则表现为L1和A1、A3的相应增加。
若银行购进金银外汇,则出售金银和外汇的个人会增加一笔存款或现金,表现为L2和A1、A3的相应增加。
第08章(热力学第二定律)习题答案

思 考 题8-1 根据热力学第二定律判断下列哪种说法是正确的.(A) 热量能从高温物体传到低温物体,但不能从低温物体传到高温物体.(B) 功可以全部变为热,但热不能全部变为功.(C) 气体能够自由膨胀,但不能自动收缩.(D) 有规则运动的能量能够变为无规则运动的能量,反之则不行. [ C ]8-2 有人说: “不可逆过程就是不能往反方向进行的过程” 对吗?为什么?[不可逆过程并不是一定不能往反方向进行的过程,而是往反方向进行的过程中用任何 方法都不能使系统和外界同时复原]8-3 有人设计一台卡诺热机(可逆的).每循环一次可从 400 K 的高温热源吸热1800 J ,向 300 K 的低温热源放热 800 J.同时对外作功 1000 J,这样的设计是(A) 可以的,符合热力学第一定律.(B) 可以的,符合热力学第二定律.(C) 不行的,卡诺循环所作的功不能大于向低温热源放出的热量.(D) 不行的,这个热机的效率超过理论值. [ D ][卡诺热机效率最大: % 25 1 12 = - = T T h ] 8-4 某人设想一台可逆卡诺热机, 循环一次可以从400K 的高温热源吸热1800J, 向300K 的低温热源放热 800J, 同时对外作功 1000J. 试分析这一设想是否合理?为什么?[ 违背熵 增原理 ]8-5 下列过程是否可逆,为什么?(1) 通过活塞(它与器壁无摩擦),极其缓慢地压缩绝热容器中的空气;(2) 用旋转的叶片使绝热容器中的水温上升(焦耳热功当量实验).解:(1)是可逆过程。
此过程是无损耗的准静态过程,当活塞(它与器壁无摩擦),极其缓慢地 绝热膨胀时,系统和外界都可复原,故是可逆过程。
(2)是不可逆过程。
功可完全转化为热,但在无外界影响下,热能却不能完全转化为 机械能。
8-6 关于可逆过程和不可逆过程的判断:(A) 可逆热力学过程一定是准静态过程.(B) 准静态过程一定是可逆过程.(C) 不可逆过程就是不能向相反方向进行的过程.(D) 凡有摩擦的过程,一定是不可逆过程.以上四种判断,其中正确的是哪些? [ A,D ]8-7 在所给出的四个图象中,哪个图象能够描述一定质量的理想气体,在可逆绝热过 程中,密度随压强的变化? [ D ]88 从统计的意义来解释, 不可逆过程实质上是一个怎样的状态转变过程?一切实际 过程都向着什么方向进行? [ 从几率较小的状态到几率较大的状态;状态的几率增大 (或 熵值增加) ]89 由绝热材料包围的容器被隔板隔为两半,左边是理想气体,右边真空.如果把隔 板撤去,气体将进行自由膨胀过程,达到平衡后气体的温度及熵如何变化? [ 温度不变; 熵增加 ]810 在一个孤立系统内, 一切实际过程都向着什么方向进行?这就是热力学第二定律 的统计意义. 从宏观上说, 一切与热现象有关的实际过程都是可逆的吗? [ 状态几率增大; 都是不可逆的 ]811 所谓第二类永动机,从功能量转换角度来讲,是一种什么形式的机器?它不可能 制成是因为违背了热学中的哪条定律? [ 从单一热源吸热,在循环中不断对外作功的热 机;热力学第二定律 ]812 熵是什么的定量量度?若一定量的理想气体经历一个等温膨胀过程, 它的熵将如 何变化? [ 大量微观粒子热运动所引起的无序性(或热力学系统的无序性) ;增加] 思考题 8-7图。
08热力学第二定律习题解答

第八章热力学第二定律一选择题1. 下列说法中,哪些是正确的?( )(1)可逆过程一定是平衡过程;(2)平衡过程一定是可逆的;(3)不可逆过程一定是非平衡过程;(4)非平衡过程一定是不可逆的。
A. (1)、(4)B. (2)、(3)C. (1)、(3)D. (1)、(2)、(3)、(4)解:答案选A。
2. 关于可逆过程和不可逆过程的判断,正确的是( )(1) 可逆热力学过程一定是准静态过程;(2) 准静态过程一定是可逆过程;(3) 不可逆过程就是不能向相反方向进行的过程;(4) 凡是有摩擦的过程一定是不可逆的。
A. (1)、(2) 、(3)B. (1)、(2)、(4)C. (1)、(4)D. (2)、(4)解:答案选C。
3. 根据热力学第二定律,下列哪种说法是正确的?( )A.功可以全部转换为热,但热不能全部转换为功;B.热可以从高温物体传到低温物体,但不能从低温物体传到高温物体;C.气体能够自由膨胀,但不能自动收缩;D.有规则运动的能量能够变成无规则运动的能量,但无规则运动的能量不能变成有规则运动的能量。
解:答案选C。
4 一绝热容器被隔板分成两半,一半是真空,另一半是理想气体,若把隔板抽出,气体将进行自由膨胀,达到平衡后:( )A. 温度不变,熵增加;B. 温度升高,熵增加;C. 温度降低,熵增加;D. 温度不变,熵不变。
解:绝热自由膨胀过程气体不做功,也无热量交换,故内能不变,所以温度不变。
因过程是不可逆的,所以熵增加。
故答案选A 。
5. 设有以下一些过程,在这些过程中使系统的熵增加的过程是( )(1) 两种不同气体在等温下互相混合;(2) 理想气体在等体下降温;(3) 液体在等温下汽化;(4) 理想气体在等温下压缩;(5) 理想气体绝热自由膨胀。
A. (1)、(2)、(3)B. (2)、(3)、(4)C. (3)、(4)、(5)D. (1)、(3)、(5) 解:答案选D 。
二 填空题1.在一个孤立系统内,一切实际过程都向着 的方向进行。
第08章 植物的生殖生理习题答案

第八章植物的生殖生理一、名词解释1.春化作用:低温促进植物开花的作用。
2.去春化作用:已春化的植物或萌动种子,在春化过程结束之前,如置于高温条件下,春化效果即行消失,这种现象叫去春化作用。
3.光周期与光周期现象:在一天中,白天和黑夜的相对长度叫光周期。
植物对光周期的反应叫光周期现象。
4.光周期诱导:植物只需要一定时间适宜的光周期处理,以后即使处于不适宜的光周期下,仍然可以长期保持刺激的效果,这种现象称为光周期诱导。
5.诱导周期数:植物达到开花所需要的适宜光周期数。
不同植物所需的诱导周期数不同。
6.临界日长:诱导短日植物开花所需的最长日照时数,或诱导长日植物开花所需的最短日照时数。
7.临界暗期:昼夜周期中短日植物能够开花所必需的最短暗期长度,或长日植物能够开花所必需的最长暗期长度。
8.长日植物:日长必须长于临界日长才能开花的植物。
9.短日植物:日长必须小于临界日长才能开花的植物。
10.日中性植物:在任何日照长度下都能开花的植物。
11.花熟状态:植物在能感受环境条件的刺激而诱导开花时所必需达到的生理状态。
12.双受精现象:在精核与卵细胞互相融合形成合子的同时,另一个精核与胚囊中的极核细胞融合形成具有3n的胚乳核,这种现象叫双受精现象。
13.花粉识别蛋白:能够感受柱头上感受蛋白的刺激而决定花粉是否萌发,存在于花粉外壁上的一种膜蛋白。
识别蛋白是一种糖蛋白。
14.花粉的群体效应:在人工培养花粉时,单位面积上花粉越多,花粉的萌发和花粉管的伸长越好。
二、填空题1.低温光周期2.Gassner 柴拉轩3.低4.茎尖生长点5.Garner Allard6.长日照植物短日植物日中性植物7.开花素赤霉素8.不开或延迟开开9.短日照延长光照(或暗期中闪红光)10.延长早熟缩短迟熟11.雌雄雌雄12.雄雌14.长短15.长日植物短日植物16.低温17.淀粉蔗糖脯氨酸18.蛋白质表膜三、选择题1.A 2.B 3.B 4.A 5.C 6.C 7.A 8.B 9.B 10.A 11.B 12.C 13.A 14.C四、是非判断与改正1.(⨯)短于临界日长条件下2.(⨯)光期若短于2~4小时短日植物也不能成花3.(⨯)愈短4.(√)5.(√)6.(⨯)可以开花7.(√)8.(⨯)长于9.(√)10.(⨯)引早熟种11.(√)12.(⨯)会缩短13.(⨯)外壁蛋白。
第08章--复杂反应动力学--习题及答案

第八章 复杂反应动力学8-1.对于平行反应 CB A 21−→−−→−k k ┤,设E a 、E 1、E 2分别为总反应的表观活化能和两个平行反应的活化能,证明存在以下关系式:E a = (k 1E 1 + k 2E 2)/(k 1 + k 2) 。
证明: 总速率: - d[A]/d t = k 1[A] + k 2[A] = (k 1 + k 2)[A] = k '[A]其中 k ' = k 1 + k 2 = Ae x p(-E '/RT ), ∵2'd 'ln d RTE T k = 又∵Tk k k k T k k T k d )d(1d )dln(d 'ln d 212121+⋅+=+=⎪⎪⎭⎫⎝⎛+⨯+=⎪⎭⎫ ⎝⎛+⨯+=T k k k T k k k k k T k T kk k d d d d 1d d d d 1222111212121⎪⎭⎫ ⎝⎛+⨯+=⎪⎭⎫ ⎝⎛+⨯+=222211212211211d ln d d ln d 1RT E k RT E k k k T k k T k k k k21221121k k E k E k RT ++⨯=所以 212211'k k E k E k E ++=8-2.醋酸高温裂解制乙烯酮,副反应生成甲烷 CH 3COOH —k 1→CH 2=CO +H 2O CH 3COOH —k 2→CH 4+CO 2已知在1189k 时k 1=4.65s -1,k 2=3.74s -1。
试计算: (1)99%醋酸反应需要的时间;(2)在1189 K 时,乙烯酮的最高效率? 如何提高选则性? 解: A B C t =0 a 0 0 t =t x y z(1) ln(a /x )=(k 1+k 2)t x =(1-0.99)a =0.01at =[ln(a /0.01a )]/(k 1+k 2) =(ln100)/(4.65+3.74)=0.5489s (2) y /z =k 1/k 2=4.65/3.74=1.243 z =0.4414a 解得 :y +z =a -x =0.99a y =0.5486a收率,就是产率=产品量/转化反应物量=0.5486a /0.99a =55.42%由于k 1与k 2 相差不大,说明两者解离能相差不大,改变温度效果不好。
08第8章 时间序列习题解答

开始具有直线趋势时,可用直线趋势模型 ˆt m at bt m ,m 1,2, , y
at 2St(1) St( 2) , ( St(1) St( 2) ), bt 1
进行预测。
0.3 时,预测的标准误差
-50-
S2
ˆ (y
t 2
(1) (1) St yt (1 ) St 1 , ( 2) (1) ( 2) St St (1 ) St 1 ,
(8.1)
式中 S t 为一次指数的平滑值; S t
(1)
( 2)
为二次指数的平滑值。当时间序列 { yt } 从某时期 (8.2) (8.3)
第8章
时间序列习题解答
8.1 解 用 t 1,,8,9,,12 分别表示 1974 年,…,1981,1982,…,1985 年, yt ( t 1,,8 )表示已知的 8 个观测值。 (1)取预测公式
yt yt 1 yt 2 , t 3,,8,9,,11 , 3 ˆt 。 其中 yt ( t 9,10,11 )分别取为递推预测的预测值 y ˆ t 1 y
( 0) ( 0) S1( 0) S 2 S3
(8.4)
y1 y2 y3 636.2 . 3
(8.5)
三次指数平滑法的预测模型为
ˆt m at bt m Ct m2 ,m 1,2, , y
其中
-51-
(1) ( 2) ( 3) at 3St 3St St , [(6 5 ) St(1) 2(5 4 ) St( 2) (4 3 ) St(3) ], bt 2 2(1 ) 2 [ St(1) 2St( 2) St(3) ]. ct 2 2(1 ) 由式(8.6) ,可得到 t 23 时,有 a23 2572.2613 , b23 259.3374 , c23 8.9819 ,
数学分析课本(华师大三版)-习题及答案08

第八章 不定积分习题§1 不定积分概念与基本积分公式1. 验证下列等式,并与(3)、(4)两式相比照:(1)()()C x f dx x f +=⎰/; (2)()()C x f x df +=⎰2. 求一曲线()x f y =,使得在曲线上每一点()y x ,处的切线斜率为x 2,且通过点()5,2.3. 验证x x y sgn 22=是x 在()+∞∞-,上的一个原函数. 4. 据理说明为什么每一个含有第一类间断点的函数没有原函数? 5. 求下列不定积分:(1)⎰⎪⎪⎭⎫ ⎝⎛-+-dx x x x 32311; (2)⎰⎪⎪⎭⎫ ⎝⎛-dx x x 21; (3)⎰gxdx 2; (4)()⎰+dx x x232;(5)⎰-dx x2443; (6)()⎰+dx x x 2213; (7)⎰xdx 2tan ; (8)⎰xdx 2sin ;(9)⎰-dx x x x sin cos 2cos ; (10)⎰⋅dx x x x22sin cos 2cos ;(11)⎰•dt t t 2310; (12)⎰dx x x x ;(13)⎰⎪⎪⎭⎫⎝⎛+-+-+dx x x x x 1111; (14)()⎰+dx x x 2sin cos ; (15)()⎰•dx x x 2cos cos ; (16)()⎰--dx e e x x 3§2 换元积分法与分部积分法1. 应用换元积分法求下列不定积分:(1)()⎰+dx x 43cos ; (2)⎰dx xex 22;(3)⎰+dx x 121; (4)()⎰+dx x n1;(5)⎰⎪⎪⎭⎫⎝⎛-+-dx x x 2231131; (6)⎰+dx x 322;(7)⎰-dx x 38; (8)⎰-dx x3571; (9)⎰dx x x 2sin ; (10)⎰⎪⎭⎫ ⎝⎛+dx x 42sin 12π;(11)⎰+dx x cos 11; (12)⎰+dx x sin 11;(13)⎰xdx csc ; (14)⎰-dx xx 21;(15)⎰+dx x x 44; (16)⎰dx x x ln 1;(17)()⎰-dx x x 3541; (18)⎰-dx x x 283; (19)()⎰+dx x x 11; (20)⎰xdx cot ;(21)⎰xdx 5cos ; (22)⎰dx x x cos sin 1;(23)⎰-+dx e e xx 1; (24)⎰+--dx x x x 83322;(25)()⎰++dx x x 3212; (26)⎰+dx ax 221;(27)()⎰+dx ax23221; (28)⎰-dx xx 251;(29)⎰-dx xx31; (30)⎰++-+dx x x 1111.2. 应用分部积分法求下列不定积分:(1)⎰xdx arcsin ; (2)⎰xdx ln ; (3)⎰xdx x cos 2; (4)⎰dx x x3ln ;(5)()⎰dx x 2ln ; (6)⎰dx x arctan ; (7)()⎰⎥⎦⎤⎢⎣⎡+dx x x ln 1ln ln ; (8)()⎰dx x 2arcsin ;(9)⎰xdx 3sec ; (10)()⎰>±022a dx a x .3. 求下列不定积分:(1)()[]()()⎰-≠1/ααdx x f x f ; (2)()()[]⎰+dx x f x f2/1;(3)()()⎰dx x f x f /; (4)()()⎰dx x f e x f /.4. 证明:(1)若 ,3,2,tan ==⎰n xdx I n n ,则21tan 11----=n n n I x n I ; (2)若()⎰=xdx x n m I n m sin cos ,,则当0≠+n m 时,()()(),3,2,,2,1sin cos ,21sin cos ,1111=-+-++-=-+-++=-++-m n n m I nm n n m x x n m I nm m n m x x n m I n m n m5. 利用上题的递推公式计算:(1)⎰xdx 3tan ; (2)⎰xdx 4tan ;(3)⎰xdx x 42sin cos .6. 导出下列不定积分对于正整数n 的递推公式:(1)⎰=dx e x I kx n n ; (2)()⎰=dx x I nn ln ; (3)()⎰=dx x I n n arcsin ; (4)⎰=xdx e I nx n sin α. 7. 利用上题的递推公式计算:(1)⎰dx e x x 23; (2)()⎰dx x 3ln ; (3)()⎰dx x 3arcsin ; (4)⎰xdx e x 3sin . §3有理函数和可化为有理函数的不定积分1. 求下列不定积分:(1)⎰-dx x x 13; (2)⎰+--dx x x x 12722; (3)⎰+dx x 113; (4)⎰+dx x 114;(5)()()⎰+-dx xx 22111; (6)()⎰++-dx x xx 221222.2. 求下列不定积分:(1)⎰-dx x cos 351; (2)⎰+dx x 2sin 21;(3)⎰+dx x tan 11; (4)⎰-+dx xx x 221;(5)⎰+dx x x 21; (6)⎰+-dx xxx 1112. 总练习题求下列不定积分: (1)⎰--dx xx x 4312; (2)⎰xdx x arcsin ; (3)⎰+dx x 11; (4)⎰xdx e x 2sin sin ;(5)⎰dx ex; (6)⎰-dx x x 112;(7)⎰+-dx x x tan 1tan 1; (8)()⎰--dx x xx 322; (9)⎰dx x 4cos 1; (10)⎰xdx 4sin ; (11)⎰+--dx x x x 43523; (12)()⎰+dx x 1arctan ; (13)⎰+dx x x 247; (14)⎰++dx x x x1tan tan tan 2; (15)()⎰-dx x x 10021; (16)⎰dx xx2arcsin ; (17)⎰⎪⎭⎫⎝⎛-+dx x x x 11ln (18) ⎰dx xx 7cos sin 1; (19)⎰⎪⎭⎫⎝⎛+-dx x x e x 211;(20)⎰=dx uv I n n ,其中x b a v x b a u 2211,+=+=,求递推形式解.习题答案§1 不定积分概念与基本积分公式2.12+=x y .5.(1)C x x x x +-+-342342; (2)C x x x +-+3334ln 3; (3)C gx+2; (4)C x x x +•++6ln 629ln 94ln 4; (5)C x +arcsin 23; (6)()C x x +-arctan 31; (7)C x x +-tan ; (8)()C x x +-2sin 241;(9)C x x +-cos sin ; (10)C x x +--cot tan ;(11)C t+90ln 90; (12)C x +815158; (13)C x +arcsin 2; (14)C x x +-2cos 21; (15)C x x +⎪⎭⎫ ⎝⎛+3sin 31sin 21; (16)C e e e e x xx x ++----33313331; §2 换元积分法与分部积分法1.(1)()C x ++43sin 31; (2)C e x +2241; (3)C x +-12ln 21; (4)()C n x n ++++111;(5)()C x x++3arcsin 313arcsin ;(6)C x ++2ln 222; (7)()C x +--33892; (8)()C x +--3257103; (9)C x +-2cos 21; (10)C x +⎪⎭⎫ ⎝⎛+-42cot 21π;(11)C x+2tan; (12)C x x +-sec tan ; (13)C x x ++-cot csc ln ; (14)C x +--21;(15)C x +2arctan412; (16)C x +ln ln ;(17)()C x +--251101; (18)C x x ++-22ln28144;(19)C xx+-1ln; (20)C x +sin ln ; (21)C x x x ++-53sin 51sin 32sin ;(22)C x +tan ln ; (23)C e x+arctan ; (24)C x x ++-83ln 2; (25)()C x x x ++-+++2123121ln ;(26)C a x x +++22ln ; (27)C ax ax ++222;(28)()()()C x x x+---+--2522322121511321;(29)C x x x x x x ++------11ln 3625676616161216567; (30)C x x x +++++-11ln414.2.(1)C x x x +-+21arcsin ; (2)C x x x +-ln ; (3)C x x x x x +-+sin 2cos 2sin 2;(4)()C x x ++-1ln 2412; (5)()C x x x x x ++-2ln 2ln 2; (6)()C xx x +-+2arctan 1212;(7)()C x x +ln ln ; (8)()C x x x x x +--+2arcsin 12arcsin 22;(9)()C x x x x +++tan sec ln tan sec 21; (10)C x a x a a x x +⎪⎭⎫ ⎝⎛+±±±22222ln 21.3.(1)()()C x f +++111αα; (2)()()C x f +arctan ; (3)()C x f +ln . 5.(1)C x x ++cos ln tan 212; (2)C x x x ++-tan tan 313;(3)C x x x x +--4sin 641sin cos 611633. 6.(1)11--=n kx n n I kn e x k I ; (2)()1ln --=n nn nI x x I ;(3)()()()2121arcsin 1arcsin -----+=n n nn I n n x x n x x I ;(4)()()[]21221cos sin sin 1---+-+=n n ax n I n n x n x a x e an I . 7.(1)C x x x e x+⎪⎭⎫⎝⎛-+-83434321232;(2)()()[]C x x x x +-+-6ln 6ln 3ln 23;(3)()()C x x x x x x x +----+222316arcsin 6arcsin 13arcsin ;(4)()C x x x x x e x+-+-cos 3sin 3cos sin 3sin 10123. §3有理函数和可化为有理函数的不定积分1.(1)C x x x x +-+++1ln 2323; (2)()C x x +--34ln 2; (3)()C x x x x +-++-+312arctan 3111ln 6122; (4)C x x x x x x +-++-++22212arctan 421212ln 82; (5)()()C x x x x x ++---+--141arctan 211ln 811ln 4122; (6)()()C x x x x ++-+++-12arctan 251222352; 2.(1)C x +⎪⎭⎫ ⎝⎛2tan 2arctan 21; (2)C x +⎪⎪⎭⎫ ⎝⎛tan 26arctan 66; (3)C xx x +++2sin cos ln 21; (4)C x x x x +-++--21432512arcsin87; (5)C x x x ++++221ln ; (6)C x x x x +---+22111ln. 总练习题(1)C x x x +--4312134534132454; (2)C x x x x x +-+-22141arcsin 41arcsin 21; (3)()C x x ++-1ln 22; (4)()C x e x +-1sin 2sin ;(5)()C x ex+-12; (6)C x+1arccos ;(7)C x x ++sin cos ln ; (8)()C x x x +-----221232ln ; (9)C x x ++3tan 31tan ; (10)C x x x ++-4sin 3212sin 4183; (11)C x x x +-++-2112ln 32; (12)()C x x x x x ++++-+22ln 1arctan ;(13)()C x x ++-2ln 214144; (14)C x x +⎪⎪⎭⎫ ⎝⎛+-31tan 2arctan 32; (15)()()()C x x x +-+------979899197114911991; (16)C xx x x +-+--211lnarcsin 1; (17)C x x x x ++⎪⎭⎫ ⎝⎛-+-11ln 212; (18)C x x +⎪⎭⎫⎝⎛+5tan 511tan 2; (19)C xe x++21; (20)()()[]121121122--++=n n n I b a b a n u v b n I典型习题解答1.(§1 第5题(13))求⎰⎪⎪⎭⎫ ⎝⎛+-+-+dx x x x x 1111 解:C x dx x xx x dx x x x x +=⎪⎪⎭⎫⎝⎛--+-+=⎪⎪⎭⎫⎝⎛+-+-+⎰⎰arcsin 211111111222.(§2 第1题(21))求⎰xdx 5cos解:()C x x x x d x xdx ++-=-=⎰⎰53225sin 51sin 32sin sin sin 1cos3.(§2 第1题(23))求⎰-+dx e e x x 1解:C e e de dx e e xx x x x+=+=+⎰⎰-arctan 112 4.(§2 第2题(9))求⎰xdx 3sec()C x x x x xdx xdxxdx x x xdxx x x xdxx x x x xd xdx +++=∴+-=--=-==⎰⎰⎰⎰⎰⎰⎰tan sec ln 21tan sec 21sec sec sec tan sec sec 1sec tan sec sec tan tan sec tan sec sec 33223解:5.(§2 第题(2))若()⎰=xdx x n m I n m sin cos ,,则当0≠+n m 时,()()(),3,2,,2,1sin cos ,21sin cos ,1111=-+-++-=-+-++=-++-m n n m I nm n n m x x n m I nm m n m x x n m I n m n m证明:()()()()()()()2,1sin cos ,,21sin cos ,cos sin 11cos sin 111sin cos cos cos 1sin 111sin cos sin cos 11sin 1sin cos 1sin cos ,11112112211211111-+-++-=-+-++=∴+--+-++=-+-++=-+++=+=-++--+--+--++-+-⎰⎰⎰⎰⎰n m I n m n n m x x n m I n m I nm m n m x x n m I xdx x n m xdx x n m n x x xdx x x n m n x x xdx x m n xn x x n x xd n m I n m n m mn m n n m m n n m m n n m n m 同理, 6.(§3 第1题(4))求⎰+dx x 114解:()()⎰⎰⎰⎰-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=+--+=+211211211112111224224x x x x d x x x x d dx x x x dx xC xx x x x x +++-+--=2121ln 24121arctan221。
《电机学》习题解答(吕宗枢) 08章
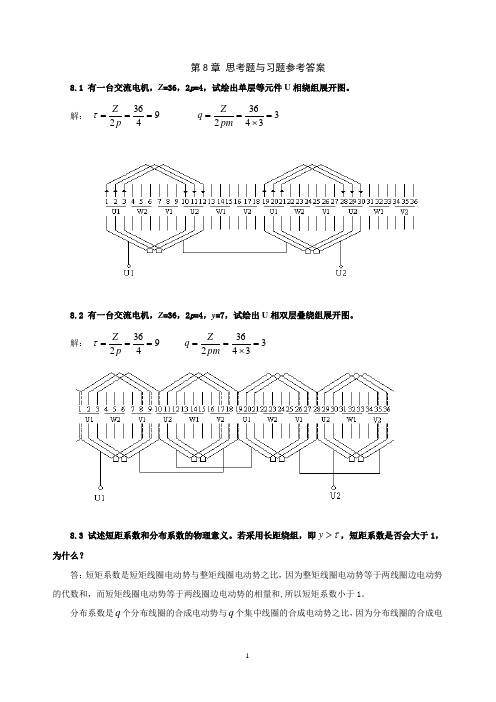
第8章 思考题与习题参考答案8.1 有一台交流电机,Z =36,2p =4,试绘出单层等元件U 相绕组展开图。
解: 94362===p Z τ 334362=⨯==pm Z q8.2 有一台交流电机,Z =36,2p =4,y =7,试绘出U 相双层叠绕组展开图。
解: 94362===p Z τ 334362=⨯==pm Z q8.3 试述短距系数和分布系数的物理意义。
若采用长距绕组,即τ>y ,短距系数是否会大于1,为什么?答:短矩系数是短矩线圈电动势与整矩线圈电动势之比,因为整矩线圈电动势等于两线圈边电动势的代数和,而短矩线圈电动势等于两线圈边电动势的相量和,所以短矩系数小于1。
分布系数是q 个分布线圈的合成电动势与q 个集中线圈的合成电动势之比,因为分布线圈的合成电动势等于q 个线圈电动势的相量和,而集中线圈的合成电动势等于q 个线圈电动势的代数和,所以分布系数数小于1。
即使采用长矩绕组,短矩系数仍然小于1。
因为长距线圈电动势仍然等于两线圈边电动势的相量和,它一定小于两线圈边电动势的代数和。
8.4 一台三相交流电机接于电网,每相感应电动势的有效值E 1=350V ,定子绕组的每相串联匝数N =312,基波绕组系数k w 1=0.96,求每极磁通1Φ。
解:根据11144.4Φ=W fNk E 可知 00526.096.03125044.435044.4111=⨯⨯⨯==ΦW fNk E Wb 8.5 一台三相交流电机, f N =50H Z ,2p =4,Z =36,定子为双层叠绕组,并联支路数a =1,τ97=y ,每个线圈匝数N c = 20,每极气隙磁通1Φ=7.5×10-3Wb ,求每相绕组基波感应电动势的大小。
解: 20363602360=⨯=⨯=Z p α 334362=⨯==pm Z q 94.070sin )9097sin()90sin(1==⨯=⨯= τyk y 96.010sin 330sin 220sin 32203sin 2sin 2sin 1==⨯==ααq q k q 9.096.094.01=⨯=W k 240120342=⨯⨯==a pqN N c V fNk E W 360105.79.02405044.444.43111=⨯⨯⨯⨯⨯=Φ=-8.6 有一台三相同步发电机,2极,转速为3000r/min ,定子槽数Z=60,每相串联匝数N =20,每极气隙磁通1Φ=1.505Wb ,求:(1)定子绕组基波感应电动势的频率;(2)若采用整距绕组,则基波绕组系数和相电动势为多少?(3)如要消除5次谐波电动势,则线圈节距y 应选多大,此时的基波电动势为多大?解:(1)Hz pn f 50603000160=⨯== (2)302602===p Z τ 6603601360=⨯=⨯=Z p α 1032602=⨯==pm Z q 因为采用整距绕组,故 11=y k 95537.03sin 1030sin 26sin 102610sin 2sin 2sin 11==⨯=== ααq q k k q w V fNk E W 6384505.195537.0205044.444.4111=⨯⨯⨯⨯=Φ=(3)取τ54=y 951.072sin )9054sin()90sin(1==⨯=⨯= τy k y V fNk E W 16.6071505.1951.095537.0205044.444.4111=⨯⨯⨯⨯⨯=Φ=8.7 为什么说交流绕组产生的磁动势既是时间的函数,又是空间的函数?答:单相绕组产生的磁动势沿空间(气隙圆周)按余弦规律分布,所以是空间的函数,其幅值大小又随时间按正弦规律变化,所以又是时间的函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.10习题8.10.1 概念题1.(1)对类内各成员访问的控制规则是怎样的?(2)私有成员、保护成员、公有成员各怎样标明?(3)如果有的成员未有标明,则系统默认为何种成员?答:(1)对类内各成员进行访问的控制规则是:公有成员、保护成员和私有成员,在类内不分彼此,相互之间均可自由进行访问。
在类外只可通过对象访问其公有成员,而不可访问其私有成员和保护成员。
对不可访问成员,不管类内类外,都不可进行访问。
(2)私有成员、保护成员、公有成员分别用private、protected、public标明。
(3)若有的成员未标明,则系统默认为是私有成员。
2.试定义一个描述时间的类。
私有数据成员有小时、分、秒。
公有成员函数有写入函数、读出函数、显示函数和计算总秒数的函数。
写入函数和读出函数在类外定义。
答:描述时间的类定义如下:class clock{private:int hour;int minute;int second;public:void put(int h,int m,int s);void get(int &h,int &m,int &s);void show(){cout<<hour<<":"<<minute<<":"<<second<<endl;}int total(){return (hour*3600+minute*60+second);}};void clock::put(int h,int m,int s){hour=h; minute=m; second=s;}void clock::get(int &h,int &m,int &s){h=hour; m=minute; s=second;}3.什么情况下要作类的引用性声明?答:类类型也应该“先定义后使用”。
但在无法做到先定义时,可先作一个类的引用性声明,然后使用。
过后再对该类作定义。
4.面向对象程序设计的文件是怎样组织的?答:一般根据类的定义、类的成员函数定义、类的使用三方面划分为相应的三个文件,即:类定义文件(*.h)、类实现文件(*.cpp)和类使用文件(*.cpp)。
前一个文件是头文件,后两个文件是源文件。
源文件必须包含头文件。
5.怎样对对象进行初始化或赋值?答:对对象初始化可以用下列两种方法:(1)用成员函数对对象进行初始化。
(2)用构造函数对对象进行初始化。
同类对象可以直接整体进行赋值。
6.(1)什么叫做本对象?this指针指向什么?(2)*this是什么意思,表示什么?答:(1)类的数据成员的具体数值是属于对象的,对这些具体数值进行操作的成员函数也是属于对象的。
这些具体的数据成员和成员函数所属对象就是这些成员的本对象。
this 指针指向本对象。
(2)*this是this指针所指,也就是所指的本对象。
*this表示本对象的当前值。
7.(1)对一个类而言,友元可以有几种情况?有何特权?(2)友元如何定义?答:(1)对一个类而言,友元可以有三种情况:(a)将某个普通函数声明为本类的友元函数;(b)将某个类的成员函数声明为本类的友元函数;(c)将某个类声明为本类的友元类,致使该类所有成员函数都成为本类的友元函数。
在类内,所有这些友元声明,只是在函数的原型或类的引用性声明的前面加上一个friend而已。
有了这个声明,则作为本类的友元函数,就可直接访问本类中的任何成员(公有成员、保护成员和私有成员)。
这就是作为本类的友元函数在本类中所获得的特权。
(2)友元函数或友元类本身的定义,则在类外该怎么定义就怎么定义,与友元不友元无关。
8.下面程序的输出结果应该是5,但因程序不完整,不能运行。
试将其补充完整。
#include<iostream>#include<cmath>using namespace std;class point{private:double x,y;public:point(double a=0,double b=0){x=a; y=b;}};double disdt(point pot){return sqrt(pot.x*pot.x+pot.y*pot.y);}int main(){point a(3,4);cout<<disdt(a)<<endl;return 0;}答:补充完整后的程序如下:(补充部分为醒目用了黑体字)#include<iostream>#include<cmath>using namespace std;class point{private:double x,y;public:point(double a=0,double b=0){x=a; y=b;}friend double disdt(point pot);};double disdt(point pot){return sqrt(pot.x*pot.x+pot.y*pot.y);}int main(){point a(3,4);cout<<disdt(a)<<endl;return 0;}9.为什么要设置静态数据成员和静态成员函数?答:描述类属性的数据作为类的数据成员,前面用关键词static进行修饰。
这叫做静态数据成员。
显然,静态数据成员不属于对象,而属于类。
是为描述类属性的需要而设置的。
在类外,因想通过类来访问私有静态数据成员,而设置了公有静态成员函数。
这样,在类外,通过类调用公有静态成员函数,就可以实现间接访问私有静态数据成员的目的。
因此公有静态成员函数是类属对外接口。
10.在类内外怎样访问静态数据成员?静态成员函数在类内外怎样访问和被访问?答:(1)在类内静态成员函数可以访问静态数据成员和静态成员函数。
(2)在类内,非静态成员函数可以访问静态数据成员和静态成员函数;但静态成员函数访问非静态数据成员和非静态成员函数时必须提供对象,一般是将对象别名传递给静态成员函数形参。
(3)在类外可以对公有静态成员函数进行访问。
既可以用类名进行访问,又可以用对象名进行访问。
11.试问下列程序运行结果如何?#include<iostream>using namespace std;class A{private:int u;static int s;public:A(int x){u=x; s+=x;}static void show(){cout<<"s="<<s<<endl;}void display(){cout<<"u="<<u<<" s="<<s<<endl;}};int A::s=1000;int main(){A::show();A a1(5);a1.show();a1.display();A a2(8);a2.show();a2.display();return 0;}答:程序运行结果如下:s=1000s=1005u=5 s=1005s=1013u=8 s=10138.10.2程序设计题1.定义一个复数类complex。
私有数据成员有实部、虚部;公有成员函数有写入、读出、求模。
声明两个complex型对象cpx1和cpx2。
在主函数中将输入的实部和虚部写入cpx1,算出复数cpx1之模。
用cpx1对cpx2赋值。
读出cpx1的实部、虚部、模,输出之。
调用显示函数输出cpx2的实部、虚部、模。
#include<iostream>#include<cmath>using namespace std;class complex{private:double real;double imag;public:void put(double r,double i);void get(double &r,double &i);double mo(){return sqrt(real*real+imag*imag);}void show(){if(imag<0) cout<<real<<imag<<"i\n";else if(imag>0) cout<<real<<'+'<<imag<<"i\n";else cout<<real<<endl;cout<<"模="<<mo()<<endl;}};void complex::put(double r,double i){real=r; imag=i;}void complex::get(double &r,double &i){r=real;i=imag;}int main(){double x,y,u,v;complex cpx1,cpx2;cout<<"请输入复数的实部和虚部。
"<<endl;cin>>x>>y;cpx1.put(x,y);cpx1.get(u,v);cout<<"cpx1实部="<<u<<'\t'<<"虚部="<<v<<"\t\t"<<"模="<<cpx1.mo()<<endl;cout<<"cpx1=";cpx1.show();cpx2=cpx1;cout<<"cpx2=";cpx2.show();return 0;}2.设计一个描述时刻的类clock。
私有数据成员有时、分、秒;公有成员函数有写入、读出、显示等函数。
用有参初始化对象c1:1时2分3秒。
用无参初始化对象c2:4时5分6秒。
将数据7时8分9秒写入对象c3。
用c1向对象c4整体赋值。
最后,调用读出函数读出c1和c2的各数据;调用显示函数显示c3和c4的各数据。
#include<iostream>using namespace std;class clock{private:int hour,minute,second;public:clock(int x,int y,int z);clock();void put(int x,int y,int z){hour=x; minute=y; second=z;}void get(int &x,int &y,int &z){x=hour; y=minute; z=second;}void show();};clock::clock(int x,int y,int z){hour=x; minute=y; second=z;cout<<"调用有参构造函数!"<<endl;}clock::clock(){hour=4; minute=5; second=6;cout<<"调用无参构造函数!"<<endl;}void clock::show(){cout<<hour<<":"<<minute<<":"<<second<<endl;}int main(){clock c1(1,2,3),c2,c3,c4;c3.put(7,8,9);c4=c1;int h1,m1,s1,h2,m2,s2;c1.get(h1,m1,s1);c2.get(h2,m2,s2);cout<<"get读得的c1数据为:"<<h1<<":"<<m1<<":"<<s1<<endl;cout<<"get读得的c2数据为:"<<h2<<":"<<m2<<":"<<s2<<endl;cout<<"show 显示c3数据为:"; c3.show();cout<<"show 显示c4数据为:"; c4.show();return 0;}3.定义一个描述同学情况的类。
