cic滤波器原理详解
CIC插值滤波器的FPGA设计与实现

CIC插值滤波器的FPGA设计与实现摘要:基于多速率信号处理原理,设计了用于下变频的CIC插值滤波器,由于CIC 滤波器结构只用到加法器和延迟器,没有乘法器,很适合用FPGA来实现,所以本文分析了CIC滤波器的原理,性能及影响参数,借助MATLAB设计符合系统要求CIC 滤波器,并利用Modelsim软件建模仿真,验证CIC滤波器性能是否达到要求。
(一)CIC滤波器基本原理A.CIC滤波器的基本单元CIC滤波器主要由积分滤波Integrator和梳状滤波Comb两个基本单元部分构成。
典型的CIC滤波器的结构,它由两个基本单元I(积分滤波器)和C(梳状滤波器)级联构成。
本设计主要针对插值滤波器,所以插值滤波器的结构示意图如图1-1所示:图 1-1 3级级联的CIC插值滤波器结构示意图积分器和梳状滤波器之间是一个采样率转换器,对于CIC插值器而言,它完成在每一个样值后补上R-1个0值的工作,,对于CIC抽取器来说,它完成在实际的抽取工作,每R个样值中取样一个。
R(插值倍数),M(延迟因子,一般取1或者2)以及N(级联级数)是影响CIC 滤波器的三个参数,它们的值需根据通带性能的需求而设定。
(二)CIC插值滤波器的设计流程根据CIC滤波器的原理,本设计的流程如图2-1所示:图2-1 CIC 插值滤波器的设计流程图(三)模型的建立和测试A .位宽策略对于数字滤波器,一个不得不考虑的问题是为防止溢出每一级所需的位宽。
对于抽取器来说,CIC 滤波器的输出增益为(*)NG R M = (3-1)所以,在全精度的情况下,最后一级输出的位宽为2log (*)out in B B N R M =+ (3-2)其中in B 表示输入数据的宽度,为了保证精度,每一个积分器和梳状滤波器的输入输出位宽都为out B 。
对于插值器而言,输出增益为212,1,2,....2(*)/,1, 2......2i i N i N i N G R M R i N N N --⎛⎫== ⎪ ⎪=++⎝⎭ (3-3)因此,第i 级为避免溢出所需要的位宽为2log ()i in i W B G =+ (3-4)最后一级输出位宽为22log (*)log out in B B N R M R =+- (3-5)在实际当中,当差分延时M=1时,为保证稳定,所有积分器的位宽在理论值的基础上加一。
cic滤波器阶数和级数

CIC滤波器阶数和级数什么是CIC滤波器?CIC(Cascaded Integrator-Comb)滤波器是一种数字滤波器结构,常用于高速数据采样系统中的抽取滤波。
CIC滤波器具有简单的结构和低成本的优点,且能够实现高度的抽取比率。
CIC滤波器是一种结构紧凑的滤波器,由级联的积分器和组合器构成。
积分器将输入信号进行积分,而组合器则通过取差来减小输出的冗余部分。
这种结构使CIC滤波器能够实现高阶滤波器,同时保持较低的计算复杂度。
滤波器阶数CIC滤波器的阶数是指滤波器内部级联的积分器和组合器的数量。
阶数越高,滤波器的频率响应越陡峭,对高频噪声的抑制能力也越强。
然而,阶数的增加会使滤波器的延迟增加,因此在选择CIC滤波器的阶数时需要考虑频率响应和延迟之间的权衡。
滤波器级数CIC滤波器的级数是指滤波器多个CIC结构级联的数量。
级数越多,滤波器的整体增益越大,抽取比率也越高。
通过级联多个CIC结构,可以实现更高的滤波器抽取比率,而不需要增加单个CIC结构的阶数。
CIC滤波器的设计步骤设计CIC滤波器的步骤主要包括选择滤波器的阶数和级数、计算滤波器的延迟和频率响应,以及优化滤波器的性能。
1. 选择滤波器的阶数和级数首先,需要确定CIC滤波器的阶数和级数。
阶数和级数的选择取决于应用的需求,包括滤波器的抽取比率、频率响应和延迟等方面的要求。
2. 计算滤波器的延迟根据滤波器的抽取比率和级数,可以计算出滤波器的延迟。
延迟是指从输入信号进入滤波器到输出信号出现的时间延迟。
3. 计算滤波器的频率响应根据滤波器的抽取比率、阶数和级数,可以计算得到滤波器的频率响应。
频率响应描述了滤波器对不同频率信号的强度衰减或增益。
4. 优化滤波器的性能根据实际需求,可以对滤波器进行性能优化。
优化可以包括调整滤波器的参数,如阶数和级数,以及对滤波器的设计进行仿真和验证。
CIC滤波器的应用领域CIC滤波器广泛应用于高速数据采样系统中,特别是在射频接收器和数字信号处理系统中。
CIC滤波器的原理与设计

CIC滤波器的原理与设计CIC 的冲击响应{1,010,()n D h n ≤≤-=其他,D 为CIC 滤波器的阶数(即抽取因子), Z 变换后11()1Dz H z z ---=-,当积分梳状滤波器的阶数不等于抽取器的抽取倍数时,令N=DM(N 为滤波器的 阶数,D 为抽取倍数)则积分梳状滤波器的传递函数为:)1(11)(1DM z zz H ----=M 是梳状滤波器中的延时因子,故称M 为差分延时因子;其频率总响应为12()()()jw jw jw H e H e H e ==sin(/2)sin(/2)wDM w=1()()22wDM w DM Sa Sa-⋅⋅x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:DM e H j =)(0; 一般数字滤波器的指标:即:CIC 幅频特性响应曲线图由其频率响应函数可以看出其主瓣电平最大为D,旁瓣电平为21.51()sin(3/2)/sin(3/2)sin(3/2)j DMH e DM DM ωπωπππ=⋅==,()20lg()()20lg ()a pa p a s a s H j H j H j H j ααΩ=ΩΩ=Ω通带最大衰减阻带最小衰减00()20lg ()()20lg ()ps j a p jw a j a s jw a H e H eH e H e αα==旁瓣与主瓣的差值 (用dB 数表示)为: dB A DM s 46.1323lg 20lg201===πα 可计算出旁瓣与主瓣的差值约为13.46,意味着阻带衰减很差,单级级联时旁瓣电平很大,为降低旁瓣电平,增加阻带衰减采用级联的方式,N 级频率响应为:)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Qj Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦⎤⎢⎣⎡=,可得到N 级CIC 的旁瓣抑制dB Q Q A DM Q Q s )46.13(23lg 20)lg(201⨯=⋅==πα 分析一下发现在Q 级联时多出了Q DM 这个处理增益,因此分析一下尽量减少带内容差(通带衰减),即,在通带内,幅度应尽量平缓;下面就它的幅平响应曲线来分析:1、设在红线w1处抽取的信号带宽很窄,为无混叠信号的带宽,能很好的对窄带信号进行滤波,去除掉高频信号噪声;且在绿线w2=2pi/DM-w1处衰减值足够大,则在其信号带宽内,红线到绿线,信号给CIC 滤 波器带来的混叠就可以忽略,计算此时阻带衰减:)2/sin()2/sin(lg20()(lg 2022012w DM w DMe H e H A jw j ==·引入带宽比例因子b=B/(fs/DM ), B 为抽取信号的带宽,D 为抽取因子,M 为延时因子;fs 为输入端采样率,则w1=b*2pi/DM ;带入可化简得:b A lg 201-≈; (假设b=0.01;即fs=100MHz ,D=20,信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽内的阻带衰减能达到40dB;;并不怎么大,适用于较粗略的滤波,适合放在第一级抽取;如果采用级联的方式可以加大无混叠信号带宽;但是满足的通带不够窄;2、在红线w1处幅度不能下降太多,通带内幅值容差不能太大,否则会引起高频失真;设该带内容差为sδ,则,)()(lg 2010jw j s e H e H =δ将w1带入可简化得)sin(lg20b b s ππδ≈,当N 级时,其带内容差也会增大;由上面分析可知,阻带衰减和带内容差,只与带宽比例因子b 有关,Df B b s /=,分析可知,在信号带宽一定的前提下,应尽可能采用小的抽取因子,或增大输入采样率;故一般把它放在抽取系统的第一级,所以在配置CIC 时,信号带宽,采样率,抽取因子,综合考虑,下面是阻带衰减和通带衰减的一个表:带宽比例因子b在w1处的通带衰减(dB )级数(N )12 3 4 5 6 1/128 0.00 0.00 0.00 0.00 0.00 0.01 1/64 0.00 0.01 0.01 0.01 0.02 0.02 1/32 0.01 0.03 0.04 0.06 0.07 0.08 1/16 0.06 0.11 0.17 0.22 0.28 0.34 1/8 0.22 0.45 0.67 0.90 1.12 1.35 1/40.911.822.743.654.565.47差分延迟M带宽比例因子b 在w2处的混叠衰减(dB ) 级数(N ) 1 2 3 4 5 6 1 1/128 42.1 84.2 126.2 168.3 210.4 252.5 1 1/64 36.0 72.0 108.0 144.0 180.0 215.9 1 1/32 29.8 59.7 89.5 119.4 149.2 179.0 1 1/16 23.6 47.2 70.7 94.3 117.9 141.5 1 1/8 17.1 34.3 51.4 68.5 85.6 102.8 1 1/4 10.5 20.9 31.4 42.8 52.3 62.7 2 1/128 48.1 96.3 144.4 192.5 240.7 288.8 2 1/64 42.1 84.2 126.2 168.3 210.4 252.5 2 1/32 36.0 72.0 108.0 144.0 180.0 216.0 2 1/16 29.9 59.8 89.6 119.5 149.4 179.3 2 1/8 23.7 47.5 71.2 95.0 118.7 142.5 21/417.835.653.471.389.1106.9表1:大抽取因子表2:大抽取因子下由CIC 频幅响应图可以发现,幅频特性的零点位于1/M 处(M 取值为整数),这说明差分因子M 决定了零点的位置;抽取因子D 狭定了抽取后信号的采样频率,它同差分延时因子M 一起还决定了主瓣和旁瓣的宽度;级数Q 可以用来控制阻带衰减,Q 越大阻带衰减越大,通带内的混叠就越小,但Q 越大,通带内主瓣衰减也越大,所以Q 不可太大,不宜超过5级。
CIC滤波器的原理与设计
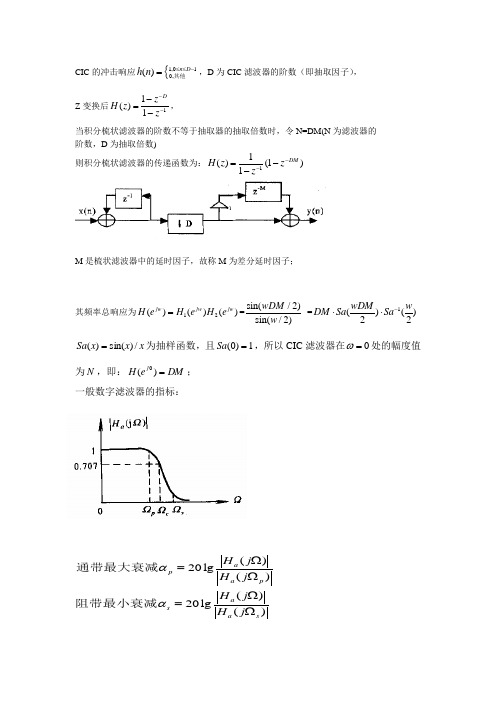
CIC 的冲击响应{1,010,()n D h n ≤≤-=其他,D 为CIC 滤波器的阶数(即抽取因子),Z 变换后11()1Dz H z z ---=-,当积分梳状滤波器的阶数不等于抽取器的抽取倍数时,令N=DM(N 为滤波器的 阶数,D 为抽取倍数)则积分梳状滤波器的传递函数为:)1(11)(1DM z zz H ----=M 是梳状滤波器中的延时因子,故称M 为差分延时因子;其频率总响应为12()()()jw jw jwH e H e H e ==sin(/2)sin(/2)wDM w =1()()22wDM wDM Sa Sa -⋅⋅x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:DM e H j =)(0; 一般数字滤波器的指标:()20lg()()20lg ()a pa p a s a s H j H j H j H j ααΩ=ΩΩ=Ω通带最大衰减阻带最小衰减即:CIC 幅频特性响应曲线图由其频率响应函数可以看出其主瓣电平最大为D ,旁瓣电平为21.51()sin(3/2)/sin(3/2)sin(3/2)j DMH e DM DM ωπωπππ=⋅==,旁瓣与主瓣的差值 (用dB 数表示)为: dB A DM s 46.1323lg 20lg201===πα 可计算出旁瓣与主瓣的差值约为13.46,意味着阻带衰减很差,单级级联时旁瓣电平很大,为降低旁瓣电平,增加阻带衰减采用级联的方式,N 级频率响应为:)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Qj Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦⎤⎢⎣⎡=, 可得到N 级CIC 的旁瓣抑制 dB Q Q A DM Q Qs )46.13(23lg 20)lg(201⨯=⋅==πα 分析一下发现在Q 级联时多出了Q DM 这个处理增益,因此分析一下尽量减少带容差(通带衰减),即,在通带,幅度应尽量平缓;下面就它的幅平响应曲线来分析:00()20lg ()()20lg()ps j a p jw a j a s jw a H e H eH e H e αα==1、设在红线w1处抽取的信号带宽很窄,为无混叠信号的带宽,能很好的对窄带信号进行滤波,去除掉高频信号噪声;且在绿线w2=2pi/DM-w1处衰减值足够大,则在其信号带宽,红线到绿线,信号给CIC 滤 波器带来的混叠就可以忽略,计算此时阻带衰减:)2/sin()2/sin(lg 20()(lg 2022012w DM w DM e H e H A jw j ==·引入带宽比例因子b=B/(fs/DM ), B 为抽取信号的带宽,D 为抽取因子,M 为延时因子;fs 为输入端采样率,则w1=b*2pi/DM ;带入可化简得:b A lg 201-≈; (假设b=0.01;即fs=100MHz ,D=20,信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽的阻带衰减能达到40dB;;并不怎么大,适用于较粗略的滤波,适合放在第一级抽取;如果采用级联的方式可以加大无混叠信号带宽;但是满足的通带不够窄;2、在红线w1处幅度不能下降太多,通带幅值容差不能太大,否则会引起高频失真;设该带容差为s δ,则,)()(lg 2010jw j s e H e H =δ将w1带入可简化得)sin(lg 20b bs ππδ≈,当N 级时,其带容差也会增大;由上面分析可知,阻带衰减和带容差,只与带宽比例因子b 有关,Df Bb s /=,分析可知,在信号带宽一定的前提下,应尽可能采用小的抽取因子,或增大输入采样率;故一般把它放在抽取系统的第一级,所以在配置CIC 时,信号带宽,采样率,抽取因子,综合考虑,下面是阻带衰减和通带衰减的一个表:表1:大抽取因子下的通带衰减由CIC频幅响应图可以发现,幅频特性的零点位于1/M处(M取值为整数),这说明差分因子M决定了零点的位置;抽取因子D狭定了抽取后信号的采样频率,它同差分延时因子M一起还决定了主瓣和旁瓣的宽度;级数Q可以用来控制阻带衰减,Q越大阻带衰减越大,通带的混叠就越小,但Q越大,通带主瓣衰减也越大,所以Q不可太大,不宜超过5级。
累积梳状(CIC)滤波器分析与设计
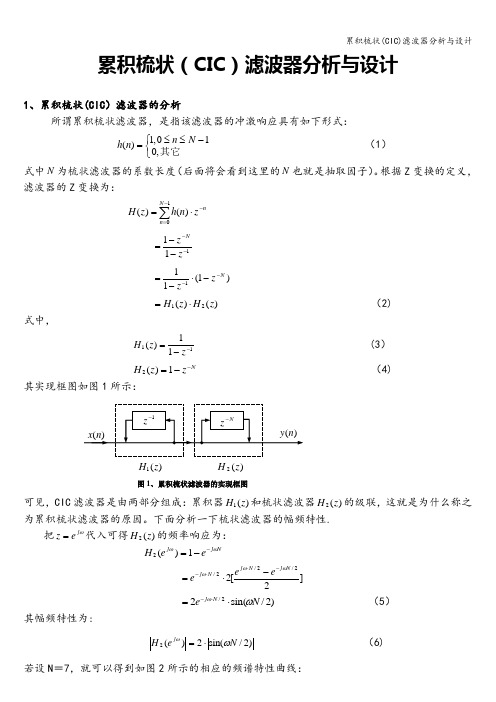
累积梳状(CIC )滤波器分析与设计1、累积梳状(CIC )滤波器的分析所谓累积梳状滤波器,是指该滤波器的冲激响应具有如下形式: ⎩⎨⎧-≤≤=其它,010,1)(N n n h (1)式中N 为梳状滤波器的系数长度(后面将会看到这里的N 也就是抽取因子)。
根据Z 变换的定义,滤波器的Z 变换为:∑-=-⋅=10)()(N n n z n h z H111----=z z N)1(111Nz z---⋅-=)()(21z H z H ⋅= (2) 式中,1111)(--=zz H (3) N z z H --=1)(2 (4) 其实现框图如图1所示:可见,CIC 滤波器是由两部分组成:累积器)(1z H 和梳状滤波器)(2z H 的级联,这就是为什么称之为累积梳状滤波器的原因。
下面分析一下梳状滤波器的幅频特性.把ωj e z =代入可得)(2z H 的频率响应为: N j j e e H ωω--=1)(2 ]2[22/2/2/N j N j N j e e eωωω-⋅⋅--⋅=)2/sin(22/N e N j ωω⋅=⋅- (5) 其幅频特性为:)2/sin(2)(2N e H j ωω⋅= (6) 若设N =7,就可以得到如图2所示的相应的频谱特性曲线:)(2z H)(1z H图1、累积梳状滤波器的实现框图由图2可以清楚地看到:)(2ωj e H 的形状犹如一把梳子,故把其形象地称之为梳状滤波器。
同样可以求得累积器)(1z H的频率响应为:ωj e z H --=11)(112/2/2/]2[2---=ωωωj j j e e e 12/)2(sin 2-⋅=ωωj e (7) 故CIC 滤波器的总频率响应为:)()()(21ωωωj j j e H e H e H ⋅= )2/sin(/)2/sin(ωωN = )2()2(1ωω-⋅⋅=Sa NSa N (8)式中,x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:N e H j =)(0 (9)CIC 滤波器的幅频特性如图3所示:在)~0(π区间上称)/2~0(N π的区间为CIC 滤波器的主瓣,而其它区间称为旁瓣。
cic滤波器原理

cic滤波器原理
CIC滤波器是一种数字滤波器,其原理基于累加器和差分器组成的级联结构。
CIC滤波器的工作原理如下:
1. 累加器阶段:输入信号经过累加器,累加器将输入信号进行递增操作,得到一个累加的输出。
2. 差分器阶段:累加器的输出信号经过差分器,差分器进行减法运算,得到相邻两个时间点上的差分输出。
3. 重采样阶段:差分器的输出信号经过重采样,根据重采样比率进行下采样操作,得到最终的输出信号。
CIC滤波器的特点:
1. CIC滤波器具有很高的差分非线性,可以有效抑制高频分量。
2. CIC滤波器在频率域上具有矩形频率响应,可以实现理想的低通滤波器功能。
3. CIC滤波器的实现简单,运算量少,适用于实时处理和硬件实现。
4. CIC滤波器具有固定频率响应,不需要频率域上的运算,适用于离散时间系统。
CIC滤波器的应用:
1. 信号预处理:用于消除高频噪声和干扰,提高信号的质量。
2. 降采样:用于降低采样率,减少数据存储和处理的开销。
3. 高通滤波:用于提取输入信号中的高频部分。
4. 低通滤波:用于去除输入信号中的高频部分。
总之,CIC滤波器通过累加器和差分器的级联结构,实现了一种简单有效的数字滤波器,其原理基于累加和差分操作,适用于信号预处理、降采样和频率域滤波等应用。
FPGA的CIC滤波器的设计

FPGA的CIC滤波器的设计1.原理概述CIC滤波器由差分器、积分器和组合器三部分组成,可有效实现信号的重采样和滤波功能。
其基本原理是将输入信号通过差分器进行差分运算,然后经过积分器进行累积运算,最后通过组合器实现滤波和重采样。
CIC滤波器的特点是具有高的通带增益和截止频率,且不需要乘法器和存储器,适合在FPGA中实现。
2.设计步骤(1)确定CIC滤波器的设计参数,包括增益因子、积分阶数、截止频率等。
(2)根据设计参数计算滤波器的结构参数,包括输入和输出数据宽度、积分器的阶数和阶间差值等。
(3)根据计算结果,设计CIC滤波器的硬件结构,包括差分器、积分器和组合器的实现方法。
(4) 使用HDL语言(如Verilog或VHDL)编写FPGA的CIC滤波器的代码,同时进行功能仿真和波形仿真。
(5)在FPGA开发板上进行综合、布局布线和验证,实现CIC滤波器的硬件设计。
3.设计关键技术(1)差分器设计:差分器实现差分运算,可以简单采用异或门或加减器实现。
需要注意输入信号的幅度范围和差分器的输出范围。
(2)积分器设计:积分器实现累积运算,需要考虑积分阶数、数据宽度和溢出等问题。
可以采用寄存器与加法器的串行或并行结构实现。
(3)组合器设计:组合器实现滤波和重采样功能,需要根据设计参数确定组合器的截止频率和增益系数。
可以采用多级组合器结构实现。
(4)输入输出接口设计:FPGA的CIC滤波器需要与外部系统进行数据交换,因此需要设计合适的输入输出接口,包括数据接口、时钟接口和控制接口等。
4.实现优化技术(1)折叠积分器:为了减少资源占用和延迟,可以采用折叠积分器结构,将多级积分器合并为一个积分器实现。
(2)级联结构:为了增加滤波器的阶数和降低截止频率,可以采用级联结构,将多个CIC滤波器级联实现。
(3)变系数设计:为了实现可调节的滤波参数,可以设计可变系数的CIC滤波器,在运行时动态调整增益因子和积分阶数。
综上所述,FPGA的CIC滤波器设计是一项复杂的数字信号处理任务,需要深入理解CIC滤波器的原理和设计方法,结合FPGA的硬件实现技术进行设计和优化。
(完整版)CIC滤波器的原理与设计
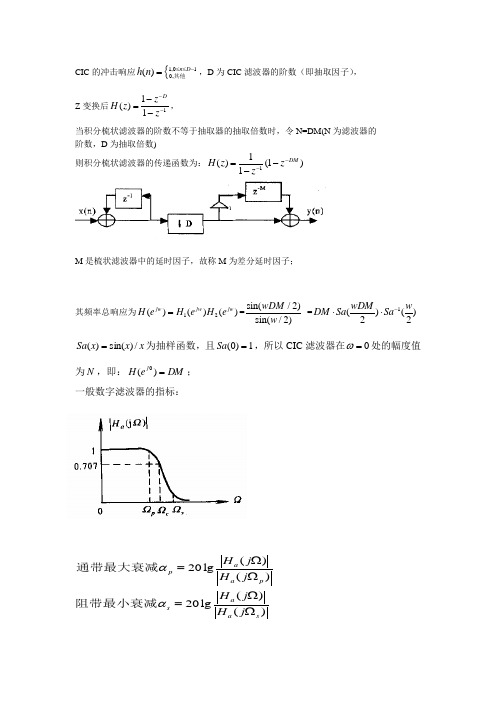
CIC 的冲击响应{1,010,()n D h n ≤≤-=其他,D 为CIC 滤波器的阶数(即抽取因子),Z 变换后11()1Dz H z z ---=-,当积分梳状滤波器的阶数不等于抽取器的抽取倍数时,令N=DM(N 为滤波器的 阶数,D 为抽取倍数)则积分梳状滤波器的传递函数为:)1(11)(1DM z zz H ----=M 是梳状滤波器中的延时因子,故称M 为差分延时因子;其频率总响应为12()()()jw jw jwH e H e H e ==sin(/2)sin(/2)wDM w =1()()22wDM wDM Sa Sa -⋅⋅x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:DM e H j =)(0; 一般数字滤波器的指标:()20lg()()20lg ()a pa p a s a s H j H j H j H j ααΩ=ΩΩ=Ω通带最大衰减阻带最小衰减即:CIC 幅频特性响应曲线图由其频率响应函数可以看出其主瓣电平最大为D ,旁瓣电平为21.51()sin(3/2)/sin(3/2)sin(3/2)j DMH e DM DM ωπωπππ=⋅==,旁瓣与主瓣的差值 (用dB 数表示)为: dB A DM s 46.1323lg 20lg201===πα 可计算出旁瓣与主瓣的差值约为13.46,意味着阻带衰减很差,单级级联时旁瓣电平很大,为降低旁瓣电平,增加阻带衰减采用级联的方式,N 级频率响应为:)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Qj Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦⎤⎢⎣⎡=, 可得到N 级CIC 的旁瓣抑制 dB Q Q A DM Q Qs )46.13(23lg 20)lg(201⨯=⋅==πα 分析一下发现在Q 级联时多出了Q DM 这个处理增益,因此分析一下尽量减少带内容差(通带衰减),即,在通带内,幅度应尽量平缓;下面就它的幅平响应曲线来分析:00()20lg ()()20lg()ps j a p jw a j a s jw a H e H eH e H e αα==1、设在红线w1处抽取的信号带宽很窄,为无混叠信号的带宽,能很好的对窄带信号进行滤波,去除掉高频信号噪声;且在绿线w2=2pi/DM-w1处衰减值足够大,则在其信号带宽内,红线到绿线,信号给CIC 滤波器带来的混叠就可以忽略,计算此时阻带衰减:)2/sin()2/sin(lg 20()(lg 2022012w DM w DM e H e H A jw j ==·引入带宽比例因子b=B/(fs/DM ), B 为抽取信号的带宽,D 为抽取因子,M 为延时因子;fs 为输入端采样率,则w1=b*2pi/DM ;带入可化简得:b A lg 201-≈; (假设b=0.01;即fs=100MHz ,D=20,信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽内的阻带衰减能达到40dB;;并不怎么大,适用于较粗略的滤波,适合放在第一级抽取;如果采用级联的方式可以加大无混叠信号带宽;但是满足的通带不够窄;2、在红线w1处幅度不能下降太多,通带内幅值容差不能太大,否则会引起高频失真;设该带内容差为s δ,则,)()(lg 2010jw j s e H e H =δ将w1带入可简化得)sin(lg 20b bs ππδ≈,当N 级时,其带内容差也会增大;由上面分析可知,阻带衰减和带内容差,只与带宽比例因子b 有关,Df Bb s /=,分析可知,在信号带宽一定的前提下,应尽可能采用小的抽取因子,或增大输入采样率;故一般把它放在抽取系统的第一级,所以在配置CIC 时,信号带宽,采样率,抽取因子,综合考虑,下面是阻带衰减和通带衰减的一个表:表1:大抽取因子下的通带衰减由CIC频幅响应图可以发现,幅频特性的零点位于1/M处(M取值为整数),这说明差分因子M决定了零点的位置;抽取因子D狭定了抽取后信号的采样频率,它同差分延时因子M一起还决定了主瓣和旁瓣的宽度;级数Q可以用来控制阻带衰减,Q越大阻带衰减越大,通带内的混叠就越小,但Q越大,通带内主瓣衰减也越大,所以Q不可太大,不宜超过5级。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
级联积分梳状(Cascade Integrator Comb,CIC)[1]滤波器结构简单、标准化,是高速抽取器中十分简单有效的抗混叠滤波单元,已被广泛使用于多抽样率信号处理系统中。
其组成只有积分器、加法器、寄存器,没有乘法器,使得CIC滤波器非常适合在具有较强实时性和并行处理能力的FPGA 上实现。
但是其阻带衰减和通带波纹的相互抑制限制了其滤波性能。
锐化级联积分梳状滤波器[2]、CIC 滤波器的部分锐化[3]、在CIC 滤波器级联分解的基础上级联一级余弦滤波器[4]、二级补偿CIC 滤波器( TSC -CIC)[5]、内插二阶多项式级联积分梳状滤波器(ISOP-CIC)[6]都是用来进行CIC滤波器改进的技术。
但上述CIC 滤波器的改进或只是降低了通带衰减,或只是提高了阻带衰减,或同时降低通带衰减、提高阻带衰减,但是占用硬件逻辑资源较多。
