初中数学八年级数学试卷
江陵县初中八年级数学试卷

一、选择题(每题4分,共40分)1. 下列各数中,有理数是()A. √16B. √-1C. πD. √0.252. 已知a > b,下列不等式中正确的是()A. a - b > 0B. a + b < 0C. a - b < 0D. a + b > 03. 如果a、b、c是三角形的三边,且a + b = c,那么下列结论正确的是()A. a > bB. a < bC. a = bD. a、b的大小无法确定4. 下列各式中,分式有意义的是()A. 1/xB. 1/(x - 1)C. 1/(x + 1)D. 1/(x^2 - 1)5. 已知一次函数y = kx + b(k ≠ 0),下列说法正确的是()A. 当k > 0时,函数的图像在第二、四象限B. 当k < 0时,函数的图像在第一、四象限C. 当b > 0时,函数的图像在第一、二象限D. 当b < 0时,函数的图像在第三、四象限6. 已知平行四边形ABCD,对角线AC和BD相交于点O,下列结论正确的是()A. OA = OCB. OB = ODC. OA = OBD. OC = OD7. 在△ABC中,∠A = 60°,∠B = 45°,则∠C的度数是()A. 75°B. 105°C. 120°D. 135°8. 下列各数中,绝对值最小的是()A. -2B. -3C. 0D. 19. 已知x^2 - 5x + 6 = 0,则x的值是()A. 2B. 3C. 4D. 610. 下列函数中,是二次函数的是()A. y = x^2 + 2x + 1B. y = 2x^2 - 3x + 1C. y = 3x^2 + 4x - 5D. y = 2x^2 - 3二、填空题(每题5分,共50分)11. (1)-8的相反数是______;(2)√9的值是______;(3)2的立方是______。
初中数学八年级试卷及答案

一、选择题(每题4分,共40分)1. 下列各数中,有理数是()A. √16B. √25C. √-9D. √-42. 已知a=3,b=-2,则a-b的值是()A. 5B. -5C. 1D. -13. 下列各组数中,互为相反数的是()A. 3和-5B. -3和3C. -3和5D. 3和54. 如果a=2,那么方程2x-a=0的解是()A. x=2B. x=1C. x=0D. x=-15. 在直角坐标系中,点P(-2,3)关于x轴的对称点是()A.(-2,-3)B.(2,3)C.(2,-3)D.(-2,3)6. 下列函数中,是正比例函数的是()A. y=2x+1B. y=3x-4C. y=5xD. y=x²+27. 在等腰三角形ABC中,AB=AC,若∠B=40°,则∠A的度数是()A. 40°B. 50°C. 60°D. 70°8. 一个长方体的长、宽、高分别为a、b、c,则它的体积V=()A. abcB. a²bC. b²cD. c²a9. 若|a|=5,|b|=3,则a+b的值可能是()A. 8B. 2C. -8D. -210. 在下列各式中,正确的是()A. √9=±3B. √16=±4C. √-4=2D. √-9=-3二、填空题(每题5分,共30分)11. 有理数a的绝对值是3,那么a的值是______。
12. 如果a=-2,那么|a|+|a|的值是______。
13. 在直角坐标系中,点M(2,-3)关于原点的对称点是______。
14. 若x²=16,则x的值是______。
15. 一个等腰三角形的底边长为8,腰长为6,则这个三角形的面积是______。
三、解答题(每题10分,共30分)16. 解方程:3x-5=2x+4。
17. 已知一个等腰三角形的底边长为10,腰长为13,求这个三角形的周长。
万唯初中数学八年级试卷

一、选择题(每题3分,共30分)1. 下列各数中,绝对值最小的是()A. -3B. -2C. 0D. 12. 已知二次函数y=ax^2+bx+c的图像开口向上,且a≠0,则下列说法正确的是()A. b>0B. b<0C. c>0D. c<03. 在直角坐标系中,点P(-2,3)关于y轴的对称点是()A.(-2,-3)B.(2,3)C.(2,-3)D.(-2,-3)4. 一个等腰三角形的底边长为6cm,腰长为8cm,则该三角形的周长为()A. 20cmB. 22cmC. 24cmD. 26cm5. 若a^2+b^2=100,且a+b=10,则ab的值为()A. 5B. 10C. 20D. 506. 在△ABC中,∠A=30°,∠B=45°,则∠C的度数为()A. 75°B. 105°C. 120°D. 135°7. 下列方程中,x=2是它的解的是()A. x-2=0B. x+2=0C. 2x=4D. 2x+2=08. 若a、b、c是等差数列,且a+b+c=15,a+c=9,则b的值为()A. 3B. 6C. 9D. 129. 在等腰三角形ABC中,AB=AC,∠B=50°,则∠C的度数为()A. 50°B. 60°C. 70°D. 80°10. 下列函数中,y=√x的定义域是()A. x≥0B. x<0C. x>0D. x≤0二、填空题(每题5分,共20分)11. 已知a=-3,b=4,则a^2+b^2的值为______。
12. 在直角坐标系中,点P(-3,5)到原点的距离是______。
13. 一个正方形的边长为5cm,则它的对角线长为______cm。
14. 若等差数列的前三项分别为3,5,7,则该数列的公差为______。
15. 若等比数列的第一项为2,公比为3,则该数列的第五项为______。
全国初二初中数学专题试卷带答案解析

全国初二初中数学专题试卷班级:___________ 姓名:___________ 分数:___________一、解答题1.如图,将矩形纸片ABCD的四个角向内折起,点A,点B落在点M处,点C,点D落在点N处,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3 cm,EF=4 cm,求AD的长.2.如图,在△ABC中,∠A=90°,D是AC上的一点,BD=DC,P是BC上的任意一点,PE⊥BD,PF⊥AC,E,F为垂足.试判断线段PE,PF,AB之间的数量关系,并说明理由.3.如图,在¨ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF,BF(1)求证:四边形BFDE是矩形;(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.4.如图,已知点E是▱ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.(1)连接AC,BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形;(2)在(1)的条件下,若△AFD是等边三角形,且边长为4,求四边形ABFC的面积.5.(10分)如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.(1)四边形ADCE是菱形;(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)6.如图,在矩形AFCG中,BD垂直平分对角线AC,交CG于D,交AF于B,交AC于O.连接AD,BC.(1)求证:四边形ABCD是菱形;(2)若E为AB的中点,DE⊥AB,求∠BDC的度数;(3)在(2)的条件下,若AB=1,求菱形ABCD的对角线AC,BD的长.7.如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.(1)求证:四边形ADCF是菱形;(2)若BC=8,AC=6,求四边形ABCF的周长.8.如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.(1)求证:△AEF≌△DEB;(2)求证:四边形ADCF是菱形;(3)若AC=4,AB=5,求菱形ADCF的面积.9.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.10.(8分)如图,在正方形ABCD中,对角线AC、BD相交于O,E、F分别在OD、OC上,且DE=CF,连结DF、AE,AE的延长线交于DF于点M,求证:AM⊥DF.11.如图,P,Q,R,S四个小球分别从正方形的四个顶点A,B,C,D同时出发,以同样的速度分别沿AB,BC,CD,DA的方向滚动,其终点分别是B,C,D,A.(1)不管滚动多长时间,求证:连接四个小球所得的四边形PQRS总是正方形.(2)四边形PQRS在什么时候面积最大?(3)四边形PQRS在什么时候面积为原正方形面积的一半?并说明理由.12.如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.(1)试找出一个与△AED全等的三角形,并加以证明.(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,试求PG+PH的值,并说明理由.13.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.求证:(1)四边形OCED是矩形;(2)OE=BC.14.如图①,在△ABC中,AB=AC,点P是BC上任意一点(不与B,C重合),PE⊥AB,PF⊥AC,BD⊥AC.垂足分别为E,F,D.(1)求证:BD=PE+PF.(2)当点P在BC的延长线上时,其他条件不变.如图②,BD,PE,PF之间的上述关系还成立吗?若不成立,请说明理由.15.已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.(1)求证:AE=EC;(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.16.如图,在Rt△ABC中,∠B=90°,BC=,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.(3)当t为何值时,△DEF为直角三角形?请说明理由.=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移17.(1)如图,纸片□ABCD中,AD=5,S□ABCD至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为( )A.平行四边形B.菱形C.矩形D.正方形(2)如图,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.①求证:四边形AFF'D是菱形;②求四边形AFF'D的两条对角线的长.18.如图,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG于E,BF∥DE交AG于F,探究线段AF、BF、EF三者之间的数量关系,并说明理由.19.两个长为2 cm,宽为1 cm的矩形摆放在直线l上(如图①),CE=2 cm,将矩形ABCD绕着点C顺时针旋转α角,将矩形EFGH绕着点E逆时针旋转相同的角度.(1)当旋转到顶点D,H重合时(如图②),连接AE,CG,求证:△AED≌△GCD;(2)当α=45°时(如图③),求证:四边形MHND为正方形.全国初二初中数学专题试卷答案及解析一、解答题1.如图,将矩形纸片ABCD的四个角向内折起,点A,点B落在点M处,点C,点D落在点N处,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3 cm,EF=4 cm,求AD的长.【答案】5cm【解析】首先利用三个角是直角的四边形是矩形易证四边形为矩形,得到接下来结合全等三角形的判定证明,根据全等三角形的对应边相等得到然后通过线段之间的转换得到由勾股定理得到的长,进而求得的长.试题解析:由折叠的性质知同理可得∴四边形为矩形.又又2.如图,在△ABC中,∠A=90°,D是AC上的一点,BD=DC,P是BC上的任意一点,PE⊥BD,PF⊥AC,E,F为垂足.试判断线段PE,PF,AB之间的数量关系,并说明理由.【答案】PE+PF=AB,理由见解析【解析】首先过作于,交于,证明四边形是矩形,进而得到接下来根据已知求出推出根据的判定定理证最后再结合全等三角形的对应边相等得到并结合线段的和差关系即可证明结论.试题解析:理由如下:过点作于,交于,如图所示:∴四边形是矩形.又在和中,3.如图,在¨ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF,BF(1)求证:四边形BFDE是矩形;(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.【答案】(1)证明见解析;(2)证明见解析.【解析】(1)根据平行四边形的性质,可得AB与CD的关系,根据平行四边形的判定,可得BFDE是平行四边形,再根据矩形的判定,可得答案;(2)根据平行线的性质,可得∠DFA=∠FAB,根据等腰三角形的判定与性质,可得∠DAF=∠DFA,根据角平分线的判定,可得答案.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD.∵BE∥DF,BE=DF,∴四边形BFDE是平行四边形.∵DE⊥AB,∴∠DEB=90°,∴四边形BFDE是矩形;(2)∵四边形ABCD是平行四边形,∴AB∥DC,∴∠DFA=∠FAB.在Rt△BCF中,由勾股定理,得BC===5,∴AD=BC=DF=5,∴∠DAF=∠DFA,∴∠DAF=∠FAB,即AF平分∠DAB.【点睛】本题考查了平行四边形的性质,利用了平行四边形的性质,矩形的判定,等腰三角形的判定与性质,利用等腰三角形的判定与性质得出∠DAF=∠DFA是解题关键.4.如图,已知点E是▱ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.(1)连接AC,BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形;(2)在(1)的条件下,若△AFD是等边三角形,且边长为4,求四边形ABFC的面积.【答案】(1)见解析;(2)4【解析】由为平行四边形,根据平行四边形的对边平行得到与平行,根据两直线平行内错角相等得到一对角相等,由为的中点,得到两条线段相等,再由对应角相等,利用可得出进而得出即可得出四边形是平行四边形,再判定对角线相等,即可得出平行四边形是矩形.由等边三角形的性质得出得出由矩形的性质得出得出即可得出四边形的面积试题解析:∵四边形为平行四边形,又∵点为的中点,在和中,又∴四边形为平行四边形.为的外角,又即∴四边形为矩形.解:∵四边形是矩形,又是等边三角形,5.(10分)如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.(1)四边形ADCE是菱形;(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)【答案】(1)证明见试题解析;(2).【解析】(1)先证明四边形ADCE是平行四边形,再证明邻边相等,即可得出结论;(2)过点D作DF⊥CE,垂足为点F;可得出△BCD是等边三角形,得出∠BDC=∠BCD=60°,CD=BC=6,再由CE∥AB,得出∠DCE=∠BDC=60°,在Rt△CDF中,由三角函数求出DF即可.试题解析:(1)∵AE∥CD,CE∥AB,∴四边形ADCE是平行四边形,又∵∠ACB=90°,D是AB的中点,∴CD=AB=BD=AD,∴平行四边形ADCE是菱形;(2)过点D作DF⊥CE,垂足为点F,如图所示:DF即为菱形ADCE的高,∵∠B=60°,CD=BD,∴△BCD是等边三角形,∴∠BDC=∠BCD=60°,CD=BC=6,∵CE∥AB,∴∠DCE=∠BDC=60°,又∵CD=BC=6,∴在Rt△CDF中,DF=CDsin60°=6×=.【考点】菱形的判定与性质.6.如图,在矩形AFCG中,BD垂直平分对角线AC,交CG于D,交AF于B,交AC于O.连接AD,BC.(1)求证:四边形ABCD是菱形;(2)若E为AB的中点,DE⊥AB,求∠BDC的度数;(3)在(2)的条件下,若AB=1,求菱形ABCD的对角线AC,BD的长.【答案】(1)见解析;(2)60°;(3)BD=1,AC=【解析】根据垂直平分线的性质,可以得到由矩形的性质,得到根据平行线的性质,利用证明从而得到,结合上步所求,由四边相等的四边形是菱形即可得出结论.由题意,可以得到垂直平分从而得出结合题意可得的度数,进而求得的度数;根据菱形的性质,得到由此在中,求得的值,进而可得的值.试题解析:垂直平分∵四边形是矩形,∴四边形是菱形.为的中点,垂直平分又为等边三角形,由菱形性质知,在中,7.如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.(1)求证:四边形ADCF是菱形;(2)若BC=8,AC=6,求四边形ABCF的周长.【答案】(1)证明见解析;(2)28.【解析】(1)根据旋转可得AE=CE,DE=EF,可判定四边形ADCF是平行四边形,然后证明DF⊥AC,可得四边形ADCF是菱形;(2)首先利用勾股定理可得AB长,再根据中点定义可得AD=5,根据菱形的性质可得AF=FC=AD=5,进而可得答案.试题解析:(1)∵将△ADE 绕点E 旋转180°得到△CFE , ∴AE=CE ,DE=EF ,∴四边形ADCF 是平行四边形,∵D 、E 分别为AB ,AC 边上的中点, ∴DE 是△ABC 的中位线, ∴DE ∥BC , ∵∠ACB=90°, ∴∠AED=90°, ∴DF ⊥AC ,∴四边形ADCF 是菱形;(2)在Rt △ABC 中,BC=8,AC=6, ∴AB=10,∵D 是AB 边上的中点, ∴AD=5,∵四边形ADCF 是菱形, ∴AF=FC=AD=5,∴四边形ABCF 的周长为8+10+5+5=28.【考点】1.菱形的判定与性质;2.旋转的性质.8.如图,在Rt △ABC 中,∠BAC=90°,D 是BC 的中点,E 是AD 的中点, 过点A 作AF ∥BC 交BE 的延长线于点F .(1)求证:△AEF ≌△DEB ;(2)求证:四边形ADCF 是菱形;(3)若AC=4,AB=5,求菱形ADCF 的面积. 【答案】(1)证明见解析;(2)证明见解析;(3)【解析】(1)根据AAS 证明即可判定.(2)先证明四边形ADCF 是平行四边形,再证明DA=DC 即可. (3)利用S 菱形ADCF =2S △ADC =S △ABC 即可求解. 试题解析:(1)∵AF ∥BD , ∴∠AFE=∠DBE , ∵E 是AD 中点, ∴AE=ED ,在△BDE 和△FAE 中,,∴△AFE ≌△DBE .(2)连接CF .∵△AFE ≌△DBE , ∴AF=BD ∵∠BAC=90°,BD=CD , ∴AD=DC=DB ,∴AF ∥CD ,AF=DC ,∴四边形ADCF 是平行四边形, ∵DA=CD ,∴四边形ADCF 是菱形. (3)∵S △ABC =×AB×AC=10,∵四边形ADCF 是菱形,BD=DC ,S △ABC =2S △ADC ,∴S菱形ADCF =2S△ADC=10.【考点】1.全等三角形的判定与性质;2.菱形的判定与性质.9.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.【答案】(1)BM+DN=MN成立.(2)DN-BM=MN.【解析】(1)、在MB的延长线上,截得BE=DN,连接AE得到△ABE≌△AND,从而得到AE=AN,然后证明△AEM≌△ANM,得到ME=MN,从而得出答案;(2)、在DC上截取DF=BM,连接AF得到△ABM≌△ADF,然后证明△MAN≌△FAN,得到所求的答案.试题解析:(1)、BM+DN=MN成立.如下图1,在MB的延长线上,截得BE=DN,连接AE,易证:△ABE≌△AND,∴AE=AN.∴∠EAB=∠NMD.∴∠BAD=90°,∠NAM=45°∴∠BAM+∠NMD=45°.∴∠EAB+∠BAM=45°.∴∠EAM=∠NAM又AM为公共边,∴△AEM≌△ANM,∴ME=MN,∴ME=BE+BM=DN+BM.∴DN+BM=MN.(2)、DN-BM=MN.如图2,在DC上截取DF=BM,连接AF.∵AB=AD,∠ABM=∠ADF=90°,∴△ABM≌△ADF(SAS)∴AM=AF,∠MAB=∠FAD.∴∠MAB+∠BAF=∠FAD+∠BAF=90°,即∠MAF=∠BAD=90°.又∠MAN=45°,∴∠NAF=∠MAN=45°.∵AN=AN,∴△MAN≌△FAN.∴MN=FN,即MN=DN-DF=DN-BM;【考点】三角形全等的证明与应用.10.(8分)如图,在正方形ABCD中,对角线AC、BD相交于O,E、F分别在OD、OC上,且DE=CF,连结DF、AE,AE的延长线交于DF于点M,求证:AM⊥DF.【答案】证明见试题解析.【解析】根据DE=CF,可得出OE=OF,继而证明△AOE≌△DOF,得出∠OAE=∠ODF,然后利用等角代换可得出∠DME=90°,即得出了结论.试题解析:∵四边形ABCD是正方形,∴CO=DO,又∵DE=CF,∴OD﹣DE=OC﹣CF,即OF=OE,在△AOE和△DOF中,∵AO=DO,∠AOD=∠DOF,OE=OF,∴△AOE≌△DOF(SAS),∴∠OAE=∠ODF,∵∠OAE+∠AEO=90°,∠AEO=∠DEM,∴∠ODF+∠DEM=90°,即可得AM⊥DF.【考点】1.正方形的性质;2.全等三角形的判定与性质.11.如图,P,Q,R,S四个小球分别从正方形的四个顶点A,B,C,D同时出发,以同样的速度分别沿AB,BC,CD,DA的方向滚动,其终点分别是B,C,D,A.(1)不管滚动多长时间,求证:连接四个小球所得的四边形PQRS总是正方形.(2)四边形PQRS在什么时候面积最大?(3)四边形PQRS在什么时候面积为原正方形面积的一半?并说明理由.【答案】(1)见解析;(2)当P,Q,R,S在出发时或在到达终点时面积最大;(3)当P,Q,R,S四点运动到正方形ABCD各边中点时,四边形PQRS的面积为原正方形面积的一半.【解析】根据已知可确定进而根据正方形的性质,可判定之间是否全等,从而可初步判断四边形的形状,判断出四边形为菱形后,只需证明其中有一个角等于,便可证明四边形为正方形.当在出发时或在到达终点时面积最大,此时的面积就等于原正方形的面积.当四点运动到正方形四边中点时,四边形的面积是原正方形面积的一半.试题解析:∵四边形是正方形,.又∵不管滚动多长时间,∴不管滚动多长时间,四边形是菱形.又∴不管滚动多长时间,四边形总是正方形.当在出发时或在到达终点时面积最大,此时的面积就等于原正方形的面积.当四点运动到正方形四边中点时,四边形的面积是原正方形面积的一半.理由:设原正方形的边长为当时,在中,由勾股定理,得即解得同理可得∴当四点运动到正方形各边中点时,四边形的面积为原正方形面积的一半.12.如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.(1)试找出一个与△AED全等的三角形,并加以证明.(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,试求PG+PH的值,并说明理由.【答案】(1)△AED≌△CEB′;证明见解析;(2)4.【解析】(1)由折叠的性质知,CB′=BC=AD,∠B=∠B′=∠D=90°,∠B′EC=DEA,则由AAS得到△AED≌△CEB′;(2)延长HP交AB于M,则PM⊥AB,PG=PM,PG+PH=HM=AD,∵CE=AE=CD-DE=8-3=5在Rt△ADE中,由勾股定理得到AD=4,∴PG+PH=HM=AD=4.试题解析:(1)△AED≌△CEB′证明:∵四边形ABCD为矩形,∴B′C=BC=AD,∠B′=∠B=∠D=90°,又∵∠B′EC=∠DEA,∴△AED≌△CEB′;(2)由折叠的性质可知,∠EAC=∠CAB,∵CD∥AB,∴∠CAB=∠ECA,∴∠EAC=∠ECA,∴AE=EC=8-3=5.在△ADE中,AD==4,延长HP交AB于M,则PM⊥AB,∴PG=PM.∴PG+PH=PM+PH=HM=AD=4.【考点】1.翻折变换(折叠问题);2.直角三角形全等的判定;3.矩形的性质.13.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.求证:(1)四边形OCED是矩形;(2)OE=BC.【答案】见解析【解析】根据菱形的定义即可证得;根据平行四边形的对边相等即可证得.试题解析:∴四边形是平行四边形.∵四边形是菱形,∴四边形是矩形.(2)∵四边形是菱形,∵四边形是矩形,14.如图①,在△ABC中,AB=AC,点P是BC上任意一点(不与B,C重合),PE⊥AB,PF⊥AC,BD⊥AC.垂足分别为E,F,D.(1)求证:BD=PE+PF.(2)当点P在BC的延长线上时,其他条件不变.如图②,BD,PE,PF之间的上述关系还成立吗?若不成立,请说明理由.【答案】(1)见解析;(2)不成立,此时PE=BD+PF,理由见解析【解析】过点作交的延长线于点.可得矩形所以再由证明得出不成立,此时试题解析:如图,过点作交的延长线于点.∴四边形是矩形.又.即不成立,此时理由:过过点作交的延长线于点.与(1)同理可得15.已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.(1)求证:AE=EC;(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.【答案】解:(1)证明:连接AC,∵BD,AC是菱形ABCD的对角线,∴BD垂直平分AC。
八年级初中数学试卷电子版

一、选择题(每题3分,共30分)1. 若a > b,则下列不等式中正确的是:A. a + 1 > b + 1B. a - 1 < b - 1C. a + 2 > b + 2D. a - 2 < b - 22. 下列各数中,不是有理数的是:A. 3/4B. √2C. -5D. 0.253. 在直角坐标系中,点P(-2,3)关于x轴的对称点是:A.(-2,-3)B.(2,3)C.(2,-3)D.(-2,3)4. 下列函数中,是反比例函数的是:A. y = x + 2B. y = 2xC. y = 3/xD. y = 45. 一个等腰三角形的底边长为6cm,腰长为8cm,则这个三角形的面积是:A. 24cm²B. 30cm²C. 36cm²D. 48cm²6. 下列图形中,不是轴对称图形的是:A. 正方形B. 等边三角形C. 长方形D. 等腰梯形7. 若x² - 5x + 6 = 0,则x的值为:A. 2或3B. 1或4C. 2或4D. 1或38. 下列关于平行四边形的说法正确的是:A. 对角线互相垂直B. 对边相等C. 对角相等D. 以上都是9. 在△ABC中,∠A = 45°,∠B = 60°,则∠C的度数是:A. 75°B. 105°C. 120°D. 135°10. 下列函数中,是二次函数的是:A. y = x² + 3x + 2B. y = x³ + 2x² + 3x + 1C. y = x² - 4x + 5D. y = 2x² + 5x - 3二、填空题(每题3分,共30分)1. 若a = 2,b = -3,则a² - b² = _______。
2. 下列各数中,最小的数是:-3/4, 0, -√2, 2。
初中八年级上册数学动点问题试卷附答案

初中八年级上册数学动点问题试卷附答案
一、选择题
1. 一辆汽车以每小时60千米的速度向东行驶,经过2小时后改变方向,以每小时40千米的速度向北行驶,求其位移。
A. 40千米
B. 80千米
C. 100千米
D. 120千米
答案:D. 120千米
2. 一辆自行车向前行驶30分钟后,记下此时的位置。
然后车辆停下来,待30分钟后,以相同的时间和速度往后倒退,到达原点。
求此自行车的位移。
A. 0千米
B. 5千米
C. 10千米
D. 15千米
答案:A. 0千米
二、填空题
1. 一个物体从A点出发,以每秒2米的速度向东行驶10秒,
然后改变方向,以每秒3米的速度向南行驶15秒,最后以每秒4
米的速度向西行驶20秒。
求物体的位移为______米。
答案:-20
2. 一架飞机以每秒200米的速度向东飞行30秒,然后改变方向,以每秒300米的速度向南飞行40秒,最后以每秒400米的速
度向西飞行50秒。
求飞机的位移为______米。
答案:-4000
三、解答题
1. 一个人从原点出发,以每小时5千米的速度向西行驶1小时,然后改变方向,以每小时8千米的速度向南行驶2小时,最后以每
小时10千米的速度向东行驶3小时。
求此人的位移和位移方向。
答案:位移为-23千米,位移方向为东南方向。
2. 一个物体以每秒10米的速度向北行驶30秒,然后改变方向,以每秒15米的速度向东行驶40秒,最后以每秒20米的速度向南
行驶50秒。
求物体的位移和位移方向。
答案:位移为20米,位移方向为南方。
江苏省苏州市西安交通大学苏州附属初级中学2024~2025学年上学期八年级数学试卷(无答案)
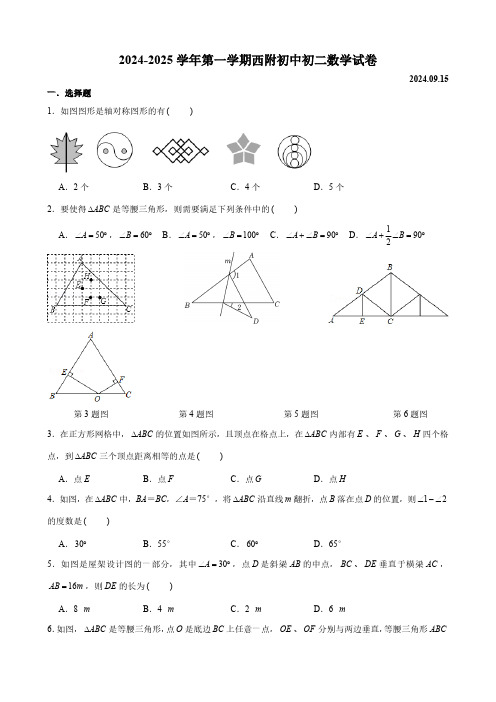
2024-2025学年第一学期西附初中初二数学试卷2024.09.15一.选择题1.如图图形是轴对称图形的有 A .2个B .3个C .4个D .5个2.要使得是等腰三角形,则需要满足下列条件中的 A ., B ., C . D .第3题图 第4题图 第5题图 第6题图3.在正方形网格中,的位置如图所示,且顶点在格点上,在内部有、、、四个格点,到三个顶点距离相等的点是 A .点B .点C .点D .点4.如图,在中,BA =BC ,∠A =75°,将沿直线翻折,点落在点的位置,则的度数是 A .B .55°C .D .65°5.如图是屋架设计图的一部分,其中,点是斜梁的中点,、垂直于横梁,,则的长为 A .8 B .4 C .2 D .6 6.如图,是等腰三角形,点是底边上任意一点,、分别与两边垂直,等腰三角形()ABC ∆()50A ∠=︒60B ∠=︒50A ∠=︒100B ∠=︒90A B ∠+∠=︒1902A B ∠+∠=︒ABC ∆ABC ∆E F G H ABC ∆()E F G HABC ∆ABC ∆m B D 12∠-∠()30︒60︒30A ∠=︒D AB BC DE AC 16AB m =DE ()m m m mABC ∆O BC OE OF ABC的腰长为5,面积为12,则的值为 A .4B .C .15D .87.如图“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪“能三等分任一角.这个三等分角仪由两根有槽的棒,组成,两根棒在点相连并可绕转动,点固定,,点、可在槽中滑动,若,则的度数是 A .B.C .D .第7题图 第9题图 第10题图8.已知,,是的三边长,且,则的形状为 A .钝角三角形 B .等边三角形 C .直角三角形 D .等腰直角三角形9.如图,点是内任意一点,,点和点分别是射线和射线上的动点,周长的最小值是,则的度数是 A .B .C .D .10.如图,在中,,,点从点出发以每秒的速度向点运动,点从点同时出发以每秒的速度向点运动,其中一个动点到达端点时,另一个动点也随之停止运动,当是以为底的等腰三角形时,运动的时间是 A .2.5秒B .3秒C .3.5秒D .4秒二、填空题11.一个汽车牌照号码在水中的倒影为,则该车牌照号码为 .12.如图所示是的方格纸,请在其中选取一个白色的方格并涂黑,使图中阴影部分是一个轴对称图形,这样的涂法有 种.13.已知等腰三角形的两边长分别为4和8,则它的周长是 .14.如果等腰三角形的两个角的比是,那么底角的度数为 .15.等腰三角形腰长为,腰上的高为.那么这个三角形的顶角是 度.OE OF +()245OA OB O O C OC CD DE ==D E 75BDE ∠=︒CDE ∠()70︒75︒80︒85︒a b c ABC ∆222a b c ab ac bc ++=++ABC ∆()P AOB ∠5OP cm =M N OA OB PMN ∆5cm AOB ∠()25︒30︒35︒40︒ABC ∆20AB cm =12AC cm =P B 3cm A Q A 2cm C APQ ∆PQ ()45⨯2:56cm 3cm第12题图 第16题图 第17题图 第18题图16.如图,在中,,,是上一点,将沿折叠,使点落在边上的处,则等于 .17.已知,是的平分线,点为上一点,过作直线,垂足为点,且直线交于点,如图所示.若,则 .18.如图所示,是一钢架,且,为了使钢架更加坚固,需在其内部添加一些钢管,,,添加的钢管长度都与相等,则最多能添加这样的钢管 根.三、作图题19.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点和(格点为网格线的交点),以及过格点的直线.(1)画出关于直线对称的△;(2)将向右平移1个单位长度,再向下平移3个单位长度,画出平移后的△;(3)填空: .20.如图:(1)在AB 公路一侧有C 、D 两村庄,想在公路上找一点P ,使C 、D 、P 三点组成的三角形的周长最短。
2023-2024学年全国初中八年级下数学人教版期中考试试卷(含答案解析)

20232024学年全国初中八年级下数学人教版期中考试试卷(含答案解析)(考试时间:90分钟,满分:100分)一、选择题(每题2分,共20分)1. 下列哪个选项是正确的?A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=62. 下列哪个选项是正确的?A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=63. 下列哪个选项是正确的?A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=64. 下列哪个选项是正确的?A. 3x+5y=10B. 2x4y=8D. 4x2y=65. 下列哪个选项是正确的?A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=66. 下列哪个选项是正确的?A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=67. 下列哪个选项是正确的?A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=68. 下列哪个选项是正确的?A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=69. 下列哪个选项是正确的?A. 3x+5y=10C. 5x+3y=15D. 4x2y=610. 下列哪个选项是正确的?A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=6二、填空题(每题2分,共20分)1. 2x+3y=6,求x的值。
2. 3x+5y=10,求y的值。
3. 4x2y=6,求x的值。
4. 5x+3y=15,求y的值。
5. 2x4y=8,求x的值。
6. 3x+5y=10,求y的值。
7. 4x2y=6,求x的值。
8. 5x+3y=15,求y的值。
9. 2x4y=8,求x的值。
10. 3x+5y=10,求y的值。
三、解答题(每题5分,共25分)1. 解方程组:2x+3y=63x+5y=102. 解方程组:5x+3y=153. 解方程组:2x4y=83x+5y=104. 解方程组:3x+5y=104x2y=65. 解方程组:5x+3y=152x4y=8四、计算题(每题10分,共30分)1. 计算:2x+3y=63x+5y=102. 计算:4x2y=65x+3y=153. 计算:2x4y=83x+5y=10五、应用题(每题10分,共20分)1. 应用题:2x+3y=62. 应用题: 4x2y=6 5x+3y=15答案解析:一、选择题1. A2. B3. C4. D5. A6. B7. C8. D9. A10. B二、填空题1. x=12. y=23. x=24. y=35. x=26. y=27. x=28. y=39. x=210. y=2三、解答题1. x=1, y=22. x=2, y=33. x=2, y=24. x=2, y=35. x=2, y=2四、计算题1. x=1, y=22. x=2, y=33. x=2, y=2五、应用题1. x=1, y=22. x=2, y=38. 简答题(每题5分,共25分)1. 简述一元二次方程的一般形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 1 2 -1 XXXXXX 学年度第二学期期中试卷 八年级数学 (满分:150分 测试时间:120分钟) 题号 一 二 三 总分 合分人 1-8 9-18 19 20 21 22 23 24 25 26 27 28 得分 一、选择题(本大题共8小题,每小题3分,共24分,每小题仅有一个答案正确,请把你认为正确的答案前的字母填 入下表相应的空格 ) 1.如图,数轴上所表示的不等式组的解集是 ( ) A 、x ≤2 B 、-1≤x ≤2 C 、-1<x ≤2 D 、x >-1 2.在代数式①x 2 ;②5y x + ; ③a -21 ;④1-πx 中,属于分式的有 ( ) A 、①② B、①③ C 、①③④ D、①②③④ 3.若反比例函数k y x =的图象经过点(-1,3),则这个函数的图象一定经过点( ) A 、(13,3) B 、(13-,3) C 、(-3,-1) D 、(3,-1) 4.若a b b -=13,则a b 的值为 ( ) A 、 32 B 、 23 C 、 34 D 、 43 5.如图所示,点P 是反比例函数y=k x 图象上一点,过点P 分别作x 轴、y•轴的垂线, 如果构成的矩形面积是4,那么反比例函数的解析式是 ( ) A 、y=-2x B 、 y=2x C 、y=-4x D 、y=4x
题号 1 2 3 4 5 6 7 8 答案 得分 评卷人 学校
姓名 考试号
班级
密
封
6.不等式2
1x <2的非负整数解有 ( ) A 、 4个 B 、 5个 C 、3个 D 、2个
7.下列四个三角形,与左图中的三角形相似的是 ( )
8.如果从一卷粗细均匀的电线上截取1米长的电线, 称得它的质量为a 克,再称得剩余电线的质量为b 克, 那么原来这卷电线的总长度是 ( )
A 、 b+1 米
B 、(b a +1)米
C 、(a+b a +1)米
D 、(a b
+1)米 二、填空题(本大题共10小题,每小题3分,共30分,把答案填在题目中的横线上)
9.不等式13x -≥-的解集为 。
10.若当x 满足条件___________,分式1
21+x 有意义。
11.点A 在函数6y x
=-的图像上,则点A 的坐标可为 。
(写出一个即可) 12.在比例尺为1︰20000的地图上测得AB 两地间的图上距离为8cm ,则AB 两地
间的实际距离为 km 。
13.已知反比例函数32m y x
-=(x<0),当m 时,y 随x 的增大而增大。
14. 使不等式2010
x x +>⎧⎨->⎩成立的最小整数解是 。
15.如图,点D 、E 分别在△ABC 的边AB 、AC 上,且AB=9,
AC=6,AD=3,若使△ADE 与△ABC 相似,则AE 的长为_______。
16.甲、乙两班学生参加植树造林,已知甲班每天比乙班多植树6棵,甲班植80棵树所用的天数与乙班植70棵树所用的天数相等。
若设甲班每天植树x 棵,则根据题意可列出方程 。
(第7题) A 、 B 、 C 、 D 、 得分 评卷人
17.若关于x 的方程51122
m x x ++=--有增根,则m= 。
或演算步骤)
.(本题满分8分) 解不等式(组),并把解集表示在数轴上。
(1)1132x x --< (2)34312
x x x +≥⎧⎪⎨-+>⎪⎩
.(本题满分8分) 解分式方程214111
x x x +-=--
21.(本题满分8分)如图,已知D 、E 分别是△ABC 的 边AC 、AB 上的点,若∠A=350,∠C=850,∠ADE=600,
1)请说明:△ADE ∽△ABC 2)若AD=4,AE=3,BE=5,求AC 长。
22.(本题满分8分) 先化简代数式211()1211
a a a a a a ++÷--+-,然后选取一个使原式有意义的a 值代入求值。
23.(本题满分10分)甲、乙两地相距360千米。
新修的高 速公路开通后,在甲乙两地之间行驶的长途客运车平均车速 提高了50%,而从甲地到乙地的时间缩短了2小时。
试确定原来的平均车速。
得分
评卷人 得分 评卷人
得分
评卷人
24.(本题满分10分)如图,已知A (-4,2)、B (n ,-4)是一次函数y kx b =+的图像与反比列函数m y x =的图像 的两个交点。
(1)求m 、n 的值; (2)求一次函数的关系式; (3)根据图像写出使一次函数的值小于反比例函数的值的x 的取值范围。
25.(本题满分10分)先阅读理解下面的例题,再按要求完 成问题。
例题:解一元二次不等式x 2-9>0。
解:把x 2-9分解因式,得:(x+3)(x-3)>0 由有理数的乘法法则“两数相乘,同号得正”有(1)3030x x +>⎧⎨->⎩或(2)3030x x +<⎧⎨-<⎩
解不等式组(1),得3x >;解不等式组(2),得3x <- 所以x 2-9>0的解集为3x >或3x <-。
请你根据上面的解法,求分式不等式011<-+x x 的解集。
得分 评卷人 得分 评卷人 学校
姓名 考试号
班级
密
封
26.(本题满分10分)制作一种产品,需先将材料加热达到得分评卷人
60℃后,再进行操作。
设该材料温度为y(℃),从加热开始计算的时间为x(分钟)。
据了解,该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图)。
已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃。
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
27.(本题满分12分)
得分评卷人
如图,是一个运算流程。
(1)分别计算x=2,-2,时y的值。
(2)若需要经过两次运算,才能运算出y,求x的取值范围。
(3)若无论运算多少次,都无法运算出y,试探究x的取值范围。
28.(本题满分12分)阅读理解:对于任意正实数a 、b ,∵2()a b ≥0, ∴2a ab b -≥0,∴a b +≥2ab 只有当a =b 时,等号成立。
结论:在a b +≥2ab (a 、b 均为正实数)中,若ab 为定值p ,则a+b ≥2p ,只有当a =b 时,a+b 有最小值2p 。
根据上述内容,回答下列问题:
(1)若m >0,只有当m = 时,1m m
+有最小值 ; 若m >0,只有当m = 时,2m
m 8+有最小值 。
(2)如图,已知直线L 1:112
y x =+与x 轴交于点A ,过点A 的另一直线L 2与双曲线8(0)y x x
-=>相交于点B (2,m ),求直线L 2的解析式。
(3)在(2)的条件下,若点C 为双曲线上任意一点,作CD ∥y 轴交直线L 1
于点D ,试求当线段CD 最短时,点A 、B 、C 、D 围成的四边形面积。
得分
评卷人。
