广东专插本(高等数学)模拟试卷40(题后含答案及解析)
广东专插本(高等数学)模拟试卷30(题后含答案及解析)

广东专插本(高等数学)模拟试卷30(题后含答案及解析)题型有:1. 选择题 2. 填空题 4. 解答题 5. 综合题选择题在每小题给出的四个选项中,只有一项是符合要求的。
1.函数f(χ)=χ3sinχ是( )A.奇函数B.偶函数C.有界函数D.周期函数正确答案:B2.设函数在χ=0处连续,则a= ( ) A.0B.1C.2D.3正确答案:B3.有( )A.一条垂直渐近线,一条水平渐近线B.两务垂直渐近线,一条水平渐近线C.一条垂直渐近线,两条水平渐近线D.两条垂直渐近线,两条水平渐近线正确答案:A4.设函数f?(2χ-1)=eχ,则f(χ)= ( )A.B.C.D.正确答案:D5.下列微分方程中,其通解为y=C1cosχ+C2sinχ的是( ) A.y?-y?=0B.y?+y?=0C.y?+y=0D.y?-y=0正确答案:C填空题6.设函数f(χ)=2χ+5,则f[f(χ)-1]=______。
正确答案:4χ+137.如果函数y=2χ2十aχ+3在χ=1处取得极小值,则a=______。
正确答案:-48.设f(χ)=e2χ,则不定积分=_____。
正确答案:eχ+C9.设方程χ-1+χey确定了y是的隐函数,则dy=______。
正确答案:10.微分方程y?-y?=0的通解为______。
正确答案:y=C1+C2eχ(C1,C2为任意常数)解答题解答时应写出推理、演算步骤。
11.求极限。
正确答案:由于当χ→0时,χ4是无穷小量,且,故可知,当χ→0时,1-e-32-3χ2,故所以12.已知参数方程。
正确答案:所以则13.求不定积分∫χ.arctanxdx。
正确答案:14.已知函数f(χ)处处连续,且满足方程求。
正确答案:方程两边关于χ求导,得f(χ)=2χ+sin2χ+χ.cos2χ.2+(-sin2χ).2 =2χ+2χcos2χ,f?(χ)=2+2cos2χ+2χ.(-2sin2χ)=2(1+cos2χ)-4χsin2χ,所以,。
广东专插本(高等数学)模拟试卷54(题后含答案及解析)

广东专插本(高等数学)模拟试卷54(题后含答案及解析) 题型有:1. 选择题 2. 填空题 4. 解答题 5. 综合题选择题在每小题给出的四个选项中,只有一项是符合要求的。
1.设函f(χ)=( ) A.-1B.0C.1D.不存在正确答案:D解析:极限不存在,本题应选D.2.设函数f(χ)=lnsinχ,则df(χ)=( )A.B.-cotχdχC.cotχdχD.tanχdχ正确答案:C解析:d(lnsinχ)=cosχdχ=cotχdχ,故应选C.3.f′(χ2)=(χ>0),则f(χ)=( )A.2χ+CB.2+CC.χ2+CD.+C正确答案:B解析:令t=χ2则χ=,f′(χ)=(χ>0),f(χ)=∫f′(χ)dχ=+C,故应选B.4.如果使函数f(χ)=在点χ=0处连续,应将其在点χ=0处的函数值补充定义为( )A.0B.2C.-1D.1正确答案:D解析:若f(χ)在χ=0处连续需补充定义f(0)=1,故本题选D.5.设pn=,qn=,n=1,2,…,则下列命题中正确的是( )A.若an条件收敛,则Pn与qn都收敛B.若an绝对收敛,则Pn与qn都收敛C.若an条件收敛,则Pn与qn的敛散性都不定D.若an绝对收敛,则Pn与qn的敛散性都不定正确答案:B解析:an绝对收敛都收敛,an条件收敛都发散,一个收敛,一个发散an发散,故本题选B.填空题6.设=6,则a=_______.正确答案:-1解析:=6,则(1+0)(1+2.0)(1+3.0)+a=0,a=-1.7.已知曲线y=χ2+χ-2上点M处的切线平行于直线y-5χ-1,则点M的坐标为_______.正确答案:(2,4)解析:y′=2χ+1=5,则χ=2,故M点坐标为(2,4).8.已知f(χ)=χ2+cosχ+∫01f(χ)dχ,则f(χ)=_______.正确答案:χ+cosχ++sin1解析:令f(χ)=χ2+cosχ+C,则f(χ)=χ2+cosχ+(χ2+cosχ+C)dχ,f(χ)=即C=,C=+sin1,故f(χ)=χ+cosχ++sin1.9.微分方程y?-y′=0的通解为_______.正确答案:y=C1+C2eχ解析:微分方程的特征方程为λ2-λ=0,则特征根为λ1=0,λ2=1,故微分方程的通解为y=C1+C2eχ(C1,C2为任意常数).10.若函数f(χ)=在χ=0处连续,则a=_______.正确答案:6解析:即=3,故a=6.解答题解答时应写出推理、演算步骤。
2020年广东省专插本考试《高等数学》真题+答案

广东省2020年普通高等学校本科插班生招生考试《高等数学》试题本试卷共2⻚,20⻚题,满分100分。
考试时间120一、单项选择题(本大题共5小题,每小题3分,共15分。
每小题只有一个符合题目要求)1.设lim x→0[cos x −f(x)]=1, 则下列等式正确的是( )A.lim x→0f(x)=1 B.lim x→0f(x)cos x =1C.lim x→0f(x)=−1 D.lim x→0[f(x)+cos x ]=12.函数f(x)=2x 3−3x 2的极小值点为( ) A.x =−1 B.x =0 C.x =1 D.x =23.已知3x 是函数f(x)的一个原函数,则f(x)=( ) A.3x B.3x ln 3 C.x3xD.3x ln 34.设平⻚区域D ={(x,y )|x 2+y 2≤1,y ≥0},则∬(x 2+y 2)4dσD( ) A.π10 B.π9 C.π5 D.2π95.设级数∑a n ∞n=1 满⻚0≤a n ≤15n ,则下列级数发散的是( )A.∑3a n ∞n=1B. ∑a n ∞n=1+3C.∑(a n ∞n=1+√n23) D.∑(a n ∞n=1−√n3) 二、填空题。
6.若函数f(x)={(1+a )x 2, x ≤1a (x −2)3+3, x >1 在x=1处连续,则常数a= . 7.曲线x 22+y 2=3在点(2,−1)处的切线方程为y= . 8.微分方程 y n +3y ’−4y =0的通解为y= .9.设二元函数f (x,y )在点(0,0)的某个邻域内有定义,且当x ≠0时,f(x,0)−f(0,0)x=3x +2,则f ’x (0,0)= 。
10.设函数f(x)在(−∞,+∞)内可导,且满足f(x)=f ‘(x),f(0)=m ,如果∫f(x)e xdx =81−1,则m=____________。
三、计算题。
11.求极限limx→0∫tarctantdtx0x 312.已知y 是x的函数,且y ′=ln √x +√ln x +2ln 2,求d 2y dx 2|x =e13.求不定积分∫(cos x −x sin x 2)dx14.设函数f(x)={x 31+x 2, x ≤1x, x >1,求定积分∫f(x +2)dx 0−315.求二元函数z =3xy 2+x 2y的全微分dz ,并求ð2zðxðy16.计算∬ydσD ,其中D 是由直线y =x,y =−2与y =0,y =2x 围成的有界闭区域。
广东省2017年普通高等学校本科插班生招生考试试题与详细解答
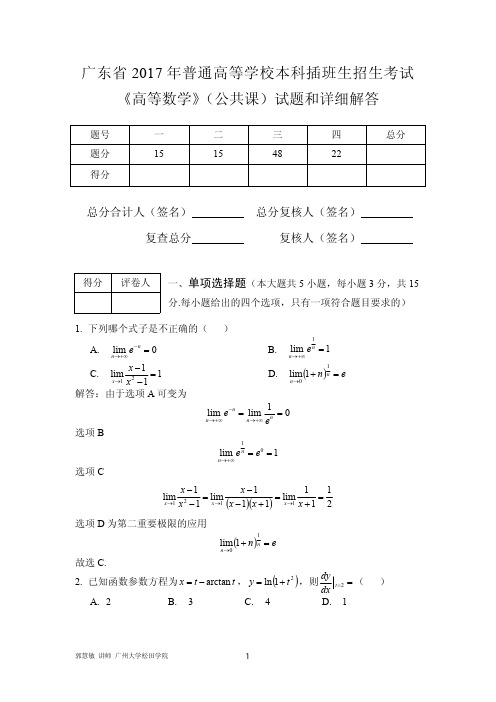
题号
一
二
三
四
总分
题分
15
15
48
22
得分
总分合计人(签名) 复查总分
总分复核人(签名) 复核人(签名)
得分 评卷人 一、单项选择题(本大题共 5 小题,每小题 3 分,共 15
分.每小题给出的四个选项,只有一项符合题目要求的)
n
选项 C
lim
x1
x 1 x2 1
lim
x1
x
x 1
1x 1
lim
x1
x
1 1
1 2
选项 D 为第二重要极限的应用
lim1
n
1 n
e
n0
故选 C.
2.
已知函数参数方程为 x t arctan t , y ln 1 t 2
,则 dy dx
8
5. 已知 1 dx 1x2 f x, y dy ,转换成极坐标的形式( )
1
0
A.
2
d
1 f r cos , r sin dr
0
0
B.
0
d
1 0
f
r
cos
,
r
sin
rdr
C.
2
d
1 f r cos , r sin rdr
1. 下列哪个式子是不正确的( )
A. lim en 0 n
1
B. lim e n 1 n
C.
lim
x1
x 1 x2 1
广东大专高数试题及答案

广东大专高数试题及答案一、选择题(每题5分,共20分)1. 函数y=f(x)是奇函数,则下列说法正确的是()。
A. f(-x) = f(x)B. f(-x) = -f(x)C. f(0) = 0D. f(x) = 0答案:B2. 极限lim(x→0) (sin x/x)的值为()。
A. 0B. 1C. 2D. 3答案:B3. 曲线y=x^2在点(1,1)处的切线斜率为()。
A. 2B. 1C. 0D. -1答案:A4. 函数y=ln(x)的导数是()。
A. 1/xB. xC. ln(x)D. x^2答案:A二、填空题(每题5分,共20分)5. 设函数f(x)=x^3-3x+2,则f'(x)=________。
答案:3x^2-36. 已知函数y=x^2-4x+c,若其图像与x轴有交点,则c的取值范围为________。
答案:c≤47. 曲线y=x^3-6x^2+11x-6在点(2,0)处的切线方程为________。
答案:y=-3x+128. 函数y=e^x的不定积分是________。
答案:e^x + C三、解答题(每题15分,共30分)9. 求函数y=x^2-4x+c在区间[0,2]上的最小值。
解:函数y=x^2-4x+c的导数为y'=2x-4。
令y'=0,解得x=2。
当0≤x<2时,y'<0,函数单调递减;当x>2时,y'>0,函数单调递增。
因此,函数在x=2处取得最小值,即y_min=c-4。
10. 求极限lim(x→∞) (1+1/x)^x。
解:lim(x→∞) (1+1/x)^x = e^lim(x→∞) (x*ln(1+1/x))。
由于lim(x→∞) (x*ln(1+1/x)) = lim(x→∞) (ln(1+1/x)/1/x) =lim(x→∞) (1/(1+1/x) * 1/x) = 0,所以原极限的值为e^0=1。
广东省2010~2020年专插本考试《高等数学》真题及答案

广东省2010年普通高校本科插班生招生考试《高等数学》试题一、单项选择题(本大题共5小题,每小题3分,共15分)1.设函数()y f x =的定义域为(,)-∞+∞,则函数1[()()]2y f x f x =--在其定义域上是()A .偶函数B .奇函数C .周期函数D .有界函数2.0x =是函数1,0()0,0x e x f x x ⎧⎪<=⎨≥⎪⎩的()A .连续点B .第一类可去间断点C .第一类跳跃间断点D .第二类间断点3.当0x →时,下列无穷小量中,与x 等价的是()A .1cos x-B .211x +-C .2ln(1)x x ++D .21x e -4.若函数()f x 在区间[,]a b 上连续,则下列结论中正确的是()A .在区间(,)a b 内至少存在一点ξ,使得()0f ξ=B .在区间(,)a b 内至少存在一点ξ,使得()0f ξ'=C .在区间(,)a b 内至少存在一点ξ,使得()()()()f b f a f b a ξ-'=-D .在区间(,)a b 内至少存在一点ξ,使得()()()b af x dx f b a ξ=-⎰5.设22(,)f x y xy x y xy +=+-,则(,)f x y y∂∂=()A .2y x-B .-1C .2x y-D .-3二、填空题(本大题共5小题,每小题3分,共15分)6.设a ,b 为常数,若2lim()21x ax bx x →∞+=+,则a b +=.7.圆²²x y x y =++在0,0()点处的切线方程是.8.由曲线1y x=是和直线1x =,2x =及0y =围成的平面图形绕x 轴旋转一周所构成的几何体的体积V =.9.微分方程5140y y y '--'='的通解是y =.10.设平面区域22{(,)|1}D x y x y =+≤D={x ,y )x ²+y'≤1},则二重积分222()Dx y d σ+=⎰⎰.三、计算题(本大题共8小题,每小题6分,共48分)11.计算22ln sin lim(2)x xx ππ→-.12.设函数22sin sin 2,0()0,0x x x f x xx ⎧+≠⎪=⎨⎪=⎩,用导数定义计算(0)f '.13.已知点1,1()是曲线12xy ae bx =+的拐点,求常数a ,b 的值.14.计算不定积分cos 1cos xdx x -⎰.15.计算不定积分ln 51x e dx -⎰.16.求微分方程sin dy yx dx x+=的通解.17.已知隐函数(,)z f x y =由方程231x xy z -+=所确定,求z x ∂∂和z y∂∂.18.计算二重积分2Dxydxdy ⎰⎰,其中D 是由抛物线²1y x =+和直线2y x =及0x =围成的区域.四、综合题(本大题共2小题,第19小题10分,第20小题12分,共22分)19.求函数0Φ()(1)xx t t dt =-⎰的单调增减区间和极值。
2015年广东专插本(高等数学)真题试卷(题后含答案及解析)精选全文完整版

精选全文完整版2015年广东专插本(高等数学)真题试卷(题后含答案及解析) 题型有:1. 选择题 2. 填空题 4. 解答题 5. 综合题选择题在每小题给出的四个选项中,只有一项是符合要求的。
1.若当χ→0时,kχ+2χ2+3χ3与χ是等价无穷小,则常数k=( ) A.0B.1C.2D.3正确答案:B解析:=k=1,故本题选B.2.已知函数f(χ)在χ0处有二阶导数,且f′(χ0)=0,f?(χ0)=1,则下列结论正确的是( )A.χ0为f(χ)的极小值点B.χ0为f(χ)的极大值点C.χ0不是f(χ)的极值点D.(χ0,f(χ0))是曲线y=f(χ)的拐点正确答案:A解析:由f(χ)在χ0处有二阶导数,f?(χ0)=1>0且f′(χ)=0,则χ0为f(χ)的极小值点.3.设F(χ)是f(χ)的一个原函数,C为任意实数,则∫f(2χ)dχ=( ) A.F(χ)+CB.F(2χ)+CC.F(2χ)+CD.2F(2χ)+C正确答案:C解析:∫f(2χ)dχ=∫(2χ)d(2χ)=F(2χ)+C,故本题选C.4.若函数f(χ)=+kχ在区间[0,1]上满足罗尔(Rolle)定理的条件,则常数k=( )A.-1B.0C.1D.2正确答案:C解析:由f(χ)在[0,1]上满足罗尔定理知,f(0)=f(1),即1=k,故本题选C.5.下列级数中,收敛的是( )A.B.C.D.正确答案:D解析:级数为公比小于1的几何级数,是收敛的;级数为p>1的p-级数,也是收敛的,故级数是收敛的.填空题6.曲线y=(1-)χ的水平渐进线为y=_______.正确答案:e-5解析:=e-5,则y=e-5为曲线的一条水平渐近线.7.设函数y=f(χ)由参数方程所确定,则=_______.正确答案:2解析:8.广义积分=_______.正确答案:解析:9.微分方程y′-χy=0满足初始条件y|χ=0=1的特解为y=_______.正确答案:解析:对微分方程分离变量为χdχ,则ln|y|=χ2+C,C为任意常数.即y=,又y|χ=0=1,故C=0,特解为y=.10.设函数f(χ)=log2χ(χ>0),则=_______.正确答案:解析:解答题解答时应写出推理、演算步骤。
广东省2020年普通高等学校本科插班生招生考试真题、详细答案及考点详解

广东省2020年普通高等学校本科插班生招生考试高等数学真题、详细答案及考点详解一、单项选择题(本大题共5小题,每小题3分,共15分.每小题只有一个选项符合题目要求)1.设()[]1cos lim 0=-→x f x x ,则下列等式正确的是间断点是()A.()1lim 0=→x f x B.()1cos lim 0=→x x f x C.()1lim 0-=→x f x D.()[]1cos lim 0=+→x x f x 解答:根据初等函数的连续性,可得()[]()()()0lim 1lim 0cos lim cos lim cos lim 0=⇒=-=-=-→→→→→x f x f x f x x f x x x x x x 因此()()1cos lim ,0cos lim 0=+=→→x x f x x f x x 故选D.本题考试内容:初等函数的连续性;考试要求:会利用函数的连续性求极限.2.函数()2332x x x f -=的极小值是()A.1-=xB.0=xC.1=x D.2=x 解答:对函数进行一阶导数求导,可得()()16662-=-='x x x x x f 令()()⇒=-=-='016662x x x x x f 10==x x 或而()612-=''x x f 因此()060<-=''f ,即x =0为极大值点()066121>=-=''f ,即x =1为极小值点从而极小值为()1321-=-=f ,故选A.本题考试内容:函数极值与极值点;考试要求:理解函数极值的概念,掌握求函数的极值、最值的方法,并会应用函数极值的方法求解应用题.3.已知x 3是函数()x f 的一个原函数,则()=x f ()A.x 3B.3ln 3xC.13-x x D.3ln 3x 解答:根据原函数的定义,可知()()()3ln 33x x x f x f =⇒='故选B.本题考试内容:原函数与不定积分的定义;考试要求:理解原函数与不定积分的概念及其关系.4.设平面区域(){}0,1|,22≥≤+=y y x y x D ,则()=+⎰⎰σd y x D422()A.10π B.9πC.5πD.92π解答:使用极坐标计算二重积分,由于平面区域如下图所示令⎩⎨⎧==θθsin cos r y r x ,其中⎩⎨⎧≤≤≤≤πθ010r ,因此()()10sin cos 1904222210422ππθθθσπ==⋅+=+⎰⎰⎰⎰⎰dr r d r r r dr d y xD故选A.本题考试内容:极坐标系下二重积分的计算;考试要求:掌握直角坐标系与极坐标系下二重积分的计算.5.设级数∑∞=1n n a 满足nn a 510≤≤,则下列级数发散的是()A.∑∞=13n naB.∑∞=+13n n aC.∑∞=⎪⎪⎭⎫ ⎝⎛+1321n n n a D.∑∞=⎪⎪⎭⎫⎝⎛-131n n n a 解答:根据正项级数的比较审敛法,由于n n a 510≤≤,由于∑∞=151n n 收敛,因此∑∞=1n na 收敛,再根据级数的性质,可以对下列选项进行判断A 选项:∑∑∞=∞==1133n n n n a a ,因此根据级数的性质可知,∑∞=13n n a 收敛;B 选项:321113a a a a a n n n n ---=∑∑∞=∞=+,因此,级数增加(减去)有限项,不改变敛散性,因此∑∞=+13n n a 收敛;C 选项:∑∑∑∑∑∞=∞=∞=∞=∞=+=+=⎪⎪⎭⎫ ⎝⎛+13211321132111n n n n n n n n n a n a n a ,其中∑∞=1321n n 为p -级数(132<=p ),故∑∞=1321n n 发散,而∑∞=1n n a 收敛,因此根据级数收敛的性质可知∑∞=⎪⎪⎭⎫ ⎝⎛+1321n n n a 发散;D 选项:∑∑∑∑∑∞=∞=∞=∞=∞=+=+=⎪⎪⎭⎫ ⎝⎛+123113113111n n n n n n n n n a n a n a ,其中∑∞=1231n n 为p -级数(123>=p ),故∑∞=1231n n 收敛,而∑∞=1n n a 收敛,因此根据级数收敛的性质可知∑∞=⎪⎪⎭⎫ ⎝⎛+1321n n n a 收敛,故选D.本题考试内容:收敛级数的基本性质;考试要求:掌握几何级数(等比级数)、调和级数、p -级数的敛散性;理解收敛级数的基本性质.二、填空题(本大题共5小题,每小题3分,共15分)6.若函数()()()⎪⎩⎪⎨⎧>+-≤+=1,321,132x x a x x a x f 在1=x 处连续,则常数=a .解答:根据函数极限的充分必要条件可知,()()()Ax f x f A x f x x x ==⇔=+→-→→111lim lim lim 而()()a x a x f x x +=+=-→-→11lim lim 211,()()332lim lim 311+-=+-=+→+→a x a x f x x 因此()().131lim lim 11=⇒+-=+⇒=+→-→a a a x f x f x x 本题考试内容:函数在一点连续的充分必要条件;考试要求:掌握判断函数(分段函数)在一点处连续的方法.7.曲线3222=+y x 在()1,2-点处的切线方程为=y .解答:隐函数求导,因此()122|20212=--='⇒-='⇒='⋅+-,y y x y y y x 从而切线方法为()().3211-=⇒-⋅=--x y x y 本题考试内容:求导方法:函数的四则运算求导方法、隐函数的求导法;考试要求:熟练掌握隐函数的求导方法.8.微分方程043=-'+''y y y 的通解为=y .解答:特征方程为()()0140432=-+⇒=-+r r r r 故1,421=-=r r 故通解为.241x x e C e C y +=-本题考试内容:二阶常系数线性齐次微分方程;考试要求:会求二阶常系数线性齐次微分方程的通解和特解.9.设二元函数()y x f ,在点()0,0的某个领域有定义,且当0≠x 时,()()230,00,+=-x xf x f ,则()='0,0x f .解答:根据偏导数的定义,()()()230,00,0,+=-='x x f x f x f x 因此().20,0='x f 本题考试内容:多元函数的定义;考试要求:理解一阶偏导数和全微分的概念.10.设函数()x f 在()+∞∞-,内可导且满足()()x f x f '=,()m f =0,如果()811=⎰-dx e x f x ,则=m .解答:使用分离变量法,可得:()()()()()()()()⎰⎰=⇒=⇒=⇒'=dx x df x f dx x f x df x f dx x df x f x f 1因此()()Cx e x f C x x f +=⇒+=ln 由于()m f =0,因此()m C m e f C ln 0=⇒==从而()xmx me ex f ==+ln ,将此式子代入()811=⎰-dx e x f x,可得().482888111111=⇒=⇒=⇒=⇒=⎰⎰⎰---m m dx m dx e me dx e x f x xx本题考试内容:可分离变量的微分方程;考试要求:会求可分离变量的微分方程.三、计算题(本大题共8小题,每小题6分,共48分)11.求极限xdt t t xx ⎰→0arctan lim.解:使用洛必达法则00arctan 01arctan limarctan lim=⋅==→→⎰xx xdt t t x xx 本题考试内容:洛必达法则和变上限的定积分;考试要求:熟练掌握应用洛必达法则求未定式极限的方法以及掌握变上限定积分求导数的方法.12.已知y 是x 的函数,且2ln 2ln ln ++='x x y ,求.|22e x dxyd =解:使用复合函数求导法,可得x x x xx x x y ln 212101ln 21211+=+⋅+⋅=''则.1ln 2121|22ee e e dx y d e x =+==本题考试内容:求导方法——复合函数的求导法;考试要求:熟练掌握复合函数求导方法.13.求不定积分().sin 2cos 2⎰-dx x x x 解:根据不定积分的性质,可得()dxx x dx x dx x x x ⎰⎰⎰-=-22sin 2cos sin 2cos 其中12sin 2122cos 212cos C x x xd xdx +==⎰⎰22222cos 21sin 21sin C x dx x dx x x +-==⎰⎰因此()C x x dx x x x +-=-⎰22cos 212sin 21sin 2cos (其中21C C C +=).本题考试内容:基本积分公式、换元积分法——第一换元法(凑微分法);考试要求:熟练掌握不定积分的基本积分公式、熟练掌握不定积分的第一换元法.14.设函数()⎪⎩⎪⎨⎧>≤+=1,1,123x x x x x x f ,求定积分().203dx x f ⎰-+解:令2+=x t ,从而2-=t x ,dt dx =,当3-=x 时,1-=t ;当0=x 时,2=t ,从而原式可变为()().23|210122122111232103=+=++==+⎰⎰⎰⎰---t dt t dt t t dt t f dx x f 本题考试内容:定积分的性质、定积分的计算——换元积分法;考试要求:掌握定积分的基本性质以及掌握定积分的换元法.15.求二元函数y x xy z 223+=的全微分dz ,并求.2yx z∂∂∂解:y x y x z 232+=∂∂,226yx xy y z -=∂∂,因此dyy x xy dx y x y dz ⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫ ⎝⎛+=222623.2662222yxy y x xy x y x z -=⎪⎪⎭⎫ ⎝⎛-∂∂=∂∂∂本题考试内容:全微分以及高阶偏导数;考试要求:掌握二元函数一阶偏导数与二阶偏导数的求法,掌握二元函数全微分的求法.16.计算σd y D⎰⎰,其中D 是由直线x y =,2-=x y 与0=y ,2=y 围成的有界区域.解:x则有界区域可写为Y-型区域⎩⎨⎧+≤≤≤≤220y x y y 因此原二重积分可变为().4|2|202222220=====⎰⎰⎰⎰⎰⎰++y ydy dy x y dx y dy d y y yy yDσ本题考试内容:直角坐标系下二重积分的计算;考试要求:掌握直角坐标系下二重积分的计算方法.17.求微分方程22sec yxdx dy =,满足初始条件1|0==x y 的特解.解:使用分离变量法,可得⎰⎰=⇒=⇒=xdx dy y xdx dy y yx dx dy 222222sec sec sec 因此C x y +=tan 313将1|0==x y 代入上式,可得310tan 131=⇒+=⨯C C 从而可得微分方程特解为.1tan 331tan 3133+=⇒+=x y x y 本题考试内容:可分离变量方程;考试要求:会求分离变量微分方程的通解和特解.18.判断级数∑∞=12!2n n n n 的收敛性.解:由于∑∞=12!2n n n n 为正项级数,()()()()()1021lim !2!121lim !2!121lim lim 22122121<=+=++=++=∞→+∞→+∞→+∞→n n n n n n n n n n a a n n n n n n n nn n 因此根据比值判别法可知:∑∞=12!2n n n n 收敛.本题考试内容:常数项级数审敛法;考试要求:掌握正项级数的比值审敛法.四、综合题(本大题共2小题,第19小题10分,第20小题12分,共22分)19.设有界平面图形G 由曲线ax e y =和直线0==x e y ,围成,其中a >0,若G 的面积等于1(1)求a 的值;(2)求G 绕y 轴旋转一周而成的旋转体体积V .解:(1)由题设可得平面图形G ,如下图所示因此aa a e a e e e a a e e a ex dx e e S a a a ax a ax1111|1011010=+-=⎪⎪⎭⎫ ⎝⎛--⋅=⎪⎭⎫ ⎝⎛-=-=⋅⎰又因为平面G 的面积为1,因此.111=⇒==a aS ye1/ax(2)要求G 绕y 轴旋转一周,因此根据公式可得()()().2|21|ln 2ln 21ln 2|ln ln 11111121212-=--=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⋅-⋅-=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⋅⋅-⋅===⎰⎰⎰⎰⎰e y e e dy y y y y e dy y e dy y y y y y dy y dy x V ee eee ee ey πππππππ本题考试内容:定积分的应用——平面图形的面积、旋转体的体积;考试要求:掌握直角坐标系下用定积分计算平面图形的面积以及平面图形绕坐标轴旋转所生的旋转体体积的方法.20.设函数()bxeax f +=1,其中b a ,为常数,且0≠ab (1)判别()x f 在区间()+∞∞-,内单调性;(2)求曲线()x f y =的拐点;(3)求曲线()x f y =的水平渐近线方程.解:(1)函数()bxeax f +=1定义域为()+∞∞-,,而()()211bxbx bx e abe e a x f +-='⎪⎭⎫⎝⎛+='因此,当0>ab 时,函数()bxeax f +=1定义域为()+∞∞-,单调递减;当0<ab 时,函数()bxeax f +=1定义域为()+∞∞-,单调递增.(2)由于()()()()()()()324222*********bx bx bx bx bx bx bx bx bx bx e e e ab e e e ab e e ab e abe x f +--=++++-='⎪⎪⎭⎫ ⎝⎛+-=''令()()()01132=+--=''bx bxbx e e e ab x f ,且0≠ab ,可得0010=⇒=⇒=-x e e ebx bx显然()x f ''在x =0左右两端异号,因此把x =0代入原式,可得()2100ae af =+=因此,拐点为⎪⎭⎫⎝⎛2,0a .(3)当0>b 时,()01limlim =+=+∞→+∞→bx x x e a x f ,()a e ax f bx x x =+=-∞→-∞→1lim lim ;当0<b 时,()a e a x f bx x x =+=+∞→+∞→1lim lim ,()01lim lim =+=-∞→-∞→bx x x e ax f ,因此水平渐近线为0==y a y 和.本题考试内容:函数单调性的判定法、曲线的凹凸性、拐点以及函数曲线的水平渐近线:掌握利用导数判定函数单调性的方法,会判定曲线的凹凸性、会求曲线的拐点以及会求曲线的水平渐近线.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东专插本(高等数学)模拟试卷40(题后含答案及解析)
题型有:1. 选择题 2. 填空题 4. 解答题 5. 综合题
选择题在每小题给出的四个选项中,只有一项是符合要求的。
1.设函数f(χ)=则= ( )
A.1
B.0
C.2
D.不存在
正确答案:D
2.设函数f(χ)在χ=1可导,则= ( )
A.f?(1)
B.2f?(1)
C.3f?(1)
D.-f?(1)
正确答案:C
3.设函数y=2cosχ,则y?= ( )
A.2cosχln2
B.-2cosχsin2
C.-ln2.2cosχ.sinχ
D.-2cosχsinχ
正确答案:C
4.设2f(χ)cosχ=[f(χ)]2,f(0)=1,则f(χ)= ( ) A.cosχ
B.2-cosχ
C.1+sinχ
D.1-sinχ
正确答案:C
5.设函数z=eχy,则dz= ( )
A.eχydχ
B.(χdy+ydχ)eχy
C.χdy+ydχ
D.(χ+y)eχy
正确答案:B
填空题
6.=_____。
正确答案:
7.曲线处的切线方程为_____。
正确答案:
8.函数y=f(χ)由参数方程,所确定,则_____。
正确答案:
9.已知,则a=_______,b_______。
正确答案:-1,2
10.微分方程y?-2y?+y=0的通解为______。
正确答案:y=C1e2+C2χeχ(C1,C2为任意常数)
解答题解答时应写出推理、演算步骤。
11.求极限。
正确答案:
12.设是连续函数,求a,b的值。
正确答案:由于当χ<0,χ>0时,f(χ)为初等函数,则连续,现只需使f(χ)在χ=0连续即可,由连续定义,得
即b=1,a为任意实数。
13.已知函数z=χ2eχy,求。
正确答案:
14.求微分方程y?+2y?+y=0满足初始条件y(0)=0,y?(0)=1的特解。
正确答案:微分方程的特征方程为r2+2r+1=0,得特征根为r=-1,且为二重根,故方程通解为y=(C1+C2χ)e-χ,又由初始条件y(0)=0,y?(0)=1,得C1=0,C2=1,故原微分方程的特解为y=χe-χ。
15.求不定积分。
正确答案:
16.求。
正确答案:因2+2cos2χ=2(1+cos2χ)=4cos2χ,所以
17.求,其中D为y=χ,y=χ+a,y=a和y=3a(a>0)为边的平行四边形。
正确答案:首先画出积分区域D,把它看作y型,则
已知曲线y=χ2,试求:
18.曲线在点(1,1)处的切线方程与法线方程;
正确答案:(1)根据导数的几何意义,曲线y=χ2在点(1,1)处切线的斜率
为曲线y=χ2在点(1,1)处法线的斜率为所以切线方程为y-1=2(χ-1),即2χ-y-1=0。
则法线方程为
即χ+2y-3=0。
19.曲线上哪一点处的切线与直线y=4χ-1平行?
正确答案:(2)设所求的点为M0(χ0,y0),曲线y=χ2在点(χ0,y0)处切
线的斜率为切线与直线y=4χ-1平行时,它
们的斜率相等,即2χ0=4,所以χ0=2,此时y0=4,故在点M0(2,4)处的切线与直线y=4χ-1平行。
综合题
设平面图形D是由曲线y=eχ,直线y=e及y轴所围成的,求:
20.平面图形D的面积;
正确答案:平面图形D如图所示,取χ为积分变量,且χ∈[0,1]。
平面图形D的面积为。
21.平面图形D绕y轴旋转一周所形成的旋转体的体积。
正确答案:平面图形D绕y轴旋转一周所生成的旋转体的体积为
22.设函数(χ>0),其中f(χ)在区间[a,+∞)上连续,f?(χ)在(a,+∞)内存在且大于零,求证:F(χ)在(a,+∞)内单调递增。
正确答案:
∴F(χ)在(a,+∞)内单调递增。
