波动习题 (1)
波动习题(1)
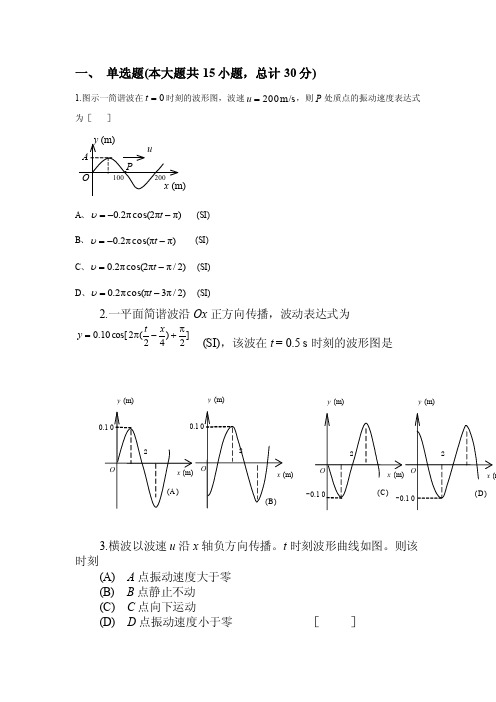
一、 单选题(本大题共15小题,总计30分)1.图示一简谐波在0=t 时刻的波形图,波速m/s 200=u ,则P 处质点的振动速度表达式为[ ]A 、)ππ2cos(π2.0--=t υ (SI)B 、)ππcos(π2.0--=t υ (SI)C 、)2/ππ2cos(π2.0-=t υ (SI)D 、)2/π3πcos(π2.0-=t υ (SI)2.一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y(SI),该波在t = 0.5 s 时刻的波形图是3.横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 [ ]y (m)y (m)- y (m) y (m)4.若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C 为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B [ ]5.将一根长绳子一端固定,用手握另一端使其拉成水平.维持拉力恒定,使绳一端在垂直于绳子的方向上作简谐运动,则[ ] A 、振动频率越高,波长越长 B 、振动频率越低,波长越长 C 、振动频率越高,波速越大 D 、振动频率越低,波速越大6.一质点作简谐运动,已知振动频率为f ,则振动动能的变化频率是[ ] A 、f 4 B 、f 2 C 、2/f D 、4/f7.沿着相反方向传播的两列相干波,其表达式为 )/(π2cos 1λνx t A y -=和 )/(π2c o s 2λνx t A y +=. 在叠加后形成的驻波中,各处简谐振动的振幅是[ ] A 、A B 、A 2C 、)/π2cos(2λx AD 、|)/π2cos(2|λx A8.设声波在介质中的传播速度为u ,声源的频率为S ν.若声源S 不动,而接收器R 相对于介质以速度R υ沿着S 、R 连线向着声源S 运动,则位于S 、R 连线中点的质点P 的振动频率为[ ]A 、S νB 、S Ruu νv + C 、S R u uνv + D 、S Ru uνv -9.一机车汽笛频率为750 Hz ,机车以时速90公里远离静止的观察者.观察者听到的声音的频率是(设空气中声速为340 m/s )[ ] A 、810 Hz B 、699 Hz C 、805 Hz D 、695 Hz10.一辆机车以30 m/s 的速度驶近一位静止的观察者,如果机车的汽笛的频率为550 Hz ,此观察者听到的声音频率是(空气中声速为330 m/s )[ ] A 、605 Hz B 、600 Hz C 、504 Hz D 、500 Hz11.在同一介质中两列相干的平面简谐波的平均能流密度(波的强度)之比是4/21=I I ,则两列波的振幅之比是[ ] A 、16/21=A A B 、4/21=A A C 、2/21=A A D 、4/1/21=A A12.当机械波在介质中传播时,一介质质元的最大变形量发生在[ ] A 、介质质元离开其平衡位置最大位移处 B 、介质质元离开其平衡位置(2/2A )处(A 是振动振幅)C 、介质质元在其平衡位置处D 、介质质元离开其平衡位置A 21处(A 是振动振幅)12.当一平面简谐机械波在弹性介质中传播时,下述各结论哪个是正确的[ ] A 、介质质元的振动动能增大时,其弹性势能减小,总机械能守恒B 、介质质元的振动动能和弹性势能都作周期性变化,但二者的相位不相同C 、介质质元的振动动能和弹性势能的相位在任一时刻都相同,但二者的数值不相等D 、介质质元在其平衡位置处弹性势能最大13.一平面简谐波在弹性介质中传播时,某一时刻介质中某质元在负的最大位移处,则它的能量是[ ]A 、动能为零,势能最大B 、动能为零,势能为零C 、动能最大,势能最大D 、动能最大,势能为零14.一平面简谐波在弹性介质中传播,在介质质元从平衡位置运动到最大位移处的过程[ ]A 、它的动能转换成势能B 、它的势能转换成动能C 、它从相邻的一段质元获得能量其能量逐渐增大D 、它把自己的能量传给相邻的一段质元,其能量逐渐减小15.一平面简谐波以速度u 沿x 轴正方向传播,在t t '=时波形曲线如图所示.则坐标原点O 的振动方程为[ ]A 、]2π)(cos[+'-=t t b u a y B 、]2π)(2cos[-'-=t t b u a y πC 、]2π)(cos[+'+=t t b u a y πD 、]2π)(cos[-'-=t t b u a y π二、 填空题(本大题共10小题,总计30分)1.一平面简谐波的表达式为 )37.0125cos(025.0x t y -= (SI),其角频率ω =______,波速u =________,波长λ = _2.一平面简谐波(机械波)沿x 轴正方向传播,波动表达式为)21cos(2.0x t y π-π=(SI),则x = -3 m 处媒质质点的振动加速度a 的表达式为_____________。
大学物理 振动与波、波动光学练习题

06振动与波、波动光学练习题 一、选择题 1 一物体作简谐振动,振动方程为)4cos(πω+=t A y在4T t =(T 为周期)时刻,物体的加速度为 [ ]2222321)(,321)(,221)(,221)(ωωωωA D A C A B A A -- 2 两个质点各自作简谐振动,它们的振幅相同、周期相同,第一个质点的振动方程为)cos(1αω+=t A y 。
当第一个质点从相对平衡位置的正位移处回到平衡位置时,第二个质点正在最大位移处,则第二个质点的振动方程为 [ ])cos()(),23cos()()2cos()(),2cos()(2222παωπαωπαωπαω++=-+=-+=++=t A y D t A y C t A y B t A y A 3一质点沿y 轴作简谐振动,振动方程为)SI (),32cos(1042παπ++⨯=-t y ,从t = 0时刻起,到质点位置在x = -2 cm 处,且向x 轴正方向运动的最短时间间隔为[ ]s 61)(s,31)(s,21)(s,41)(s,81)(E D C B A 4 已知两个简谐振动曲线如图所示,1x 相位比2x 的相位 [ ]ππππ超前,落后,超前,落后)()(2)(2)(D C B A5题图 7题图5 一质点作简谐振动,周期为T 。
质点由平衡位置向X 轴正方向运动时,由平衡位置到二分之一最大位移这段路程所需要的时间为 [ ],8)(6)(12)(4)(T D T C T B T A ,,, 6 在下面几种说法中,正确的说法是: [ ](A )波源不动时,波源的振动周期与波动的周期在数值上是不同的,(B )波源振动的速度与波速相同,(C) 在波传播方向上的任一质点的振动相位总是比波源的相位滞后,(D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前。
7一平面简谐波,沿X 轴负方向传播,角频率为ω,波速为u 。
设4T t =时刻的波形如图所示,则该波的表达式为: [ ]])(cos[)(),(cos )(]21)(cos[)(),(cos )(πωωπωω++=+=+-=-=ux t A y D u x t A y G u x t A y B ux t A y A 8 当机械波在媒质中传播时,一媒质质元的最大变形量发生在 [ ](A)媒质质元离开其平衡位置最大位移处,(B )媒质质元离开其平衡位置)2/2(A 处,(C )媒质质元在其平衡位置处,(D )媒质质元离开其平衡位置A/2处(A 是振动振幅)。
波动习题

六、练习题(一)选择题1、频率是200Hz 的波,它在骨头中的波长是(骨头中的波速3400m/s ):A 17mB 170mC 0.17mD 1.7m2、频率为30KHz 的机械波属于A 次声波B 声波C 物质波D 超声波3、对于频率为1000Hz ,人的听觉范围声强级A 0dB 到120dB B 0dB 到12dBC 10dB 到12dBD 12dB 到12db4、机械波在通过不同介质时,不会发生变化的物理量是A 波速B 强度C 波长D 频率5、频率为10Hz 的机械波属于A 次声波B 声波C 超声波D 物质波6、波源振动方程0.04cos(2.5)s t m π=,以100m/s 的速度在介质中传播,波动方程为 A 0.04cos 2.5()100x s t m π=-; B 0.04cos 2.5()100x s t m π=+; C 0.04cos(2.5)s t m π=; D 0.04cos(2.5100)s t m π=⨯。
7、波源振动方程0.04cos(2.5)s t m π=,以100m/s 的速度在介质中传播,距波源20m 处质点的振动方程为A 0.04cos 2.5(20)s t m π=-;B 0.04cos 2.5(0.2)s t m π=-;C 0.04cos 2.5(20)s t m π=+;D 0.04cos 2.5(0.2)s t m π=+。
8、波源振动方程0.04cos(2.5)S t m π=,以100m/s 的速度在介质中传播,在波源起振后1.0S 距波源20m 处质点的振动速度A V=0.04m/sB V ≠0C V=2m/sD V=09、设有波动方程0.02cos 2(1000.25)S t x m π=-,则波长A 4.0m λ=;B 0.25m λ=;C 0.5m λπ=;D 0.50m λ=。
10、设有波动方程0.02cos 2(1000.25)S t x m π=-,频率为A 200Hz ν=;B 100Hz ν=;C 50Hz ν=;D 0.50Hz ν=。
物理波动试题

物理波动试题波动是物理学中重要的一个分支,它涉及到波的传播、干涉、衍射等现象。
本试题将涵盖波动的基本概念、公式和应用,旨在考察学生对波动知识的理解和应用能力。
1.简答题(每题10分)(1)什么是波动?简要说明波动的特点及分类。
波动是指能量或信息沿着空间传播的现象。
特点:波动是在介质中传播的,介质不随波传播而移动;波动是由某种原因(振动源)激发产生的;波动可以传播能量和动量;波动可以壁相互作用产生干涉、衍射等现象。
分类:机械波和电磁波。
(2)什么是机械波?它们传播的基本特点是什么?机械波是指需要介质来传播的波动现象。
机械波传播的基本特点是:需要介质来传播,介质的微小部分进行振动,振动的能量沿波的传播方向传递。
(3)什么是波长和频率?它们之间的关系是怎样的?波长是指一次完整振动所对应的距离,用符号λ表示。
频率是指在单位时间内波动上通过某一点的次数,用符号f表示。
它们之间的关系可以由式子v = fλ表示,其中v代表波速。
波速等于波长乘以频率。
(4)什么是相位差?简要说明相位差对波动干涉的影响。
相位差是指两个波源相对于某一点的等效相位差。
它是由波源到该点距离的变化与波长之比所决定。
相位差对波动干涉的影响是:当相位差为整数倍的倍数时,波峰和波峰或波谷和波谷同时到达干涉点,形成增强干涉;当相位差为奇数倍的半数时,波峰和波谷同时到达干涉点,形成减弱干涉。
2.计算题(每题20分)(1)一根被两端固定的弦子上,泛起了两个频率相同且弦长相同的基本振动波。
若两波的相位差为π/4,求出相邻两个波腹之间的距离。
解析:相邻两个波腹之间的距离等于半个波长,即λ/2。
根据相位差为π/4,可以得出相位差对应的距离变化为λ/8。
所以,λ/2 = λ/8,化简可得λ = 4d,其中d为波腹之间的距离。
所以相邻两个波腹之间的距离为4d。
(2)一个平面波以速度v在某介质中传播,当波长λ减小一倍,频率f变为2f,则速度v变为多少?解析:根据波速公式v = fλ,代入新的波长和频率,得到新的波速v' = 2v。
1振动波练习题

一、选择题1、一物体作简谐振动,振动方程为)4/cos(πω+=t A x 。
在t=T/4(T 为周期)时刻,物体的加速度为 (A) 2221ωA -(B) 2221ωA (C) 2321ωA - (D) 2321ωA [ ] 2、对一个作简谐振动的物体,下面哪种说法是正确的?(A) 物体位于平衡位置且向负方向运动时,速度和加速度为零。
(B) 物体位于平衡位置且向正方向运动时,速度最大,加速度为零。
(C) 物体处在运动负方向的端点时,速度和加速度都达到最大值。
(D) 物体处在正方向的端点时,速度最大,加速度为零。
[ ]3、弹簧振子在光滑水平面上作谐振动时,振动频率为v 。
今将弹簧分割为等长的两半,原物体挂在分割后的一支弹簧上,这一系统作谐振动时,振动频率为(A) v (B) v 2(C) 2v (D) 0.5v [ ] 4、一质点沿x 轴作简谐振动,振动方程为))(316cos(1042SI t x ππ+⨯=-。
从t=0时刻起,到质点位置在x =-2cm 处,且向x 轴正方向运动的最短时间间隔为(A) 1/8s (B) 1/4s (C) 1/2s(D) 1/3s (E) 1/6s [ ]5、一质点作简谐振动,周期为T 。
当它由平衡位置向X 轴正方向运动时,从二分之一最大位移处到最大位移处这段路程所需要的最短时间为(A) T/4 (B) T/12(C) T/6 (D) T/8 [ ]6、一弹簧振子在光滑水平面上作谐振动,弹簧的倔强系数为k ,物体的质量为m ,振动的角频率为ω=(k/m )1/2,振幅为A ,当振子的动能和势能相等的瞬时,物体的速度为 (A)A ω2 (B) 2/A ω (C) A ω21 (D) A ω [ ] 7、 一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是(A) 动能为零,势能最大。
(B) 动能为零,势能为零。
(C) 动能最大,势能最大。
人教版高中物理选修一《波的描述》练习题(含解析)(1)

课时分层作业(十二)波的描述(建议用时:25分钟)考点一波的图像1.下列选项为一列横波在某介质中传播时某一时刻的波形图,已知波的传播方向向右,能正确描述各质点继续振动时运动方向的是()C[处在位移最大处的质点一定向平衡位置运动,因此,A、D两项错误,利用“上下坡”法可判断C项正确,B项错误.]2.(多选)如图所示,实线为某时刻一横波的图像,虚线是短暂时间间隔Δt 后的波的图像,且已知波传播得很慢,则由图像可判断出()A.波传播速度的大小B.波的传播方向C.各质点的速度D.各质点的振动方向BD[据题意,由于Δt很小,而且波传播得很慢,因而波传播了很小的距离,即波向右传播,只要确定了传播方向,那么各质点的振动方向就完全确定,不确定,B、D两项正确,A、C两项错误.] 但由于Δs、Δt未知,因而v=ΔsΔt3.如图所示为一列简谐横波在某一时刻的波形图,已知质点A在此时刻的振动方向如图中箭头所示,则以下说法中正确的是()A.波向左传播,质点B向下振动,质点C向上振动B.波向右传播,质点B向上振动,质点C向下振动C.波向左传播,质点B向上振动,质点C向上振动D.波向右传播,质点B向下振动,质点C向下振动C[解决该题有许多方法,现用“上下坡法”判断,若波向右传播,则A 质点处于下坡,应向上振动.由此可知波向左传播.同理可判断C向上振动,B 向上振动,故C项正确.]考点二波长、频率和波速4.一列简谐横波沿x轴正方向传播,频率为5 Hz,图中A、B两质点的横坐标分别为x=2 cm和x=16 cm.某时刻的波形如图所示,从该时刻算起,当质点B的位移和速度与图示时刻质点A的运动状态相同时,所需的最短时间为()A.0.08 s B.0.12 sC.0.14 s D.0.16 sC[由题图可知,波长λ=20 cm,速度v=λf=0.2×5 m/s=1 m/s.质点A的运动状态传播16 cm-2 cm=14 cm所需的最短时间为t=0.14 s,选项C正确.] 5.平静湖面传播着一列水面波(横波),在波的传播方向上有相距3 m的甲、乙两个小木块随波上下运动,测得两个小木块每分钟都上下30次,甲在波谷时,乙在波峰,且两木块之间有一个波峰.这列水面波()A.频率是30 Hz B.波长是3 mC.波速是1 m/s D.周期是0.1 sC[据题意,甲在波谷时,乙在波峰,且两木块之间有一个波峰,则1.5λ=3 m,得λ=2 m.由小木块每分钟振动30次得小木块振动的频率f=3060Hz=0.5 Hz,周期为T=1f=2 s,故波速v=λf=2×0.5 m/s=1 m/s.由以上分析可知C项正确.]6.小明将不同规格的橡皮筋A、B系在一起,连接点为O,请两个同学抓住橡皮筋的两端,并将橡皮筋靠近瓷砖墙面水平拉直.小明用手抓住O点,上下快速抖动.某时刻橡皮筋形状如图所示,下列判断正确的是()A.两种橡皮筋中的波长相同B.两种橡皮筋中波的频率相同C.两种橡皮筋中的波速相同D.此时两种橡皮筋中a、b两质点的运动方向相反B[由题图可知,橡皮筋A的波长为橡皮筋B的波长的两倍,选项A错误;两橡皮筋的振动为受迫振动,橡皮筋中波的频率相同,都为小明抖动的频率,选项B正确;由v=λf知,橡皮筋A的波速为橡皮筋B的波速的两倍,选项C错误;由同侧法可判断,此时两种橡皮筋中a、b两质点的运动方向相同,选项D 错误.]7.一列简谐横波沿直线由a向b传播,相距10.5 m的a、b两处的质点振动图像如图中a、b所示,则()A.该波的振幅可能是20 cmB.该波的波长可能是8.4 mC.该波的波速可能是10.5 m/sD.该波由a传播到b可能历时7 sD [题中给出了两个质点的振动图像,从图中直接可以看出振动的振幅为10 cm ,周期为4 s ,选项A 错误;因为波是沿着a 向b 传播,所以从振动图像可以看出,T =4 s ,b 比a 至少晚振动34个周期,则a 、b 间距离与波长的关系为s =⎝ ⎛⎭⎪⎫n +34λ,(n =0,1,2,…),波由a 传播到b 历时t =nT +34T (n =0,1,2,…),再利用v =λT ,可得选项B 、C 错误,D 正确.]考点三 机械波的多解问题8.(多选)一列简谐波在某一时刻的波形如图所示,经过一段时间,波形变成如图中虚线所示,已知波速大小为1 m/s.则这段时间可能是( )A .1 sB .2 sC .3 sD .4 sAC [如果这列波向右传播,则传播的距离为nλ+14λ(n =0,1,2,…),λ=4 m .则这段时间可能为1 s 、5 s 、9 s 、…,故选项A 正确;如果这列波向左传播,则传播的距离为nλ+34λ(n =0,1,2,…),则这段时间可能为3 s 、7 s 、11 s 、…,故选项C 正确.]9.(多选)一列横波在t =0时刻的波形如图实线所示,在t =1 s 时的波形如图中虚线所示.由此可以判定此波的( )A .波长一定是4 cmB .周期一定是4 sC.振幅一定是2 cmD.传播速度一定是1 cm/sAC[解有关波动图像的题目,一般可分为两类:一类是读图,可以直接从图上读出振幅和波长,此题便可读出波长是4 cm,振幅是2 cm,故A、C选项正确;另一类是根据图像给定的条件,去计算波速、周期,判定波传播的方向,判定某一质点的运动情况及判定某一时刻的波形图.这类问题的解决,是建立在正确读图和对波动的正确理解上的,是较深层次的考查.此题表示出在1 s时间内图像的变化,这1 s时间与周期的关系是nT+14T=1 s(n=0,1,2,3,…)是不确也不确定,D选项也错误.]定解.因此B选项错误.同理传播速度v=λT(建议用时:15分钟)10.(多选)一列简谐波在某时刻的波形如图所示,则下列说法中正确的是()A.此列波的振幅是0.1 mB.x=15 m处质点的位移是0.1 mC.若A质点的速度沿y轴正方向,则B质点的速度也沿y轴正方向D.A质点的加速度沿y轴负方向,B、C两质点的加速度沿y轴正方向ACD[从波形图中可以直接读出振幅、某质点的位移,并判断某质点运动的方向.故选项A、C、D正确.]11.(多选)一列简谐横波在某时刻的波形如图所示,此时刻质点P的速度为v,经过0.2 s后它的速度大小、方向第一次与v相同,再经过1.0 s它的速度大小、方向第二次与v相同,则下列判断中正确的是()A .波沿x 轴负方向传播,且波速为10 m/sB .若某时刻N 质点到达波谷处,则Q 质点一定到达波峰处C .质点M 与质点Q 的位移大小总是相等、方向总是相反D .从图示位置开始计时,在3 s 时刻,质点M 偏离平衡位置的位移y =-10 cmBD [假设P 点向下振动,则第一次速度与v 相同需要经过大于半个周期的时间,第二次速度与v 相同需要经过小于半个周期的时间,与题目中给的时间不符合,所以P 点应向上振动,根据同侧法判断该机械波应该向右传播,选项A 错误;根据题意得,两次速度与v 相同时间加在一起共一个周期即质点P 的振动周期为0.2 s +1.0 s =1.2 s ,所以波的传播周期也为1.2 s ,波长为12 m ,所以波的传播速度为10 m/s.N 、Q 相距λ2,由于对称性,N 、Q 速度大小相等,方向相反,所以N 到波谷,Q 到波峰,选项B 正确;经过34T 波向右平移34λ,可以发现M 、Q 均为正位移,选项C 错误;3 s =⎝ ⎛⎭⎪⎫2+12T ,所以图形正好与本题图关于x 轴对称,所以此时刻质点M 偏离平衡位置的位移y =-10 cm ,选项D 正确.]12.如图所示是一列横波在某一时刻的波形图,若波沿x 轴正方向传播,则:(1)质点A 的振动方向、质点C 的振动方向、质点D 的振动方同各是怎样的?(2)再经过34T ,质点A 通过的路程是多少?质点C 的位移是多少? [解析] (1)由“带动看齐法”(或“上下坡法”)知,波沿x 轴正方向传播时,质点A 向上振动,质点C 向下振动,质点D 在正方向最大位移处,速度为零.(2)再经过34T ,质点A 通过的路程为3A =3×2 cm =6 cm ;质点C 到达正向最大位移处,即C 的位移是2 cm ,方向沿y 轴正方向.[答案] 见解析13.一列简谐横波在x 轴上传播,a 、b 是x 轴上相距s ab =6 m 的两质点.t =0时,b 点正好到达最高点,且b 点到x轴的距离为4 cm ,而此时a 点恰好经过平衡位置向上运动,已知这列波的频率为25 Hz.(1)求经过时间1 s ,a 质点运动的路程;(2)设a 、b 在x 轴上的距离大于一个波长,求该波的波速.[解析] (1)质点a 一个周期运动的路程s 0=4A =0.16 m,1 s 内的周期数n =ft =25,则1 s 内运动的路程s =ns 0=4 m.(2)若波由a 传向b ,则s ab =⎝ ⎛⎭⎪⎫n +34λ,v =λf =6004n +3m/s(n =1,2,…);若波由b 传向a ,则s ab =⎝ ⎛⎭⎪⎫n +14λ,v =λf =6004n +1m/s(n =1,2,…). [答案] (1)4 m (2)见解析。
大学物理第十一章波动光学习题答案

第十一章 波动光学习题11-1 在杨氏双缝实验中,双缝间距d =0.20 mm ,缝屏间距D =1.0 m ,若第2级明条纹离屏中心的距离为6.0 mm ,试求:(1)入射光的波长;(2)相邻两明条纹间的距离。
解:(1)由λk d D x =明知, λ22.01010.63⨯⨯= 30.610m m 600n m λ-=⨯= (2)3106.02.010133=⨯⨯⨯==∆-λd D x mm 11-2 在双缝装置中,用一很薄的云母片(n =1.58)覆盖其中的一条缝,结果使屏幕上的第7级明条纹恰好移到屏幕中央原零级明纹的位置。
若入射光的波长为550 nm ,求此云母片的厚度。
解:设云母片厚度为e ,则由云母片引起的光程差为e n e ne )1(-=-=δ 按题意 λδ7= ∴610106.6158.1105500717--⨯=-⨯⨯=-=n e λm 6.6=m μ 11-3 在折射率n 1=1.52的镜头表面涂有一层折射率n 2=1.38的MgF 2增透膜,如果此膜适用于波长λ=550 nm 的光,问膜的最小厚度应取何值?解:设光垂直入射增透膜,欲透射增强,则膜上、下两表面反射光应满足干涉相消条件,即λ)21(22+=k e n ),2,1,0(⋅⋅⋅=k 222422)21(n n k n k e λλλ+=+=)9961993(38.14550038.125500+=⨯+⨯=k k o A令0=k ,得膜的最薄厚度为996o A 。
11-4 白光垂直照射在空气中厚度为0.4μm 的玻璃片上,玻璃的折射率为1.50。
试问在可见光范围内(λ= 400~700nm ),哪些波长的光在反射中增强?哪些波长的光在透射中增强?解:(1)222n d j λδλ=+= 24 3,480n m 21n d j j λλ===- (2)22(21) 22n d j λλδ=+=+ 22n d j λ= 2,600n m j λ==;3,400nm j λ== 11-5 白光垂直照射到空气中一厚度为380 nm 的肥皂膜上,设肥皂膜的折射率为1.33,试问该膜的正面呈现什么颜色?背面呈现什么颜色? 解:由反射干涉相长公式有42221ne ne k k λδλλ=+==-, ),2,1(⋅⋅⋅=k 得4 1.3338002674nm 2214 1.3338003404nm 231k k λλ⨯⨯===⨯-⨯⨯===⨯-,红色,紫色所以肥皂膜正面呈现紫红色。
大学物理波动光学综合练习题(含答案)
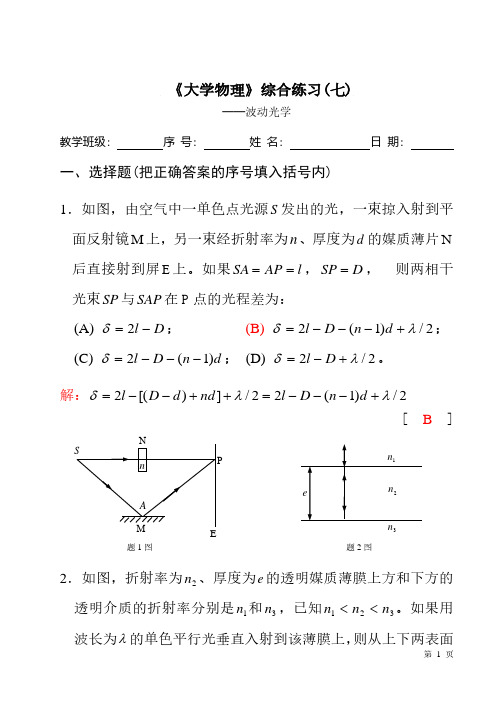
《大学物理》综合练习(七)——波动光学教学班级: 序 号: 姓 名: 日 期:一、选择题(把正确答案的序号填入括号内)1.如图,由空气中一单色点光源S 发出的光,一束掠入射到平面反射镜M 上,另一束经折射率为n 、厚度为d 的媒质薄片N 后直接射到屏E 上。
如果l AP SA ==,D SP =, 则两相干光束SP 与SAP 在P 点的光程差为:(A) D l −=2δ; (B) 2/)1(2λδ+−−−=d n D l ;(C) d n D l )1(2−−−=δ; (D) 2/2λδ+−=D l 。
解:2/)1(22/])[(2λλδ+−−−=++−−=d n D l nd d D l[ B ]2.如图,折射率为2n 、厚度为e 的透明媒质薄膜上方和下方的透明介质的折射率分别是1n 和3n ,已知321n n n <<。
如果用波长为λ的单色平行光垂直入射到该薄膜上,则从上下两表面3题1图 题2图反射的光束的光程差是(A) e n 22; (B) 2/22λ−e n ;(C) 2/322λ−e n ; (D) 222/2n e n λ−。
解:两反射面均有半波损失,e n 22=δ。
[ A ]3.设在双缝干涉实验中,屏幕E 上的P 点是亮条纹,如将缝2S 盖住,并在21S S 连线的垂直平分面处放一反射镜M (如图),则此时:(A) P 点处为暗条纹;(B) P 点处仍然是亮条纹;(C)无干涉条纹; (D)无法确定P 点是亮条纹还是暗条纹。
解:光在M 处发射有半波损失,故P 点处为暗条纹。
[ A ]4.用波长为λ的平行单色光垂直照射图示装置观察空气层上下表面反射光形成的等厚干涉条纹。
以下各图画出可能出现的暗条纹的形状和位置。
试判断哪一图是实际观察到的干涉暗条纹。
题3图解:λλλδ42247max =+⨯= 4max =k (明),故图(C )正确。
[ C ]5.在迈克尔耳逊干涉仪的一条光路中,放入一折射率为n 、厚度为d 的透明薄片,放入前后两条光路的光程差的改变量为(A) d n )1(−; (B) nd ; (C) d n )1(2−; (D) nd 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 单选题(本大题共15小题,总计30分)1.图示一简谐波在0=t 时刻的波形图,波速m/s 200=u ,则P 处质点的振动速度表达式为[ ]A 、)ππ2cos(π2.0--=t υ (SI)B 、)ππcos(π2.0--=t υ (SI)C 、)2/ππ2cos(π2.0-=t υ (SI)D 、)2/π3πcos(π2.0-=t υ (SI)2.一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是3.横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 [ ]y (m)y (m)- y (m) y (m)4.若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C 为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B [ ]5.将一根长绳子一端固定,用手握另一端使其拉成水平.维持拉力恒定,使绳一端在垂直于绳子的方向上作简谐运动,则[ ] A 、振动频率越高,波长越长 B 、振动频率越低,波长越长 C 、振动频率越高,波速越大 D 、振动频率越低,波速越大6.一质点作简谐运动,已知振动频率为f ,则振动动能的变化频率是[ ] A 、f 4 B 、f 2 C 、2/f D 、4/f7.沿着相反方向传播的两列相干波,其表达式为)/(π2cos 1λνx t A y -=和 )/(π2c o s 2λνx t A y +=.在叠加后形成的驻波中,各处简谐振动的振幅是[ ] A 、A B 、A 2C 、)/π2cos(2λx AD 、|)/π2cos(2|λx A8.设声波在介质中的传播速度为u ,声源的频率为S ν.若声源S 不动,而接收器R 相对于介质以速度R υ沿着S 、R 连线向着声源S 运动,则位于S 、R 连线中点的质点P 的振动频率为[ ]A 、S νB 、S Ruu νv + C 、S R u uνv + D 、S Ru uνv -9.一机车汽笛频率为750 Hz ,机车以时速90公里远离静止的观察者.观察者听到的声音的频率是(设空气中声速为340 m/s )[ ] A 、810 Hz B 、699 Hz C 、805 Hz D 、695 Hz10.一辆机车以30 m/s 的速度驶近一位静止的观察者,如果机车的汽笛的频率为550 Hz ,此观察者听到的声音频率是(空气中声速为330 m/s )[ ] A 、605 Hz B 、600 Hz C 、504 Hz D 、500 Hz11.在同一介质中两列相干的平面简谐波的平均能流密度(波的强度)之比是4/21=I I ,则两列波的振幅之比是[ ] A 、16/21=A A B 、4/21=A A C 、2/21=A A D 、4/1/21=A A12.当机械波在介质中传播时,一介质质元的最大变形量发生在[ ] A 、介质质元离开其平衡位置最大位移处B 、介质质元离开其平衡位置(2/2A )处(A 是振动振幅)C 、介质质元在其平衡位置处D 、介质质元离开其平衡位置A 21处(A 是振动振幅)12.当一平面简谐机械波在弹性介质中传播时,下述各结论哪个是正确的[ ] A 、介质质元的振动动能增大时,其弹性势能减小,总机械能守恒B 、介质质元的振动动能和弹性势能都作周期性变化,但二者的相位不相同C 、介质质元的振动动能和弹性势能的相位在任一时刻都相同,但二者的数值不相等D 、介质质元在其平衡位置处弹性势能最大13.一平面简谐波在弹性介质中传播时,某一时刻介质中某质元在负的最大位移处,则它的能量是[ ]A 、动能为零,势能最大B 、动能为零,势能为零C 、动能最大,势能最大D 、动能最大,势能为零14.一平面简谐波在弹性介质中传播,在介质质元从平衡位置运动到最大位移处的过程[ ]A 、它的动能转换成势能B 、它的势能转换成动能C 、它从相邻的一段质元获得能量其能量逐渐增大D 、它把自己的能量传给相邻的一段质元,其能量逐渐减小15.一平面简谐波以速度u 沿x 轴正方向传播,在t t '=时波形曲线如图所示.则坐标原点O 的振动方程为[ ]A 、]2π)(cos[+'-=t t b u a y B 、]2π)(2cos[-'-=t t b u a y πC 、]2π)(cos[+'+=t t b u a y πD 、]2π)(cos[-'-=t t b u a y π二、 填空题(本大题共10小题,总计30分)1.一平面简谐波的表达式为 )37.0125cos(025.0x t y -= (SI),其角频率ω =______,波速u =________,波长λ = _2.一平面简谐波(机械波)沿x 轴正方向传播,波动表达式为)21cos(2.0x t y π-π=(SI),则x = -3 m 处媒质质点的振动加速度a 的表达式为_____________。
3. 一列平面简谐波沿x 轴正向无衰减地传播,波的振幅为 2×10-3 m ,周期为0.01 s ,波速为400 m/s . 当t = 0时x 轴原点处的质元正通过平衡位置向y 轴正方向运动,则该简谐波的表达式为________________。
4. A ,B 是简谐波波线上的两点。
已知,B 点振动的相位比A 点落后π31,A 、B 两点相距0.5 m ,波的频率为 100 Hz ,则该波的波长 λ = ___________m ,波速 u = ________m/s 。
5.一球面波在各向同性均匀介质中传播,已知波源的功率为100 W ,若介质不吸收能量,则距波源10 m 处的波的平均能流密度为________.6. 已知波源的振动周期为4.00×10-2 s ,波的传播速度为300 m/s ,波沿x 轴正方向传播,则位于x 1 = 10.0 m 和x 2 = 16.0 m 的两质点振动相位差为__________。
7. 两相干波源S 1和S 2的振动方程分别是t A y ωcos 1=和)21cos(2π+=t A y ω。
S 1距P 点3个波长,S 2距P 点21/4个波长。
两波在P 点引起的两个振动的相位差是_________。
8. S 1,S 2为振动频率、振动方向均相同的两个点波源,振动方向垂直纸面,两者相距λ23(λ为波长)如图。
已知S 1的初相为π21。
(1)若使射线S 2C 上各点由两列波引起的振动均干涉相消,则S 2的初相应为______________________。
(2)若使S 1 S 2连线的中垂线MN 上各点由两列波引起的振动均干涉相消,则S 2的初位相应为_______________________。
9两个相干点波源S 1和S 2,它们的振动方程分别是)21cos(1π+=t A y ω和)21cos(2π-=t A y ω。
波从S 1传到P 点经过的路程等于2个波长,波从S 2传到P 点的路程等于27个波长。
设两波波速相同,在传播过程中振幅不衰减,则两波传到P 点的振动的合振幅为____。
10. 一平面简谐波沿Ox 轴正方向传播,波长为λ。
若如图P 1点处质点的振动方程为)2cos(1φν+π=t A y ,则P 2点处质点的振动方程为____________________________;与P 1点处质点振动状态相同的那些点的位置是______________________。
三、 计算题(本大题共5小题,总计40分)1..(8分) 一波长为λ的简谐波沿Ox 轴正方向传播,在λ21=x 的P 处质点的振动方程是210)cos 21sin 23(-⨯-=t t y P ωω (SI),求该简谐波的表达式. 2.一振幅为 10 cm ,波长为200 cm 的简谐横波,沿着一条很长的水平的绷紧弦从左向右行进,波速为 100 cm/s .取弦上一点为坐标原点,x 轴指向右方,在0=t 时原点处质点从平衡位置开始向位移负方向运动.求以SI 单位表示的波动表达式(用余弦函数)及弦上任一点的xOP 1 P 2 L 1 L 23133图最大振动速度3.已知一平面简谐波的表达式为 )24(πcos x t A y += (SI). (1) 求该波的波长λ,频率ν和波速u 的值;(2) 写出s 2.4=t 时刻各波峰位置的坐标表达式,并求出此时离坐标原点最近的那个波峰的位置;(3) 求s 2.4=t 时离坐标原点最近的那个波峰通过坐标原点的时刻t .1分4. 沿x 轴负方向传播的平面简谐波在t = 2 s 时刻的波形曲线如图所示,设波速u = 0.5 m/s 。
求:原点O 的振动方程。
5:如图所示,两相干波源在x 轴上的位置为S 1和S 2,其间距离为d = 30 m ,S 1位于坐标原点O 。
设波只沿x 轴正负方向传播,单独传播时强度保持不变。
x 1 = 9 m 和x 2 = 12 m 处的两点是相邻的两个因干涉而静止的点。
求两波的波长和两波源间最小相位差。
5206图。
