浙江省高考数学圆锥曲线历年高考真题版
浙江高考圆锥曲线

浙江高考圆锥曲线1.(2013)年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))如图,点)1,0(-P 是椭圆)0(1:22221>>=+b a by a x C 的一个顶点,1C 的长轴是圆4:222=+y x C 的直径.21,l l 是过点P 且互相垂直的两条直线,其中1l 交圆2C 于两点,2l 交椭圆1C 于另一点D (1) 求椭圆1C 的方程; (2)求ABD ∆面积取最大值时 (2) 直线1l 的方程.【答案】解:(Ⅰ)由已知得到1b =,且242a a =∴=, 所以椭圆的方程是2214xy +=; (Ⅱ)因为直线12l l ⊥,且都过点(0,1)P -,所以设1:110l y kx kx y =-⇒--=,直线21:10l y x x ky k k=--⇒++=,所以圆心(0,0)到直线1:110l y kx kx y =-⇒--=的距离为d =所以直线1l 被圆224x y +=所截的弦AB ==由22222048014x ky k k x x kx x y ++=⎧⎪⇒++=⎨+=⎪⎩, 28||4D P k x x DP k +=-∴==+所以11||||22ABDS AB DP ∆====2324313k ==≤=++252k k =⇒=⇒=时等号成立,此时直线1:1l y x =-2、:的长轴是圆的一个顶点,:)是椭圆点21221)0(141-,0(C C b a y x C P >>=+ 21,l l 是过点,11A C l P 于另一点交椭圆,其中且互相垂直的两条直线面积最大值时直线。
求于另一点交椭圆AB ABP B C l ∆12解设),,(),,(2211y x B y x A 直线AB 的方程为b kx y +=将其代入1422=+y x 整理得448)41(222-+++b kbx x k 22212214144,418kb x x k kb x x +-=+-=+∴由∴⊥PB PA 1)1())(1(11112122121222112211-=+++++=++⋅++=+⋅+x x b x x b k x x k x b kx x b kx x y x y 即0)1(1422=-+-b b ,解得舍去)或(153-==b b ,),(过定点又直线53,0Q AB 2222222214125453241)44)(41(464582121k k kb k b k x x PQ S PAB++⋅=+-+-⋅=-⋅=∴∆ 令则),52(2542≥+=t k t PAB S ∆=tt t t 2594153225945322+⋅=+⋅,时当52=t ,PAB S ∆最大, 53=y AB 的直线方程为于此时。
专题11+圆锥曲线-十年高考(2009-2018)之高三数学分项与解读(浙江专版)+Word版含解析
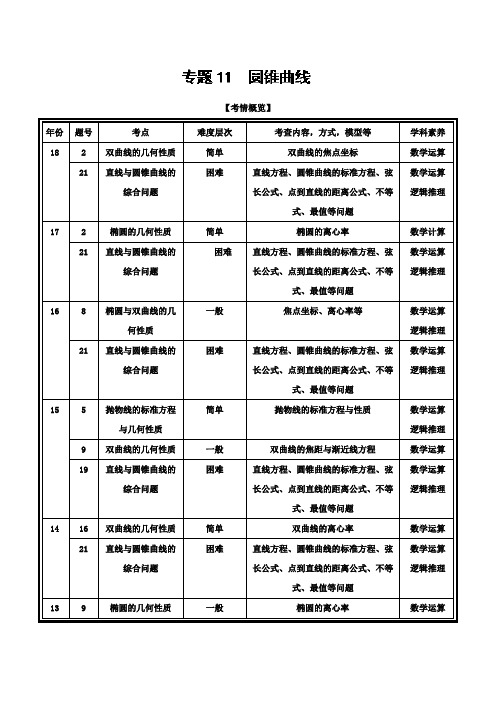
【考情概览】【应试策略】1.平面直角坐标系xOy 中,椭圆C :()222210x y a b a b +=>> E :22x y =的焦点F 是C 的一个顶点.(I )求椭圆C 的方程;(II )设P 是E 上的动点,且位于第一象限,E 在点P 处的切线l 与C 交与不同的两点A ,B ,线段AB 的中点为D ,直线OD 与过P 且垂直于x 轴的直线交于点M . (i )求证:点M 在定直线上;(ii )直线l 与y 轴交于点G ,记PFG △的面积为1S ,PDM △的面积为2S ,求12S S的最大值及取得最大值时点P 的坐标.【答案】(Ⅰ)1422=+y x ;(Ⅱ)(i )见解析;(ii )12S S 的最大值为49,此时点P 的坐标为)41,22((Ⅱ)(i )设)0)(2,(2>m m m P ,由y x 22=可得x y =/, 所以直线l 的斜率为m ,因此直线l 的方程为)(22m x m m y -=-,即22m mx y -=. 设),(),,(),,(002211y x D y x B y x A ,联立方程222241m y mx x y ⎧=-⎪⎨⎪+=⎩得014)14(4322=-+-+m x m x m ,由0>∆,得520+<<m 且1442321+=+m m x x , 因此142223210+=+=m m x x x , 将其代入22m mx y -=得)14(2220+-=m m y ,因为mx y 4100-=,所以直线OD 方程为x m y 41-=. 联立方程⎪⎩⎪⎨⎧=-=m x x m y 41,得点M 的纵坐标为M 14y =-,即点M 在定直线41-=y 上. (ii )由(i )知直线l 方程为22m mx y -=,令0=x 得22m y -=,所以)2,0(2m G -, 又21(,),(0,),22m P m F D ))14(2,142(2223+-+m m m m , 所以)1(41||2121+==m m m GF S , )14(8)12(||||2122202++=-⋅=m m m x m PM S ,所以222221)12()1)(14(2+++=m m m S S , 令122+=m t ,则211)1)(12(2221++-=+-=t tt t t S S , 当211=t,即2=t 时,21S S 取得最大值49,此时22=m ,满足0>∆, 所以点P 的坐标为)41,22(,因此12S S 的最大值为49,此时点P 的坐标为)41,22(.【应试策略】定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少,或者将该问题涉及的几何式转化为代数式或三角问题,证明该式是恒定的. 定点、定值问题同证明问题类似,在求定点、定值之前已知该值的结果,因此求解时应设参数,运用推理,到最后必定参数统消,定点、定值显现. 2.如图,已知抛物线,过直线上任一点作抛物线的两条切线,切点分别为.(I )求证:; (II )求面积的最小值.【答案】(1)见解析(2) 面积取最小值【解析】试题分析:(1)设,的斜率分别为,由切线条件,易得,即,由两根之积可得所以;(2),而,同理可得,即,然后求最值即可.(II)由(I)得,所以综上,当时,面积取最小值.【应试策略】圆锥曲线的最值与范围问题的常见求法(1)几何法:若题目的条件和结论能明显体现几何特征和意义,则考虑利用图形性质来解决;(2)代数法:若题目的条件和结论能体现一种明确的函数关系,则可首先建立目标函数,再求这个函数的最值.在利用代数法解决最值与范围问题时常从以下五个方面考虑:①利用判别式来构造不等关系,从而确定参数的取值范围;②利用已知参数的范围,求新参数的范围,解这类问题的关键是在两个参数之间建立等量关系;③利用隐含或已知的不等关系建立不等式,从而求出参数的取值范围;④利用基本不等式求出参数的取值范围;⑤利用函数的值域的求法,确定参数的取值范围.3.已知点1,2P t⎛⎫⎪⎝⎭在椭圆22:12xC y+=内,过P的直线l与椭圆C相交于A,B两点,且点P是线段AB的中点,O为坐标原点.(Ⅰ)是否存在实数t,使直线和直线OP的倾斜角互补?若存在,求出的值,若不存在,试说明理由;(Ⅱ)求OAB面积S的最大值.【答案】( Ⅰ)存在;(Ⅱ)max2S=.【解析】试题分析:试题解析:(Ⅰ)存在.由解得,,(或由解得,)当时,显然不符合题意;当时,设直线的斜率为,只需,即,解得,均符合题意.(Ⅱ)由(1)知的方程是,所以,【应试策略】解析几何中存在性问题的求解方法:1.通常采用“肯定顺推法”,将不确定性问题明朗化,其步骤为:假设满足条件的元素(点、直线、曲线或参数)存在,用待定系数法设出,列出关于特定参数的方程组,若方程组有实数解,则元素(点、直线、曲线或参数)存在,否则(点、直线、曲线或参数)不存在. 2.反证法与验证法也是求解存在性问题的常用方法.【真题展示】一、选择题1.【2018年,浙江卷2】双曲线221 3=x y -的焦点坐标是( )A .(0),0)B .(−2,0),(2,0)C .(0,,(0D .(0,−2),(0,2)【.答案】B【解析】∵2314c =+=,∴双曲线2213x y -=的焦点坐标是(2,0)-,(2,0).2.【2017年,浙江卷2】椭圆22194x y +=的离心率是A B C .23D .59【答案】B【解析】试题分析:e ==B . 3.【2013年.浙江卷.理9】如图,F 1,F 2是椭圆C 1:24x +y 2=1与双曲线C 2的公共焦点,A ,B 分别是C 1,C 2在第二、四象限的公共点.若四边形AF 1BF 2为矩形,则C 2的离心率是( ).A .32 D 【答案】D【解析】椭圆C 1中,|AF 1|+|AF 2|=4,|F 1F 2|=又因为四边形AF 1BF 2为矩形,所以∠F 1AF 2=90°.所以|AF 1|2+|AF 2|2=|F 1F 2|2,所以|AF 1|=2-|AF 2|=2+所以在双曲线C 2中,2c =2a =|AF 2|-|AF 1|=e ==,故选D . 4. 【2011年.浙江卷.理8】已知椭圆22122:1(0)x y C a b a b +=>>与双曲线222:14y C x -=有公共的焦点,2C 的一条渐近线与以1C 的长轴为直径的圆相交于,A B 两点,若1C 恰好将线段AB 三等分,则(A)2132a =(B )213a = (C )212b =(D )22b =5. 【2010年.浙江卷.理8】设1F 、2F 分别为双曲线22221(0,0)x y a b a b-=>>的左、右焦点.若在双曲线右支上存在点P ,满足212PF FF =,且2F 到直线1PF 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为(A )340x y ±= (B )350x y ±= (C )430x y ±= (D )540x y ±= 【答案】C【解析】利用题设条件和双曲线性质在三角形中寻找等量关系,得出a 与b 之间的等量关系,可知答案选C ,本题主要考察三角与双曲线的相关知识点,突出了对计算能力和综合运用知识能力的考察,属中档题 6.【2015高考浙江,理5】如图,设抛物线24y x =的焦点为F ,不经过焦点的直线上有三个不同的点A ,B ,C ,其中点A ,B 在抛物线上,点C 在y 轴上,则BCF ∆与ACF ∆的面积之比是( )A.11BF AF -- B.2211BF AF -- C.11BF AF ++ D.2211BF AF ++【答案】A. 【解析】11--===∆∆AF BF x x AC BC S S A B ACF BCF ,故选A. 【考点定位】抛物线的标准方程及其性质7.【2016高考浙江理数】已知椭圆C 1:22x m +y 2=1(m >1)与双曲线C 2:22x n–y 2=1(n >0)的焦点重合,e 1,e 2分别为C 1,C 2的离心率,则( )A .m >n 且e 1e 2>1B .m >n 且e 1e 2<1C .m <n 且e 1e 2>1D .m <n 且e 1e 2<1 【答案】A【考点】1、椭圆的简单几何性质;2、双曲线的简单几何性质.【易错点睛】计算椭圆1C 的焦点时,要注意222c a b =-;计算双曲线2C 的焦点时,要注意222c a b =+.否则很容易出现错误.8.【2012年.浙江卷.理8】如图,F 1,F 2分别是双曲线C :22221x y a b-=(a ,b >0)的左、右焦点,B 是虚轴的端点,直线F 1B 与C 的两条渐近线分别交于P ,Q 两点,线段PQ 的垂直平分线与x 轴交于点M .若|MF 2|=|F 1F 2|,则C 的离心率是( )A .3 B .2【答案】B9.【2009年.浙江卷.理9】过双曲线22221(0,0)x y a b a b-=>>的右顶点A 作斜率为1-的直线,该直线与双曲线的两条渐近线的交点分别为,B C .若12AB BC =,则双曲线的离心率是 ( )A 【答案】C【解析】对于(),0A a ,则直线方程为0x y a +-=,直线与两渐近线的交点为B ,C ,22,,(,)a ab a ab B C a b a b a b a b ⎛⎫- ⎪++--⎝⎭,则有22222222(,),,a b a b ab ab BC AB a b a b a b a b ⎛⎫=-=- ⎪--++⎝⎭,因222,4,AB BC a b e =∴=∴= 哦;。
浙江历年高考数学试题及答案汇编十圆锥曲线

浙江历年高考数学试题及答案汇编十圆锥曲线1.若双曲线的方程为$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$,则双曲线的离心率为$\sqrt{1+\frac{b^2}{a^2}}$。
2.图中给出的是一个斜三角形$ABP$,要求点$P$在平面$a$内运动,使得$\triangle ABP$的面积为定值。
根据题意可知,$\triangle ABP$的面积等于$\frac{1}{2}AB\cdot h$,其中$h$为$P$到$AB$的距离。
因此,$h$是一个定值,而$AB$是一个斜线段,所以$P$的轨迹是一条与$AB$垂直的直线。
3.设椭圆的焦点分别为$F_1$、$F_2$,椭圆上任意一点$P$到$F_1$、$F_2$的距离之和为常数$2a$($2a$为椭圆的长轴),即$|PF_1|+|PF_2|=2a$。
根据题意可得$|F_2A|+|F_2B|=12$,因此$|AB|=2a=24-|F_2A|-|F_2B|=12$。
4.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的两个焦点$F_1$、$F_2$的直线为双曲线的准线,且与$x$轴的夹角为$\theta=\arctan\frac{b}{a}$。
由于双曲线的左、右支分别对称,不妨考虑右支。
右支的渐近线方程为$y=\pm\frac{b}{a}x$。
过$F_1$的直线的斜率为$\tan(\theta+\frac{\pi}{4})=\frac{a}{b}$,因此该直线的方程为$y-\frac{b}{a}x=2b$。
将该直线与双曲线的渐近线联立,解得交点坐标为$B(\frac{2a^2}{b},\frac{2ab}{b})$。
同理,过$F_2$的直线的方程为$y+\frac{b}{a}x=2b$,将其与双曲线的渐近线联立,解得交点坐标为$C(-\frac{2a^2}{b},-\frac{2ab}{b})$。
浙江十年(2014-2023)单独考试招生文化考试数学真题分类汇编 圆锥曲线含详解

专题06圆锥曲线考点01椭圆1.(2023年浙江)中国刺绣作为一项传统手工技艺,是中国传统文化的重要组成部分.某个椭圆形的刺绣艺术品的尺寸如图所示,则这个椭圆的离心率是()u 53u 56u 52u 552.(2023年浙江)椭圆的标准方程为2+26=1,焦点在x 210,则n=____.3.(2022年浙江)椭圆22221(0)x y a b a b+=>>的焦距为离心率3e =,过点(2,0)-的直线与椭圆交于A ,B 两点,且线段AB 的中点坐标为01,2y ⎛⎫- ⎪⎝⎭.求:(1)椭圆的标准方程;(4分)(2)0y 的值.(6分)4.(2021年浙江)若椭圆2214x y m +=的一个焦点为(0,3)-,则椭圆的离心率为()A.355 B.413 C.313D.313135.(2021年浙江)如图,(4,0)F 为椭圆的右焦点,M 是椭圆上的点,若△OMF是正三角形,则椭圆长轴长为.6.(2020年浙江)若椭圆22221(0)x y a b a b +=>>的焦距为2,离心率为2.斜率为1的直线经过椭圆的左焦点,交椭圆于A ,B 两点.(1)求椭圆的标准方程;(5分)(2)求||AB 的值.(5分)7.(2019年浙江)椭圆标准方程为221244x y t t+=+-,一个焦点为()3,0-,则t 的值为()A.1- B.0C.1D.38.(2019年浙江)已知椭圆中心在原点且对称轴为坐标轴,它与双曲线2213y x -=有且仅有两个公共点,它们的离心率之积为1,则椭圆标准方程为________.9.(2018年浙江)方程+32+2+−32+2=10所表示的曲线为()A.圆B.椭圆C.双曲线D.抛物线10.(2018年浙江)如图所示,椭圆22+22=1的两个焦点坐标为1−2,0,22,0,两个顶点和两个焦点构成一个正方形,求:(1)椭圆的标准方程和离心率;(4分)(2)以点A (a ,0)为顶点,且关于x 轴对称的内接等腰直角三角形的周长.(6分)11.(2017年浙江)已知椭圆方程:224312x y +=,下列说法错误的是()A.焦点为()0,1-,()0,1B.离心率12e =C.长轴在x 轴上D.短轴长为2312.(2016年浙江)椭圆22116x y m +=的离心率34e =,则m 的值为A.7B 7C.7或25D.7或256713.(2015年浙江)若()0,πβ∈,则方程22sin 1x y β+=所表示的曲线是()A .圆B .椭圆C .双曲线D .椭圆或圆14.(2014年浙江)两边靠墙的角落有一个区域,边界线正好是椭圆轨迹的部分,如图所示.现要设计一个长方形花坛,要求其不靠墙的顶点正好落在椭圆的轨迹上.(1)根据所给条件,求出椭圆的标准方程;(3分)(2)求长方形面积S 与边长x 的函数关系式;(3分)(3)求当边长x 为多少时,面积S 有最大值,并求其最大值.(4分)考点02双曲线1.(2023年浙江)如图所示,双曲线的标准方程为22−22=1(>0,>0),1,2为双曲线的两个焦点,实轴长为23,且双曲线经过点(−2,−2);(1)求双曲线的标准方程;(3分)(2)若点M 在双曲线的渐近线上,ΔB 12的面积为122,求点M 的坐标;(4分)(3)点P (m,n )在双曲线右支上,点N 的坐标为(1,n ),求∣B 1∣∣P∣的值.(3分)2.(2022年浙江)己知双曲线221412x y -=的两个焦点为12,F F ,以线段12F F 为直径的圆与双曲线在第一象限的交点为P ,则12F PF △的面积为()A .43B .63C .12D .243.(2021年浙江)已知双曲线的渐近线方程为2y x =±,实轴长为4,则双曲线标准方程是()A.221416x y -= B.221416y x -=或2214x y -=C.2214x y -= D.221416x y -=或2214y x -=4.(2020年浙江)双曲线221x y -=与直线1x y -=交点的个数为()A .0B .1C .2D .45.(2020年浙江)已知双曲线22221x y a b -=的渐近线方程为y =,则该双曲线的离心率为___________.6.(2019年浙江)双曲线22221x y a b-=的实轴长为10,焦距为26,则双曲线的渐近线方程为()A.135y x =±B.125y x =±C.512y x =±D.513y x =±7.(2018年浙江)双曲线216−29=1的焦点坐标为()A.±7,0B.0,±7C.±5,0D.0,±58.(2018年浙江)双曲线22−28=1e =3,则实半轴长9.(2017年浙江)设动点M 到()1F =的距离减去它到)2F 的距离等于4,则动点M 的轨迹方程为()A.22149x y -=(2x ≤-)B.22149x y -=(2x ≥)C.22149x y -=(2y ≥) D.22149x y -=(3x ≥)10.(2017年浙江)双曲线2212516y x -=的两条渐近线方程为______.11.(2016年浙江)已知双曲线22221x y a b -=的离心率52e =,实轴长为4,直线l 过双曲线的左焦点1F 且与双曲线交于,A B 两点,83AB =.(1)求双曲线的方程;(2)求直线l 的方程.12.(2015年浙江)焦点在x 轴上,焦距为8的双曲线,其离心率2e =.则双曲线的标准方程为()A .221412x y -=B .221124x y -=C .221412y x -=D .221124y x -=13.(2014年浙江)双曲线22149x y -=的离心率e =()A .23B .32C .132D .133考点03抛物线1.(2023年浙江)截至2023年2月,被誉为“中国天眼”的500米口径的射电望远镜(FAST),已经发现超740颗脉冲星,为世界各国探索宇宙星空,提供了中国智慧和中国力量.如图所示,这个射电望远镜的轴截面是一个开口向上的抛物线的一部分.当抛物线口径AB 为300米时,抛物线的深度OC 为56.25米,则这个抛物线的标准方程为()A.x 2=400yB.x 2=200yC.y 2=400xD.y 2=200x2.(2022年浙江)己知点(2,2)M 在抛物线22y px =上,则抛物线的焦点坐标为()A .(1,0)-B .(1,0)C .1,02⎛⎫⎪⎝⎭D .1,02⎛⎫-⎪⎝⎭3.(2021年浙江)已知抛物线顶点为原点,准线l :13y =-.(1)求抛物线的标准方程;(4分)(2)过焦点F 的直线与抛物线相交于A ,B 两点,若83AB =,求直线AB 的方程.4.(2020年浙江)若直线y x b =+经过抛物线24x y =的焦点,则b 的值是()A .2-B .1-C .1D .25.(2019年浙江)已知抛物线的顶点在原点,焦点坐标为()3,0F .(1)求抛物线的标准方程;(2)若抛物线上点M 到焦点的距离为4,求点M 的坐标.6.(2018年浙江)抛物线2=12的焦点到其准线的距离是()A.18B.14C.12D.17.(2017年浙江)1992年巴塞罗那奥运会开幕式中,运动员安东尼奥·雷波洛以射箭方式点燃主会场的圣火成为历史经典.如图所示,如果发射点A 离主火炬塔水平距离60m AC =,塔高20m BC =.已知箭的运动轨迹是抛物线,且离火炬塔水平距离20m EC =处达到最高点O .(1)若以O 为原点,水平方向为x 轴,1m 为单位长度建立直角坐标系。
2005-2019年浙江高考理科数学历年真题之圆锥曲线大题(学生版)

2005-2019年浙江高考理科数学历年真题之圆锥曲线大题(学生版)1、(2005年)如图,已知椭圆的中心在坐标原点,焦点12,F F 在x 轴上,长轴12A A 的长为4,左准线l 与x 轴的交点为M ,|MA 1|∶|A 1F 1|=2∶1. (Ⅰ)求椭圆的方程;(Ⅱ)若直线1l :x =m (|m |>1),P 为1l 上的动点,使12F PF ∠ 最大的点P 记为Q ,求点Q 的坐标(用m 表示).2、(2006年)如图,椭圆by a x 222+=1(a >b >0)与过点A (2,0)、B(0,1)的直线有且只有一个公共点T ,且椭圆的离心率e=23。
(Ⅰ)求椭圆方程;(Ⅱ)设F 1、F 2分别为椭圆的左、右焦点,M 为线段AF 2的中点, 求证:∠ATM=∠AF 1T 。
3、(2007年)如图,直线y kx b =+与椭圆2214x y +=交于A B ,两点,记AOB △的面积为S . (I )求在0k =,01b <<的条件下,S 的最大值; (II )当2AB =,1S =时,求直线AB 的方程.4、(2008年)已知曲线C 是到点P ()和到直线距离相等的点的轨迹。
是过点Q (-1,0)的直线,M 是C 上(不在上)的动点;A 、B 在上, 轴(如图)。
(Ⅰ)求曲线C 的方程; (Ⅱ)求出直线的方程,使得为常数。
83,21-85-=y l l ,MA l MB x ⊥⊥l QAQB25、(2009年)已知椭圆1C :22221(0)y x a b a b+=>>的右顶点为(1,0)A ,过1C 的焦点且垂直长轴的弦长为1. (I )求椭圆1C 的方程;(II )设点P 在抛物线2C :2()y x h h =+∈R 上,2C 在点P 处的切线与1C 交于 点,M N .当线段AP 的中点与MN 的中点的横坐标相等时,求h 的最小值.6、(2010年)已知1>m ,直线,02:2=--m my x l 椭圆21222,,1:F F y mx C =+ 分别为椭圆C 的左、右 焦点.(I )当直线l 过右焦点F 2时,求直线l 的方程;(II )设直线l 与椭圆C 交于A ,B 两点,21F AF ∆,21F BF ∆的重心分别为G ,H.若原点O 在以线段GH为直径的圆内,求实数m 的取值范围.OxyAP MN7、(2011年)已知抛物线1:C 2x =y ,圆2:C 22(4)1x y +-=的圆心为点M 。
04__17浙江高考历年圆锥曲线大题

2018年04月10日wan****.121的高中数学组卷一.解答题(共21小题)1.如图,已知抛物线x2=y,点A(﹣,),B(,),抛物线上的点P(x,y)(﹣<x<),过点B作直线AP的垂线,垂足为Q.(Ⅰ)求直线AP斜率的取值范围;(Ⅱ)求|PA|•|PQ|的最大值.2.如图,设抛物线y2=2px(p>0)的焦点为F,抛物线上的点A到y轴的距离等于|AF|﹣1,(Ⅰ)求p的值;(Ⅱ)若直线AF交抛物线于另一点B,过B与x轴平行的直线和过F与AB垂直的直线交于点N,AN与x轴交于点M,求M的横坐标的取值范围.3.如图,已知抛物线C1:y=x2,圆C2:x2+(y﹣1)2=1,过点P(t,0)(t>0)作不过原点O的直线PA,PB分别与抛物线C1和圆C2相切,A,B为切点.(Ⅰ)求点A,B的坐标;(Ⅱ)求△PAB的面积.注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则称该直线与抛物线相切,称该公共点为切点.4.已知椭圆上两个不同的点A,B关于直线y=mx+对称.(1)求实数m的取值范围;(2)求△AOB面积的最大值(O为坐标原点).5.如图,设椭圆C:(a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限.(Ⅰ)已知直线l的斜率为k,用a,b,k表示点P的坐标;(Ⅱ)若过原点O的直线l1与l垂直,证明:点P到直线l1的距离的最大值为a﹣b.6.如图,点P(0,﹣1)是椭圆C1:+=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1,l2是过点P且互相垂直的两条直线,其中l1交圆C 2于A、B两点,l2交椭圆C1于另一点D.(1)求椭圆C1的方程;(2)求△ABD面积的最大值时直线l1的方程.7.已知抛物线C的顶点为O(0,0),焦点F(0,1)(Ⅰ)求抛物线C的方程;(Ⅱ)过F作直线交抛物线于A、B两点.若直线OA、OB分别交直线l:y=x﹣2于M、N两点,求|MN|的最小值.8.如图,椭圆C:=1(a>b>0)的离心率为,其左焦点到点P(2,1)的距离为,不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP 平分.(Ⅰ)求椭圆C的方程;(Ⅱ)求△APB面积取最大值时直线l的方程.9.如图,在直角坐标系xOy中,点P(1,)到抛物线C:y2=2px(P>0)的准线的距离为.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB 被直线OM平分.(1)求p,t的值.(2)求△ABP面积的最大值.10.已知抛物线C1:x2=y,圆C2:x2+(y﹣4)2=1的圆心为点M(Ⅰ)求点M到抛物线C1的准线的距离;(Ⅱ)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.11.如图,设P是抛物线C1:x2=y上的动点.过点P做圆C2:x2+(y+3)2=1的两条切线,交直线l:y=﹣3于A,B两点.(Ⅰ)求C2的圆心M到抛物线 C1准线的距离.(Ⅱ)是否存在点P,使线段AB被抛物线C1在点P处的切线平分?若存在,求出点P的坐标;若不存在,请说明理由.12.已知m是非零实数,抛物线C:y2=2px(p>0)的焦点F在直线上.(I)若m=2,求抛物线C的方程(II)设直线l与抛物线C交于A、B,△AA1F,△BB1F的重心分别为G,H,求证:对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外.13.已知m>1,直线l:x﹣my﹣=0,椭圆C:+y2=1,F1、F2分别为椭圆C的左、右焦点.(Ⅰ)当直线l过右焦点F2时,求直线l的方程;(Ⅱ)设直线l与椭圆C交于A、B两点,△AF1F2,△BF1F2的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.14.已知椭圆C1:(a>b>0)的右顶点A(1,0),过C1的焦点且垂直长轴的弦长为1.(Ⅰ)求椭圆C1的方程;(Ⅱ)设点P在抛物线C2:y=x2+h(h∈R)上,C2在点P处的切线与C1交于点M,N.当线段AP的中点与MN的中点的横坐标相等时,求h的最小值.15.已知抛物线C:x2=2py(p>0)上一点A(m,4)到其焦点的距离为.(Ⅰ)求p与m的值;(Ⅱ)设抛物线C上一点p的横坐标为t(t>0),过p的直线交C于另一点Q,交x轴于M点,过点Q作PQ的垂线交C于另一点N.若MN是C的切线,求t的最小值.16.如图,椭圆=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=.(Ⅰ)求椭圆方程;(Ⅱ)设F1、F2分别为椭圆的左、右焦点,求证:.17.如图,直线y=kx+b与椭圆=1交于A,B两点,记△AOB的面积为S.(I)求在k=0,0<b<1的条件下,S的最大值;(Ⅱ)当|AB|=2,S=1时,求直线AB的方程.18.如图,椭圆=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=.(Ⅰ)求椭圆方程;(Ⅱ)设F1、F2分别为椭圆的左、右焦点,M为线段AF2的中点,求证:∠ATM=∠AF1T.19.如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.(Ⅰ)求椭圆的方程;(Ⅱ)若直线l1:x=m(|m|>1),P为l1上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用m表示).20.如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|:|A1F1|=2:1.(Ⅰ)求椭圆的方程;(Ⅱ)若点P在直线l上运动,求∠F1PF2的最大值、21.已知双曲线的中心在原点,右顶点为A(1,0)点P、Q在双曲线的右支上,支M(m,0)到直线AP的距离为1(Ⅰ)若直线AP的斜率为k,且,求实数m的取值范围;(Ⅱ)当时,△APQ的内心恰好是点M,求此双曲线的方程.2018年04月10日wan****.121的高中数学组卷参考答案一.解答题(共21小题)1.;2.;3.;4.;5.;6.;7.;8.;9.;10.;11.;12.;13.;14.;15.;16.;17.;18.;19.;20.;21.;。
2018年高考数学试题分类汇编之圆锥曲线解析版

FM = (0 , 2) , FN = (3 , 4) .
则 FM FN = (0 ,2 ) ? (3 , 4 ) =8 .
故选: D
x2 6.(全国卷一理)( 11)已知双曲线 C:
y2 1 ,O 为坐标原点, F 为 C 的右焦点,过 F 的直线与 C 的
3
两条渐近线的交点分别为 M、N.若 △ OMN 为直角三角形,则 |MN |=
2018 年高考数学试题分类汇编之圆锥曲线(解析版)
一、选择题
1.(浙江卷)( 2)双曲线 x2 3
2
y =1 的焦点坐标是
A . (- 2 ,0) ,( 2 , 0) B . (- 2, 0), (2, 0) C. (0, - 2 ), (0, 2 ) D. (0, - 2), (0, 2)
解:∵双曲线方程可得双曲线的焦点在
4)已知椭圆
C
:
x a2
y 4
1的一个焦点为 (2 ,0) ,则 C 的离心率为
1 A.
3
1 B.
2
2 C.
2
解:椭圆的一个焦点为( 2,0),可得 a2-4=4,解得 a
22 D.
3
2 2,
c c 2, e
a
2
.
2
故选: C
5.(全国卷一理)(
8)设抛物线
C: y2=4x 的焦点为
F,过点( –2, 0)且斜率为
故选: B
x2 7.(全国卷二文)( 6)双曲线 a2
y2 b2
1( a
0, b
0) 的离心率为
3 ,则其渐近线方程为
A . y 2x
B. y 3x
C. y
2x
2
(完整版)圆锥曲线高考真题

(完整版)圆锥曲线⾼考真题(1)求M 的⽅程(2)C ,D 为M 上的两点,若四边形ACBD 的对⾓线CD ⊥AB ,求四边形ACBD 的⾯积最⼤值.2.设1F ,2F 分别是椭圆()222210y x a b a b+=>>的左右焦点,M 是C 上⼀点且2MF 与x 轴垂直,直线1MF 与C 的另⼀个交点为N.(1)若直线MN 的斜率为34,求C 的离⼼率;(2)若直线MN 在y 轴上的截距为2,且15MN F N =,求a,b .3.已知椭圆C :,直线不过原点O 且不平⾏于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M .(1) 证明:直线OM 的斜率与的斜率的乘积为定值;(2)若过点(),延长线段OM 与C 交于点P ,四边形OAPB 能否平⾏四边⾏?若能,求此时的斜率,若不能,说明理由.4.已知抛物线C :22y x = 的焦点为F ,平⾏于x 轴的两条直线12,l l 分别交C 于A ,B 两点,交C 的准线于P ,Q 两点.(1)若F 在线段AB 上,R 是PQ 的中点,证明AR ∥FQ ;(2)若△PQF 的⾯积是△ABF 的⾯积的两倍,求AB 中点的轨迹⽅程.5.已知抛物线C :y 2=2x ,过点(2,0)的直线l 交C 与A ,B 两点,圆M 是以线段AB 为直径的圆.(1)证明:坐标原点O 在圆M 上;(2)设圆M 过点P (4,-2),求直线l 与圆M 的⽅程.6.已知斜率为k 的直线l 与椭圆22143x y C +=:交于A ,B 两点,线段AB 的中点为()()10M m m >,.(1)证明:12k <-;(2)设F 为C 的右焦点,P 为C 上⼀点,且FP FA FB ++=0u u u r u u u r u u u r .证明:FA u u u r,FP u u u r ,FB u u u r 成等差数列,并求该数列的公差.7.已知椭圆2222:1(0)x y C a b a b +=>>的离⼼率为,且经过点(0,1),圆22221:C x y a b +=+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
省高考数学圆锥曲线真题
04. 若椭圆122
22=+b
y a x (a >b >0)的左、右焦点分别为F 1、F 2,线段F 1F 2被抛物线y 2=2bx 的焦点分成5∶
3的两段,则此椭圆的离心率为
(A)
1716 (B)17174 (C)5
4 (D)552
05.过双曲线)0,0(122
22>>=-b a b
y a x 的左焦点且垂直于x 轴的直线与双曲线相交于M 、
N 两点,以MN 为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于 .
07. 已知双曲线22
221(0,0)x y a b a b -=>>的左、右焦点分别为12,F F ,P 是准线上一点,且
1212,||||4PF PF PF PF ab ⊥⋅=,则双曲线的离心率是
(A )2 (B )3 (C )2 (D )3
08.如图,AB 是平面α的斜线段...
,A 为斜足,若点P 在平面α运动,使得ABP △的面积为定值,则动点P 的轨迹是( )
A .圆
B .椭圆
C .一条直线
D .两条平行直线
09. 过双曲线
22
221(0,0)x y
a b a b
-=>>的右顶点A 作斜率为1-的直线,该直线与双曲线的两条渐近线的交点分别为,B C .若1
2
AB BC =,则双曲线的离心率是( )
A 2
B 351010. (13)设抛物线)0(22
>=p px y 的焦点为F ,点)2,0(A 。
若线段FA 的中点B 在抛物线上,则B 到该抛物线准线的距离为 。
11. 已知椭圆C 1:2222=1x y a b + (a >b >0)与双曲线C 2:22
14
y x -
=有公共的焦点,C 2的一条渐近线与以C 1的长轴为直径的圆相交于A ,B 两点, 若C 1恰好将线段AB 三等分,则( )
A .a 2
=
132 B .a 2=13 C .b 2=12
D .b 2
=2 11. 设F 1,F 2分别为椭圆2
213
x y +=的左、右焦点,点A ,B 在椭圆上.若125F A F B =,则点A 的坐标是________.
A B P α (第10题)
12. F 1,F 2分别是双曲线C :2
2
221x y a b
-=(a,b >0)的在左、右焦点,B 是虚轴的端点,直线F 1B 与C
的两条渐近线分别教育P,Q 两点,线段PQ 的垂直平分线与x 轴交与点M ,若|MF 2|=|F 1F 2|,则C 的离心
率是
A.
3
B 2
04. 已知双曲线的中心在原点,右顶点为A (1,0),点P 、Q 在双曲线的右支上,点M (m ,0)到直线AP 的距离为1,
(1)若直线AP 的斜率为k ,且|k |∈
], 数m 的取值围; (2)当m =2+1时,△APQ 的心恰好是点M ,求此双曲线的方程。
05. 如图,已知椭圆的中心在坐标原点,焦点F 1、F 2在x 轴上,长轴A 1A 2的长为4,左准线x l 与轴的交点为M ,|MA 1|∶|A 1F 1|=2∶1. (Ⅰ)求椭圆的方程;
(Ⅱ)若直线11),1|(|:l P x m x l 为>=上的动点,使21PF F ∠最大的点P 记为Q ,求点Q 的坐标(用m 表示).
06.如图,椭圆b
y a x 2
22+=1(a >b >0)与过点A (2,0)B(0,1)的直线有且只有一个公共点T ,且
椭圆的离心率e=
2
3
.(Ⅰ)求椭圆方程; (Ⅱ)设F 1、F 2分别为椭圆的左、右焦点,M 为线段AF 1的中点,求证:∠ATM=∠AF 1T.
07如图,直线y kx b =+与椭圆2
214
x y +=交于A 、B 两点,记ABC ∆的面积为S 。
(Ⅰ)求在0k =,01b <<的条件下,S 的最大值; (Ⅱ)当||2,1AB S ==时,求直线AB 的方程。
08. 已知曲线C 是到点1328P ⎛⎫- ⎪⎝⎭
,和到直线5
8
y =-
距离相等的点的轨迹. l 是过点(10)Q -,
的直线,M 是C 上(不在l 上)的动点;A B ,在l 上,MA l ⊥,MB x ⊥轴(如图).
(Ⅰ)求曲线C 的方程; (Ⅱ)求出直线l 的方程,使得2
QB
QA
为常数.
09已知椭圆1C :22
221(0)y x a b a b
+=>>的右顶点为(1,0)A ,过1C 的
焦点且垂直长轴的弦长为1. (I )求椭圆1C 的方程;
(II )设点P 在抛物线2C :2
()y x h h =+∈R 上,2C 在点P 处
的切线与1C 交于点,M N .当线段AP 的中点与MN 的中 点的横坐标相等时,求h 的最小值.
A
B O
Q
y
x
l
M (第20题)
10.已知1>m ,直线,02:2
=--m my x l 椭圆21222,,1:F F y m
x C =+ 分别为椭圆C 的左、右焦点. (I )当直线l 过右焦点F 2时,求直线l 的方程;
(II )设直线l 与椭圆C 交于A ,B 两点,21F AF ∆,21F BF ∆的重心
分别为G ,H.若原点O 在以线段GH 为直径的圆,数m 的取值围.
11. 已知抛物线C 1:x 2
=y ,圆C 2 :x 2
+(y -4)2
=1的圆心为点M .
(1)求点M 到抛物线C 1的准线的距离;
(2)已知点P 是抛物线C 1上一点(异于原点),过点P 作圆C 2的两条切线,交抛物线C 1于A ,B 两点,若过M ,P 两点的直线l 垂直于AB ,求直线l 的方程.
12. 如图,椭圆
22
22
:1(0)
x y
C a b
a b
+=>>的离心率为
1
2
,其左焦点到点P(2,1)的距离为10,
不过原点
....O的直线l与C相交于A,B两点,且线段AB被直线OP平分。
(Ⅰ)求椭圆C的方程;
(Ⅱ)求△APB面积取最大值时直线l的方程。
