关于城市宽箱梁横向分布系数的取值分析
新规范横向分布系数

关于新规范横向分布系数以及偏载系数的计算关于横向分布调整系数:一、进行桥梁的纵向计算时:a) 汽车荷载○1对于整体箱梁、整体板梁等整体结构其分布调整系数就是其所承受的汽车总列数,考虑纵横向折减、偏载后的修正值。
例如,对于一个跨度为230米的桥面4车道的整体箱梁验算时,其横向分布系数应为4 x 0.67(四车道的横向折减系数) x1.15(经计算而得的偏载系数)x0.97(大跨径的纵向折减系数) =2.990。
汽车的横向分布系数已经包含了汽车车道数的影响。
○2多片梁取一片梁计算时按桥工书中的几种算法计算即可,也可用程序自带的横向分布计算工具来算。
计算时中梁边梁分别建模计算,中梁取横向分布系数最大的那片中梁来建模计算。
b) 人群荷载○1对于整体箱梁、整体板梁等整体结构人群集度,人行道宽度,公路荷载填所建模型的人行道总宽度,横向分布系数填1 即可。
因为在桥博中人群效应= 人群集度x人行道宽度x人群横向分布调整系数。
城市荷载填所建模型的单侧人行道宽度,若为双侧人行道且宽度相等,横向分布系数填2,因为城市荷载的人群集度要根据人行道宽度计算。
○2多片梁取一片梁计算时人群集度按实际的填写,横向分布调整系数按求得的横向分布系数填写,一般算横向分布时,人行道宽度已经考虑了,所以人行道宽度填1。
c) 满人荷载○1对于整体箱梁、整体板梁等整体结构满人宽度填所建模型扣除所有护栏的宽度,横向分布调整系数填1。
与人群荷载不同,城市荷载不对满人的人群集度折减。
○2多片梁取一片梁计算时满人宽度填1,横向分布调整系数填求得的。
注:1、由于最终效应:人群效应= 人群集度x人行道宽度x人群横向分布调整系数。
满人效应= 人群集度x满人总宽度x满人横向分布调整系数。
所以,关于两项的一些参数,也并非一定按上述要求填写,只要保证几项参数乘积不变,也可按其他方式填写。
2 、新规范对满人、特载、特列没作要求。
所以程序对满人工况没做任何设计验算的处理,用户若需要对满人荷载进行验算的话,可以自定义组合。
小箱梁的恒载横向分配系数

小箱梁的恒载横向分配系数在桥梁工程中,小箱梁作为一种常见的结构形式,其恒载横向分配系数是设计过程中不可忽视的重要参数。
这一系数关系到桥梁结构的稳定性、安全性以及经济性。
本文将从专业角度出发,深入探讨小箱梁恒载横向分配系数的相关知识,力求为读者提供全面、准确的理解。
一、小箱梁的基本概念小箱梁,顾名思义,是一种截面形状类似于箱子的梁体结构。
它通常由上下翼缘板和腹板组成,形成一个闭合的截面。
这种结构形式具有较高的抗扭刚度和横向稳定性,因此在桥梁工程中得到广泛应用。
二、恒载横向分配系数的意义恒载横向分配系数是指在小箱梁桥梁中,恒载(如自重、桥面铺装等)在横向(即与桥梁轴线垂直的方向)上的分配比例。
这一系数的确定对于桥梁的结构设计至关重要,它直接影响到梁体的内力分布、变形情况以及支座的反力等。
三、影响恒载横向分配系数的因素1. 梁体截面形式:不同截面形式的小箱梁,其横向刚度和传力路径有所差异,从而导致恒载横向分配系数的变化。
2. 支座布置方式:支座的布置方式和间距对梁体的横向受力特性有显著影响,进而影响到恒载的横向分配。
3. 桥面铺装及附属设施:桥面铺装、护栏等附属设施的重量也是恒载的一部分,它们的布置和重量会影响到恒载的横向分配。
四、恒载横向分配系数的计算方法恒载横向分配系数的计算通常基于结构力学原理,采用有限元分析等方法进行。
在计算过程中,需要充分考虑梁体的截面特性、支座条件以及恒载的分布情况等因素。
具体的计算步骤和公式因工程实际情况而异,这里不再赘述。
五、工程实例分析以某实际桥梁工程为例,该工程采用小箱梁结构形式,通过详细的计算分析确定了恒载横向分配系数。
在设计过程中,工程师们充分考虑了梁体的截面形式、支座布置方式以及桥面铺装等附属设施的重量等因素,确保了桥梁结构的安全性和经济性。
这一实例为我们提供了宝贵的实践经验和参考依据。
六、总结与启示通过对小箱梁恒载横向分配系数的深入探讨,我们可以得出以下结论:首先,恒载横向分配系数是桥梁设计中不可忽视的重要参数;其次,该系数的确定受多种因素影响,需要综合考虑各种因素的作用;最后,在实际工程中,应根据具体情况采用合适的计算方法和分析手段来确定恒载横向分配系数。
宽幅装配式箱梁桥荷载横向分布系数计算

邬晓光等:宽幅装配式箱梁桥荷载横向分布系数计算
77
ofthewideassembledboxgirderbridgeareobtained.Takinganassemblyboxgirderbridgewitha widthspanratioof0.87inGuizhouasthebackground,thecalculationmethodsofGM method, ANSYSfiniteelementmethodandelasticallysupportednonthrustframemethodareadopted respectively.andcompareswiththeresultsofloadtestofrealbridge.Thecalculationresultsof equivalentelasticallysupportednonthrustframeareclosetothoseofloadtestmethod,andthe errorislessthan10%.ComparedwiththeresultsofGM methodandANSYSfiniteelement method,thecalculation resultsofequivalentelastically supported nonthrustframearemore accurate,convenientand efficient.Equivalentelastically braced nonthrustframe modelcan accuratelycalculatethetransverseloaddistributioncoefficientofassembledboxgirderbridgewith largewidthspanratio,andithasgoodapplicabilityforgeneralassembledboxgirderbridgewith widespanratioandmeetstheactualengineeringrequirements. Keywords:assembled bridge;load transversedistribution;energy analogy;elasticbraced non thrustframe;solidfiniteelement
宽箱梁的数值计算分析

宽箱梁的数值计算分析摘要:本文以某多箱室连续梁桥为例,讨论了宽箱梁的计算方法,并通有限元计算软件对比分析不同计算方法对宽箱梁计算结果的影响。
以该桥的分析计算分析结果为例,从而为宽箱梁的计算提供可靠的计算依据。
关键词: 宽箱梁;单梁法;刚性横梁法;梁格法;数值分析Abstract: Taking a more box chamber continuous girder bridge as an example, discusses the calculation method of wide box girder, and through a comparative analysis of the finite element calculation software of different calculation methods for wide box girder of the calculated results influence. With the analysis of the calculation results of the bridge as an example, the calculation of wide box girder so as to provide reliable calculation basis.Keywords: Wide box girder, Single-beam method; Rigid beam method; Grillage method; Numerical analysis1.前言近年来,为适应交通功能现代化的需求,我国高速、高等级公路与城市立交工程建设迅猛发展;并随着桥梁建设材料性能与施工工艺水平的不断进步,为了缓解城市交通的压力,桥梁道路不断地拓宽。
这就使得桥梁建设不得不跟着道路不断拓宽。
对于城市道路,由于美观的要求,桥梁形式一般以箱梁为主,箱梁主要的结构优点是:截面抗弯、抗扭刚度大,结构在施工和使用过程中都具有良好的稳定性,并能很好适应管线等公共设施的布置。
城市高架桥斜腹板宽箱梁横向框架计算分析

城市高架桥斜腹板宽箱梁横向框架计算分析摘要:结合某市政高架桥工程实例,建立斜腹板宽箱梁的横向框架模型计算分析,并与规范理论计算公式进行对比,为今后的桥梁设计提供一些参考。
关键词:斜腹板;宽箱梁;横向框架0引言随着城市交通的迅速发展,在城市中新建的高架桥越来越多。
为了满足不断增长的交通需求,新建的城市高架桥多采用双向6车道或双向8车道。
预应力混凝土连续箱梁广泛应用于城市高架桥,箱梁横桥向受力直接决定箱梁顶、底板的厚度与横向配筋情况。
本文根据某城市市政高架桥一联3x40m跨预应力混凝土连续箱梁,建立横向框架模型计算分析。
1工程概况本联高架桥桥跨布置为3X40m,单幅桥宽20m。
上部结构主梁采用等高度单箱三室预应力混凝土连续箱梁,按部分预应力A类构件设计,采用C50混凝土支架现浇施工。
主梁梁高采用2.2m;箱梁跨中顶板厚0.25m,底板厚0.22m,腹板厚0.45m,箱梁支点处顶板加厚至0.45m,底板加厚至0.42m,腹板加厚至0.8m。
2计算分析2.1横向框架计算模型横向框架模型采用桥梁博士V3.6.0版本进行建模计算。
模型采用杆系单元,沿箱梁纵桥向选取单位长度,汽车荷载在结构横向上动态加载。
在箱梁腹板中轴线处设置竖向弹性支撑与侧向约束,可将弹性支承近似为刚性支承,框架模型单元划分如下图所示。
图表1结构计算模型图2.2计算参数(1)道路等级:城市快速路。
(2)设计荷载:城-A级;设计安全等级:一级,结构的重要性系数:1.1。
(3)二期恒载:桥面铺装按10cm厚沥青铺装层考虑,荷载取值为2.4kN/m2;单侧防撞护栏荷载取值为13kN/m,单侧声屏障荷载取值5kN/m,单侧花槽荷载取值1kN/m,计算时考虑双侧设置防撞护栏及声屏障。
(4)均匀温差:整体升温26度,整体降温27度。
(5)非均匀温差:按规范,竖向日照正温差T1=+14℃,T2=5.5℃;竖向日照反温差T1=-7.0℃,T2=-2.75℃。
桥宽12.5米单箱单室框架分析横向分布系数计算(1)
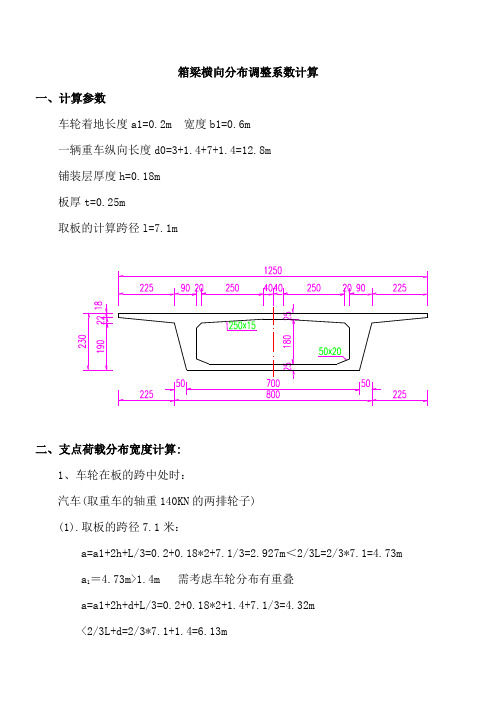
箱梁横向分布调整系数计算一、计算参数车轮着地长度a1=0.2m 宽度b1=0.6m一辆重车纵向长度d0=3+1.4+7+1.4=12.8m铺装层厚度h=0.18m板厚t=0.25m取板的计算跨径l=7.1m二、支点荷载分布宽度计算:1、车轮在板的跨中处时:汽车(取重车的轴重140KN的两排轮子)(1).取板的跨径7.1米:a=a1+2h+L/3=0.2+0.18*2+7.1/3=2.927m<2/3L=2/3*7.1=4.73ma1=4.73m>1.4m 需考虑车轮分布有重叠a=a1+2h+d+L/3=0.2+0.18*2+1.4+7.1/3=4.32m<2/3L+d=2/3*7.1+1.4=6.13m取a1=6.13m2、车轮在顶板的支承处时:a=a1+2h+t=0.2+0.18*2+0.25=0.81m3、车轮在顶板的支承附近时,距支点的距离为x时a=a1+2h+t+2x=0.2+0.18*2+0.25+2x =(0.81+2x)m 4、车轮在悬臂板的支承附近时,当c值不大于2.5m时: a=a1+2h+2c=0.2+0.18*2+2*(0.18+x)=(0.92+2x)m 荷载分布宽度图示:三、折线横向分布系数计算:1、板跨中处(1)q11*a=P,则:q11=P/a=140*2/2/6.13=22.82、板跨中距支点x处(1)0.81+2x=2*7.1/3=4.73时,x=1.96q11*a=P,则:q11=P/a=140*2/2/6.13=22.83、板跨中距支点0.275m处,分布宽度开始重叠(0.81+2x=1.4时,x=0.295)q2*a=P,则:q2=P/a=140/2/1.4=504、板支承处q3*a=P,则:q3=P/a=140/2/0.81=86.425、悬臂板根部,q4*a=P,则:q4=P/a=140/2/0.92=76.16、悬臂板距支点0.24米处,分布宽度开始有重叠(0.92+2x=1.4时,x=0.24)q5*a=P,则:q5=P/a=140/2/1.4=507、悬臂板距支点的距离为1.25米处时a=a1+2h +2c=0.92+2*1.25 =3.42 ma=3.42m>1.4m 需考虑车轮分布有重叠a=3.42+1.4=4.82m则:q6=P/a=140*2/2/4.82=29.05汽车加载有效区域 1 11.5 分布系数。
横向分布系数和偏载系数

一、 横向分布如图3—2—1a所示,梁桥的上部结构由承重结构(①~④号主梁)及传力结构(横隔梁、行车道板)两大部分组成,各片主梁靠横隔梁和行车道板连成空间整体结构,当桥上作用荷载(桥面板上作用2个车轴,前轴轴重为P1,后轴轴重为P2)时,各片主梁共同参与工作,形成了各片主梁之间的内力分布。
在计算恒载时,除主梁的自重外,一般将桥面铺装、人行道、栏杆等的重量近似平均分配给各片主梁,即计算出桥面铺装、人行道、栏杆等的总重量除以梁的片数(本例4片梁),得到每片主梁承担的桥面铺装、人行道、栏杆的重量。
由于人行道、栏杆等构件一般位于边梁上(①、④号主梁),精确计算时,也可考虑它们的重量在各梁间的分布,即中梁(②、③号主梁)也分担一部分人行道、栏杆的重量。
在计算活载时,需要考虑活载在各片主梁间的分布。
《标准》规定,车道荷载的横向分布系数应按设计车道数布置车辆荷载进行计算。
车辆荷载的横向布置如图3—2—1c所示。
对于车道荷载,最外车轮距人行道缘石之距不得小于0.5m,车道荷载的横向轮距为1.8m,两列车道荷载车轮的横向间距不得小于1.3m。
如图3—2—1b所示,在车道荷载的作用下,①号边梁所分担的荷载,也就是说,①号边梁所分担的荷载R1为轴重P1的。
若将第i号梁所承担的力R i表示为系数m i与轴重P的乘积(R i=m i×P),则m i称为第i号梁的荷载横向分布系数。
由此,1号梁的横向分布系数。
荷载所引起的各片主梁的内力大小(横向分布)与桥梁的构造特点、荷载的作用位置有关,因此求解荷载作用下各主梁的内力是一个空间问题,目前广泛采用的方法是将复杂的空间问题转化为平面问题。
本节将着重介绍几种横向分布系数的计算方法。
二、杠杆法基本原理:杠杆法忽略了主梁之间横向结构的联系作用,即假设桥面板在主梁上断开,把桥面板看作沿横向支承在主梁上的简支梁或悬臂梁。
如图3—2—1b所示,由于杠杆法忽略了主梁之间横向结构的联系作用,当桥上作用车道荷载时,左边的轮重P1/2仅传递给1号和2号梁,右边的轮重P1/2传递给2号梁和3号梁。
横向分布系数和偏载系数

一、 横向分布如图3—2—1a所示,梁桥的上部结构由承重结构(①~④号主梁)及传力结构(横隔梁、行车道板)两大部分组成,各片主梁靠横隔梁和行车道板连成空间整体结构,当桥上作用荷载(桥面板上作用2个车轴,前轴轴重为P1,后轴轴重为P2)时,各片主梁共同参与工作,形成了各片主梁之间的内力分布。
在计算恒载时,除主梁的自重外,一般将桥面铺装、人行道、栏杆等的重量近似平均分配给各片主梁,即计算出桥面铺装、人行道、栏杆等的总重量除以梁的片数(本例4片梁),得到每片主梁承担的桥面铺装、人行道、栏杆的重量。
由于人行道、栏杆等构件一般位于边梁上(①、④号主梁),精确计算时,也可考虑它们的重量在各梁间的分布,即中梁(②、③号主梁)也分担一部分人行道、栏杆的重量。
在计算活载时,需要考虑活载在各片主梁间的分布。
《标准》规定,车道荷载的横向分布系数应按设计车道数布置车辆荷载进行计算。
车辆荷载的横向布置如图3—2—1c所示。
对于车道荷载,最外车轮距人行道缘石之距不得小于0.5m,车道荷载的横向轮距为1.8m,两列车道荷载车轮的横向间距不得小于1.3m。
如图3—2—1b所示,在车道荷载的作用下,①号边梁所分担的荷载,也就是说,①号边梁所分担的荷载R1为轴重P1的。
若将第i号梁所承担的力R i表示为系数m i与轴重P的乘积(R i=m i×P),则m i称为第i号梁的荷载横向分布系数。
由此,1号梁的横向分布系数。
荷载所引起的各片主梁的内力大小(横向分布)与桥梁的构造特点、荷载的作用位置有关,因此求解荷载作用下各主梁的内力是一个空间问题,目前广泛采用的方法是将复杂的空间问题转化为平面问题。
本节将着重介绍几种横向分布系数的计算方法。
二、杠杆法基本原理:杠杆法忽略了主梁之间横向结构的联系作用,即假设桥面板在主梁上断开,把桥面板看作沿横向支承在主梁上的简支梁或悬臂梁。
如图3—2—1b所示,由于杠杆法忽略了主梁之间横向结构的联系作用,当桥上作用车道荷载时,左边的轮重P1/2仅传递给1号和2号梁,右边的轮重P1/2传递给2号梁和3号梁。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于城市宽箱梁横向分布系数的取值分析
摘要:变截面连续箱梁桥、连续刚架桥的设计,一般均将桥跨结构视作弹性梁元,采用平面杆系程序计算。
荷载偏心用增大系数法考虑,增大系数的取值对于宽跨比很大的城市桥梁具有很大的任意性。
本文以某实桥为背景,采用ANSYS 结构分析通用程序计算了多个特征断面各腹板的横向分布系数。
据此,对照了按荷载横向分布简化算法的计算结果,所得出的结论,可为同类工程设计提供参考。
关键词:宽箱梁;横向分布;空间分析;简化算法
Abstract: The variable cross section continuous box girder bridges, continuous rigid frame bridge design, generally will bridge structure as an elastic beam element, the plane pole-system program calculation. Eccentric load by increasing the coefficient method to consider, increase coefficient for width span ratio of big city bridges with large arbitrariness. Taking a bridge as the background, using the ANSYS general structural analysis program calculates the multiple features of the web section of transverse distribution coefficient. Accordingly, controlled by lateral load distribution algorithm of calculation results, the conclusion, for similar engineering design to provide a reference.
Key words: wide box beam; transverse distribution; spatial analysis; simplified algorithm
1概述
实桥位于某高速公路交点,为三跨(42m+80m+42m)预应力混凝土上承式
拱梁组合体系桥。
主梁两侧边墩处各有一片端横梁,宽1.3m,主墩中心及中跨跨中两侧各有两片横梁,宽0.4m,边跨及中跨在主拱与主梁的结合处均设置横梁,宽0.6m。
主梁采用单箱三室断面,箱梁顶宽25.5m、底宽17.3m,腹板中距为5.75m 及5.8m,两边悬臂4.1m,跨中梁高2.0m。
主拱腿采用钢筋混凝土单箱三室断面,宽17.3m,高1.4m,腹板中距与主梁相同。
副拱采用实心矩形断面,宽17.3m,高0.6m。
为保持沪杭高速公路车流畅通,主桥采用中心转体施工。
主桥总体及主梁断面见图1。
图1主桥总体及主梁断面示意图单位:cm
2ANSYS板壳元空间分析
由于主桥为对称结构,计算模型取1/2模型,模型单元为SHELL63弹性壳单元,
共有574个单
元、545个节点,如图2所示。
支承条件:主墩固接,边墩为竖向约束,跨中为对称约束。
首先获得桥面单元各节点的位移影响面,由位移影响面推算箱梁各腹板的荷载分布。
分析中提取了9个断面来分析荷载横向分布,这些断面如图2中以SEC1~SEC9表示。
分析中发现:SEC4,SEC6与SEC2荷载横向分布特征相似,SEC7与SEC3荷载横向分布特征相似,SEC8的荷载横向分布特征介于SEC6与SEC9之间。
限于篇幅仅将SEC1~SEC3,SEC5及SEC9特征断面边、中腹板的荷载横向分布影响线列如图3示。
由图3可知:SEC1断面为支点断面,荷载横向分布呈现杠杆原理;SEC2断面由于主拱的支撑作用纵向跨径减小,宽跨比为25.5/20=1.275/1,箱梁断面各腹板偏载明显,荷载横向界于杠杆分布与刚性横梁分布之间;SEC3断面位于边跨有强大横梁(高3.78m)的跨中,荷载横向分布呈现刚性横梁原理;SEC5断面由于副拱的支撑作用纵向跨径明显减小,宽跨比达25.5/5.8=4.4/1,荷载横向分布呈现杠杆原理;SEC9断面位于中跨跨中,宽跨比25.5/40.36=0.63/1,箱梁断面各腹板呈现共同受力特性,荷载横向分布近似刚性横梁法。
按双向六车道、城-A级车道荷载,对上述各断面边、中腹板的荷载横向分布影响线进行动态规划法加载,获得各腹板的荷载横向分布系数值见表1。
表1 更特征断面横向分布系数值
图2计算模型
3与简化计算方法的比较
3·1与一次刚度换算法的比较一次刚度换算法[1],即把非简支梁体系的某一桥跨变换为跨度相同的等刚度常截面简支梁。
为了简化分析方便,将图2中的各断面几何特征值列成表2。
首先应用一次刚度换算法原理得到SEC1~SEC9计算断面的换算惯矩,其次将箱梁全断面划分为四片刚度相等的I梁,最后应用考虑抗扭的弹性支承连续梁法[1]得到SEC1~SEC3,SEC5及SEC9特征断面各I梁(即边、中腹板)荷载横向分布影响线,如图4所示。
对上述各断面边、中腹板的荷载横向分布影响线进行动态规划法加载,获得各腹板的荷载横向分布系数值,分别与增大系数法、ANSYS板壳元分析法比较见表3。
表2 各断面几何特征值
图4各特征断面荷载横向分布影响线
表3
3·2计算结果比较
(1) ANSYS板壳元空间分析法,通过对整个结构进行模拟,能比较精确地反映各断面的荷载
横向分布特性:支点断面及宽跨比较大断面SEC5近似杠杆分布、跨中断面SEC3及SEC9近似刚性
横梁法。
但必须借助有限元通用程序来完成。
因此,作为校核简化算法的计算结果是有效的,但不
便于工程应用。
(2)一次刚度换算法,通过等刚度思想将超静定变截面结构等效为简支常截面结构。
与图3比较可知图4中:SEC1支点断面按刚性横梁分布与实际杠杆分布不符,横向分布系数边腹板偏小24.5%,中腹板偏小16.9%;SEC3断面影响线反映的横向结构刚度比实际偏小,而SEC9反映的比实际偏大;荷载作用于各断面悬臂端时,对边、中腹板荷载分布的影响未得到如实反映。
(3)增大系数法[1],按现行考虑活载偏载取增大系数1.15,则边、中腹板的横向分布系数按六车道控制均为0.9488(6×0.55×1.15÷4=0.9488)。
由表3可知:增大系数法所取横向分布系数值与ANSYS空间分析法值偏差因不同断面、不同腹板而不同,支点断面(SEC1)及宽跨比很大的断面(SEC5)较大,跨中断面(SEC3,SEC9)及宽跨比较小的断面(SEC2)较小,中腹板偏差较小而边腹板偏差较大(44%)。
4结语
一次刚度换算法能较简便地估算结构纵向各断面的荷载横向分布,跨中断面可根据等效刚度按考虑抗扭的弹支连梁法计算;但在支点断面刚度较难精确等效,可采用实际断面刚度按杠杆法计算荷载横向分布;建议在用平面杆系程序分析本实桥相似的宽箱梁结构时,采用沿桥跨变化的活载横向分布系数,以使分析结果与
实际相符及确保结构安全、经济;由于本文结论仅是在对某实桥进行分析的基础上得出,其它桥型可供参考。
参考文献
[1]胡肇滋.桥跨结构简化分析———荷载横向分布·北京:人民交通出版社,1996。
