反比例函数与四边形经典例题与练习
反比例函数与平行四边形

反比例函数与平行四边形例2、(08威海市)如图3-1,点A (m ,m +1),B (m +3,m -1)都在反比例函数x k y =的图象上. (1)求m ,k 的值;(2)如果M 为x 轴上一点,N 为y 轴上一点, 以点A ,B ,M ,N 为顶点的四边形是平行四边形,试求直线MN 的函数表达式. 分析:点A (m ,m +1),B (m +3,m -1)都在反比例函数xk y =的图象上,所以有)1)(3()1(-+=+m m m m k =,解得12,3==k m 。
于是点A(3, 4), B(6, 2), 过A 、B两点分别作X 、Y 轴的垂线,垂足分别是M 、N,如图3-2,显然AM 和BN 互相平分,因此四边形ABMN 是平行四边形。
这个平行四边形恰是符合题意的四边形。
因为M (3,0),N (0,2),根据待定系数法可求出直线MN 的解析式为232+-=x y . 注意应用反比例函数的另一个表达形式)0(≠=k k xy 。
根据点的坐标在函数图象上,则点的坐标满足函数解析式。
如果直接把点的坐标代入解析式x k y =中,有m k m =+1和31+=-m k m ,由此求m 和k 容易出错。
反比例函数的另一个表达形式是)0(≠=k k xy 即两个变量的积一定。
据此得)1)(3()1(-+=+m m m m k =,求m ,k 的值就比较简单。
(2)以点A ,B ,M ,N 为顶点的四边形是平行四边形,同学们往往盲目的在坐标轴上寻找点M 和点N, 当我们由m 的值写出了点A 点B的坐标A(3, 4)、B(6, 2), 并且在坐标轴上标出对应的坐标时,不难发现AM 和BN 互相平分,由此M 和N 点的确定使人大有“踏破铁鞋无处觅,得来全不费工夫”的感觉,真爽。
点评: 本例题把反比例函数图象与性质与一元二次方程、平行四边形性质判定结合。
64 反比例函数中的平行四边形问题

反比例函数中的平行四边形问题1、如图,在平面直角坐标系中,反比例函数y=的图象过等边三角形BOC的顶点B,OC=2,点A在反比例函数图象上,连接AC、AO.(1)求反比例函数解析式;(2)若四边形ACBO的面积为3,求点A的坐标.解:(1)作BD⊥OC于D,如图,∵△BOC为等边三角形,∴OD=CD=OC=1,∴BD=OD=,∴B(﹣1,﹣),把B(﹣1,﹣)代入y=得k=﹣1×(﹣)=,∴反比例函数解析式为y=;(2)设A(t,),∵四边形ACBO的面积为3,∴×2×+×2×=3,解得t=,∴A点坐标为(,2).2、如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A、B在x轴上,点C、D在第二象限,点M是BC中点.已知AB=6,AD=8,∠DAB=60°,点B的坐标为(﹣6,0).(1)求点D和点M的坐标;(2)如图①,将▱ABCD沿着x轴向右平移a个单位长度,点D的对应点D′和点M的对应点M′恰好在反比例函数y=(x>0)的图象上,请求出a的值以及这个反比例函数的表达式;(3)如图②,在(2)的条件下,过点M,M′作直线l,点P是直线l上的动点,点Q是平面内任意一点,若以B′,C′,P、Q为顶点的四边形是矩形,请直接写出所有满足条件的点Q的坐标.解:(1)∵AB=6,点B的坐标为(﹣6,0),∴点A(﹣12,0),如图1,过点D作DE⊥x轴于点D,则ED=AD sin∠DAB=8×=4,同理AE=4,故点D(﹣8,4),则点C(﹣2,4),由中点公式得,点M(﹣4,2);(2)图象向右平移了a个单位,则点D′(a﹣8,4)、点M′(a﹣4,2),∵点D′M′都在函数上,∴(a﹣8)×4=(a﹣4)×2,解得:a=12,则k=(12﹣8)×4=16,故反比例函数的表达式为=;(3)由(2)知,点M′的坐标为(8,2),点B′、C′的坐标分别为(6,0)、(10,4),设点P(m,2),点Q(s,t);①当B′C′是矩形的边时,如图2,求解的矩形为矩形B′C′PQ和矩形B′C′Q′P′,过点C′作C′H⊥l交于点H,C′H=4﹣2=2,直线B′C′的倾斜角为60°,则∠M′PC′=30°,PH=C′H÷tan∠M′PC′=2=6,故点P的坐标为(16,2),由题意得:点P、Q′关于点C′对称,由中点公式得,点Q的坐标为(12,﹣4);同理点Q、Q′关于点M′对称,由中点公式得,点Q′(4,6);故点Q的坐标为:(12,﹣4)或(4,6);②当B′C′是矩形的对角线时,∵B′C′的中点即为PQ的中点,且PQ=B′C′,∴,解得:,,故点Q的坐标为(4,2)或(12,2);综上,点Q的坐标为:(12,﹣4)或(4,6)或(4,2)或(12,2).3、如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,4).反比例函数y=(x>0)的图象经过点D,点P是一次函数y=kx+4﹣4k(k≠0)的图象与该反比例函数图象的一个公共点.(1)求反比例函数的解析式;(2)通过计算,说明一次函数y=kx+4﹣4k(k≠0)的图象一定过点C;(3)对于一次函数y=kx+4﹣4k(k≠0),当随x的增大而增大时,确定点P横坐标的取值范围(不必写过程).解:(1)∵四边形ABCD是平行四边形,∴AD=BC,∵B(4,1),C(4,4),∴BC⊥x轴,AD=BC=3,而A点坐标为(1,0),∴点D的坐标为(1,3).∵反比例函数y=(x>0)的函数图象经过点D(1,3),∴3=,∴m=3,∴反比例函数的解析式为y=;(2)当x=4时,y=kx+4﹣4k=4k+4﹣4k=4,∴一次函数y=kx+4﹣4k(k≠0)的图象一定过点C;(3)设点P的横坐标为a,∵一次函数y=kx+4﹣4k(k≠0)过C点,并且y随x的增大而增大时,∴k>0,P点的纵坐标要小于4,横坐标大于4,当纵坐标小于4时,∵y=,∴<4,解得:a>,则a的范围为a>1或a<.4、小亮在研究矩形的面积S与矩形的边长x,y之间的关系时,得到如表数据:x0.51 1.5234612y126■32 1.510.5结果发现一个数据被墨水涂黑了,(1)被墨水涂黑的数据为;(2)y与x的函数关系式为,且y随x的增大而;(3)如图是小亮画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形OABC的面积记为S1,矩形ODEF的面积记为S2,请判断S1与S2的大小关系,并说明理由;(4)在(3)的条件下,DE交BC于点G,反比例函数y=的图象经过点G交AB于点H,连接OG、OH,则四边形OGBH的面积为.解:(1)从表格可以看出xy=6,∴墨水盖住的数据是6÷1.5=4;故答案为4;(2)由xy=6,得到y=,y随x的增大而减少;故答案为y=;减少;(3)S1=OA•OC=k=6,S2=OD•OF=k=6,∴S1=S2;=OA•OB=6,S△OCG=OD•OG=×2=1,S△OCG=OA•OH=×2=1,(4)∵S四边形OCBA=S四边形OCBA﹣S△OCG﹣S△OAH=6﹣1﹣1=4;∴S四边形OGBH故答案为4;5、如图,在平面直角坐标系中,四边形ABCD是平行四边形,点A、B在x轴上,点C、D在第二象限,点M是BC中点.已知AB=6,AD=8,∠DAB=60°,点B的坐标为(﹣6,0).(1)求点D和点M的坐标;(2)如图①,将▱ABCD沿着x轴向右平移a个单位长度,点D的对应点D′和点M的对应点M′恰好在反比例函数y=(x>0)的图象上,请求出a的值以及这个反比例函数的表达式;(3)如图②,在(2)的条件下,过点M,M′作直线l,点P是直线l上的动点,点Q是平面内任意一点,若以B′,C′,P、Q为顶点的四边形是矩形,请直接写出所有满足条件的点Q的坐标.解:(1)∵AB=6,点B的坐标为(﹣6,0),∴点A(﹣12,0),如图1,过点D作DE⊥x轴于点D,则ED=AD sin∠DAB=8×=4,同理AE=4,故点D(﹣8,4),则点C(﹣2,4),由中点公式得,点M(﹣4,2);(2)图象向右平移了a个单位,则点D′(a﹣8,4)、点M′(a﹣4,2),∵点D′M′都在函数上,∴(a﹣8)×4=(a﹣4)×2,解得:a=12,则k=(12﹣8)×4=16,故反比例函数的表达式为=;(3)由(2)知,点M ′的坐标为(8,2),点B ′、C ′的坐标分别为(6,0)、(10,4),设点P (m ,2),点Q (s ,t );①当B ′C ′是矩形的边时,如图2,求解的矩形为矩形B ′C ′PQ 和矩形B ′C ′Q ′P ′,过点C ′作C ′H ⊥l 交于点H ,C ′H =4﹣2=2,直线B ′C ′的倾斜角为60°,则∠M ′PC ′=30°,PH =C ′H ÷tan ∠M ′PC ′=2=6,故点P 的坐标为(16,2),由题意得:点P 、Q ′关于点C ′对称,由中点公式得,点Q 的坐标为(12,﹣4);同理点Q 、Q ′关于点M ′对称,由中点公式得,点Q ′(4,6);故点Q 的坐标为:(12,﹣4)或(4,6);②当B ′C ′是矩形的对角线时,∵B ′C ′的中点即为PQ 的中点,且PQ =B ′C ′,∴,解得:,,故点Q 的坐标为(4,2)或(12,2);综上,点Q的坐标为:(12,﹣4)或(4,6)或(4,2)或(12,2).6、已知,在直角坐标系中,平行四边形OABC的顶点A,C坐标分别为A(2,0),C(﹣1,2),反比例函数y=的图象经过点B(m≠0)(1)求出反比例函数的解析式(2)将▱OABC沿着x轴翻折,点C落在点D处,作出点D并判断点D是否在反比例函数y=的图象上(3)在x轴是否存在一点P使△OCP为等腰三角形?若存在,写出点P的坐标;若不存在,请说明理由.解:(1)分别过点C、B作x轴的垂线,垂足分别为:E、F,∵四边形OABC为平行四边形,则∠COE=∠BAF,CO=AB,∴Rt△COE≌Rt△BAF,∴AF=OE=1,故点B(1,2),故m=2,则反比例函数表达式为:y=;(2)翻折后点D的坐标为:(﹣1,﹣2),∵(﹣1)•(﹣2)=2,∴D在反比例函数y=的图象上;(3)当OP=OC时,点P(,0);当OC=PC时,点P(﹣2,0);当OP=PC时,设点P(m,0),则m2+(m+1)2+4,解得:m=﹣2.5;综上,点P的坐标为:(,0)或(﹣2,0)或(﹣2.5,0).7、如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,4).反比例函数y=(x>0)的图象经过点D,点P是一次函数y=kx+4﹣4k(k≠0)的图象与该反比例函数图象的一个公共点.(1)求反比例函数的解析式;(2)通过计算,说明一次函数y=kx+4﹣4k(k≠0)的图象一定过点C;(3)对于一次函数y=kx+4﹣4k(k≠0),当随x的增大而增大时,确定点P横坐标的取值范围(不必写过程).解:(1)∵四边形ABCD是平行四边形,∴AD=BC,∵B(4,1),C(4,4),∴BC⊥x轴,AD=BC=3,而A点坐标为(1,0),∴点D的坐标为(1,3).∵反比例函数y=(x>0)的函数图象经过点D(1,3),∴3=,∴m=3,∴反比例函数的解析式为y=;(2)当x=4时,y=kx+4﹣4k=4k+4﹣4k=4,∴一次函数y=kx+4﹣4k(k≠0)的图象一定过点C;(3)设点P的横坐标为a,∵一次函数y=kx+4﹣4k(k≠0)过C点,并且y随x的增大而增大时,∴k>0,P点的纵坐标要小于4,横坐标大于4,当纵坐标小于4时,∵y=,∴<4,解得:a>,则a的范围为a>1或a<.8、如图,A为反比例函数y=(其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA,AB,且OA=AB.过点B作BC⊥OB,交反比例函数y=(其中x>0)的图象于点C,连接OC交AB于点D,则的值为.解:过点A作AH⊥x轴,垂足为H,AH交OC于点M,如图,∵OA=AB,AH⊥OB,∴OH=BH=OB,设OH=BH=a,则A(a,),C(2a,),∵AH∥BC,∴MH=BC=,∴AM=AH﹣MH=﹣=,∵AM∥BC,∴△ADM∽△BDC,∴==.9、如图,点A(1,3)为双曲线上的一点,连接AO并延长与双曲线在第三象限交于点B,M为y轴正半轴上一点,连接MA并延长与双曲线交于点N,连接BM、BN,已知△MBN的面积为,则点N 的坐标为.解:连接ON,∵点A(1,3)为双曲线上,∴k=3,即:y=;由双曲线的对称性可知:OA=OB,=S△MAO,S△NBO=S△NAO,∴S△MBO=S△BMN=,∴S△MON设点M(0,m),N(n,),∴mn=,即,mn=,①设直线AM的关系式为y=kx+b,将M(0,m)A(1,3)代入得,b=m,k=3﹣m,∴直线AM的关系式为y=(3﹣m)x+m,把N(n,)代入得,=(3﹣m)×n+m,②由①和②解得,n=,当n=时,=,∴N(,),故答案为:(,).10、如图,等边△OAB的边AB与y轴交于点C,点A是反比例函数y=(x>0)的图象上一点,且BC=2AC,则等边△OAB的边长为.解:设点A(a,),等边三角形的边长为b,过点A作x轴的平行线交y轴于点M,过点B作y轴的平行线交AM的延长线于点E,过点O作ON⊥AB 与点N,则AN=AB=b,ON=b,∵AN=b,AC=b,∴CN=AN﹣AC=b,∵CM∥BE,∴=,即=,则AE=3a,∵∠OCN=∠ACM=∠ABE,∴△ONC∽△AEB,∴=,即=,解得:BE=a,AB2=AE2+BE2,则b2=9a2+a2=a2,∵点A(a,),∴AB2=a2+=a2,解得:a2=3,b=2,故答案为2.11、如图,直线y=mx﹣1交y轴于点B,交x轴于点C,以BC为边的正方形ABCD的顶点A(﹣1,a)在双曲线y=﹣(x<0)上,D点在双曲线y=(x>0)上,则k的值为.解:∵A(﹣1,a)在双曲线y=﹣(x<0)上,∴a=2,∴A(﹣1,2),∵点B在直线y=mx﹣1上,∴B(0,﹣1),∴AB==,∵四边形ABCD是正方形,∴BC=AB=,设C(n,0),∴=,∴n=﹣3(舍)或n=3,∴C(3,0),∴点B向右平移3个单位,再向上平移1个单位,∴点D是点A向右平移3个单位,再向上平移1个单位,∴点D(2,3),∵D点在双曲线y=(x>0)上,∴k=2×3=6,故答案为:6.12、如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转α度,tanα=,交反比例函数图象于点C,则点C的坐标为.解:如图,过B作BF⊥AC于F,过F作FD⊥y轴于D,过A作AE⊥DF于E,则△AEF∽△FDB,∵tanα=,∴==,∴设BD=a,则EF=2a,∵点A(2,3)和点B(0,2),∴DF=2﹣2a,OD=OB﹣BD=2﹣a,∴AE=2DF=4﹣4a,∵AE+OD=3,∴4﹣4a+2﹣a=3,解得a=,∴F(,),设直线AF的解析式为y=kx+b,则,解得,∴y=x+,∵点A在反比例函数y=的图象上,∴y=,解方程组,可得或,∴C(﹣,﹣),故答案为(﹣,﹣).13、如图,点A是双曲线y=﹣在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动点C的位置也不断变化,但点C始终在双曲线y=上运动,则k的值为.解:作AD⊥x轴于D,CE⊥x轴于E,连接OC,如图,∵AB过原点,∴点A与点B关于原点对称,∴OA=OB,∵△CAB为等腰三角形,∴OC⊥AB,∴∠ACB=120°,∴∠CAB=30°,∴OA=OC,∵∠AOD+∠COE=90°,∠AOD+∠OAD=90°,∴∠OAD=∠COE,∴Rt△AOD∽Rt△OCE,∴=()2=()2=3,=×|﹣6|=3,而S△OAD=1,∴S△OCE即|k|=1,而k>0,∴k=2.14、以矩形OABC的顶点O为坐标原点建立平面直角坐标系,使点A、C分别在x、y轴的正半轴上,双曲线y=(x>0)的图象经过BC的中点D,且与AB交于点E,过OC边上一点F,把△BCF沿直线BF 翻折,使点C落在矩形内部的一点C′处,且C′E∥BC,若点C′的坐标为(2,4),则tan∠CBF的值为.解:连接OD、OE.设BC=BC′=m,则EC′=m﹣2.∵CD=BD,==S矩形ABCD,∴S△CDO==S△CDO=S矩形ABCD,∵S△AOE∴AE=EB,∵C′(2,4),∴AE=EB=4,在Rt△BEC′中,∵BC′2=BE2+EC′2,∴m2=42+(m﹣2)2,∴m=5,∴E(5,4),∴B(5,8),则BC=5,延长EC′交y轴于G,则EG⊥y轴,∴C′G=2,CG=4,∴在Rt△FGC′中,C′F2=C′G2+FG2,即(4﹣FG)2=22+FG2,∴FG=,∴CF=4﹣=,∴tan∠CBF===.故答案是:.15、如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数y=(k≠0)的图象过点C,则该反比例函数的表达式为;解:如图,过点C作CE⊥y轴于E,在正方形ABCD中,AB=BC,∠ABC=90°,∴∠ABO+∠CBE=90°,∵∠OAB+∠ABO=90°,∴∠OAB=∠CBE,∵点A的坐标为(﹣4,0),∴OA=4,∵AB=5,∴OB==3,在△ABO和△BCE中,,∴△ABO≌△BCE(AAS),∴OA=BE=4,CE=OB=3,∴OE=BE﹣OB=4﹣3=1,∴点C的坐标为(3,1),∵反比例函数y=(k≠0)的图象过点C,∴k=xy=3×1=3,∴反比例函数的表达式为y=.故答案为:y=.16、如图,点A在双曲线y=的第一象限的那一支上,AB垂直于y轴与点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为.解:连DC,如图,∵AE=3EC,△ADE的面积为3,∴△CDE的面积为1,∴△ADC的面积为4,设A点坐标为(a,b),则AB=a,OC=2AB=2a,而点D为OB的中点,∴BD=OD=b,=S△ABD+S△ADC+S△ODC,∵S梯形OBAC∴(a+2a)×b=a×b+4+×2a×b,∴ab=,把A(a,b)代入双曲线y=,∴k=ab=.故答案为:.17、如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y=交于E,F两点,若AB=2EF,则k的值是.解:作FH⊥x轴,EC⊥y轴,FH与EC交于D,如图,由直线y=﹣x+2可知A点坐标为(2,0),B点坐标为(0,2),OA=OB=2,∴△AOB为等腰直角三角形,∴AB=2,∴EF=AB=,∴△DEF为等腰直角三角形,∴FD=DE=EF=1,设F点横坐标为t,代入y=﹣x+2,则纵坐标是﹣t+2,则F的坐标是:(t,﹣t+2),E点坐标为(t+1,﹣t+1),∴t(﹣t+2)=(t+1)•(﹣t+1),解得t=,∴E点坐标为(,),∴k=×=.故答案为.。
2023年中考数学高频考点突破——反比例函数与四边形综合

2023年中考数学高频考点突破——反比例函数与四边形综合1.如图,已知反比例函数y=(x>0)的图象与一次函数y=﹣x+b的图象分别交于A(1,3)、B两点.(1)求m、b的值;(2)若点M是反比例函数图象上的一动点,直线MC⊥x轴于C,交直线AB于点N,MD⊥y轴于D,NE⊥y轴于E,设四边形MDOC、NEOC的面积分别为S1、S2,S=S2﹣S1,求S的最大值.2.已知:如图所示,正比例函数y=ax的图象与反比例函数y=的图象交于点A(3,2).(1)试确定上述正比例函数和反比例函数的表达式;(2)M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x 轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,求M点坐标.3.如图,四边形OABC是面积为4的正方形,函数(x>0)的图象经过点B.(1)求k的值;(2)将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′、NA′BC.设线段MC′、NA′分别与函数(x>0)的图象交于点E、F,求线段EF所在直线的解析式.4.如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点Q的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.5.如图,已知点A在函数(x>0)的图象上,点B在函数(x<0)的图象上,点C在函数(x<0)的图象上,且AB∥x轴,BC∥y轴,四边形ABCD是以AB、BC为一组邻边的矩形.(1)若点A的坐标为(,2),求点D的坐标;(2)若点A在函数(x>0)上移动,矩形ABCD的面积是否变化?如果不变,求出其面积;(3)若矩形ABCD四个顶点A、B、C、D分别在>0,x>0),<0,x<0),>0,x<0),<0,x>0)上,请直接写出k1、k2、k3、k4满足的数量关系式.6.如图,一次函数y=x﹣1的图象与反比例函数y=(x>0)的图象交于点B(3,a),与x轴交于点A.点C在反比例函数y=(x>0)的图象上的一点,CD⊥x轴,垂足为D,CD与AB交于点E,OA=AD.(1)求a,k的值;(2)若点P为x轴上的一点,求当PB+PC最小时,点P的坐标;(3)F是平面内一点,是否存在点F使得以A、B、C、F为顶点的四边形是平行四边形?若存在,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.7.如图,已知,A(0,4),B(﹣3,0),C(2,0),过A作y轴的垂线交反比例函数的图象于点D,连接CD,AB∥CD.(1)证明:四边形ABCD为菱形;(2)求此反比例函数的解析式;(3)求sin∠DAC的值.8.如图,直线y=x与双曲线y=(k≠0)交于A,B两点,点A的坐标为(m,﹣3),点C是双曲线第一象限分支上的一点,连接BC并延长交x轴于点D,且BC=2CD.(1)求k的值并直接写出点B的坐标;(2)点G是y轴上的动点,连接GB,GC,求GB+GC的最小值;(3)P是x轴上的点,Q是平面内一点,是否存在点P,Q,使得A,B,P,Q为顶点的四边形是矩形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.9.如图,在△AOB中,∠OAB=90°,AO=AB,OB=2.一次函数交y轴于点C(0,﹣1),交反比例函数于A、D两点.(1)求一次函数和反比例函数的解析式;(2)求△OAD的面积;(3)问:在直角坐标系中,是否存在一点P,使以O,A,D,P为顶点的四边形是平行四边形?若存在,直接写出点PP的坐标;若不存在,请说明理由.10.如图在平面直角坐标系中,已知直线y=﹣x+2及双曲线y=(k>0,x>0).直线交y轴于A点,x轴于B点,C、D为双曲线上的两点,它们的横坐标分别为a,a+m (m>0).(1)如图①连接AC、DB、CD,当四边形CABD为平行四边形且a=2时,求k的值.(2)如图②过C、D两点分别作CC′∥y轴∥DD'交直线AB于C',D',当CD∥AB 时,①对于确定的k值,求证:a(a+m)的值也为定值.②若k=6,且满足m=a﹣4+,求d的最大值.11.如图1,已知A(﹣1,0),B(0,﹣2),平行四边形ABCD的边AD、BC分别与y轴、x轴交于点E、F,且点E为AD中点,双曲线y=(k为常数,k≠0)经过C、D 两点.(1)求k的值;(2)如图2,点G是y轴正半轴上的一个动点,过点G作y轴的垂线,分别交反比例函数y=(k为常数,k≠0)图象于点M,交反比例函数y=﹣(x<0)的图象于点N,当FM=FN时,求G点坐标;(3)点P在双曲线y=上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求出满足要求的所有点Q的坐标.12.综合与探究如图1,反比例函数的图象y=﹣经过点A,点A的横坐标是﹣2,点A关于坐标原点O的对称点为点B,作直线AB.(1)判断点B是否在反比例函数y=﹣的图象上,并说明理由;(2)如图1,过坐标原点O作直线交反比例函数y=﹣的图象于点C和点D,点C 的横坐标是4,顺次连接AD,DB,BC和CA.求证:四边形ACBD是矩形;(3)已知点P在x轴的正半轴上运动,点Q在平面内运动,当以点O,B,P和Q为顶点的四边形为菱形时,请直接写出此时点P的坐标.13.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数(k>0,x>0)的图象上,点D的坐标为(4,3).设AB所在直线解析式为y=ax+b(a≠0).(1)求反比例和一次函数解析式;(2)若将菱形ABCD沿x轴正方向平移m个单位,在平移中若反比例函数图象与菱形的边AD始终有交点,求m的取值范围;(3)在直线AB上是否存在M、N两点,使以MNOD四点的四边形构成矩形?若不存在,请说明理由,若存在直接求出M、N(点M在点N的上方)两点的坐标.14.如图,在平面直角坐标系xOy中,一次函数y=﹣x+5的图象与反比例函数y=(k >0)的图象交于A、B两点(点A在点B左边),交x轴于点C,延长AO交反比例函数y=(k>0)的图象于点E,点F为第四象限内一点,∠AFE=90°,连接OF.(1)填空:FO AO(填“>”、“=”或“<”);(2)连接CF,若AF平分∠OAC.①若△AFC的面积为10,求k的值;②连接BF,四边形AOFB能否为菱形?若能,直接写出符合条件的k的值;若不能,说明理由.15.如图1,在平面直角坐标系中,直线l:y=﹣2x+2与x轴交于点A,将直线l绕着点A 顺时针旋转45°后,与y轴交于点B,过点B作BC⊥AB,交直线l于点C.(1)求点A和点C的坐标;(2)如图2,将△ABC以每秒3个单位的速度沿y轴向上平移t秒,若存在某一时刻t,使A、C两点的对应点D、F恰好落在某反比例函数的图象上,此时点B对应点E,求出此时t的值;(3)在(2)的情况下,若点P是x轴上的动点,是否存在这样的点Q,使得以P、Q、E、F四个点为顶点的四边形是菱形?若存在,请直接写出符合题意的点Q的坐标;若不存在,请说明理由.16.如图,一次函数y1=x+1的图象与反比例函数y2=的图象相交于点A(m,2),B 两点,分别连接OA,OB.(1)求这个反比例函数的表达式;(2)请根据函数图象的轴对称性,直接写出点B的坐标为;当y1>y2,则自变量x的取值范围是;(3)在平面直角坐标系内,是否存在一点P,使以点O,A,B,P为顶点的四边形为菱形?若存在,请直接写出点P的坐标;若不存在,请说明理由.17.如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B在反比例函数y=的第一象限内的图象上,OA=6,OC=10,动点P在x轴的上方,且满足S=.△PAO(1)若点P在这个反比例函数的图象上,求点P的坐标;(2)连接PO、PA,求PO+PA的最小值;(3)若点Q是平面内一点,使得以A、B、P、Q为顶点的四边形是菱形,则请你直接写出满足条件的所有点Q的坐标.18.如图,在平面直角坐标系中,四边形ABCO为矩形,B(5,4),D(﹣3,0),点P 从点A出发,以每秒1cm的速度沿AB方向向终点B运动;点Q从点D出发,以每秒2cm的速度沿DC方向向终点C运动,已知动点P、Q同时出发,当点P、Q有一点到达终点时,P、Q都停止运动,设运动时间为t秒.(1)用含t的代数式表示:BP=cm,CQ=cm;(2)函数y=的图象在第一象限内的一支双曲线经过点P,且与线段BC交于点M,若出△POM的面积为7.5cm2,试求此时t的值;(3)点P、Q在运动过程的中,是否存在某一时刻t,使坐标平面上存在点E,以P、Q、C、E为顶点的四边形刚好是菱形?若存在,请求出所有满足条件的t的值,若不存在,请说明理由.19.如图,在平面直角坐标系中,一次函数y=kx+b的图象与双曲线交于点M(﹣4,m)、N(n,﹣4),与x轴交于A.(1)求k、b的值.(2)①将直线y=kx+b向上平移4个单位分别交x轴、y轴于点B、C,画出这条直线.②P是平面直角坐标系中的一点,若以A、B、C、P为顶点的四边形是平行四边形,求P点的坐标.20.如图1,在平面直角坐标系中,菱形ABCD的顶点D在第二象限,其余顶点都在第一象限,AB∥x轴,过点A作AE⊥CD,垂足为E.(1)若点A(6,8),点E(6,14).①求AO的长;②线段MN在y轴上移动(点M在点N的上方),MN=2,当四边形AEMN的周长最小时,求点M的坐标;(2)如图2,反比例函数y=(x>0)的图象经过点E,与边AB交于点F,AO⊥AD,AO=AB,DE=4CE,连结OE,OF,EF,且S△EOF=.求反比例函数的表达式.参考答案与试题解析1.【解答】解:(1)把A(1,3)的坐标分别代入y=、y=﹣x+b,∴m=xy=3,3=﹣1+b,∴m=3,b=4.(2)由(1)知,反比例函数的解析式为y=,一次函数的解析式为y=﹣x+4,∵直线MC⊥x轴于C,交直线AB于点N,∴可设点M的坐标为(x,),点N的坐标为(x,﹣x+4),其中,x>0,又∵MD⊥y轴于D,NE⊥y轴于E,∴四边形MDOC、NEOC都是矩形,∴S1=x•=3,S2=x•(﹣x+4)=﹣x2+4x,∴S=S2﹣S1=(﹣x2+4x)﹣3=﹣(x﹣2)2+1.其中,x>0,∵a=﹣1<0,开口向下,∴有最大值,∴当x=2时,S取最大值,其最大值为1.2.【解答】解:(1)∵点A(3,2)为正比例函数与反比例函数的交点,∴将x=3,y=2代入正比例解析式y=ax得:3a=2,解得:a=,将x=3,y=2代入反比例解析式y=得:=2,解得:k=6,∴正比例函数解析式为y=x,反比例函数解析式为y=;(2)过M作MN⊥x轴于N点.∵M(m,n)(0<m<3)是反比例函数图象上的一动点,且四边形OCDB为矩形,∴mn=6,BM=m,BO=DC=MN=n,又A(3,2),∴AC=2,OC=3,又mn=6,=S矩形OCDB﹣S△BMO﹣S△AOC=3n﹣mn﹣×2×3=3n﹣6=6,∴S四边形OADM解得:n=4,由mn=6,得到4m=6,解得:m=,则M坐标为(,4).3.【解答】解:(1)∵四边形OABC是面积为4的正方形,∴OA=OC=2,∴点B坐标为(2,2),将x=2,y=2代入反比例解析式得:2=,∴k=2×2=4.(2)∵正方形MABC′、NA′BC由正方形OABC翻折所得,∴ON=OM=2AO=4,∴点E横坐标为4,点F纵坐标为4.∵点E、F在函数y=的图象上,∴当x=4时,y=1,即E(4,1),当y=4时,x=1,即F(1,4).设直线EF解析式为y=mx+n,将E、F两点坐标代入,得,∴m=﹣1,n=5.∴直线EF的解析式为y=﹣x+5.4.【解答】解:(1)设正比例函数解析式为y=kx,将点M(﹣2,﹣1)坐标代入得k=,所以正比例函数解析式为y=x,同样可得,反比例函数解析式为;(2)当点Q在直线OM上运动时,设点Q的坐标为Q(m,m),=OB•BQ=×m×m=m2,于是S△OBQ=|(﹣1)×(﹣2)|=1,而S△OAP所以有,m2=1,解得m=±2,所以点Q的坐标为Q1(2,1)和Q2(﹣2,﹣1);(3)因为四边形OPCQ是平行四边形,所以OP=CQ,OQ=PC,而点P(﹣1,﹣2)是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值,(8分)因为点Q在第一象限中双曲线上,所以可设点Q的坐标为Q(n,),由勾股定理可得OQ2=n2+=(n﹣)2+4,所以当(n﹣)2=0即n﹣=0时,OQ2有最小值4,又因为OQ为正值,所以OQ与OQ2同时取得最小值,所以OQ有最小值2,由勾股定理得OP=,所以平行四边形OPCQ周长的最小值是2(OP+OQ)=2(+2)=2+4.(或因为反比例函数是关于y=x对称,所以当Q在反比例函数时候,OQ最短的时候,就是反比例与y=x的交点时候,联立方程组即可得到点Q坐标)5.【解答】解:(1)∵点A的坐标为(,2),AB∥x轴,∴B点纵坐标为2,又点B在函数(x<0)的图象上,∴当y=2时,x=﹣1.5,∴B(﹣1.5,2),∵BC∥y轴,∴C点横坐标为﹣1.5,又点C在函数(x<0)的图象上,∴当x=﹣1.5时,y=﹣4,∴C(﹣1.5,﹣4).∵AD⊥y轴,∴D(0.5,﹣4).(2)若点A在函数(x>0)上移动,矩形ABCD的面积不变.理由如下:如图,设AB、CD与y轴分别交于F、G,BC、AD与x轴分别交于E、H,设A(a,),则B(﹣3a,),C(﹣3a,﹣),D(a,﹣).∵矩形ABCD的面积=矩形AFOH的面积+矩形BFOE的面积+矩形CEOG的面积+矩形DHOG的面积=1+3+6+2=12.(3)设A(t,),则B(,),C(,),D(t,),又∵点D在y=的图象上,t•=k4,∴k1k3=k2k4.6.【解答】解:(1)∵一次函数y=x﹣1的图象与反比例函数y=(x>0)的图象交于点B(3,a),∴a=3﹣1,∴a=2.∴B(3,2),∴k=3×2=6;(2)令y=0,则x﹣1=0,∴x=1.∴A(1,0),∴OA=1,∵OA=AD,∴AD=1,∴OD=2,∴点C的横坐标为2,由(1)知:k=6,∴反比例函数y=(x>0)的解析式为y=.∴y==3,∴C(2,3).设点C关于x轴的对称点C′,则C′(2,﹣3),连接BC′,交x轴于点P,如图,则此时PB+PC最小.设直线BC′的解析式为y=kx+b,∴,解得:,∴直线BC′的解析式为y=5x﹣13.令y=0,则5x﹣13=0,∴x=.∴P(,0);(3)存在点F使得以A、B、C、F为顶点的四边形是平行四边形,理由:①当四边形ABFC为平行四边形时,如图,由(2)知:AD=1,C(2,3),B(3,2),OD=2,∴CD=3,DM=2,BM=1.过点F作FG⊥x轴,过点B作MH∥x轴交CD于点M,交FG于点H,∵CD⊥x轴,FG⊥x轴,∴CD∥FG.∵四边形ABFC为平行四边形,∴AC∥FB,AC=FB.∴∠ACD=∠BFH.在△ACD和△BFH中,,∴△ACD≌△BFH(AAS),∴AD=BH=1,CD=FH=3.∴MH=MB+BH=2.∵CD⊥x轴,FG⊥x轴,MH∥x轴,∴四边形MDGH为矩形,∴GH=DM=2,DG=MH=2,∴OG=OD+DG=4,FG=FH+HG=5,∴F1(4,5);②当四边形ABCF为平行四边形时,如图,设直线y=x﹣1与y轴交与点N,则N(0,﹣1),∴ON=1.∵OA=1,∴OA=ON,∴∠OAN=45°,∴∠EAD=∠OAN=45°,∵CD⊥x轴,∴∠AED=45°.∴DE=AD=1.∵CD=3,∴CE=CD﹣DE=2,过点B作BM⊥CE于点M,则BM=1,∵∠CEB=∠AED=45°,∴ME=BM=1,∴CM=1,∴BM=CE,M为CE的中点,∴∠CBE=90°.∵四边形ABCF为平行四边形时,∴CB∥AE,∴∠EAB+∠ABC=180°∴∠EAB=90°,∴∠FAO=45°,∴OF=OA=1,∴F2(0,1);③当四边形ACBF为平行四边形时,如图,过点B作BG⊥x轴,过点F作MH∥x轴,交BG的延长线于点H,过点A作AM⊥MH 于点M,同①可求得:OB=3,BG=2,△ACD≌△FBH,∴BH=CD=3,FH=AD=1,四边形AMHG为矩形,∴MH=AG=2,AM=GH=BH﹣BG=1,∴MF=MH﹣FH=1,∴F3(2,﹣1).综上,存在点F使得以A、B、C、F为顶点的四边形是平行四边形,符合条件的点F的坐标F1(4,5),F2(0,1),F3(2,﹣1).7.【解答】(1)证明:由题意得AD⊥AO,BC⊥AO,∴AD∥BC,∵AB∥CD,∴四边形ABCD是平行四边形,∵A(0,4),B(﹣3,0),C(2,0),∴BC=2﹣(﹣3)=5,AO=4,BO=3,CO=2,在Rt△ABO中,AB===5,∴AB=BC,∴四边形ABCD是菱形;(2)解:过点D作DH⊥x轴于H,则四边形AOHD是矩形,∴DH=AO=4,OH=AD,∵四边形ABCD是菱形,∴AD=AB=5,∴OH=5,∴D(5,4),∵反比例函数的图象于点D,∴4=,∴k=20,∴此反比例函数的解析式为y=;(3)解:在Rt△ACO中,AC===2∵四边形ABCD是菱形,∴AD∥BC,∴∠DAC=∠ACO,∴sin∠DAC=sin∠ACO===.8.【解答】解:(1)将点A的坐标为(m,﹣3)代入直线y=x中,得﹣3=m,解得:m=﹣2,∴A(﹣2,﹣3),∴k=﹣2×(﹣3)=6,∴反比例函数解析式为y=,由,得或,∴点B的坐标为(2,3);(2)如图1,作BE⊥x轴于点E,CF⊥x轴于点F,∴BE∥CF,∴△DCF∽△DBE,∵BC=2CD,BE=3,∴=,∴=,∴CF=1,∴C(6,1),作点B关于y轴的对称点B′,连接B′C交y轴于点G,则B′C即为BG+GC的最小值,∵B′(﹣2,3),C(6,1),∴B′C==2,∴BG+GC=B′C=2;(3)存在.理由如下:当点P在x的正半轴上时,如图,设点P1的坐标为(a,0),过点B作BE⊥x轴于点E,∵∠OEB=∠OBP1=90°,∠BOE=∠P1OB,∴△OBE∽△OP1B,∴=,∵B(2,3),∴OB==,∴=,∴点P1的坐标为(,0),当点P在x的负轴上时,如图2,设点P2的坐标为(a,0),过点A作AH⊥x轴于点H,同理证得点P2的坐标为(﹣,0),当四边形AP3BQ3或是矩形四边形AP4BQ4时,OA=OP4=,∴点P的坐标为(﹣,0)或(,0),综上所述,点P的坐标为(,0)或(﹣,0)或(﹣,0)或(,0).9.【解答】解:(1)作AF垂直于x轴,垂足为点F,∵AO=AB,AF⊥OB,∴,∵∠OAB=90°,AO=AB,∴∠AOB=45°,∴AF=OF=1,∴点A(1,1),设一次函数解析式为y1=k1x+b,反比例函数解析式为,将点A(1,1)和C(0,﹣1)代入y1=k1x+b,得y1=2,b=﹣1,∴一次函数的解析式为y1=2x﹣1.将点A(1,1)代入,得k2=1,∴反比例函数的解析式为,即一次函数解析式为y1=2x﹣1,反比例函数解析式为;(2)将两个函数联立得,整理得2x2﹣x﹣1=0,解得,x2=1,∴y1=﹣2,y2=1,∴点,∴,即△OAD的面积为;(3)存在,①以OA为对角线时,∵O(0,0),A(1,1),D(﹣,﹣2),∴将A点向右平移个单位,向上平移2个单位得到P点的坐标,即P(,3),②以OD为对角线时,∵O(0,0),A(1,1),D(﹣,﹣2),∴将D点向右平移1个单位,向上平移1个单位得到P点的坐标,即P(,﹣1),③以AD为对角线时,∵O(0,0),A(1,1),D(﹣,﹣2),∴将D点向左平移1个单位,向下平移1个单位得到P点的坐标,即P(﹣,﹣3),综上所述,点P的坐标为,,.10.【解答】(1)解:∵直线y=﹣x+2交y轴于A点,交x轴于B点,∴点A(0,2),点B(4,0),∵C、D为双曲线上的两点,∴点C(2,),点D(2+m,),∵四边形CABD为平行四边形,∴AD与BC互相平分,∴=,=,解得:m=4,k=6;(2)①证明:∵CC′∥y轴∥DD',CD∥AB,∴四边形CDD'C'是平行四边形,∴CC'=DD',∵C、D为双曲线上的两点,∴点C(a,),点D(a+m,),∵CC′∥y轴∥DD',∴点C'的横坐标为a,点D的横坐标为a+m,∴点C'(a,﹣a+2),点D'(a+m,﹣a﹣m+2),∴+a﹣2=+a+m﹣2,∴k=a(a+m),∴当k为定值时,a(a+m)为定值;②解:∵k=6,∴6=a(a+m),∴a2+am=12,∵m=a﹣4+,∴a2+a(a﹣4+)=12,∴d=﹣2a2+4a+12=﹣2(a﹣1)2+14,∴当a=1时,d的最大值为14.11.【解答】解:(1)∵A(﹣1,0),B(0,﹣2),E为AD中点,∴x D=1,设D(1,t),又∵DC∥AB,∴C(2,t﹣2),∴t=2t﹣4,∴t=4,∴k=4;(2)由(1)得C(2,2),∵B(0,﹣2),∴直线BC的解析式为y=2x﹣2,当y=0时,x=1,∴F(1,0),∴OF=1,设点G的坐标为(0,m),∵MN∥x轴,∴M(,m),N(﹣,m),∵FM=FN,∴1﹣(﹣)=﹣1,解得:m=或m=0(不合题意舍去),∴点G的坐标为(0,);(3)∵由(1)知k=4,∴反比例函数的解析式为y=,∵点P在双曲线上,点Q在y轴上,∴设Q(0,y),P(x,),①当AB为边时:如图1,若ABPQ为平行四边形,则=0,解得x=1,此时P1(1,4),Q1(0,6);如图2,若ABQP为平行四边形,则=,解得x=﹣1,此时P2(﹣1,﹣4),Q2(0,﹣6);②如图3,当AB为对角线时,AP=BQ,且AP∥BQ;∴=,解得x=﹣1,∴P3(﹣1,﹣4),Q3(0,2);故点Q的坐标为(0,6)或(0,﹣6)或(0,2).12.【解答】(1)解:结论:点B在反比例函数y=﹣的图象上.理由:∵反比例函数的图象y=﹣经过点A,点A的横坐标是﹣2,∴A(﹣2,4),∵A,B关于原点对称,∴B(2,﹣4),∵x=2时,y=﹣=﹣4,∴点B在反比例函数y=﹣的图象上;(2)证明:由题意,C(4,﹣2),D(﹣4,2),∵C,D关于原点对称,∴OC=OD,∵A,B关于原点对称,∴OA=OB,∴四边形ADBC是平行四边形,∵CD==4,AB==4,∴AB=CD,∴四边形ADBC是矩形;(3)解:如图,当四边形OBP1Q1是菱形时,P1(4,0).当四边形OBQ2P2是菱形时,P2(2,0).当四边形OP3BQ3是菱形时,P3(5,0),综上所述,满足条件的点P的坐标为(4,0)或(2,0)或(5,0).13.【解答】解:(1)如图,延长AD交x轴于F,由题意得AF⊥x轴,∵点D的坐标为(4,3),∴OF=4,DF=3,∴OD=5,∴AD=5,∴点A坐标为(4,8),∴k=xy=4×8=32,由菱形的性质得到B(0,5),设直线AB的方程为:y=ax+b(a≠0),则,解得,故反比例解析式为y=;直线AB的方程为:y=x+5;(2)将菱形ABCD沿x轴正方向平移m个单位,使得点D落在函数y=(x>0)的图象D'点处,∴点D'的坐标为(4+m,3),∵点D'在y=的图象上,∴3=,解得m=,∴0≤m;(3)如图,存在,理由:∵四边形ABCD是菱形,∴OB=OD=5,过D作DE⊥x轴于E,过N作NF⊥y轴于F,过M作MH⊥y轴于H,∴∠DEO=∠ONB=∠NOD=90°,∴∠BON+∠BOD=∠BOD+∠DOE=90°,∴△BON≌△DOE(AAS),∴BN=DE=3,ON=OE=4,=OB•NF=BN•ON,∴S△OBN∴NF=,∵点N在直线AB上,∴N(﹣,),设M(n,n+5),∴MH=n,OH=n+5,∵BM2=BH2+MH2,∴22=(n+5﹣5)2+n2,∴n=±,∵n>0,∴M(,).14.【解答】解:(1)∵反比例函数y=(k>0)的图象是中心对称图形,∴AO=EO,在Rt△AEF中,∠AFE=90°,AO=EO,∴FO=,故答案为:=;(2)①如图,连接CF,由(1)可知,FO=AO,∴∠OAF=∠OFA,∵AF平分∠OAC,∴∠OAF=∠BAF,∴∠OFA=∠BAF,∴OF∥AC,=S△AFC=10,∴S△AOC对于y=﹣x+5,令y=0,则0=﹣x+5,∴x=5,∴C(5,0),∴OC=5,设A(m,﹣m+5),m>0,∴S=﹣,=10,又∵S△AOC∴﹣,∴m=1,∴﹣m+5=﹣1+5=4,∴A(1,4),∵A(1,4)在反比例函数y=上,∴k=1×4=4;②如图,连接BF,由①可知,OF∥AB,FO=AO,当AO=AB时,此时四边形AOFB是菱形,将y=﹣x+5由y=联立,得:,解得:或,∴A(),B(),∴OA+()2=25﹣2k,AB2=50﹣8k,当AO=AB时,OA2=AB2,即25﹣2k=50﹣8k,∴k=,综上所述,当四边形AOFB为菱形时,k=.15.【解答】解:(1)∵y=﹣2x+2与x轴交于点A,∴0=﹣2x+2,得x=1,∴点A(1,0);过点C作CH⊥y轴于点H,∴∠CHB=∠BOA=90°∵将直线l绕着点A顺时针旋转45°后,与y轴交于点B,∴∠BAC=45°,又∵BC⊥AB,∴∠BAC=∠ACB=45°,∴AB=BC,∵∠OBA+∠OAB=90°,∠OBA+∠CBH=90°,∴∠OAB=∠CBH,在△AOB和△BHC中,∴△AOB≌△BHC(AAS),∴BH=AO=1,CH=BO,设OB=a,则OH=a+1,∴点C(a,﹣a﹣1),∵点C在直线l上,∴﹣a﹣1=﹣2a+2,∴a=3,∴C(3,﹣4);(2)将△ABC以每秒3个单位的速度沿y轴向上平移t秒,A(1,0),B(0,﹣3),C(3,﹣4)∴点D(1,3t),点E(0,﹣3+3t),点F(3,﹣4+3t),∵点A、C两点的对应点D、F正好落在某反比例函数的图象上,∴1×3t=3×(﹣4+3t),∴t=2;(3)由(2)知E(0,3),F(3,2),∴EF=,当EF=EP=时,则OP=1,∴P(1,0)或(﹣1,0),当P(1,0)时,由平移的性质得,点Q(4,﹣1),当P(﹣1,0)时,由平移的性质得,点Q(2,﹣1),当EF=FP=时,同理得P(3﹣,0)或(3+,0),∴Q(﹣,1)或(,1),当PE=PF时,设P(x,0),则9+x2=4+9﹣6x+x2,解得x=,∴P(,0),∴Q(),综上:Q(4,﹣1)或(2,﹣1)或(﹣,1)或(,1)或().16.【解答】解:(1)将A(m,2)代入y1=x+1得,2=m+1,∴m=1,∴A(1,2),将A(1,2)代入y2=得,k=1×2=2,∴y2=;(2)根据函数图象的轴对称性知,点A与B关于直线y=﹣x对称,过A作AC∥y轴,过B作BC∥x交于C,则C(﹣1,﹣1),∴B(﹣2,﹣1),当y1>y2,则自变量x的取值范围是x>1或﹣2<x<0,故答案为:(﹣2,﹣1),x>1或﹣2<x<0;(3)存在,如图,∵OA=OB,∴点P在AB上方时,四边形OAPB是菱形,∵O(0,0),A(1,2),B(﹣2,﹣1),由平移的性质得P(﹣1,1),∴以点O,A,B,P为顶点的四边形为菱形,点P的坐标为(﹣1,1).17.【解答】解:(1)设点P的纵坐标为m,=.∵S△PAO∴,∴m=4,∵四边形OABC是矩形,OA=6,OC=10,∴B(6,10),∴k=6×10=60,∵点P在这个反比例函数的图象上,∴点P的横坐标为=15,∴P(15,4);(2)如图,点P在直线y=4上运动,作点O关于直线y=4的对称点O',连接O'A,此时PO+PA的最小值即为AO'的长,在Rt△AOO'中,由勾股定理得,AO'==10,∴PO+PA的最小值为10;(3)当AP=AB=10时,如图,AG=4,∴PG=2,∴P(6﹣2,4),∴Q(6﹣2,14),当点P在G的右侧时,同理Q'(6+2,14),当BA=BP时,如图,由勾股定理得PG=8,∴P(﹣2,4),∵PQ=10,∴Q(﹣2,﹣6),同理,当P在G的右侧时,Q'(14,﹣6),当PA=PB时,点P在AB的垂直平分线y=5上,点P又在直线y=4上,故不存在,综上:Q(6﹣2,14)或(6+2,14)或(﹣2,﹣6)或(14,﹣6).18.【解答】解:(1)根据题意得:AP=tcm,AB=5cm,∴BP=(5﹣t)cm,∵DC=DO+OC=3+5=8,DQ=2tcm,∴CQ=DC﹣DQ=(8﹣2t)cm,故答案为:(8﹣2t);当BP=CQ时,四边形PQCB是矩形,∴5﹣t=8﹣2t,解得:t=3,∴当t=3时,四边形PQCB为矩形;故答案为:(5﹣t);3;(2)∵点P的坐标为(t,4),点P在反比例函数的图象上,∴k=4t,∴y=,∴点M的坐标为(5,),∴BM=4﹣,连接PM,如图1所示:∴△POM的面积S=矩形AOCB的面积﹣△AOP的面积﹣△PBM的面积﹣△OCM的面积=5×4﹣×t×4﹣×(5﹣t)×(4﹣)﹣×5×=﹣t2+10,∵点Q从点D运动到点C用是为4秒,点P从点A运动到点B用时为5秒,∴0≤t≤4,∴S=﹣t2+10(0≤t≤4);(3)存在;t的值为或,点E的坐标为(,4)或(3﹣2,4);理由如下:∵点P的坐标为(t,4),点Q的坐标为(2t﹣3,0),点C的坐标为(5,0),∴PQ2=(t﹣3)2+42,PC2=(t﹣5)2+42,CQ2=(8﹣2t)2;分情况讨论:①当PQ=PC时,(t﹣3)2+42=(t﹣5)2+42,解得:t=4(不合题意,舍去);②当PQ=CQ时,(t﹣3)2+42=(8﹣2t)2,解得:t=,或t=(不合题意,舍去),∴t=;若四边形PQCE为菱形,则PE∥CQ,点E在直线AB上,如图2所示:∴AE=AP+PE=t+8﹣2t=8﹣t=8﹣=,此时点E的坐标为(,4);③当PC=CQ时,(t﹣5)2+42=(8﹣2t)2,解得:t=,或t=(不合题意,舍去),∴t=;若四边形PQCE为菱形,则PE∥CQ,点E在直线AB上,如图3所示:∴AE=PE﹣AP=8﹣2t﹣t=83=﹣3+2,此时点E的坐标为(3﹣2,4);综上所述:存在某一时刻,使坐标平面上存在点E,以P、Q、C、E为顶点的四边形刚好是菱形,t的值为或,点E的坐标为(,4)或(3﹣2,4).19.【解答】解:(1)把x=﹣4,y=m代入中,得,∴点M(﹣4,2),把x=n,y=﹣4代入中,得,∴点N(2,﹣4),∴将点M(﹣4,2),点N(2,﹣4)代入y=kx+b中,得,解得,∴k=﹣1,b=﹣2;(2)①将直线y=﹣x﹣2向上平移4个单位,得y=﹣x+2,当x=0时,y=2,∴点C坐标为(0,2),当y=﹣x+2=0时,x=2,∴点B坐标为(2,0),平移后的直线如图所示:②以A、B、C、P为顶点的四边形是平行四边形,分情况讨论:当CA,CB为边时,AP∥CB且AP=CB,点P坐标为(0,﹣2),当BC,BA为边时,AP∥CB且AP=CB,点P坐标为(﹣4,2),当AC,AB为边,AC∥BP且AC=BP,∴点P坐标为(4,2),综上,满足条件的点P坐标为(0,﹣2)或(﹣4,2)或(4,2).20.【解答】解:(1)①∵点A(6,8),∴AO==10;(2)∵点A(6,8),点E(6,14),∴AE=6,∵四边形AEMN的周长=AE+MN+ME+AN,AE=6,MN=2,∴四边形AEMN的周长=8+AN+ME,∴当AN+ME有最小值时,四边形AEMN的周长有最小值,如图,将A向上平移两个单位得到A',连接A'M,作点A'关于y轴的对称点A'',连接A''E,∴AA'=2=MN,A'(6,10),∴四边形ANMA'是平行四边形,∴AN=A'M,∴AN+ME=A'M+ME,∵点A'与点A''关于y轴对称,∴A''M=A'M,点A''(﹣6,10),∴AN+ME=A''M+ME,∴点M,点E,点A''共线时,A''M+ME的最小值为A''E的长,∵点A''(﹣6,10),点E(6,14),∴直线A''E的解析式为:y=x+12,当x=0时,y=12,∴点M(0,12);(3)如图,延长EA交x轴于N,过点F作FH⊥x轴于H,设AB=AO=5a,∵四边形ABCD是菱形,∴DC∥AB,DC=AB=5a=AD,∵DE=4CE,∴DE=4a,CE=a,∵AB∥x轴,∴DE∥AB∥x轴,∵AE⊥CD,∴AE⊥x轴,AE⊥AB,∴∠DEA=∠ANO=90°,∴AE==3a,∵AD⊥AO,∴∠DAE+∠OAN=90°=∠OAN+∠AON,∴∠DAE=∠AON,又∵AD=AO=AB,∴△ANO≌△DEA(AAS),∴DE=AN=4a,AE=ON=3a,∴点A(3a,4a),点E(3a,7a),∵反比例函数y=(x>0)的图象经过点E,与边AB交于点F,∴k=21a2,点F(a,4a),==×3a×7a+(7a+4a)×(a﹣3a)﹣×4a×a,∵S△EOF∴a=1,∴k=21,∴反比例函数解析式为y=.。
中考数学复习考点知识归类讲解与练习17 反比例函数中的四边形问题

1 / 37中考数学复习考点知识归类讲解与练习 专题17 反比例函数中的四边形问题知识对接考点一、反比例函数中的四边形问题类型1单支双曲线上一点两垂直形成的矩形面积专项训练 一、单选题1.如图,四边形OABF 中,∠OAB =∠B =90°,点A 在x 轴上,双曲线k y x=过点F ,交AB 于点E ,连接EF .若34BF OA =,S △BEF =9,则k 的值为( )A.8 B.12 C.16 D.20 【答案】A【分析】设点F(a,ka),由34BFOA=得点E和点B,再结合S△BEF=9求k的值.【详解】解:设点F(a,ka ),∵34 BF OA=∴点B(4a,ka),点E(4a,4ka),∴BF=3a,BE=34ka,∵S△BEF=9,∴12•3a•34ka=9,∴k=8.故选:A.【点睛】本题考查了反比例图象上点的坐标,三角形的面积,采用了设而不求的方法求k的取值.2.如图,函数kyx=(k>0)的图象经过矩形OABC的边BC的中点E,若四边形ODBC的面积为6,则k的值为()A.2 B.3 C.4 D.6 【答案】C【分析】根据反比例函数kyx=(k>0)的图象经过矩形OABC的边BC的中点E,可得到点D是AB的中点,进而得出11232AOD OCBDS S k===四边形,求出k即可.【详解】设B(2m,2n),∵E为BC中点,四边形OCBA是矩形,∴E(2m,n)∵函数kyx=(k>0)的图象经过矩形OABC的边BC的中点E,∴k=2mn,又点D在函数kyx=(k>0)的图象上,∴点D坐标为(m,2n)∴点D是AB的中点,∴S△AOD=13S四边形OCBD=163⨯=2=12|k|,∴k=4或k=﹣4<2(舍去),3 / 37故选:C . 【点睛】考查反比例函数图象上点的坐标特征,反比例函数k 的几何意义,以及矩形的性质,求出△OAD 的面积是解决问题的关键.3.如图,△ABO 的顶点A 在函数k y x=(x >0)的图象上,∠ABO =90°,过AO 边的三等分点M 、N 分别作x 轴的平行线交AB 于点P 、Q .若四边形MOBP 的面积为5,则k 的值为()A .9B .12C .15D .18【答案】D 【分析】根据已知条件,证明ABO APM △△,得到49APMABOS S=△△,推出9ABO S =△,又根据函数图象上点的几何意义,知道2ABO kS =△,从而推得k 值. 【详解】解:∵M 、N 为AO 边的三等分点,且//NQ OB ,//MP OB ∴11,9023AN AM AO AQN APM ==∠=∠= 在ABO APM △与△中:5 / 3790PAM BAOAPM ABO ∠=∠⎧⎨∠=∠=⎩∴ABO APM △△222439APM ABO S AM S AO ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭△△ 又∵四边形MOBP 的面积为5 即5ABOAPMMOBP S S S=-=四边形∴9ABO S =△又∵A 在函数k y x=(x >0)的图象上,∠ABO =90°∴2ABO kS =△ ∴18k =∵函数图象在第一象限 ∴0k > ∴18k = 故选:D 【点睛】本题考查反比例函数图象上点的几何意义,以及相似三角形的相关判定和性质,根据图形进行数形结合是解题关键.4.如图,点A 是反比例函数图象上一点,过点A 作AB y ⊥轴于点B ,点C D 、在x 轴上,且//BC AD ,四边形ABCD 的面积为3,则这个反比例函数的解析式为()A.6yx=B.6yx=-C.3yx=D.3yx=-【答案】D【分析】过A点向x轴作垂线,与坐标轴围成的四边形的面积是定值|k|,由此可得出答案.【详解】解:过点A向x轴作垂线,如图,四边形ABCD的面积为3,根据反比例函数系数k的几何意义可得:3k=,又∵反比例的函数图象在第二象限,∴3k=-,即这个反比例函数的解析式为3yx=-.故选D.【点睛】此题考查了反比例函数的几何意义,解答本题关键是掌握在反比例函数中k所代表的几何意义,属于基础题,难度一般.7 / 375.如图,在平面直角坐标系中,ABCO 为平行四边形,(6,2)A ,(2,4)B ,反比例函数(0)ky k x=≠的图象经过四边形OABC 的顶点C ,则k 的值是()A .3-B .3C .8D .8-【答案】D 【分析】连接OB ,AC ,根据O ,B 的坐标易求P 的坐标,再根据平行四边形的性质:对角线互相平分即可求出则C 点坐标,根据待定系数法即可求得k 的值. 【详解】解:连接OB ,AC ,相交于点P , ∵四边形OABC 是平行四边形, ∴AP =CP ,OP =BP , ∵B (2,4), ∴P 的坐标(1,2), ∵A (6,2),∴C 的坐标为(-4,2),∵反比例函数(0)ky k x=≠的图象经过点C ,∴k=-4×2=-8,故选:D.【点睛】本题考查的是反比例函数图象上点的坐标特点,平行四边形的性质,求得C点的坐标是解答此题的关键.6.如图,四边形OABC是平行四边形,点A的坐标为A(3,0),∠COA= 60°,D为边AB的中点,反比例函数y =k(x > 0)的图象经过C,D两点,直线CD与y轴相交于点xE,则点E的坐标为()A.(0,B.(0,C.(0,5)D.(0,6)【答案】B【分析】作CE⊥x轴于点E,过B作BF⊥x轴于F,过D作DM⊥x轴于M,设C的坐标为(x),表示出D的坐标,将C、D两点坐标代入反比例函数的解析式,解关于x的方程求出x即可得到点C、D的坐标,进而求得直线CD的解析式,最后计算该直线与y轴交点坐标即可得出结果.【详解】解:作CE⊥x轴于点E,则∠CEO=90°,过B作BF⊥x轴于F,过D作DM⊥x轴于M,则BF=CE,DM∥BF,BF=CE,∵D为AB的中点,∴AM=FM,∴DM=12BF,∵∠COA=60°,∴∠OCE=30°,∴OC=2OE,CE,∴设C的坐标为(x),∴AF=OE=x,CE=BF,OE=AF=x,DM,∵四边形OABC是平行四边形,A(3,0),∴OF=3+x,OM=3+12x,即D点的坐标为(3+12x),9 / 37把C、D的坐标代入y=kx得:k=x=(3+12x,解得:x1=2,x2=0(舍去),∴C(2,,D(4,设直线CD解析式为:y=ax+b,则24a ba b⎧=+⎪⎨+⎪⎩,解得ab⎧=⎪⎨⎪=⎩∴直线CD解析式为:y x=+∴当x=0时,y=∴点E的坐标为(0,.故选:B.【点睛】本题主要考查了平行四边形的性质、运用待定系数法求函数的解析式以及含30度角的直角三角形的性质.根据反比例函数图象经过C、D两点,得出关于x的方程是解决问题的关键.7.如图,四边形AOBC和四边形CDEF都是正方形,边OA在x轴上,边OB在y轴上,点D在边CB上,反比例函数y=8x-在第二象限的图象经过点E,则正方形AOBC和正方形CDEF的面积之差为()A.12B.10C.8D.6【答案】C【分析】设正方形AOBC的边长为a,正方形CDEF的边长为b,则E(b-a,a+b),再根据反比例函数图象上点的坐标特征得(a+b)•(b-a)=8,因为S正方形AOBC =a2,S正方形CDEF=b2,从而求得正方形AOBC和正方形CDEF的面积之差为8.【详解】解:设正方形AOBC的边长为a,正方形CDEF的边长为b,则E(a﹣b,a+b),∴(a+b)•(a﹣b)=8,整理为a2﹣b2=8,∵S正方形AOBC =a2, S正方形CDEF=b2,∴S正方形AOBC ﹣S正方形CDEF=8,故答案为:C.【点睛】本题考查了反比例函数图象上点的坐标特征:反比例函数y=kx(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=|k|;也考查了正方形的性质.8.如图,四边形AOBC和四边形CDEF都是正方形,边OA在y轴上,边OB在x 轴上,点11 / 37F在边AC上,反比例函数y=10x在第一象限的图象经过点E,则正方形AOBC和正方形CDEF 的面积之差为()A.12 B.10 C.6 D.4【答案】B【分析】设正方形AOBC的边长为a,正方形CDEF的边长为b,则E(a﹣b,a+b),代入反比例函数解析式即可求解.【详解】解:设正方形AOBC的边长为a,正方形CDEF的边长为b,则E(a﹣b,a+b),∴(a+b)•(a﹣b)=10,整理为a2﹣b2=10,∵S正方形AOBC=a2,S正方形CDEF=b2,∴S正方形AOBC﹣S正方形CDEF=10,故选:B.【点睛】本题考查了反比例函数图象上点的坐标特征:反比例函数kyx(k是常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.13 / 379.如图,在平面直角坐标系中,函数y =2x(x >0)的图象经过矩形OABC 的边BC 的中点D ,且与边AB 相交于点E ,则四边形ODBE 的面积为( )A .32B .2C .3D .4【答案】B 【分析】由矩形的性质求出S △OAB =S △OBC ,反比例函数系数k 的几何意义△OAE 和△OCD 的面积各为1,根据等底同高,面积和差求出四边形OEBD 的面积为2. 【详解】解:连接OB ,如图所示:∵OB 是矩形OABC 的对角线, ∴S △OAB =S △OBC又∵点D 、E 在反比例函数y =2x(x >0)的图象上,∴1212OAE OCD S S ∆∆==⨯=,又∵CD=BD ,OC 是△OCD 和△OBD 的高, ∴S △OCD =S △OAB =1, 又∵S △OBC =S △OCD +S △OBD , ∴S △OAB =S △OBC =2 又∵S △OBE =S △OAB ﹣S △OAE , ∴S △OBE =2﹣1=1, 又∵S 四边形OEBD =S △ODE +S △OBE , ∴S 四边形OEBD =1+1=2, 故选:B . 【点睛】本题考查了矩形的性质,反比例函数的性质,三角形的面积和差法,等底同高法两个三角形的面积相等相关知识点,重点掌握反比例函数系数k 的几何意义,难点是作辅助线将不规则的四边形转化成三角形求解.10.如图,在平面直角坐标系中,反比例函数y =k x(x >0)的图象经过矩形OABC 的边BC 的中点D ,且与边AB 相交于点E ,点B 的坐标为(4,2),则四边形ODBE 的面积为()A .32B .2C .3D .4【答案】D 【分析】15 / 37首先根据条件求出反比例函数的k 值,再根据其几何意义对面积进行转换即可. 【详解】∵B (4,2),D 为BC 的中点,∴D (2,2),把点D (2,2)代入反比例函数解析式得k =4, ∴反比例函数解析式为4y x=(x >0),则E (4,1),∴S 四边形OEBD =S 矩形OABC -S △OCD -S △OAE =4×2-12×2×2-12×4×1=4故选:D . 【点睛】本题考查了求反比例函数解析式及反比例函数k 的几何意义,灵活利用k 的几何意义求解面积是解题关键. 二、填空题11.如图,反比例函数()0ky x x =>的图象经过长方形OABC 对角线的交点M ,分别与AB ,BC 相交于点D ,E .若四边形ODBE 的面积为3,则k 的值为________.【答案】1 【分析】设M 点的坐标为(,)m n ,根据矩形性质求得,A B 的坐标,根据矩形的性质以及反比例函数k的几何意义2OCE OAD kS S ==△△,根据S 四边形ODBE =S 矩形ABCD OCE OAD S S --△△,以及已知条件即可求得k .【详解】四边形ABCD 是矩形,BC y ∴⊥轴,BA x ⊥轴,由反比例函数k 的几何意义可知,,E D 在反比例函数图像上,2OCE OAD k S S ∴==△△ 设M 点的坐标为(,)m n ,而点M 在反比例函数图像上,则mn k =, 又矩形OABC 对角线的交点M ,M ∴为OB 的中点∴(2,2)B m n ,(2,0)A m ,(0,2)C n ,S 矩形ABCD =224AB OA n m mn ⨯=⨯=,∴S 四边形ODBE =S 矩形ABCD 114322OCE OAD S S k k k k --=--=△△, S 四边形ODBE =3,∴33k =,解得1k =, 故答案为:1. 【点睛】本题考查了反比例函数k 的几何意义,矩形的性质,中点坐标公式,设点的坐标求解是解题的关键.12.如图,已知在平面直角坐标系xOy 中,Rt OAB ∆的直角顶点B 在x 轴的正半轴上,点A 在第一象限,反比例函数(0)ky x x =>的图象经过OA 的中点C .交AB 于点D ,连接CD .若17 / 37ACD ∆的面积是3,则四边形OBDC 的面积是______.【答案】5 【分析】作辅助线,构建直角三角形,利用反比例函数k 的几何意义得到12OCE OBD S S k ∆∆==,根据OA 的中点C ,利用中线的性质和三线合一得到△OCE 和△OAB 的面积比为1:4,代入可得结论. 【详解】解:连接OD ,BC ,过C 作//CE AB ,交x 轴于E ,90ABO ∠=︒,反比例函数(0)k y x x=>的图象经过OA 的中点C ,12COE BOD S S k∆∆∴==,3ACD OCD S S ∆∆==,ABC OBC S S ∆∆=,AC OC BC ==,//CE AB ,∴CE ⊥OB , ∴OE =BE ,∴14OCE OAB S S ∆∆=,4OCE OAB S S ∆∆∴=,1143322k k ∴⨯=++,4k ∴=,14482OAB S ∆∴=⨯⨯=,∴四边形OBDC 的面积为5OAB ACD S S ∆∆-=,故答案为:5.【点睛】本题考查了反比例函数比例系数k 的几何意义:在反比例函数k y x=图象中任取一点,过这一个点向x 轴和y 轴分别作垂线,与坐标轴围成的矩形的面积是定值||k .在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是1||2k ,且保持不变.13.如图,过点P (2,3)分别作PC ⊥x 轴于点C ,PD ⊥y 轴于点D ,PC 、PD 分别交反比例函数y 2x=(x >0)的图象于点A 、B ,则四边形BOAP 的面积为 ___.【答案】4 【分析】根据反比例函数系数k 的几何意义可得S △DBO =S △AOC =12|k |=1,再利用矩形OCPD 的面积减去△BDO 和△CAO 的面积即可.19 / 37解:∵B、A 两点在反比例函数y 2x=(x >0)的图象上, ∴S △DBO =S △AOC =12×2=1, ∵P (2,3),∴四边形DPCO 的面积为2×3=6, ∴四边形BOAP 的面积为6-1-1=4, 故答案为4. 【点睛】此题主要考查了反比例函数k 的几何意义,关键是掌握在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是12|k |,且保持不变.14.如图,反比例函数的图象与矩形ABCO 的边AB 交于点G ,与边BC 交于点D ,过点A ,D 作//DE AF ,交直线0y kx k 于点E ,F ,若OE OF =,BG =,则四边形ADEF 的面积为 ______ .【答案】3 【分析】延长DE 交x 轴于K ,作DH OA ⊥于H ,证得OEKOFA ,即可证得KEOADKADEFADEOS S SS四边形四边形,设3(,)G a a ,用a 表示OA 和AB,根据三角形面积公式求得即【详解】解:延长DE 交x 轴于K ,作DH OA ⊥于设3(,)G a a ,则OA a =,3AGa, 3BGGA , 33BGa,333DH AB AG BGa,//DE AF ,EKOFAO ,在OEK ∆和OFA ∆中,EKO FAO EOK FOA OEOF,()OEKOFA AAS ,OK OAa ,2AKa ,112322KEO ADK ADEF ADEO S S S S AK DH a ∆∆∴=+==⋅=⨯=+四边形四边形故答案为:3+ 【点睛】21 / 37本题考查了反比例函数综合,全等三角形的判定与性质,三角形面积公式,证得KEOADKADEFADEOS S SS四边形四边形是解题的关键.15.如图,两个反比例函数3y x =和1y x =在第一象限内的图象依次是C 1和C 2,设点P 在C 1上,PC ⊥x 轴于点C ,交C 2于点A ,PD ⊥y 轴于点D ,交C 2于点B ,则四边形PAOB 的面积为_______.【答案】2 【分析】根据反比例函数k 值的几何意义即可求解. 【详解】∵C 2:y =1x 过A ,B 两点, C 1:y =3x过P 点, ∴S △ACO = S △BOD =12,S 矩形DPCO =3,∴S 四边形PAOB = S 矩形DPCO - S △ACO - S △BOD =3-12-12=2, 故答案为:2. 【点睛】本题主要考查反比例函数的图像和性质,解题的关键是熟知反比例函数k 值的几何意义. 三、解答题16.如图,点A 是坐标原点,点D 是反比例函数()60y x x=>图像上一点,点B 在x轴上,AD BD =,四边形ABCD 是平行四边形,BC 交反比例函数()60y x x=>图像于点E .(1)平行四边形ABCD 的面积等于______;(2)设D 点横坐标为m ,试用m 的代数式表示点E 的坐标;(要有推理和计算过程) (3)EB 的最小值为______.【答案】(1)12;(2)1)m ;(3)【分析】(1)作DH AB ⊥于H ,设(,)D m n .首先证明2AB m =,根据反比例函数的几何意义求出6mn =即可解决问题.(2)利用(1)中结论,根据2CD AB m ==得到点C 坐标,求出直线BC 的解析式,构建方程组确定点E 的坐标.(3)作EF x ⊥轴于F ,CG x ⊥轴于G .利用平行线分线段成比例得到CEFGBE BF=BE AD =,求出AD 的最小值即可解决问题. 【详解】解:(1)如图,作DH AB ⊥于H ,设(,)D m n .DA DB =,DH AB ⊥,AH BH m ∴==,23 / 37点D 在6y x=上,6mn ∴=,212ABCD S AB DH mn ∴=⋅==平行四边形.故答案为12. (2)由题意6(,)D m m , 由(1)可知2AB m =, 四边形ABCD 是平行四边形,2CD AB m ∴==,6(3,)C m m∴, (2,0)B m ,设直线BC 的解析式为y =kx +b ,∴6302mk b m mk b ⎧=+⎪⎨⎪=+⎩,解得:2612k m b m ⎧=⎪⎪⎨⎪=-⎪⎩,∴直线BC 的解析式为2612y x m m=-, 由26612y xy x m m⎧=⎪⎪⎨⎪=-⎪⎩,解得1)x m y ⎧=⎪⎨=⎪⎩或(1x my ⎧=⎪⎨=⎪⎩,1)E m ∴. (3)作EF x ⊥轴于F ,CG x ⊥轴于G .//EF CG ,∴CE FG BE BF ==BE ∴,要使得BE 最小,只要AD 最小,AD m ==,AD ∴的最小值为BE ∴=【点睛】本题属于反比例函数综合题,考查了等腰三角形的性质,平行四边形的性质,一次函数的性质,待定系数法等知识,解题的关键是学会构建一次函数,利用方程组确定交点坐标,属于中考压轴题.17.如图,在平面直角坐标系xOy 中,点,A B 在反比例函数(0)ky x x =>的图像上(点B 的横坐标大于点A 的横坐标),点A 的坐标为(2,4),过点A 作AD x ⊥轴于点D ,过点B 作BC x ⊥轴于点C ,连接,OA AB .25 / 37(1)求反比例函数k y x=的表达式;(2)若点D 是OC 的中点,求四边形OABC 的面积. 【答案】(1)8y x=;(2)10 【分析】(1)反比例函数待定系数法求解析式,将已知点A 的坐标代入反比例函数k y x=即可; (2)四边形OABC 的面积可以拆解为AOD △和四边形ABCD 【详解】(1)把2,4x y ==代入ky x=得42k =,8k ∴=.∴反比例函数的表达式是8y x=. (2)∵点D 是OC 的中点,24OC OD ∴==.当4x =时824y ==.2BC ∴=.1124(24)21022AODOABC ABCD S SS ∴=+=⨯⨯+⨯+⨯=四边形四边形.【点睛】本题考查了用待定系数法求反比例函数的解析式,第二问考查了求反比例函数图像上的点的特点,解题的关键是求出点B的坐标.18.如图,将一个长方形放置在平面直角坐标系中,OA=2,OC=3,E是AB中点,反比例函数图象过点E且和BC相交点F.(1)直接写出点B和点E的坐标;(2)求直线OB与反比例函数的解析式;(3)连接OE、OF,求四边形OEBF的面积.【答案】(1)B(2,3),E(2,32);(2)33,2y x yx==;(3)3【分析】(1)根据OA=2,OC=3,得到点B的坐标;根据E是AB的中点,求得点E的坐标,(2)运用待定系数法求直线OB的解析式,再进一步运用待定系数法求得反比例函数的解析式;(3)根据反比例函数的解析式求得点F的横坐标,再进一步根据四边形的面积等于矩形的面积减去两个直角三角形的面积进行计算.【详解】解:(1)∵OA=2,OC=3,E是AB中点,∴B(2,3),E(2,32);27 / 37(2)设直线OB 的解析式是y =k 1x , 把B 点坐标代入,得k 1=32,则直线OB 的解析式是y =32x .设反比例函数解析式是y =2k x, 把E 点坐标代入,得k 2=3, 则反比例函数的解析式是y =3x; (3)由题意得F y =3,代入y =3x , 得F x =1,即F (1,3).则四边形OEBF 的面积=矩形OABC 的面积﹣△OAE 的面积﹣△OCF 的面积=2×3﹣12⨯1×3﹣12⨯2×32=3. 【点睛】本题考查反比例函数系数k 的几何意义、待定系数法求反比例函数解析式、矩形的性质、反比例函数图象上点的坐标特征、待定系数法求一次函数解析式,灵活应用是关键,本题是中考的常考题型19.如图,已知反比例函数()0ky x x=>的图象经过点()4,2A ,过A 作AC y ⊥轴于点C .点B 为反比例函数图象上的一动点,过点B 作BD x ⊥轴于点D ,连接AD .直线BC 与x 轴的负半轴交于点E . (1)求k 的值;(2)若3BD OC =,求四边形ACED 的面积.【答案】(1)8k ;(2)6. 【分析】(1)利用待定系数法即可解决问题.(2)分别求出点B 、C 坐标,再求出直线BC 的解析式,进而求出E 点坐标,DE 的长,即可利用梯形面积公式解决问题. 【详解】解:(1)∵反比例函数()0k y x x=>的图象经过点()4,2A , ∴24k =, 解得:8k ,∴反比例函数解析式为:()80y x x=>. (2)∵AC y ⊥轴,()4,2A , ∴2OC =, ∴36BD OC==, ∵BD x ⊥轴,∴点B 的纵坐标为6,代入8y x=中,得:86x=,解得:43x =,29 / 37∴4,63B ⎛⎫ ⎪⎝⎭, ∵()0,2C ,设直线BC 的解析式为:y kx b =+,则有4632k b b ⎧+=⎪⎨⎪=⎩,解得:32k b =⎧⎨=⎩,∴直线BC 的解析式为:32y x =+, 令0y =,得:320x +=, 解得:23x =-,∴2,03E ⎛⎫- ⎪⎝⎭,∴42233DE ⎛⎫=--= ⎪⎝⎭,∵//AC DE ,∴()()11422622ACEDS AC DE OC =+=⨯+⨯=四边形.【点睛】本题为反比例函数与一次函数综合题,考查了待定系数法求反比例函数、一次函数解析式,熟练掌握待定系数法,理解函数图象上点的坐标特点是解题关键.20.如图,将一个矩形放置在平面直角坐标系中,OA =2,OC =3,E 是AB 的中点,反比例函数图象过点E 且与BC 相交于点F . (1)求反比例函数的解析式;(2)连接OE 、OF ,求四边形OEBF 的面积.【答案】(1)3y x =;(2)3. 【分析】(1)根据题意求得E 点坐标,再根据待定系数法即可求得函数解析式; (2)根据OAE OCF OEBF OABC S S S S =--四边形矩形△△即可求得四边形的面积. 【详解】解:(1)由题意得()2,3B , ∴32,2E ⎛⎫⎪⎝⎭,设反比例函数的解析式是()0k y k x=≠, 把E 点坐标代入,得3k =, 所以反比例函数的解析式是3y x =;(2)由题意得3F y =,代入3y x =,得1F x =,即()1,3F ,∴336322OAE OCFOEBF OABCS S S S=--=--=四边形矩形△△.【点睛】本题考查待定系数法求反比例函数解析式,反比例函数k与图形面积,矩形的性质.(1)中能正确求得E点坐标是解题关键;(2)中掌握割补法是解题关键.21.如图,在平面直角坐标系中,正比例函数y=mx与反比例函数y=3nx-的图象交于A、PBD关于直线AP对称,连接AB,作CD∥y轴交直线AP于点C.(1)求m、n的值和点A的坐标;(2)求sin∠CDB的值;(3)连接AD、BC,求四边形ABCD的面积.【答案】(1)m=﹣2,n=﹣3,A;(2;(3)60【分析】(1)把P点的坐标分别代入y=mx与y=3nx-即可求得;(2)根据反比例函数和正比例函数的对称性求得A的坐标,即可得出AB∥y轴,AB=然后通过证得△CDP≌△ABP,得到AB=CD=CP=AP,即可证得四边形ABCD是菱形,31 / 37根据勾股定理求得AP ,即可求得PC ,解直角三角形即可求得结论;(3)由菱形的性质可知S 四边形ABCD =4S △CPB ,求得△CPB 的面积,即可求得四边形ABCD 的面积.【详解】解:(1)∵正比例函数y =mx 与反比例函数y =3n x-的图象交于A 、P点,,解得,m =﹣2,n =﹣3;由题意可知A 与P 关于原点对称,且P,∴A;(2)∵BA,∴AB ∥y 轴,∴AB =∵CD ∥y 轴,∴AB ∥CD ,∴∠CDP =∠ABP ,∵点BD 关于直线AP 对称,∴AC ⊥BD ,PD =PB ,在△CDP 和△ABP 中,CDP ABP PD PB CPD APB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△CDP ≌△ABP (ASA ),33 / 37∴AB =CD =CP =AP ,又∵AC ⊥BD ,PD =PB ,∴四边形ABCD 是菱形,∵P,A,∴PC PA =∴sin∠CDB =PC CD; (3)∵P,B,∴PB∴S 四边形ABCD=114446022CPB S PB PC ∆=⨯⋅=⨯.【点睛】本题是反比例函数与一次函数的交点问题,主要考查了待定系数法求函数的解析式,轴对称的性质,反比例函数与正比例函数的对称性,菱形的判定和性质,三角形面积以及解直角三角形等,证得四边形是菱形是解题的关键.22.如图,已知矩形OABC 的顶点()8,6B -在反比例函数k y x =的图象上,点A 在x 轴上,点C 在y 轴上,点P 在反比例函数k y x =的图象上,其横坐标为()8a a <-,过点P 作PE x ⊥轴于点E ,PF y ⊥轴于点F ,交AB 于点G .(1)求反比例函数的解析式;(2)若四边形PEAG 为正方形,求点P 的坐标;(3)连接OP 交AB 于点M ,若:3:2BM MA =,求四边形PEAM 与四边形BMOC 的面积比.【答案】(1)48y x =-;(2)()12,4-;(3):3:8PEAM BMOC S S =四边形四边形. 【分析】(1)把顶点()8,6B -代入反比例函数k y x =中得,利用待定系数法解题;(2)设点48,a P a ⎛⎫ ⎪⎝⎭-,分别解出48PE a =-,8PG a =--,根据正方形的性质PE PG =,代入解题即可;(3)根据反比例函数的几何意义,四边形PEAM 的面积与BMO ∆的面积相等,结合等高的BMO ∆与MAO ∆的面积之比为3∶2,设BMO ∆的面积为3x ,则MAO ∆的面积为2x ,由此解得8BMOC S x =四边形,据此解题.【详解】解:(1)把顶点()8,6B -代入反比例函数k y x =中得,8648k =-⨯=-,48y x∴=-; (2)设点48,a P a ⎛⎫ ⎪⎝⎭-,根据题意可知48PE a =-,8PG a =--,35 / 37∵四边形PEAG 为正方形,∴PE PG =,即848aa =---, ∴112a =-,24a =(舍),∴点P 的坐标为()12,4-;(3)根据反比例函数的几何意义,可知BAO ∆和PEO ∆的面积均为24,∴四边形PEAM 的面积与BMO ∆的面积相等,由:3:2BM MA =,根据等高的BMO ∆与MAO ∆的面积之比为3∶2,设BMO ∆的面积为3x ,则MAO ∆的面积为2x ,∴3BMO PEAM S S x ∆==四边形,∴5BAO BCO S S x ∆∆==,∴8BMOC S x =四边形,∴:3:8PEAM BMOC S S =四边形四边形.【点睛】本题考查待定系数法解反比例函数的解析式、反比例函数系数k 的几何意义、矩形的性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.23.如图,在平面直角坐标系xOy 中,一次函数y =kx +b (k ≠0)的图象分别交x 轴,y 轴于A (3,0),B (0,﹣3)两点,将直线AB 向上平移7个单位长度后,刚好与反比例函数m y x=(m ≠0)的图象只有一个交点C ,与y 轴交于点D ,连接AD ,BC . (1)求直线AB 的函数表达式;(2)求点C 的坐标及四边形ABCD 的面积.【答案】(1)y=x-3;(2)点C 坐标为(-2,2);四边形ABCD 的面积为17.5 .【分析】(1)把A 、B 的坐标代入y=kx+b 可以得到关于k 、b 的方程组,解方程组得到k 与b 的值即可得到AB 的函数表达式;(2)由题意可得CD 的函数表达式,与反比例函数表达式联立得到关于x 的一元二次方程,由判别式等于0可以求得m ,从而得到C 点坐标,然后由四边形ABCD 的面积等于三角形BCD 面积加上三角形BDA 面积可以得到最终答案.【详解】解:(1)由题意可得:303k b b +=⎧⎨=-⎩,解之可得:k=1,b=-3, ∴直线AB 的函数表达式为y=x-3;(2)由题意可得CD 的函数表达式为:y=x-3+7即y=x+4, ∴x+4=m x,即x (x+4)=m , 240x x m ∴+-=,由题意得:()24410m ∆=-⨯⨯-=,解得:m=-4,37 / 37 ∴24402x x x ++==-,,y=-2+4=2,∴点C 坐标为(-2,2),在y=x+4中令x=0得y=4,∴D 点坐标为(0,4),∴四边形ABCD 的面积=BDC ABD SS + =11727322⨯⨯+⨯⨯=7+10.5=17.5.【点睛】本题考查一次函数与反比例函数的综合应用,熟练掌握一次函数解析式的求法及平移、一元二次方程特殊解的求法、由坐标轴与直线所围图形面积的求法是解题关键.。
苏科版八年级下册第十一章反比例函数中的四边形问题训练(一)

4. A
解:如图,过点 C 作 ⊥ 轴于 E,
在正方形 ABCD 中, = ,∠ ∴ ∠ + ∠ = 90°, ∵ ∠ + ∠ = 90°, ∴∠ =∠ , ∵点 A 的坐标为( − 4,0), ∴ = 4, ∵ = 5, ∴ = 52 − 42 = 3, 在△ 和△ 中,
(1)求点 D 的坐标; (2)求经过点 C 的反比例函数的关系式.
5 / 21
不要因为长期埋头科学,而失去对生活、对美、对待诗意的感受能力。—— 达尔文
17. 如图,在平面直角坐标系中,▱ABCD 的顶点 A、B、
D 的坐标分别为(2,0)、(6,0)、(0,3),顶点 C 在函数 = ( > 0)的图象上.
(1)填空:无论 k 值取何值时,四边形 ABCD 的形状一定是
;
(2)①当点 B 坐标为( , 1)时,四边形 ABCD 的形状一定是
的 m 值,能使四边形 ABCD 为矩形的点 B 共有
个;
;②填空:对①中
(3)四边形 ABCD 能不能是菱形?若能,直接写出 B 点的坐标;若不能,说明理由.
16. 如图,四边形 ABCD 为菱形,已知 (0,4), ( − 3,0).
∠ =∠ ∠ =∠ ,
=
∴△ ≌△ ( ), ∴ = = 4, = = 3, ∴ = − = 4 − 3 = 1, ∴点 C 的坐标为(3,1),
= 90°,
∵反比例函数 = ( ≠ 0)的图象过点 C,
∴ = = 3 × 1 = 3, ∴反比例函数的表达式为 = 3.
初三数学反比例函数与四边形(难题)
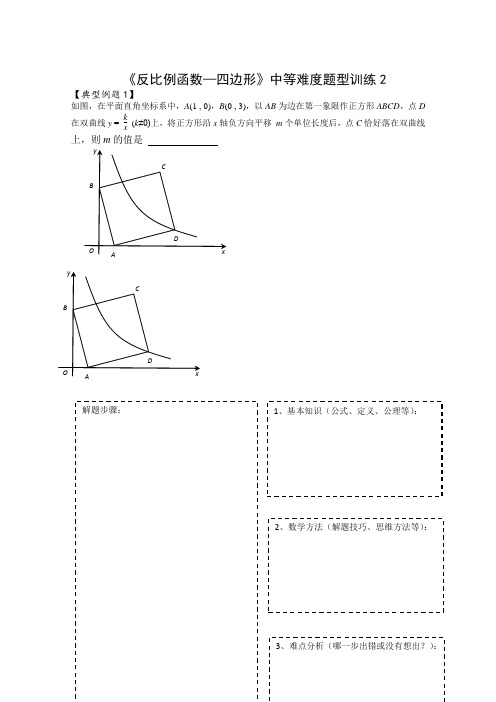
《反比例函数—四边形》中等难度题型训练2【典型例题1】如图,在平面直角坐标系中,A (1 , 0),B (0 , 3),以AB 为边在第一象限作正方形ABCD ,点D在双曲线y = kx(k ≠0)上,将正方形沿x 轴负方向平移 m 个单位长度后,点C 恰好落在双曲线上,则m 的值是【类型训练1A 】如图,在平面直角坐标系中,A (2 , 0),B (0 , 6),以AB 为边在第一象限作矩形ABCD ,AD=10,点D 在双曲线y = kx(k ≠0)上,将矩形沿x 轴负方向平移 a 个单位长度后,点C 恰好落在双曲线上,则a 的值是3、难点分析(哪一步出错或没有想出?):【类型训练1B】(2016达州)如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为.解题步骤:1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):3、难点分析(哪一步出错或没有想出?):【变式训练1】如上图,已知反比例函数xy 1 的图像上有一点P (P 点在第一象限),过点P分别作x 轴和y 轴的垂线,垂足分别为A 、B ,使四边形OAPB 为正方形。
又在反比例函数的图像上有一点P 1,过点P 1分别作BP 和y 轴的垂线,垂足分别为A 1、B 1,使四边形BA 1P 1B 1为正方形,则点P 1的坐标是 。
【变式训练2】正方形的A 1B 1P 1P 2顶点P 1、P 2在反比例函数xy 2=(x >0)的图象上,顶点A 1、B 1分别在x 轴、y 轴的正半轴上,再在其右侧作正方形P 2P 3A 2B 2,顶点P 3在反比例函数xy 2=(x >0)的图象上,顶点A 2在x 轴的正半轴上,则点P 3的坐标为 .1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):【变式训练3】如图,已知平行四边形OABC的面积为18,对角线AC 、OB 交于点D ,双曲线y = kx(k >0)经过C 、D 两点,则k =_________【变式训练4】如图,已知梯形ABCO 的底边AO 在x 轴上,BC ∥AO ,AB ⊥AO ,过点C 的双曲线ky x 交OB 于D ,且OD :DB =1 :2,若△OBC 的面积等于3,则k 的值【变式训练5】如图,在平面直角坐标系中,菱形ABOC 的顶点O 在坐标原点,边BO 在x 轴的负半轴上,∠BOC =60°,顶点C 的坐标为(m,,反比例函数ky x的图像与菱形对角线AO 交于D 点,连接BD ,当BD ⊥x 轴时,k 的值是xAxA【变式训练6】如图,边长为2的正方形ABCD 的顶点A 在y轴上,顶点D 在反比例函数xk y(x >0)的图像上,已知点B 的坐标是(56,511),则k 的值为【变式训练7】如图,菱形ABCD 的四个顶点均在坐标轴上,对角线AC 、BD 交于原点O ,DF ⊥AB 交AC 于点G ,反比例函数xy 3(x >0)经过线段DC 的中点E ,若BD = 4,则AG 的长为3341、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):【变式训练8】已知反比例函数y = kx图象经过点A (-1,-3),点P 是反比例函数图象在第一象限上的动点,以OA 、OP 为邻边作平行四边形OABP ,则平行四边形OABP 周长的最小【变式训练9】如图,反比例函数xky(x >0)的图象与矩形OABC 的边长AB 、BC 分别交于点E 、F ,已知S △FOC =3 且AE=BE ,则(1)k = . (2)、△OEF 的面积的值为29.3、难点分析(哪一步出错或没有想出?):1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):【变式训练10】如图,点A在双曲线23(0)y xx=>上,点B 在双曲线(0)ky xx=>上(点的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k=________3、难点分析(哪一步出错或没有想出?):解题步骤:1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):3、难点分析(哪一步出错或没有想出?):【变式训练11】如图,点A B 、在函数4(0)y x x=>的图象上,过点A B 、分别向x y 、轴作垂线.记矩形AEFP 面积为1S ,矩形BPCD 面积为S 2,阴影部分图形的面积恰好等于1S ,则12S S +=【变式训练12】如图,在平面直角坐标系中,点A 在函数)0,0(>>=x k xky 的图象上,过点A 作AB ∥x 轴交y 轴于点B ,连结OA ,过点B 作BC ∥OA 交x 轴于点C ,若△BOC 的面积是2,则k = .解题步骤: 1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):3、难点分析(哪一步出错或没有想出?):【变式训练13】如图,在平面直角坐标系中,矩形OEFG 的顶点F 的坐标为(4,2),将矩形OEFG 绕点O 逆时针旋转,使点F 落在y 轴上,得到矩形OMNP ,OM 与GF 相交于点A .若经过点A 的反比例函数)0(>=x xky 的图象交EF 于点B ,则点B 的坐标为解题步骤: 1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):3、难点分析(哪一步出错或没有想出?):【变式训练14】如图,平面直角坐标系中,平行四边形OABC 的顶点C (3,4),边OA 落在x 正半轴上,P 为线段AC 上一点,过点P 分别作DE ∥OC ,FG ∥OA 交平行四边形各边如图.若反比例函数xky的图象经过点D ,四边形BCFG 的面积为8,则k 的值为解题步骤: 1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):3、难点分析(哪一步出错或没有想出?):【变式训练15】如图,两个反比例函数x k y 1=和xky 2=(其中k 1>k 2>0)在第一象限内的图象依次是C l 和C 2,设点P 在C 1上,PC ⊥x 轴于点C ,交C 1于点A ,PD 上y 轴于点D ,交C 2于点B ,则四边形PAOB 的面积为解题步骤: 1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):3、难点分析(哪一步出错或没有想出?):【变式训练16】如图,矩形OABC的顶点A 在y轴上,C 在x 轴上,双曲线与AB 交于点D ,与BC 交于点E ,DF x ⊥轴于点F ,EG y ⊥轴于点G ,交DF 于点H ,若矩形OGHF 和矩形HDBE 的面积分别是1和2,则k 的值为xH FG E D CA OB yxH FG E D CA OB y【变式训练17】两个反比例函数y=x k 和y =x 1在第一象限内的图象如图所示,点P 在y =x k 的图象上,PC ⊥x 轴于点C ,交y =x 1的图象于点A ,PD ⊥y 轴于点D ,交y =x1的图象于点B ,当点P 在y =xk的图象上运动时,以下结论:①△ODB 与△OCA 的面积相等;②四边形P AOB 的面积不会发生变化;③P A 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是________________3、难点分析(哪一步出错或没有想出?):【变式训练18】如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A、C分别在x轴、y轴上,反比例函数(k≠0,x>0)的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:①△OCN≌△OAM;②ON=MN;③四边形DAMN与△MON面积相等;④若∠MON=45°,MN=2,则点C的坐标为(0,).其中正确结论的是①③④解题步骤:1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):3、难点分析(哪一步出错或没有想出?):【变式训练19】如图,正方形ABCD的边BC 在x 轴上,E 是对角线AC 、BD 的交点,反比例函数y = 2x(x >0)的图象经过A 、E 两点,则点D 的坐标为____________.【变式训练20】已知矩形OABC的面积为3100,它的对角线OB 与双曲线xky 相交于点D ,且OB ∶OD =5∶3,则k =_____【变式训练21】在矩形AOBC 中,OA =4,OB =6.分别以OB、OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是边BC 上的一个动点(不与端点重合),过F 点的反比例函数y = kx(k >0)的图象与AC 边交于点E ,将△CEF 沿EF 对折后,C 点恰好落在OB 上,则k =____________.【变式训练22】如图,点A(x 1,y 1)、B(x 2,y 2)都在双曲线y = kx(x >0)上,且x 2-x 1=4,y 1-y 2=2;分别过点A 、B 向x 轴、y 轴作垂线段,垂足分别为C 、D 、E 、F ,AC 与BF 相交于G 点,四边形FOCG 的面积为2,五边形AEODB 的面积为14,那么双曲线的解析式为_______________.【变式训练23】已知P 是函数y =12x (x >0)图象上一点,P A ⊥x 轴于点A ,交函数y =1x(x >0)图象于点M ,PB ⊥y 轴于点B ,交函数y = 1x(x >0)图象于点N (点M 、N 不重合).当△OMN 为直角【变式训练24】 (2013年武汉)如图,已知四边形ABCD 是平行四边形,BC =2AB ,A ,B 两点的坐标分别是(-1,0),(0,2),C ,D 两点在反比例函数)0(<=x xky 的图象上,则k 的值等于 .【变式训练25】如图,矩形OABC 的顶点A 、C 分别在x 、y 轴的正半轴上,点D 为对角线OB 的中点,反比例函数xky,在第一象限内的图象经过点D ,且与AB 、BC 分别交于E 、F 两点.若四边形BEDF 的面积为6,则k 的值为解题步骤: 1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):3、难点分析(哪一步出错或没有想出?):【变式训练26】如图,在平面直角坐标系中,正方形ABCD 的顶点O 在坐标原点,点B 的坐标为(1,4),点A 在第二象限,反比例函数xky的图象经过点A ,则k 的值是解题步骤: 1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):3、难点分析(哪一步出错或没有想出?):【变式训练27】(2015•凉山州)以正方形ABCD 两条对角线的交点O 为坐标原点,建立如图所示的平面直角坐标系,双曲线xy 3经过点D ,则正方形ABCD 的面积是解题步骤: 1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):3、难点分析(哪一步出错或没有想出?):【变式训练28】已知反比例函数xky =在第二象限内的图象如图所示,经过图象上两点A 、E 分别引y 轴与x 轴的垂线,交于点C ,且与y 轴与x 轴分别交于点M 、B .连接OC 交反比例函数图象于点D ,且21 ODCD ,连接OA ,OE ,如果△AOC 的面积是15,则△ADC 与△BOE 的面积和为解题步骤: 1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):3、难点分析(哪一步出错或没有想出?):【变式训练29】如图,矩形AOBC 的顶点坐标分别为A (0,3),O (0,0),B (4,0),C (4,3),动点F 在边BC 上(不与B 、C 重合),过点F 的反比例函数xky =的图象与边AC 交于点E ,直线EF 分别与y 轴和x 轴相交于点D 和G .给出下列命题:①若k =4,则△OEF 的面积为;②若821=k ,则点C 关于直线EF 的对称点在x 轴上;③满足题设的k 的取值范围是0<k ≤12;④若DE •EG =1225,则k =1.其中正确的命题的序号是 (写出所有正确命题的序号).1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):【变式训练30】如图,四边形OABC 是矩形,ADEF 是正方形,点A 、D 在x 轴的正半轴上,点C 在y 轴的正半轴上,点F 在AB 上,点B 、E 在反比例函数xky 的图象上,OA =1,OC =6,则正方形ADEF 的边长3、难点分析(哪一步出错或没有想出?):解题步骤: 1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):3、难点分析(哪一步出错或没有想出?):【变式训练31】(2013•自贡)如图,在函数)0(8>=x xy 的图象上有点P 1、P 2、P 3…、P n 、P n+1,点P 1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P 1、P 2、P 3…、P n 、P n+1分别作x 轴、y 轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为S 1、S 2、S 3…、S n ,则S 1= ,S n = .(用含n 的代数式表示)解题步骤: 1、基本知识(公式、定义、公理等):2、数学方法(解题技巧、思维方法等):3、难点分析(哪一步出错或没有想出?):。
苏教版八年级数学下复习反比例函数的四边形压轴题

反比例函数和四边形压轴题精选【精讲精练】y=2x 和反比例函数的图象交于点A (m ,-2).(1)求反比例函数的解析式;(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x 的取值范围;(3)若双曲线上点C (2,n )沿OA B ,判断四边形OABC 的形状并放在平面直角坐标系的第二象限内,若∠A=90°,AB=AC ,且A 、B (1(2DEF 位置,若B 、C 两点的对应点E 、F 的解析式; (3轴上的点M 和反比例函数图象上的点P ,的坐标;若不存在,请说明理由.,∠ADC=90°,AD=8,BC=6,点M 从点D 2从点B 出发,以每秒1个单位长度的速度向点运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N 作NP ⊥AD 于点P ,连接交NP 于点Q (1)AM=(2t 的值(3的直角顶点A (1)求k (2)如图2,过O 点作OD ⊥AC 于D 点,求22CD AD -的值; (3)如图3,点P 为x 轴上一动点.在(1)中的双曲线上是否存在一点Q ,使得△PAQ 是以点A 为直角顶点的等腰三角形.若存在,求出点P 、点Q 的坐标,若不存在,请说明理由.ABCD 中,AB=3,BC=4.动点P 从点A 出发沿AC 向终点C 运动,同时动点Q 从点B 出发沿BA 向点A 运动,到达A 点后立刻以原来的速度沿AB 返回.点P ,Q 运动速度均为每秒1个单位长度,当点P 到达点C 时停止运动,点Q 也同时停止.连结PQ ,设运动时间为t (t >0)秒.(1)求线段AC 的长度;(2)当点Q从B点向A点运动时(未到达A点),求△APQ的面积S关于t的函数关系式,并写出t的取值范围;(3)伴随着P,Q两点的运动,线段PQ的垂直平分线为l:①当l经过点A时,射线QP交AD于点E,求AE的长;②当l经过点B时,求t的值.1,已知点A(a,0),B(0,b),且a、b()230a b++=,?ABCD的边AD与y轴交于点E,且E为AD中点,双曲线kyx=经过C、D两点.(1)求k的值;(2)点P在双曲线k(3MN⊥HT,交°)如图①摆放,点(1)求∠(2)如图′F′,DE′交AC,试判断的值是否随着的变化而变化?如果不变,请求出从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把另一个与(1的完美分(2ACB的(3为底边的等腰三角形,求完美分割线CD的长。
反比例函数与特殊平行四边形--专题训练

反比例函数与特殊平行四边形1.如图,在平面直角坐标系中,O为坐标原点,已知▱AOBC的边OA在x轴上,BC与y轴正半轴交于点D,A(−9,0),C(−6,4),反比例函数y=k(x>0)经过点B.动点P从点B出发,沿B−O−D的折线以每秒1个单位x的速度匀速运动,动点Q同时从点A出发,沿A−O以每秒1个单位的速度匀速运动,点P,Q中有一个点到达终点,另一个点运动随即而停止.(1)求反比例函数的表达式.(2)在反比例函数的图象是否存在一点E,使得以B,D,P,E为顶点的四边形是平行四边形?若存在,请求出点P的坐标:若不存在,请说明理由.(3)过动点Q的直线始终与x轴垂直且与折线ACB交于点M,当t≥5时,在坐标平面内是否存在点N,使得以P,Q,M,N为顶点的四边形为菱形?若存在,请直接写出t的值;若不存在,请说明理由.2.(1)已知直线y =kx −2和抛物线y =x 2−2x +3,①当k =4时,求直线与抛物线的交点坐标;②当k 为何值时,直线与抛物线只有一个交点?(2)已知点A(a,0)是x 轴上的动点,B(0,42),以AB 为边在AB 右侧做正方形ABCD ,当正方形ABCD 的边与反比例函数y =4个交点时,试求a 的取值范围.3.在平面直角坐标系中,过点P (0,a )作直线l 分别交y =m x (m >0、x >0)、y =nx (n <0、x <0)于点M 、N ,(1)若m =2,MN ∥x 轴,S △MON =6,求n 的值;(2)若a =5,PM =PN ,点M 的横坐标为4,求m -n 的值;(3)如图,若m =4,n =-6,点A(d ,0)为x 轴的负半轴上一点,B 为x 轴上点A 右侧一点,AB =4,以AB 为一边向上作正方形ABCD ,若正方形ABCD 与y =m x (m >0、x >0)、y =n x (n <0、x <0)都有交点,求d 的范围.4.如图所示,一次函数y=kx+b的图象与反比例函数y=m交于A(1,t+2),B(﹣2t,﹣1)两点.x(1)求一次函数和反比例函数的函数表达式;(2)点C(x1,y1)和D(x2,y2)是反比例函数y=m x图象上任意两点,①若x1<x2<0,p=y1+y28,q=2x,试判断p、q的大小关系,并说明理由;1+x2②若x1<﹣4,0<x2<1,过C、D两点分别作直线AB的垂线,垂足分别为E、F,当x1x2=﹣4时,判断四边形CEFD的形状,并说明理由.5.正方形ABCD的顶点A(1,1),点C(3,3),反比例函数y=k(x>0).x(x>0)的关系式;(1)如图1,双曲线经过点D时求反比例函数y=kx(2)如图2,正方形ABCD向下平移得到正方形A′B′C′D′,边A'B'在x轴上,反比例函数y=k(x>0)的图象分x别交正方形A′B′C′D′的边C'D′、边B′C′于点F、E,①求△A'EF的面积;②如图3,x轴上一点P,是否存在△PEF是等腰三角形,若存在直接写出点P坐标,若不存在明理由.6.如图1,在平行四边形ABCD中,AD//x轴,AD=7,原点O是对角线AC的中点,顶点A的坐标为(﹣3,3),反比例函数y=kx(k≠0)在第一象限的图象过四边形ABCD的顶点D.(1)D点坐标为,k=.(2)①平行四边形ABCD的顶点B是否在反比例函数的图象上?为什么?②如图2,连接BD并延长,设直线BD解析式为y=k1x,根据图象直接写出不等式k1x<k x的x的取值范围;(3)是否存在两点P、Q分别在反比例函数图象的两支上,使得四边形AQCP是菱形?若存在,求出P、Q两点的坐标.7.如图,四边形ABCD的四个顶点分别在反比例函数y=mx 与y=nx(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P,已知点B的横坐标为4.(1)当m=4,n=16时.①若点P的纵坐标为2,求直线AB的函数表达式.②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.(2)四边形ABCD能否成为正方形?若能,求此时m、n之间的数量关系:若不能,试说明理由.8.如图,直线y=12x与y=kx(k>0)在第一象限内的交于点P(a,12a),且OP=20.(1)求a,k的值;(2)A为x正半轴上的点,B为直线y=12x上的一点,C为平面内一点;①当四边形OABC是以点P为对角线交点的矩形时,求直线AC的解析式;②当四边形OABC是以点P为对角线交点的菱形时,直接写出点A、C的坐标,并判断点C是否在y=kx上.9.如图所示,M、N、P在第二象限,横坐标分别是﹣4、﹣2、﹣1,双曲线y=k过M、N、P三点,且MN=xNP.(1)求双曲线的解析式;于另一点Q,求Q点坐标;(2)过P点的直线l交x轴于A,交y轴于B,且PA=4AB,且交y=kx(3)以PN为边(顺时针方向)作正方形PNEF,平移正方形使N落在x轴上,点P、E对应的点P′、E'正好落上,求F对应点F′的坐标.在反比例函数y=bx10.我们知道求函数图象的交点坐标,可以联立两个函数解析式组成方程组,方程组的解就是交点的坐标.如:求直线y=2x+3与y=﹣x+6的交点坐标,我们可以联立两个解析式得到方程组{y=2x+3y=−x+6,解得{x=1y=5,所以直线y=2x+3与y=﹣x+6的交点坐标为(1,5).请利用上述知识解决下列问题:(1)已知直线y=kx﹣2和抛物线y=x2﹣2x+3,①当k=4时,求直线与抛物线的交点坐标;②当k为何值时,直线与抛物线只有一个交点?(2)已知点A(a,0)是x轴上的动点,B(0,42),以AB为边在AB右侧做正方形ABCD,当正方形ABCD的边与反比例函数y4个交点时,试求a的取值范围.谢谢观看。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
读史使人明智,读诗使人灵秀,数学使人周密,科学使人深刻,伦理使人庄重,逻辑使人善1
图 5E D C
B A 反比例函数和梯形
1.如图,将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去,结果如下表,则a n =
(用含n 的代数式表示). 所剪次数
1 2 3 4 …
n
正三角形个数 4 7
10 13 … a n
2.如图5,在梯形ABCD 中,AB ∥DC , DB 平分∠ADC ,过点A 作AE ∥BD ,交CD 的
延长线于点E ,且∠C =2∠E . (1)求证:梯形ABCD 是等腰梯形.
(2)若∠BDC =30°,AD =5,求CD 的长.
2.如图3,在梯形ABCD 中,AD BC ∥,EA AD ⊥,M 是AE 上一点,BAE MCE =∠∠,
45MBE = ∠.
(1)求证:BE ME =.
(2)若7AB =,求MC 的长.
3.(7分)如图7,在梯形ABCD 中,AD ∥BC , AD DC AB ==,
120ADC ∠= .(1)(3分)求证:DC BD ⊥
(2)(4分)若4AB =,求梯形ABCD 的面积. 解:
图3
A
B
C
D
M
E
A D
B
C
读史使人明智,读诗使人灵秀,数学使人周密,科学使人深刻,伦理使人庄重,逻辑使人善2
4.如图,△AOB 和△COD 均为等腰直角三角形,∠AOB =∠COD =90º,D 在AB 上. (1)求证:△AOB ≌△COD ;(4分) (2)若AD =1,BD =2,求CD 的长.(3分)
5.如图,四边形OABC 是面积为4的正方形,函数k
y x
=(x >0)的图象经过点B .
(1)求k 的值;
(2)将正方形OABC 分别沿直线AB 、BC 翻折,得到正方形MABC ′、MA ′BC .设线段MC ′、
NA ′分别与函数k
y x
=(x >0)的图象交于点E 、F ,求线段EF 所在直线的解析式.
6.已知反比例函数y =
8
m x
-(m 为常数)的图象经过点A (-1,6). (1)求m 的值;
(2)如图9,过点A 作直线AC 与函数y =
8
m x
-的图象交于点B ,与x 轴交于点C ,且AB =2BC ,求点C 的坐标.
A
B
C D 图 O
读史使人明智,读诗使人灵秀,数学使人周密,科学使人深刻,伦理使人庄重,逻辑使人善3
D B C E
N
O A
M y
x
7.(湖南郴州)如图1,已知正比例函数和反比例函数的图像都经过点M (-2,1-),且P
(1-,-2)为双曲线上的一点,Q 为坐标平面上一动点,PA 垂直于x 轴,QB 垂直于y 轴,垂足分别是A 、B .
(1)写出正比例函数和反比例函数的关系式;
(2)当点Q 在直线MO 上运动时,直线MO 上是否存在这样的点Q ,使得△OBQ 与△OAP 面积相等?
如果存在,请求出点的坐标,如果不存在,请说明理由;
(3)如图2,当点Q 在第一象限中的双曲线上运动时,作以OP 、OQ 为邻边的平行四边形OPCQ ,
求平行四边形OPCQ 周长的最小值.
8(江苏省南通市)已知双曲线k y x =与直线1
4y x =相交于A 、B 两点.第一象限上的点M (m ,n )
(在A 点左侧)是双曲线k
y x
=上的动点.过点B 作BD ∥y 轴于点D.过N (0,-n )作NC ∥x
轴交双曲线k
y x
=于点E ,交BD 于点C.
(1)若点D 坐标是(-8,0),求A 、B 两点坐标及k 的值.
(2)若B 是CD 的中点,四边形OBCE 的面积为4,求直线CM 的解析式.
(3)设直线AM 、BM 分别与y 轴相交于P 、Q 两点,且MA =pMP ,MB =qMQ ,求p -q 的值.
图1
x y B
()
A O M Q P 图2 x
y ()
B
C
A O
M P Q
读史使人明智,读诗使人灵秀,数学使人周密,科学使人深刻,伦理使人庄重,逻辑使人善4
9.(2012上海)如图,在直角坐标平面内,函数m
y x
=
(0x >,m 是常数)的图象经过(14)A ,,()B a b ,,
其中1a >.过点A 作x 轴垂线,垂足为C ,过点B 作y 轴垂线,垂足为D ,连结AD ,DC ,CB .
(1)若ABD △的面积为4,求点B 的坐标; (2)求证:DC AB ∥;
10.如图,已知双曲线y=k/x 与直线y=kx 交于A 、B 两点,点A 在第一象限,试解答下列问题:
(1)若点A 的坐标为(4,2),则点B 的坐标为: .
(2)若点A 的横坐标为m ,则点B 的坐标可表示为: .
(3) 过原点O 作另一条直线l ,交双曲线于P,Q 两点,点P 在第一象限,如图2所示,试说明ABPQ 一定是平行四边形?
(4) 设点A 、P 的横坐标分别为m 、n, 四边形APBQ 可能是矩形吗?可能是正方形吗?若可能,求m ,n 应满足的条件;若不可能,请说明理由.
11.如图2,已知:∠MON=30°,点123,,A A A 在射线ON 上,点123,,B B B …..在射线OM 上,△112A B A 、△223A B A 、△334A B A ……均为等边三角形,若1OA =l ,则△667A B A 的边长为( )
x
C
O D B
A y
读史使人明智,读诗使人灵秀,数学使人周密,科学使人深刻,伦理使人庄重,逻辑使人善5
A 、6
B 、12
C 、32
D 、64
12.平行于直线y x =的直线l 不经过第四象限,且与函数3
(0)y x x
=>和图象交于点A ,过点A
作AB y ⊥轴于点B ,AC x ⊥轴于点C ,四边形ABOC 的周长为8.求直线l 的解析式.
13 如图,A,B 是双曲线y =k /x 上的点,A,B 两点的横坐标分别是a,2a ,线段AB 的延长线交于x 轴于点c ,若△AOC 的面积为9,则k 的值为____
A
B
O
C
y x
3
(0)y x x
=>
l。
