1.2.1函数的概念(第一课时)
人教版必修1函数的概念教案(第一课时)

1.2.1 函数的概念第一课时一,教材的地位与作用函数是描述客观世界变化规律的重要数学模型。
高中阶段不仅把函数看成变量之间的依赖关系,同时还用集合与对应的语言来刻画函数,函数的思想方法将贯穿于高中数学课程的始终。
函数的概念是抽象概括出的概念,通过大量的实例,培养学生从“特殊到一般”的综合归纳的能力,培养学生分析问题的能力,引导学生如何发现事物的本质,如何找到问题的突破口来解决问题。
二,教学目标1,知识与技能:(1)理解函数的概念及其符号表示,能够辨别函数的例证和反例(2)会求简单函数的定义域与值域(3)掌握构成函数的三要素,学会判别两个函数是否相等,理解函数的整体性2,过程与方法:(1)通过实例,进一步体会函数是描述变量之间的依赖关系的重要数学模型,在此基础上学习用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;(2)通过函数概念学习的过程,培养学生从“特殊到一般”的分析问题能力以及抽象概括能力3,情感态度与价值观让学生体会现实世界充满变化,感受数学的抽象概括之美。
三,教学重点与难点1,教学重点:函数的概念,构成函数的三要素2,教学难点:函数符号y=f(x)的理解四,教学方法分析1,教法分析:遵循建构主义观点的教学方式,即通过大量实例,按照从“特殊到一般”的认识规律,提出问题,大胆猜想,确定方向分组研究尝试验证,归纳总结,通过搭建新概念与学生原有认识结构间的桥梁,使学生在心理上得到认同,建立新的认识结构。
2,学法分析:倡议学生主动观察,积极思考,提出问题,大胆猜测,从而自主归纳小结。
在学习中培养自我的从“特殊到一般”的分析问题能力,感受数学的抽象概括之美。
五、教学过程1,复习回顾回顾初中所学函数(如一次函数y=ax+b a≠0等)及函数的概念:(传统定义:设在一个变化过程中有两个变量x与y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说y是x的函数,x叫做自变量);指出用函数可以描述变量之间的依赖关系;强调函数是描述客观世界变化规律的重要数学模型。
人教版数学高二-新课标 《函数的概念》 教学设计

1.2.1 函数的概念(第一课时)课 型:新授课 教学目标:(1)通过丰富实例,学习用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;(2)了解构成函数的三要素;(3)能够正确使用“区间”的符号表示某些集合。
教学重点:理解函数的模型化思想,用集合与对应的语言来刻画函数。
教学难点:理解函数的模型化思想,用集合与对应的语言来刻画函数。
教学过程:一、问题链接:1. 讨论:放学后骑自行车回家,在此实例中存在哪些变量?变量之间有什么关系? 2.回顾初中函数的定义:在一个变化过程中,有两个变量x 和y ,对于x 的每一个确定的值,y 都有唯一的值与之对应,此时y 是x 的函数,x 是自变量,y 是因变量。
表示方法有:解析法、列表法、图象法. 二、合作探究展示: 探究一:函数的概念:思考1:(课本P 15)给出三个实例:A .一枚炮弹发射,经26秒后落地击中目标,射高为845米,且炮弹距地面高度h (米)与时间t (秒)的变化规律是21305h t t =-。
B .近几十年,大气层中臭氧迅速减少,因而出现臭氧层空洞问题,图中曲线是南极上空臭氧层空洞面积的变化情况。
(见课本P 15图)C .国际上常用恩格尔系数(食物支出金额÷总支出金额)反映一个国家人民生活质量的高低。
“八五”计划以来我们城镇居民的恩格尔系数如下表。
(见课本P 16表)讨论:以上三个实例存在哪些变量?变量的变化范围分别是什么?两个变量之间存在着怎样的对应关系? 三个实例有什么共同点?归纳:三个实例变量之间的关系都可以描述为:对于数集A 中的每一个x ,按照某种对应关系f ,在数集B 中都与唯一确定的y 和它对应,记作::f A B → 函数的定义:设A 、B 是两个非空的数集,如果按照某种确定的对应关系f ,使对于集合A 中的任意一个数x ,在集合B 中都有唯一确定的数()f x 和它对应,那么称:f A B →为从集合A 到集合B 的一个函数(function ),记作:(),y f x x A =∈其中,x 叫自变量,x 的取值范围A 叫作定义域(domain ),与x 的值对应的y 值叫函数值,函数值的集合{()|}f x x A ∈叫值域(range )。
函数的概念-导学案

1.2.1函数的概念(第一课时)[预习内容]:认真阅读教材 P 15—18页。
深入理解本节的学习目标及重难点,认真独立完成本节的题目。
一.教学目标:1. 进一步体会函数是描述变量之间的依赖关系的重要数学模型,在此基础上学习用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;2. 了解构成函数的要素;3. 能够正确使用“区间”的符号表示某些集合。
重点:函数的概念;难点:对抽象符号()x f 的理解。
二.自学引入;1、初中学过函数的概念----你能叙述吗?函数有哪几种表示方法?初中学过哪些具体函数?例如:思考(1)1=y 是函数吗?(2)函数x y =与xx y 2=是同一个函数吗? 现在从集合的对应关系进一步学习函数及其构成。
2、阅读教材15-16页三个函数实例完成填空由实例一可知:对于数集 任一时间t 按照对应关系 在数集 中都有唯一确定的高度h 和它对应.由实例二可知:对于数集 每一时刻t 按照对应关系 在数集 中都有唯一确定的臭氧洞面积s 和它对应.由实例三可知:对于数集 每一时刻按照按对应关系 在 数集 中都有唯一确定的恩格尔系数和它对应.以上三个实例有什么不同点 其共同点是:3、从集合的观点叙述函数的概念。
一般地,设A ,B 是__________数集,如果按照__________________________,使对于集合中A __________________,在集合B 中都有________________________,那么就称B A f →:为从集合A 到集合B 的一个函数,记作.),(A x x f y ∈=其中,x 叫做自变量,x 的取值范围A 叫做函数的 ;与x 的值相对应的y 值叫做函数值,函数值的集合})({A x x f ∈叫做函数的 .显然,值域是集合B 的子集.4、概念理解概念巩固(1)1=y 是函数吗?(2)函数x y =与xx y 2=是同一个函数吗? (3)一次函数的定义域 值域反比例的定义域 值域 值域(4)要使函数y ,∴此函数的定义域为________. (5)还要有实际意义;一种练习本的单价为0.6元,买本子的个数x 与应付钱数y 之间的函数关系为________,其中x 的允许取值范围是________. 5、函数相等如果两个函数的定义域相同,并且对应关系完全一致,那么就称这两个函数相等.(1)只要两个函数的定义域相同,对应法则相同,其值域就 故判断两个函数是否相等时,一看定义域,二看对应法则.如y =1与y =x x不是相等函数,因为 y =3t +4与y =3x +4是相等函数,因为(2)求函数的定义域,一般是转化为解不等式或不等式组的问题,注意定义域是一个集合,其结果必须用集合或区间来表示.6.阅读教材P17填表.上是数轴上某一线段或射线上的所有点所对应的实数的取值集合,如{x |a <x ≤b }=(a ,b ],{x |x ≤b }=(-∞,b ].(1)实数a ,b 都叫相应区间的 。
函数的定义

对应法则: y ax
4ac b 2 y , 当a 0 4a B 2 4 ac b y , 当a 0 4a
2
bx c
x
函数的三要素:①定义域 ②值域 ③对应关系 函数的三要素作为判断两个函数是否是 同一函数的判断依据
, a (, a) _______ ( a , ) [ a , ) ( , ) 符号 _________ ______ _
判断:(正确的打“√”,错误的打“×”) (1)区间表示数集,数集一定能用区间表示. ( )
(2)数集{x|x≥2}可用区间表示为[2,+∞]. ( )
1.2 函数及其表示
1.2.1 函数的概念 第一课时 函数的概念
实例1 一枚炮弹发射后,经过26s落到地面击中目标.炮弹的射高为 845m,且炮弹距地面的高度h(单位:m)随时间t(单位:s)变化的 规律是
h 130t 5t 2 .
(1)你能得出炮弹飞行1s、5s、10s、20s时距离地面多高吗? (2)t的变化范围是多少? (3)可以得出什么结论?
(3)设 A= Z,B= Z, f:
x . x
【解题探究】1.当已知的对应关系用图象表示时,怎样判断其是否为函数 关系? 2.一般依据什么来说明一个对应关系是不是函数关系?
(1)是 (2)是 (3)不是
类型 二 用区间表示数集 【典型例题】 1.用区间表示数集{x|x≤2或x>3}为____________.
【拓展提升】用区间表示数集的两个注意点 (1)弄清区间的含义,掌握一般区间形式所对应的数集. (2)注意数集中的符号“≤”“≥”“<”及“>”与区间中的符号 “[”“]”“(”“)”的对应关系.
§1.2.1函数的概念(第1课时) 集体备课
§1.2.1函数的概念(第一课时)一、教学目标1. 通过实例,进一步体会函数是描述变量之间的依赖关系的重要数学模型,在此基础上学习用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;2. 了解构成函数的要素;3. 能够正确使用“区间”的符号表示某些集合;二、教学重点与难点:重点:理解函数的模型化思想,用集合与对应的语言来刻画函数;难点:符号“y=f(x)”的含义,区间表示;三、学法与教学用具1、学法:学生通过自学、思考、交流、讨论和概括,从而更好地完成本节课的教学目标 .2、教学用具:电脑投影仪 .四、教学思路(一)复习引入1、复习初中所学函数的概念,强调函数的模型化思想;(先提问后放幻灯片设在一个变化过程中有两个变量x与y,如果对于x的每一个值,y都有唯一的值与它对应,则称x是自变量,y是x的函数;2、阅读引例,体会函数是描述客观事物变化规律的数学模型的思想:引例1:一枚炮弹发射后,经过26s落到地面击中目标,炮弹的射高为845m,且炮弹距地面的高度h(单位:m)随时间t(单位:s)变化的规律是:h=130t-5t2 (*)(板书)这里,炮弹飞行时间t的变化范围是数集A={t|0≤t≤26},炮弹距地面的高度h的变化范围是数集B ={h|0≤h≤845}.从问题的实际意义可知,对于数集A中的任意一个时间t,按照对应关系(*),在数集B中都有唯一的高度h和它对应。
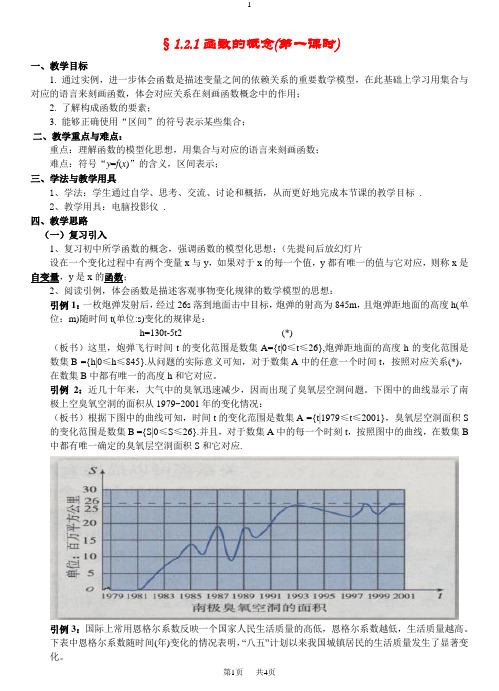
引例2:近几十年来,大气中的臭氧迅速减少,因而出现了臭氧层空洞问题。
下图中的曲线显示了南极上空臭氧空洞的面积从1979~2001年的变化情况:(板书)根据下图中的曲线可知,时间t的变化范围是数集A ={t|1979≤t≤2001},臭氧层空洞面积S 的变化范围是数集B ={S|0≤S≤26}.并且,对于数集A中的每一个时刻t,按照图中的曲线,在数集B 中都有唯一确定的臭氧层空洞面积S和它对应.引例3:国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高。
高中数学新课标人教A版必修一:1.2.1 函数的概念 课件 (共16张PPT)

3 两个函数相同:当且仅当三要素相同。
例1 y= x 3 + 2 x 是函数吗?
——函数的定义域和值域均为非空的数集
例2 y=± x 是函数吗?
——对于函数定义域中每一个x,值域中都有 唯一确定的y和它对应。(不是函数)
练习:下列图形哪个可以表示函数的图象?
y
0x
A
y
0x
B
y
0x
C
四、如何求函数的定义域
想 f(1)表示什么意思? 一 想 f(1)与f(x)有什么区别?
一般地,f(a)表示当x=a时的函数值,是一个常量。 f(x)表示自变量x的函数,一般情况下是变量。 14
例:已知函数f(x)=3x2-5x+2.求f(0),f(a)和 f(a+1)
想一想 f[f(0)]等于多少?
练习:f(x)=|x+1|,则f(-1) +f(1)等于多少?
六、小结
1 函数的概念
2 定义域的求法 3 对函数符号y=f(x)的理解
七、布置作业
一、复习回顾
初中时学过函数的概念,它是怎样叙述的? 设在一个变化过程中,有两个变量x和y,
如果对于x的每一个值,y都有唯一的值与 它对应.那么就说y是x的函数. 其中x叫做 自变量,y是函数值。
想一想
y=1(x∈R)是函数吗?
Go to 13
研究函数y 1 x
为了研究的方便,取几组特殊的x值和对应的y值
当x=1时,y=1
当x=2时,y
1 2
当xБайду номын сангаас3时,y 1
3
A
B
y1
x
1
1
1
2
2
(绝对经典)1.2.1函数的概念

a, b
x a x b 写成开区间
a, b
x a x b 写成左闭右开区间a,b
x a x b 写成左开右闭区间 a,b
另外还有 ,,a,,a,,,b,,b
例 1.已知函数 f x x 1 1
函数值的集合 f x x A 叫做函数的值域,注意,值域是 B 的子集。
指出下列函数的定义域和值域,对应法则
(1) y 2x 1
(2) f x x2 2x 2
(3) g(x) 3 x
(4) h x 1 x 1
区间的概念及其写法介绍
当 a b 得时候
(3)求 f x 1 并指出其中 x 的范围。
例 2.下列函数中,哪些函数与函数 f x x 相同
2
(1) g x x
(2) h x x2
(3) t t2
t
(4) k s 3 s3
1.2.1函数的概念
定义:一般地,设 A, B 是非空数集,如果按照某种确定的对应关系 f ,使对于集合 A 中
的任意一个数 x ,在集合 B 中,都有唯一确定的数 f x 和它对应,那么就称 f : A B
为从集合 A 到集合 B 的一个函数,记作
y f x,xA
其中 x 叫做自变量, x 的取值范围 A 叫定义域,与 x 的值相对应的 y 值叫做函数值,
x 2
(1)求 f x 的定义域;
(2)求
f
3 ,
f
2 3
(3)求 f x 1 并指出其中 x 的范围。
例 1.已知函数 f x x 1 1 x 20
函数的概念(一)

第一章集合与函数的概念1.2 函数及其表示1.2.1 函数的概念(第一课时)一、学习目标1、正确理解函数的概念,能用集合与对应的语言来刻画函数,了解构成函数的三要素;2、会判断某个对应关系能否构成函数关系,会求定义域,函数值。
二、学习过程(一)复习引入新课1.初中学习过哪些函数?函数解析式(对应关系)定义域值域2、初中函数的概念在某变化过程中,有两个变量x、y,如果每一个x ,相应地有唯一的一个y 值与之对应,那么x是自变量,y是因变量。
此时就称y 是x 的函数。
(二)尝试学习1、阅读课本15页到16页,归纳概括出三个实例的共同特征。
2、函数的定义设A 、B 是两个( )的( )集,如果按照某种对应关系f ,使对于集合A 中的( )数x ,在集合B 中都有( )的数f(x)和它对应,那么就称f: A →B 为从集合A 到集合B 的一个函数, 记作 :y=f(x),x ∈A 。
其中x 叫做自变量,x 的取值范围A 叫做函数的( ),与x 的值对应的y 值叫做函数值,函数值的集合 ( )叫做( )值域是集合B 的( )集。
注意:(1)可以“一对一”,“多对一”,但不可以“一对多”; (2)函数的三要素:定义域、值域、对应关系;(3)y=f(x)表示y 是x 的函数,可简记为f(x),有时也可以用 F (x ),g(x)来表示函数; (4)f(a)表示自变量x=a 时的函数值; 3、讲解课本17页例1(三)分组讨论、合作释疑1、下列图像中不能作为函数y=f(x)的图像的是( )xyo xy oxy oxy oBACD的定义域、求函数312)(2-+-=x x x f )]1([,21)(3f f x x x f 求、已知函数++=(四)小组展示,教师点拨小结(1)求定义域要注意:①偶次方根下的被开方数为非负数,分式中分母不为零; ②如果f(x)由几部分组成,定义域应为使各部分都有意义的x 的集合的交集 ;③在实际问题中,要考虑自变量具有实际意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{x|0≤x≤10}
关系.( y=4.9x2 )
{y|0≤y≤490}
{x|0≤x≤24}
{t|-2≤t≤9}
对于集合A中的每一个元素 x,在集合B中都有唯一的元素 y 和它对应,
记作: f:A→B
函数的概念
1. 定义 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的 任意一个数x,在集合B中都有唯一确定 的数 f(x)和它对应,那么就称f:A→B为 从集合A到集合B的一个函数
在这些变化着的现象中,都存在着两个变量,当 一个变量变化时,另一个变量随之发生变化.
在初中数学中有没有学过类似的知识? 函数
函数的概念
初中函数的概念
设在一个变化过程中有两个变量x与y, 如果对 于x的每一个值, y都有唯一的值与它对应, 那么就 说 y是 x的函数, x叫做自变量.
下面再来看一些函数的实际例子。
函数的概念
年份
22001188
22001177
22001166 2015 2015 2014 2014 2013 2013
人数(万人)
1177.5.5
1166..11
15.6 1144..88 14.0 14.0 13.8 13.8
函数的概念
年份 2018 2017 2016 2015 2014 2013
函数的概念
问题2:一物体在490米高的位置从静止开始下落, 下落的距离y(m)与下落时间x(s)之间近似地满足关 系式y=4.9x2. 若一物体下落2s,你能求出下落的距离吗?
函数的概念
问题3:某市一天24小时的气温变化图:
4时的气温是多少?全天的最高气温是多少?
函数的概念
在上面的三个问题中,是否确定了函数关系?
x
定义域{x|x≠0},值域{y|y≠0}.
函数的概念
2.已学函数的定义域和值域
⑶二次函数f(x)=ax2+bx+c (a≠0)
理 17.5万人 16.1万人 15.6万人 14.8万人 14.0万人 13.8万人
A
2018 2017 2016 2015
2014 2013
B
17.5
(1)会不会出现某个年份没
16.1 15.6
有与之对应的人数?
14.8 14.0
(2)会不会出现某个年份有
13.8 两个人数与之对应?
函数的概念
函数的概念
1. 定义 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的 任意一个数x,在集合B中都有唯一确定 的数 f(x)和它对应,那么就称f:A→B为 从集合A到集合B的一个函数
函数的概念
1. 定义 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的 任意一个数x,在集合B中都有唯一确定 的数 f(x)和它对应,那么就称f:A→B为 从集合A到集合B的一个函数
函数的概念
能否用集合语言来阐述这三个问题的共同特点?
年份 2018 2017 2016 2015 2014 2013
理 17.5万人 16.1万人 15.6万人 14.8万人 14.0万人 13.8万人
一个物体在490米高的位置从静止 开始下落,下落的距离y(m)与时间 x(s)的关系.( y=4.9x2 )
函数的概念
1. 定义 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的 任意一个数x,在集合B中都有唯一确定 的数 f(x)和它对应,那么就称f:A→B为 从集合A到集合B的一个函数
函数的概念
1. 定义 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的 任意一个数x,在集合B中都有唯一确定 的数 f(x)和它对应,那么就称f:A→B为 从集合A到集合B的一个函数
年份 人数(万人)
非空数集A
非空数集B
2018 17.5万人
2017 2016
16.1万人 15.6万人
{2013,2014 ,2015,2016,2017,2018}{17.5,16.1,15.6,14.8,14.0,13.8}
2015 14.8万人
2014 14.0万人
2013 13.8万人
一个物体在490米高的位置从静止开 始下落,下落的距离y(m)与时间x(s)的
与x值相对应的y的值叫做函数值,
函数值的集合{ f (x) | x A}叫做函数
的值域.
函数的概念
思考:
• 一次函数,反比例函数、二次函数 的定义域、值域各是什么?
函数的概念
2.已学函数的定义域和值域
⑴ 一次函数f(x)=ax+b(a≠0) 定义域R,值域R.
⑵ 反比例函数f (x) k (k 0)
函数的概念
问题1:2010—2018年,我国普通高等学校在四川本科招
生人数情况如下:
年份 2018 2017 2016 2015 2014 2013
理 17.5万人 16.1万人 15.6万人 14.8万人 14.0万人 13.8万人
试回答下列问题: (1)2013年我国在四川本科招生人数为多少? (2)哪一年的四川本科招生人数为15.6人? (3)2018年的四川招生人数与2017年相比增加了多少?
为什么?
年份 2018 2017 2016 2015 2014 2013
理 17.5万人 16.1万人 15.6万人 14.8万人 14.0万人 13.8万人
一个物体在490米高的位置从静止 开始下落,下落的距离y(m)与时间 x(s)的关系.( y=4.9x2 )
函数的概念
在上述的每一个问题中都含有两个变 量,当一个变量的取值确定后,另一个变 量的值随之惟一确定,每一个问题确定了 一个函数关系.
记作: y=f (x),xA
函数的概念
设A、B是非空的数集,如果按照某个确定的对应关 系f,使对于集合A中的任意一个数x,在集合B中 都有唯一确定的数 f(x)和它对应,那么就称 f:A→B为从集合A到集合B的一个函数, 记作: y=f (x),xA
其中,x叫做自变量,x的取值范围A叫
做函数的定义域;
函数的概念
1.2.1 函数的概念
第一课时
函数的概念
清晨,SUN从东方冉冉升起;
SUN
随着二氧化碳的大量排放,地球正在逐渐变暖;
中国的国内生产总值在逐年增长.
想一想:
上述三个现象中,从数学的角度看,你认为有哪些 共同特点?
函数的概念
清晨,太阳从东方冉冉升起; 随着二氧化碳的大量排放,地球正在逐渐变暖; 中国的国内生产总值在逐年增长.
