微波技术基础第二章课后答案
电磁场与微波技术第一二三章课后习题及部分答案

第 1 章 习 题1、 求函数()D Cz By Ax u +++=1的等值面方程。
解:根据等值面的定义:标量场中场值相同的空间点组成的曲面称为标量场的等值面,其方程为)( ),,(为常数c c z y x u =。
设常数E ,则,()E D Cz By Ax =+++1, 即:()1=+++D Cz By Ax E针对不同的常数E (不为0),对应不同的等值面。
2、 已知标量场xy u =,求场中与直线042=-+y x 相切的等值线方程。
解:根据等值线的定义可知:要求解标量场与直线相切的等值线方程,即是求解两个方程存在单解的条件,由直线方程可得:42+-=y x ,代入标量场C xy =,得到: 0422=+-C y y ,满足唯一解的条件:02416=⨯⨯-=∆C ,得到:2=C ,因此,满足条件的等值线方程为:2=xy3、 求矢量场z zy y y x xxy A ˆˆˆ222++=的矢量线方程。
解:由矢量线的微分方程:zy x A dz A dy A dx ==本题中,2xy A x =,y x A y 2=,2zy A z =, 则矢量线为:222zy dzy x dy xy dx ==,由此得到三个联立方程:x dy y dx =,z dz x dx =,zy dz x dy =2,解之,得到: 22y x =,z c x 1=,222x c y =,整理, y x ±=,z c x 1=,x c y 3±=它们代表一簇经过坐标原点的直线。
4、 求标量场z y z x u 2322+=在点M (2,0,-1)处沿z z y xy xx t ˆ3ˆˆ242+-=方向的方向导数。
解:由标量场方向导数的定义式:直角坐标系下,标量场u 在可微点M 处沿l 方向的方向导数为γβαcos cos cos zu y u x u l u ∂∂+∂∂+∂∂=∂∂α、β、γ分别是l 方向的方向角,即l 方向与z y xˆˆˆ、、的夹角。
廖承恩《微波技术基础》习题解答(最全的版本)

w.
λ=
2π υ p 1 = = = β f f µε r ε 0
ww
sc oc 2-5 在长度为 d 的无耗线上测得 Z in (d ) 、 Z in (d ) 和接实际负载时的
Z in (d ) ,证明
sc oc 假定 Z in (d ) = j100Ω , Z in (d ) = − j 25Ω , Z in (d ) = 75∠30°Ω ,求 Z L 。
解: ΓL =
Z L − Z0 =0.2-0.4j=0.4472exp(-j1.11)=0.4472∠-63.44° ZL + Z0 VSWR = ρ =
1+ | ΓL | = 2.618 1− | ΓL |
幅分布图,并求其最大值和最小值。
解:
ΓL =
ww
w.
V ( d ) = VL+ e jβd (1+ | ΓL | e j ( Φ L − 2 βd ) ) 1 ∴V (3λ / 4) = VL+ e j 3π / 2 (1 + e j (π −3π ) ) = VL+ ( −4 / 3) = 600 3 + VL = −450V
w.
60 23 ln = 33.3Ω 2.25 10
网
2 × 10 −1 = 552.6Ω 2 × 10 −3
co m
解法二:在空气中υ p 所以 Z 0 =
= 3 ×108
1 1 = = 55.6Ω 8 υ p C1 3 × 10 × 60 × 10 −12
L1 =
Z0 55.6 = = 1.85 × 10 − 7 H 8 υ p 3 × 10
课
Ω;其输入端电压为 600V、试画出沿线电压、电流和阻抗的振
微波技术习题解答

微波技术习题解答第1章练习题1.1 无耗传输线的特性阻抗Z0= 100()。
根据给出的已知数据,分别写出传输线上电压、电流的复数和瞬时形式的表达式:(1) R L= 100 (),I L = e j0(mA);(2) R L = 50(),V L = 100e j0(mV);(3) V L = 200e j0 (mV),I L = 0(mA)。
解:本题应用到下列公式:(1)(2)(3)(1) 根据已知条件,可得:V L = I L R L = 100(mV),复数表达式为:瞬时表达式为:(2) 根据已知条件,可得:复数表达式为:瞬时表达式为:(3) 根据已知条件,可得:复数表达式为:瞬时表达式为:1.2 无耗传输线的特性阻抗Z0 = 100(),负载电流I L = j(A),负载阻抗Z L = j100()。
试求:(1) 把传输线上的电压V(z)、电流I(z)写成入射波与反射波之和的形式;(2) 利用欧拉公式改写成纯驻波的形式。
解:根据已知条件,可得:V L = I L Z L = j(j100) = 100(V),1.3 无耗传输线的特性阻抗Z0 = 75(),传输线上电压、电流分布表达式分别为试求:(1) 利用欧拉公式把电压、电流分布表达式改写成入射波与反射波之和的形式;(2) 计算负载电压V L、电流I L和阻抗Z L;(3) 把(1)的结果改写成瞬时值形式。
解:根据已知条件求负载电压和电流:电压入射波和反射波的复振幅为(1) 入射波与反射波之和形式的电压、电流分布表达式(2) 负载电压、电流和阻抗V L = V(0) = 150j75,I L = I(0) = 2 + j(3) 瞬时值形式的电压、电流分布表达式1.4 无耗传输线特性阻抗Z0 = 50(),已知在距离负载z1= p/8处的反射系数为 (z1)= j0.5。
试求(1) 传输线上任意观察点z处的反射系数(z)和等效阻抗Z(z);(2) 利用负载反射系数 L计算负载阻抗Z L;(3) 通过等效阻抗Z(z)计算负载阻抗Z L。
微波技术与天线习题答案第二章电子工业出版社

第二章2-1 答: 将微波元件等效为网络进行分析,就是用等效电路网络参数代替原微波元件对原系统的影响。
它可将复杂的场分析变成简单易行的路分析,为复杂的微波系统提供一种简单便捷的分析工具。
2-2 答: 波导等效为双线的等效条件是两者的传输功率相等,由于模式电压,电流不唯一,导致等效特性阻抗,等效输入阻抗也不唯一,而归一化阻抗仅由反射系数确定,反射系数是可唯一测量的微波参量。
因而归一化阻抗也是唯一可确定的物理量。
故引入归一化阻抗的概念。
2-3 答: 归一化电压U 与电流I 和不归一电压U ,电流I 所表示的功率要相等,由此可得U I,的定义为U I ,2-4 答: (a) 由121220.02U U I U I ==+ 得 10[]0.021A ⎡⎤=⎢⎥⎣⎦ (b) 由12212200U U I I I =+= 得 1200[]01A ⎡⎤=⎢⎥⎣⎦(c) 由12121U nU I I n== 得 0[]01/n A n ⎡⎤=⎢⎥⎣⎦ (d) 由 传输线方程已知终端条件的解双曲函数的形式,将j γβ=,11(),()z l z l U z U I z I ''==''==代入得1202122cos sin sin cos U lU jZ lI l I j U lI Z ββββ=+=+ 即 00cos sin []sin /cos ljZ l A j l Z l ββββ⎡⎤=⎢⎥⎣⎦当 /2l θβπ==时 0100[]0.010j A j ⎡⎤=⎢⎥⎣⎦(e) 将 l θβπ== 代入(d)中解 可得2-5 解: (a) 01/00[]00/0j n jn a j n j n ⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦(b) 010*******02020100/.0[]/0/00/.jZ jZ Z Z A j Z j Z Z Z -⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦2-6 解: (a)等效电路如图所示由 1221222U U j I I j U I =-+=+ 得 11221211()2211()22U I I j j U I I j j =-+-=+-即 1/21/2/2/2[]1/21/2/2/2j j jj Z j j j j --⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦ (b)等效电路如图所示 由1212U jI I jU == 得12210()()()0U j I U j I =+--=-+ ∴0[]0j Z j -⎡⎤=⎢⎥-⎣⎦(c)等效电路如图所示由 1221222U U J I I j U I =+=- 得 112212()22()22j jU I I j j U I I =---=-+-∴ /2/2[]/2/2j j Z j j --⎡⎤=⎢⎥-⎣⎦2-7 证: 由 111112U Z I Z I =+ ① 2121222U Z I Z I =+ ② 将 22L U Z I =-代入 ② 得 122122L IZ Z Z I -=+ ∴ 212121112111122in LU I Z Z Z Z Z I I Z Z ==+=-+ 2-8 证: 由 111112I Y U Y U =+ ① 212122I Y U Y U =+ ②将 22L I Y U =-代入②得 22121/L Y Y Y UU -=+ 即212122LU Y U Y Y =-- 代入①有 2-9 证: 由互易时 det[A]=1 可得即 12A x = 且 20xB +≠ 0B ≠2-10 证: ∵11121221212222U a U a I I a U a I =+=+ 且22L U Z I = ∴ 1112212111212122222122//L in L U a U I a a Z a Z I a U I a a Z a ++===++ 2-11 解: 设波节处的参考面为1T ' 则将参照面1T '内移到1T 1min1/4l θβπ==∴ 1211110.2j S S e j θ'==-由对称性可知 22110.2S j S =-= 由无耗网络的性质可知 22121112111,/2S S θθπ=-=± ∴ 12210.98S S ==±=±∴ 0.20.98[]0.980.2j S j -±⎡⎤=⎢⎥±-⎣⎦ 2-12 解: 插入相移 21arg S θπ== 插入衰减 2211()10lg0.175L dB dB S ==电压传输系数 210.98j T S e π== 输入驻波比 11111 1.51S S ρ+==-2-13 解: 由 0[]0j a j ⎡⎤=⎢⎥⎣⎦ 可知 0[]0j S j -⎡⎤=⎢⎥-⎣⎦ 由1212U jI I jU == 可得12210()()()0U j I U j I =+--=-+ 即 0[]0j Z j -⎡⎤=⎢⎥-⎣⎦由1221I jU I jU =-= 得 0[]0j Y j ⎡⎤=⎢⎥⎣⎦2-14 解: 插入驻波比 即为输入驻波比 即 111112212211111112212211,,[]011j S a a a aS aS a a a a ρ+⎡⎤+--===⎢⎥-+++⎣⎦∴ 1111, 2.622j S S j ρ====+2-15 解: 11l θβ= 111211122122[]j j j S e S e S S e S θθθ---⎡⎤'=⎢⎥⎣⎦2-16 解: 11l θβ=内移 22l θβ=外移 30θ=不动∴ 11211222122()111213()2212223313233[]j j j j j j j j S e S e S e S S e S e S e S e S e S θθθθθθθθθθ-----⎡⎤⎢⎥'=⎢⎥⎢⎥⎣⎦由 [][]S P S P '= 也可求得 其中 120000001j j e P e θθ-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦2-17 解: 代入式 (2-44a)可得∴ 2/31/3[]1/32/3S ±⎡⎤=⎢⎥±⎣⎦由 [][][1]S S +≠ 可知该网络是互易有耗的。
《微波技术与天线》傅文斌 习题答案第2章

第2章 微波传输线2.1什么是长线?如何区分长线和短线?举例说明。
答 长线是指几何长度大于或接近于相波长的传输线。
工程上常将1.0>l 的传输线视为长线,将1.0<l 的传输线视为短线。
例如,以几何长度为1m 的平行双线为例,当传输50Hz 的交流电时是短线,当传输300MHz 的微波时是长线。
2.2传输线的分布参数有哪些?分布参数分别与哪些因素有关?当无耗传输线的长度或工作频率改变时分布参数是否变化?答 长线的分布参数一般有四个:分布电阻R 1、分布电感L 1、分布电容C 1、分布电导G 1。
分布电容C 1(F/m )决定于导线截面尺寸,线间距及介质的介电常数。
分布电感L 1(H/m )决定于导线截面尺寸,线间距及介质的磁导率。
分布电阻R 1(Ω/m )决定于导线材料及导线的截面尺寸。
分布电导G 1(S/m ) 决定于导线周围介质材料的损耗。
当无耗传输线(R 1= 0,G 1= 0)的长度或工作频率改变时,分布参数不变。
2.3传输线电路如图所示。
问:图(a )中ab 间的阻抗0=ab Z 对吗?图(b )中问ab 间的阻抗∞=ab Z 对吗?为什么?答 都不对。
因为由于分布参数效应,传输线上的电压、电流随空间位置变化,使图(a )中ab 间的电压不一定为零,故ab 间的阻抗ab Z 不一定为零;使图(b )中a 点、b 点处的电流不一定为零,故ab 间的阻抗ab Z 不一定为无穷大。
2.4平行双线的直径为2mm ,间距为10cm ,周围介质为空气,求它的分布电感和分布电容。
解 由表2-1-1,L 1=1.84×10-6(H/m ),C 1=6.03×10-12(F/m )2.5写出长线方程的的解的几种基本形式。
长线方程的解的物理意义是什么? 答(1)复数形式()()()z L L z L L I Z U I Z U z U ββj 0j 0e 21e 21--++= ()()()z L L z L L I Z U Z I Z U Z z I ββj 00j 00e 21e 21---+=(2)三角函数形式()z Z I z U z U L L ββsin j cos 0+=()z I z Z U z I L Lββcos sin j+= (3)瞬时形式()()A z t A t z u ϕβω++=cos , ()B z t B ϕβω+-+cos ()()A z t Z A t z i ϕβω++=cos ,0()B z t Z B ϕβω+--cos 0其中,()L L I Z U A 021+=,()L L I Z U B 021-= 物理意义:传输线上的电压、电流以波动的形式存在,合成波等于入射波与反射波的叠加。
廖承恩《微波技术基础》习题解答(最全的版本)

(2) (3)
(4)
sc oc 当 Z in (d ) = j100Ω , Z in (d ) = − j 25Ω , Z in (d ) = 75∠30°Ω 时
1562 . 5 +1875 × 75 ×
3 + 62 . 5 j 2
sc oc 2-6 在长度为 d 的无耗线上测得 Z in (d ) = j50Ω , Z in (d ) = − j 50Ω ,接 实
第二三四六七章习题解答 第二章习题解答
2-1 某双导线的直径为 2mm,间距为 10cm,周围介质为空气,求 其特性阻抗。某同轴线的外导体内直径为 23mm,内导体外直径为 10mm, ,求其特性阻抗;若在内外导体之间填充εr 为 2.25 的 介 质 , 求其特性阻抗。
解:双导线:因为直径为 d=2mm=2×10-3m 间距为 D=10cm=10-1m 所以特性阻抗为
ZL = Z0
2 — 12 画出图 2— 1 所示电路沿线电压、电流和阻抗的振幅分布图,
所以 ΓL =
Z L '− Z 02 450 − 450 = =0 Z L '+ Z 02 450 + 450
电磁场与微波技术第一二三章课后习题及部分答案剖析

第 1 章 习 题1、 求函数()D Cz By Ax u +++=1的等值面方程。
解:根据等值面的定义:标量场中场值相同的空间点组成的曲面称为标量场的等值面,其方程为)( ),,(为常数c c z y x u =。
设常数E ,则,()E D Cz By Ax =+++1, 即:()1=+++D Cz By Ax E针对不同的常数E (不为0),对应不同的等值面。
2、 已知标量场xy u =,求场中与直线042=-+y x 相切的等值线方程。
解:根据等值线的定义可知:要求解标量场与直线相切的等值线方程,即是求解两个方程存在单解的条件,由直线方程可得:42+-=y x ,代入标量场C xy =,得到: 0422=+-C y y ,满足唯一解的条件:02416=⨯⨯-=∆C ,得到:2=C ,因此,满足条件的等值线方程为:2=xy3、 求矢量场z zy y y x xxy A ˆˆˆ222++=的矢量线方程。
解:由矢量线的微分方程:zy x A dz A dy A dx ==本题中,2xy A x =,y x A y 2=,2zy A z =,则矢量线为:222zy dzy x dy xy dx ==,由此得到三个联立方程:x dy y dx =,z dz x dx =,zy dz x dy =2,解之,得到: 22y x =,z c x 1=,222x c y =,整理, y x ±=,z c x 1=,x c y 3±=它们代表一簇经过坐标原点的直线。
4、 求标量场z y z x u 2322+=在点M (2,0,-1)处沿z z y xy xx t ˆ3ˆˆ242+-=方向的方向导数。
解:由标量场方向导数的定义式:直角坐标系下,标量场u 在可微点M 处沿l 方向的方向导数为γβαcos cos cos zuy u x u l u ∂∂+∂∂+∂∂=∂∂α、β、γ分别是l 方向的方向角,即l 方向与z y xˆˆˆ、、的夹角。
微波技术课后习题答案-第二章习题参考答案11
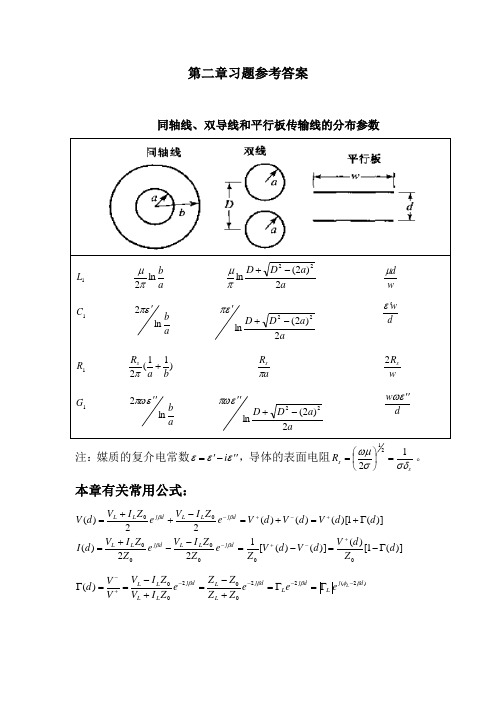
第二章习题参考答案同轴线、双导线和平行板传输线的分布参数注:媒质的复介电常数εεε''-'=i ,导体的表面电阻ss R σδσωμ1221=⎪⎭⎫⎝⎛=。
本章有关常用公式:)](1[)()]()([122)()](1)[()()(22)(00000000d Z d V d V d V Z e Z Z I V e Z Z I V d I d d V d V d V e Z I V e Z I V d V d j L L d j L L dj L L d j L L Γ-=-=--+=Γ+=+=-++=+-+-+-+-ββββ )2(2200200)(d j L d j L dj L L d j L L L L L e e e Z Z Z Z e Z I V Z I V VV d βφβββ----+-Γ=Γ=+-=+-==ΓL Lj L j L L L L L e e Z Z Z Z Z Z Z Z φφΓ=+-=+-=Γ0000dtg jZ Z dtg jZ Z Z d Z L L in ββ++=000)()(1)(1)()()(0d d Z d I d V d Z in Γ-Γ+==LL VV VSWR Γ-Γ+==11minmax2.1无耗或者低耗线的特性阻抗为110C L Z = 平行双导线的特性阻抗:aDa a D D a a D D Z r r rln 11202)2(ln 11202)2(ln 112222000εεεμεπ≈-+=-+=已知平行双导线的直径mm a 22=,间距cm D 10=,周围介质为空气(1=r ε),所以特性阻抗)(6.5521100ln 120ln11200Ω==≈a D Z rε 同轴线的特性阻抗:ab a b Z r rln 60ln 121000εεμεπ==已知同轴线外导体的内直径2mm b 23=,内导体的外直径2mm a 10=,中间填充空气(1=r ε):特性阻抗)(50210223ln 60ln 600Ω===abZ r ε中间填充介质(25.2=r ε):特性阻抗)(3.33210223ln 25.260ln 600Ω===a b Z r ε2.2对于无耗传输线线有相位常数μεωωβ===k C L 11,所以可求出相速度v k C L v p =====μεωβω1111,等于电磁波的传播速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答:圆波导 易于实现单模传输,但由于模极化面是不稳定的存在着模的极化简并,故实用中不用圆波导作为传输线。但是利用 模的极化简并可以构成一些特殊的波导元器件,如极化衰减器、极化变化器和微波铁氧体环行器等。
解:由于 ,空气填充,其工作波长 为
波导波长
利用上题中导出的
所以归一化负载阻抗
2-18什么叫做激励和耦合?
答:所谓激励就是在波导中建立所需波型的方法。相应地,从波导中取出所需波型的能量的方法称为耦合。激励和耦合是可逆的,激励装置也可以用作耦合装置。
2-19波导中的激励可以由哪几种方式?激励装置是什么?电磁场能否激励的判据是什么?
答:当波沿Z轴不能传播时呈截止状态,处于此状态时的波长叫截止波长,定义为 ;
当工作波长大于截止波长时,波数 ,此时电磁波不能在波导中传播;
当工作波长小于截止波长时,波数 ,此时电磁波能在波导传播;
2-7矩形波导中的截止波长 和波导波长 ,相速度 和群速度 有什么区别和联系?它们与哪些因素有关?
答:波导波长为 , 为截止波长
解:工作波长
波导波长
相移常数
故经过 后,产生的相移量 为
所以,中心频率上的时延 为
2-16已知空气填充BJ-100波导,工作波长 ,当终端接负载 时,测得驻波比 ,第一个电场波节点距负载 ,试求:
(1)波导中传输的波型;
(2)终端负载阻抗的归一化值。
解:(1) BJ-100为矩形波导,其横截面尺寸 。
,
根据矩形波导单模传输的条件,波导的尺寸由下式确定 ,
即
故可选用BJ-100,其模横截面尺寸为
选定尺寸后,计算 、 和
2-11空气填充的矩形波导BJ-100,其尺寸为 ,工作波长 ,问波导可能存在几种波型。若波导的横截尺寸变为 ,情况又怎样?
解:利用矩形波导的截止波长的计算公式,计算各种波型的截止波长;然后由传输条件 来判断波导中可能存在的波型。
2-20圆波导中的波型指数 和 的意义是什么,它们与矩形波导中的波型指数有何不同?
答:圆波导中m代表场沿圆周方向分布的整驻波数,n代表沿半径方向场分量出现的最大值个数。而在矩形波导中,m和n分别代表场强沿x轴和y轴方向分布的半波数。
2-21欲在圆波导中得到单模传输,应选择哪种波型,为什么?
答:在圆波导中实现单模传输一般选择 波型,因为 模的截止波长最长,易于实现单模传输。
2-1波导为什么不能传输TEM波?
答:一个波导系统若能传输TEM波型,则在该系统中必须能够存在静电荷静电核或恒定电流,而在单导体所构成的空心金属波导馆,不可能存在静电荷或恒定电流,因此也不可能传输TEM波型。
2-2什么叫波型?有哪几种波型?
答:波型是指每一种能够单独地在规则波导中存在的电磁场的一种分布状态。
几个低次模的截止波长分别为
根据波导中波的传输条件 ,故只能传输 波。
(2)矩形波导BJ-100, 波的波导波长为
第一个电场波节点距负载为 ,波节点处的归一化阻抗为 ,即
故
则
2-17已知一矩形波导馈电系统, ,空气填充,工作频率 ,端接负载 ,测得馈线上的驻波比 ,第一个电场最小点距负载 ,试求:终端负载阻抗的归一化值;
根据场的横向分量与纵向分量之间的关系式划分波型,主要有三种:
TEM波( , ),TE波( , ),TM波( , )
2-3何谓TEM波,TE波和TM波?其波阻抗和自由空间波阻抗有什么关系?
答: , 的为TEM波; , 为TE波; , 为TM波。
TE波阻抗:
TM波阻抗:
其中 为TEM波在无限答煤质中的波阻抗。
答:激励方式有三种,它们是电场激励、磁场激励和电流激励;激励装置为探针激励、环激励、小孔或缝激励,电子流激励。杆激励为电场激励,环为磁场激励,孔激励根据孔开在波导的不同位置,可能为单一的磁场激励或同时存在电场和磁场激励。
波导的激励原则是指使激励装置产生被激励波型的某一场分量或壁电流,从而使该波型在波导中建立。
所以可能存在的模式有: , , , 和 。
当尺寸为 时,各波型的截止波长为
所以可能存在的模式有: , , , , , , , , ,
2-12在空气填充的矩形波导,测得相邻两波节点之间的距离为22mm,求 。
解:因为在波导中相邻两波节之间的距离为 ,所以得到
2-13矩形波导BJ-100,其横截面尺寸为 ,在波导中传输 波,工作波长 ,试求截止波长 、相速 、群速 、传输功率P和波型阻抗 。
群速为 ,相速为 ,且 ,与c,工作波长 ,截止波长 有关。
2-8在矩形波导中不存在 和 这两种波型,为什么?
答:根据TM波的特点 , ,由TM波的场分量表达式可知
在m=0或n=0时, ,不符合TM波的特点。
2-9在空气填充的矩形波导( )中,要求只传输 波型,其条件是什么?若波导尺寸不变,而填充 , 的介质,只传输 波型的条件又是什么?
解:由于 的截止波长 ,而 的截止波长为a, 的截止波长为2b。若要保证单模传输 ,则由传输条件 , 与 均被截止,故有
同时
若波导中全填充 , 的介质,则ห้องสมุดไป่ตู้长变为 ,因此单模传输条件变为
同时
2-10一空气填充的矩形波导,要求只传输 波型,信号的工作频率为 ,试确定波导的尺寸,并求出 、 和 。
解:工作频率为 ,空气填充,速度 ,因此工作波长
解:
波的截止波长
波长的相速度
波的波导波长
波的传输功率
而 的 与 为
故
波的波型阻抗
由于
故
若用 表示 ,则有
所以,传输功率
2-14矩形波导的横截面尺寸为a=23mm,b=10mm,传输频率为10GHz的 波,求截止波长、波导波长、相速和波阻抗。如果频率稍微增大,上述参量如何变化?如果波导尺寸a和b发生变化,上述参量又如何变化?
解:矩形波导的截止波长为 ,
工作波长为
波导波长为
相速为
波阻抗为
当频率增大时,截止波长不变,波导波长降低,相速降低,波阻抗降低;
当a增大时,截止波长增大,波导波长降低,相速降低,波阻抗降低;
当b增大时,对各个参量无影响。
2-15若矩形波导横截面尺寸 ,有中心频率 的脉冲调制波通过 长的波导,求中心频率上的时延 。
2-4试将关系式 ,推导为 。
解:由 的场分量关系式 ( 与z无关)得:
利用关系式 可推出:
2-5波导的传输特性是指哪些参量?
答:传输特性是指传输条件、传播常数、传播速度、波导波长、波形阻抗、传输功率以及损耗和衰减等。
2-6何为波导的截止波长 ?当工作波长 大于或小于 时,波导的电磁波的特性有何不同?
