典型相关分析的实例(专业知识)
关于两组数据的相关性分析

关于两组数据的相关性分析我通过查阅资料和同学们分组讨论等总结性阐述了关于两组变量间相关关系的统计分析。
通过学习和阐述我对两组数据的相关性分析的问题有了比较深的了解.
研究典型相关分析的原理、典型成分的计算方法及计算步骤.把两组变量X与y转化为具有最大相关性的若干对典型成分,直到两组变量的相关性被分解.通过典型相关系数及其显著性检验.选择典型成分分析两组变量的相关性.实例表明只有第一个典型相关系数能通过显著性检验,而其它两个典型相关系数显著为零,放应选取第一对典型成分F,和Gl傲分析.典型相关分析是研究两组随机变量之间相关性的一种统计分析方法,它将两组随机变量间的相关信息更加充分地挖掘出来,分别在两组随机变量中提取相关性最大的两个成分,通过测定这两个成分之间的相关关系,可以推测两组随机变量的相关关系.典型相关分析的方法由霍特林于1936年首次提出.在许多实际问题中,需要研究两组变量之间的相关性.例如:研究成年男性体型与血压之间的关系;研究国民经济的投入要素与产出要素这两组变量之间的联系情况;研究临床症状与所患疾病;研究原材料质量与相应产品质量;研究居民营养与健康状况的关系;研究人体形态与人体功能的关系;研究身体特征与健身训练结果的关系.首先,我们应该进行变量指标的选择,如成年男性体型与血压之间的关系中,体型可用身高、体重、体型
指数等指标来表示,血压可用收缩压、舒张压、脉率等指标来表示;又如身体特征与健身训练结果的关系中,身体特征可用体重、腰围、脉搏表示,而训练结果可用单杠、弯曲、跳高等指标来体现.其次是样本数据的收集.最后,利用典型相关分析的原理进行研究.
相信这个对我以后的统计学的研究会有很大的帮助.。
《SPSS统计分析》第10章 相关分析

12.990 16.290 17.990 19.290
12.500 15.800 17.500 18.800
11.500 14.800 16.500 17.800
2.200 5.500 7.200 8.500
3.300 5.000 6.300
3.300
1.700 3.000
5.000 1.700
1.300
3.分析两个变量间线性关系的程度。往往因为第三个变量的作用,使相关系数不能真正反映两个 变量间的线性程度。 这是应该控制一个变量的变化求另两个变量间的相关系数,也就是说, 在第三个变量不变的情况下,两个变量的线性程度。
CORRELATIONS /VARIABLES=VCP with HEIGHT WEIGHT /PRINT=TWOTAIL NOSIG /MISSING=PAIRWISE .
6.300 3.000 1.300
1.800 1.500 3.200 4.500
2.700 6.000 7.700 9.000
5.000 8.300 10.000 11.300
12.000 15.300 17.000 18.300
9: 9 14.790 14.300 13.300
4.000 1.800 1.500 3.200 4.500
返回
典型相关分析
返回
典型相关分析概念
典型相关分析是用来描述两组随机变量间关 系的统计分析方法。
通过线性组合,可以将一组变量组合成一个 新的综合变量。虽然每组变量间的线性组合有无 数多个,但通过对其施加一些条件约束,能使其 具有确定性。
典型相关分析就是要找到使得这两个由线性 组合生成的变量之间的相关系数最大的系数。
学习通过编程解决偏相关问题
典型相关分析
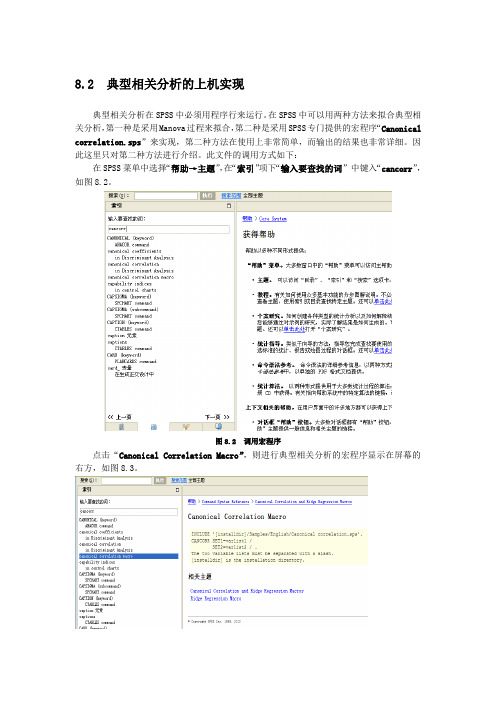
8.2 典型相关分析的上机实现典型相关分析在SPSS中必须用程序行来运行。
在SPSS中可以用两种方法来拟合典型相关分析,第一种是采用Manova过程来拟合,第二种是采用SPSS专门提供的宏程序“Canonical correlation.sps”来实现,第二种方法在使用上非常简单,而输出的结果也非常详细。
因此这里只对第二种方法进行介绍。
此文件的调用方式如下:在SPSS菜单中选择“帮助→主题”,在“索引”项下“输入要查找的词”中键入“cancorr”,如图8.2。
图8.2 调用宏程序点击“Canonical Correlation Macro”,则进行典型相关分析的宏程序显示在屏幕的右方,如图8.3。
图8.3 典型相关分析的宏程序此宏程序包含两个命令,每个命令用英文句点结束。
第一句是调用Cancorr.sps 程序命令。
第二句命令是执行典型相关分析程序,并定义典型相关分析中的两个变量组,每个变量名之间以空格分开。
子命令以“/”线开头,不要误打为“\”。
执行程序时,先选择这些命令,用光标点击运行菜单命令或点运行按钮,即可得到所有典型相关分析的结果。
在完成典型相关分析以后,会自动形成新的典型变量,第一对典型变量分别被命名为S1_CV001和S2_CV001,意为第一组(set1)的第一个典型变量和第二组的第一个典型变量。
其他典型变量S1_CV002和S2_CV002也是以同样形式标注分组属性及其序号的。
这些典型变量连同原来的观测变量将被自动存入一个暂时文件cc__tmp1中。
可通过命令打开此文件使用典型变量,最好将此文件另取文件名存为一个永久性文件,因为在下一次运行Cancrr 命令时,又会产生新的暂存文件将此覆盖。
8.3 典型相关分析的案例分析为了研究城镇居民家庭收入来源与消费性支出的关系,选取了反映城镇居民家庭收入来源与消费性支出的两组变量,收入组变量为:1x :工资性收入; 2x :经营净收入;3x :财产性收入; 4x :转移性收入;消费性支出组变量为:1y :食品; 2y :衣着;3y :居住; 4y :家庭设备用品及服务; 5y :医疗保健; 6y :交通和通信; 7y :教育文化娱乐服务; 8y :其它商品和服务;搜集了2010年我国各地区城镇居民家庭平均每人收入来源和全年消费性支出数据资料,如表8-1所示。
典型相关分析、冗余分析

两组变量的个数和性质可以是不同的
典型相关的基本思想
Nk心理
设有两组观测变量,通过权重与观测变量 对应相乘、然后将各项相加,分别对每一 组先建立一个线性组合,称典型变式。 每一个典型变式的值又构成一个新的典型 变量。
二者是一个事物的两个方面 变式:关系形式;变量:关注数值
Nk心理
冗余指数
不对称:典型相关平方相同;但两个变 式对自己一方观测变量的代表比例不同
冗余指数
变式与观测变量之间的测量,既是整体 指标(总方差百分比),又是平均指标 (平均每个观测变量方差的百分比)
冗余分析
典型相关:两个多元集团两元间分析; 冗余分析:这两元之间关系的分析
Spss实例与操作
Nk心理
典型冗余分析
冗余
如果一个变量可以由另一个变量的方差来解 释或预测,那么就说这个方差部分与另一变 量方差冗余 即:变量的这个方差部分可以由另一个变量 的一部分方差所预测或解释 常用相关形容词关系(不确切),相关系数 的平方(确定系数)属于冗余分析的范畴, 因为冗余是重叠方差
Nk心理
冗余
冗余
两个变式中的冗余:典型相关系数取平方。 它不是一侧变式与另一侧观测变量的共享方 差比,而是两侧对应变式之间的共享方差比
第二组变式1对第一组变量的 平均解释比例: 交叉负载 乘方 1 X1 -0.548 0.3003 X2 0.299 0.0894 合计 0.3897 平均值 0.1949
典型相关分析的统计指标
冗余指数(manova)
Nk心理
1.典型变式序号(CAN.VAR);2、3.每个变式所代表的某分组 的方差比例和累计方差比例,DE因变量组,CO自变量组;4、 5.另一组解释的方差比例以及累计方差比例
统计学专业基础课与专业课之间的典型相关分析

统计学专业基础课与专业课之间的典型相关分析摘要本文基于统计学系0301-0302两个班的66名学生17门课程(包括专业基础课和专业课)的考试成绩,运用典型相关分析法研究了统计学系基础课和专业课的相关程度。
通过运用统计分析软件SAS运行得到变量间的相关系数以及标准化后的典型相关系数,进而求出典型相关变量。
最后结合分析结果和实际情况对教学提了一点小小的建议。
关键词:基础课;专业课;典型相关分析;典型相关系数Canonical Correlation Analysis Between The Major and BasicSubjects of The Statistics MajorAbstractWith the method of canonical correlation analysis,I study about the correlation between the major and basic subjects of the statistics major.The research is based on the examination scores of66students of classes0301and0302who are in the major of statistics,including only17 subjects,the major and basic subjects.The article then gives the standard canonical correlations between the variables from which we can know the canonical correlative variables.In the end,I give some suggestions about education,according to the output of the analysis and the matter of fact.Key word:basic subject,major,canonical correlation,canonical coefficients1引言对于统计学系的学生来说,对数学理论的理解和掌握要求比较高,而且更重要的是要做到融会贯通,举一反三,学会理论联系实际,并利用统计分析的方法来解决日常生产生活中的问题,因而专业基础课程(如数学分析和高等代数等)的学习无疑是相当重要的,因为它直接关系到后续专业课的学习效果。
相关性分析报告(correlationanalysis)

相关性分析(correlation analysis)➢概述相关性分析可以用来验证两个变量间的线性关系,从相关系数r我们可以知道两个变量是否呈线性关系、线性关系的强弱,以及是正相关还是负相关。
➢适用场合·当你有成对的数字数据时;·当你画了一张散点图,发现数据有线性关系时;·当你想要用统计的方法测量数据是否落在一条线上时。
➢实施步骤尽管人工可以进行相关性分析,然而计算机软件可以使计算更简便。
按照以下的介绍来使用你的软件。
分析计算出相关性系数r,它介于-l到1之间。
·如果r接近0则两个变量没有线性相关性;·当r接近-l或者1时,说明两个变量线性关系很强;·正的r值代表当y值很小时x值也很小,当y值很大时r值也很大;·负的r值代表当y值很大时x值很小,反之亦然。
➢示例图表5.39到图表5.42给出了两个变量不同关系时的散点图。
图表5.39给出了一个近似完美的线性关系,r=0.98;图表5.40给出了一个弱的负线性相关关系,R=-0. 69,与图表5.39比较,数据散布在更宽的范围内;在图表5.41中,两个变量不相关,r=0.l5;在图表5.42中,相关性分析计算出相同的r值——=0.15,但是,在这个情况下显然两个变量是相关的,尽管不是线性的。
➢注意事项·如果,r=0,则变量不相关,但是可能有弯曲的相关性,如图表5.42那样。
为避免这种情况,首先画出数据的散点图来判断它们的关系。
相关性分析只对于存在线性关系的变量有意义。
·相关性分析可以证实两个变量间关系的强弱,但不能计算出那条回归线,如果想找到最符合的线,请参阅回归分析。
·对于系数的决定,回归分析中使用r2,它是相关系数r一的平方。
END。
护理典型案例分析范文(精选3篇)

护理典型案例分析范文(精选3篇)(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如工作总结、工作计划、合同协议、条据文书、策划方案、句子大全、作文大全、诗词歌赋、教案资料、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays for everyone, such as work summaries, work plans, contract agreements, doctrinal documents, planning plans, complete sentences, complete compositions, poems, songs, teaching materials, and other sample essays. If you want to learn about different sample formats and writing methods, please stay tuned!护理典型案例分析范文(精选3篇)护理典型案例分析范文第1篇“参与式方法”教学过程分组:教师可根据班级情况进行分组。
典型相关分析模型

即
XX
YY
66.552 49.719 57.038 2.205 35.257 42.971 34.086
49.719 62.695 77.848 2.576 42.971 66.638 40.610
XY
36.729 53.562 40.300 50.610 63.329 75.019 1.079 2.524
故得 第一对典型相关变量
0.61 0.667 0.827 = 0.111 0.288 0.019 0.108 0.032 0.332
X 0.031 X 1 0 .019 X 2 0.058 X 3 0 .072 X 4 a1 b1Y 0 .121Y1 0 .021Y2 0 .021Y3
则主要由脉搏次数所决定。 又由于第一典型相关系数 1 0.957 为正且很接近于 1、
X4, X3
Y1与 的系数
皆为正,说明每分钟的脉搏次数与胸围和吸烟量有非常密切的正相关关系,即胸围 越大、吸烟量越多,心跳就越快。
X 0 .031 X 1 0.019 X 2 0 .058 X 3 0.072 X 4 , a1
由于 X 4 , X 3 的系数相对较大,表明该项指标主要由胸围和每日的吸烟量所决定。 而做为与该项指标有最大线性相关关系的健康状况综合性指标
b1Y 0.121Y1 0.021Y2 0.021Y3
( 10.14 ) ( 10.15 ) ( 10.16 )
a Cov X , Y b a XY b
a D X a a XX a
bDY b b YY b
两综合性指标
a X
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
内容详尽
21
B矩阵(q×q)
0.2611 -0.0560 -0.0337 -0.0551 -0.0312 -0.0053 0.5572 0.1009 0.0034 -0.0543 -0.0632 -0.0843 0.0859 0.0013 0.1743 -0.1175 -0.0007 0.1183 0.2550 0.1490 -0.1052 0.1390 0.3531 0.2912 0.5573
Corr(X)=R11 Corr(X,Y)=R12
Corr(Y,X)=R21
R21 R12
内容详尽
Corr(Y)=R22
9
简单相关系数 描述两组变量的相关关系的缺点
➢只是孤立考虑单个X与单个Y间的相关 ,没有考虑X、Y变量组内部各变量间的 相关。
➢两组间有许多简单相关系数(实例为30 个),使问题显得复杂,难以从整体描 述。
内容详尽
10
(二)典型相关分析的思想
采用主成分思想寻找第i对典型(相关)变 量(Ui,Vi):
Ui
ai1 X1*
ai
2
X
* 2
ai
,
p
X
* p
aX *
Vi bi1Y1* bi2Y2* bi,qYq* bY *
i 1, 2, m,min( p, q) m
典型相关系数 i Corr(Ui ,Vi )
典型相关是简单相关、多重相关的推广; 或者说简单相关系数、复相关系数是典型相 关系数的特例。
内容详尽
3
典型相关是研究两组变
量之间相关性的一种统计分析 方法。也是一种降维技术。
由Hotelling (1935, 1936)最早 提出,Cooley and Lohnes (1971)、 Kshirsagar (1972)和 Mardia, Kent, and Bibby (1979) 推动了它
内容详尽
20
A矩阵(p×p)
0.5298 0.4586 0.3053 0.3986 -0.2919 -0.1778 -0.0912 -0.0701 -0.1669 -0.1939 -0.0007 -0.0168
0.2274 0.2739 0.5489 0.0840 0.5238 0.4468 0.0966 0.0376 0.0510 0.3877 -0.2523 -0.1759 -0.0915 -0.0979 -0.0669 -0.0377 0.0061 -0.0806 0.0949 0.1421 0.1757 -0.0210 0.2171 0.3142
身高(cm)、坐高、体重(kg)、胸围、 肩宽、盆骨宽分别为X1,X2,…,X6;
机能指标脉搏(次/分)、收缩压 (mmHg) 、舒张压(变音)、 舒张压(消 音)、肺活量(ml)分别为Y1,Y2,…, Y5。现欲研究这两组变量之间的相关 性。
内容详尽
6
内容详尽
7
简单相关系数矩阵
内容详尽
8
简单相关系数公式符号
b12 X2 b22
b13
X3
b23
典型典加型权相系典关数型系变数量
11
ρ11
η11
c11
Y1
c21
c12
22
ρ22
η2 2
c22
Y2
• 1与2是三个X变项的线性组合。
• η1与η2代表两内个容详Y尽变项的线性组合。
14
二、典型相关系数及其检验
内容详尽
15
(一)求解典型相关系数的步骤
1.
求X,Y变量组的相关阵
内容详尽
22
3. 求矩阵A、B的λ(相关系数 的平方)
A I B I 0
A、B有相同的非零特征值
内容详尽
23
B矩阵求λ (典型相关系数的平方)
典型相关分析
Canonical Correlation Analysis
内容详尽
1
一、引言
内容详尽
2
(一)何时采用典型相关分析
1. 两个随机变量Y与X
简单相关系数
2. 一个随机变量Y与一组随机变量X1,X2,…,
Xp
多重相关(复相关系数)
3. 一组随机变量Y1,Y2,…,Yq与另一组随
机变量X1,X2,…,Xp 典型(则)相关系数
2 =Corr(U2,V2)(与U1、V1 无关; 使U2与V2
间最大相关)
..... ……
第五对典型相关变量间的典型相关系数为:
5 =Corr(U5,V5) (与U1、V1 、…、 U4、V4
无关; U5与V5 间最大相关)
有:
1 2 5 0
内容详尽
12
典型相关变量的性质
1, i j
1, i j
典型变量系数或典型权重 a、b
内容详尽
11
X*1,X*2,…,X*p和Y*1,Y*2,…,Y*q分别为X1, X2,…,Xp和Y1,Y2,…,Yq的正态离差标准化值。 记第一对典型相关变量间的典型相关系数为:
1 =Corr(U1,V1)(使U1与V1 间最大相关)
第二对典型相关变量间的典型相关系数为:
数。
内容详尽
17
(二)典型相关系数计算实例
1. 求X,Y变量组的相关阵 R=
R11
R21
R12
R22
内容详尽
18
Corr(X)=R11 Corr(X,Y)=R12
Corr(Y,X)=R21
内容详尽
Corr(Y)=R22
19
2. 求矩阵A、B
A (R11)1 R12 (R22 )1 R21 B (R22 )1 R21(R11)1 R12
(1) Corr(Ui ,U j ) 0, i j Corr(Vi ,Vj ) 0, i j
(2)
典型相关系数, i j
Corr
(U
i
,V
j
)
0,
i j
【除前面(i 1)个CanR之外的最大者】
3 Ui、Vi的均数为0,方差为1。
内容详尽
13
(三)典型相关分析示意图
X1 b11 b21
的应用。
内容详尽
4
实例(X与Y地位相同)
X1, X2, …, Xp
Y1, Y2, …, Yq
1 临床症状
所患疾病
2 原材料质量
相应产品质量
3 居民营养
健康状况
4 生长发育(肺活量) 身体素质(跳高)
5 人体形态
人体功能
内容详尽
5
1985年中国28 省市城市男生
(19~22岁)的调查数据。记形态指标
R=
R11
R21
R12
R22
;
2. 求矩阵 A、B
A (R11)1 R12 (R22 )1 R21 B (R22 )1 R21(R11)1 R12
可以证明A、B有相同的非零特征根;
内容详尽
16
3. 求A或B的λi(相关系数的平方)与 i ,
i=1,…,m,即 i i2 ;
4. 求A、B关于λi的特征根向量即变量加权系
