数字信号处理 - 2012年最新程佩青第三版ppt课件合集
合集下载
数字信号处理程佩青第三版课件(全套课件)

j0n
M 0, 1, 2
表明复指数序列具有以2为周期的周期性,在 以后的研究中,频率域只考虑一个周期就够了。
7. 周期序列
如果对所有n存在一个最小的正整数N,使下面等
式成立: x(n) x(n N)
则称x(n)为周期序列,最小周期为N。
例:
x(n) sin( n)
4
x(n) sin[ (n 8)],
4
N 8
一般正弦序列的周期性
设 x(n) Asin( 0n )
式中,A为幅度,ω0为数字域频率,为初相。
那么 x(n N ) Asin[ 0 (n N ) ] Asin( 0n 0N )
如果 x(n) x(n N)
则 Asin( 0n ) Asin[ 0 (n N) ]
N (2 /0 )k N,k均取整数
xa(t) 0
xa(nT)
t
2T
0
t
T
这里 n 取整数。对于不同的 n 值,xa(nT) 是 一个有序的数字序列,该数字序列就是离散时间信 号。注意,这里的n取整数,非整数时无定义,另 外,在数值上它等于信号的采样值,即
x(n) xa (nT ), n
离散时间信号的表示方法:公式表示法、图形 表示法、集合符号表示法,如
线性卷积的计算
y(n) x(m)h(n m) x(n) h(n) m
计算它们的卷积的步骤如下: (1)折叠:先在哑变量坐标轴k上画出x(k)和
h(k),将h(k)以纵坐标为对称轴折叠成 h(-k)。 (2)移位:将h(-k)移位n,得h(n-k)。当n为
正数时,右移n;当n为负数时,左移n。 (3)相乘:将h(n-k)和x(k)的对应取样值相乘。 (4)相加:把所有的乘积累加起来,即得y(n)。
数字信号处理程佩青第三版课件第三章离散付氏变换-1

解 法 一 : 数 值 解
N1
X(k) x(n)WNnk
n0
7
3
x(n)W8nk
W
n 8
k
n0
n0
j2 k j2 2 k j2 3 k
1 e8 e8 e8
X (0 ) 4X ( 1 ) 1 j 2 1X (2 ) 0X (3 ) 1 j 2 1
X (4 ) 0X (5 ) 1 j 2 1X (6 ) 0X (7 ) 1 j 2 1
关于离散傅里叶变换(DFT):
序列x(n)在时域是有限长的(长度为N),它的离 散傅里叶变换X(k)也是离散、有限长的(长度也 为N)。
n为时域变量,k为频域变量。 离散傅里叶变换与离散傅里叶级数没有本质区别,
2、序列的移位
D F S [ x ( n m ) ] W N m k X ( k ) e j2 N m k X ( k )
N 1
证 : D F S [x(n m )] x(n m )W N n k
n 0
令inmN1mx(i)WNk(im)
im
N1
W N m k x(i)W N ki W N m kX(k)
同样,利用对称性
若 y (n ) x 1 (n )x 2 (n )
则
N 1
Y(k)D F S[y(n)] y(n)W N nk
n 0
N 1N l01X1(l)X2(kl)
N 1N l01X2(l)X1(kl)
§3.5 离散傅里叶变换
——有限长序列的离散频域表示
在进行DFS分析时,时域、频域序列都是无限 长的周期序列
x2 m … 5 4 3 2 1 0 5 4 3 2 1 0 … 10 x2 1m … 0 5 4 3 2 1 0 5 4 3 2 1 … 8 x2 2m … 1 0 5 4 3 2 1 0 5 4 3 2 … 6 x2 3m … 2 1 0 5 4 3 2 1 0 5 4 3 … 10 x2 4m … 3 2 1 0 5 4 3 2 1 0 5 4 … 14 x2 5m … 4 3 2 1 0 5 4 3 2 1 0 5 … 12
N1
X(k) x(n)WNnk
n0
7
3
x(n)W8nk
W
n 8
k
n0
n0
j2 k j2 2 k j2 3 k
1 e8 e8 e8
X (0 ) 4X ( 1 ) 1 j 2 1X (2 ) 0X (3 ) 1 j 2 1
X (4 ) 0X (5 ) 1 j 2 1X (6 ) 0X (7 ) 1 j 2 1
关于离散傅里叶变换(DFT):
序列x(n)在时域是有限长的(长度为N),它的离 散傅里叶变换X(k)也是离散、有限长的(长度也 为N)。
n为时域变量,k为频域变量。 离散傅里叶变换与离散傅里叶级数没有本质区别,
2、序列的移位
D F S [ x ( n m ) ] W N m k X ( k ) e j2 N m k X ( k )
N 1
证 : D F S [x(n m )] x(n m )W N n k
n 0
令inmN1mx(i)WNk(im)
im
N1
W N m k x(i)W N ki W N m kX(k)
同样,利用对称性
若 y (n ) x 1 (n )x 2 (n )
则
N 1
Y(k)D F S[y(n)] y(n)W N nk
n 0
N 1N l01X1(l)X2(kl)
N 1N l01X2(l)X1(kl)
§3.5 离散傅里叶变换
——有限长序列的离散频域表示
在进行DFS分析时,时域、频域序列都是无限 长的周期序列
x2 m … 5 4 3 2 1 0 5 4 3 2 1 0 … 10 x2 1m … 0 5 4 3 2 1 0 5 4 3 2 1 … 8 x2 2m … 1 0 5 4 3 2 1 0 5 4 3 2 … 6 x2 3m … 2 1 0 5 4 3 2 1 0 5 4 3 … 10 x2 4m … 3 2 1 0 5 4 3 2 1 0 5 4 … 14 x2 5m … 4 3 2 1 0 5 4 3 2 1 0 5 … 12
数字信号处理第三版课件第一章
❖ 设有序列x(n), 则x(-n)是以n=0为纵轴将x(n)反褶后的序列。
x(n)
3 2 11
-4 -3 -2 -1 0 1 2 3 4 5 6 n
3 x(-n)
2 1
-4 -3 -2 -1 0 1 2 3 4 5 6 n
x(n)
3
3
3
2
2
2
…1
1
1
…
-4 -3 -2 -1 0 1 2 3 4 5 6 n
-4 -3 -2 -1 0 1 2 3 4 5 6 n
2
x(n)= (n) +2(n-1)+3(n-2) x(m) (n m)
3 2
m0
1
(其中,x(0)=1, x(1)=2, x(2)=3)
-4 -3 -2 -1 0 1 2 3 4 5 6 n
2、单位阶跃序列u(n) -Unit step sequence
❖ x(mn) 为抽取序列(m>1) ❖ x(n/m)为插值序列(m<1)
例如:x(n)与x(2n)
x(n)
2 1
5 4 3
-2 -1 0 1 2
n
x(2n)
5
3
1
-2 -1 0 1 2
n
注意:
x(n) = x(t)|t=nT x(2n) = x(t)|t=2nT x(n/2) = x(t)|t=nT/2
❖ 一般,采样间隔是均匀的,用x(nT)表示离散时间信号在nT 点上的值,n为整数。由于x(nT)顺序存放在存储器中,我们通 常直接用x(n)表示离散时间信号-序列。
x(t)|t=nT=x(nT)
…… 0 T 2T 3T 4T 5T 6T 7T 8T 9T ……
x(n)
3 2 11
-4 -3 -2 -1 0 1 2 3 4 5 6 n
3 x(-n)
2 1
-4 -3 -2 -1 0 1 2 3 4 5 6 n
x(n)
3
3
3
2
2
2
…1
1
1
…
-4 -3 -2 -1 0 1 2 3 4 5 6 n
-4 -3 -2 -1 0 1 2 3 4 5 6 n
2
x(n)= (n) +2(n-1)+3(n-2) x(m) (n m)
3 2
m0
1
(其中,x(0)=1, x(1)=2, x(2)=3)
-4 -3 -2 -1 0 1 2 3 4 5 6 n
2、单位阶跃序列u(n) -Unit step sequence
❖ x(mn) 为抽取序列(m>1) ❖ x(n/m)为插值序列(m<1)
例如:x(n)与x(2n)
x(n)
2 1
5 4 3
-2 -1 0 1 2
n
x(2n)
5
3
1
-2 -1 0 1 2
n
注意:
x(n) = x(t)|t=nT x(2n) = x(t)|t=2nT x(n/2) = x(t)|t=nT/2
❖ 一般,采样间隔是均匀的,用x(nT)表示离散时间信号在nT 点上的值,n为整数。由于x(nT)顺序存放在存储器中,我们通 常直接用x(n)表示离散时间信号-序列。
x(t)|t=nT=x(nT)
…… 0 T 2T 3T 4T 5T 6T 7T 8T 9T ……
《数字信号处理-第三版》电子课件 第2章 信号的采样与重建

•按采样周期对模拟信号采样,并保持一定的时间间隔。 •理想的采样保持器输出是一阶梯型的波形,阶梯前沿的幅值与此 时刻的模拟信号保持一致。
• A/D转换器模块——模拟数字转换与量化
•图中小圆圈处的电平为量化电平,以最接近于当前实际电平的二 进制数码表示。 •A/D转换输出为数字信号(时间上离散,幅度上量化)
由于 s2时 X a, j T 1Xaj
所以
Yj T 1Xa(j )G (j )Xa(j )
这就是说,在时域低通滤波器的输出为 ytxat
注:实际上,理想低通滤波器是不可能实现的,但在满足一定精度的情 况下,总可用一个可实现网络去逼近。
y(t)xatgt n xa()(nT )g(t)d
3 s 0 . 5 i n 、 2 n c 0 . 3 n o 、 4 c 0 s . 5 o n 、 1 s 0 s . 7 0 i n n
离散时间序列仅由3个归一化数字角频率为 0.3 、 0.5、 0.7
的正弦序列组成。
v n 8 c 0 . 3 o n 5 c s 0 . 5 o n 0 . 6 s 1 4 s 0 . 7 0 i 3 n n 5
语音 音乐 视频
一些典型的数字信号处理系统
上限频率 fmax 500Hz
采样频率 fs 1-2 kHz
1kHz 2kHz 4kHz 20kHz 4MHz
2-4kHz 4-10 kHz 8-16 kHz 40-96 kHz 8-10 MHz
15
ቤተ መጻሕፍቲ ባይዱ
2、采样的恢复(恢复模拟信号)
如果采样频率高于奈奎斯特采样频率,即信号最高频率谱不超过折叠频率
滤除Ωs/2以上的分量,平滑滤波器应当逼近
H(j)sin /T2/2ejT
• A/D转换器模块——模拟数字转换与量化
•图中小圆圈处的电平为量化电平,以最接近于当前实际电平的二 进制数码表示。 •A/D转换输出为数字信号(时间上离散,幅度上量化)
由于 s2时 X a, j T 1Xaj
所以
Yj T 1Xa(j )G (j )Xa(j )
这就是说,在时域低通滤波器的输出为 ytxat
注:实际上,理想低通滤波器是不可能实现的,但在满足一定精度的情 况下,总可用一个可实现网络去逼近。
y(t)xatgt n xa()(nT )g(t)d
3 s 0 . 5 i n 、 2 n c 0 . 3 n o 、 4 c 0 s . 5 o n 、 1 s 0 s . 7 0 i n n
离散时间序列仅由3个归一化数字角频率为 0.3 、 0.5、 0.7
的正弦序列组成。
v n 8 c 0 . 3 o n 5 c s 0 . 5 o n 0 . 6 s 1 4 s 0 . 7 0 i 3 n n 5
语音 音乐 视频
一些典型的数字信号处理系统
上限频率 fmax 500Hz
采样频率 fs 1-2 kHz
1kHz 2kHz 4kHz 20kHz 4MHz
2-4kHz 4-10 kHz 8-16 kHz 40-96 kHz 8-10 MHz
15
ቤተ መጻሕፍቲ ባይዱ
2、采样的恢复(恢复模拟信号)
如果采样频率高于奈奎斯特采样频率,即信号最高频率谱不超过折叠频率
滤除Ωs/2以上的分量,平滑滤波器应当逼近
H(j)sin /T2/2ejT
数字信号处理程佩青第三版课件第六章IIR滤波器的设计方法

可整理ppt
6.2 最小与最大相位延时系统、最小 与最大相位超前系统
LSI系统的系统函数:
M
M
(1cmz1)
(zcm)
H(z)KmN1
Kz(NM)
m1 N
(1dkz1)
(zdk)
k1
ቤተ መጻሕፍቲ ባይዱk1
频率响应:
M
(ejcm)
H(ej)Kej(NM)m N 1
H(ej)ejarg[H(ej)]
(ejdk)
可k 整1理ppt
H (ej)H (ej)ej(j)
H ( e j ) 为幅频特性:表示信号通过该滤波器
后各频率成分的衰减情况
( j) 为相频特性:反映各频率成分通过滤波
器后在时间上的延时情况
可整理ppt
理想滤波器不可实现,只能以实际滤波器逼近
通带: c
11H(ej)1
阻带: st H(ej) 2
过渡带: cst
c :通带截止频率 s t :阻带截止频率
1 :通带容限
2 :阻带容限
可整理ppt
通带最大衰减: 1
12 0lgH H ((e ejj 0 c)) 2 0lgH (ej c) 2 0lg (11)
阻带最小衰减: 2
220lgH H ((e ej j0 st)) 20lgH (ejst) 20lg2
第六章 IIR滤波器的设计
可整理ppt
1
主要内容
理解数字滤波器的基本概念 了解最小相位延时系统 理解全通系统的特点及应用 掌握冲激响应不变法 掌握双线性变换法 掌握Butterworth、Chebyshev低通滤波器的特点 了解利用模拟滤波器设计IIR数字滤波器的设计过程 了解利用频带变换法设计各种类型数字滤波器的方法
6.2 最小与最大相位延时系统、最小 与最大相位超前系统
LSI系统的系统函数:
M
M
(1cmz1)
(zcm)
H(z)KmN1
Kz(NM)
m1 N
(1dkz1)
(zdk)
k1
ቤተ መጻሕፍቲ ባይዱk1
频率响应:
M
(ejcm)
H(ej)Kej(NM)m N 1
H(ej)ejarg[H(ej)]
(ejdk)
可k 整1理ppt
H (ej)H (ej)ej(j)
H ( e j ) 为幅频特性:表示信号通过该滤波器
后各频率成分的衰减情况
( j) 为相频特性:反映各频率成分通过滤波
器后在时间上的延时情况
可整理ppt
理想滤波器不可实现,只能以实际滤波器逼近
通带: c
11H(ej)1
阻带: st H(ej) 2
过渡带: cst
c :通带截止频率 s t :阻带截止频率
1 :通带容限
2 :阻带容限
可整理ppt
通带最大衰减: 1
12 0lgH H ((e ejj 0 c)) 2 0lgH (ej c) 2 0lg (11)
阻带最小衰减: 2
220lgH H ((e ej j0 st)) 20lgH (ejst) 20lg2
第六章 IIR滤波器的设计
可整理ppt
1
主要内容
理解数字滤波器的基本概念 了解最小相位延时系统 理解全通系统的特点及应用 掌握冲激响应不变法 掌握双线性变换法 掌握Butterworth、Chebyshev低通滤波器的特点 了解利用模拟滤波器设计IIR数字滤波器的设计过程 了解利用频带变换法设计各种类型数字滤波器的方法
数字信号处理程佩青第三版课件第二章z变换与离散时间傅里叶变换DTFT

(4 z)(z 1/ 4)
解:x(n) 1
2 j
z2
z n 1dz
c (4 z)(z 1/ 4)
c (Rx , Rx )
其中:F(z)
z2
zn1
z n 1
(4 z)(z 1/ 4)
(4 z)(z 1/ 4)
当n 1时
F (z)在围线c内只有一阶极点z 1
4
x(n)
Re
s[F
(
z
即X(z)在z=处收敛
0 4 Re[z]
x(n)是一个因果序列,即x(n) 0,n 0
同样当n 0时,由F (z)
z n 1
在c外无
(4 z)(z 1/ 4)
极点,且分母阶次比分子阶次高两阶以上,由
围线外极点留数为0可得x(n) 0
当n 0时 F(z)
z n 1
(4 z)(z 1/ 4)
z
4
4
z
z n 1
z
1/
4
z
4
4n2
15
x(n) 4n u(n 1) 4n2 u(n 2)
15
15
j Im[z]
C
1/ 4 0
4 Re[z]
例2:X (z)
z2
,z 4,求其z反变换
(4 z)(z 1/ 4)
j Im[z]
解: 收敛域是圆的外部
C
x(n)是右边序列
1/ 4
又lim X (z) 1, z
第二章 z变换和DTFT
本章主要内容:
1、z变换的定义及收敛域 2、z变换的反变换 3、z变换的基本性质和定理 4、离散信号的DTFT 5、z变换与DTFT的关系 6、离散系统的z变换法描述
数字信号处理-程佩青-PPT第一章
7)任意序列
x(n)能够表达成单位取样序列旳移位加权和,也可表达 成与单位取样序列旳卷积和。
x(n) x(m) (n m) x(n) (n)
m
例:x(n) 2 (n 1) (n) 1.5 (n 1) (n 2) 0.5 (n 3)
3、序列旳周期性
若对全部n存在一种最小旳正整数N,满足 x(n) x(n N ) n
m
x(m)T[ (n m)],线性性
T[ ai xi (n)] i
m
x(m)h(n m),
移不变性
aiT[xi (n)] i
m
x(n) h(n)
h(n) T[ (n)] h(n m) T[ (n m)]
x(n)
LSI y(n)
h(n)
y(n) x(n) h(n)
一种LSI系统能够用单位抽样响应h(n)来表征,任意输 入旳系统输出等于输入序列和该单位抽样响应h(n)旳 卷积和。
结论: 若有限长序列x(n)旳长度为N,h(n)旳长度为M, 则其卷积和旳长度L为:
L=N+M-1
互换律
4、LSI系统旳性质
x(n)
y(n)
h(n)
h(n)
y(n)
x(n)
y(n) x(n) h(n) h(n) x(n)
结合律
x(n) h1(n)
y(n) h2(n)
x(n) h2(n)
例:
x(n)=0.9
ne
j 3
n
6)正弦序列
x(n) Asin(0n )
模拟正弦信号:
xa (t) Asin(t )
x(n) xa (t) tnT Asin(nT )
0 T / fs 0:数字域频率
数字信号处理程佩青第三版第三章离散傅里叶变换精品PPT课件
1 N
N
1
X~
(k
)e
j
2 N
nk
k 0
N 1 ~x (k )WNnk
k 0
j 2
WN e N
二、DFS离散傅里级数的推导 意义
• 用数字计算机对信号进行频谱分析时, 要求信号必须以离散值作为输入,而且 上面讨论可知:只有第四种形式(DFS)对 数字信号处理有实用价值。
• 但如果将前三种形式要么在时域上采样 ,要么在频域上采样,变成离散函数, 就可以在计算机上应用。所以我们要先 了解如何从以上三种形式推出DFS.
• 周期连续时间信号 FS 非周期离散频谱密 度函数。
• 周期为Tp的周期性连续时间函数 x(t) 可展 成傅里叶级数X (jkW0) ,是离散非周期性频 谱 , 表 示为:
例子
• 通过以下 变 换 对 可 以 看 出 时 域 的 连 续 函 数造成频域是非周期的频谱函数,而频 域的离散频谱就与时域的周期时间函数
1.由非周期连续时间信号推出DFS
• 连续信号x(t)经过抽样为x(nT), 对离散
的时间信号进行DTFT得到周期连续频
谱密度函数。再经过抽样,得到周期
性离散频谱密度函数即为DFS.
x(t)
取样
x(t)
D T
F
T
X(ejw) t
采样
t X(ejΩT)
Ω w
2.周期性连续时间信号函数
• 周期性连续时间信号函数经采样后,得 到周期性的离散时间函数(DFS)。
三、本章主要讨论
• 离散傅里叶变换的推导 • 离散傅里叶变换的有关性质 • 离散傅里叶变换逼近连续时间信号的问题
第二节 傅里叶变换的几种形式
• 傅里叶变换: 建立以时间t为自变量的“信号” 与 以 频 率 f 为 自 变 量 的 “ 频 率 函 数 ”(频 谱) 之 间 的 某 种 变 换 关 系 .
全套电子课件:数字信号处理(第三版)
5、本书的主要内容
经典的数字信号处理限于线性时不变系统理 论, 数字滤波和FFT是常用方法。
随机信号处理:基于平稳高斯随机信号 目前DSP研究热点: 时变非线性系统、非平
稳信号、 非高斯信号 处理方法的发展:自适应滤波、 离散小波 变换、 高阶矩分析、盲处理、分形、混沌
理论
课程介绍
基础理论:离散时间信号与系统(ch1)(复习和强化)
(4)可以实现多维信号处理
利用庞大的存储单元,可以存储二维的图像信号或多维的阵列信号,实现二维或 多维的滤波及谱分析等。 4G移动通信:MIMO和OFDM
缺点
(1)增加了系统的复杂性。它需要模拟接口以及比较复杂的数字系统。 (2)应用的频率范围受到限制。主要是A/D转换的采样频率的限制。 (3)系统的功率消耗比较大。数字信号处理系统中集成了几十万甚至更多的晶体管 ,而模拟信号处理系统中大量使用的是电阻、电容、电感等无源器件,随着系统的复 杂性增加这一矛盾会更加突出。
其常中用zZ为[x(复n)变]表量示,对以序其列实x(部n)为的横Z坐变标换,,虚即部为纵坐标构成的平面为z平面。
Z[ x(n)] x(n) z n n
这种变换也称为双边 Z 变换,与此相应还有单边 Z 变换,单边 Z变换只是 对单边序列(n>=0部分)进行变换的Z变换,其定义为
X ( z) x(n) z n n0
上个世纪80年代用Apple II计算机用雷米兹交替算法设计一256阶的FIR滤波 器需要20多小时。
上个世纪90年代已经可以实时地在PC机上实现音视频的编解码。
4、DSP的发展与运用(续)
DSP发展的主要表现: (1) 由 简 单 的 运 算 走 向 复 杂 的 运 算 , 目 前 几十位乘几十位的全并行乘法器可以在数 个纳秒的时间内完成一次浮点乘法运算, 这无论在运算速度上和运算精度上均为复 杂的数字信号处理算法提供了先决条件;
数字信号处理程佩青PPT
二阶多项式
H ( z ) A k1 1 1 1 k k z z 1 1 2 2 k k z z 2 2 A kH k ( z )
当 M N 时 , 共 有 N 2 1 节
当零点为奇数时:
有一个 2k 0
当极点为奇数时:
有一个 2k 0
H ( z ) A k1 1 1 1 k k z z 1 1 2 2 k k z z 2 2 A kH k ( z )
k 1
k 1
k 1
A为 常 数
M M 1 2 M 2
p k 和 c k 分 别 为 实 数 零 、 极 点 N N 1 2 N 2
q k , q k * 和 d k , d k * 分 别 为 复 共 轭 零 、 极 点
将共轭成对的复数组合成二阶多项式,系数即为实数。 为采用相同结构的子网络,也将两个实零点/极点组合成
N1
H(z) h(n)zn n0
N n 2 1 0 1 h (n )z n h N 2 1 z N 2 1 n N N 1 1 1 h (n )z n 2 令 n N 1 m
N n 2 1 0 1 h (n ) z n z (N 1 n ) h N 2 1 z N 2 1
h(n)偶对称,取“+”
h(n)奇对称,取“
”,且
h
N 1 2
0
N为偶数时
N1
H(z) h(n)zn
N1 2
N1
h(n)zn h(n)zn
n0
n0
nN
N1
2
2
h(n)znz(N1n)
n0
四、数字滤波器的格型结构
格型结构的优点:
1)模块化结构便于实现高速并行处理
2)m阶格型滤波器可以产生1阶到m阶的m个横向 滤波器的输出性能
H ( z ) A k1 1 1 1 k k z z 1 1 2 2 k k z z 2 2 A kH k ( z )
当 M N 时 , 共 有 N 2 1 节
当零点为奇数时:
有一个 2k 0
当极点为奇数时:
有一个 2k 0
H ( z ) A k1 1 1 1 k k z z 1 1 2 2 k k z z 2 2 A kH k ( z )
k 1
k 1
k 1
A为 常 数
M M 1 2 M 2
p k 和 c k 分 别 为 实 数 零 、 极 点 N N 1 2 N 2
q k , q k * 和 d k , d k * 分 别 为 复 共 轭 零 、 极 点
将共轭成对的复数组合成二阶多项式,系数即为实数。 为采用相同结构的子网络,也将两个实零点/极点组合成
N1
H(z) h(n)zn n0
N n 2 1 0 1 h (n )z n h N 2 1 z N 2 1 n N N 1 1 1 h (n )z n 2 令 n N 1 m
N n 2 1 0 1 h (n ) z n z (N 1 n ) h N 2 1 z N 2 1
h(n)偶对称,取“+”
h(n)奇对称,取“
”,且
h
N 1 2
0
N为偶数时
N1
H(z) h(n)zn
N1 2
N1
h(n)zn h(n)zn
n0
n0
nN
N1
2
2
h(n)znz(N1n)
n0
四、数字滤波器的格型结构
格型结构的优点:
1)模块化结构便于实现高速并行处理
2)m阶格型滤波器可以产生1阶到m阶的m个横向 滤波器的输出性能
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x(n) xa (nT ), n
离散时间信号的表示方法:公式表示法、图形 表示法、集合符号表示法,如
x(n) ...1,2,3,7,8,9,...
二、常用序列
1. 单位抽样序列(n)
(n)
1, n 0, n
0 0
(t) 1/
0 t
(n)
1
0
n
(t)
(1)
t
0
2. 单位阶跃序列u(n)
等效为翻褶、移位、相乘和相加四个步骤。
1.2 线性移不变系统
x(n) 离散时间系统 y(n) T[•]
系统可定义为将输入序列x(n)映射成输出序列y(n)的 唯一变换或运算,并用T[]表示,即
y(n) T[x(n)]
在时域离散系统中,最重要、最常用的是线性时不变系统。
1.2.1 线性系统
若系统满足可加性与比例性,则称此系统为 离散时间线性系统。
n 0
2. 序列的乘法
x1(n)
n
0
x(n) x1(n) x2 (n) x2(n)
n
同序号的序列值逐项对应相乘 0
x1(n) ·x2(n)
n 0
3. 序列的移位
x(n)
y(n) x(n n0 )
n
0
当 n0>0 时,序列右移 ——延迟
x(n-2)
n
当 n0<0 时,序列左移 0 ——超前
u(n)
1, n 0, n
0 0
u(n) 0
u(t)
1
…
n
0
t
(n)与u(n)之间的关系
(n) u(n) u(n 1)
u(n) (n k) k 0
令n-k=m,有
n
u(n) (m) m
3. 矩形序列RN(n)
RN
(n)
1, 0,
0 n N 1 其它n
N为矩形序
列的长度
RN (n) u(n) u(n N )
4
x(n)
sin[
(n
8)],
4
N 8
一般正弦序列的周期性
设 x(n) Asin(0n )
式中,A为幅度,ω0为数字域频率,为初相。
那么 x(n N ) Asin[0 (n N ) ] Asin(0n 0 N )
如果 x(n) x(n N )
则 Asin(0n ) Asin[0 (n N ) ]
xa (t) sin(t), xa (t) tnT sin(nT )
T
fS
Ω为模拟角频率,单位为弧度/秒。T为信号的采 样周期,fs为信号的采样频率。
6. 复指数序列
x(n) e( j0 )n
这里ω为数字域频率,单位为弧度。当 =0时,
上式可表示成 x(n) e j0n
上式还可写成 x(n) cos(0n) j sin(0n)
0
m
点间补(m-1)个零值点,表示零值插值。
——插值序列
n n
6. 累加(等效积分)
n
y(n) x(k) k
7. 差分运算
前向差分 x(n) x(n 1) x(n) 后向差分 x(n) x(n) x(n 1)
8. 卷积和
y(n) x(n) h(n) x(m)h(n m) m
4. 序列的翻转
x(-n)是x(n)的翻转序列。x(-n)是以纵 轴(n=0)为对称轴将序列x(n)加以翻转。
x(n)
n 0
x(-n) n
0
5. 尺度变换
x(mn) 是 x(n) 序列每隔
m点取一点形成的,相当于 时间轴n压缩了m倍。
——抽取序列
x(n)
0 x(2n)
x n 是 x(n) 序列相邻抽样
2 无理数时,则正弦序列无周期。例如,sin 1 n
0
4
用单位采样序列来表示任意序列
x(n) x(m) (n m) m
(n
m
)
1,
0,
nm nm
三、 序列的运算
1. 序列的加法
x(n) x1(n) x2 (n)
同序号的序列值逐项对应相加
x1(n)
n 0
x2(n)
n 0
x1(n) +x2(n)
e e j0 2M n
j0n
M 0, 1, 2
表明复指数序列具有以2为周期的周期性,在 以后的研究中,频率域只考虑一个周期就够 了。
7. 周期序列
如果对所有n存在一个最小的正整数N,使下面等
式成立: x(n) x(n N )
则称x(n)为周期序列,最小周期为N。
例:
x(n) sin( n)
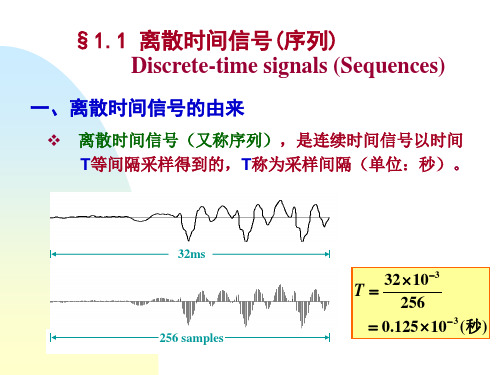
1.1 离散时间信号——序列
信号是传递信息的函数。针对信号的自变量和函数值的 取值,可分为三种信号:
(1)连续时间信号
-----自变量取连续值,而函数值可连续可离散。当函 数值是连续的,又常称模拟信号,如语音信号、电视信号 等。
(2)离散时间信号
-----自变量取离散值,而函数值连续。
(3)数字信号
-----自变量和函数值均取离散值。它是信号幅度离散 化了的离散时间信号。
一、离散时间信号——序列的概念
离散时间信号是对模拟信号 xa(t) 进行等间隔 采样获得的,采样间隔为T,得到:
xa(t) tnT xa(nT), n
xa(t) 0
xa(nT)
t
2T
0
t
T
这里 n 取整数。对于不同的 n 值,xa(nT) 是 一个有序的数字序列,该数字序列就是离散时间信 号。注意,这里的n取整数,非整数时无定义,另 外,在数值上它等于信号的采样值,即
R4(n)
N 1
RN (n) (n m) m0
n 012 3
4. 实指数序列
x(n) anu(n) ,a为实数
0<a<1
a>1
n
n
0
0
-1<a<0
a<-1
0
n0
n
a<-1或-1<a<0,序列的幅值摆动
5. 正弦序列
x(n) Asin(n )
式中,ω为数字域频率,单位为弧 如度果。正弦序列是由模拟信号xa(t)采样得到的, 那么
N (2 / 0 )k N,k均取整数
正弦序列的周期性讨论: N (2 /0 )k
2 整数时,则正弦序列有周期,当k=1时,周 0 期为 2 0
2 0
有 理ቤተ መጻሕፍቲ ባይዱ数 时 , 设 2 0 = P/Q, 要 使
N=(2/0)k=(P/Q)k 为 最 小 正 整 数 , 只 有
k=Q,即N=P 时,所以正弦序列的周期为P
第一章 离散时间信号与系统
学习目标
• 掌握序列的概念及其几种典型序列的定义,掌握序 列的基本运算,并会判断序列的周期性。
• 掌握线性/移不变/因果/稳定的离散时间系统的概 念并会判断,掌握线性移不变系统及其因果性/稳 定性判断的充要条件。
• 理解常系数线性差分方程及其用迭代法求解单位 抽样响应。
• 了解对连续时间信号的时域抽样,掌握奈奎斯特 抽样定理,了解抽样的恢复过程。
离散时间信号的表示方法:公式表示法、图形 表示法、集合符号表示法,如
x(n) ...1,2,3,7,8,9,...
二、常用序列
1. 单位抽样序列(n)
(n)
1, n 0, n
0 0
(t) 1/
0 t
(n)
1
0
n
(t)
(1)
t
0
2. 单位阶跃序列u(n)
等效为翻褶、移位、相乘和相加四个步骤。
1.2 线性移不变系统
x(n) 离散时间系统 y(n) T[•]
系统可定义为将输入序列x(n)映射成输出序列y(n)的 唯一变换或运算,并用T[]表示,即
y(n) T[x(n)]
在时域离散系统中,最重要、最常用的是线性时不变系统。
1.2.1 线性系统
若系统满足可加性与比例性,则称此系统为 离散时间线性系统。
n 0
2. 序列的乘法
x1(n)
n
0
x(n) x1(n) x2 (n) x2(n)
n
同序号的序列值逐项对应相乘 0
x1(n) ·x2(n)
n 0
3. 序列的移位
x(n)
y(n) x(n n0 )
n
0
当 n0>0 时,序列右移 ——延迟
x(n-2)
n
当 n0<0 时,序列左移 0 ——超前
u(n)
1, n 0, n
0 0
u(n) 0
u(t)
1
…
n
0
t
(n)与u(n)之间的关系
(n) u(n) u(n 1)
u(n) (n k) k 0
令n-k=m,有
n
u(n) (m) m
3. 矩形序列RN(n)
RN
(n)
1, 0,
0 n N 1 其它n
N为矩形序
列的长度
RN (n) u(n) u(n N )
4
x(n)
sin[
(n
8)],
4
N 8
一般正弦序列的周期性
设 x(n) Asin(0n )
式中,A为幅度,ω0为数字域频率,为初相。
那么 x(n N ) Asin[0 (n N ) ] Asin(0n 0 N )
如果 x(n) x(n N )
则 Asin(0n ) Asin[0 (n N ) ]
xa (t) sin(t), xa (t) tnT sin(nT )
T
fS
Ω为模拟角频率,单位为弧度/秒。T为信号的采 样周期,fs为信号的采样频率。
6. 复指数序列
x(n) e( j0 )n
这里ω为数字域频率,单位为弧度。当 =0时,
上式可表示成 x(n) e j0n
上式还可写成 x(n) cos(0n) j sin(0n)
0
m
点间补(m-1)个零值点,表示零值插值。
——插值序列
n n
6. 累加(等效积分)
n
y(n) x(k) k
7. 差分运算
前向差分 x(n) x(n 1) x(n) 后向差分 x(n) x(n) x(n 1)
8. 卷积和
y(n) x(n) h(n) x(m)h(n m) m
4. 序列的翻转
x(-n)是x(n)的翻转序列。x(-n)是以纵 轴(n=0)为对称轴将序列x(n)加以翻转。
x(n)
n 0
x(-n) n
0
5. 尺度变换
x(mn) 是 x(n) 序列每隔
m点取一点形成的,相当于 时间轴n压缩了m倍。
——抽取序列
x(n)
0 x(2n)
x n 是 x(n) 序列相邻抽样
2 无理数时,则正弦序列无周期。例如,sin 1 n
0
4
用单位采样序列来表示任意序列
x(n) x(m) (n m) m
(n
m
)
1,
0,
nm nm
三、 序列的运算
1. 序列的加法
x(n) x1(n) x2 (n)
同序号的序列值逐项对应相加
x1(n)
n 0
x2(n)
n 0
x1(n) +x2(n)
e e j0 2M n
j0n
M 0, 1, 2
表明复指数序列具有以2为周期的周期性,在 以后的研究中,频率域只考虑一个周期就够 了。
7. 周期序列
如果对所有n存在一个最小的正整数N,使下面等
式成立: x(n) x(n N )
则称x(n)为周期序列,最小周期为N。
例:
x(n) sin( n)
1.1 离散时间信号——序列
信号是传递信息的函数。针对信号的自变量和函数值的 取值,可分为三种信号:
(1)连续时间信号
-----自变量取连续值,而函数值可连续可离散。当函 数值是连续的,又常称模拟信号,如语音信号、电视信号 等。
(2)离散时间信号
-----自变量取离散值,而函数值连续。
(3)数字信号
-----自变量和函数值均取离散值。它是信号幅度离散 化了的离散时间信号。
一、离散时间信号——序列的概念
离散时间信号是对模拟信号 xa(t) 进行等间隔 采样获得的,采样间隔为T,得到:
xa(t) tnT xa(nT), n
xa(t) 0
xa(nT)
t
2T
0
t
T
这里 n 取整数。对于不同的 n 值,xa(nT) 是 一个有序的数字序列,该数字序列就是离散时间信 号。注意,这里的n取整数,非整数时无定义,另 外,在数值上它等于信号的采样值,即
R4(n)
N 1
RN (n) (n m) m0
n 012 3
4. 实指数序列
x(n) anu(n) ,a为实数
0<a<1
a>1
n
n
0
0
-1<a<0
a<-1
0
n0
n
a<-1或-1<a<0,序列的幅值摆动
5. 正弦序列
x(n) Asin(n )
式中,ω为数字域频率,单位为弧 如度果。正弦序列是由模拟信号xa(t)采样得到的, 那么
N (2 / 0 )k N,k均取整数
正弦序列的周期性讨论: N (2 /0 )k
2 整数时,则正弦序列有周期,当k=1时,周 0 期为 2 0
2 0
有 理ቤተ መጻሕፍቲ ባይዱ数 时 , 设 2 0 = P/Q, 要 使
N=(2/0)k=(P/Q)k 为 最 小 正 整 数 , 只 有
k=Q,即N=P 时,所以正弦序列的周期为P
第一章 离散时间信号与系统
学习目标
• 掌握序列的概念及其几种典型序列的定义,掌握序 列的基本运算,并会判断序列的周期性。
• 掌握线性/移不变/因果/稳定的离散时间系统的概 念并会判断,掌握线性移不变系统及其因果性/稳 定性判断的充要条件。
• 理解常系数线性差分方程及其用迭代法求解单位 抽样响应。
• 了解对连续时间信号的时域抽样,掌握奈奎斯特 抽样定理,了解抽样的恢复过程。
