2017年育苗杯数学竞赛初赛模拟试题
广东省育苗杯数学竞赛初赛试题以及答案汇编

广东省育苗杯数学竞赛初赛试题[初赛考试日期:xx年xx月xx日(星期五)]说明:第1-10题,每题7分;第11-15题,每题10分;共120分。
1、根据算24点的游戏规则,选用加、减、乘、除四种运算,(可加括号),使下列四个数计算的结果是24,每个数必须用一次且只能用一次。
请上横线上写出正确的算式。
(1)6,6,6,10 (2)3,8,8,2=24 =242、计算:1.4×7.7×3+5.8×7.7-15.4×2=()3、计算:[(2015×2016×861.52)+(2016×2015×1154.48)]÷(2015×2016)=()4、计算:(1234567+2345671+3456712+4567123+5671234+6712345+7123456)÷7=()5、若A×B×C×D=2016,其中A、B、C、D是四个互不相同的自然数,那么(A+B+C+D)最大值是()6、A、B都是自然数,且B比A大42。
如果14A+1.5B=2016,则A=(),B=()。
7、某市出租车收费标准是起步价10元(在3km以内),超过3km后,每1 km收费2.5元(不足1 km按1 km计算)。
现在乘客乘出租车走了8.2 km,应付()元。
8、将右面这个展开图围成一个正方体后,与红色的面相对的面是()色。
9、某特战队小分队以每小时8千米的行军速度到某地执行反恐任务,途中休整30分钟后继续前进,在出发后5.5小时后,通讯员骑摩托车以每小时58千米的速度追赶他们。
照这样的速度()小时可以追上。
10、火车站大楼顶上的大钟5时敲5下,8秒钟敲完,到11时敲响11下,敲完需要()分钟。
11、红星小学五年级有12人参加植树活动,男生每人栽了5棵树,女生每人栽了3棵树,一共栽了52棵树,那么参加植树活动的12人当中,男生有()人,女生有()人。
(完整版)2003年--2016年广东育苗杯初赛和复赛试题及答案

2003年广东省小学五年级数学《育苗杯》初赛试题(每题8分,共120分)_____市(县、区) 镇小学姓名得分______1、一个数比1.2大,而比1.3小,这个数可以是_______。
(只要求写出符合条件的一个数)2、把625620四舍五入到万位,是_________万。
3、写出方程未知数的解:已知3.6 x-0.9 x=10.8,则x=_______。
4、360×72+36×280=_________。
5、0.25×0.125×0.5×64=_________。
6、2003-2002+2001-2000+1999-1998+1997=_________。
7、7.5与6.2的和乘2.3,再减去27.46,差是多少?列出式子是_______________________,差是________。
8、如图,由三个长为10cm,宽为5cm的长方形拼成的图形,这个图形的周长为________cm。
9、学校图书馆有科技书650本,文艺书本数比科技书本数的3倍多45本,图书馆有科技书、文艺书共_________本。
10、学校计划买20个排球,按商场价计算要用360元;现决定多买15个,那么一共需用_________元。
11、右图摆着两层小立方体,把有阴影的部分取走(取到底),还剩_______个小立方体。
12、在下面算式中补上括号,使式子成立:(1) 1260 ÷ 36 - 8 × 2 =63(2) 1260 ÷ 36 - 8 × 2 =9013、学校兴趣小组的同学参加数学竞赛,得100分的有4人;得99分的有3人;得97分的有3人;得96分的有4人。
这次数学竞赛中,学校数学小组的同学平均分为_________分。
14、一个等腰三角形中,有一个内角的度数是另一个内角的4倍,则这个等腰三角形的顶角是_________度。
2017年广东省育苗杯数学竞赛初赛试
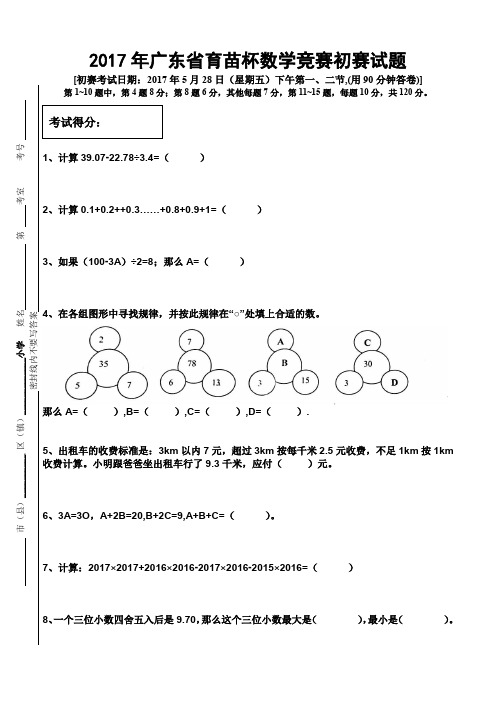
2017年广东省育苗杯数学竞赛初赛试题 [初赛考试日期:2017年5月28日(星期五)下午第一、二节,(用90分钟答卷)] 第1~10题中,第4题8分;第8题6分,其他每题7分,第11~15题,每题10分,共120分。
1、计算39.07-22.78÷3.4=( ) 2、计算0.1+0.2++0.3……+0.8+0.9+1=( ) 3、如果(100-3A )÷2=8;那么A=( ) 4、在各组图形中寻找规律,并按此规律在“○”处填上合适的数。
那么A=( ),B=( ),C=( ),D=( ). 5、出租车的收费标准是:3km 以内7元,超过3km 按每千米2.5元收费,不足1km 按1km 收费计算。
小明跟爸爸坐出租车行了9.3千米,应付( )元。
6、3A=3O ,A+2B=20,B+2C=9,A+B+C=( )。
7、计算:2017×2017+2016×2016-2017×2016-2015×2016=( ) 8、一个三位小数四舍五入后是9.70,那么这个三位小数最大是( ),最小是( )。
市(县__________ 区(镇)_____________小学 姓名 第 考室 考号密封线内不要写答案9、2015年6月1日是星期一,那么,2017年10月1日是星期()。
10、如果用1×2和1×3两种规格的长方形地板砖铺满右面的底面,要使地板砖数尽量少,要怎样铺?至少需要地板砖()。
11、直线上有A、B、C三个点,AB长26厘米,BC长18厘米,那么线段AC的长是()厘米。
12、李明用小正方体(由右图)拼搭图形,至少要准备()个这样的小正方体才能拼搭成一个从上面、正面、侧面看到的都是“田”字的立体图形。
13、小明全家人的年龄加在一起,刚好是89岁,小明的爸爸比妈妈大3岁,小明比妹妹大4岁,但是6年前他们全家人的年龄加在一起刚好是66岁,今年爸爸()岁,妈妈()岁,小明()岁,妹妹()岁。
2017年全国初中数学联赛试题-含详细解析

2017年全国初中数学联合竞赛试题说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设7分和0分两档;第二试各题,请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.第一试(A)一、选择题(本题满分42分,每小题7分)1. 已知实数a b c ,,满足2133903972a b c a b c ++=++= ,,则32b ca b+=+ ( ) A .2 B .1 C .0 D .1− 2. 已知△ABC 的三边长分别是a ,b ,c ,有以下三个结论:(1) (2)以a 2,b 2,c 2为边长的三角形一定存在;(3)以|a -b |+1,|b -c |+1,|c -a |+1为边长的三角形一定存在. 其中正确结论的个数为( )A .0B .1C .2D .33. 若正整数a ,b ,c 满足a b c ≤≤且()2abc a b c =++,则称(a ,b ,c )为好数组.那么,好数组的个数为( )A .1B .2C .3D .44. 设O 是四边形ABCD 的对角线AC ,BD 的交点,若∠BAD +∠ACB =180︒,且BC =3,AD =4,AC =5,AB =6,则DOOB=( ) A .109 B .87 C .65 D .435. 设A 是以BC 为直径的圆上的一点,AD ⊥BC 于点D ,点E 在线段DC 上,点F 在CB的延长线上,满足∠BAF =∠CAE .已知BC =15,BF =6,BD =3,则AE =( ) A .43 B .213 C .214 D .2156. 对于正整数n ,设a n 是最接近n 的整数,则1a 1+1a 2+1a 3+…+1a 200=( )A .1917B .1927C .1937D .1947二、填空题(本题满分28分,每小题7分)7.成立的实数a 的值为______.8. 如图,平行四边形ABCD 中,∠ABC =72︒,AF ⊥BC 于点F ,AF 交BD 于点E ,若DE =2AB ,则∠AED =______.9. 设m ,n 是正整数,且m >n .若9m 与9n 的末两位数字相同,则m -n 的最小值为____.10. 若实数x ,y 满足x 3+y 3+3xy =1,则x 2+ y 2的最小值为______.第一试(B)一、选择题(本题满分42分,每小题7分)1.已知二次函数y =ax 2+bx +c (c ≠0)的图象与x 轴有唯一交点,则二次函数y =a 3x 2+b 3x +c 3的图象与x 轴的交点个数为( )A .0B .1C .2D .不确定 2.题目与(A )卷第1题相同. 3.题目与(A )卷第3题相同.4.已知正整数a ,b ,c 满足a 2-6b -3c +9=0,-6a +b 2+c =0,则a 2+b 2+c 2=( ) A .424. B .430. C .441. D .460.5.设O 是四边形ABCD 的对角线AC ,BD 的交点,若∠BAD +∠ACB =180,且BC =3,AD =4,AC =5,AB =6,DOOB=( )A .43B .65C .87D .1096.题目与(A )卷第5题相同.二、填空题(本题满分28分,每小题7分) 1.题目与(A )卷第1题相同.2.设O 是锐角三角形ABC 的外心,D ,E 分别为线段BC ,OA 的中点,∠ACB =7∠OED ,∠ABC =5∠OED ,则∠OED =______. 3.题目与(A )卷第3题相同. 4.题目与(A )卷第4题相同.第二试(A)一、(本题满分20分)已知实数x ,y 满足x + y =3,1x +y 2+1x 2+y =12,求x 5+y 5的值.二、(本题满分25分)如图,△ABC 中,AB >AC ,∠BAC =45︒,E 是∠BAC 的外角平分线与△ABC 的外接圆的交点,点F 在AB 上且EF ⊥AB .已知AF =1,BF =5,求△ABC 的面积.三、(本题满分25分)求所有的正整数数对(a ,b ),使得a 3=49×3b +8.第二试(B)一、(本题满分20分)已知实数a ,b ,c 满足a ≤b ≤c ,a +b +c =16,a 2+b 2+c 2+14abc = ,求c 的值.二、(本题满分25分)求所有的正整数m ,使得22m -1-2m +1是完全平方数.三、(本题满分25分)如图,O 为四边形ABCD 内一点,∠OAD =∠OCB ,OA ⊥OD ,OB ⊥OC .求证:AB 2+CD 2=AD 2+BC 2.7。
2017年“育苗杯”模拟测试卷(一)

2017年“育苗杯”模拟测试卷(一)姓名:分数:说明:第1题——第10题,每题7分;第11——15题,每题10分。
时间:15:00——16:301、计算:2015.05×601+1550×201.505+201505×2.44﹦()2、2011.2012×2011.2012-2012.2012×2010.2012=( )3、幼儿园中班的小朋友分苹果,如果每人分5个,还剩22个;如果每人分7个,还差18个。
中班小朋友有()人,苹果有()个。
4、五(1)班参加数学竞赛,初赛成绩是:全班平均90分,男生平均88分,女生平均93分。
这个班女生有18人,那么,男生有()人。
5、大小两桶油,大桶所装油的重量是小桶所装油的2.2倍。
如果从大桶中取出12千克倒入小桶,则两桶所装油的重量正好相等,原来大桶装有油()千克,小桶装有油()千克。
6、小东做了一个长方体模型,表面积是250平方厘米。
这个长方体恰好能分割成两个完全一样的正方体。
那么:(1)其中一个正方体的体积是()立方厘米;(2)原来这个长方体的体积是()立方厘米7、把一条彩带对半剪开,再取其中的一段对半剪开,这样剪了3次,最短的一段是4厘米。
这条彩带原来长()米。
8、16千克砂糖的价钱相当于1.6千克茶叶的价钱,如果4元可买5千克砂糖,那么16元可买()千克茶叶。
9、小明的爸爸买来三种水果:苹果、梨子和柑果。
其中32个不是苹果,44个不是梨子。
已知苹果的个数和梨子个数的和是48个。
梨子有()个。
10、(1+2+3+……+2000+2015)×(1+2+3+……+9+10)的积是()数。
(填“奇数”或“偶数”)11、将1、2、3、……2014、2015作如下位置的排列(横向为行):1 8 9 16 17 24 →↓↑→↓2 7 10 15 18 23 ↓↑…3 6 11 14 19 22 ↓↑…4 5 12 13 20 21 ↓→↑…那么2015应排第()行中的第()个数。
育苗杯竞赛练习题

育苗杯竞赛练习题姓名____________ 成绩________________1、一个长方形周长为2米,沿较长边的中点连线把这个长方形剪开,分成两个同样的小长方形,它们周长的和比原长方形的周长增加了6分米。
原长方形的面积是__________。
2、一个学生做两个整数的乘法时,把其中一个因数的4误作为1,得出的乘积是525;另一个学生也在做这道乘法,他也把这个3、一个减法算式里,被减数、减数、差这三个数的和是160,已知差是减数的7倍,则差是____________。
用相等的速度从学校到书店要走1小时,已经走了35分钟,还剩1000米。
从学校到书店一共有米。
4、王叔叔第一次买东西时,用去袋中钱的一半;然后去银行取款180元,取款后再去买衣服,又用去袋中钱的一半,剩下150元,王叔叔第一次买东西时,袋中原有钱元。
5、有两只老龟,十年前一位专家说:“这两只老龟年龄之和是500岁,年龄之差是60岁。
”按这位专家的说法,今年那只最老的龟是_____岁。
6、A、B、C、D表示0~9中四个不同的数字,用ADDD、BCD、AB的形式分别表示四位数、三位数、两位数。
已知:BCD+CCD=ADDD。
则AB+AC+AD+BC+BD+CD= 。
7、一个除法式子里,被除数、除数、商与余数这四个数的和是1996。
已知商是12,余数是69,则除数是。
8、公园计划把一块长方形的地种上草。
如果这块地的长增加4.5米,或它的宽增加2.5米,这块地的面积都将增加31.5平方米。
这块地的面积是。
8、今天长途班车比往常早到站了。
汽车站立即派人骑自行车将随班车的邮件送往邮局,自行车走了半小时,遇到邮局派出取邮件的摩托车,车手接过邮件后,一点也不耽搁调头就返回邮局,结果比往常早到了14分钟。
如果摩托车每天去车站取邮件的出发时间和行驶速度都一样,那么今天长途班车比往常到站时间提早了分钟。
9、一块长170厘米,宽114厘米的长方形木板,要反它锯成长为40厘米、宽为30厘米的小长方形。
2017年育苗杯数学竞赛初赛模拟试题

2017年育苗杯数学竞赛初赛模拟试题[初赛考试日期:2015年4月24日(星期五)下午第一、二节,(用90分钟答卷)]说明:第1~10题,每题7分;第11~15,每题10分,共120分。
1、计算:29292929×88888888÷10101010÷11111111= 。
2、计算:2017×201820182018—2018×201720172017= 。
3、计算:32.2÷2.7+386÷54-4.88÷0.27 。
4、在两位数中,个位数字与十位数字奇偶性不同的数共有 个。
5、一个正方体的表面展开图如图1所示,则图中“广”字所在的面的对面所标的字是 。
图16、如图2,大正方形的面积是400平方厘米,则圆环的面积是 平方厘米。
(π取3.14)图27、有一袋苹果,分给家里的人,每人3个还剩3个,每人4个还缺2个,则有 口人, 个苹果。
8、甲乙丙三同学在2016年育苗杯初赛中,平均分为86。
甲乙的平均分为82,乙丙的平均分为90,则甲丙的平均分是。
9、一辆自行车有两个轮子,一辆三轮车有三个轮子。
车棚里放着自行车和三轮车共10辆,数数车轮共有26个。
则有自行车辆,三轮车辆。
10、某市收取每月煤气费的规定是:如果煤气的用量不超过60立方米,按0.8元/立方米收费,如果超过60立方米,超过部分按1.2元/立方米收费。
已知某用户4月份的煤气费平均0.88元/立方米,那么4月份该用户应缴煤气费元。
11、小明利用暑假到一家自行车厂勤工俭学,讲好了干7个星期,老板给他一辆自行车外加200元作报酬,后因他只做了4个星期,老板给了他一辆自行车外加20元钱的报酬,则一辆自行车的价值是元。
12、要生产一批机器零件350个,若甲先做2天,乙加入合作,又经过2天完成任务;若乙先做2天,甲加入合作,需要再经过3天完成任务,则甲每天做个零件,乙每天做个零件。
2017年全国初中数学联赛(初三组)初赛试卷参考答案及评分细则详解

2017年全国初中数学联赛(初三组)初赛试卷参考答案及评分细则详解2017年全国初中数学联赛(初三组)初赛试卷试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准。
选择题和填空题只设7分和分两档;解答题,请严格按照本评分标准规定的评分档次给分,不要再增加其他中间档次。
如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数。
一、选择题(本题满分42分,每小题7分)1、设实数a、b满足a-b=-1,则a³-b³+3ab的值为(B)A、-3B、-1C、1D、3解析:a³-b³+3ab=(a-b)(a²+ab+b²)+3ab=-(a-b)=-12、若实数a为常数,关于x的不等式组{x+a²≤2a x≤-7}的整数解只有8个,则a的值为(C)A、-1B、0C、1D、2解析:{x+a²≤2a x≤-7}⇒-7≤x≤-a²+2a⇒1≤-a²+2a⇒(a-1)≤0⇒a≤1因为a是常数,所以a=13、在菱形ABCD中,AB=4,E为AB的中点,若在线段BD上取一点P,则PA+PE∠A=60°,的最小值是(D)A、23B、4C、25D、27解析:如图,连结AC,EC交BD于点P,则点P是所求的菱形ABCD中,AB=4,∠A=60°,E为AB的中点DE=√3×AB/2=2√3CE=DE+DC=2√3+4AE=√(CE²+AC²)=√(28²+16)=4√10PA+PE∠A=AE×sin(∠APE)=4√10×sin(60°+∠BPD)令∠BPD=θ,则∠APE=60°+θPA+PE∠A=4√10×(cosθ+√3sinθ)=4√10×(sinθ+√3cosθ+2)/24√10×(sin(θ-60°)+2)/2=2√10×(√3cosθ+sinθ+1)≥2√10所以最小值为2√10,即274、对于任意实数a,b,c,用M{a,b,c}表示三个数的平均数,用min{a,b,c}表示这三个数中最小的数,若M{2x+y+2,x+2y,2x-y}=min{2x+y+2,x+2y,2x-y},则x+y=(A)A、-4B、-2C、2D、4解析:不妨设a最小,则M{a,b,c}=aa+b+c=3ab-a)+(c-a)=ab-a≥0,c-a≥0b=a,c=a2x+y+2=x+2y=2x-yx=-3,y=-1x+y=-45、如图,RtΔABC的斜边AB与⊙O相切于点P,直角顶点C在⊙O上,若AC=22,BC=4,则⊙O的半径是(B)A、3B、23C、4D、26解析:如图,由射影定理得:BC²=AC×DCCD=4²/22BD²=CD²+BC²=48BO=BD/2=√48/2=2√3OP=OB-√AB²-AP²=2√3-√22²-4²=2√3-2r=OP=2√3-2=2(√3-1)=2∙236、不超过1142无明显问题的段落,不需修改)即有:x2kx5x 2x25x k x 2将两式相减,得:10x52x化XXX:2x210x50由于方程只有一个公共实根,所以判别式为0,即:24250解得:2或 5又因为x2kx k的实根为0或k,所以:当2时,实根为0,k,所以实根之和为k;当5时,实根为0,k,所以实根之和为k;综上所述,关于x的方程x2kx k所有的实根之和为k k0.题目一:已知方程组 $\begin{cases}\alpha^2-k\alpha+5=0 \\\alpha^2+5\alpha-k=0\end{cases}$,求所有实数根的和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年育苗杯数学竞赛初赛模拟试题[初赛考试日期:2015年4月24日(星期五)下午第一、二节,(用90分钟答卷)]说明:第1~10题,每题7分;第11~15,每题10分,共120分。
考试得分:
1、计算:29292929×88888888÷10101010÷11111111= 。
2、计算:2017×201820182018—2018×201720172017= 。
3、计算:32.2÷2.7+386÷54-4.88÷0.27 。
4、在两位数中,个位数字与十位数字奇偶性不同的数共有个。
5、一个正方体的表面展开图如图1所示,则图中“广”字所在的面的对面所标的字是。
图1
6、如图2,大正方形的面积是400平方厘米,则圆环的面积是平方厘米。
(π取
3.14)
图2
7、有一袋苹果,分给家里的人,每人3个还剩3个,每人4个还缺2个,则有口人,
个苹果。
8、甲乙丙三同学在2016年育苗杯初赛中,平均分为86。
甲乙的平均分为82,乙丙的平均分
为90,则甲丙的平均分是。
9、一辆自行车有两个轮子,一辆三轮车有三个轮子。
车棚里放着自行车和三轮车共10辆,数
数车轮共有26个。
则有自行车辆,三轮车辆。
10、某市收取每月煤气费的规定是:如果煤气的用量不超过60立方米,按0.8元/立方米收费,
如果超过60立方米,超过部分按1.2元/立方米收费。
已知某用户4月份的煤气费平均0.88元/立方米,那么4月份该用户应缴煤气费元。
11、小明利用暑假到一家自行车厂勤工俭学,讲好了干7个星期,老板给他一辆自行车外加
200元作报酬,后因他只做了4个星期,老板给了他一辆自行车外加20元钱的报酬,则一辆自行车的价值是元。
12、要生产一批机器零件350个,若甲先做2天,乙加入合作,又经过2天完成任务;若乙先
做2天,甲加入合作,需要再经过3天完成任务,则甲每天做个零件,乙每天做个零件。
13、某旅行团计划租车出行,若租用45座的客车,则15人没座;若租用相同数量的60座客
车,除多出一辆车外,其余恰好坐满。
已知45座客车租金250元/天,60座客车租金300元/天,若要使每个人都有座位,则租用辆座车更合算。
13、电气机车和磁悬浮列车各一列,从相距298千米的两地同时出发相向而行,磁悬浮列车的
速度比电气机车速度的5倍还快20千米/小时,半小时后两车相遇。
则电气机车和磁悬浮列车的速度分别为
和。
15、假设一对刚出生的雌雄小兔过两个月就能生下一对雌雄小兔。
以后每月生下一对雌雄小兔。
如果小明养了初生的一对小兔,问:经过一年他有对小兔。
