光学系统设计-习题
工程光学习题答案(附试题样本)
第一章习题1、已知真空中的光速c＝3 m/s，求光在水（n=1.333）、冕牌玻璃（n=1.51）、火石玻璃（n=1.65）、加拿大树胶（n=1.526）、金刚石（n=2.417）等介质中的光速。
解：则当光在水中，n=1.333时，v=2.25 m/s,当光在冕牌玻璃中，n=1.51时，v=1.99 m/s,当光在火石玻璃中，n＝1.65时，v=1.82 m/s，当光在加拿大树胶中，n=1.526时，v=1.97 m/s，当光在金刚石中，n=2.417时，v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像，若将屏拉远50mm，则像的大小变为70mm,求屏到针孔的初始距离。
解：在同种均匀介质空间中光线直线传播，如果选定经过节点的光线则方向不变，令屏到针孔的初始距离为x，则可以根据三角形相似得出：所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃（设n=1.5），下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片，要求在玻璃板上方任何方向上都看不到该金属片，问纸片最小直径应为多少？解：令纸片最小半径为x,则根据全反射原理，光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射，而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为：(1)其中n2=1, n1=1.5,同时根据几何关系，利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为：(2)联立（1）式和（2）式可以求出纸片最小直径x=179.385mm，所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0，求光纤的数值孔径（即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角）。
解：位于光纤入射端面，满足由空气入射到光纤芯中，应用折射定律则有：n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射，使得光束可以在光纤内传播，则有：(2)由（1）式和（2）式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上，求其会聚点的位置。
光学设计简答题习题详解
h1 h2 f1 ' = = 24.306, f 2 ' = = −54.167 u1 '−u1 u 2 '−u2
tg W =
(40 − 30) / 2 ∴ 2W = 11.42° 50
40 / 2 ∴ 2W = 43.6° tg W = 50
30
30
H1 H1’
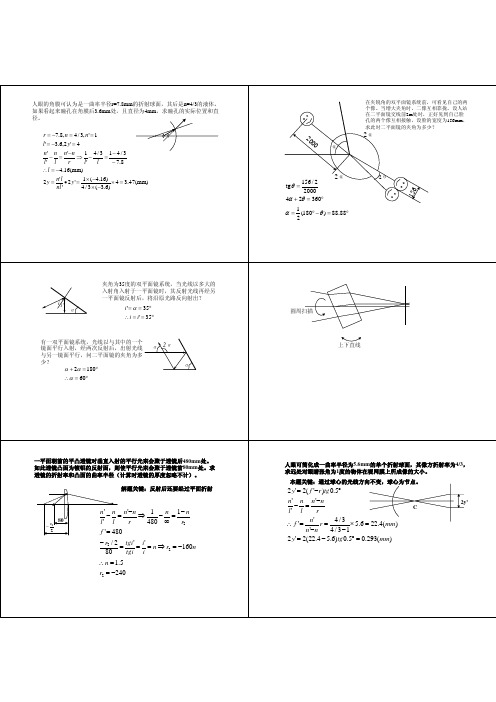
有一焦距为50mm的放大镜，直径D＝40mm，人眼瞳孔离放大镜20mm来观看位于物方 焦平面上的物体。瞳孔直径为4mm。问此系统中，何者为孔阑、何者为渐晕光阑，并 求入瞳、出瞳和渐晕光阑的像的位置和大小；并求能看到半渐晕时的视场范围。 本题在像方做较为方便。位于物方 焦面上的物成像于无穷远，由像方 无穷远轴上点判断，瞳孔为孔阑， 放大镜为渐晕光阑。 入瞳：瞳孔经放大镜所成的像
l p ' = 26.25 mm
tg W ' =
40 / 2 =1 20
2 y = 2 f ' tg W ' = 100(mm)
tg W ' = 20 ∴ 2W ' = 2 × tg −1 (20 tg 1.6°) = 58.3799° tg W
有一4倍的伽利略望远镜(目镜为负)，物镜焦距160mm，直径40mm，眼瞳在 目镜后10mm，直径5mm，为出瞳。目镜直径10mm。(1)何为渐晕光阑？其在 物空间和像空间的像位置和大小？(2)无渐晕时视场角？(3)半渐晕时视场角？
一个光学系统，对100倍焦距处的物面成一缩小到1/50的像，物方孔径角为sinU≈u=0.005， 物面的照度为1000lx，反射率为ρ=0.75，系统的透过率为K=0.8，求像面的照度。
L= E' = =(
M
π
(完整)应用光学习题解答分解
一、填空题1、光学系统中物和像具有共轭关系的原因是 。
2、发生全反射的条件是。
3、 光学系统的三种放大率是 、 、 ，当物像空间的介质的折射率给定后,对于一对给定的共轭面，可提出 种放大率的要求。
4、 理想光学系统中，与像方焦点共轭的物点是 。
5、物镜和目镜焦距分别为mm f 2'=物和mm f 25'=目的显微镜,光学筒长△= 4mm ，则该显微镜的视放大率为 ，物镜的垂轴放大率为 ，目镜的视放大率为 。
6、 某物点发出的光经理想光学系统后对应的最后出射光束是会聚同心光束，则该物点所成的是(填“实”或“虚"）像。
7、人眼的调节包含 调节和 调节。
8、复杂光学系统中设置场镜的目的是。
9、要使公共垂面内的光线方向改变60度，则双平面镜夹角应为 30 度.10、近轴条件下，折射率为1.4的厚为14mm 的平行玻璃板,其等效空气层厚度为 10 mm 。
11、设计反射棱镜时，应使其展开后玻璃板的两个表面平行,目的是 保持系统的共轴性 。
12、有效地提高显微镜分辨率的途径是 提高数值孔径和减小波长 。
13、近轴情况下,在空气中看到水中鱼的表观深度要比实际深度 小 。
一、填空题1、光路是可逆的2、光从光密媒质射向光疏媒质，且入射角大于临界角I 0，其中，sinI 0=n 2/n 1。
3、垂轴放大率；角放大率；轴向放大率；一4、轴上无穷远的物点5、－20；－2； 106、实7、视度瞳孔8、在不影响系统光学特性的的情况下改变成像光束的位置,使后面系统的通光口径不致过大.9、3010、1011、12、13、小二、简答题1、什么是共轴光学系统、光学系统物空间、像空间？答:光学系统以一条公共轴线通过系统各表面的曲率中心，该轴线称为光轴，这样的系统称为共轴光学系统.物体所在的空间称为物空间，像所在的空间称为像空间.2、如何确定光学系统的视场光阑？答：将系统中除孔径光阑以外的所有光阑对其前面所有的光学零件成像到物空间。
光学设计作业答案
现代光学设计作业学号：**********姓名：***一、光学系统像质评价方法 (2)1.1 几何像差 (2)1.1.1 光学系统的色差 (3)1.1.2 轴上像点的单色像差─球差 (4)1.1.3 轴外像点的单色像差 (5)1.1.4 正弦差、像散、畸变 (7)1.2 垂直像差 (7)二、光学自动设计原理 (9)2.1 阻尼最小二乘法光学自动设计程序 (9)2.2 适应法光学自动设计程序 (11)三、ZEMAX光学设计 (13)3.1 望远镜物镜设计 (13)3.2 目镜设计 (17)四、照相物镜设计 (22)五、变焦系统设计 (26)一、光学系统像质评价方法所谓像差就是光学系统所成的实际像和理想像之间的差异。
由于一个光学系统不可能理想成像，因此就存在光学系统成像质量优劣的问题，从不同的角度出发会得出不同的像质评价指标。
（1）光学系统实际制造完成后对其进行实际测量✧星点检验✧分辨率检验（2）设计阶段的评价方法✧几何光学方法：几何像差、波像差、点列图、几何光学传递函数✧物理光学方法：点扩散函数、相对中心光强、物理光学传递函数下面就几种典型的评价方法进行说明。
1.1 几何像差几何像差的分类如图1-1所示。
图1-1 几何像差的分类1.1.1 光学系统的色差光波实际上是波长为400~760nm 的电磁波。
光学系统中的介质对不同波长光的折射率不同的。
如图1-2，薄透镜的焦距公式为()'121111n f r r ⎛⎫=-- ⎪⎝⎭(1-1) 因为折射率n 随波长的不同而改变，因此焦距也要随着波长的不同而改变，这样，当对无限远的轴上物体成像时，不同颜色光线所成像的位置也就不同。
我们把不同颜色光线理想像点位置之差称为近轴位置色差，通常用C 和F 两种波长光线的理想像平面间的距离来表示近轴位置色差，也成为近轴轴向色差。
若l ′F 和l ′c 分别表示F 与C 两种波长光线的近轴像距，则近轴轴向色差为'''FC F C l l l ∆=- (1-2)图1-2 单透镜对无限远轴上物点白光成像当焦距'f 随波长改变时，像高'y 也随之改变，不同颜色光线所成的像高也不一样。
工程光学习题解答--第二章-理想光学系统
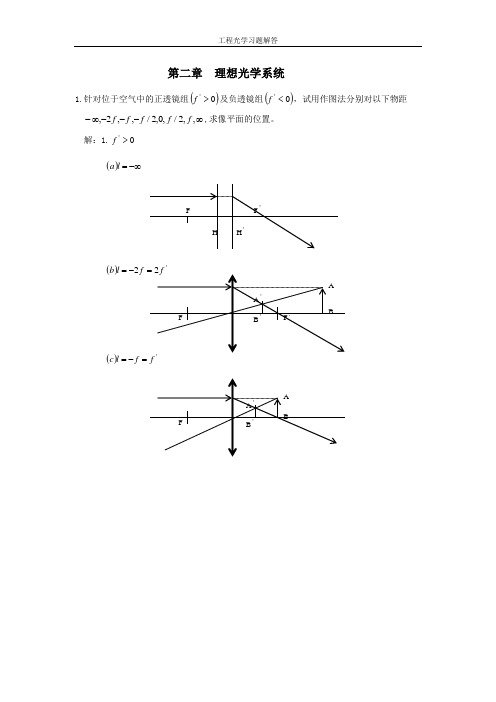
第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ，试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。
解：1.0'>f ()-∞=l a()'2f l b -=()f f l c=-=()/f l d -=()0=l e()/f lf =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’＝75mm,被摄景物位于（以F 点为坐标原点）=x ,2,4,6,8,10,m m m m m -----∝-处，试求照相底片应分别放在离物镜的像方焦面多远的地方。
解： （1）x= -∝ ，xx ′=ff ′ 得到：x ′=0 （2）x ′=0.5625 （3）x ′=0.703 （4）x ′=0.937 （5）x ′=1.4（6）x ′=2.813.设一系统位于空气中，垂轴放大率*-=10β，由物面到像面的距离（共轭距离）为7200mm ， 物镜两焦点间距离为1140mm 。
求该物镜焦距，并绘出基点位置图。
解:∵ 系统位于空气中，f f -='10''-===ll y y β 由已知条件：1140)('=+-+x f f7200)('=+-+x l l解得：mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上，当透镜向物体移近18mm 时，物体将被放大*-4，试求透镜的焦距，并用图解法校核之。
解：方法一：31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二： 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三： 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像，放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上，则见像向透镜方向移动，放大率为原先的3/4倍，求两块透镜的焦距为多少？ 解：⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像，像高为物高的一半，今将物面向物体移近100mm ， 则所得像与物同大小，求该正透镜组的焦距。
(完整版)光学系统与像差全套答案
2.解：由vcn =得：光在水中的传播速度:)/(25.2333.1)/(1038s m s m n c v =⨯==水水光在玻璃中的传播速度:)/(818.165.1)/(1038s m s m n c v =⨯==玻璃玻璃3.一高度为1.7米的人立于离高度为5米的路灯(设为点光源)1.5米处，求其影子长度。
解：根据光的直线传播。
设其影子长度为x ,则有xx+=5.157.1可得x =0.773米 4.一针孔照相机对一物体于屏上形成一60毫米高的像。
若将屏拉远50毫米，则像的高度为70毫米。
试求针孔到屏间的原始距离。
解：根据光的直线传播,设针孔到屏间的原始距离为x ，则有xx 605070=+可得x =300（毫米）5. 有一光线以60°的入射角入射于的磨光玻璃球的任一点上， 其折射光线继续传播到球表面的另一点上，试求在该点反射和折射的光线间的夹角。
解：根据光的反射定律得反射角''I =60°，而有折射定律I n I n sin sin ''=可得到折射角'I =30°，有几何关系可得该店反射和折射的光线间的夹角为90°。
6、若水面下200mm 处有一发光点，我们在水面上能看到被该发光点照亮的范围(圆直径)有多大？解：已知水的折射率为 1.333,。
由全反射的知识知光从水中到空气中传播时临界角为：nn m I 'sin ==333.11=0.75，可得m I =48.59°，m I tan =1.13389，由几何关系可得被该发光点照亮的范围(圆直径)是2*200*1.13389=453.6(mm)7、入射到折射率为的等直角棱镜的一束会聚光束(见图1-3)， 若要求在斜面上发生全反射，试求光束的最大孔径角解：当会聚光入射到直角棱镜上时，对孔径角有一定的限制，超过这个限制，就不会 发生全反射了。
由nI m 1sin =，得临界角 26.41=m I 得从直角边出射时，入射角74.34590180=---=m I i由折射定律nU i 1sin sin =，得 5.68U =即 11.362U =8、有一光线入射于和的平面分界面上， 平面的法线为，求反射光线和折射光线。
光学系统设计-习题
n 1 1 1 n r1 r2
。
同心透镜的特点：球心 由透镜主面公式：
C1 , C2 重合在一起， d r1 r2
dr (r1 r2 )r1 1 lH r1 n(r2 r1 ) n 1d n(r2 r1 ) n 1(r1 r2 ) dr2 (r1 r2 )r2 r2 n(r2 r1 ) n 1d n(r2 r1 ) n 1(r1 r2 )
该透镜为双凸透镜
d 15mm
n1 1 n 2 n 1 .5 n1 n 1.33 2
由 f1 而 f2
n1r1 20 40m m n1 n1 1.5 1
f1 f 2
r1 n1 1.5 20 60m m n1 1.5 1 n1
x 8m x 6m x 4m x 2m
x' 0.703mm x' 0.9375mm x' 1.406mm x' 2.813mm
2. 已知一个同心透镜r1=50mm，厚度d=10mm，n=1.5163，求 它的主平面和焦点位置。
解：
1 1 ( n 1) 2 d 1 0.51632 10 ( n 1) 0.5163 (1 / 50 1 / 60) f' nr1 r2 1.5163 50 40 r1 r2
n2 r2 1.5 （ 15 ） 132.35m m n2 n2 1.33 1.5
r2 n2 1.33 （ 15 ） 117.35m m n2 n2 1.33 1.5
光学例题2012。12.9
1.有一玻璃球，折射率为，今有一光线射到球面上，入射角为60°，求反射光线和折射光线的夹角。
2. 水槽有水20cm深，槽底有一个点光源，水的折射率为1.33，水面上浮一不透明的纸片，使人从水面上任意角度观察不到光，则这一纸片的最小面积是多少？3. 空气中的玻璃棒，n’＝1.5163，左端为一半球形，r＝-20mm。
轴上有一点光源，L＝-60mm。
求U＝－2°的像点的位置。
4. 简化眼把人眼的成像归结为只有一个曲率半径为5.7mm，介质折射率为1.333的单球面折射，求这种简化眼的焦点的位置和光焦度。
5. 有一玻璃球，折射率为n＝1.5，半径为R，放在空气中。
(1)物在无穷远时，经过球成像在何处？(2) 物在球前2R处时像在何处？像的大小如何？6. 一个半径为100mm的玻璃球，折射率为1.53。
球内有两个气泡，看来一个恰好在球心，另一个在球的表面和球心之间，求两个气泡的实际位置。
7. 一个玻璃球直径为60mm，折射率为1.5，一束平行光入射在玻璃球上，其会聚点应该在什么位置？8. 一球面反射镜，r＝-100mm，求β＝0，－0.1，－1，5，10情况下的物距和像距。
9. 一球面镜对其前面200mm处的物体成一缩小一倍的虚像，求该球面镜的曲率半径。
10. 垂直下望池塘水底的物时，若其视见深度为1m，求实际水深，已知水的折射率为4/3。
11. 有一等边折射率三棱镜，其折射率为1.65，求光线经该棱镜的两个折射面折射后产生最小偏向角时的入射角和最小偏向角。
12. 身高为1.8m的人站在照相机前3.6m处拍照，若拟拍成100mm高的像，照相机镜头的焦距为多少？13. 单透镜成像时，若共轭距为250mm，求下列情况下透镜的焦距：(1) 实物，β＝-4；(2) 实物，β＝-1/4；(3) 虚物，β＝-4。
14. 设一个光学系统处于空气中，β＝-10，由物面到像面的距离为7200mm，物镜两焦点距离为1140mm，求透镜的焦距。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
nr1r2 f' ( n 1 ) n( r2 r1 ) ( n 1 )d 149.27mm
n 1 l'H f ' d 13.99mm nr1 n 1 lH f ' d 5.25mm nr2
l l lH 5005.25mm
6、设计照相物镜的焦距等于75mm，底片尺寸正方形， 边长为55mm，求该照相物镜的最大视场角等于多数？ 解：
' 1 ' 2
3
f f f2 f 0
' 1 ' 2 ' 2
28.87
d 1 f 1' f 2' 28 .87 78.87 d 2 f 1' f 2' 28 .87 21.13
173.19 f 1' f 2' f ' { 173.19
0, 若能成实像，则 l2 则成实像的条件是 2 x1 又 x2 所以， 2 x1 f 2
2
由于实物成实像的情况 ，所以对于 1来说， l1 x1 f1 0 即 x1 f1 f1
由于
f1 0 而 1
所以对于这两个条件不 能同时满足
得到
f ' 100mm
4.一薄透镜组焦距为100 mm，和另一焦距为50 mm的薄透镜 组合，其组合焦距仍为100 mm，问两薄透镜的相对位置。 解：
5、一块厚透镜，n=1.6，r1=120mm，r2=-320mm， d=30mm，试求该透镜焦距和基点位置。如果物距 l1=-5m时，问像在何处？ 解：
d 1 78.87 f ' 173.19 28.87
d 2 21.13 f ' 173.19 28.87 舍去
3. 有一正薄透镜对某一物成倒立的实像，像高为物高的一 半，今将物面向透镜移近100mm，则所得像与物同大小，求 该正透镜组的焦距。 解：
f 1 1 x1 2 f 源自 2 1 x2 x2 x1 100
f ' 587.37 f 587.37
主面位置： r1 d 50 10 lH 50 n(r1 r2 ) (n 1)d 1.5163 (40 50) _(1.5163 1) 10
l' H r2 d 40 n( r1 r2 ) (n 1)d
1 f 2 50 mm 4 物体所处的位置 -50mm x1 100mm x1
即，物体放在 L1左面150mm以内
(3) 假如双子系统由正负透镜组合
A
1时，如果 1 0， 2 0时，
即 f 2 0 x2 f 2 x2 即 x1 f 2 f 2 f ( f 2 / f1)
若透镜为无焦系统，则 Φ 即
n(r2 r1 ) (n 1)d 0
1 0 f
d
n (r2 r1 ) n 1
此时构成望远镜系统分 别有 f f ' lH lF lF lH 主面和焦面都在无穷远 处
F1
O1
F2
O2
d
证明同心透镜两主面重合在一起，其光焦度为
Φ0
f
且
0,
d f1 f 2 x1 0 x2 x1 0 x2 x1
由于无焦系统的 F1 和 F2 重合 如果物体在透镜1的前焦面上， 对于透镜2来说，
x2 x1
也就是说，物体经过双子无焦系统之后，像在第二个子系统的后焦面上。 由双子无焦系统公式
' f ' 2 f2 xF f 1' f 2' f ' 又d f 1' ( f 2' ) f 1' f 2'
全部代入(1)式
求出
( f 2 f )
2 ' 1 ' 2
f 2 f 2' f f f 2' 2 3 f 1' f 2' 2
f 2 200 2 f1 100 f1 100 1 f 2 200 2
F1
1
2
F1
F2
4
F2
50 x1 100mm x1 50mm
(2) 若需物体成实像，也就是说 l 0 2
x2 f 2 f 2 2 x1 f 2 4x1 0 l2
筒长＝d＋后工作距离
65 50 15mm d L lk
而有双子系统像方焦面公式
d f lF 1 f1
对于无限远物体成像，像面恰好是系统的焦面，
lk lF
而由主面坐标
15 35 1 f ＝50 1
而 d f1 f 2
d f 2 lH
H
f 2 240mm
H1 H1
H2 H2
F
lk lF
L
n2 n1
d
f
设计一个对无限远成像的短焦距物镜。焦距 f 35m m ,筒长 L 65 mm ， 50mm 。求理想系统的结构参数，并 要求有大于焦距的后工作距离 lk 画出理想光路示意图。
f1 35mm
H 2 H lF f 50 35 15mm lH
由
1
2
f 2 lH
d
像 面
F
F1
H'
f 2 25mm
d
L
f
lk lF
由双组元构成一个无焦系统，其中 f1 100mm ，f 2 200m m 。当物 放在透镜1前焦面上并用平行光照明时，（1）求像的位置和放大倍率； （2）确定物体成实像时物面位置应处的范围；（3）当采用一正、一负组 元组成无焦系统时，它能成实像吗？ (1) 此为双子无焦系统
1. 已知照相物镜的焦距f′=75mm，被摄景物位于距
离x=-∞,-10,-8,-6,-4,-2m处，试求照相底片应 分别放在离物镜的像方焦面多远的地方?
f '2 752 x' 解： xx' ff ' x x x x' 0 x 10m x' 0.5625mm
55 2 y 38.89mm 2
'
y ' 38.89 tg ' 0.5185 f 75
视场角2 54.8
设计一个对无限远成像的长焦距物镜。焦距 f 1200 m m ,由物镜第一面顶 点到像面的距离（简称筒长） L 700 mm ，由物镜最后一面到像面的距 400mm 。若按最简单的薄透镜系统考虑，试求 离（称后工作距离）lk 系统的理想光学参数，并画出理想的光路图 因为筒长小于焦距（一般长焦距透镜多如此），所以应该采用一种远距型的系统，这种系 统是正负组分离，而且正组在前的结构。 考虑简单的双子系统，即二元组合系统的基本关系式。 筒长＝d＋后工作距离 由双子系统像方焦距
n2 r2 1.5 （ 15 ） 132.35m m n2 n2 1.33 1.5
r2 n2 1.33 （ 15 ） 117.35m m n2 n2 1.33 1.5
＝d f1 f 2 15 60 (132.35) 177.35mm
f1
B.
f1
0
1
若 f1 0, f 2 0
x2 f 2 0 若成实像， 则l2 f 同样， x1 1
而
x1 f1
0
f1
f1
单透镜能构成无焦系统吗？如果可能的话，试求 望远透镜结构参数之间的关系，并画出光学结构 图。
透镜中心厚度 d , 折射率为 n 1 1 c1 c2 r1 r2 单折射球面参量 r1 n 1 nr 球面 2： f 2 2 1 n 球面1： f1 r n n f1 nr 1 n 1 r f 2 2 1 n n(r2 r1 ) (n 1)d 光学间隔： d f1 f 2 n 1 nr 1r2 而焦距 ： f f n 1n(r2 r1 ) (n 1)d 1 d (n 1) 2 光焦度： 1 2 1 2 (n 1)(c1 c2 ) dc1c2 f n n
对于无限远成像，像面正好是系统的焦面
700 d 400 d (1 ) f lF f1
d 300 mm
(1)
lk lF
代入（1）式得到
f1 450mm
n1
1
2
n2
像面
又由双子系统主面公式
H 2 H ( f 'lk ) (1200 400) lH 800m m
F
C1 C2
F
O1
lH
f
H H’
- lH
d
O2
f
, r2 15mm, d 15mm, n 1.5 一透镜的结构参数为： r1 20mm
当透镜一边是空气，另一边是水（ n 1.33）时，求透镜的物像方的焦距。
透镜的结构参数为： r1 20mm, r2 15mm
f f1 f 2 40 (132 .35) 29.85mm 177 .35 f ' f1f 2 39.7mm
2. 由一个正透镜组和一个负透镜组构成的摄远系统，前组 正透镜的焦距f1′=100，后 组负透镜的焦距f2 ′=-50， 要求由第一组透镜到组合系统像方焦点的距离与系统的组 合焦距 之比为1∶1.5，求二透镜组之间的间隔d应为多少? 组合焦距等于多少?