民航客运量的多元线性回归分析
Spss对民航客运量的多元回归分析:

Spss对民航客运量的多元回归分析:1.首先方法选择:进入法。
然后分析相关性表格:国民收入,消费额,民航航线里程,来华旅游人数都与民航客运量高度相关,而铁路客运量和民航客运量的相关性较低。
通过观察调整后的判定系数为0.994,拟合优度较高,不被解释的变量较少。
回归方程的显著性小于0.05,说明被解释变量与解释变量的线性关系是显著的。
可以建立线性方程。
在显著性系数中,铁路客运量的sig 大于0.05,所以是不显著的,说明自变量铁路客运量对因变量的影响是不明显的,应该移除该变量。
回归方程:ˆY =-195.945+0.519X 1-0.771X 2+0.001X 3+15.983X 4+0.344X 52.方法选择:后退法。
然后分析相关性表格:由表可以看出:除了铁路客运量的相关性较低外,其余变量的相关性都较高。
采用后退法后,调整变量更高,拟合优度更高。
回归方程的显著性为0,认为被解释变量和解释的变量线性关系是显著的,可以建立线性方程。
在剔除变量铁路客运量后,剩余变量的sig 都变得更小,显著性更显著。
回归方程为:ˆY =-153.930+0.509X 1-0.754X 2+15.980X 4+0.347X 53.方法选择:逐步回归法。
然后分析相关性表格:铁路客运量相关性较低,其他变量相关性都较高。
采用逐步法后,调整值很高,拟合优度很高。
说明可以用该模型预测。
sig 值小于0.05,说明显著性很高。
采用逐步回归法后,变量得显著性很高。
变量为国民收入和民航航线里程。
回归方程为:ˆY =-299.004+0.083X 1+17.316X 4。
民航客运量影响因素回归分析

技术论坛TECHNOLOGY FORUM中国航班CHINA FLIGHTS 54民航客运量影响因素回归分析冉龄玉|重庆交通大学经济与管理学院摘要:经济、信息以及科技的全球化,让出行不再困难。
乘坐飞机是居民在远距离出行时主要考虑的方式之一。
本文为探究国内民航客运量的影响因素,通过回归分析构建了国内民航客运量的影响因素最小二乘回归模型。
为了对国内民航客运量进行有效地评估和预测,本文以计量经济学的理论方法,从多元线性回归的角度,对上述影响民航业发展的因素进行分析,构建回归模型来探究民航业的变化走向以及成因问题。
关键词:民航;影响因素;回归分析1引言融合于各种出行方式的信息科技让国民出行不再困难。
移动支付、国民信息化的社会生活方式以及便捷的出行方式,加快了国民的生活节奏,也加快了中国融入世界的进程。
中国的发展与变化大大刺激了国内民航业的发展。
国内航空公司在2018年发布的公报中显示,当年实现了营业收入比去年增长了14.5个百分点,全年营业额达6130.2亿元。
影响民航客运量的因素涉及社会发展的各个方面。
研究民航客运量的影响因素,对扩大民航市场、增加民航的服务量和营业额有着十分重要的实际意义。
不少学者从相关分析方法入手,对影响民航客运量的因素有哪些进行了探究。
纪跃芝[1]认为历史阶段的不同导致影响因素发生变化,得到主要因素为民航航线里程、入境旅游人数;彭立南[2]发现第三产业增加值以及外国人入境旅游人数对民航客运量有着重大影响。
李丽华[3]采用逐步回归法和岭回归法构建民航客运量的多元线性回归模型,其结论中的因素为:国民总收入(消费支出额)、铁路客运量和入境旅游人数。
蔡文婷[4]等人通过对影响航空运输客运量的因素进行灰色综合关联法分析,对影响因素进行重要程度分析,得到因素重要性排序:国内旅游收入、人均GDP、机场吞吐量、外贸进出口总额、城镇居民可支配收入、铁路客运量、航线数量、国内游客。
张艳[5]等人得到的结论与蔡文婷[4]等人的结论中包含相同的因素。
基于线性模型的民航客运量影响因素与预测研究

基于线性模型的民航客运量影响因素与预测研究
随着我国经济的发展和低空交通发展的不断壮大,民航运输在我国的重要性越来越受
到重视。
因此,掌握民航客运量的影响因素,对于民航运输管理和未来规划具有重要意义。
本文基于线性模型,研究了民航客运量的影响因素及其预测。
首先,本文收集了2010年至2019年我国民航客运量及其相关因素的数据,包括GDP、旅游人数、燃油价格、航线数量、机场数量等。
对于变量选择,本文采用相关性分析和逐
步回归的方法,得出了影响因素为GDP、旅游人数、航线数量和机场数量。
这些因素与民
航客运量的关系呈现出线性相关性。
接着,本文利用多元线性回归模型对影响因素进行分析。
模型的结果表明,影响民航
客运量的最显著因素是GDP,其次是旅游人数和航线数量。
在机场数量的影响上,与预期
不同,其影响程度较小。
在预测方面,本文使用了回归模型的方法,预测了未来3年的民航客运量。
预测结果
表明,未来3年我国民航客运量将保持高速增长态势。
其中,2020年预测值为6.27亿人次,2021年预测值为6.91亿人次,2022年预测值为7.58亿人次。
这也进一步验证了本文建立的模型的可靠性和准确性。
综上所述,本文基于线性模型,通过对影响民航客运量的因素进行分析和预测,提出
了一些对于民航管理和未来规划的建议。
其中,对于政府部门,应该加大对于民航运输基
础设施建设的投入,以保障日益增长的市场需求;对于航空公司,则应该根据市场需求,
加强航线的拓展和优化服务,提高核心竞争力。
基于多元线性回归的客车销售量影响因素信息化分析
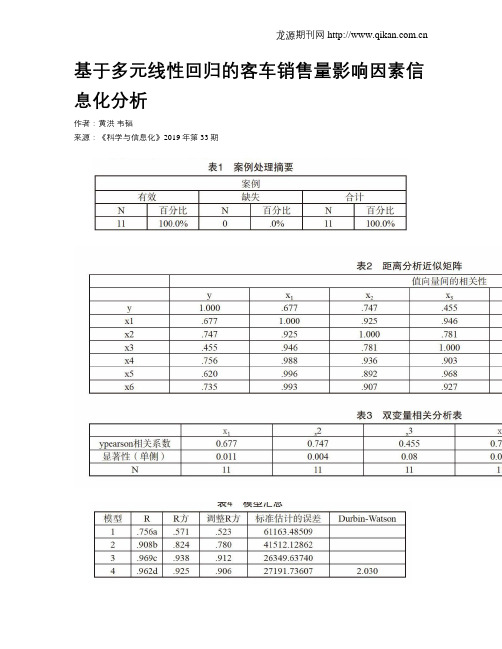
基于多元线性回归的客车销售量影响因素信息化分析作者:黄洪韦韬来源:《科学与信息化》2019年第33期摘要本文通过回归分析的方法对2008~2018年的相关数据进行分析,以客车销售量为因变量构建多元线性回归方程。
分析结果表明,民用汽车保有量和公路总里程对客车销量有着较大影响,变量间存在着线性关系。
客车生产企业在制定中长期计划和发展策略时,应重点考虑这两个变量对销量的影响。
关键词客车;销量;变量;回归分析我国客车工业起步较晚,直到20世纪90年代初,仍停留卡车底盘改装阶段,但随着经济发展和技术进步,客车行业的技术水平取得了长足的进步,随之而来的是产品产量和销量井喷式发展,逐渐成为客车生产和出口第一大国。
2005~2014年十年间,年均复合增速约10%,2014年客车销售量达到了顶峰的606918辆。
然而从2015年开始,国内客车市场容量接近饱和,销量增速转负。
2016年中国客车销售53.92万辆,同比减少9.9%。
之后更是一路下滑,2017年国内客车市场累计销售543413辆,同比下降2.98%,客车业的“严冬”仍将继续。
本文通过对中国客车销量影响因素进行研究,希望研究结果能够对客车行业的发展以及客车企业经营策略的制定提供借鉴。
1 客车销售影响因素分析我国汽车运输行业的发展与经济的发展既相互促进又相互制约,客运发展比货运发展受经济发展的影响更大,国内生产总值和汽车保有量的增长二者之间呈正相关的规律[1]。
经济的增长对客车行业发展的促进作用显著,2008年国家的“四万亿”政策大量投资导致2009年中国新建公路、改建公路分别增长23%和18%,国内客车需求在2010年得到集中释放,销量与2009年相比增长了25%[2]。
2018年前6月,累计出口客车30198辆,累计同比增长5.98%[3]。
世界經济的增长对我国客车出口的影响也不容忽视,尤其是客车出口权重最大的亚洲、美洲和非洲地区。
对美国、德国、日本、韩国等国家汽车产量增长率与实际GDP增长率都具有显著的正向相关性[4]。
影响民航客运量因素的相关性分析及实证研究

影响民航客运量因素的相关性分析及实证研究[摘要]本文利用1989—2011年的统计数据对我国民航客运量及各影响因素进行了研究。
首先分析了影响民航客运量的相关因素,通过相关性分析进行了证明。
在此基础上,通过建立多元线性回归模型,发现第三产业增加值以及外国人入境旅游人数对民航客运量有着重大影响。
对回归模型进行了合理解释,给出了一些建议,以达到提高我国民航旅客运输业的市场竞争力的目的。
[关键词]民航客运;相关性分析;多元回归分析民航运输是我国运输行业中不可或缺的一部分,是满足社会公众需要、发展旅游业、促进对外交往不可缺少的工具。
其发展程度反映了国家的经济发展水平。
在经济全球化趋势越发显著的当今,研究客运量发展及其相关影响因素很有现实意义。
影响民航客运量的因素源于诸多方面,根据文献资料,可以得出影响民航客运量的主要因素有第三产业增加值、城市居民消费水平、外国人入境旅游人数、铁路客运量、定期航班航线里程。
本文拟从相关性分析入手,通过实证分析,得出一些建议。
1 影响因素的相关性分析从历年《中国统计年鉴》中采集1989—2011年的民航客运量及影响因素的数据,使用Pearson相关系数计算公式计算民航客运量与各影响因素的相关系数,以此分析它们的相关性。
Pearson相关系数的计算公式为:通过计算得出,第三产业增加值与民航客运量的相关系数为0.995,城市居民消费水平与民航客运量的相关系数为0.985,外国人入境旅游人数与民航客运量的相关系数为0.955,铁路客运量与民航客运量的相关系数为0.933,定期航班航线里程与民航客运量的相关系数为0.955。
可见,这些因素与民航客运量有很强的相关性,说明对民航客运量有着重大影响。
2 民航客运量与相关影响因素的多元线性回归模型根据相关性分析,可以发现各影响因素彼此相关度也很高。
通过建立多元线性回归模型,进一步分析影响因素与民航客运量的关系。
以y表示因变量民航客运量(万人),以x1表示第三产业增加值(亿元)、x2表示城市居民消费水平(绝对元)、x3表示外国人入境旅游人数(万人)、x4表示铁路客运量(万人)、x5表示定期航班航线里程(万千米)。
我国各阶段民航客运量的回归分析模型

题目我国各阶段民航客运量的回归分析模型学生姓名张栋栋学号 ********** 所在学院数学与计算机科学学院专业班级数应1101班指导教师李晓康 __ ____完成地点陕西理工学院 ___2015年5月10日我国各阶段的民航客运量的回归分析模型张栋栋(陕西理工学院数学与计算机科学学院数学与应用数学2011级数应1班,陕西 汉中 723000)指导教师:李晓康[摘 要] 为了研究我国民航客运量的变化规律及其原因,通过对我国部分年份民航客运量数据进行统计和收集,运用多元线性回归分析的方法并建立相关模型,找出影响我国民航客运量的主要因素,并对模型进行评价分析,为以后我国民航发展提供科学依据。
[关键词] 民航客运量 回归分析 相关性 阶段1.引言民航业作为科技型新兴产业,在我国众多行业中占有重要以及特殊的地位.伴随着整个国民经济的发展而不断发展壮大,民航产业作为国民经济的重要行业,同时作为民用相对先进方便的交通运输方式,是我国运输行业中必不可少的一部分,它的发展程度深刻反映了一个国家的经济水平,也对我国贸易和旅游业有着巨大的贡献,也越来越受到国家的重视[8]。
我国航空业起步较晚,但发展速度较快,民用航空业伴随着经济的增长也不断迅猛壮大,运输能力显著增强,据工信部提出到2020年民用飞机年产收入将超过1000亿元,然而面对难得的机遇,要求航空企业制定合理的决策,促进民航企业进行更好地进行收益管理。
目前国内很多学者的研究范围包括对我国民航空间格局与竞争态势的研究,对我国民航客运价格定价机制与制改革的探讨,以及运用各种共统计方法对民航客运需求的研究。
本文在一定的数据分析上,针对一定的时间段我国民航客运量的部分影响因素:国内生产总值、居民消费、铁路客运量、民航航线历程、来华旅游人数,并分两个时间段对我国民航客运量的变化趋势及成因做出了研究,运用多元回归分析的方法对后续民航客运分析与预测打下基础,并且对每个建立的模型进行了对比,得到一个最好的关于我国民航客运量的回归模型,根据模型对我国目前民航运输业发展中面临的问题提出有效建议,提高我国民航的市场竞争力,最后对全文进行评价及总结。
我国民航客运量的因素分析
-56.288 200.864
.102
.018
1.456
-2.806
.908
-1.267
30.802
9.980
.518
.328
.134
.302
t -.280 5.683
-3.092 3.086 2.454
Sig. .782 .000 .005 .005 .022
多元线性回归分析
由回归分析得 回归方程为: yˆ 56.2880.102x1 2.806x2 30.802x3 0.328x4
yˆ 638.5070.023x1 0.01x2 19.892x3 0.294x4
多重共线性分析
模型
1
(常量)
x1
x2
x3
x4
a. 因变量: y
系数a
非标准化系数
标准系数
B
标准 误差 试用版
-56.288
200.864
.102
.018
1.456
-2.806
.908
-1.267
30.802
系数a
非标准化系数
B
标准 误差
标准系数 试用版
440.059
136.182
.069
.002
.991
354.269
213.272
.061
.016
.870
.269
.509
.121
158.874
219.303
.064
.015
.910
-.487
.593
-.220
.333
.156
.307
t 3.231
36.823 1.661 3.785 .528 .724 4.217 -.822 2.142
我国民航客运量影响因素分析及建模预测
我国民航客运量影响因素分析及建模预测在我国的民航业发展中,客运量一直是一个非常关键的指标。
因为随着社会经济的不断发展,民航客运量的增长需要充分考虑各种影响因素,从而制定出符合实际的发展策略。
本文将分析我国民航客运量的主要影响因素,并建立相应的预测模型,以期为我国民航业的可持续发展提供参考。
一、民航客运量影响因素分析1.宏观经济因素宏观经济因素是影响民航客运量的主要因素之一。
随着经济的不断增长,人民生活水平的提高以及旅游行业的发展,民航客运量也会相应增长。
此外,宏观经济、货币和财政等也会对民航客运量产生一定影响。
2.航空公司和航班因素航空公司的管理、经营和市场推广等因素都会直接影响到民航客运量的增长。
航班数量、航线网络、航班时刻的选择等也会对客运量产生影响。
航班的准点率、航班的服务质量等也是影响客运量的因素之一。
3.旅游业发展随着旅游业的发展和国际旅游的兴起,民航客运量也会相应增长。
旅游业的繁荣将引起人们的出游热情,提高机票需求量。
4.城市规划和交通发展城市规划和交通发展也是影响民航客运量的因素之一。
城市的繁荣和发展将带动航空客运的需求量,而交通工具密集度高的地区机场的使用率也会相应较高。
二、建模预测为了预测我国民航客运量的发展趋势,我们可以通过建立回归模型或时间序列模型来进行预测。
1.回归模型回归模型是一种基于相关分析的建模方法,可以通过分析各个影响因素对民航客运量的影响程度,建立预测模型。
例如,通过多元线性回归分析,可以得出民航客运量与宏观经济因素、旅游业发展和城市规划等因素的相关系数。
2.时间序列模型时间序列模型是一种基于历史数据的建模方法,可以将历史数据分析后得出的规律应用于未来的预测中。
例如,通过ARIMA模型或Holt-Winter模型等时间序列模型,可以预测出未来几年民航客运量的变化趋势。
三、结论综上所述,我国民航客运量的增长需要考虑各种影响因素,从而制定出符合实际的发展策略。
宏观经济因素、航空公司和航班因素、旅游业发展和城市规划和交通发展等都是影响民航客运量的主要因素。
北航数理统计大作业(逐步回归)
北京航空航天大事BEIHANG UNIVERSITY应用数理统计第一次大作业学号:______姓名:______________班级: __________20 15年12月民航客运量得多元线性回归分析摘要:本文为建立以民航客运量为因变量得多元线性回归模型,选取了199 6年至2013年得统计数据,包含国民生产总值,民航航线里程,过夜入境旅游人数,城镇居民可支配收入等因素,利用统计•软件SPSS对各因素进行了筛选分析,采用逐步回归法得到最优多元线性回归模型,并对模型得回归显著性、拟合度以及随机误差得正态性进行了检验,并采用201 4年得数据进行检验,得到得结果达到预期,证明该模型建立就是较为成功得.关键词:多元线性回归,逐步回归法,民航客运量0、符号说明变量符号民用航空客运量Y国民生产总值X,民航航线里程X3城镇居民人均可支配收入X51、引言随着社会得进步,人民生活水平得提高,如何获得更快捷方便得交通成为人们日益关注得问题•因为航空得安全性,快速且价格水平越来越倾向大众,越来越多得人们选择航空这种交通方式。
近年来,我国得航空客运量已经进入世界前列,为掌握航空客运得动态,合理安排班机数量•科学地对我国民航客运量得影响因素得分析,并得出其回归方程,进而能够估计航空客运量就是非常有必要得。
本文收集整理了与我国航空客运量相关得历年数据,运用SPSS软件对数据进行分析,研究199 6年起至20 13年我国民航客运量y(万人)与国民生产总值Xi(亿元)、铁路客运量X2(万人)、民航航线里程X3 (万公里)、入境过夜旅游人数X4 (万人)、城镇居民人均可支配 收入X5 (元)得关系。
采用逐步回归法建立线 性模型,选出较优得线性回归模型。
2、数据得统计与分析本文在进行统计时,查阅《中国统计摘要》,《中国统计年鉴2 0 14》以及中国 知网数据查询中得数据,收集了 19 96年至201 3年各个自变量因素得数据,分析它们 之间得联系。
影响民航客运量的相关因素分析
影响民航客运量的相关因素分析摘要:民航客运量受到很多因素的影响,本文选取了国民收入、铁路客运量、民航里程数与来华旅游入境人数四个具有代表性的指标,通过运用线性回归的方法来对这些影响因素进行相关的定量分析,并建立相关模型。
试图为我国的民航业的发展提供一些有参考价值的预测和信息。
关键词:民航客运量、影响因素、线性回归、定量分析一、航空业现状与影响因素分析航空运输作为现代化运输方式,其发展程度直接能反映一个国家的经济水平。
我国航空业发展起步较晚,最近几年虽然发展非常迅速,但是和国际上的航空公司相比还是有很大差距,而随着改革开放的进一步加深,民航业要面临更多的激烈竞争。
因此,加强对民航业的重视与研究,提高民航业的改革和发展,可以有效提升民航业的竞争力。
(一)民航客运量的现状分析近年来,我国的民航业发展迅速,在起步的近20年的时间里,平均增长速度在年15%左右,最近两年增速加快。
但是相对于国内航线的迅猛发展,国际航线却很疲软。
进入21世纪以来,我国航空业开始采用统一的标准,2002年实行政企分离以来,我国航空运输量呈现明显的增长趋势。
(二)民航客运量影响因素分析影响民航客运量的因素有很多,综合有关学者和该领域的专家的观点和意见,我们得出有着最直接影响的是国民收入、铁路客运量、民航里程数与来华旅游入境人数四个指标。
国民收入是一个国家整体经济的直接反映,而航空业在本国的发展更是与经济的好坏息息相关;铁路客运作为我国客运最为重要的运输,会和航空业形成一定的竞争;民航里程数反映了行业的发展水平,最后入境旅游人数也是与航空客运量有直接关联。
二、数据来源与分析本文主要以中国统计年鉴2002-2012历年的数据作为数据来源,从中采集了国民收入、铁路客运量、民航里程数与来华旅游入境人数历年的数据,如下图一:数据分析:以年份为横轴,作出四个解释变量和被解释变量的走势图。
为了避免异方差,这里我们对原始数据去自然对数处理。
从图中我们可以看出四个解释变量和被解释变量的走势相同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘要: 为了对民航业务量做出准确地评估和预测, 利用多元线性回归分析方法对民航客运量的变化趋势及成因建立 并从国民收入、 消费额、 铁路客运量、 民航航线里程、 来华旅游入境人数等方面进行了多元线 了多元线性回归模型, 性回归分析。 关键词: 回归分析; 最小二乘法; 回归方程; 显著性检验; 民航客运量 中图分类号: O212 文献标识码: A 文章编号: 1006 - 0707 ( 2012 ) 08 - 0081 - 04
)
在此条件下可以得到关于回归系数的估计及 σ 估计的 进一步的结果, 比如, 它们分别是回归系数及 σ 的最小方差 而且还可以作回归的显著性检验及区间 无偏估 计 等, 估计 1. 3 1. 3. 1
[7 ]
∑( y
i =1
i
珋 -y )2 =
∑( y
i =1
i
- yi )
2
)
n
n
n
+
∑( y
i =1
[8 ] - 1 ) 时, 接受 H0 , 则认为回归方程不显著 。
E( β i ) = β i , var( β i ) = c ij σ
)
2
c ij σ2 ) β i ~ N( β i ,
)
据此构造 t 统计量 ti = 其中 σ = βi c ii σ 槡 1 e2 i = n - p - 1∑ i =1
2 差, 通常认为 ε ~ N( 0 , σ )。
1 ) 解释变量 x1 , x2 , …, x m,是随机变量, x i2 , 观测值( x i1 , …, x im ) 为常数。 2 ) 方差齐性及不相关的假定条件为[1]
{
E( ε i ) = 0 , i = 1, 2, …, n COV( ε i , εj ) = = j ( i, j = 1, 2, …, n) {0σ,, ii ≠ j
^
2
2. 1
民航客运量模型的建立与求解
民航客运量模型的建立与求解 1 ) 数据来源 x1 表示国民收入总 以预测值 y 表示民航客运量( 万人) ,
21 . 578 x4 + 0 . 435 x5
2
( 20 )
b. 复相关系数 R = 0 . 999 , 决定系数 R = 0 . 988 , 由相关 系数来看回归方程高度显著 。 c. 方差分析表中, F = 1 128 . 303 , P 值 = 0 . 000 表明回归 x2 , x3 , x4 , x5 整体上对 y 有高度线性 方程高度显著, 说明 x1 , 关系。 d. 回归系数的显著性检验 。自变量 x1 , x2 , x3 , x4 , x5 对 y 均有显著影响, 其中 x3 铁路客运量的 P 值 = 0 . 006 最大, 可 这充分说 是仍然在 1 % 的显著性水平上对 y 具有高度显著, 明在多元回归分析中, 不能仅凭相关系数的大小而决定变量 的取舍。
2 2 … ε n ~ N( 0 , σ ) iid
2, …, n, 其中 i = 1 , 这个模型称为多元线性回归模型 。 令
y1 1 x11 x12 y2 1 x21 x22 Y = , X = yn 1 x n1 x n2 β0 ε1 β1 ε2 β = , ε = βm εn
y1 = y2 = yn = ε , ε
1
β0 + β1 x11 + β2 x12 + … + β p x1m + ε1 β0 + β1 x21 + β2 x22 + … + β p x2m + ε2 ( 2) β0 + β1 x n1 + β2 x n2 + … + β p x nm + ε n
2
。
( 17 )
回归系数的 F 检验
对多元线性回归方程的显著性检验就是看随机变量 x1 , x2 , …, x m 从 整 体 上 对 y 是 否 有 明 显 的 影 响。 因 此 提 出 原 假设 H0 : β1 = β2 = … = β m = 0 x2 , …, xm 如果原假设被接受, 则表明随机变量 y 与 x1 ,
[7 ]
。
2
之间的关系由线性回归模型表示不合适 。 一般用 F 检验来 判别, 为了建立对 H0 进行检验的 F 统计量, 用总离差平方和 ( 5)
2
3 ) 正态分布的假定条件为
{
i = 1, 2, …, n ε i ~ N( 0 , σ ), …, ε1 , ε2 , ε n 相互独立
2
的分解式, 即
c ii σ 槡 按照一元线性回归系数区间估计的推导过程, 可得 β j 置信水 平为 1 - α 的置信区间为
)
是回归标准差。 当原假设 H0i : β i = 0 成立时, 式( 10 ) 构造的 t i 统计量服 查出双 从自由度为 n - m - 1 的 t 分布。 给定显著性水平 α, 侧检验的临界值 t α / 2 。当 t i ≥ t α / 2 时拒绝原假设 H0i : β i = 0 , 认为 β i 显著不为 0 , 认为 β i 显著不为 0 , 自变量 x i 对因变量 y 的线性效果显著; 反之认为 β i 为 0 , 自变量 x i 对因变量 y 的 线性效果不显著 1. 3. 2
2
83 张 艳, 等: 民航客运量的多元线性回归分析
x2 , …, x m 的样本复相关系数 为 y 关于 x1 ,
[5 ]
。
结果见表 4 ~ 6 。 5 ) 回归诊断 a. 回归方程为 y = 450 . 9 + 0 . 354 x1 - 0 . 561 x2 - 0 . 007 3 x3 +
2 0, 1]区间内, R2 距离 1 越 样本决定系数 R 的取值在[
近, 表明拟合的效果越好; R 距离 0 越近, 表明拟合的效果越 R 检验可以更清楚直观的反映回归拟 差。与 F 检验相比, 合的效果, 但是并不能做为严格的显著性检验 。称 R = 槡 R2 = SST 槡 SSR ( 18 )
i
珋 -y )2
( 12 )
简写为 SST = SSR + SSE 此时用 F 检验统计量 F = SSR / m SSE / ( n - m - 1 ) ( 14 ) ( 13 )
。 回归系数的 t 检验
回归方程的显著性检验 在多元线性回归问题中, 回归方程显著并不能说明每个
F 在正态性假设下, 当 H0 : β1 = β2 = … = β m = 0 成立时, n - m - 1 ) 的 F 分布, 服从自由度为( m, 于是可利用 F 统计 量对回归方程的总体显著性进行检验 。 对于给定的数据, 当 i = 1, 2, ..., n, 计算出 SSR 和 SSE, 进而得到对应 F 的值, 见 一般列在下面的方差分析表中, 再由给定的显著性水平 α, n - m - 1) 。 查 F 分布表, 得到临界值 F α ( m, 表1 方差来源 自由度 回归 残差 总和 m n - m -1 n -1 方差分析表 均方 F值
2
( 4)
x i2 , …, x im , yi ) ( i = 1, 在实际问题中, 获得 n 组关于( x i1 , 2, …, n) 观测数据, 则
Markov ) 条件, M 这个称为高斯 - 马尔柯夫( Gauss简记为 G条件。在此条件下, 可以得到关于回归系数方程一些重要性 质, 比如, 得到关于回归系数的最小二乘估计是回归系数的
2012 年 8 月 第 33 卷 第 8 期 四 川 兵 工 学 报 【信息科学与控制工程】
民航客运量的多元线性回归分析
张 艳, 苗 刚, 李盈科
( 新疆农业大学 数理学院, 乌鲁木齐 830052 )
在实际问题中,常遇到研究一个随机变量与多个变量 之间的相关关系, 如, 某产品的销售额不仅受到投入的广告 费用的影响, 还与产品价格、 消费者收入状况、 社会保障及其 它可替代产品的价格等其他因素有关系 。 研究这种一个随 机变量同多个变量之间关系的方法主要是多元回归分析法 。 目前, 我国国民收入实现了快速增长, 民航业蓬勃发展, 为了对民航业务量做出准确地评估和预测, 民航客运量的变 化趋势及成因成为航空公司关心的主要问题 。 影响我国民 航客运量的因素, 不仅有经济因素、 政治因素, 还有天气因 素、 季节因素, 这些因素对我国民航客运量的变化影响程度 各有不同, 而这些因素的不同组合也会产生不同的效果 。 本 文从国民收入、 消费额、 铁路客运量、 民航航线里程、 来华旅 游入境人数等几个方面出发, 运用多元回归分析法来研究其 变化趋势及成因问题。
[4 , 8 ]
)
1 ( yi - yi ) n - p - 1∑ i =1
)
)
n
2
)
ti =
βi - βi
~ t( n - m - 1 )
( 15 )
)
)
1. 4. 2
( βi - tα /2 槡 c ii σ, c ii σ) βi + tα /2 槡 拟合优度
)
( 16 )
拟合优度用于检验回归方程对样本观测值的吻合程度 。 在多元线性回归中, 定义样本相关系数为 R2 = SSR SSE = 1 - SST SST
[3 ]
)
i = 1, 2, …, m
( 6)
平方和 SSR SSE SST
如果接受原假设 H0i , 则 x i 不显著; 否则 x i 是显著的。
SSR /m SSR /m SSE / ( n - m -1) SSE / ( n - m -1)
2 T β ~ N( β, σ ( X X)
