基于总变分和各向异性扩散方程的图像恢复模型

合集下载

处理及建议PDE

处理及建议PDE偏微分方程(Partial Differential Equations，PDE)在现代科学中扮演了重要的角色，它是从基本自然规律、应用数学、数学物理以及工程技术中产生的，很多问题都可以用偏微分方程来描述。

偏微分方程现已经应用于图像处理和计算机视觉的许多方面，包括图像恢复、图像分割、抠图、运动物体跟踪、物体检测等等。

偏微分方程在图像处理领域中的应用，具体涉及到微分几何、变分理论、数值分析等多个数学领域。

图像处理的目的，就是对数字化后的图像信息进行某些运算或处理，以提高图像的质量或达到人们所要求的预期效果。

用偏微分方程进行图像处理的基本思想就是根据实际问题，建立数学模型(变分模型或PDE模型)。

而变分方法将研究问题归结为一个泛函求极值问题，目的是使图像能量最小化。

由于偏微分方程可以准确对图像建模，从而能够很好的解决图像处理中许多复杂的问题，比如，用偏微分方程进行图像处理是对图像进行整体处理，在去除噪声的同时可以较好地保持边缘形状和位置不变。

在计算方面，可以很好地利用现在已有的一些非常完备的数值分析和偏微分方程的计算方法来进行运算。

使用偏微分方程的突出优点就是图像处理和分析的速度、准确性和稳定性都有很大提高。

使用偏微分方程方法进行图像处理不仅对偏微分方程理论研究提出了新的研究课题，而且对图像处理、信号分析等问题的发展起到了重要的促进作用，因此，它有着重要的理论价值，又有着广阔的应用前景。

总的来说，基于扩散方程的图像恢复技术的发展过程经历了从均匀线性扩散到线性非均匀扩散，再到非线性扩散，以及边缘增强、关联增强扩散的各向异性扩散的过程，近年来还出现了向前向后扩散、复数域扩散等方法，这些基于偏微分方程的图像恢复方法都有比较完善的理论框架。

除了在图像恢复方面有应用外，偏微分方程在图像分割、抠图、修补、边缘检测方面也有着广泛的应用。

偏微分方程在图像处理中的应用

偏微分方程在图像处理中的应用近年来，随着计算机技术的飞速发展，图像处理技术在各个领域得到了广泛应用。

而偏微分方程作为数学分析中的重要工具，也在图像处理中发挥着重要的作用。

本文将探讨偏微分方程在图像处理中的应用。

一、图像去噪图像去噪是图像处理中的一个重要问题，而偏微分方程可以通过模型来实现图像的去噪。

常见的偏微分方程去噪模型有总变分模型和非局部模型。

总变分模型是一种基于全变分的去噪方法，它通过最小化图像的总变分来实现去噪。

总变分是图像灰度在空间上的变化程度的度量，通过控制总变分的大小，可以实现去除图像中的噪声。

非局部模型则是通过对图像进行非局部相似性的测量，将图像的每个像素点与其周围像素点进行比较，从而实现去噪的效果。

二、图像增强图像增强是指通过一系列的处理方法，改善图像的质量和视觉效果。

偏微分方程可以通过图像的梯度信息来实现图像的增强。

梯度是指图像中像素灰度变化的速率，是图像中最重要的特征之一。

通过计算图像的梯度，可以得到图像中每个像素点的亮度变化情况，从而实现图像的增强。

常见的偏微分方程增强模型有梯度扩散模型和非线性扩散模型。

梯度扩散模型通过对图像的梯度进行扩散，使得图像中的细节信息得到增强。

非线性扩散模型则是通过对图像的梯度进行非线性的处理，进一步增强图像的细节信息。

三、图像分割图像分割是将图像分成若干个具有独立特征的区域的过程。

偏微分方程可以通过对图像的边缘进行检测，实现图像的分割。

边缘是图像中灰度变化突然的地方，是图像分割中最重要的特征之一。

通过对图像的边缘进行检测，可以将图像中的不同区域分割开来。

常见的偏微分方程分割模型有基于水平集的模型和基于变分的模型。

基于水平集的模型通过对图像中的边缘进行演化，实现图像的分割。

基于变分的模型则是通过最小化图像的能量函数，将图像分割成不同的区域。

四、图像恢复图像恢复是指通过一系列的处理方法，从损坏或噪声严重的图像中恢复出原始图像。

偏微分方程可以通过最小化图像的能量函数，实现图像的恢复。

基于曲率驱动扩散(CDD)的图像修复模型

（ｎｕｎｖｒｔ，ｆ３０９Ｃｉ）Ａｈｉｉｓｙｅ２０３，ｈｎｕｅｉＨｅｉａ
Ａｓｒｃ：ｈＶ（ｔａａｏａｉｐｉｔｇｍｏｅｆｌｔｒａｚｅｃｎｅｔｉｒｃｌｗｅｅｂｏｅｃｌｉｌｇｒｔｎｔｅｂｔｔｅＴＴｏａＶｒｔｎ１ｎａｉｄｌａｓＯｅｌｅｔｏｎｃｖｔｐｎｉｅ，ｈｎｔｒｋｎｓｅｓａｅｈａＴｌｉｉ）ｎｎｉｉｈｉｙｉｐｈａｒａｈ
维普资讯
研究开发
基于曲率驱动扩散（Ｄ的图像修复模型ＣＤ）
李莉（徽大学，徽合肥２０３）安安３０９
摘要：于Ｔ总体变分）复模型不能满足“ 接性准则” 由Ｖ（修连。针对这个问题，ｈｎ和ＳｅＣａｈｎ提出了基于曲率驱动扩散（Ｄ修复模ＣＤ）
ｐｉｔｇｍｏｅｗｈｃｓｆｕｄｄｏｒａｕｅｉｖｎＤｉｕｉｎａｎｉｄｌｉｈｉｏｎｅｎＣｕｖｔｒ—ＤｒｅｆｓｓｎｌｏｆＣＤＤ）Ｔｈ．ｅＣＤＤｄｌｍｐｒｕｖｔｒａｅｉｔｅＴＶｍｏｅ，ｔｕ，ｍｏｅｏｔａｃｒａｕｅｂｓｄｏｌｈｄｌｈｓｉｓ
或创造艺术效果。
图１当ｌｗ时．Ｖ的修复结果不满足 “ 接性准则” ＞Ｔ连
ＴＶ修复模型是最小化一个基于总变分模的能量范函，记Ｄ为待修复区域，为待修复区域的外邻域，在不考虑噪声的情况Ｅ

基于总变分和各向异性扩散方程的图像恢复模型

维普资讯
２００６年１Ｏ月
西安电子科技大学学报（自然科学版）
Ｊ０ＵＲＮＡＬ０ＦＸＩＡＮＵＮＩＤＩＶＥＲＳＩＴＹ
０ｃ．０６ｔ２０
第３３卷
第５期
Ｖｏ．３ＮＯ５１３．
基于总变分和各向异性扩散方程的图像恢复模型
特征也被保留．
关键词：总变分；向异性扩散方程；噪；节特征各去细
中图分类号：Ｐ９．１Ｔ３１４
文献标识码：Ａ
文章编号：０１２０（０６０ —７９０１０ —４０２０）５０５ —４
Ｉａｅｒｓｏａｉｎｕｉｈｅｔｔｌｖｒａｉｏａａｉｔｏｎｔｎｓｔｏｃｄｆｕｉｎｅａｉｎｈｅａｉｏｒｐｉｉｆｓｏｑｕｔｏ
ＬＩＭｉ，ＦＥＮＧｉｇ— ｈｕｎＸａｎｃ
（ｃｏｌｆＳｉｎｅＳｈｏｃｅｃ．ＸｉｉｎＵｎｖｏｄａｉ．．Ｘｉａ７０７ｎ１０１．Ｃｈｎ）ｉａＡｂｔａｔＷｅｐｏｏｅａｎｗｄｌｆｒｉｇｅｔｒｔｎｓｒｃ：ｒｐｓｅｍｏｅｏｍａｅｒｓｏａｉ，ｗｈｃｏｉｅｈｏａａｉｔｎｍｉｉａｉｎｏｉｈｃｍｂｎｓｔｅｔｔｌｒａｉｎｚｔｖｏｏ
李敏，冯象初
（西安电子科技大学理学院．西西安陕７０７）１０１
摘要：提出了一个基于总变分和各向异性扩散方程的图像恢复模型．模型通过引进 “ 粹的 ” 向异该纯各性扩散方程的扩散项．实现了偏微分方程去噪方法中非线性扩散方程与能量泛函变分法的有机结合．实验表明该模型不但能够提高去噪性能。而且可增强边缘并保持边缘的位置；够保持图像中的纹理特征能和不能用边缘刻画的大尺度细小特征．得处理后的图像清晰度和对比度大大增强，且有意义的细节使而

联合各向同性扩散和全变分模型的图像恢复模型

如下：０ｕ１＝Ｒ＋ｒ．（．１１）
其中ｕ，）（：ｘＱｃＲＲ为描述真实场景的初始图像，是甜的退化，称为观察到的图像，ｒ／是加性白高斯噪声，Ｒ是线性模糊算子．给定ｕ在已知图像退化模型为（１１）．的前提下，从中恢复是一个经典的反问题．本文仅仅考虑Ｒ为单位算子的情形，即Ｕ＝，ｏ＋７．图像恢复的传统方法主要是进行图像滤波．经典的图像滤波有均值滤波、中值滤波、维纳滤波等．由于图像的大部分信息存在于图像的边缘和纹理处，因此要求在进行图像恢复的过程中，尽可能多地保留图像
可变权重联合各向同性扩散和金变分模型的图像恢复模型，该权重参数依赖于图像曲面的几何特征。
最后，通过数值实验论证了算法的有效性。
【关键词】向同性扩散；全变分模型；图像恢复；图像曲面；抛物型偏微分方程各
【中圈分类号】５．１１１【文献标识码】Ａｆ文章编号】０８１８（０２０－０５０１０ — ７Ｘ２１）３００－５
Ｍａ．０１ｒ２２
联合各向同性扩散和全变分模型的图像恢复模型
辛
【摘
巧，许
璐，胡卫敏
（伊犁师范学院数学与统计学院，应用数学研究所，新疆伊宁８５０）３００
要】本文首先简单回顾了基于抛物型偏微分方程的图像恢复模型。在此基础上，提出了一个通过
的边缘和纹理信息，而图像的边缘与噪声在频带上的会混叠，这导致了图像去噪和边缘保持成为一对矛盾．
经典的滤波方法，特别是频率域的方法很难处理这类问题．最近２年来，以物理中热扩散模型为基础，发０

【计算机应用】_图像修复_期刊发文热词逐年推荐_20140724

Байду номын сангаас
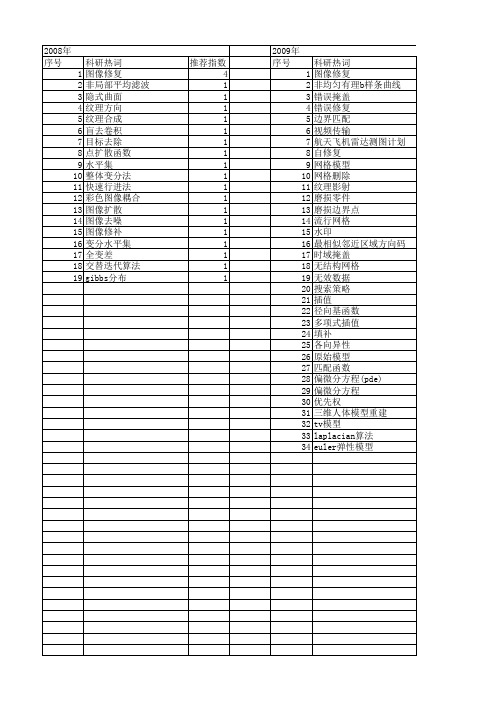
推荐指数 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
科研热词图像修复非均匀有理b样条曲线错误掩盖错误修复边界匹配视频传输航天飞机雷达测图计划自修复网格模型网格删除纹理影射磨损零件磨损边界点流行网格水印最相似邻近区域方向码时域掩盖无结构网格无效数据搜索策略插值径向基函数多项式插值填补各向异性原始模型匹配函数偏微分方程(pde) 偏微分方程优先权三维人体模型重建 tv模型 laplacian算法 euler弹性模型
2008年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
科研热词图像修复非局部平均滤波隐式曲面纹理方向纹理合成盲去卷积目标去除点扩散函数水平集整体变分法快速行进法彩色图像耦合图像扩散图像去噪图像修补变分水平集全变差交替迭代算法 gibbs分布
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39
推荐指数 6 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

基于各向异性扩散方程的局部非纹理图像修整与去噪

ｉｇｅｉｐｉｔｇｓｈｍｅｂｓｄｏｎｓｔｏｉｉｕｉｎｅｕｔｎ，ｈｃａｉｌｅｕｌｅｏｓｄｐｅｅｅｅｇｓｅｅｔｅｙｗｈｌｍａｎａｎｉｃｅａｅｎａｉｏｒｐｃｄｆｓｑａｉｗｉｈｃｎｓｍｕｔｏｓｙｄｎｉｅａｒｓｒｄｅｆｃｉｌｉｎｏｏｎａｎｖｖｅｆｌｇｉｈｓｉｇａｅ．ｈｓｈｅｎｉｄｃｔｄｔｅｒｔａｌｎｘｅｍｅｔｌ．ｉｉｎｔｅｍｉｓｒａＴｉａｂｅｎｉａｅｏｅｉｌａｄｅｐｒｎａｙｌｎｎｓｈｃｙｉｌ
Ａｂｔｃ：Ｉｇｎａｎｉｇｉａｎｅｐｌｔｎｗｉｈｇｅｓｓａｄｆｌｉｎｉｏｍａｉｎｌｓｎｏｔｎａｃｒｉｇｔｔｓｒｏｎ－ｓｒｔｍａｅｉｐｉｔｓｎｉｔｒｏａｉｈｃｕｓｅｎｉｓｎａａｎｏｌｍｆｒｔ－ｉｇｐｒｉｃｏｄｎｏｉｕｒｕｄｏｏｏｓ
区域，图像修整属于图像恢复的范畴。利用变分方法导出的各向异性扩散方程对于图像边缘的良好保持特性，而在图像处理中得到了广泛的应用。基于这一思想，本文提出了一种基于各向异性扩散方程的图像修整算法：在填补修整区域的同时，可有效地去除噪声，同时保持边缘信息。理论分析和实验结果表明了这一点。关键词：图像处理；图像修整；图像去噪；变分；向异性扩散方程各

图像修复的方向梯度TV模型研究

图像修复的方向梯度TV模型研究王相海;王爽;方玲玲【摘要】基于PDE（Partial Differential Equation）的图像修复因其所具有的局部自适应特性、形式上的规范性和模型建立的灵活性而受到关注,而如何在有效的进行修复受损图像的同时很好的保留图像的细节信息成为图像修复所追求的目标.本文首先对TV（total variation）模型进行了分析和讨论,针对TV模型在图像修复时会对图像过度平滑、容易丢失细节信息等问题提出了一种改进模型,该模型通过对非线性扩散项引入方向梯度和边缘引导函数,自适应的调整了模型在图像边缘和区域信息丰富区域的平滑力度;通过计算每一次迭代时待修复点33邻域内的各向灰度差分,确定最小灰度差分的方向,从而确定了该点邻域内的图像纹理走向.本文模型克服了TV模型的弱点,在有效进行破损图像修复的同时,很好的保持了边缘和纹理细节信息.通过峰值信噪比和归一化均方误差的统计结果验证了所提模型的稳定性和有效性.%Image Inpainting based on the partial differential equation （PDE） has received considerable attention because it has the local self-adapting characteristics,formal normalization,and modelingflexibility.However,how to effectively repair the image as well as keep details of image is the pursued goal of image inpainting.In this paper,we firstly analyzes and discusses the TV-model,on this basic,proposes an improved model,which introduces direction gradient and guide-function of edge into the non-linear diffusion parts and adaptively adjusts the smooth intensity of the model in edge and texture information-rich regions of images;by calculating the gray level difference of the repaired point in the 33 neighborhood by each iteration to determine the directionof the smallest gray difference,so we can determine the direction of the image texture point in the neighborhood.This model not only overcomes over smoothness produced in the TV-model,but also avoids losing details and information,and greatly maintain a good image of the edge and texture details.Experimental results illustrate the effectiveness and stability of the proposed model by PSNR and NMSE.【期刊名称】《吉林师范大学学报（自然科学版）》【年(卷),期】2012(033)002【总页数】7页(P1-7)【关键词】图像修复;变分模型;方向梯度;边缘引导函数;灰度差分【作者】王相海;王爽;方玲玲【作者单位】辽宁师范大学计算机与信息技术学院,辽宁大连116029／苏州大学江苏省计算机信息处理技术重点实验室,江苏苏州215006;辽宁师范大学计算机与信息技术学院,辽宁大连116029;苏州大学江苏省计算机信息处理技术重点实验室,江苏苏州215006／苏州大学计算机科学与技术学院,江苏苏州215006【正文语种】中文【中图分类】TP391多媒体技术的快速发展使图像的存储和使用更加灵活方便，但同时也会因网络传输和使用不当等带来图像质量下降和局部信息的缺失等问题［1］．近年来图像修复（Image Inpainting）作为一种修复图像丢失或破坏的信息技术成为一个新的研究领域，特别是在去除图像的划痕或破损以及修补图像处理过程中因目标物体或文字的移走而出现的信息空白区等问题成为当前亟待解决的热点问题．基于偏微分方程的全变分图像处理方法近年因其所具有的良好的边缘保持特性而受到越来越多人的关注．基于偏微分方程（PDE，Partial Differential Equation）的图像修复对于修复小尺度的图像受损区域取得了很好的效果，它主要是利用物理学中热扩散方法将待修复信息周围的原有效信息延伸到待修复区域，把修复问题转化为能量泛函的建立问题，通过求解最小平方能量泛函，获得图像的近似解，以达到图像修复效果［2］．基于PDE的图像修复技术最早是由Bertalmio和Sapiro等人提出的（简称BSCB方法）［3］，它是利用待修补区域的边缘信息，采用一种由粗到精的方法来估计等照度线（isophote）的方向，通过传播机制将信息传播到待修补的区域内，以便得到较好的修补效果．考虑到应用于图像修复的偏微分方程中边缘信息的重要性，Rudin等在文献［4］中提出的变分极小化模型（TV，Total Variation）作为一个经典模型，在去噪的同时能够很好的保护影像边缘；进一步Osher等人提出了基于该模型的图像修复算法，能在大量噪声情况下有效的对图像进行修复，但在图像细节的保持上有一定的欠缺，而且不完全符合图像处理的形态学原则［5，6］．此外，针对TV模型在恢复图像中会产生阶梯效应，文献［7］给出了一种基于四阶偏微分方程的盲图像恢复模型，用四阶范数来代替TV范数，构造了一种新的能量泛函，用分片平面图像来近似边界，从而消除了二阶非线性扩散所造成的阶梯效应，同时也能取得较好的图像恢复效果，但该模型在图像细节的恢复上仍不能令人满意．针对这一问题，文献［8］提出了一个非局部算子，将其与TV模型相结合，根据非局部泛函，通过基于块距离的度量，在全局搜索与之最相似的点，使得丢失信息能正确填充，修复效果得到改善．但算法需要全局搜索，计算复杂度很高，而且对于计算的权重大小很难把握．本文针对TV修复模型的不足，构建了一个基于方向梯度的自适应扩散函数，进而提出一种具有边缘引导特性的变分模型，并对其离散化过程进行了研究．该模型在有效进行图像修复的同时，能很好的保留图像边缘和纹理细节信息．此外，在峰值信噪比和归一化均方误差上，模型都表现出很好的特性，仿真实验结果验证了模型的有效性．记D为待修补区域，E为待修补区域的外邻域（见图1）．记修复后E∪D区域内的图像值为u，定义代价函数为：满足如下噪声约束条件：其中A（E）为区域E的面积，E内的初始图像值u0包含方差为σ的高斯白噪声．采用Lagrange乘子法将有约束条件的极值问题转化为无约束条件的极值问题，得到下列新的代价函数：由计算函数极值的变分方法可知，若计算如（2）式所示的二维最简泛函的极值时，函数F应满足（3）式：这样式⑴中的第一项可以表示为：其中，φ（·）为一个非负递减的严格凸函数，并且满足φ（0）=0和因此可得总变分模型的一般形式为：（4）式对应的Euler-Lagrange方程为：进一步，对模型进行变分最小化［9］．在式（4）中，令φ（|▽u|）=|▽u|，得到如下的最小化能量函数：其中，∫E∪D|▽u|dxdy为正则项，表示图像u的总变分范数（TV范数），该项主要是对能量进行估计，起到平滑图像、消除噪声和保留边缘的作用，它可以使图像中出现不连续的部分，但不允许存在震荡，因此，可用来去除噪声；∫E（u－u0）2dxdy反映了被恢复图像u与原图像u0之间的差别，称其为逼近项．λ（λ＞0）为均衡系数，用来平衡正则项和逼近项．式（5）对应的Euler-Lagrange方程时间演化形式为：其中．由于待修复的区域内信息已丢失，所以在修复区域内部无法做去噪操作，但在待修复区域外部，模型可以进行该操作．若不考虑去噪问题，可取λ=0，即：为了满足能量函数达到最小值，应满足假设v=（V（1），V（2））=▽u/|▽u|，点O为待修复点，其对应八邻域点分别为WN、W、WS、S、ES、E、EN和N（参见图2）．首先，计算待修复点O和周围四邻域点N、W、S、E的中间位置点n、w、s、e，进一步计算对应的，具体计算过程如下（以点e为例）：综上，基于TV模型的修复方法本质上是一种各向异性的扩散算法，其各向异性权重与当前的梯度绝对值呈反比，用来保证修复结果与原图的相似性，以免产生过度平滑．基于该原理，在图像边缘处，边缘两边的值并不会彼此扩散，而是沿着边缘的法线进行扩散，从而实现修复的效果．但由于该种分析方法考虑邻域信息时，只是使用待修复区域外围的环状区域，因此着眼点过于局部，整体的修复效果得不到保证，图像细节保持上有一定的欠缺．针对TV模型应用于图像修复时丢失图像细节等情况，本文在模型的扩散项中添加了上、下、左、右四个方向的梯度，同时增加了用以调节各向异性的扩散系数λ：其中，σ为大于0的极小参数，主要用来防止|▽uα|为0时，1/|▽uα|没有意义的情况；|▽uα|分别包括|▽uE|，|▽uW|，|▽uN|和|▽uS|，对于图2中的E、W、N和S 点，有：其中，uEx、uWx、uNx和uSx分别表示对应点在x方向上的偏导数，而uEy、uWy、uNy和uSy则为对应点在y方向上的偏导数．这样，新模型在进行图像修复时，可在|▽u|取值较大的地方，即图像的边缘方向上尽可能不进行平滑，而在图像的平坦区域，即垂直于梯度的方向上（边缘的切线方向），则尽可能的进行大范围的平滑处理．调节各向异性扩散程度的参数是根据待修复图像点的3×3邻域内的各方向的像素灰度差分决定的．例如在X方向上，像素点间的灰度差分越小，说明受到这一方向的像素点的相关度就越大，对应的参数值λ就越大，这样就会更好地保持图像细节．在PM模型［11］中，传导系数g（|▽u|）能够在平滑过程中根据图像的局部特征而自适应的进行调整：在图像比较平坦的区域，传导系数会自动增大，从而能够平滑平坦区域中的不规则的、较小的噪声；而在图像的边缘附近区域，传导系数会自动减小，从而保留了边缘的局部信息．本文在所提出的模型中增加了相其中median为取中值操作．当|▽u|＜K时，表明为图像的灰度变化平缓的区域，而当|▽u|≥K时，则认为是图像的边缘区域［11］．边缘引导函数g（|▽u|）的引入，使该修复模型在图像灰度缓变的区域进行较多的扩散，而在图像的边缘则不再扩散，使其沿着图像边缘扩散到待修复区域内．从而在修复图像内容同时，可以较好的保持图像的边缘．在模型的离散化过程中，通过计算每一次迭代时待修复点3*3邻域内的各向灰度差分来确定最小灰度差分的方向，从而确定该点邻域内的图像纹理走向．具体过程如下：首先，采用图2的结构和半点格式对模型进行离散化，参见公式（6）～（8）．其次，设E点坐标为（i，j）（参见图3），由（9）式可得：最后，计算待修复点O的附近邻域内各向灰度差分：其中，L、H、HL和LH是待修复点O的水平方向、竖直方向和对角线方向上的灰度差分值．取min（L，H，LH，HL），并在最小灰度差分值方向上乘以调解系数λ，其中λ是大于1的阈值（本文中实验中取值为3）．为了避免在图像的平坦区|▽u|的值为零所导致的div（▽u/▽u|）运算无意义，在实际计算中，采用了如下正则化梯度：上述离散化模型算法实现的具体步骤如下：Step1初始：设待修复图像I的范围为I0～In，选取空间步长h、时间步长Δt和扩散调解系数λ．Step2由式（12）计算边缘检测阈值K．判断图像范围内某一像素Ix（初始时：Ix=I0）是否位于修补区域内，若不是，转向Step2．4，否则，执行如下过程：Step2．1由式（6）（7）计算待修复点与邻域点的中间位置梯度模值|▽u|和一阶导数值V（1），V（2），并利用式（8）和（11）分别计算待修复点的上、下、左、右四方向的梯度和传导函数g（|▽u|）．Step2．2由式（13）计算待修复点的四个方向上的灰度差分值，并确定差分值最小值的主方向．Step2．3利用式（14）对像素值进行更新．Step2．4若Ix=In，表明已处理完整个图像，转向Step3，否则置Ix=Ix+1，返回执行Step2．1．Step3．结束本文的仿真实验是在MATLAB R2007b下进行的．为了验证算法的有效性，我们对TV基本模型和本文提出模型的图像修复结果进行了比较．实验中对三幅不同大小的图像分别进行了不同程度的破坏，其中，图像A主要进行了划痕破坏；图像B主要进行了任意涂鸦的破坏；图像C主要进行了图像上已存在文字的破坏；然后采用两种模型对每幅待修复图像进行修复处理，如图4～6所示．从图中可以看出，采用TV模型处理后的图像，虽然较好的保持了边缘，但图像表面仍残留着部分难以去除的破坏部分，一定程度上影响了视觉效果．而采用本文提出的模型，不但很好去除图像中的破坏部分，而且使原图像中的大量细节和边缘信息得以保留．更进一步地，我们随机选取图像A修复效果放大效果图与TV模型进行对比，不难看出本文改进模型在保持图像细节和边缘上均具有较好的效果，如图7所示．另外，考虑到图像中没有足够的信息来保证修复的唯一正确性，这样对修复结果的判断就会带有很多主观因素，当然也就没有唯一完全正确的评价标准．本文采用图像的峰值信噪比（PSNR）和归一化均方误差（NMSE）进行图像修复后的统计结果（参见表1），PSNR和NSME的计算公式如下： NMSE=其中u'（i，j）是修复后的影像，u（i，j）是原始图像；m和n为图像的长和宽．从统计结果可以看出，本文提出模型修复后的图像与原图像（受损图像）相比会得到失真更少、修复效果更好的图像．本文针对TV修复模型在图像修复时存在的细节保留不足和边缘断裂的缺陷，通过对非线性扩散项的改造，引入了方向梯度和边缘引导函数，提出了基于方向梯度的具有边缘检测的变分模型．在模型的离散化过程中，采用灰度差分方法进行待修复点图像纹理走向的确定．克服了TV修复模型容易产生的小块局部修复效果和丢失细小纹理边缘信息的弱点，在有效的修复破损图像的同时，边缘和细节都很好的予以保持，在峰值信噪比上也均有提高．【相关文献】［1］张红英，彭启琮．数字图像修复技术综述［J］．中国图像图形学报，2007，12（1）：1～10．［2］DING H Y，BIAN Z F．Remote Sensing Image Restoration Based on TV Regularization and Local Constraints［J］．Acta Photonica Sinica．2009，6 （38）：1577～1580．［3］BERTALMIO M，BERTOZZI A L，SAPIRO G，et al．Fluid Dynamics，and Image and Video Inpainting［C］．Proc．IEEE CVPR＇01，2001，1：355～362．［4］RUDIN L I，OSHER S，FATEMI E．Nonlinear total variation based noise removal algorithms［J］．Physica D，1992，60：259～268．［5］OSHER S，FEDIKIW R．Level set methods and dynamic implicit surfaces［M］．New York：Springer，2003．［6］MARQUINA A，OSHER S．Explicit algorithm for a new time dependent model based on level set motion for nonlinear deblurring and noise removal［J］．SIAM Journal on Scientific Computing．2000，22：387～405．［7］马少贤，江成顺．基于四阶偏微分方程的盲图像修复模型［J］．中国图象图形学报，2010，15（1）：26～30．［8］李莉，王卫卫．基于偏微分方程的图像修复（硕士学位论文）．西安电子科技大学，西安，2010．［9］LEONID I R，STANLEY O，EMAD F．Nonlinear total variation based noise removal algorithms［J］．Physica D：Nonlinear Phenomena，1992，60（1-4）：259～268．［10］PERONA P，MALIK J．Scale-space and edge detection using anisotropic diffusion ［J］．IEEE Transaction on Pattern Anal Machine Intell，1990，12 （7）：629～639．［11］SAPIRO G．Geometric Partial Differential Equations and Image Analysis ［M］．Cambridge University Press，2001．。

基于图像亮度局部约束的总变分图像去噪法

第２卷第５ｇ６１ｌ
２１０１年９月
数
据
采
集
与
处
理
Ｖｏ．２１６Ｎｏ．５
Ｊｕｎｌｏｔｑｉｉｉｎ＆ＰｏｅｓｎｏｒａｆＤａａＡｃｕｓｔｏｒｃｓｉｇ
Ｓｐｅ．２１０１
文章编号：０４９３（０１０ —５４０１０— ０７２１）５０６— ５
在图像获取或传输的过程中，常会由于传感经
器自身的噪声或传输信道的问题而使图像受到噪声的污染。对于许多图像处理的应用而言，例如边缘检测、图像分割、目标识别等等，噪声的去除是第１步需要完成的，者说去噪有利于后续的图像处或
ｕｉｉｅｏｃｎｓｒｉｈｅｎｕｅｉａｏｕｉｎａａｈｉｅａｉｔｐ．Ｅｘｐｒｍｅｓｓｔｌｚｄｔｏｔａｎｔｍｒｃｌｓｌｔｏｔｅｃｔｒｔｏｎｓｅｅｉｎｔｈｏｗｈａｈｔｔｔｅ
Ａｂｔａｔｓｒｃ：Ａｅｉｇｅｏｓｎｅｈｄｉｐｏｏｅｎｗｍａｅｄｎｉｉｇｍｔｏｓｒｐｓｄ，ｗｈｃｏｉｈｃｍｂｎｓｔｅｔｔｌａｉｔｎｔｅ — ｉｅｈｏａｒａｉｈｏｖｏｒｔｈｏａｎｅｓｔｏｎｏｓｒｉｔ．Ｔｏｏｅｃｍｅｔｅｗｅｋｅｓｔａｈｏａａｉ— ｙｗｉｈｔｅｌｃｌｉｔｎｉｙｂｕｄｃｎｔａｎｓｖｒｏｈａｎｓｈｔｔｅｔｔ１ｖｒａｔｎｉｇｅｏｉｇｍｅｈｄｉｅｓｏｐｏｕｅｆｌｅｅｇｓｏａｅｎａｄｌｃｌｖｒａｃｒｉｍａｅｄｎｓｎｔｏｓａｙｔｒｄｃａｓｄｅ，ｌｃｌｍａｎｏａａｉｎｅａｅｏ

基于偏激分方程(PDE)的图像去噪的方法综述

基于偏激分方程(PDE)的图像去噪的方法综述摘要:偏微分方程(PDE)方法,是图像处理中的一种较新的方法,有着很强的数学基础,在图像处理中的应用发展非常快。

本文将近几年应用较多的几种图像去噪方法进行了系统的概括总结,指出了该领域的学者是如何一步步进行改进得到新方法的,并对该领域的发展做了新的展望。

关键词:图像去噪偏微分方程平滑滤波总变差1 引言图像去噪是数字图像处理中的一个经典问题。

随着数字图像处理技术的发展,大量数字图像经由信道传输或通过介质保存。

图像在传输或存储过程中受到外界物理条件的限制,所产生的噪声会影响图像的视觉效果。

而在众多的应用领域中,又需要清晰的、高质量的图像,因此,图像去噪是一类重要的图像处理问题,同时也是其它图像处理的重要预处理过程,对后继处理带来很大的影响。

基于偏微分方程(PDE)的方法进行图像处理因具有各向异性的特性,自适应性强,能够在平滑噪声的同时更好的保持边缘与纹理等细节性息,故在过去的二十几年中获得了巨大的发展。

这个领域的实质性的创始工作归功于和各自独立的研究。

他们严格地介绍了尺度空间理论并指出图像与具有递增方差的高斯函数做卷积实现低通滤波和求解以原图像为初值的热传导方程等价。

然而由于高斯滤波是各向同性扩散,在去除噪音的同时模糊了边界。

改进滤波技术,在去噪的同时能完好的保存边缘等重要信息,一直是这一领域的目标。

本文详细介绍了现存的基于PDE的图像去噪的主要方法,并指出了它们之间的联系。

2 图像去噪模型偏微分方程与图像去噪的结合产生了许多模型,大体上可以分为两大类:一种是基本的迭代格式,随着时间的变化更新,使得图像向所要得到的效果逐步逼近,这种算法的代表为的方程以及对其改进的后续工作。

该方法在前向扩散的同时具有向后扩散的功能,所以具有平滑图像和边缘锐化的能力,并且扩散系数有很大的选择空间。

但是该方法是病态问题,在应用中不稳定。

另一种是基于变分法的思想,确定图像的能量函数,通过求能量函数的最小值,使得图像达到平滑状态,现在得到广泛应用的总变差TV(Total Variation)模型[4]就是这一类。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

! " " /年% "月第, ,卷!第#期
!
西安电子科技大学学报（自然科学版） ! "#$%& ’!" (!) * + * &%!#% * , -$ . * /0
!
U 1 G ) ! " " / V 3 4 ) , ,!W 3 ) #
基于总变分和各向异性扩散方程的图像恢复模型
李 ! 敏! 冯象初
第 # 期 !!!!!!!!!!!!!! 李 ! 敏等 ! 基于总变分和各向异性扩散方程的图像恢复模型
( / %
廓进行平滑和去噪 ) 这样就使得图像在边缘两侧及区域内部得到充分的平滑 ! 从而使得图像的细节特征得到较好的保持 ) 把" 纯粹的 # 各向异性扩散方程的扩散项式 $ % 引入总变分 Z 模型 ! 从而使得新模型避免了这种强扩散 ! # $ 同时发挥了 " 纯粹的 # 各向异性扩散方程的优势 ) 数值实验结果表明这种结合可提高原变分模型的去噪性能 ! 改善恢复图像的视觉质量 ) # " !! 新模型的推导用式 $ % 中的扩散项 # 方程 ’ $ & # %中的 : $ & # !得到新模型的 + 0: 6 = 0 0 (%代替式 $ / 6 = " " (% O T # # #
#
" # #
! ! $ " " " " " " " " 3" 4 4 4 4 4 4% 5 3! 52 5 5 5! 5 其中" ! & ’ ’ 1 ! ! ! ! % !6 ’1 " " " " " 42 42 5 5# 在数值计算中 ! 为避免图像平坦区域梯度为零的情况! 一般都采取参数提升梯度! 即
图像恢复模型 # 大大改观了原始图像的恢复质量 # 提高了去噪性能 )
:! 预备知识
! " !! 总变分模型其模型可写为 !! 对于带噪图像来说 # ! " " % !# " 1"2% 其中" 是原始干净图像 ’ 通常为标准偏差为! 高斯白噪声 ’ % 是图像中加入的噪声 # " " 为带噪的观测图像 )
! # # " 0 1 2 3 3 4 3 50 1 6 7 8 1 7 9 6 : 6 ; 8< 8 6 = ) 9 6 > ; 8 % " " ( %# ? 2 6 8 ; !( $ # 5 6 ’ ( & # 2 ( 7A B 3 3 C 7;8 7 DE 3 : 7 4 5 3 B 6 E ; 7 B 7 C G 3 B ; G 6 3 8 D 2 6 1 21 3 E H 6 8 7 C G 2 7 G 3 G ; 4 = ; B 6 ; G 6 3 8E 6 8 6 I ; G 6 3 8 !@ A F & D 6 G 2G 2 7% J B 7 ; 8 6 C 3 G B 3 6 1: 6 5 5 J C 6 3 87 J ; G 6 3 83 5. 4 = ; B 7 IL; 8 :M 3 B 7 4 NM) O J 7 G 3 G 2 7 6 8 G B 3 : J 1 G 6 3 83 5 G 2 7 A A K 8 7 D: 6 5 5 J C 6 3 8G 7 B E# G 2 6 CE 3 : 7 4 1 ; 88 3 G 3 8 4 7 E 3 = 78 3 6 C 7H J G ; 4 C 37 8 2 ; 8 1 77 : 7 C; 8 :Q 7 7 2 7 6 B 4 3 1 ; 4 6 G ) PB F AG P . 8 :6 G 1 ; 8; 4 C 3Q 7 7 G 7 R G J B 7 C ; 8 : 4 ; B 7 $ C 1 ; 4 7 5 6 8 7 5 7 ; G J B 7 C G 2 ; G ; B 78 3 G 1 2 ; B ; 1 G 7 B 6 I ; 7 :H : 7 C ) S 7 1 ; J C 73 5 A F P7 F # # G 2 7 C 7 5 ; = 3 B ; H 4 71 2 ; B ; 1 G 7 B 6 C G 6 1 C 8 3 G3 8 4 3G 2 7A B 3 1 7 C C 7 :6 E ; 7 C4 3 3 QE J 1 21 4 7 ; B 7 B; 8 :C E 3 3 G 2 7 B H J G P: F # ; 4 C 3C 6 8 6 5 6 1 ; 8 G: 7 G ; 6 4 C; B 7Q 7 G B 7 C J 4 G 6 8 6 8; 7 ; 4 6 8 6 C 6 3 8 ) F A F A A F= $ ’ ’ ’ 7 % ) & 0 ’ G 3 G ; 4 = ; B 6 ; G 6 3 8 ; 8 6 C 3 G B 3 6 1: 6 5 5 J C 6 3 87 J ; G 6 3 8 8 3 6 C 7B 7 E 3 = ; 4 : 7 G ; 6 4 ! A K 89
数字图像处理技术已广泛应用于许多科学和工程领域 ) 而图像质量自然也成为评判这些应用成果价值的客观指标 ) 但是 # 由于实际中设备的不完善和物理的限制 # 所获得的图像通常达不到期望的质量 ) 因此# 原始图像的恢复是非常必要的 ) 近! 由于人类视觉对图像恢复水平的高追求 # 数学方法处理图像已成为 " 年来 # 一个重要的课题 # 其中 # 偏微分方程 ! 和泛函分析备受青睐 ) + O T" 具体到基于偏微分方程的去噪方法大致可分为两类 $ 基于非线性尺度空间 ! 即非线性扩散方程" 的方法
" 8 "
!
& # "3" # ! : 4: 5! ! "" #" 2#"
4;
E 6 8 ’" "#1
8
8
8
8
8
"
"
%为期望值 ) ) 9 是常数 ! & 为窗函数 ! %$ 纯粹的 " 各向异性扩散方程 ! " #! !
/% 提出 * 纯粹的 + 各向异性扩散方程 $ ( . 4 = ; B 7 I和 M 3 B 7 4等发展了 + 7 B 3 8 ; $ M ; 4 6 Q 扩散的思想 ! & # " " ": 6 =" " " # 4! : ’ "! ! # # !! ! 5#& "! : 1 ) ( #1" " "" 4! " 4! 4! !! 5! 5# 5#& "! ! "" *
" 4! 5
4: 51 "$" #" #: "
" "
": 4: # 5! 6
" # /
$! %# $: %6 " 4 : 4 5 5
当离散式 " 时! 如果 /#
那么由扩散项 : " & # 即当 " 1 "! 6 = " " (#所提供的扩散可能会很大 ! # #
" 1"时! # " % % % % # " # 6 = "! 6 ( 1 "! -: " & ! ! % ! , "( ,( "( # " " # ( (# 42 52 # 就等价于各向同性的热扩散 ) 它意味着式 " # 会在图像相对平坦的区域内形成一种强扩散 ! 从 ( / !! 这时式 " 而使得图像在这些区域中局部地变成常数 ) 式" # 仍然把图像看成是空间中分片连续的函数 ! 因此在扩 / S V
! 西安电子科技大学理学院 " 陕西西安 !( # % " " ( % 摘要 ! 提出了一个基于总变分和各向异性扩散方程的图像恢复模型 ) 该模型通过引进" 纯粹的# 各向异性扩散方程的扩散项 ! 实现了偏微分方程去噪方法中非线性扩散方程与能量泛函变分法的有机结合 ) 实而且可增强边缘并保持边缘的位置 $ 能够保持图像中的纹理特征验表明该模型不但能够提高去噪性能 ! 和不能用边缘刻画的大尺度细小特征 ! 使得处理后的图像清晰度和对比度大大增强 ! 而且有意义的细节特征也被保留 ) 关键词 ! 总变分 $ 各向异性扩散方程 $ 去噪 $ 细节特征中图分类号 ! " # * + , ’ %) %!! 文献标识码 ! .!! 文章编号 ! % " " % $ ! " " ! " " / " # $ " ( # ’ $ " -
" # -
其中" #为尺度: 下" 4! "" 4! : 4! 5#为初始的灰度图像 ! 5! 5#的平滑版本 ) "" "" 式" # 右边的扩散项可转化为图像灰度曲面梯度正交方向’ 上的扩散项 ! 即 -
": 6 = #
" 1 "# " # #
" #
"3 " "
% " #
!
! "! "# # "" # # "" "! "# # # ! "3 # 1" 1" ’ ’! " # "! # !