流体力学--习题解答及习题课讲义
流体力学习题解答讲解

2.在现实生活中可视为牛顿流体的有水 和空气 等。
3.流体静压力和流体静压强都是压力的一种量度。
它们的区别在于:前者是作用在某一面积上的总压力;而后者是作用在某一面积上的平均压强或某一点的压强。
4.均匀流过流断面上压强分布服从于水静力学规律。
5.和液体相比,固体存在着抗拉、抗压和抗切三方面的能力。
7.流体受压,体积缩小,密度增大 的性质,称为流体的压缩性 ;流体受热,体积膨胀,密度减少 的性质,称为流体的热胀性 。
8.压缩系数β的倒数称为流体的弹性模量 ,以E 来表示12.液体静压强分布规律只适用于静止、同种、连续液体。
13.静止非均质流体的水平面是等压面,等密面和等温面。
14.测压管是一根玻璃直管或U 形管,一端连接在需要测定的容器孔口上,另一端开口,直接和大气相通。
16.作用于曲面上的水静压力P 的铅直分力z P 等于其压力体内的水重。
17.通过描述物理量在空间的分布来研究流体运动的方法称为欧拉法。
18. 流线不能相交(驻点处除外),也不能是折线,因为流场内任一固定点在同一瞬间只能有一个速度向量,流线只能是一条光滑的曲线或直线。
20.液体质点的运动是极不规则的,各部分流体相互剧烈掺混,这种流动状态称为紊流。
21.由紊流转变为层流的临界流速k v 小于 由层流转变为紊流的临界流速kv ',其中kv '称为上临界速度,k v 称为下临界速度。
23.圆管层流的沿程阻力系数仅与雷诺数有关,且成反比,而和管壁粗糙无关。
25.紊流过渡区的阿里特苏里公式为25.0)Re68(11.0+=d k λ。
26.速度的大小、方向或分布发生变化而引起的能量损失,称为局部损失。
29.湿周是指过流断面上流体和固体壁面接触的周界。
31.串联管路总的综合阻力系数S 等于各管段的阻抗叠加。
32.并联管路总的综合阻力系数S 与各分支管综合阻力系数的关系为3211111s s s s ++=。
管嘴与孔口比较,如果水头H 和直径d 相同,其流速比V 孔口/V 管嘴等于82.097.0,流量比Q 孔口/Q 管嘴等于82.060.0。
工程流体力学习题课1-第2-3-4章-部分习题解答

2 2 d2
习题3-14解题示意图1
Dr W-X Huang, School of Chemical Engineering, Sichuan University, Chengdu 610065, P.R. China
工程流体力学——习题课(1)——第 2-3-4 章部分习题解答
Fx1 =
y x
H1
D
H2
图 3-26 习题 3-11 附图
1 1 ρ gH1 × ( DL) = × 1000 × 9.8 × 4 × (4 × 10) = 784000 N=784kN 2 2 1 D 1 4 Fx 2 = ρ gH 2 × ( L) = × 1000 × 9.8 × 2 × × 10 = 196000 N=196kN 2 2 2 2
H
h
由此得: H ≥ 122mm + h ≥ 244mm (2) 结合以上正负压操作时结果有:
p / ρ g ≤ h ≤ H − | p| / ρ g
图 3-23 习题 3-8 附图
→ 122mm ≤ h ≤ 178mm
Dr W-X Huang, School of Chemical Engineering, Sichuan University, Chengdu 610065, P.R. China
工程流体力学——习题课(1)——第 2-3-4 章部分习题解答
F1-6
习题 3-8 旋风除尘器如图 3-23 所示,其下端出灰口管段长 H,部分插入 水中,使旋风除尘器内部与外界大气隔开,称为水封;同时要求出灰管内液面 不得高于出灰管上部法兰位置。设除尘器内操作压力 ( 表 压 ) p = −1.2 kPa~ 1.2kPa。 净化空气 (1) 试问管段长 H 至少为多少 mm? (2) 若H=300mm,问其中插入水中的部分h应在 什么范围?(取水的密度 ρ =1000kg/m3) 含尘 解:(1) 正压操作时,出灰管内液面低于管外液 面,高差为 h′ = p / ρ g ;为实现水封,出灰管插入深 度 h 必须大于此高差,即
(完整版)流体力学习题解析
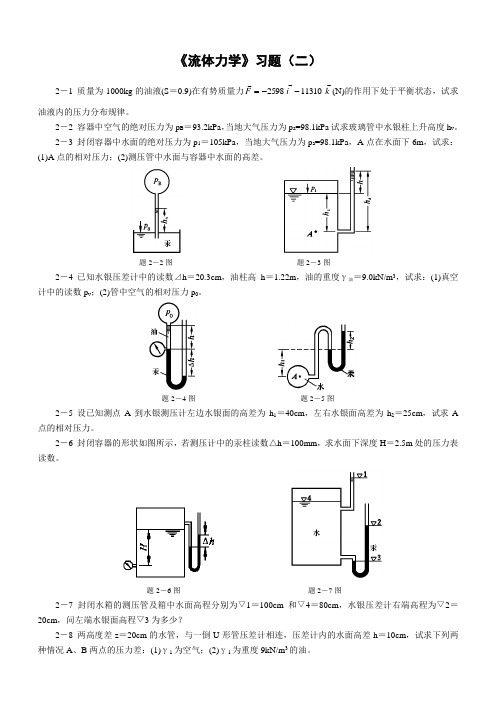
《流体力学》习题(二)2-1 质量为1000kg 的油液(S =0.9)在有势质量力k i F 113102598--=(N)的作用下处于平衡状态,试求油液内的压力分布规律。
2-2 容器中空气的绝对压力为p B =93.2kPa ,当地大气压力为p a =98.1kPa 试求玻璃管中水银柱上升高度h v 。
2-3 封闭容器中水面的绝对压力为p 1=105kPa ,当地大气压力为p a =98.1kPa ,A 点在水面下6m ,试求:(1)A 点的相对压力;(2)测压管中水面与容器中水面的高差。
题2-2图 题2-3图 2-4 已知水银压差计中的读数⊿h =20.3cm ,油柱高h =1.22m ,油的重度γ油=9.0kN/m 3,试求:(1)真空计中的读数p v ;(2)管中空气的相对压力p 0。
题2-4图 题2-5图 2-5 设已知测点A 到水银测压计左边水银面的高差为h 1=40cm ,左右水银面高差为h 2=25cm ,试求A 点的相对压力。
2-6 封闭容器的形状如图所示,若测压计中的汞柱读数△h =100mm ,求水面下深度H =2.5m 处的压力表读数。
题2-6图 题2-7图 2-7 封闭水箱的测压管及箱中水面高程分别为▽1=100cm 和▽4=80cm ,水银压差计右端高程为▽2=20cm ,问左端水银面高程▽3为多少?2-8 两高度差z =20cm 的水管,与一倒U 形管压差计相连,压差计内的水面高差h =10cm ,试求下列两种情况A 、B 两点的压力差:(1)γ1为空气;(2)γ1为重度9kN/m 3的油。
题2-8图题2-9图2-9 有一半封闭容器,左边三格为水,右边一格为油(比重为0.9)。
试求A、B、C、D四点的相对压力。
2-10 一小封闭容器放在大封闭容器中,后者充满压缩空气。
测压表A、B的读数分别为8.28kPa和13.80kPa,已知当地大气压为100kPa,试求小容器内的绝对压力。
流体力学习题讲解(修)

【3-3】 水流通过如图所示管路流入大气,已知:U形测压管中水银柱高差Δh=0.2m,h1=0.72m H2O,管径d1=0.1m,管嘴出口直径d2=0.05m,不计管中水头损失,试求管中流量qv。 【解】 首先计算1-1断面管路中心的压强。因为A-B为等压面,列等压面方程得: 则 (mH2O) 列1-1和2-2断面的伯努利方程
1-5:如 图 所 示 容 器, 上 层 为 空 气, 中 层 为 的 石 油, 下 层 为 的 甘 油, 试 求: 当 测 压 管 中 的 甘 油 表 面 高 程 为 时 压 力 表 的 读 数。
已知:H = 1 m h = 5 m D = 50 mm 喷嘴 d = 30 mm 不计摩擦损失 求: 1、真空室中的 压强 p2 , 2、排出水的流量 qV 。
解:取 5 个过流断面如图。
对1—1,3—3 断面列伯努利方程得:
流体力学-习题
1-1. 一 底 面 积 为45x50cm2 , 高 为 1cm 的 木 块, 质 量 为5kg , 沿 涂 有 润 滑 油 的斜 面 向 下 作 等 速 运 动, 木 块 运 动 速 度u=1m/s , 油 层 厚 度1cm , 斜 坡 角 22.620 (见 图 示), 求 油 的 粘 度 。
则:
由连续方程知:
即:
再对 1—1,2—2 断面列伯努利方程得:
解得:
真空室压强 p2 低于大气压,降至 0.345105 Pa 后, 蓄水池中的水被压上来。
流量为:
v — 吸水管中的流速
对 4—4 和 5—5 断面列伯努利方程求 v :
解得:
排出水的流量:
3-2:注 液 瓶 为 了 使 下 部 管 口 的 出 流 量 不 随 时 间 而 变, 在 上 部 瓶 塞 中 插 人 通 气 管, 试 分 析 出 流 量 恒 定 的 原 理 和 调 节。
流体力学__第二章习题解答

第2章 流体静力学2.1 大气压计的读数为100。
66kPa (755mmHg),水面以下7.6m 深处的绝对压力为多少?知:a a KP P 66.100= 3/1000m kg =水ρ m h 6.7= 求:水下h 处绝对压力 P解:aa KP ghP P 1756.71000807.96.100=⨯⨯+=+=ρ 2.2 烟囱高H=20m ,烟气温度t s =300℃,压力为p s ,确定引起火炉中烟气自动流通的压力差。
烟气的密度可按下式计算:p=(1。
25-0.0027t s )kg/m 3,空气ρ=1。
29kg/m 3。
解:把t 300s C =︒代入3s (1.250.0027)/s t kg m ρ=-得3s (1.250.0027)/s t kg m ρ=-33(1.250.0027300)/0.44/kg m kg m=-⨯=压力差s =-p ρρ∆a ()gH ,把31.29/a kg m ρ=,30.44/s kg m ρ=,9.8/g N kg =,20H m =分别代入上式可得s =-20p Pa ρρ∆⨯⨯a ()gH=(1.29-0.44)9.8166.6Pa =2.3 已知大气压力为98.1kN/m 2。
求以水柱高度表示时:(1)绝对压力为117.2kN/m2时的相对压力;(2)绝对压力为68。
5kN/m 2时的真空值各为多少? 解:(1)相对压力:p a =p-p 大气=117.72-98.1=19.62KN/2m以水柱高度来表示:h= p a/ g ρ=19。
62* 310 /(9.807* 310)=2.0m (2)真空值:2v a p =p p=98.168.5=29.6/m KN --以水柱高度来表示:h= p a/ g ρ=29。
6* 310 /(9.807* 310)=3。
0m2。
4 如图所示的密封容器中盛有水和水银,若A 点的绝对压力为300kPa ,表面的空气压力为180kPa,则水高度为多少?压力表B 的读数是多少?解:水的密度1000 kg/m 3,水银密度13600 kg/m 3A 点的绝对压力为:)8.0(20g gh p p H g o h A ρρ++=300⨯310=180⨯310+1000⨯9。
完整版流体力学课后习题作业答案

第四章作业答案4-3水在变直径竖管中流动,已知粗管直径d i =300mm ,流速v i =6m/s 。
两断面相距 3m,为使两断面的压力表读值相同。
试求细管直径(水头损失不计) 。
解:4— 4 变直径管段 AB ,d A =0.2m,d B =0.4m ,高差△ h=1.5m ,测得 p A =30kPa ,p B =40kPa , B 点 处断面平均流速 v B =1.5m/s ,试判断水在管中的流动方向。
解:Ad B 21.5 (0.4)2 6m/sH AZ A 邑2 A0臾兰 4.90md A 20.2g2g 9.8 2gH BZ B -P B240 1.525.69mB1.5 g2g9.819.6H B >H A ,水由B 流向A; 水头损失5.69-4.90=0.79m 4— 5用水银压差计测量水管中的点流速u ,如读值 △ h=60mm ,( 1)求该点流速;(2)3若管中流体是 0.8kg /m 的油,△ h 不变,不计水头损失,则该点的流速是多少?解:(1)u <2g 12.6 h J‘19.6 12.6 0.06 3.85m/s⑵u :2g 12.8 h v'19.6 12.8 0.06 4.34m/s4—6利用文丘里管的喉管处负压抽吸基坑中的积水,已经知道管道直径 d [ 100mm ,喉管直径d 2 50mm ,h 2m ,能量损失忽略不计。
试求管道中流量至少为多大,才能抽出基坑中的积水?p 1p 2解:由题意知,只有当(乙-)(Z 2 -) h 时,刚好才能把水吸上来,由文丘里流gg量计原理有Q k* (z _P L ) (Z 2 ~P ^),其中kv g gP i P i2V i 2g Vi 2Z 2P 2v ?d 2v 1d 12300 62—4.837m 2g235.5mmv 2 9.74m/s22V 2 2g代入数据,有Q 12.7l/s。
4-8管道流动管径为d=150mm,喷嘴出口直径d D=50mm,各点高差h1=2m,h2=4m,h3=3m,不计水头损失,求A、B、C、D各点压强。
流体力学课后习题与答案

第三、四章 流体动力学基础习题及答案3-8已知流速场u x =xy 2, 313y u y =-, u z =xy, 试求:(1)点(1,2,3)的加速度;(2)是几维流动;(3)是恒定流还是非恒定流;(4)是均匀流还是非均匀流?解:(1)411633x x x x x x y z u u u u a u u u xy t x y z ∂∂∂∂=+++==∂∂∂∂25333213313233312163. 06m/s y y z x y a y u y a yu xu xy xy xy a =-===+=-====(2)二元流动 (3)恒定流(4)非均匀流41xy 33-11已知平面流动速度分布为x y 2222cxu u x ycy x y =-=++,, 其中c 为常数。
求流线方程并画出若干条流线。
解:2222-xdx=ydyx ydx dydx dy cy cx u u x y x y =⇒-=⇒++积分得流线方程:x 2+y 2=c方向由流场中的u x 、u y 确定——逆时针3-17下列两个流动,哪个有旋?哪个无旋?哪个有角变形?哪个无角变形?(1)u x =-ay,u y =ax,u z =0 (2)z 2222,,0,a c x ycy cxu u u x y x y =-==++式中的、为常数。
z 2222,,0,a c x y cy cxu u u x y x y =-==++式中的、为常数。
解:(1)110 ()()22yx x y z u u a a a xy ωωω∂∂===-=+=∂∂有旋流动 xy 11()()0 22y x xy zx u u a a x y εεε∂∂=+=-==∂∂ 无角变形 (2)222222222222222222211()2()2()22()()12()2()0 0 2()y x z x y u u x y c cx x y c cy x y x y x y c x y c x y x y ωωω∂⎡⎤∂+-+-=-=+⎢⎥∂∂++⎣⎦⎡⎤+-+====⎢⎥+⎣⎦无旋流动2222xy 22222112()()()022()()y x u u c x y c x y x y x y x y ε∂⎡⎤∂---=+==-≠⎢⎥∂∂++⎣⎦ 有角变形4—7变直径管段AB ,d A =0.2m,d B =0.4m ,高差△h=1.5m ,测得p A =30kPa ,p B =40kPa ,B 点处断面平均流速v B =1.5m/s ,试判断水在管中的流动方向。
流体力学题及答案讲解学习

C (c) 盛有不同种类溶液的连通器DC D水油BB (b) 连通器被隔断AA(a) 连通容器1. 等压面是水平面的条件是什么?2. 图中三种不同情况,试问:A-A 、B-B 、C-C 、D-D 中哪个是等压面?哪个不是等压面?为什么?3 已知某点绝对压强为80kN/m 2,当地大气压强p a =98kN/m 2。
试将该点绝对压强、相对压强和真空压强用水柱及水银柱表示。
4. 一封闭水箱自由表面上气体压强p 0=25kN/m 2,h 1=5m ,h 2=2m 。
求A 、B 两点的静水压强。
速?答:与流线正交的断面叫过流断面。
过流断面上点流速的平均值为断面平均流速。
引入断面平均流速的概念是为了在工程应用中简化计算。
8.如图所示,水流通过由两段等截面及一段变截面组成的管道,试问:(1)当阀门开度一定,上游水位保持不变,各段管中,是恒定流还是非恒定流?是均匀流还是非均匀流?(2)当阀门开度一定,上游水位随时间下降,这时管中是恒定流还是非恒定流?(3)恒定流情况下,当判别第II 段管中是渐变流还是急变流时,与该段管长有无关系?9 水流从水箱经管径分别为cmd cm d cm d 5.2,5,10321===的管道流出,出口流速sm V /13=,如图所示。
求流量及其它管道的断面平均流速。
解:应用连续性方程(1)流量:==33A v Q 4.91s l /103-⨯(2) 断面平均流速s m v /0625.01= , s m v /25.02= 。
10如图铅直放置的有压管道,已知d 1=200mm ,d 2=100mm ,断面1-1处的流速v 1=1m/s 。
求(1)输水流量Q ;(2)断面2-2处的平均流速v 2;(3)若此管水平放置,输水流量Q 及断面2-2处的速度v 2是否发生变化?(4)图a 中若水自下而上流动,Q 及v 2是否会发生变化?解:应用连续性方程 (1)4.31=Q s l / (2)s m v /42= (3)不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
流 体 力 学习题解答及习题课第2章2-1 解:A B p p gh ρ=+ 则()()4442.710 2.9100.421.36109.807e a a v A B Hg e v p p p p p p h g g p p m g ρρρ+---==+⨯+⨯===⨯⨯2-2 解:111a p gh p gh ρρ++煤水= 则:()11a p p gh ρρ=+-水煤 同理:222a p gh p gh ρρ++煤水= 则:()22a p p gh ρρ=+-水煤而:12p p gH ρ=+煤 则:()()12a a p gh p gh gH ρρρρρ+-=+-+水煤水煤煤可得:第一章 流体及其主要物理性质例1:已知油品的相对密度为0.85,求其重度。
解:3/980085.085.0m N ⨯=⇒=γδ例2:当压强增加5×104Pa 时,某种液体的密度增长0.02%,求该液体的弹性系数。
解:0=+=⇒=dV Vd dM V M ρρρρρd dV V -=Pa dp d dp V dV E p84105.2105%02.01111⨯=⨯⨯==-==ρρβ例3:已知:A =1200cm 2,V =0.5m/sμ1=0.142Pa.s ,h 1=1.0mm μ2=0.235Pa.s ,h 2=1.4mm 求:平板上所受的内摩擦力F绘制:平板间流体的流速分布图及应力分布图 解:(前提条件:牛顿流体、层流运动)dy du μτ= ⎪⎪⎩⎪⎪⎨⎧-=-=⇒2221110h u h u V μτμτ 因为 τ1=τ2 所以sm h h Vh u h uh u V /23.02112212211=+=⇒=-μμμμμN h uV A F 6.411=-==μτ第二章 流体静力学例1:如图,汽车上有一长方形水箱,高H =1.2m ,长L =4m ,水箱顶盖中心有一供加水用的通大气压孔,试计算当汽车以加速度为3m/s 2向前行驶时,水箱底面上前后两点A 、B 的静压强(装满水)。
解:分析:水箱处于顶盖封闭状态,当加速时,液面不变化,但由于惯性力而引起的液体内部压力分布规律不变,等压面仍为一倾斜平面,符合0=+s gz ax 等压面与x 轴方向之间的夹角g a tg =θPaL tg H h p A A 177552=⎪⎭⎫ ⎝⎛⋅+==θγγ PaL tg H h p B B 57602=⎪⎭⎫ ⎝⎛⋅-==θγγ例2:(1)装满液体容器在顶盖中心处开口的相对平衡分析:容器内液体虽然借离心惯性力向外甩,但由于受容器顶限制,液面并不能形成旋转抛物面,但内部压强分布规律不变:Cz gr p +-⋅=)2(22ωγ利用边界条件:r =0,z =0时,p =0作用于顶盖上的压强:g r p 222ωγ=(表压)(2)装满液体容器在顶盖边缘处开口的相对平衡压强分布规律:Cz gr p +-⋅=)2(22ωγ边缘A 、B 处:r =R ,z =0,p =0g R C 222ωγ-=作用于顶盖上的压强:()2222r R gp --=ωγ例3:已知:r 1,r 2,Δh求:ω0 解:212120=-s z gr ω (1)222220=-s z gr ω (2)因为 h z z s s ∆==21所以212202r r h g -∆=ω例4已知:一圆柱形容器,直径D =1.2m ,完全充满水,顶盖上在r 0=0.43m 处开一小孔,敞开测压管中的水位a =0.5m ,问此容器绕其立轴旋转的转速n 多大时,顶盖所受的静水总压力为零?已知:D =1.2m ,r 0=0.43m ,a =0.5m 求:n解:据公式 )(Z d z Y d y X d x dp ++=ρ 坐标如图,则 x X 2ω=,y Y 2ω=,g Z -= 代入上式积分:C z gr p +-⋅=)2(22ωγ (*)由题意条件,在A 点处:r =r 0,z =0,p =γa 则 C gr a +-⋅=)02(202ωγγ 所以 )2(202gr a C ωγ-⋅=所以 )2()2(20222gr a z gr p ωγωγ-⋅+-⋅= 当z =0时: )2(220222gr a gr p ωγωγ-⋅+=它是一旋转抛物方程:盖板上静压强沿径向按半径的二次方增长。
而 02)2(22202220=⋅⎥⎥⎦⎤⎢⎢⎣⎡-⋅+=⋅==⎰⎰⎰r d r g r a g r r d r p p d AP RRAπωγωγπ 所以0)2(2202320=⎥⎥⎦⎤⎢⎢⎣⎡-+⎰dr r g r a g r Rωω 即 02)2(420220242=⎥⎥⎦⎤⎢⎢⎣⎡-+Rr g r a r g ωω 则 2202022224042Rr ga ga r R -=⇒=+-ωωω所以 22024212Rr ga n -==ππω代入数据得:n =7.118转/秒例5:闸门宽1.2m ,铰在A 点,压力表G 的读数为-14700Pa ,在右侧箱中装有油,其重度γ0=8.33KN/m 3,问在B 点加多大的水平力才能使闸门AB 平衡? 解:把p 0折算成水柱高:m p h 5.1980014700-=-==γ相当于液面下移1.5m ,如图示虚构液面则左侧:()()N A h Pc 7056022.11298001=⨯⨯+⨯==γ压力中心距A 点:3.11-2=1.11m右侧:设在B 点加水平力F 使闸门AB 平衡,对A 点取矩 ∑ M A =0即 AB F h P h PD D +=2211 KNF 87.25233.1992.1911.156.70=⨯-⨯=例6:一示压水箱的横剖面如图所示,压力表的读数为0.14个大气压,圆柱体长 L =1.2m ,半径R =0.6m求:使圆柱体保持如图所示位置所需的各分力(圆柱体重量不计)。
解:水平分力:→N A h P x c x 2.119952.16.07.19800=⨯⨯⨯==γ垂直分力:↑第三章 流体运动学与动力学基础例1:已知:⎪⎩⎪⎨⎧=+-=+=0z y x u t y u t x u 求:t =0 时,A (-1,1)点流线的方程。
解: t y dy t x dx +-=+积分:ln(x+t)=-ln(-y+t)+C → (x+t) (-y+t)=C` 当t =0时,x =-1,y =1,代入上式得: C`=1 所以,过A (-1,1)点流线的方程为:xy =-1例2、伯努利方程式的应用实例 例2-1 : 一般水力计算问题有一喷水装置如图示。
已知h 1=0.3m ,h 2=1.0m ,h 3=2.5m ,求喷水出口流速,及水流喷射高度h (不计水头损失)。
解:① 以3-3断面为基准面,列1-1、3-3两断面的能量方程:()320320000h h p p h h +=⇒++=+++γγ以2-2断面为基准面,列2-2、4-4两断面的能量方程: ()g V h h p 200024120+++=++γ 所以,()()()[]()sm h h h h g h h g p gV /57.63.05.28.9222212321204=-⨯⨯=+-+=+-=γ② mg V h 20.2224==例2-2: 节流式流量计已知:U 形水银压差计连接于直角弯管, d 1=300mm ,d 2=100mm ,管中流量Q =100L/s 试问:压差计读数Δh 等于多少? (不计水头损失)解:以0-0断面为基准面,列1-1、2-2两断面的能量方程:()2g V 2g V 0222211++∆+=++γγp h z p ()2g V V 212221-+∆+=-h z p p γ又s m A Q V /42.13.014.31.04211=⨯⨯==, s m A Q V /74.121.014.31.04222=⨯⨯==由等压面a -a 得压强关系:h p z p H g ∆-=-γγ21 则 z h p p H g γγ+∆=-21所以 ()6.1942.174.1222-+∆+=+∆h z z h Hg γγγmmm h Hg 649649.018.8==-=∆γγγ例2-3: 毕托管原理水从立管下端泄出,立管直径为d =50mm ,射流冲击一水平放置的半径R =150mm 的圆盘,若水层离开盘边的厚度δ=1mm 求:流量Q 及汞比压计的读数Δh 。
水头损失不计。
分析:1-1: p 1(=0), V 1(?), z 1(√)2-2: p 2(=0), V 2(?), z 2(√) 3-3: p 3( ?), V 3(=0), z 3(√)(驻点) 每点都有一个未知数,可对任何两点列方程。
解:以圆盘为基准面,列1-1、2-2两断面的能量方程:2gV 022g V 032221++=++δ ①列1-1、3点的能量方程:02g V 03321++=++γp ②据连续性方程:212241V R V d Q ⋅=⋅=δππ ③③代入①式:2242222/4.766416s m d R g V =⎪⎪⎭⎫⎝⎛-=δ (忽略δ/2)V 2=8.74m/s, V 1=4.196m/sV 1代入②式: mp 898.32g V 3213=+=γ所以:s L V A V A Q /23.82211=⋅=⋅=h p H g ∆=⋅+γγ5.13mmm p h Hg 396396.098006.1398005.19800898.35.13==⨯⨯+⨯=⋅+=∆γγ例2-4: 流动吸力图示为一抽水装置,利用喷射水流在吼道断面上造成的负压,可将M 容器中的积水抽出。
已知:H 、b 、h (不计损失),求:吼道有效断面面积A 1与喷嘴出口断面面积A 2之间应满足什么样的条件能使抽水装置开始工作?解:以1-1为基准面,列0-0、1-1断面的能量方程:2g V 211+=γp h 以0`-0`为基准面,列1-1、2-2断面的能量方程:()2g V 2g V 22211=++-γp h H 要使抽水机工作:bp ≥-γ1则:()gH V b h g V 2,221=+=又因为:2211V A V A ⋅=⋅所以:b h HV V A A +==1221例3:水头线(局部损失不计)例4:已知:Q =0.001m 3/s ,D =0.01mH w 吸=1m ,h w 排=25m 求:H =?p B =?N 泵=? 解:取1-1、2-2断面列伯努利方程:O mH h z z H w 21232)(=+-=取1-1、B 断面列伯努利方程:W QH N Pap sm V VA Q h p B w B6.31332001.09800108.9/74.122gV 7.0042=⨯⨯==⨯-=∴=⇒=+++=γγ泵吸例5:动量方程已知:一个水平放置的90º弯管输送水 d 1=150mm ,d 2=75mm p 1=2.06×105Pa ,Q =0.02m 3/s 求:水流对弯管的作用力大小和方向(不计水头损失) 分析:1-1: p 1(√), V 1(可求), z 1(√) 2-2: p 2(?), V 2(可求), z 2(√)解:s m d QA Q V /132.142111===π s m d Q A Q V /527.442222===π取1-1、2-2两断面列伯努利方程对选取的控制体列动量方程: x 方向:)0(111V Q R A p x -=-ρ y 方向:)0(222-=-V Q A p R y ρ所以,N R N R y x 9583663== NR R R y x 378622=+=66.14==xy R R arctgθ所以,水流对弯管壁的作用力为F 的反作用力F`,大小相等,方向相反。
