贵阳市四校2020届高三年级联合考试(五)文科数学-双向细目表
贵州省贵阳市大学附属中学 2020年高三数学文联考试卷含解析

贵州省贵阳市大学附属中学 2020年高三数学文联考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. i是虚数单位,复数z满足,则z=()A.1+2i B.2+i C.1-2i D.2-i参考答案:B2. 设是虚数单位,若,则的值是A、-1B、1C、D、参考答案:D3. 设函数f(x)= 则满足f(x)≤2的x的取值范围是()A.[1,2] B.[0,2] C.[1,+∞) D.[0,+∞)参考答案:D略4. 已知命题;命题,则下列命题中为真命题的是()A、 B、 C、 D、参考答案:C略5. 某程序框图如右图所示,若输出的S=57,则判断框内填A. B. C. D.参考答案:A略6. 复数(i是虚数单位)的虚部是()A. 3iB. 6iC. 3D. 6参考答案:C【分析】直接利用复数的除法的运算法则化简求解即可.【详解】解:复数2+3i.复数(i是虚数单位)的虚部是3.故选:C.【点睛】本题考查复数的除法的运算法则以及复数的基本概念,是基础题.7. 设向量的模分别为6和5,夹角为等于()A. B. C. D.参考答案:D略8. 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则它的体积可能为()A.B.C.D.参考答案:A9. 已知函数,若,则实数的取值范围是()A. B.C. D.参考答案:A略10. 已知集合,,若,则实数的值是()A.0 B.0或2 C.2 D.0或1或2B试题分析:由得,所以.故选B.考点:集合的包含关系,集合的定义.二、填空题:本大题共7小题,每小题4分,共28分11. 将参数方程(为参数)化为普通方程,所得方程是__________。
参考答案:答案:412. 已知集合,,,则= .参考答案:{3,5}13. 已知=1-mi,其中m,n是实数,i是虚数单位,则m的值为____参考答案:214. 已知双曲线(>0)的一条渐近线的方程为,则= . 参考答案:2本题考查双曲线的渐近线方程,容易题。
贵阳市四校2020届高三年级联合考试(五)理数-试卷

一、选择题(本大题共12 小题,每小题5 分,共60 分 在每小题给出的四个选项中,只有一项是符合题目要 求的) 1. 已知集合A={x x2>x},集合B ={x },则 -2<x<2
A. AB
B. BA
C. A∩B =
2. 设i 是虚数单位,z- 表示复数z 的共轭复数. 若z+2z- = 3+i,则z 的虚部为
上的
点到右焦点F2 的最大距离是3.
(1)求C 的标准方程;
Hale Waihona Puke (2)设C 的左、右顶点分别为A1,A2,过A1,A2 分别作x 轴的垂线l1,l2,直线l:y ( )与 = kx+m k≠0 C
相切,且l 与l1,l2 分别交于P,Q 两点,求证:∠PF1Q=∠PF2Q.
21. (本小题满分12 分)
; ①AF⊥GC
②BD 与GC 成异面直线且夹角为60°;
; ③BD∥MN
④BG
与平面ABCD
所成角的正切值为槡2 . 2
图1
其中正确命题的个数是
A. 1
B. 2
C. 3
D. 4
9. 在等差数列{an}中,已知a4 = a7 ,且公差d<0,则其前n 项和取得最大值时n 的值为
A. 4
B. 5
C. 6
3
A. -39 25
39 B.
25
C. -57 25
57 D.
25
5. 在(1 )( +x 5 2x-1)的展开式中,含x4 项的系数为
A. -25
B. 25
C. -15
D. 15
6.
函数f(x)=
( [ xcosx
x2 +1
x∈
-
2,2])的大致图象是
贵阳市四校2020届高三年级联合考试(五)理科数学-双向细目表
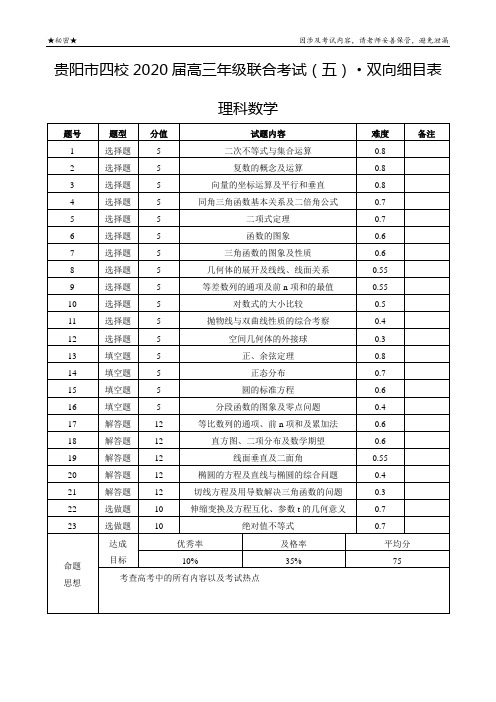
理科数学
题号
题型
分值Байду номын сангаас
试题内容
难度
备注
1
选择题
5
二次不等式与集合运算
0.8
2
选择题
5
复数的概念及运算
0.8
3
选择题
5
向量的坐标运算及平行和垂直
0.8
4
选择题
5
同角三角函数基本关系及二倍角公式
0.7
5
选择题
5
二项式定理
0.7
6
选择题
5
函数的图象
0.6
7
选择题
5
三角函数的图象及性质
0.6
8
选择题
5
几何体的展开及线线、线面关系
0.55
9
选择题
5
等差数列的通项及前n项和的最值
0.55
10
选择题
5
对数式的大小比较
0.5
11
选择题
5
抛物线与双曲线性质的综合考察
0.4
12
选择题
5
空间几何体的外接球
0.3
13
填空题
5
正、余弦定理
0.8
14
填空题
5
正态分布
0.7
15
填空题
5
圆的标准方程
0.6
16
填空题
5
分段函数的图象及零点问题
0.4
17
解答题
12
等比数列的通项、前n项和及累加法
0.6
18
解答题
12
直方图、二项分布及数学期望
贵州省五校联盟2020届高三数学第四次联考试题 文

贵州省五校联盟2020届高三第四次联考试卷文科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页。
第Ⅱ卷3至4页。
第Ⅰ卷(本卷共12小题,每小题5分,共60分)注意事项1.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮檫檫干净后,再选涂其它答案标号,不能答在试题卷上。
2.答题前认真阅读答题卡上的“注意事项”。
参考公式:如果事件A 、B 互斥,那么 )()()(B P A P B A P +=+如果事件A 、B 相互独立,那么 )()()(B P A P B A P ⋅=⋅如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中事件A 发生k 次的概率为0()1()(=-=-k p p C k P k n k kn n ,1,2,… ,)n球的表面积公式:24R S π=(R 为球的半径) 球的体积公式:334R V π= (R 为球的半径)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集{}1,2,3,4,5,6,7,8U =,{}1,3,5,7M =,{}5,6,7N =,则()U C M N ⋃ =( )(A) {5,7} (B ) {2,4} (C ){2.4.8} (D ){1,3,5,6,7} 2.“0a b >> ”是“222ab a b <+ ”成立的( )A 必要不充分条件B 充分不必要条件C 充分且必要条件D 不充分且不必要条件 3.已知函数0.5()2log (1)f x x x =+>,则)(x f 的反函数是( ) A .)2(2)(21<=--x x f xB .)2(2)(21>=--x x fxC .)2(2)(21<=--x x fx D .)2(2)(21>=--x x fx4. 若4cos ,,0,52παα⎛⎫=∈- ⎪⎝⎭则tan 4πα⎛⎫+= ⎪⎝⎭( ) A .17 B .7 C .177或D .177-或-5. 在等差数列}{n a 中,有12876=++a a a ,则此数列的前13项之和为( )A .24B .39C .52D .1046.在坐标平面内,已知)0,0(O )0,5(),2,1(Q P , OPQ ∠的平分线交x 轴于点S .记,,==则=( )A.b a PS 3132+=B.b a PS 3231+=C.b a PS 5154+=D. b a PS 5451+= 7.已知正三棱柱111ABC A B C -的侧棱长与底面边长都相等,则直线1AC 与侧面11ABB A 所成角的正弦值等于 ( )A .4 B .4.2 D .28.若过定点(1,0)M -且斜率为k 的直线与圆22450x y x ++-=在第一象限内的部分有交点,则k 的取值范围是( )A. 0k <<B.0k <<C.0k <<05k <<9.有5张音乐专辑,其中周杰伦的3张(相同), 郁可唯和曾轶可的各1张.从中选出3张送给3个同学(每人1张).不同送法的种数有( )A. 120B.60C.25D.1310.如图,双曲线)0,0(12222>>=-b a by a x 的左、右焦点分别为21F F 、.过点1F 作倾斜角为ο30的直线l ,l 与双曲线的右支交于点P .若线段1PF 的中点M 落在y 轴上,则双曲线的渐近线方程为 ( )A .x y ±=B .x y 2±=C .x y 3±=D .x y 2±= 11.四面体ABCD 的外接球球心在CD 上,且2CD =,3=AB ,在外接球面上B A 、两点间的球面距离是( ) A.π6B.π3C.2π3D.5π612.函数()f x 的定义域为R.若(1)f x +是奇函数,(1)f x -是偶函数,则( ) (A) )3(-x f 是偶函数 (B) )4(-x f 是偶函数 (C) )4()(+=x f x f (D) )5(+x f 是奇函数绝密★启用前贵州省2020届高三年级五校第二次联考试卷第Ⅱ卷(本卷共10小题,共90分)注意事项1.考生不能将答案直接答在试卷上,必须答在答题卡上。
贵阳市四校2020届高三年级联合考试(五)英语-双向细目表
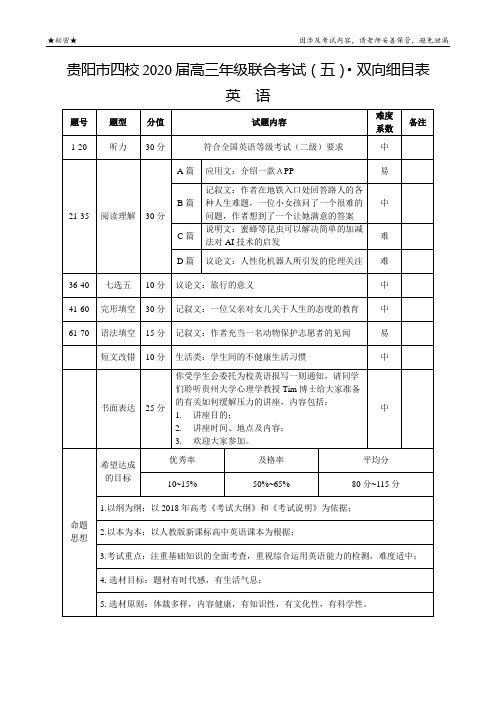
英语
题号
题型
分值
试题内容
难度系数
备注
1-20
听力
30分
符合全国英语等级考试(二级)要求
中
21-35
阅读理解
30分
A篇
应用文:介绍一款APP
易
B篇
记叙文:作者在地铁入口处回答路人的各种人生难题,一位小女孩问了一个很难的问题,作者想到了一个让她满意的答案
中
C篇
说明文:蜜蜂等昆虫可以解决简单的加减法对AI技术的启发
难
D篇
议论文:人性化机器人所引发的伦理关注
难
36-40
七选五
10分
议论文:旅行的意义
中
41-60
完形填空
30分
记叙文:一位父亲对女儿关于人生的态度的教育
中
61-70
语法填空
15分
记叙文:作者充当一名动物保护志愿者的见闻
易
短文改错
10分
生活类:学生间的不健康生活习惯
中
书面表达
25分
你受学生会委托为校英语报写一则通知,请同学们聆听贵州大学心理学教授Tim博士给大家准备的有关如何缓解压力的讲座,内容包括:
1.讲座目的;
2.讲座时间、地点及内பைடு நூலகம்;
3.欢迎大家参加。
中
命题
思想
希望达成
的目标
优秀率
及格率
平均分
10~15%
50%~65%
80分~115分
1.以纲为纲:以2018年高考《考试大纲》和《考试说明》为依据;
2.以本为本:以人教版新课标高中英语课本为根据;
2020届高三联考试卷及答案(数学文科)

2020届高三第二次联考试卷文科数学本卷分第Ⅰ卷(选择题、填空题)和第Ⅱ卷解答题两部分,满分150分. 考试用时间120分钟. 注意事项:1.答第I 卷前,考生务必将自己的姓名、班级用蓝、黑墨水钢笔签字笔写在答卷上; 2.第I 卷每小题得出答案后,请将答案填写在答题卷相应表格指定位置上. 答在第Ⅰ卷上不得分;3.考试结束,考生只需将第Ⅱ卷(含答卷)交回. 参考公式: 锥体的体积公式13V Sh =, 其中S 是锥体的底面积, h 是锥体的高.第Ⅰ卷(选择题、填空题共70分)一、选择题(共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 设全集{}{}R,(3)0,1U A x x x B x x ==+<=<-, 则下图中阴影部分表示的集合为 ( )A. {}0x x >B. {}30x x -<<C. {}31x x -<<-D. {}1x x <-2. 已知正方形ABCD 的边长为1, 则AB BC AC ++u u u r u u u r u u u r=( )A. 0B. 2C.2 D. 223. 两座灯塔A 和B 与海洋观察站C 的距离都等于a km , 灯塔A 在观察站C 的北偏东20o, 灯塔B 在观察站C 的南偏东40o,则灯塔A 与灯塔B 的距离为 ( )km A. a B.a 2 C. a 2 D. a 34. 曲线x x x f ln )(=在点1=x 处的切线方程为( )A. 22+=x yB. 22-=x yC. 1-=x yD. 1+=x y5. 设函数22(,2]()log (2,)x x f x x x ⎧∈-∞=⎨∈+∞⎩, 则满足()4f x =的x 的值是 ( )A. 2B. 16C. 2或16D. 2-或166. 设向量311(sin ,),(,cos ),432a xb x ==r r 且//a b r r , 则锐角x 为( ) A. 6π B. 4π C. 3πD. π125 7. 已知等差数列{}n a 中, 315,a a 是方程2610x x --=的两根, 则7891011a a a a a ++++等于( )A. 18B. 18-C. 15D. 128. 已知函数sin()y A x m ωϕ=++的最大值是4, 最小值是0, 最小正周期是2π, 直线3x π=是其图象的一条对称轴, 则下面各式中符合条件的解析式是( )A. 4sin(4)6y x π=+ B. 2sin(2)23y x π=++ C. 2sin(4)23y x π=++ D. 2sin(4)26y x π=++ 9. 若函数)(x f y =的图象如右下图所示, 则函数)1(x f y -=的图象大致为 ( )10. 已知0a >且21,()x a f x x a ≠=- , 当(1,1)x ∈- 时均有1()2f x < , 则实数a 的取值范围是( )A. [)∞+⎥⎦⎤ ⎝⎛,,221 0YB. (]4,11,41 Y ⎪⎭⎫⎢⎣⎡C. (]2 11,21, Y ⎪⎭⎫⎢⎣⎡ D. [)∞+⎥⎦⎤⎝⎛, 441,0Y 二、填空题(共4小题,每小题5分,满分20分) 11. 函数5||4)(--=x x x f 的定义域为_____ ________.12. 若()f n 为21n +的各位数字之和()n *∈N , 如: 因为2141197,19717+=++=, 所以(14)17f =. 记1()()f n f n =,21()(())f n f f n =, …,1()(())k k f n f f n += (k *∈N ), 则2008(8)f = .13. 如下图是由大小相同的长方体木块堆成的几何体的三视图, 则此几何体共由____ _____块木块堆成.14. 对于函数x x x f cos sin )(+=, 给出下列四个命题:① 存在)2,0(πα∈, 使34)(=αf ; 俯视图侧视图正视图D.C.A. B.② 存在)2,0(πα∈, 使)3()(αα+=+x f x f 恒成立;③ 存在R ϕ∈, 使函数)(ϕ+x f 的图象关于y 轴对称; ④ 函数f (x )的图象关于点)0,43(π对称;⑤ 若0,2x π⎡⎤∈⎢⎥⎣⎦, 则()f x ∈. 其中正确命题的序号是 .2020年文科数学答题卷二、填空题(共4小题,每小题5分,满分20分)11. 12.13. 14.第Ⅱ卷(解答题共80分)三、解答题(共6小题,满分80分) 15. (本小题满分14分)已知向量(cos ,sin )=r a αα, (cos ,sin )=rb ββ, -=r r a b .(Ⅰ) 求cos()αβ-的值; (Ⅱ) 若0πα<<, 0πβ-<<, 且5sin β=-, 求sin α.班 姓 学号 考16. (本小题满分12分)已知函数32()(4)3(6)f x x m x mx n =+--+-在定义域内是奇函数. (1) 求m , n 的值;(2) 求()f x 在区间[3,2]-上的极值和最值.17. (本小题满分14分)已知点集{}(,)L x y y ==⋅u u r r m n , 其中(22,1),(1,12)x b b =-=+u u r rm n 为向量, 点列(,)n n n P a b 在点集L 中, 1P 为L 的轨迹与y 轴的交点, 已知数列{}n a 为等差数列, 且公差为1, *N n ∈.(1) 求数列{}n a , {}n b 的通项公式;(2) 求1n n OP OP +⋅u u u r u u u u u r 的最小值;(3) 设1(2)n n n n c n n a P P +=≥⋅u u u u u u r , 求234n c c c c ++++L 的值.18. (本小题满分14分)(1) 如图1, 在三棱锥A BCD -中, ,M N 分别是ABC ∆和ACD ∆的重心, 求证://MN BD .(2) 如图2, 在三棱锥S ABC -的侧棱,,SA SB SC 上分别取,,A B C '''三点, 使12SA SA '=, 13SB SB '=, 14SC SC '=, 过,,A B C '''三点作截面将棱锥分成上、下两部分, 求这两部分的体积比. 学号 考室19. (本小题满分12分)某西部山区的某种特产由于运输的原因, 长期只能在当地销售. 当地政府通过投资对该项特产的销售进行扶持, 已知每投入x 万元, 可获得纯利润100)40(16012+--=x P 万元 (已扣除投资, 下同). 当地政府拟在新的十年发展规划中加快发展此特产的销售, 其规划方案为: 在未来10年内对该项目每年都投入60万元的销售投资, 其中在前5年中, 每年都从60万元中拨出30万元用于修建一条公路. 公路5年建成, 通车前该特产只能在当地销售; 公路通车后的5年中, 该特产既在本地销售, 也在外地销售, 在外地销售的投资收益为: 每投入x 万元, 可获纯利润)60(2119)60(1601592x x Q -+--=万元. 问仅从这10年的累积利润看, 该规划方案是否可行?20.(本小题满分14分)已知函数()22xx af x =-, 将()y f x =的图象向右平移两个单位, 得到()yg x =的图象.(1) 求函数()y g x =的解析式;(2) 若函数()y h x =与函数()y g x =的图象关于直线1y =对称, 求函数()y h x =的解析式;(3) 设1()()(),F x f x h x a=+ 设()F x 的最小值为m . 是否存在实数a , 使2m >若存在, 求出a 的取值范围, 若不存在, 说明理由.室2020年联考文科数学答案一、选择题(共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的) CDDCC BCDAC二、填空题(共4小题,每小题5分,满分20分)11. {x |45x x ≥≠且} 12. 11 13. 5 14. ①③④⑤ 三、解答题(共6小题,满分80分)15. 解:(Ⅰ)(cos ,sin )=r Q a αα, (cos ,sin )=rb ββ, ()cos cos ,sin sin ∴-=--r rαβαβa b . ………………………………………………… (2)5-=r r Q a b ,5=, …………………… (4) 即 ()422cos 5αβ--=, ()3cos 5αβ∴-=. (7)(Ⅱ)0,0,022ππαβαβπ<<-<<∴<-<Q , (8)()3cos 5αβ-=Q ,()4sin .5αβ∴-= (9)5sin 13β=-Q ,12cos 13β∴=, (10)()sin sin ∴=-+⎡⎤⎣⎦ααββ ……………………………………………………………… (12)()()sin cos cos sin =-+-αββαββ ………………………………………………… (13)412353351351365⎛⎫=⋅+⋅-= ⎪⎝⎭. ………………………………………………………………………… (14) 16. 解: (1) 依题意得()()f x f x -=-, (1)即3232()(4)()3()(6)(4)3(6)x m x m x n x m x mx n -+----+-=---+--, ……………… (2)∴22(4)2(6)0m x n -+-=, ……………………………………………………………………… (3) 故4m =,6n =. ……………………………………………………………………………………(4)(2)由(1)得3()12f x x x =-, ………………………………………………………………………(5)∴2()3123(2)(2)f x x x x '=-=-+, …………………………………………………… (6)当(3,2)x ∈--时, ()0f x '>, ()f x 单调递增; 当(2,2)x ∈-时, ()0f x '<, ()f x 单调递减;……………………………………………………………………………………………… (8)所以当2x =-时,()f x 有极大值16. (9)(3)9f -=Q , (2)16f =-, ……………………………………………………………………… (10) max ()(2)16f x f ∴=-=,min ()(2)16f x f ∴==-. (12)17.解:(1)由y =⋅u u r r m n,(22,1),(1,12)x b b =-=+u u r rm n , 得:12+=x y (2)即 :L 12+=x y Q 1P 为L 的轨迹与y 轴的交点, 1(0,1)P ∴ 则 110,1a b == (3)Q数列{}n a 为等差数列, 且公差为1, 1 (N )n a n n *∴=-∈, ………………………………… (4) 代入12+=x y , 得:2 1 (N )n b n n *=-∈ (5)(2) (1,21)n P n n --Q , 1(,21)n P n n +∴+,221121(1,21)(,21)515()1020n n OP OP n n n n n n n +∴⋅=--⋅+=--=--u u u r u u u u u r (8)Nn *∈Q , 所以当1n =时,1n n OP OP +⋅u u u r u u u u u r有最小值, 为3. (9)(3) 当2≥n 时, )12,1(--n n P n ,得:11),n n n a P P n +⋅=-u u u u u u r…………………………………(10)111(1)1n C n n n n===---, (12)23111111(1)()()12231n C C C n n n∴+++=-+-++-=--L L L . …………………… (14)18. 解: (1) 连结AM , 延长交BC 于P ; 连结AN , 延长交CD 于Q , 连结PQ . (1),M N Q 分别是ABC ∆和ACD ∆的重心,23AM AN AP AQ ∴==. ...................................................... (3) //MN PQ ∴, 且,P Q 分别是,BC CD 的中点. ..................... (5) ∴//PQ BD , (6)由公理4知: //MN BD . (7)(2) 解:sin 1sin 12SB C SBC S SB SC B SC S SB SC B SC ''∆∆''''⋅∠==''⋅∠, ……………………… (10) 设点A '到平面SBC 的距离为h ', A 点到平面SBC 的距离为h .12SA SA '=Q , 12h h '∴=. …………………………………………… (12) 1131243SB C S A B C A SB C S ABC A SBCSBC S h V V V V S h ''∆''''''----∆'⋅===⋅. .................................... (13) 故三棱锥被分成的两部分的体积比为1:23. (14)19. 解: 在实施规划前, 由题设100)40(16012+--=x P (万元), 知每年只须投入40万, 即可获得最大利润100万元. 则10年的总利润为W 1=100×10=1000(万元). …………………………………………… (3) 实施规划后的前5年中, 由题设100)40(16012+--=x P 知, 每年投入30万元时, 有最大利润8795max =P (万元). ………………………………………………………………………………………………………… (5) 前5年的利润和为8397558795=⨯(万元). (6)设在公路通车的后5年中, 每年用x 万元投资于本地的销售, 而用剩下的(60-x )万元于外地区的销售投资, ………………………………………………………………………………………………………… (7) 则其总利润为5)2119160159(5]100)40(1601[222⨯+-+⨯+--=x x x W 4950)30(52+--=x . ……………………………… (9) 当x =30时,W 2|max =4950(万元). (10)AB CD M NQPSC'B'A'CBA从而10年的总利润为495083975+(万元). (11)1000495083975>+Θ,∴该规划方案有极大实施价值. …………………………………………… (12) 20. 解: (1) 由题设,()g x (2)f x =-2222x x a--=-. (2)(2) 设点(,)x y 在()y h x =的图象上, 点11(,)x y 在()y g x =的图象上, 且与点(,)x y 关于直线1y =对称, 则112x xy y=⎧⎨=-⎩, (4)2(),2()y g x y g x ∴-=∴=-, 即22()222x x ah x --=-+. (6)(3)由题设,21()2xx F x a =-+22222x x a ---+=111()2(41)242x x a a -+-+ ………………… (7) 0a ≠Q① 当0a <时, 有114a -0<, 410a -<, 而2x0>, 12x 0>,()2F x ∴<, 这与()F x 的最小值2m >+矛盾; …………………………………………… (8) ② 当104a <≤时, 有114a -0>, 410a -≤, 此时()F x 在R 上是增函数, 故不存在最小值;……………………………………………………………………………………………………… (9) ③ 当4a ≥时, 有114a -0≤, 410a ->, 此时()F x 在R 上是减函数, 故不存在最小值;……………………………………………………………………………………………………… (10) ④当144a <<时, 有114a -0>,410a ->,()2F x ≥, (11)当且仅当2x=时取得等号,()F x 取最小值m=2. (12)又2m >+及144a <<, 得(4)(41)744144a a a a --⎧>⎪⎪⎨⎪<<⎪⎩ …………………………………………… (13) 1212,21244a a a ⎧<<⎪⎪∴<<⎨⎪<<⎪⎩. (14)。
贵州省贵阳市五校2022-2023学年高三联合考试(四)文数答案

贵阳市五校2023届高三年级联合考试(四)文科数学参考答案一、选择题(本大题共12小题,每小题5分,共60分)题号123456789101112答案BCDBDCDACDAD【解析】1.由题易知{|3}A x x =>,则{4}A B = ,故选B .2.因为1i z =+,所以11131i i 1i 22z z -=+-=++,故选C .3.由题知()f x 周期为4,(2021)(15054)(1)(1)1f f f f =+⨯==--=-,故选D.4.双曲线的一条渐近线方程为b y x a =,将(1-,代入渐近线方程得ba=,所以2e ==,故选B .5.设公比为q ,由题意26q q =+,解得3q =,所以221914n n n a q a a q ++==++,故选D .6.由图可知,输出10(110)1210552S +=+++== ,故选C .7.因为ln 5ln e 1>=,1020551-<<=,1lg 05<,所以z y x <<,故选D .8.由已知可得,5ππππcos 2cos π2cos π2cos 26666αααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=-+=+-=--=⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦2ππ119cos 22sin 11212169αα⎡⎤⎛⎫⎛⎫--=--=-⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故选A .9.记4名男生为A ,B ,C ,D ,2名女生为a ,b ,从中选择两名为:AB ,AC ,AD ,Aa ,Ab ,BC ,BD ,Ba ,Bb ,CD ,Ca ,Cb ,Da ,Db ,ab 共15个基本事件,其中恰好选取一名男生和一名女生有Aa ,Ab ,Ba ,Bb ,Ca ,Cb ,Da ,Db 共8种,所以概率为815,故选C.10.多面体所在正方体的棱长为224π12π⨯=,故选D .11.由图知2A =,再把点(0代入,可得π2sin 3ϕϕ=⇒=,由五点描图法可得πππ63ω+=,所以4ω=,故π()2sin 43f x x ⎛⎫=+ ⎪⎝⎭,所以5π5ππ2sin 12463f ⎛⎫⎛⎫=+=- ⎪⎪⎝⎭⎝⎭,故选A .12.()f x 为定义在(0)(0)-∞+∞ ,,上的偶函数,在(0)+∞,上是单调递减函数;又2(1)log 223f =+=,(lg )3f x <可化为(lg )(1)f x f <,即(|lg |)(1)f x f <,得|lg |1x >,即lg 1x >或lg 1x <-,解得10(10)10⎛⎫+∞ ⎪⎝⎭,,,故选D .二、填空题(本大题共4小题,每小题5分,共20分)题号13141516答案01-36336000【解析】13.根据题意得,22(2)(2)a b a b -=+ ,∴22224444a a b b a a b b -+=++ ,∴814a b =+410--=,∴0a b =,即夹角的余弦值为0.14.(1(1))f ,代入740x y --=得(1)3f =,即3a b +=,(1)7k f '==,即327a b +=,则1a =,2b =,所以1a b -=-.15.设公差为d ,则220(1)n n d +=++,得2d =,于是312a =,324a =,336a = ,,213a ==,4223a ==,6333a ==, ,213a q a ⇒==,553(13)36313S -==-.16.根据题意可知大圆柱的底面圆的半径20cm R =,两圆柱的高40cm h =,设小圆柱的底面圆的半径为r ,则有12π2π2rh Rh =⨯,即80π800πr =,解得10r =,所以该模型的体积为223ππ12000π(cm )V V R h r h -=-=大小,所以制作该模型所需原料的质量为12000π1⨯=36000(g).解:(1三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分))sin sin sin πcos tan .sin 3a Ab Bc C C C C C C a B +-=⇒=⇒==……………………………………………………………………………………(6分)(2)设AB 边上的中线为CD ,由已知,有向量关系:2222224||||||2||||cos 4CD CA CB CD CA CB CA CB C a b ab =+⇒=++⇒=++224423ab a b ab ab ⇒-=+⇒≥≤(当且仅当a b =时取等号)14sin .24433S ab C ⇒===△≤……………………………………………(12分)18.(本小题满分12分)解:(1)100(0.00150.00250.00150.0010)1a ⨯++++=,解得0.0035a =,平均数估计值为5000.00151006000.00351007000.00251008000.0015⨯⨯+⨯⨯+⨯⨯+⨯1009000.001100670⨯+⨯⨯=(分).…………………………………………………(6分)(2)由题意可知,样本中男生有250100251000⨯=人,则女生有75人,属于“高分选手”的有(0.10.15)10025+= 人,其中男生10人,则高分中女生为251015-=人,不属于“高分选手”的男生为251015-=人,不属于“高分选手”的女生为751560-=人,因此,得到22⨯列联表如下:属于“高分选手”不属于“高分选手”合计男生101525女生156075合计2575100因此,2K 的观测值2100(10601515)4 3.84125757525k ⨯-⨯==>⨯⨯⨯,所以有95%的把握认为该校学生属于“高分选手”与“性别”有关.……………………………………………………………………………………(12分)(1)证明:连接OA OB OC ,,,D ∵为圆锥顶点,O 为底面圆心,OD ⊥∴平面ABC ,P ∵在DO 上,OA OB OC PA PB PC ====,∴,ABC △∵是圆内接正三角形,AC BC =∴,PAC △≌PBC △,90APC BPC ∠=∠=︒∴,即PB PC PA PC ⊥⊥,19.(本小题满分12分),PA PB P PC =⊥ ,∴平面PAB .……………………………………………(6分)(2)解:设圆锥的母线为l ,底面半径为r ,圆锥的侧面积为πrl rl ==,2222OD l r =-=,解得1r l ==,,2sin 60AC r =︒=,在等腰直角三角形APC中,2AP AC ==在Rt PAO △中,2PO =,∴三棱锥P ABC -的体积为11333248P ABC ABC V PO S -==⨯=△ .…………………………………………………………………………………(12分)20.(本小题满分12分)(1)解:椭圆过点(20),,即2a =,又c =,得21b =,即椭圆方程为2214x y +=.……………………………………………………(4分)(2)证明:由2214x y y kx m ⎧+=⎪⎨⎪=+⎩,,得222(14)8440k x kmx m +++-=,2216(41)0k m ∆=-+>,设11()A x y ,,22()B x y ,,则122814kmx x k +=-+,设AB 的中点M 为00()x y ,,得0241142km x k =-=+,即2148k km +=-,所以2001141288k y kx m k k k+=+=-=-.所以AB 的中垂线方程为11182y x k k ⎛⎫+=-- ⎪⎝⎭,即138y x k ⎛⎫=-- ⎪⎝⎭,故AB 的中垂线恒过点308N ⎛⎫⎪⎝⎭.…………………………………………………(12分)21.(本小题满分12分)(1)解:11()(0)axg x a x x x-'=-=>,当0a ≤时,()0g x '>,函数在(0)+∞,上单调递增;当0a >时,10x a ⎛⎫∈ ⎪⎝⎭,时,()0g x '>,1x a ⎛⎫∈+∞ ⎪⎝⎭,时,()0g x '<,函数在10a ⎛⎫ ⎪⎝⎭,上单调递增,在1a ⎛⎫+∞ ⎪⎝⎭,上单调递减.综上所述,当0a ≤时,()g x 只有增区间为(0)+∞,.当0a >时,()g x 的增区间为10a ⎛⎫ ⎪⎝⎭,,减区间为a 1⎛⎫+∞ ⎪⎝⎭,.………………………(6分)(2)证明:由已知得2()ln (1)f x x a x =--,()f x 的定义域为(0)+∞,,当0a ≤时,存在正实数e M =,使得2()1(e 1)0f M a =-->.当0a >时,2221()ax ax f x x--'=-,令22()221480h x ax ax a a =--∆=+>,,()h x 在区间(0)+∞,上有一个零点02a x a+=.当0(0)x x ∈,时,()0h x <,当0()x x ∈+∞,时,()0h x >,所以()f x 在0(0)x ,上单调递增,在0()x +∞,上单调递减.2000011()()ln (1)2x f x f x x a x =+=--,≤∵∴.由()0h x =,得001(1)2a x x -=,所以00011()ln 22f x x x =+-.设11()ln 22F x x x =+-,当1x >时,221()02x F x x -'=>,所以()F x 在(1)+∞,上单调递增,所以()(1)0F x F >=,即0()0f x >,所以存在正实数0M x =,使得()0f M >.…………………………………………(12分)解:(1)l 的普通方程为22.(本小题满分10分)【选修4−4:坐标系与参数方程】1)y x =-,1C 的普通方程为2214y x +=.……………………………………………………………………………………(5分)(2)2C的参数方程为1cos 2sin 2x y θθ⎧=⎪⎪⎨⎪=⎪⎩,,(θ为参数).故点P 的坐标是1cos 22θθ⎛⎫ ⎪ ⎪⎝⎭,,从而点P 到直线lπ244θ⎤⎛⎫=-+ ⎪⎥⎝⎭⎦,由此当πsin 14θ⎛⎫-=- ⎪⎝⎭时,d1)-.……………………………………………………………………(10分)23.(本小题满分10分)【选修4−5:不等式选讲】解:(1)21()|1||1|21121x x f x x x x x x --⎧⎪=++-=-<⎨⎪>⎩,,,,,,≤≤∵()6f x <,∴261x x -<⎧⎨-⎩,,≤或2611x <⎧⎨-<⎩,,≤或261x x <⎧⎨>⎩,,∴31x -<-≤或11x -<≤或13x <<,故解集为(33)-,.……………………………………………………(5分)(2)∵()|1||1||(1)(1)|2f x x x x x =++-+--=≥,∴min ()2f x =,当且仅当(1)(1)0x x +-≤时取等,∵()|3|0f x a -+<有解,∴min |3|()2a f x +>=,∴|3|2a +>,∴32a +<-或32a +>,即5a <-或1a >-,故a 的取值范围是(5)(1)-∞--+∞ ,,.…………………………………………(10分)。
贵阳市四校2020届高三年级联合考试(五)文数-试卷

的题号必须与所涂题目的题号一致,在答题卡选答区域指定位置答题. 如果多做,则按所做的第一题计分.
22. (本小题满分10 分)[选修4-4:坐标系与参数方程]
{ 在平面直角坐标系xOy
中,曲线C1
的参数方程为x y
= =
, 4cosβ (β
, 4sinβ
为参数),将曲线C1
上的所有点的横坐标
缩短为原来的12 ,纵坐标缩短为原来的槡43后得到曲线C2. 以坐标原点为极点,x 轴的正半轴为极轴建立极
32 A. π
3
B. 28π
C. 16π
文科数学·第2 页(共4 页)
D. 32π
二、填空题(本大题共4 小题,每小题5 分,共20 分) 13. 设a,b,c 分别是△ABC 的内角A,B,C 的对边,已知A = , 120° a = 2槡7 ,b = 2,则c= .
14. 已知正数x,y 的等差中项为1 ,则2 + 8 的最小值为 . 2 xy
21. (本小题满分12 分)
已知函数f(x)=
,其中为常数 xsinx+2cosx+ax+2
a
.
(1)若曲线y=f(x)在(0,f(0))处的切线在两坐标轴上的截距相等,求a 的值;
(2)若对x∈[0,π],都有π<f(x)<π2,求a 的取值范围.
请考生在第22、23 两题中任选一题作答,并用2B 铅笔在答题卡上把所选题目的题号涂黑. 注意所做题目
0 40
0 25
0 15
0 10
k0
0 455
0 708
1 323
2 072
2 706
文科数学·第3 页(共4 页)
19. (本小题满分12 分)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.7
23
选做题
10
绝对值不等式
0.7
命题
思想
达成
目标
优秀率
及格率
平均分
8%
30%学
7
选择题
5
函数的图象
0.6
8
选择题
5
对数式的大小比较
0.6
9
选择题
5
三角函数的图象及性质
0.55
10
选择题
5
几何体的展开及线线、线面关系
0.5
11
选择题
5
双曲线的几何性质
0.4
12
选择题
5
空间几何体的外接球
0.2
13
填空题
5
正、余弦定理
0.8
14
填空题
5
等差中项及基本不等式
0.7
15
填空题
5
圆的标准方程
贵阳市四校2020届高三年级联合考试(五)·双向细目表
题号
题型
分值
试题内容
难度
备注
1
选择题
5
二次不等式与集合运算
0.8
2
选择题
5
复数的概念及运算
0.8
3
选择题
5
向量的坐标运算及平行和垂直
0.8
4
选择题
5
线性规划
0.8
5
选择题
5
同角三角函数基本关系及二倍角公式
0.65
6
选择题
5
等差数列的前n项和
0.6
0.55
16
填空题
5
分段函数的图象及零点问题
0.3
17
解答题
12
等比数列的通项及前n项和
0.7
18
解答题
12
由直方图求平均数及独立性检验
0.65
19
解答题
12
线面垂直及点面距
0.6
20
解答题
12
椭圆的方程及直线与椭圆的综合问题
0.35
21
解答题
12
切线方程及用导数解决三角函数的问题
0.3
22
选做题
10
