浙江大学2000年研究生高等代数试题
2000考研数学二真题及答案解析

邻域内当 x < 0 时曲线 y = f (x) 是凸的,在此去心临域内 x > 0 时曲线 y = f (x) 是凹的,
点 (0, f (0)) 是曲线 y = f (x) 的拐点,选(C).
(3)【答案】A 【分析】由选项答案可知需要利用单调性证明,关键在于寻找待证的函数. 题设中已知
f '(x)g(x) − f (x)g '(x) < 0,
f ′′′(x) = (x − [ f ′(x)]2 )′ = 1− 2 f ′(x) f ′′(x)
以 x = 0 代入,有 f ′′′(0) = 1 ,所以
= f ′′′(0) lim f ′′(x)= − f ′′(0) li= m f ′′(x) 1.
x→0
x−0
x→0 x
从而知,存在 x = 0 去心邻域,在此去心邻域内, f ′′(x) 与 x 同号,于是推知在此去心
(C)点 (0, f (0)) 是曲线 y = f (x) 的拐点.
(D) f (0) 不是 f (x) 的极值,点 (0, f (0)) 也不是曲线 y = f (x) 的拐点.
(3 ) 设 f (x), g(x) 是大于零的可导函数,且 f '(x)g(x) − f (x)g '(x) < 0, 则当 a < x < b 时,
(D) y′′′ − 2 y′′ − y′ + 2 y =0.
三、(本题满分 5 分)
∫ 设 f (ln x) = ln(1+ x) ,计算 f (x)dx .
x
四、(本题满分 5 分)
{ } 设 xoy 平面上有正方= 形 D (x, y) 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 及直线 l : x + y = t(t ≥ 0) .若
2000考研数一真题答案及详细解析

一、填空题
(1)【答案】
4
【详解】 I 1 2x x2 dx 1 1 (x 1)2 dx
0Байду номын сангаас
0
解法 1:用换元积分法:设 x 1 sin t ,当 x 0 时,sin t 1,所以下限取 ;当 x 1 2
时, sin t 0 ,所以上限取 0 .
f
(x,
y,
z)dS
若f (x, y, z)关于y为奇函数 若f (x, y, z)关于y为偶函数
其中 S1 S {y 0} .
性质 3:设 f (x, y, z) 在分块光滑曲面 S 上连续, S 关于 xoy 平面对称,则
0
S
f
(x,
y,
z)dS
2
S1
f
(x,
y,
z)dS
若f (x, y, z)关于z为奇函数 若f (x, y, z)关于z为偶函数
性无关知, r 1,, m r 1,, m m, 因此 1,, m 线性无关,充分性成立;当m
= 1时,考虑1 (1, 0)T , 1 (0,1)T 均线性无关,但1 与 1 并不是等价的,必要性不成立.
(D) 剩下(D)为正确选项. 事实上,矩阵 A 1,, m 与矩阵 B 1,, m 等价 ⇔ r A =r B ⇔ r 1,, m r 1,, m m, 因此是向量组 1,, m 线性无关的充要
1
lim
x0
2 1
ex
4
ex
sin x
x
1.
四【详解】根据复合函数的求导公式,有
z x
f1 ' y
f
2000年全国硕士研究生入学统一考试数学一、二、三、四试题完整版附答案解析及评分标准

x y2
f12)
1 y2
f2
1 y
(xf21
x y2
f
22
)
1 x2
g
y x3
g
2000 年 • 第 2 页
f1
1 y2
f2 ' xyf11
x y3
f22
1 x2
g
y x3
g .
„„5 分
五、(本题满分 6 分)
计算曲线积分 I
L
xdy ydx 4x2 y2
,其中
L
是以点(1,0)为中心,R
三、(本题满分 5 分)
1
求
lim(
x0
2
ex
4
sin x
x) .
1 ex
1
4
3
解:因
lim
x0
(
2
ex
4
sin x
2e
) lim (
x
x0
x e
4
x
sin x) 1 x
,
1 ex
e x 1
1
1
2 ex
lim (
x0
4
sin x) x
2 ex
lim (
x0
4
sin x) 2 1 1, x
(5) 设二维随机变量 X ,Y 服从二维正态分布,则随机变量 X Y 与 X Y 不相关
的充分必要条件为
(B)
(A) E(X)=E(Y)
(B) E X 2 E X 2 E Y 2 E Y 2
(C) E X 2 E Y 2
(D) E X 2 E X 2 E Y 2 E Y 2
为半径的圆周(R>1).取逆时
文档:浙江大学考研题(2000-2005按题型整理))

名词解释:1.意识2.侧抑制和感受野 4.格式塔心理学5.模式识别 6.晶体智力和流体智力7.STROOP效应8.现代人格三层次理论9.费希纳定律10.自我功效论11.人本主义心理学12.皮层的言语区 13.神经冲动的化学传导 14.知觉的恒常性15.特征整合论16.心境与应激17.正强化与负强化 18.投射测验 19.两种人格理论模式20.基于物体的选择注意21.交互作用22.等响曲线23.恩墨特定律24.样本分布25.PASS模型26.投射测验17.需要与动机28.Weiner的动机归因理论29.结构优势效应30.特征整合理论31.启动效应32.问题空间33.实验者效应34.匹配法35.启动效应36.诱动现象37.听觉适应38.差异系数39.分层随机抽样40.心理物理学41.似动现象42.实验法43.闪光融合理论44.最小可觉差45.等响曲线46.完全随机化设计47.部分报告法48平均差误法49.似动现象50.系列位置效应51.实验者效应52.被试间设计53.费希纳的对数定律54.音高量表55.实验效度56.操作定义57.感受野58.数量估计法59.双眼视差60.开窗实验61反射62错觉63模式识别64图形掩蔽65暗适应66发散思维67心境与应激68诱因理论69素质70特质简答:1.试结合实例分析知觉是对输入信息的组织和解释2.试阐述和评述智力三元论3.试评述几种主要的注意选择理论4.试阐述减法反应时和相加因素法范式的典型实验及特点并说明其对认知心理学的贡献5.阈限的定义及操作定义,6.如何正确选用回忆方法,7.非参数检验方法的特点,8.开窗实验的范式及特点,9.谈用统计法消除额外变量,10.试述感受性和感受阈限以及感觉大小与刺激强度的关系。
11.试述并评价几种主要的能力理论。
12.你如何看待短时记忆容量问题?什么是工作记忆?为什么它是认知心理学研究的关键问题?13.什么是部件认知(RBC)理论?它与传统模式识别理论相比有什么进步?有什么不足?14.什么是Stroop效应?什么是反应选择?你认为两者有关吗?为什么?15.试阐述“心理旋转”和“心理扫描”的典型实验,你认为它们对心理学的贡献主要表现在哪里?16.如何控制额外变量?17.恒定刺激法的特点?18.反应指标应该有什么要求?19.感受性与感觉域限如刺激强度与感受性的关系是什么样的?20.有两个口袋,一个口袋有2只黑球和4只白球,另一个口袋有5只黑球和3只白球,求(1)从两只口袋中各取一只白球的概率(2)从两只口袋中各取一只黑球的概率(3)从一只口袋中取一个白球从另一只口袋中去一只黑球的概率21.详述内隐记忆与外显记忆的区别。
高等代数考研真题第一章多项式

且f(x)在有理数域上不可约。
第一章多项式1 (清华2 000— 20分)试求7次多项式f(X ),使f(M 1能被(X -1)4整除,而f(X )-1能被(X 1)4整除。
2、 (南航 2001 — 20 分)(1) 设 x —2px+2 I x +3x +px+q ,求 p,q 之值。
(2) 设f(x) , g(x), h(x) € R[x],而满足以下等式2(x +1)h(x)+(x -1) f(x)+ (x -2) g(x)=02(x +1)h(x)+(x+1) f(x)+ (x+2) g(x)=02 2证明:x +1 I f(x) , x +1 I g(x)3、 (北邮2002 —12分)证明:x d - 1 I x "- 1的充分必要条件是d I n (这里里记号 d I n 表示正整数d 整除正整数n )。
4、 、(北邮 2003 —15分)设在数域 P 上的多项式 g 1(x), g 2(x) , g 3(x) , f(x),已知 g 1(x) I f(x),g 2(x) I f(x) , g 3(x) I f(x),试问下列命题是否成立,并说明理由:(〔)如果 g 1(x) ,g 2(x) , g 3(x)两两互素,则一定有 g 1(x) , g 2(x) , g 3(x) I f(X )(2)如果g1(x) , g 2(x) , g 3(x)互素,则一定有 g 1(x)g 2(x)g 3(x)I f(X )5、 (北师大2003—25分)一个大于1的整数若和其因子只有1和本身,则称之为素数。
证明P 是素数当且仅当任取正整数a ,b 若p I ab 则p I a 或p I b 。
6、 (大连理工2003 —12分)证明:次数>0且首项系数为1的多项式f(x)是某一不可约多项式的方幕主充分必要条件是,对任意的多项式g(x) , h(x),由f(x) I g(x) h(x)可以推出f(x) I g(x),或者对某一正整数 m , f(x) I h m(x)。
2000年浙江大学804数学分析考研真题【圣才出品】

2000年浙江大学804数学分析考研真题浙江大学2000年攻读硕士学位研究生入学试题考试科目:数学分析(804)一、(10分)()i 求极限10(1)lim x x e x x →-+; ()ii 设01,x a x b ==,21,2,3,2n n n x x x n ---==.求lim n n x →∞.二、(10分) ()i 设(0)f K '=,试证明00()()lim a b f b f a K b a -+→→-=-;()ii 设()f x 在[],a b 上连续,()f x ''在(),a b 内存在,试证明存在(),a b ξ∈,使得2()()()2()()24a b b a f b f a f f ξ+-''+-=.三、(15分)()i 求数项级数12n n n ∞=∑的和;()ii 试证明函数11()x n S x n ∞==∑在()1,+∞上连续.四、(15分)()i 设方程组0sin sin 0x y u v x u y v +++=⎧⎨+=⎩,确定了可微函数(,)(,)u u x y v v x y =⎧⎨=⎩,试求,,v v du x y ∂∂∂∂; ()ii 设2)()y x y F y dx x =,求(1)F '.五、(30分) ()i 计算积分20sin 1cos x x I dx x π=+⎰;()ii 求以曲面22x y z e --=为顶,平面0z =为底,柱面221x y +=为侧面的曲顶柱体的体积V ;()iii 设S 表示半球面221)z x y =+≤的上侧,求第二类曲面积分222()(2)(2)S J x y z dydz x y z dzdx x z y dxdy=++-++⎰⎰.六、(20分)()i 将函数(),()f x x x ππ=-≤≤展开成Fourier 级数;()ii 求级数211n n ∞=∑的和;()iii 计算广义积分10ln(1)x dx x -⎰.。
2000年考研真题及详解
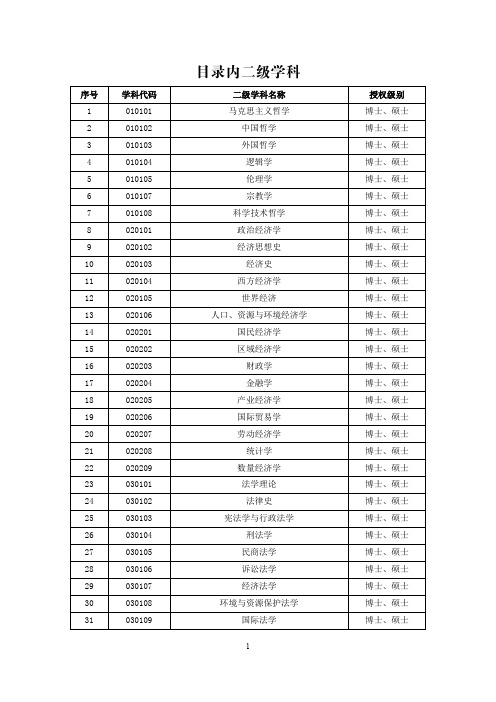
哲学
博士、硕士
2
金融工程
0202Z1 0202
应用经济学
博士、硕士
3
能源经济学
0202Z2 0202
应用经济学
博士、硕士
4
国际金融学
0202Z4 0202
应用经济学
博士、硕士
5
知识产权法学
0301Z1 0301
法学
博士、硕士
6
国防教育学
0401Z1 0401
教育学
博士、硕士
7
对外汉语教学
0501Z1 0501 中国语言文学
系统工程 模式识别与智能系统 导航、制导与控制
建筑历史与理论
4
授权级别 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士
硕士 硕士 硕士 硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士、硕士 博士 硕士 博士 硕士 硕士 硕士
化学
博士、硕士
14
海洋物理
0707Z1 0707
海洋科学
博士、硕士
15
海洋生物技术
0707Z2 0707
海洋科学
博士、硕士
16 电气检测技术及仪器 0804Z1 0804 仪器科学与技术 博士、硕士
17 软物质与功能材料 0805Z1 0805 材料科学与工程 博士、硕士
18
核工程与材料
0805Z2 0805 材料科学与工程 博士、硕士
24
财务学
1202Z1 1202
工商管理
博士、硕士
浙江大学研究生入学考试2000年试题

浙江大学研究生入学考试2000年试题一、填空题1.流体在管内会引发机械能的损失,这是由于。
2.离心泵在设计流量下工作时泵效率最高,这是由于。
而大型泵的效率通常高于小型泵的,那么是由于。
3.在进行流态化操作时,床层的压降不随气速增大而增大,这是由于。
4.某一热流体流经一段直管后,在流入同一内径的弯管段,那么弯管段的传热系数比直管段的,因为。
5.关于相同产能力,多效蒸发比单效蒸发操作费用,设备费用。
6.将相对挥发度为的某二元物系在全回流操作的塔中进行精馏,现测得全凝器中冷凝液组成为,塔顶第二层塔板上升的气相组成为,那么塔顶第一层塔板的气相默弗里板效为。
7.关于难容气体的吸收,可采取哪些方法以提高吸收速度、。
8.恒沸精馏的原理是。
9.在设计或研制新型气液传质设备时,要求设备具有、、。
10.临界湿含量于哪些因素有关?(举其中四个因素)、、、。
二、选择题1.如图1所示,高位槽A通过一并联管路向槽B输送液体,两槽液面维持恒定。
输液时要求排液管FG上的阀门k1关闭.现由于操作不慎,阀门k1未关严,试判定,与k1关闭时相较,下面哪个结论正确。
(1)D处的压力下降,总管AC内流量下降;(2)E处的压力下降,支管CF内流量增大;(3)C处的压力下降,支管CED内流量增大;(4)E处的压力上升,支管CED内流量下降。
2.随着流体流量的增大,流体通过以下哪一种流量计时,其压降转变幅度最小。
(1)孔板流量计;(2)文丘里流量计;(3)转子流量计3.离心泵的安装高度与。
(1)泵的结构无关;(2)液体流量无关;(3)吸入管路的阻力无关; (4)被输送的液体密度有关4.推导过滤大体方程式的一个最大体依据是 。
(1)滤液通过滤饼时呈湍流流动; (2)假定滤渣大小均一;(3)滤液通过滤饼时呈层流流动; (4)假设过滤介质的阻力可忽略不计5.如图2所示,冷、热流体在套管换热器中进行换热(均无相转变)。
现冷流体流量m 2减少,那么 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、 (20 分) (1) A 是正定阵, C 是实对称矩阵,证明:存在可逆矩阵 P 使得 P 1 AP, P 1CP 同时为 对角形; (2) A 是正定阵, B 是实矩阵,而 AB 是实对称的,证明: AB 正定的充要条件是 B 的 特征值全大于 0. 四、 (20 分)设 n 维线性空间 V 的线性变换 A 有 n 个互异的特征值,线性变换 B 与 A 可交换
下证不可能是情形二。 (反证法)若不然为情形二,就是 ( f ( x), g ( x)) 1 则
u ( x), v( x) P[ x]s.t u ( x) f ( x) v( x) g ( x) 1L (*)
由已知条件, f 与g 有一公共复根(设为 ) ,则 f ( ) g ( ) 0 ,将 代入 盾,故假设不正确,得证! (2)设 b 是 f ( x) 的任一根,下证 f ( ) 0 。证明见《高等代数题解精粹》钱吉林编 P20 第 42 题. 二、计算行列式
PAP E 1 (2)由(1)知 P非异s. t 2 PABP O n
1 所以 P BP 2 ,故 AB 正定 i 0, i 1, 2,L , n 得证!! O n
1 , 2 ,L , n s.t A i i i ,其中 i 为 A 的特征值,且 i j , i j , i , j 1, 2L , n 1 令 T (1 , 2 ,L , n ) s.tT AT 2 O n
1
(2)Q AB BA 则, (T AT )(T BT ) (T BT )(T AT ) ,令 C T AT , D T BT , C 为对 角矩阵,且主对角线上的元素互异,而 CD DC ,
1
1
1
1
1
1
b1 由结论“与对角矩阵可交换的矩阵只能是对角矩阵”知 D b2 ,即 O bn b1 T BT b2 , O bn
在此结论中令
1 ,知 Dn n 1
三、 (1) A 是正定矩阵, C 是实对称矩阵,证明: 可逆矩阵 P s.t PAP, PCP 同时为对角形 Proof: (1)Q A 正定, 可逆矩阵 T 使得 T AT E ,此时 T CT 还是对称的, 正交矩阵 M 使得 M T CTM 为对角形,令 P TM ,此时 PAP E PCP 是对角形,得证!
浙
江
大
学
二〇〇〇年攻读硕士研究生入学考试试题 考试科目:高等代数
编号:226
一、 (20 分) f ( x) 是数域 P 上的不可约多项式 (1) g ( x) P[ x] ,且与 f ( x) 有一个公共复根,证明 f ( x) | g ( x) ;
1 1 (2)若 c 及 都是 f ( x) 的根, b 是 f ( x) 的任一根,证明 也是 f ( x) 的根. c b 2 1 0 L 0 0 0 1 2 1 L 0 0 0 二、 (10 分)计算行列式 Dn . L L L L L 0 0 0 L 1 2 1 0 0 0 L 0 1 2
(*) 中得到 1 0 的矛
1 b
2 1 0 ...0 0 0 Dn 1 2 1 ...0 0 0 .. .. .. .. 0 0 0 ...0 1 2
Solution:我们已经知道:
1
1
O O 1 O
n 1 n 1 , (n 1) n 1 ,
1
四、设 n 维线性空间 V 的线性变换 A 有 n 个互异的特征值,线性变换 B与A 可交换的充分必要条件是 B
第 2 页 共 4 页
是 E , A , A ,L , A
1
2
n 1
的线性组合,其中 E 为恒等变换。
Proof:我们分以下四步来完成证明。 (1) 由题意知, A 有 n 个互异特征值,故
( A( ), ) ( , B ( )) 。证明: A 的核等于 B 是数域 P 上的不可约多项式 (1) g ( x) P[ x] ,且与 f ( x) 有一公共复根,证明: f ( x) | g ( x) 。
第 1 页 共 4 页
(2)若 c 及
2 n 1 的充要条件是 B 是 E , A, A ,L , A 的线性组合,其中 E 为恒等变换.
五、 (10 分)证明: n 阶幂零指数为 n 1 的矩阵都相似. (若 An 1 0 , An 2 0 而称 A 的幂零指数为 n 1 ) 六、 (20 分)设 A, B 是 n 维欧氏空间 V 的线性变换。对任意 , V ,都有
1 1 都是 f ( x) 的根, b 是 f ( x) 的任一根,证明: 也是 f ( x) 的根。 c b
Proof:(1)Q f ( x) 是数域 P 上的不可约多项式,故对于 P 上任一多项式 g ( x) 只有以下两种情形:
10 f ( x) | g ( x)
,
20
( f ( x), g ( x)) 1
1
B i bi i , i 1, 2,L , n
(3)Q A i i i A
1
k
i i k i , k 1, 2,L , n
2 n 1
(4)欲证 B 可由 E , A , A ,L , A
线性表出,只须证方程
( B 0 显然)设 B 0 B x1 E x2 A1 x3 A2 L xn An 1 有非零解即可, 将 B 作用于 i , i 1, 2,L , n 则
