中国精算师《寿险精算》章节题库(第4章 均衡净保费——第6章 毛保费与修正准备金)【圣才出品】
寿险精算习题及答案
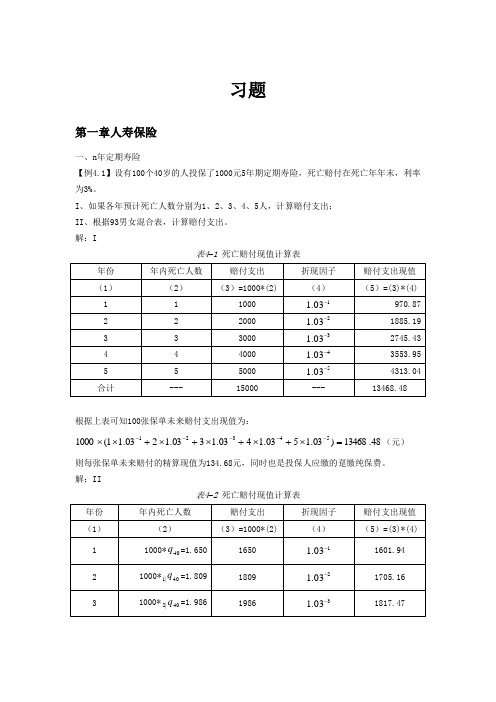
习题第一章人寿保险一、n 年定期寿险【例4.1】设有100个40岁的人投保了1000元5年期定期寿险,死亡赔付在死亡年年末,利率为3%。
I 、如果各年预计死亡人数分别为1、2、3、4、5人,计算赔付支出; II 、根据93男女混合表,计算赔付支出。
解:I表4–1 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:48.13468)03.1503.1403.1303.1203.11(100054321=⨯+⨯+⨯+⨯+⨯⨯-----(元)则每张保单未来赔付的精算现值为134.68元,同时也是投保人应缴的趸缴纯保费。
解:II表4–2 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:86.9124)03.103.103.103.103.1(1000540|4440|3340|2240|11402=⨯+⨯+⨯+⨯+⨯⨯-----q q q q q (元)则每张保单未来赔付的精算现值为91.25元,同时也是投保人应缴的趸缴纯保费。
【例4.2】某人在40岁时投保了10000元3年期定期寿险,死亡赔付在死亡年年末,利率为5%。
根据93男女混合表计算:I 、单位趸缴纯保费;II 、单位赔付现值期望的方差;III 、(总)趸缴纯保费; 解:I 、单位趸缴纯保费为,)()(424023414024040|2340|1240240|11|3:40q p v q p v vq q v q v vq q v Ak k k ++=++=⨯=∑=+]05.1001993.0)001812.01()00165.01(05.1001812.0)00165.01(05.100165.0[32⨯-⨯-+⨯-+=00492793.0=(元)。
II 、单位赔付现值期望的方差为,00444265.0)()()()(21|3:4040|2640|1440221|3:40240|)1(221|3:401|3:402=-++=-⨯=-∑=+A q v q v q v A q v AAk k k III 、趸缴纯保费为,28.49100001|3:40=⨯A (元) 【例4.3】某人在50岁时投保了100000元30年期定期寿险,利率为8%。
中国精算师《寿险精算》章节题库-人寿保险的精算现值(圣才出品)

第2章人寿保险的精算现值选择题1.30岁的人购买保额为1000元的特殊的35年期两全保险,已知条件如下:(1)在其购买保险时,其两个孩子的年龄分别是3岁和6岁;(2)特殊约定为:如果被保险人死亡时两个孩子的年龄都小于11岁,那么给付额为3000元;如果被保险人死亡时只有一个孩子的年龄小于11岁,那么给付额为2000元;(3)在被保险人死亡时立即给付保险金;(4)μ30+t=0.04,t≥0;(5)δ=0.06;(6)35E30=0.0302。
则此保单的趸缴纯保费为()元。
[2008年真题]A.638B.766C.777D.796E.800【答案】D【解析】由题意可知,该保险相当于保额1000元的35年期两全保险+1000元保额的8年期定期保险(5-8年内被保险人只有一个孩子小于11岁)+1000元保额的5年期定期保险(5年内两个孩子都小于11岁),故此保单的趸缴保险费为:=796(元)2.30岁的人购买两年期定期保险,保险金在被保险人死亡的年末给付,保单年度t 的保额为bt ,已知条件为:q30=0.1,b2=10-b1,q31=0.6,i=0 ,Z表示给付现值随机变量,则使得Var(Z)最小的b1的值为()。
[2008年真题]A.0.0B.5.0C.6.8D.8.6E.8.9【答案】C【解析】v=1,由题意得:Pr [K(30)=0]=q30=0.1,Pr [K(30)=1]=p30q31=(1-0.1)×0.6=0.54,所以E(Z)=b1×0.1+(10-b1)×0.54,E(Z)2= ×0.1+(10-b12)×0.54,故Var(Z)=E(Z2)-(E(Z))2= -6.048b1+24.84。
故当b1=6.048/(2×0.4464)=6.8时,Var(Z)最小。
3.50岁的人购买保险金在死亡时给付的特殊的递增型终身寿险,Z表示给付现值随机变量,已知:b t=1+0.1t,v t=(1+0.1t)-2,t p50·μ(50+t)=0.02 ,0≤t<50则Var(Z)的值为()。
中国精算师《寿险精算》章节题库-特殊年金与保险(圣才出品)

第12章特殊年金与保险
计算题:
1.假设每年内死亡服从均匀分布,证明式可表示为:
解:由于死亡服从均匀分布,
2.证明中定义的Z和每年支付1的n年延期连续生命年金有相同的方差。
解:每年支付1的n年延期连续生命年金的随机变量可表示为:
3.对部分现金立即偿还年金.设现值随机变量为:
证明对部分现金立即偿还年金,式可写成:
解:直接求期望可得:
4.证明:有:
解:因为
5.假设
证明:
解:
因为Z2是常量,Z1为n年定期死亡保险的现值随机变量,故
6.一份保单从(x)死亡日期开始提供每年为1的连续确定年金。
如死亡发生在保单签发后的15年内,则年金支付到保单签发后的20年年底;如死亡发生在保单签发后15至20年内,则年金支付5年。
保单签发20年后终止。
给出趸缴净保费的表达式。
解:设保单给付现值的随机变量为Z,可得:
7.某份保单规定:如被保险人在20年末还活着时可得1000元;如在保单签发后的20年内死亡,则每月可得10元的收入直至20年末,该收入的第一笔支付在死亡的月末,保单签发20年后则无支付。
给出x岁时的年缴净保费公式。
解:
8.证明:
解:
9.证明:对一个退休收入保单,记a=h+r,其中h=[a],0<r<1,则在第h+1保单年度内死亡均匀分布的假设下下式成立:
解:
10.证明:
解:。
中国精算师《寿险精算》过关必做(含真题)习题集(人寿保险的主要类型)【圣才出品】

第11章人寿保险的主要类型1.简述普通型人寿保险的主要类型。
答:按照保险责任可将普通型人寿保险分为定期寿险、终身寿险、两全保险、年金保险等四种:(1)定期寿险是以死亡为给付保险金条件,保险期限为一定年限的人寿保险。
固定年限可以为当前到未来某个固定的年龄,如至七十岁;从当前开始固定一段时间,如十年或二十年。
(2)终身寿险指以死亡为给付保险金条件,保险期限持续到死亡时刻的人寿保险。
(3)两全保险,被保险人在保险合同规定的年限内死亡或仍生存两种情况下,保险人按照合同都被付保险金。
两全保险的净保费由风险保险费和储蓄保险费组成,风险保险费用于当年死亡给付,储蓄保险费逐年积累,既可用于中途退保时支付退保金,也可用于生存给付。
两全保险不仅能使受益人得到保障,也能使被保险人享受一定的保险合同利益。
(4)年金保险指以生存为给付保险金条件,按约定分期给付生存保险金。
分期给付保险金间隔不可超过一年。
2.简述分红保险的特点。
答:分红保险有以下几项主要特点:(1)保单持有人享受经营成果。
保险公司每年将分红险种产生的部分盈余以红利的形式分配给保单持有人,投保人可与保险公司共享经营成果,增加获利机会。
(2)保单持有人承担一定的风险。
由于每年保险公司的经营状况不一样,在经营状况不好的情况下,保单持有人分到的红利就会比较少,甚至没有。
因此分红保险使保险公司和保单持有人在一定程度上共同承担了风险。
(3)定价的精算假设比较保守。
寿险产品在定价时主要以预定死亡率、预定利率和预定费用率三个因素为依据。
三个预定因素和实际情况的差距将直接影响寿险公司的经营成果。
由于寿险公司希望将部分盈余以红利形式分配给客户,所以在定价时对精算假设估计较为保守,导致保单价格较高,以期在实际经营过程中产生更多的可分配红利。
(4)保险给付、退保金中含有红利。
被保险人身故后,受益人在获得保险金额的同时还可获得未领取的累积红利及利息;满期给付时,被保险人在获得保险金额的同时也可得到未领取的累积红利及利息;退保时,分红保险的保单持有人得到的退保金也包括未领取累积红利及利息。
《寿险精算讲义》第四章均衡纯保费

答案
答案
全离散式分两次缴付的年缴纯保费计算 半连续式分两次缴付的年缴纯保费计算
例 4.5.2
对于(40)的人,投保5000元的全离散 式25年定期保险,用换算函数表和年利 率6%。在UDD假设下求:
(1)普通年缴纯保费 (2)季缴纯保费 (3)月缴纯保费
x xx
xa
x
终身寿险-普通
下面考察保险人损失L的方差
(3)Var
(
L)
Var
(v
K
1
Px
a K
1
)
Var(vK 1
Px
1 vK 1 d
)
Var(vK 1(1
Px d
)
Px d
)
(1 Px )2Var(vK 1) d
(1
Px d
)
2[
2
Ax
( Ax )2 ]
2 Ax ( Ax )2 (dax )2
60
【每年分m次缴费的年均纯保费】
在每年分m次缴付的年均纯保费P,每次 缴付纯保费为x元,其计算方法是:
用符号 P(xm)表示保险金额为一个单位的全
离散式普通终身寿险,且每年分m次缴付
的年均衡纯保费.m=2、4、12,故每次缴
纳的纯保费应该是
P(m) x
m
【每年分m次缴费的年均纯保费】
条件:在每一保单年度内,保费分m次缴纳。 终身寿险半连续式寿险为例
m年递延终身生存 保险
P1 x:n
A1 x:n
ax:n Dxn
(Nx Nxn)
P(m
ax
)
A1 x:m
axm
a x:m
Dxm N xm
保险精算第6章(2)

解出
px 0.8187.
8
按照方案二缴纳的保费精算现值为
p(1 vpx ) p(1 0.95 px )
根据净均衡原理,保险给付金精算现值和缴纳的保费精 算现值相等,即有
950 - 47.5 px p(1 0.95 px )
解出
p 512.5.
9
常见险种的完全离散净均衡保费总结
险种
保费公式
)
Var (v S 1 )
E(v2(S1) ) [E(vS1)]2
2i i2
2
i
2
15
则在分数期死亡服从均匀分布假定下,损失变量的方 差为
Var(L) Var(ZS ) E(ZK 2 ) [E(ZS )]2 Var(ZK )
2i i2
2
i
2
2 Ax
i
1 1 Ax
2
[ 2 Ax
终身人寿(终身缴费)保险 n年定期(n年缴费)寿险 n年两全(n年缴费)保险 h年缴费终身人寿保险 h年缴费n年两全保险
Px Ax ax
P1 x:n
A1 x:n
ax:n
Px:n Ax:n ax:n
h Px Ax ax:h P h x:n Ax:n ax:h
n年生存(n年缴费)保险
P1 x:n
第六章 期缴保费
1
常见险种的完全连续净均衡保费总结
险种
保费公式
终身人寿(终身缴费)保险
P( Ax ) Ax ax
n年定期(n年缴费)寿险 n年两全(n年缴费)保险
h年缴费终身人寿保险 h年缴费n年两全保险
P
(
A1 x:n
)
A1 x:n
ax:n
P( Ax:n ) Ax:n ax:n
中国精算师《寿险精算》章节题库-寿险定价概述(圣才出品)

第13章寿险定价概述简答题:1.简述寿险定价的基本原则。
答:寿险定价的基本原则包括:(l)充足性原则该原则指保险费率应高至足以弥补预计发生的各项赔付以及有关的费用。
如果费率不充足,就会导致保险人难以仅依赖收取的保险费来履行未来保险赔付的义务,进而影响保险人的盈利能力和偿付能力,最终可能使被保险人的利益受到损害。
因此寿险产品的费率不能太低。
(2)合理性原则该原则是指寿险产品的平均费率水平应该和预计发生的各项赔付及费用水平相匹配,保险人获得一个恰当的利润水平。
(3)公平性原则该原则是指保险人对被保险人所承担的保险保障和赔付责任应该和投保人所缴纳的保费对等。
公平性原则是针对每个被保险人而言,合理性原则只针对某个险种的平均费率水平而言。
(4)可行性原则每一个寿险产品在开发和定价时都有其预定的目标客户群,费率的厘定不仅仅要考虑赔付的需要,以及合理性、公平性的原则,还要考虑目标客户群的特征以及其缴纳保费的能力,这样才能提高行销的可行性。
(5)稳定性原则该原则是指保险费率在短期内应该是相对稳定的,这样既有利于保险经营,又有利于投保人续保。
(6)弹性原则该原则是指保险费率要随着实际情况的变化而有所变化。
2.了解寿险公司产品开发的过程。
答:险种开发流程可分为以下几个环节:(1)产品形态构思。
新产品形态的思路来源包括由销售渠道提供的根据客户或销售人员对现有产品的反馈、经验分析的结果、同业产品的启发、政策法规的导向等。
(2)产品可行性分析。
它是新产品开发项目前期的重要工作,其分析结果将被写入产品可行性分析报告以供公司管理层决策参考。
产品可行性分析报告主要分析该产品能否符合公司策略、适应客户需求、合法合规、符合内部运营和系统支持能力、符合公司产品盈利性标准、投入产出合理性,并对产品的主要风险点进行提示。
(3)管理层审批。
由于寿险产品的长期性,每一个新产品的上市,保险公司都必须在系统中记录相关信息,提供相应的服务,长达数年甚至上百年,因而保险公司对于新产品开发的决策通常比较谨慎。
中国精算师考试指引——考试用书及考试形式

中国精算师资格考试指南第I部分中国精算师资格考试一准精算师部分A1数学考试时间:3小时考试形式:选择题考试要求:本科目是关于风险管理和精算中随机数学的基础课程。
通过本科目的学习,考生应该掌握基本的概率统计知识,具备一定的数据分析能力,初步了解各种随机过程的性质。
考生应掌握概率论、统计模型和应用随机过程的基本概念和主要内容。
考试内容:A、概率论(分数比例约为35%)1. 概率的计算、条件概率、全概公式和贝叶斯公式(第一章)2. 联合分布律、边缘分布函数及边缘概率密度的计算(第二章)3. 随机变量的数字特征(§3.1、§3.2、§3.4)4. 条件期望和条件方差(§3.3)5. 大数定律及其应用(第四章)B、数理统计(分数比例约为25%)1. 统计量及其分布(第五章)2. 参数估计(第六章)3. 假设检验(第七章)4. 方差分析(§8.1)C、应用统计(分数比例约为10%)1. 一维线性回归分析(§8.2)2. 时间序列分析(平稳时间序列及ARIMA模型)(第九章)D、随机过程(分数比例约为20%)1. 随机过程一般定义和基本数字特征(第十章)2. 几个常用过程的定义和性质(泊松过程、更新过程、马氏过程、鞅过程和布朗运动)(第十一章)E、随机微积分(分数比例约为10%)1. 关于布朗运动的积分(§11.5、第十二章)2. 伊藤公式(§12.2)考试指定教材:中国精算师资格考试用书:《数学》肖宇谷主编,李勇权主审,中国财政经济出版社2010版,所有章节。
A2金融数学考试时间:3小时考试形式:选择题考试要求:本科目要求考生具有较好的数学知识背景。
通过学习本科目,考生应该熟练掌握利息理论、利率期限结构与随机利率模型、金融衍生工具定价理论、投资组合理论的主要内容,在了解基本概念、基本理论的基础上,掌握上述几部分内容涉及的方法和技巧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E.0.8
十万种考研考证电子书、题库视频学习平台
【答案】B
【解析】
11.给定如下条件
则 δ 满足( )。 A.100δ2-17δ+0.66=0 B.100δ2-16δ+0.60=0 C.100δ2-15δ+0.50=0 D.100δ2-15δ+0.44=0 E.100δ2-14δ+0.40=0 【答案】A 【解析】由已知,有:
A.-1.12 B.-0.6 C.-0.25 D.0.15 E.0.00 【答案】C 【解析】由已知,有:
4 / 212
圣才电子书 十万种考研考证电子书、题库视频学习平台
6.已知死亡在各个年龄中均匀分布,且满足:i=0.04,δ=0.0392,nEx=0.6,
=0.804
A.117.57 B.121.92 C.130.07 D.140.15 E.147.16 【答案】B 【解析】由已知,有 PrL(π)>0<0.5 而
是关于 k 的减函数,即 L(π)取满足条件的最高值时,k 须取 39,故
解得:π≥121.92
2.设
=0.042 , 20P35=0.0299 ,A55=0.6099, 则
即
8 / 212
圣才电子书 十万种考研考证电子书、题库视频学习平台
从而 100δ2-17δ+0.66=0。
12.对于普通终身寿险,设 k|qx=c(0.96)k+1,k=0,1,2,…。其中
,i=6%
则其年缴纯保费 Px=( )。
A.0.02199
B.0.03774
死亡是均匀分布的。计算完全连续保费
=( )。
A.0.597
B.9.598
C.0.599
D.0.600
E.0.601
【答案】E
【解析】由已知,得
10.已知 A90=0.885301,i=0.06,假设死亡均匀分布,计算 A.0.4 B.0.5 C.0.6 D.0.7
7 / 212
=( )。
圣才电子书
i=0.06。则保险人亏损现值的方差为( )。
A.0.17698
B.0.25363
9 / 212
圣才电子书
C.0.36632
十万种考研考证电子书、题库视频学习平台
D.0.43667
E.0.51898
【答案】A
【解析】
故
14.已知 A.0.002 B.0.003 C.0.006
圣才电子书
十万种考研考证电子书、题库视频学习平台
第 4 章 均衡净保费
1.现有保额为 20000 元的终身寿险保单,记 π 为每张保单的年缴净保费,L(π)表 示每张保单在签单时保险人的损失变量。设预定利率为 i=6%,签单时被保险人的年龄为 40 岁,已知 39q40=0.4939,40q40=0.5109,计算使得 Pr[L(π)>0]<0.5 的最小年缴 保费 π 的值为( )元。[2008 年真题]
3 / 212
圣才电子书 十万种考研考证电子书、题库视频学习平台
5.49 岁的人购买完全离散单位保额终身寿险,在保单签发时保险人的损失变量记为 L, 已知: A49=0.29224,2A49=0.11723 ,i=0.05,Var(L)=0.1;则 E(L)=( )。[2008 年 真题]
C.0.04399
ห้องสมุดไป่ตู้
D.0.04499
E.0.04774
【答案】B
【解析】已知 i=6%,所以 v=1/(1+i)=1/1.06=0.943396,d=i/(1+i)=0.06/1.06。
其精算现值为:
13.设一个 0 岁的整值剩余寿命服从概率为
的分布,在
其死亡年末赔付 1 单位的保单,每年年初交付保费 P,当保费按平衡原理决定时,利率
=0.0420,20P35=0.0299,A55=0.6099,则
=( )。
10 / 212
圣才电子书
D.0.008
十万种考研考证电子书、题库视频学习平台
故
=( )。
8.设 15P45=0.038, A.0.005 B.0.006 C.0.007 D.0.008 E.0.009 【答案】D 【解析】由已知,得:
,A60=0.625,计算
=( )。
6 / 212
圣才电子书 十万种考研考证电子书、题库视频学习平台
9.已知 A90=0.885301,i=0.06,α(∞)=1.000283,β(∞)=0.509855,假设
( )。[2008 年真题]
1 / 212
值分别为
圣才电子书
A.0.031;0.011
十万种考研考证电子书、题库视频学习平台
B.0.011;0.031
C.0.024;0.018
D.0.018;0.024
E.0.014;0.028
【答案】B
【解析】
解得:x=0.011,y=0.031。
则
=( )。[2008 年真题]
A.153
B.155
C.157
D.159
E.161
【答案】B
【解析】由已知,有
从而 故 故
5 / 212
圣才电子书 十万种考研考证电子书、题库视频学习平台
7.如果 A.0.040 B.0.041 C.0.042 D.0.043 E.0.044 【答案】B 【解析】由已知,有
E.0.045
【答案】C
2 / 212
圣才电子书 十万种考研考证电子书、题库视频学习平台
【解析】设该保险的均衡纯保费为 P,由题意得:
4.关于(x)的完全连续终身寿险保单,保险人的损失变量记为
,
剩余寿命 T(x)的概率密度函数为
利率 δ=0.05,那么保险人面临正损失的概率为( )。[2008 年真题] A.0.47 B.0.48 C.0.49 D.0.50 E.0.51 【答案】E 【解析】面临正损失的概率即
3.30 岁的人购买完全离散的 10 年定期保险,若死亡在 10 年内发生,则在死亡年末
给付额为 1 个单位;若被保险人在 10 年末仍生存,则所有的保费都将退还(不含利息),
已知 A30
,d=0.05,计算该保险的均衡纯保费为( )。[2008
年真题]
A.0.031
B.0.035
C.0.039
D.0.041
