角形 角平分线部分经典题型
【中考数学必备专题】几何辅助线大揭秘 之角平分线问题(含答案)
【中考数学必备专题】几何辅助线大揭秘之角
平分线问题
一、证明题(共3道,每道40分)
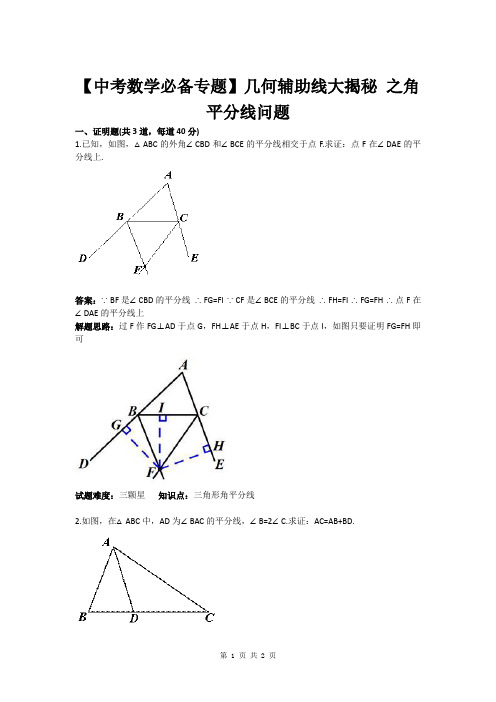
1.已知,如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F.求证:点F在∠DAE的平分线上.
答案:∵BF是∠CBD的平分线∴FG=FI ∵CF是∠BCE的平分线∴FH=FI ∴FG=FH ∴点F在∠DAE的平分线上
解题思路:过F作FG⊥AD于点G,FH⊥AE于点H,FI⊥BC于点I,如图只要证明FG=FH即可
试题难度:三颗星知识点:三角形角平分线
2.如图,在△ABC中,AD为∠BAC的平分线,∠B=2∠C.求证:AC=AB+BD.
答案:∵AD是∠BAC的平分线∴∠BAD=∠EAD 在△ABD和△AED中AB=AE ∠BAD=∠EAD AD=AD ∴△ABD≌△AED(SAS)∴BD=ED,∠B=∠AED ∵∠AED=∠B=2∠C ∴∠CDE=∠AED ﹣∠C=∠C ∴DE=CE ∴BD=CE ∵AC=AE+CE ∴AC=AB+BD
解题思路:在AC上截取AE=AB,连接DE,如图只要证明BD=CE即可
试题难度:三颗星知识点:三角形角平分线
3.已知:如图,在△ABC中,BE平分∠ABC,AD⊥BE,垂足为点D.求证:∠BAD=∠DAE+∠C.
答案:∵BE平分∠ABC,AD⊥BE ∴△ABF为等腰三角形(三线合一)∴∠BAD=∠BFD ∵∠BFD 为△ACF的外角∴∠BFD=∠DAE+∠C ∴∠BAD=∠DAE+∠C
解题思路:延长AD与BC交于点F,如图只要证明∠BFD=∠BAD即可
试题难度:三颗星知识点:三角形角平分线。
利用角平分线性质解决问题练习题

利用角平分线性质解决问题练习题角平分线是初中数学中一个重要的概念,它有着广泛的应用。
在解决一些几何问题时,我们可以利用角平分线的性质来简化计算,提高解题效率。
下面我将给出一些角平分线的问题练习题并逐一解答。
1. 题目:在三角形ABC中,角A的角平分线交BC边于点D,若AB=AC,AD=5cm,BD=3cm,求BC的长度。
解析:根据角平分线的性质,我们知道BD/DC = AB/AC。
代入已知条件,可得3/DC = 1,解得DC=3cm。
由此可以知道,BC = BD+DC = 3+3 = 6cm。
2. 题目:在平行四边形ABCD中,角A的角平分线交BC边于点E,若AB=8cm,AD=10cm,BE=6cm,求CE的长度。
解析:由于平行四边形的特性,我们可以得知AE=AD=10cm。
根据角平分线的性质,可以得到BE/EC = AB/AC,代入已知条件可得6/EC = 8/(10+AC),解得EC=16cm。
因此,CE的长度为16cm。
3. 题目:在正方形ABCD中,角A的角平分线交BC边于点E,知AE=5cm,求BE的长度。
解析:由于正方形的特性,我们知道BE=BC。
根据角平分线的性质,我们可以得到AE/EC = AB/AC,即5/EC = 1。
解得EC=5cm,因此BE也等于5cm。
4. 题目:在三角形ABC中,角A的角平分线交BC边于点D,且AD=BD,若AC=6cm,BD=2cm,求AB的长度。
解析:根据角平分线的性质,我们知道BD/DC = AB/AC。
代入已知条件可得2/DC = AB/6。
由于AD=BD,即DC=2cm。
代入可得2/2 = AB/6,解得AB=6cm。
5. 题目:在梯形ABCD中,AB∥DC,角BAD的角平分线交BC边于点E,若BE=6cm,ED=9cm,求CD的长度。
解析:根据梯形的特性,我们可以得知AD∥BC。
根据角平分线的性质,可以得到BE/EC = BA/AD。
代入已知条件可得6/EC =AB/(AD+ED),即6/EC = BA/CD。
初中数学-三角形角平分线例题

例01.已知:如图,BD 是ABC 的平分线,BC AB ,P 在BD 上,AD PM ,CD PN .求证:PN PM .分析:要证PN PM ,可以证明点P 在ADC 的平分线上. 证明:因为BD 是ABC 的平分线, 所以CBD ABD . 在ABD 和CBD 中,)()()(已知已证公共边CB AB CBD ABD BD BD 所以)(SAS CBD ABD ,所以CDB ADB (全等三角形的对应角相等) 因为CD PN AD PM ,,所以PN PM (角平分线上的点到角的两边距离相等)说明 本题也可以在证明了CBD ABD 后再证明DPN DPM . 但利用角平分线的性质定理来证明更简洁.今后证明一定要注意灵活运用所学知识.例02.已知:如图,P A 、PC 分别是ABC 外角MAC 和NCA 的角平分线,它们交于P .求证:PB 为MBN 的角平分线.分析:要证BP 为MBN 的角平分线,只须证点P 到BM 、BN 距离相等,而P A 、PC 为外角平分线,故可过P 作AC PE ,BM PD ,BN PF .证明:过点P 作AC PE ,BM PD ,BN PF 于F . 因为P A 、PC 分别是MAC 和NCA 的平分线,且BM PD ,BN PF ,∴PE PD ,PF PE (角平分线上的点到角两边距离相等).∴PF PD .又∵BN PF BM PD ,,∴点P 在MBN 的角平分线上(到角两边距离相等的点在这个角的平分线上) ∴BP 为MBN 的角平分线. 说明 当有角平分线这个条件时,常常经过角平分线上的点向角的两边作垂线,利用“角平分线上的点到角两边距离相等”来证题. 同样,要证明某射线是角平分线时,只要经过射线上一点向角的两边作垂线,再证垂线段相等.本题不能只想到应用三角形全等来解决总是,防止形成思维误区.例03.如图,已知:AD 是ABC 的角平分线,DE 、DF 分别是ABD 和ACD 的高. 求证:AF AE .分析:因为AD 为ABC 的角平分线,DE 、DF 是点D 到AB 、AC 边上的距离,∴有DF DE . 再利用直角三角形全等可证明AF AE .证明:AD 是ABC 的角平分线,DE 、DF 分别是ABD 和ACD 的高. ∴ DF DE (角平分线上的一点到这个角的两边的距离相等) 在ADE Rt 和ADF Rt 中,)()(已证公共边DF DE AD AD ∴ )(HL ADF Rt ADE Rt∴ AF AE (全等三角形的对应边相等)说明:本题也可以用AAS 来证明三角形全等,但直接使用角平分线的性质更简单.例04.已知:如图,在ABC 中, 90C ,BC AC ,AD 是A 的平分线. 求证:AB CD AC .分析:证明AB CD AC . 可用延长的方法或截取的方法,我们用截取的方法证明本题. 在AB 上取一点E ,使AE AC ,则易证ADE ACD ,由此 得到DE CD , 90DEB ,又由 45B ,得CD BE DE . 可证明本命题,那么利用角平分线的性质,作辅助线的时候,也可作AB DE 于E ,可直接得到DE CD .证明:过D 点作AB DE 垂足为E . 则 ∵AD 为角平分线,∴DE CD (角平分线上的一点到这个角的两边的距离相等) 在ACD Rt 和AED Rt 中,)()(已证公共边DE CD AD AD )(HL AED Rt ACD Rt ,∴ AE AC (全等三角形的对应边相等) ∵ CB AC (已知), 90C (已知) ∴ 45CAB B在DEB Rt 中, 90DEB , 45B , ∴ 45B EDB . ∴CD BE DE ∵BE AE AB , ∴CD AC AB .例05.已知:如图,在ABC 中,AD 平分BAC ,AB DE 于E ,AC DF 于F .求证:EF AD .分析:欲证:EF AD ,就要证9021EOF AOE AOB 所以考虑证AFO AEO由题中条件可知AEO 、AFO 已有一边(公共边)一角对应相等,只要证AF AE 即可,所以先证明AFD AED证明:∵AD 是BAC 的平分线. AB DE ,AC DF ∴ DF DE (角平分线上的点到这个两边距离相等) 在AED Rt 和AFD Rt 中)()(公共边已证AD AD DF DE ∴)(HL AFD Rt AED Rt∴AF AE (全等三角形的对应边相等) 在AEO 和AFO 中)()()(公共边已知已证AO AO FAO EAO AF AE ∴)(SAS AFO AEO∴ AOF AOE (全等三角形对应角相等) ∴9021EOF AOE ∴ EF AD (垂直定义)例06.已知:如图,在ABC 中,BE 、CF 分别平分ABC 、ACB ,且交于点O , 求证:点O 在A 的平分线上.分析:要证点O 在A 的平分线上,只需证明点O 到A 的两边的距离相等,即证OG OH .证明:过点O 分别作三边的垂线OD 、OG 、OH ,∵AB OH DC OD ,,BO 平分ABC (已知)∴OD OH (角平分线上的点到这个角两边的距离相等) 同理OG OD , ∴OG OH∴点O 在A 的平分线上(到角两边距离相等的点在这个角的平分线上)例07.写出下列命题的逆命题,并判断真假. (1)同位角相等,两直线平行. (2)如果3 x ,那么92x(3)如果ABC 是直角三角形,那么当每个内角取一个对应外角时,三角形的三个外角只有两个钝角.(4)如果C B A ABC ,那么C B BC ,C A AC ,C B A ABC . 分析:准确理解原命题、逆命题、真命题、假命题等概念,分清题设和结论,是写出逆命题的关键,对于假命题,可以举一个反例,全面地考虑问题.解答:(1)逆命题是:两直线平行,同位角相等,它是一个真命题.(2)逆命题是:如果92x ,那3 x 它是一个假命题∵9)3(2 ,∴3 x 或3 x(3)逆命题是:如果ABC 的三个外角中只有两个钝角,那么ABC 是直角三角形. 它是一个假命题,因为ABC 还可能是钝角三角形.(4)逆命题是:如果ABC 和C B A 中,C B BC ,C A AC ,C B A ABC ,那么C B A ABC ,这是一个假命题,因为有两边及其一边的对角对应相等的两个三角形不一定是全等三角形.角的平分线例1、已知:如图1,△ABC 的角平分线BM 、CN 相交于点P.求证:点P 到三边AB 、BC 、CA 的距离相等.分析:这是证明线段相等问题,由已知利用定理不难证明.证明:(略)说明:已知、求证中都没有具体说明哪些线段是距离,证明它们相等必须标出它们,这一段话要在证明中写出,同辅助线一样处理。
初中角平分线几何题

初中角平分线几何题
下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!好了,言归正传,以下是《初中角平分线几何题》全文:
1. 已知三角形ABC中∠A=60°,求∠A的角平分线与边BC的交点到B、C 两点的距离比。
2. 已知一个角的两边长度分别为6cm和8cm,求这个角的角平分线长度。
3. 一个角的两边长度分别为5cm和7cm,求这个角的角平分线与两边的交点到顶点的距离比。
4. 已知一个圆中∠AOB=120°,求∠AOB的角平分线与圆周的交点到OA、OB两条边的距离比。
5. 已知一个直角三角形ABC中∠A=90°,∠B=45°,求AB边上两个交点到
A、B两点的距离比。
三角形-角平分线部分经典题型

1.如图1所示,在△ABC 中,∠A =90°,BD 平分∠ABC ,AD =2 cm ,则点D 到BC 的距离为________cm .图1 图22.如图2所示,在Rt ΔABC 中,∠C =90°,BD 是∠ABC 的平分线,交AC 于D ,若CD =n ,AB =m ,则ΔABD 的面积是( )A .B .C .mnD .2mn3.如图,在△ABC 中,∠C =900,BC =40,AD 是∠BAC 的平分线交BC 于D ,且DC ∶DB =3∶5,则点D 到AB 的距离是 。
4.如图,已知BD 是∠ABC 的内角平分线,CD 是∠ACB 的外角平分线,由D 出发,作点D 到BC 、AC 和AB的垂线DE 、DF 和DG ,垂足分别为E 、F 、G ,则DE 、DF 、DG 的关系是 。
5.如图,已知AB ∥CD ,O 为∠A 、∠C 的角平分线的交点,OE ⊥AC 于E ,且OE=2,则两平行线间AB 、CD 的距离等于 。
6.AD 是△BAC 的角平分线,自D 向AB 、AC 两边作垂线,垂足为E 、F ,那么下列结论中错误的是( ) A 、DE=DF B 、AE=AFC 、BD=CDD 、∠ADE=∠ADF7.到三角形三条边的距离都相等的点是这个三角形的( ) A.三条中线的交点B.三条高的交点 C.三条边的垂直平分线的交点D.三条角平分线的交点8.已知△ABC 中,∠A=80°,∠B 和∠C 的角平分线交于O 点,则∠BOC= 。
9.如图,已知相交直线AB 和CD ,及另一直线EF 。
如果要在EF 上找出与AB 、CD 距离相等的点,方法是 ,这样的点至少有 个,最多有 个。
mn 31mn 213题图DCBA10.如图所示,已知△ABC 中,∠C =90°,AC =BC ,AD 平分∠CAB ,交BC 于点D ,DE ⊥AB 于点E ,且AB =6 cm,则△DEB 的周长为( )。
初一三角形角平分线经典例题

《角平分线》经典例题在直角三角形ABC中,∠A=90°,∠ABC的平分线BE交AC于E点,过E点作ED⊥BC于D点,已知AC=10cm,ΔCDE的周长为16cm,求CD的长.〔解析〕根据角平分线上的点到角的两边的距离相等可得AE=DE,从而求出DE+CE=AC,所以ΔCDE的周长=AC+CD,根据ΔCDE的周长及AC的长即可求得CD的长.解:∵BE为∠ABC的平分线,∠A=90°,DE⊥BC,∴AE=DE,∴DE+CE=AE+CE=AC=10cm,∵ΔCDE的周长为16cm,∴DE+CE+CD=16cm,∴CD=16-10=6(cm).如图(1)所示,已知∠ADC+∠ABC=180°,DC=BC.求证点C在∠DAB的平分线上.〔解析〕作CE⊥AB,CF⊥AD,垂足分别为E,F,利用∠ADC+∠ABC=180°,∠ADC+∠CDF=180°,得出∠ABC=∠CDF,进而证得ΔCBE≌ΔCDF,得出FC=EC,即可求得结论.证明:如图(2)所示,作CE⊥AB,CF⊥AD,垂足分别为E,F,∴∠BEC=∠DFC=90°,∵∠ADC+∠ABC=180°,∠ADC+∠CDF=180°,∴∠ABC=∠CDF,在ΔCBE和ΔCDF中,∴ΔCBE≌ΔCDF(AAS),∴FC=EC,∴点C在∠DAB的平分线上.如图(1)所示,已知点P 是ΔABC 三条角平分线的交点,PD ⊥AB ,若PD =5,ΔABC 的周长为20,求ΔABC 的面积.〔解析〕作PE ⊥BC 于E ,PF ⊥AC 于F ,根据角平分线的性质定理得PE =PF =PD =5,然后根据三角形面积公式和S ΔABC =S ΔPAB +S ΔPBC +S ΔPAC 得到S ΔABC =(AB +BC +AC ),再把ΔABC 的周长为20代入计算即可.解:作PE ⊥BC 于E ,PF ⊥AC 于F ,如图(2)所示,∵点P 是ΔABC 三条角平分线的交点,∴PE =PF =PD =5,∴S ΔABC =S ΔPAB +S ΔPBC +S ΔPAC=PD ·AB +PE ·BC +PF ·AC=(AB +BC +AC )=20=50.如图(1)所示,在RtΔABC 中,∠ACB =90°,且AC =b ,BC =a ,AB =c ,∠A 与∠B 的平分线交于点O ,O 到AB 的距离为OD.试探究OD 与a ,b ,c 的数量关系.〔解析〕过点O作OE⊥AC于E,OF⊥BC于F,然后根据角平分线上的点到角的两边的距离相等可得OD=OE=OF,然后证得四边形EOFC是正方形,从而证得OE=OF=FC=EC=OD,AE=AD,BD=BF,通过AB=AC-OD+BC-OD即可求解.解:如图(2)所示,过点O作OE⊥AC于E,OF⊥BC于F,∵∠BAC,∠ABC的平分线交于点O,OD⊥AB,∴OD=OE,OD=OF,∴OD=OE=OF,∵∠ACB=90°,∴四边形EOFC是正方形,∴OE=OF=FC=EC=OD,在RtΔOAE和RtΔOAD中,∴RtΔOAE≌RtΔOAD,∴AE=AD,同理BD=BF,∴AE+EC=AD+OD=AC=b,BF+CF=BD+OD=BC=a,∴AD=b-OD,BD=a-OD,∴AD+BD=a+b-2OD,即c=a+b-2OD,∴OD=(a+b-c).。
中考:角平分线、垂直平分线经典试题
中考:角平分线、垂直平分线经典试题知识考点:了解角平分线、垂直平分线的有关性质和定理,并能解决一些实际问题。
精典例题:【例题】如图,已知在△ABC 中,AB =AC ,∠B =300,AB 的垂直平分线EF 交AB 于点E ,交BC 于点F ,求证:CF =2BF 。
分析一:要证明CF =2BF ,由于BF 与CF 没有直接联系,联想题设中EF 是中垂线,根据其性质可连结AF ,则BF =AF 。
问题转化为证CF =2AF ,又∠B =∠C =300,这就等价于要证∠CAF =900,则根据含300角的直角三角形的性质可得CF =2AF =2BF 。
分析二:要证明CF =2BF ,联想∠B =300,EF 是AB 的中垂线,可过点A 作AG ∥EF 交FC 于G 后,得到含300角的Rt △ABG ,且EF 是Rt △ABG 的中位线,因此BG =2BF =2AG ,再设法证明AG =GC ,即有BF =FG =GC 。
例题图1 F EC B A例题图2 G F ECB A分析三:由等腰三角形联想到“三线合一”的性质,作AD ⊥BC 于D ,则BD =CD ,考虑到∠B =300,不妨设EF =1,再用勾股定理计算便可得证。
以上三种分析的证明略。
例题图3D F ECB A问题图321ED CB A探索与创新:【问题】请阅读下面材料,并回答所提出的问题: 三角形内角平分线性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例。
如图,△ABC 中,AD 是角平分线。
求证:ACABDC BD =。
分析:要证ACABDC BD =,一般只要证BD 、DC 与AB 、AC 或BD 、AB 与DC 、AC 所在三角形相似,现在B 、D 、C 在同一条直线上,△ABD 与△ADC 不相似,需要考虑用别的方法换比。
我们注意到在比例式ACABDC BD =中,AC 恰好是BD 、DC 、AB 的第四比例项,所以考虑过C 作CE ∥AD 交BA 的延长线于E ,从而得到BD 、CD 、AB 的第四比例项AE ,这样,证明ACABDC BD =就可以转化为证AE =AC 。
角平分线的性质练习题
角平分线的性质练习题一、选择题1. 在三角形ABC中,BD是角B的平分线,若AB=5,BC=7,AC=6,那么BD的长度为:A. 4B. 6C. 8D. 无法确定2. 如果角平分线将三角形分成两个面积相等的部分,那么这两个部分的底边分别是:A. 相等B. 不相等C. 一个底边是另一个的两倍D. 底边长度无法确定3. 在三角形ABC中,角A的平分线与BC相交于点D,若AD=4,AC=8,那么AB的长度可能是:A. 6B. 8C. 10D. 12二、填空题4. 在三角形ABC中,如果角A的平分线将BC分为BD和DC两段,BD=DC,那么三角形ABD与三角形ACD的面积之比为________。
5. 若角平分线定理告诉我们,在三角形ABC中,如果BD是角B的平分线,则AB:AC=______:______。
6. 在三角形ABC中,如果角A的平分线与BC相交于点D,且AD垂直于BC,那么角B和角C的度数之和为________。
三、简答题7. 描述角平分线定理的内容,并给出一个应用此定理的几何问题。
8. 解释为什么在三角形中,角平分线可以将对边分成的两段长度与相邻两边成比例。
四、计算题9. 在三角形ABC中,已知角A的平分线AD与BC相交于点D,且BD=3,DC=4,AB=6,求AC的长度。
10. 在三角形ABC中,角B的平分线BE与AC相交于点E,已知AE=4,EC=6,AB=5,求BC的长度。
五、证明题11. 证明:在三角形ABC中,如果BD是角B的平分线,那么AB/AC = BD/DC。
12. 证明:如果点D在三角形ABC的边BC上,且AD是角A的平分线,那么三角形ABD与三角形ACD的面积相等。
六、综合题13. 在三角形ABC中,已知角A的平分线AD与BC相交于点D,且AD=2,BD=3,DC=4,AB=5,求BC的长度,并证明你的结论。
14. 给定三角形ABC,其中角A的平分线AD与BC相交于点D,角B的平分线BE与AC相交于点E。
角平分线练习题
角平分线练习题一.选择题〔共22小题〕1.如图,BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF 的长度是〔〕A.2 B.3 C.4 D.62.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=〔〕A.30° B.35° C.45° D.60°3.观察图中尺规作图痕迹,以下说法错误的选项是〔〕A.OE是∠AOB的平分线B.OC=ODC.点C、D到OE的距离不相等 D.∠AOE=∠BOE4.如图,OP是∠AOC的平分线,点B在OP上,BD⊥OC于D,∠A=45°,假设BD=2,则AB长为〔〕A.2 B.2C.2D.35.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,假设CD=2,AB=8,则△ABD的面积是〔〕A.6 B.8 C.10 D.126.如图,Rt△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,AB=10,则△ABD 的面积等于〔〕A.30 B.24 C.15 D.10=15,7.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD则CD的长为〔〕A.3 B.4 C.5 D.68.如图,BP为∠ABC的平分线,过点D作BC、BA的垂线,垂足分别为E、F,则以下结论中错误的选项是〔〕A.∠DBE=∠DBF B.DE=DF C.2DF=DB D.∠BDE=∠BDF9.如图,OA是∠BAC的平分线,OM⊥AC于点M,ON⊥AB于点N,假设ON=8cm,则OM长为〔〕A.4cm B.5cm C.8cm D.20cm10.在正方形网格中,∠AOB的位置如下图,到∠AOB两边距离相等的点应是〔〕A.M点B.N点C.P点D.Q点11.如图,直线l、l′、l″表示三条相互穿插的公路,现方案建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有〔〕A.一处B.二处C.三处D.四处12.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,假设CD=BD,点D到边AB的距离为6,则BC的长是〔〕A.6 B.12 C.18 D.2413.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有以下结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④AD平分∠CDE;其中正确的选项是〔〕个.A.1 B.2 C.3 D.414.三条公路将A、B、C三个村庄连成一个如图的三角形区域,如果在这个区域修建一个集贸市场,要使集贸市场到三条公路的距离相等,则这个集贸市场应建的位置是〔〕A.三条高线的交点B.三条中线的交点C.三条角平分线的交点D.三边垂直平分线的交点15.如图,PD⊥AB,PE⊥AC,垂足分别为D、E,且PD=PE,则△APD与△APE全等的理由是〔〕A.SAS B.AAA C.SSS D.HL16.如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.假设BC=4cm,CD=3cm,则点D到AB的距离是〔〕A.2cm B.3cm C.4cm D.5cm17.如图,OC是∠AOB的平分线,PD⊥DA于点D,PD=2,则P点到OB的距离是〔〕A.1 B.2 C.3 D.418.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,以下结论:①∠AED=90°②∠ADE=∠CDE ③DE=BE ④AD=AB+CD,四个结论中成立的是〔〕A.①②④B.①②③C.②③④D.①③19.如下图,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在〔〕A.△ABC的三条中线的交点B.△ABC三条角平分线的交点C.△ABC三条高所在直线的交点D.△ABC三边的中垂线的交点20.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则以下结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB,其中正确的有〔〕A.2个B.3个C.4个D.1个21.如图,Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AB=12,CD=3,则△DAB的面积为〔〕A.12 B.18 C.20 D.2422.如图,AD是△ABC的角平分线,DE⊥AB于点E,S=10,DE=2,AB=4,则△ABCAC长是〔〕A.9 B.8 C.7 D.6评卷人得分二.填空题〔共13小题〕=9,23.如图,BD平分∠ABC交AC于点D,DE⊥BC于点E,假设AB=5,BC=6,S△ABC则DE的长为.24.如图,OC为∠AOB的平分线,CM⊥OB,OC=5,OM=4,则点C到射线OA的距离为.25.如图,△ABC的周长是32,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=6,△ABC的面积是.26.如图,△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是.27.如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为.28.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,CD=16,则D到AB 边的距离是.29.如图,在△ABC中,∠BAC=60°,AD平分∠BAC,假设AD=6,DE⊥AB,则DE 的长为.30.如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有处.31.如图,点O在△ABC,且到三边的距离相等,假设∠A=60°,则∠BOC=.32.如图,在Rt△ABC中,∠B=90°,CD是∠ACD的平分线,假设BD=2,AC=8,则△ACD的面积为.33.如图,BD⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF=.34.把命题“角平分线上的点到这个角两边的距离相等〞改写成“如果…,则…、〞的形式:如果,则.35.Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,假设BC=32,且BD:CD=9:7,则D到AB的距离为.评卷人得分三.解答题〔共5小题〕36.如图,DE⊥AB于E,DF⊥AC于F,假设BD=CD、BE=CF.〔1〕求证:AD平分∠BAC;〔2〕直接写出AB+AC与AE之间的等量关系.37.如图:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:〔1〕∠ECD=∠EDC;〔2〕OE是CD的垂直平分线.38.如图,四边形ABCD中,AC为∠BAD的角平分线,AB=AD,E、F两点分别在AB、AD上,且AE=DF.请完整说明为何四边形AECF的面积为四边形ABCD的一半.39.△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作一直线交AB、AC于E、F.且BE=EO.〔1〕说明OF与CF的大小关系;〔2〕假设BC=12cm,点O到AB的距离为4cm,求△OBC的面积.40.如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.〔1〕求证:AC=AE;〔2〕假设点E为AB的中点,CD=4,求BE的长.2018年09月23日tcq372的初中数学组卷参考答案与试题解析一.选择题〔共22小题〕1.如图,BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=6,则DF 的长度是〔〕A.2 B.3 C.4 D.6【解答】解:∵BG是∠ABC的平分线,DE⊥AB,DF⊥BC,∴DE=DF=6,应选:D.2.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=〔〕A.30° B.35° C.45° D.60°【解答】解:作MN⊥AD于N,∵∠B=∠C=90°,∴AB∥CD,∴∠DAB=180°﹣∠ADC=70°,∵DM平分∠ADC,MN⊥AD,MC⊥CD,∴MN=MC,∵M是BC的中点,∴MC=MB,∴MN=MB,又MN⊥AD,MB⊥AB,∴∠MAB=∠DAB=35°,应选:B.3.观察图中尺规作图痕迹,以下说法错误的选项是〔〕A.OE是∠AOB的平分线B.OC=ODC.点C、D到OE的距离不相等 D.∠AOE=∠BOE【解答】解:根据尺规作图的画法可知:OE是∠AOB的角平分线.A、OE是∠AOB的平分线,A正确;B、OC=OD,B正确;C、点C、D到OE的距离相等,C不正确;D、∠AOE=∠BOE,D正确.应选:C.4.如图,OP是∠AOC的平分线,点B在OP上,BD⊥OC于D,∠A=45°,假设BD=2,则AB长为〔〕A.2 B.2C.2D.3【解答】解:如图,过B点作BE⊥OA于E,∵OP是∠AOC的平分线,点B在OP上,BD⊥OC于D,BD=2,∴BE=BD=2,在直角△ABE中,∵∠AEB=90°,∠A=45°,∴AB=BE=2.应选:C.5.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线,假设CD=2,AB=8,则△ABD的面积是〔〕A.6 B.8 C.10 D.12【解答】解:如图,过点D作DE⊥AB于E,∵AB=8,CD=2,∵AD是∠BAC的角平分线,∠C=90°,∴DE=CD=2,∴△ABD的面积=AB•DE=×8×2=8.应选:B.6.如图,Rt△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,AB=10,则△ABD 的面积等于〔〕A.30 B.24 C.15 D.10【解答】解:如图,过D作DE⊥AB于E,∵AD平分∠BAC,∠C=90°,∴DE=DC=3,∵AB=10,∴△ABD的面积=AB•DE=×10×3=15.应选:C.=15,7.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD则CD的长为〔〕A.3 B.4 C.5 D.6【解答】解:如图,过点D作DE⊥AB于E,∵∠C=90°,AD平分∠BAC,∴DE=CD,∴S=AB•DE=×10•DE=15,△ABD解得DE=3.应选:A.8.如图,BP为∠ABC的平分线,过点D作BC、BA的垂线,垂足分别为E、F,则以下结论中错误的选项是〔〕A.∠DBE=∠DBF B.DE=DF C.2DF=DB D.∠BDE=∠BDF【解答】解:∵BP为∠ABC的平分线,DE⊥AC,DF⊥AB,∴DE=DF,B正确,不符合题意;在Rt△DBE和Rt△DBF中,,∴Rt△DBE≌Rt△DBF,∴∠DBE=∠DBF,∠BDE=∠BDF,A、D正确,不符合题意,2DF不一定等于DB,C错误,符合题意,应选:C.9.如图,OA是∠BAC的平分线,OM⊥AC于点M,ON⊥AB于点N,假设ON=8cm,则OM长为〔〕A.4cm B.5cm C.8cm D.20cm【解答】解:∵OA是∠BAC的平分线,OM⊥AC,ON⊥AB,∴OM=ON=8cm,应选:C.10.在正方形网格中,∠AOB的位置如下图,到∠AOB两边距离相等的点应是〔〕A.M点B.N点C.P点D.Q点【解答】解:从图上可以看出点M在∠AOB的平分线上,其它三点不在∠AOB的平分线上.所以点M到∠AOB两边的距离相等.应选A.11.如图,直线l、l′、l″表示三条相互穿插的公路,现方案建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有〔〕A.一处B.二处C.三处D.四处【解答】解:如下图,加油站站的地址有四处.应选:D.12.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,假设CD=BD,点D到边AB的距离为6,则BC的长是〔〕A.6 B.12 C.18 D.24【解答】解:过D作DE⊥AB于E,∵点D到边AB的距离为6,∴DE=6,∵∠C=90°,AD平分∠BAC,DE⊥AB,∴CD=DE=6,∵CD=DB,∴DB=12,∴BC=6+12=18,应选:C.13.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有以下结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④AD平分∠CDE;其中正确的选项是〔〕个.A.1 B.2 C.3 D.4【解答】解:∵∠C=90°,AD平分∠BAC,DE⊥AB,∴CD=DE,故①正确;在Rt△ACD和Rt△AED中,,∴Rt△ACD≌Rt△AED〔HL〕,∴AC=AE,∠ADC=∠ADE,∴AC+BE=AE+BE=AB,故②正确;AD平分∠CDE,故④正确;∵∠B+∠BAC=90°,∠B+∠BDE=90°,∴∠BDE=∠BAC,故③正确;综上所述,结论正确的选项是①②③④共4个.应选:D.14.三条公路将A、B、C三个村庄连成一个如图的三角形区域,如果在这个区域修建一个集贸市场,要使集贸市场到三条公路的距离相等,则这个集贸市场应建的位置是〔〕A.三条高线的交点B.三条中线的交点C.三条角平分线的交点D.三边垂直平分线的交点【解答】解:在这个区域修建一个集贸市场,要使集贸市场到三条公路的距离相等,根据角平分线的性质,集贸市场应建在∠A、∠B、∠C的角平分线的交点处.应选:C.15.如图,PD⊥AB,PE⊥AC,垂足分别为D、E,且PD=PE,则△APD与△APE全等的理由是〔〕A.SAS B.AAA C.SSS D.HL【解答】解:∵PD⊥AB,PE⊥AC,∴∠ADP=∠AEP=90°,在Rt△ADP和△AEP中,∴Rt△ADP≌△AEP〔HL〕,应选:D.16.如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.假设BC=4cm,CD=3cm,则点D到AB的距离是〔〕A.2cm B.3cm C.4cm D.5cm【解答】解:过D作DE⊥AB于E,∵在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,∴DE=DC=3cm,应选:B.17.如图,OC是∠AOB的平分线,PD⊥DA于点D,PD=2,则P点到OB的距离是〔〕A.1 B.2 C.3 D.4【解答】解:如图,过点P作PE⊥OB,∵OC是∠AOB的平分线,点P在OC上,且PD⊥OA,PE⊥OB,∴PE=PD,又PD=2,∴PE=PD=2.应选:B.18.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,以下结论:①∠AED=90°②∠ADE=∠CDE ③DE=BE ④AD=AB+CD,四个结论中成立的是〔〕A.①②④B.①②③C.②③④D.①③【解答】解:过E作EF⊥AD于F,如图,∵AB⊥BC,AE平分∠BAD,∴Rt△AEF≌Rt△AEB∴BE=EF,AB=AF,∠AEF=∠AEB;而点E是BC的中点,∴EC=EF=BE,所以③错误;∴Rt△EFD≌Rt△ECD,∴DC=DF,∠FDE=∠CDE,所以②正确;∴AD=AF+FD=AB+DC,所以④正确;∴∠AED=∠AEF+∠FED=∠BEC=90°,所以①正确.应选:A.19.如下图,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在〔〕A.△ABC的三条中线的交点B.△ABC三条角平分线的交点C.△ABC三条高所在直线的交点D.△ABC三边的中垂线的交点【解答】解:∵凉亭到草坪三条边的距离相等,∴凉亭选择△ABC三条角平分线的交点.应选:B.20.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则以下结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB,其中正确的有〔〕A.2个B.3个C.4个D.1个【解答】解:∵AD平分∠BAC∴∠DAC=∠DAE∵∠C=90°,DE⊥AB∴∠C=∠E=90°∵AD=AD∴△DAC≌△DAE∴∠CDA=∠EDA∴①AD平分∠CDE正确;无法证明∠BDE=60°,∴③DE平分∠ADB错误;∵BE+AE=AB,AE=AC∴BE+AC=AB∴④BE+AC=AB正确;∵∠BDE=90°﹣∠B,∠BAC=90°﹣∠B∴∠BDE=∠BAC∴②∠BAC=∠BDE正确.应选:B.21.如图,Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AB=12,CD=3,则△DAB的面积为〔〕A.12 B.18 C.20 D.24【解答】解:过D作DE⊥AB,∵Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,∴DE=DC=3,∴△DAB的面积=,应选:B.=10,DE=2,AB=4,则22.如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABCAC长是〔〕A.9 B.8 C.7 D.6【解答】解:过D作DF⊥AC于F,∵AD是△ABC的角平分线,DE⊥AB,∴DE=DF=2,=AB×DE=×4×2=4,∵S△ADB∵△ABC的面积为10,∴△ADC的面积为10﹣4=6,∴AC×DF=6,∴AC×2=6,∴AC=6应选:D.二.填空题〔共13小题〕23.如图,BD平分∠ABC交AC于点D,DE⊥BC于点E,假设AB=5,BC=6,S=9,△ABC则DE的长为.【解答】解:作DF⊥AB于F,∵BD平分∠ABC,DE⊥BC,DF⊥AB,∴DE=DF,,即×5×DE+×6×DE=9,∴×AB×DF+×BC×DE=S△ABC解得,DE=,故答案为:.24.如图,OC为∠AOB的平分线,CM⊥OB,OC=5,OM=4,则点C到射线OA的距离为 3 .【解答】解:过C作CF⊥AO,∵OC为∠AOB的平分线,CM⊥OB,∴CM=CF,∵OC=5,OM=4,∴CM=3,∴CF=3,故答案为:3.25.如图,△ABC的周长是32,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=6,△ABC的面积是96 .【解答】解:过O作OM⊥AB,ON⊥AC,连接AO,∵OB,OC分别平分∠ABC和∠ACB,∴OM=ON=OD=6,∴△ABC的面积为:×AB×OM+BC×DO+NO=〔AB+BC+AC〕×DO=32×6=96.故答案为:96.26.如图,△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是42 .【解答】解:过O作OE⊥AB于E,OF⊥AC于F,连接OA,∵OB,OC分别平分∠ABC和∠ACB,OD⊥BC,∴OE=OD,OD=OF,即OE=OF=OD=4,∴△ABC的面积是:S△AOB +S△AOC+S△OBC=×AB×OE+×AC×OF+×BC×OD=×4×〔AB+AC+BC〕=×4×21=42,故答案为:42.27.如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为4cm .【解答】解:∵BC=10cm,BD:DC=3:2,∴DC=4cm,∵AD是△ABC的角平分线,∠ACB=90°,∴点D到AB的距离等于DC,即点D到AB的距离等于4cm.故答案为4cm.28.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,CD=16,则D到AB 边的距离是16 .【解答】解:过D作DE⊥AB于E,则DE的长度就是D到AB边的距离.∵AD平分∠CAB,∠ACD=90°,DE⊥AB,∴DC=DE=16〔角平分线性质〕,故答案为:16.29.如图,在△ABC中,∠BAC=60°,AD平分∠BAC,假设AD=6,DE⊥AB,则DE的长为 3 .【解答】解:∵∠BAC=60°,AD平分∠BAC,∴∠DAE=∠BAC=30°.在Rt△ADE中,DE⊥AB,∠DAE=30°,∴DE=AD=3.故答案为:3.30.如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 4 处.【解答】解:∵△ABC角平分线的交点到三角形三边的距离相等,∴△ABC角平分线的交点满足条件;如图:点P是△ABC两条外角平分线的交点,过点P作PE⊥AB,PD⊥BC,PF⊥AC,∴PE=PF,PF=PD,∴PE=PF=PD,∴点P到△ABC的三边的距离相等,∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;综上,到三条公路的距离相等的点有4个,∴可供选择的地址有4个.故答案为:4.31.如图,点O在△ABC,且到三边的距离相等,假设∠A=60°,则∠BOC= 120°.【解答】解:∵点O在△ABC,且到三边的距离相等,∴点O是三个角的平分线的交点,∴∠OBC+∠OCB=〔∠ABC+∠ACB〕=〔180°﹣∠A〕=〔180°﹣60°〕=60°,在△BCO中,∠BOC=180°﹣〔∠OBC+∠OCB〕=180°﹣60°=120°.故答案为:120°.32.如图,在Rt△ABC中,∠B=90°,CD是∠ACD的平分线,假设BD=2,AC=8,则△ACD的面积为8 .【解答】解:作DH⊥AC于H,∵CD是∠ACD的平分线,∠B=90°,DH⊥AC,∴DH=DB=2,∴△ACD的面积=×AC×DH=×8×2=8,故答案为:8.33.如图,BD⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF= 150°.【解答】解:∵BD⊥AE于B,DC⊥AF于C,且DB=DC,∴AD是∠BAC的平分线,∵∠BAC=40°,∴∠CAD=∠BAC=20°,∴∠DGF=∠CAD+∠ADG=20°+130°=150°.故答案为:150°34.把命题“角平分线上的点到这个角两边的距离相等〞改写成“如果…,则…、〞的形式:如果一个点在角的平分线上,则它到这个角两边的距离相等.【解答】解:如果一个点在角平分线上,则它到角两边的距离相等.35.Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,假设BC=32,且BD:CD=9:7,则D到AB的距离为14 .【解答】解:如图,过点D作DE⊥AB于E,∵BC=32,BD:CD=9:7,∴CD=32×=14,∵∠C=90°,AD平分∠BAC,∴DE=CD=14,即D到AB的距离为14.故答案为:14.三.解答题〔共5小题〕36.如图,DE⊥AB于E,DF⊥AC于F,假设BD=CD、BE=CF.〔1〕求证:AD平分∠BAC;〔2〕直接写出AB+AC与AE之间的等量关系.【解答】〔1〕证明:∵DE⊥AB于E,DF⊥AC于F,∴∠E=∠DFC=90°,∴△BDE与△CDE均为直角三角形,∵∴△BDE≌△CDF,∴DE=DF,即AD平分∠BAC;〔2〕AB+AC=2AE.证明:∵BE=CF,AD平分∠BAC,∴∠EAD=∠CAD,∵∠E=∠AFD=90°,∴∠ADE=∠ADF,在△AED与△AFD中,∵,∴△AED≌△AFD,∴AE=AF,∴AB+AC=AE﹣BE+AF+CF=AE+AE=2AE.37.如图:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:〔1〕∠ECD=∠EDC;〔2〕OE是CD的垂直平分线.【解答】证明:〔1〕∵E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,∴EC=DE,∴∠ECD=∠EDC;〔2〕在Rt△OCE和Rt△ODE中,,∴Rt△OCE≌Rt△ODE〔HL〕,∴OC=OD,又∵OE是∠AOB的平分线,∴OE是CD的垂直平分线.38.如图,四边形ABCD中,AC为∠BAD的角平分线,AB=AD,E、F两点分别在AB、AD上,且AE=DF.请完整说明为何四边形AECF的面积为四边形ABCD的一半.【解答】解:分别作CG⊥AB与G,CH⊥AD与H,∵AC为∠BAD的角平分线,∴CG=CH,∵AB=AD,∴△ABC面积=△ACD面积,又∵AE=DF,∴△AEC面积=△CDF面积,∴△BCE面积=△ABC面积﹣△AEC面积,△BCE面积=△ACD面积﹣△CDF面积,∴△BCE面积=△ACF面积,∵四边形AECF面积=△AEC面积+△ACF面积,四边形AECF面积=△AEC面积+△BCE面积,∴四边形AECF面积=△ABC面积,又∵四边形ABCD面积=△ABC面积+△ACD面积,又∵四边形ABCD面积=2△ABC面积,∴四边形AECF面积为四边形ABCD面积的一半.39.△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作一直线交AB、AC于E、F.且BE=EO.〔1〕说明OF与CF的大小关系;〔2〕假设BC=12cm,点O到AB的距离为4cm,求△OBC的面积.【解答】解:〔1〕OF=CF.理由:∵BE=EO,∴∠EBO=∠EOB,∵△ABC中,∠ABC与∠ACB的平分线交于点O,∴∠EBO=∠OBC,∴∠EOB=∠OBC,∴EF∥BC,∴∠FOC=∠OCB=∠OCF,∴OF=CF;〔2〕过点O作OM⊥BC于M,作ON⊥AB于N,∵△ABC中,∠ABC与∠ACB的平分线交于点O,点O到AB的距离为4cm,∴ON=OM=4cm,=BC•OM=×12×4=24〔cm2〕.∴S△OBC40.如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.〔1〕求证:AC=AE;〔2〕假设点E为AB的中点,CD=4,求BE的长.【解答】〔1〕证明:∵在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB,∴CD=DE,∠AED=∠C=90°,∠CAD=∠EAD,在△ACD和△AED中∴△ACD≌△AED,∴AC=AE;〔2〕解:∵DE⊥AB,点E为AB的中点,∴AD=BD,∴∠B=∠DAB=∠CAD,∵∠C=90°,∴3∠B=90°,.∴∠B=30°,∵CD=DE=4,∠DEB=90°,∴BD=2DE=8,由勾股定理得:BE==4.。
实用文库汇编之三角形 角平分线部分经典题型
*实用文库汇编之1.如图1所示,在△ABC中,∠A =90°,BD平分∠ABC,AD=2 cm,则点D到BC的距离为________cm.*图1图22.如图2所示,在RtΔABC中,∠C=90°,BD是∠ABC的平分线,交AC于D,若CD=n,AB=m,则ΔABD的面积是()A.mn31B.mn21C.mn D.2mn3.如图,在△ABC中,∠C=900,BC=40,AD是∠BAC的平分线交BC于D,且DC∶DB=3∶5,则点D到AB的距离是。
4.如图,已知BD是∠ABC的内角平分线,CD是∠ACB的外角平分线,由D出发,作点D到BC、AC和AB 的垂线DE、DF和DG,垂足分别为E、F、G,则DE、DF、DG的关系是。
5.如图,已知AB∥CD,O为∠A、∠C的角平分线的交点,OE⊥AC于E,且OE=2,则两平行线间AB、CD的距离等于。
6.AD是△BAC的角平分线,自D向AB、AC两边作垂线,垂足为E、F,那么下列结论中错误的是( )A、DE=DFB、AE=AFC、BD=CDD、∠ADE=∠ADF7.到三角形三条边的距离都相等的点是这个三角形的()A.三条中线的交点B.三条高的交点C.三条边的垂直平分线的交点D.三条角平分线的交点8.已知△ABC中,∠A=80°,∠B和∠C的角平分线交于O点,则∠BOC= 。
9.如图,已知相交直线AB和CD,及另一直线EF。
如果要在EF上找出与AB、CD距离相等的点,方法是,这样的点至少有个,最多有个。
第3题图DC BA10.如图所示,已知△ABC 中,∠C =90°,AC =BC ,AD 平分∠CAB ,交BC 于点D ,DE ⊥AB 于点E ,且AB =6 cm,则△DEB 的周长为( )。
A.9 cm B.5 cm C.6 cm D.不能确定11.如图,AB //CD ,CE 平分∠ACD ,若∠1=250,那么∠2的度数是 .12.如图,OP 平分AOB ∠,PA OA ⊥,PB OB ⊥,垂足分别为A ,B .下列结论中不一定成立的是( )A .PA PB = B .PO 平分APB ∠C .OA OB =D .AB 垂直平分OP13.如图,已知AC ∥BD 、EA 、EB 分别平分∠CAB 和∠ABD ,CD 过点E ,则AB 与AC+BD•相等吗?说明理由.14、如图所示,已知AD 为等腰三角形ABC 的底角的平分线,∠C =90° 求证:AB =AC +CD .15、如图,在四边形ABCD 中,BC>BA ,AD=DC,BD 平分∠ABC,求证:∠A+∠C=180°D16、如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE. 求证:△ACD≌△CBE.17.已知:如图,△ABC中,∠C=90°,试在AC上找一点P,使P到斜边的距离等于PC.(画出图形,并写出画法)18.已知:OD平分∠POQ,在OP、OQ边上取OA=OB,CM⊥AD于M,CN⊥BD于N.求证:CM=CN.19.已知:如图,ΔABC的外角∠CBD和∠BCE的平分线BF、CF交于点F.求证:一点F必在∠DAE的平分线上.20.已知:如图,A、B、C、D四点在∠MON的边上,AB=CD,P为∠MON内一点,并且△PAB的面积与△PCD的面积相等.求证:射线OP是∠MON的平分线.ABCDE21.如图,ΔABC中,∠C=90°,BD平分∠ABC,DE⊥AB于E,若△BCD与△BCA的面积比为3∶8,求△ADE与△BCA的面积之比.22.已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)求证:AM平分∠DAB;(2)猜想AM与DM的位置关系如何?并证明你的结论.23.已知:如图,在ΔABC中,AD是△ABC的角平分线,E、F分别是AB、AC上一点,并且有∠EDF +∠EAF=180°.试判断DE和DF的大小关系并说明理由.24.如图1所示:AM∥DN,AE、DE分别平分∠MAD和∠AND,并交于E点.过点E的直线分别交AM、DN于B、C.(1)如图2,当点B、C分别位于点AD的同侧时,猜想AD、AB、CD之间的存在的数量关系:_______________________________.(2)试证明你的猜想.(3)若点B、C分别位于点AD的两侧时,试写出AD、AB、CD之间的关系,并选择一个写出证明过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.如图1所示,在△ABC 中,∠A =90°,BD 平分∠ABC ,AD =2 cm ,则点D 到BC 的距离为________cm . 图1 图2
2.如图2所示,在Rt ΔABC 中,∠C =90°,BD 是∠ABC 的平分线,交AC 于D ,若CD =n ,AB =m ,则ΔABD 的面积是( )
A .
B .
C .mn
D .2mn
3.如图,在△ABC 中,∠C =900,BC =40,AD 是∠BAC 的平分线交BC 于D ,且DC ∶DB =3∶5,则点D 到AB 的距离是 。
4.如图,已知BD 是∠ABC 的内角平分线,CD 是∠ACB 的外角平分线,由D 出发,作点D 到BC 、AC 和AB 的垂线DE 、DF 和DG ,垂足分别为E 、F 、G ,则DE 、DF 、DG 的关系是 。
5.如图,已知AB ∥CD ,O 为∠A 、∠C 的角平分线的交点,OE ⊥AC 于E ,且OE=2,则两平行线间AB 、CD 的距离等于 。
是△BAC 的角平分线,自D 向AB 、AC 两边作垂线,垂足为E 、F ,那么下列结论中错误的是( )
A 、DE=DF
B 、AE=AF
C 、BD=C
D D 、∠ADE=∠ADF
7.到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点
B.三条高的交点 C.三条边的垂直平分线的交点
D.三条角平分线的交点 8.已知△ABC 中,∠A=80°,∠B 和∠C 的角平分线交于O 点,则∠BOC= 。
9.如图,已知相交直线AB 和CD ,及另一直线EF 。
如果要在EF 上找出与AB 、CD 距离相等的点,方法是 ,这样的点至少有 个,最多有 个。
10.如图所示,已知△ABC 中,∠C =90°,AC =BC ,AD 平分∠CAB ,交BC 于点D ,DE ⊥AB 于点E ,且AB =6 cm,则△DEB 的周长为( )。
cm
cm cm D.不能确定
11.如图,AB
12.如图,OP 平分AOB ∠,PA OA ⊥,PB OB ⊥,垂足分别为A ,B .下列结论中不一定成立的是( )
A .PA P
B = B .PO 平分APB ∠
C .OA OB =
D .AB 垂直平分OP
13.如图,已知AC ∥BD 、EA 、EB 分别平分∠CAB 和∠ABD ,CD 过点E ,则AB 与AC+BD•相等吗?说明理由. O
B
A P
14、如图所示,已知AD为等腰三角形ABC的底角的平分线,∠C=90°
求证:AB=AC+CD.
15、如图,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC,求证:∠A+∠C=180°
16、如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE. 求证:△ACD≌△CBE.
17.已知:如图,△ABC中,∠C=90°,试在AC上找一点P,使P到斜边的距离等于PC.(画出图形,并写出画法)
18.已知:OD平分∠POQ,在OP、OQ边上取OA=OB, CM⊥AD于M,CN⊥BD于N.
求证:CM=CN.
19.已知:如图,ΔABC的外角∠CBD和∠BCE的平分线BF、CF交于点F.
求证:一点F必在∠DAE的平分线上.
20.已知:如图,A、B、C、D四点在∠MON的边上,AB=CD,P为∠MON内一点,并且△PAB的面积与△PCD 的面积相等.求证:射线OP是∠MON的平分线.
21.如图,ΔABC中,∠C=90°,BD平分∠ABC,DE⊥AB于E,若△BCD与△BCA的面积比为3∶8,求△ADE与△BCA的面积之比.
22.已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
(1)求证:AM 平分∠DAB ;
(2)猜想AM 与DM 的位置关系如何?并证明你的结论.
23.已知:如图,在ΔABC 中,AD 是△ABC 的角平分线,E 、F 分别是AB 、AC 上一点,并且有∠EDF +∠EAF =180°.试判断DE 和DF 的大小关系并说明理由.
24.如图1所示:AM ∥DN ,AE 、DE 分别平分∠MAD 和∠AND ,并交于E 点.
过点E 的直线分别交AM 、DN 于B 、C.
(1)如图2,当点B 、C 分别位于点AD 的同侧时,猜想AD 、AB 、CD 之间的存在的数量关系:_______________________________.
(2)试证明你的猜想.
(3)若点B 、C 分别位于点AD 的两侧时,试写出AD 、AB 、CD 之间的关系,并选择一个写出证明过程。
25.已知:在平面直角坐标系中,△ABC 的顶点A 、C 分别在y 轴、x 轴上,且∠ACB=90°,AC=BC.
(1)如图1,当(0,2),(1,0)A C -,点B 在第四象限时,则点B 的坐标为 ;
(2)如图2,当点C 在x 轴正半轴上运动,点A 在y 轴
正半轴上运动,点B 在第四象限时,作BD ⊥y 轴于点D , 试判断OA BD OC +与OA
BD OC -哪一个是定值, 并说明定值是多少?请证明你的结论.
结论:
证明:
26.如图,△ABC 中,∠ABC=42°,D 是BC 边上一点,DC=AB ,且∠DAB=27°。
(1)△ABC 是____________ 三角形;
(2)证明你的结论。
27.在ABC △中,AB AC =,点D 是直线BC 上一点(不与B C 、重合),以AD 为一边在AD 的右侧..
作图2
ADE △,使AD AE DAE BAC =∠=∠,,连接CE .
(1)如图1,当点D 在线段BC 上,如果90BAC ∠=°,则BCE ∠= 度;
(2)设BAC α∠=,BCE β∠=.
①如图2,当点D 在线段BC 上移动,则αβ,之间有怎样的数量关系?请说明理由;
②当点D 在直线BC 上移动,则αβ,之间有怎样的数量关系?请直接写出你的结论.
28.已知:如图,在△ABC 中,AB=AC ,∠BAC=α,且60°<α<120°.P 为△ABC 内部一点,且PC=AC ,∠PCA=120°—α.
(1)用含α的代数式表示∠APC ,得∠APC =_______________________;
(2)求证:∠BAP=∠PCB ;
(3)求∠PBC 的度数.
证明:(2)。
