二次函数中的相似三角形问题
二次函数与相似三角形问题(含答案 完美打印版)

综合题讲解 函数中因动点产生的相似三角形问题例题 如图1,已知抛物线的顶点为A (2,1),且经过原点O ,与x 轴的另一个交点为B 。
⑴求抛物线的解析式;(用顶点式...求得抛物线的解析式为x x 41y 2+-=) ⑵若点C 在抛物线的对称轴上,点D 在抛物线上,且以O 、C 、D 、B 四点为顶点的四边形为平行四边形,求D 点的坐标;⑶连接OA 、AB ,如图2,在x 轴下方的抛物线上是否存在点P ,使得△OBP 与△OAB 相似若存在,求出P 点的坐标;若不存在,说明理由。
分析:1.当给出四边形的两个顶点时应以两个顶点的连线.......为四边形的边和对角线来考虑问题以O 、C 、D 、B 四点为顶点的四边形为平行四边形要分类讨论:按OB 为边和对角线两种情况2. 函数中因动点产生的相似三角形问题一般有三个解题途径① 求相似三角形的第三个顶点时,先要分析已知三角形的边.和角.的特点,进而得出已知三角形是否为特殊三角形。
根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解。
y xEQ PC B OA 例题2:如图,已知抛物线y=ax 2+4ax+t (a >0)交x 轴于A 、B 两点,交y 轴于点C ,抛物线的对称轴交x 轴于点E ,点B 的坐标为(-1,0). (1)求抛物线的对称轴及点A 的坐标;(2)过点C 作x 轴的平行线交抛物线的对称轴于点P ,你能判断四边形ABCP 是什么四边形并证明你的结论;(3)连接CA 与抛物线的对称轴交于点D ,当∠APD=∠ACP 时,求抛物线的解析式.练习1、已知抛物线2y ax bx c =++经过5330P E ⎫⎪⎪⎝⎭,,,及原点(00)O ,.(1)求抛物线的解析式.(由一般式...得抛物线的解析式为225333y x x =-+) (2)过P 点作平行于x 轴的直线PC 交y 轴于C 点,在抛物线对称轴右侧且位于直线PC 下方的抛物线上,任取一点Q ,过点Q 作直线QA 平行于y 轴交x 轴于A 点,交直线PC 于B 点,直线QA 与直线PC 及两坐标轴围成矩形OABC .是否存在点Q ,使得OPC △与PQB △相似若存在,求出Q 点的坐标;若不存在,说明理由.(3)如果符合(2)中的Q 点在x 轴的上方,连结OQ ,矩形OABC 内的四个三角形OPC PQB OQP OQA ,,,△△△△之间存在怎样的关系为什么练习2、如图,四边形OABC 是一张放在平面直角坐标系中的矩形纸片,点A 在x 轴上,点C 在y 轴上,将边BC 折叠,使点B 落在边OA 的点D处。
二次函数中三角形问题(含问题详解)

二次函数中的三角形一.与三角形面积例1:如图,已知在同一坐标系中,直线22k y kx =+-与y 轴交于点P ,抛物线k x k x y 4)1(22++-=与x 轴交于)0,(),0,(21x B x A 两点。
C 是抛物线的顶点。
(1)求二次函数的最小值(用含k 的代数式表示); (2)若点A 在点B 的左侧,且021<⋅x x 。
①当k 取何值时,直线通过点B ;②是否存在实数k ,使ABC ABP S S ∆∆=?如果存在,请求出此时抛物线的解析式;如果不存在,请说明理由。
例2:已知抛物线)1(3)4(2-+---=m x m x y 与x 轴交于A 、B 两点,与y 轴交于C 点, (1)求m 的取值范围;(2)若0<m ,直线1-=kx y 经过点A ,与y 轴交于点D ,且25=⋅BD AD ,求抛物线的解析式; (3)若A 点在B 点左边,在第一象限内,(2)中所得的抛物线上是否存在一点P ,使直线P A 平分ACD ∆的面积?若存在,求出P 点的坐标;若不存在,请说明理由。
例3.已知矩形ABCD 中,AB =2,AD =4,以AB 的垂直平分线为x 轴,AB 所在的直线为y 轴,建立平面直角坐标系(如图)。
(1)写出A 、B 、C 、D 及AD 的中点E 的坐标;(2)求以E 为顶点、对称轴平行于y 轴,并且经过点B 、C 的抛物线的解析式; (3)求对角线BD 与上述抛物线除点B 以外的另一交点P 的坐标;(4)△PEB 的面积S △PEB 与△PBC 的面积S △PBC 具有怎样的关系?证明你的结论。
A BC DO E x y(第25题图)例4.如图1,已知直线12y x =-与抛物线2164y x =-+交于AB ,两点. (1)求A B ,两点的坐标;(2)求线段AB 的垂直平分线的解析式;(3)如图2,取与线段AB 等长的一根橡皮筋,端点分别固定在A B ,两处.用铅笔拉着这根橡皮筋使笔尖P 在直线AB 上方的抛物线上移动,动点P 将与A B ,构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P 点的坐标;如果不存在,请简要说明理由.二.与三角形形状例5. 如图,抛物线254y ax ax =-+经过ABC △的三个顶点,已知BC x ∥轴,点A 在x 轴上,点C 在y 轴上,且AC BC =.(1)求抛物线的对称轴;(2)写出A B C ,,三点的坐标并求抛物线的解析式;(3)探究:若点P 是抛物线对称轴上且在x 轴下方的动点,是否存在PAB △是等腰三角形.若存在,求出所有符合条件的点P 坐标;不存在,请说明理由.图2图1例 6.如图①,在平面直角坐标系中,点A 的坐标为(12),,点B 的坐标为(31),,二次函数2y x =的图象记为抛物线1l .(1)平移抛物线1l ,使平移后的抛物线过点A ,但不过点B ,写出平移后的一个抛物线的函数表达式: (任写一个即可).(2)平移抛物线1l ,使平移后的抛物线过A B ,两点,记为抛物线2l ,如图②,求抛物线2l 的函数表达式.(3)设抛物线2l 的顶点为C ,K 为y 轴上一点.若ABK ABC S S =△△,求点K 的坐标.(4)请在图③上用尺规作图的方式探究抛物线2l 上是否存在点P ,使ABP △为等腰三角形.若存在,请判断点P 共有几个可能的位置(保留作图痕迹);若不存在,请说明师.x 图①x 图②x 图③例7. 已知:如图,抛物线2y ax bx c =++经过(1,0)A 、(5,0)B 、(0,5)C 三点. (1)求抛物线的函数关系式;(2)若过点C 的直线y kx b =+与抛物线相交于点E (4,m ),请求出△CBE 的面积S 的值; (3)在抛物线上求一点0P 使得△ABP 0为等腰三角形并写出0P 点的坐标;(4)除(3)中所求的0P 点外,在抛物线上是否还存在其它的点P 使得△ABP 为等腰三角形?若存在,请求出一共有几个满足条件的点P (要求简要说明理由,但不证明);若不存在这样的点P ,请说明理由.例8.如图,在直角坐标系中,点A 的坐标为(-2,0),连接OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB . (1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式; (3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由;(4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方, 那么△P AB 是否有最大面积?若有,求出此时P 点的坐标及△P AB 的最大面积;若没有,请说明理由.(注意:本题中的结果均保留根号)(第25题图)三.二次函数与三角形相似 例9:已知一次函数1243--=x y 的图象分别交x 轴、y 轴于A 、C 两点, (1)求出A 、C 两点的坐标;(2)在x 轴上找出点B ,使ACB ∆∽AOC ∆,若抛物线过A 、B 、C 三点,求出此抛物线的解析式; (3)在(2)的条件下,设动点P 、Q 分别从A 、B 两点同时出发,以相同速度沿AC 、BA 向C 、A 运动,连结PQ ,使m AP =,是否存在m 的值,使以A 、P 、Q 为顶点的三角形与ABC ∆相似,若存在,求出所有m 的值;若不存在,请说明理由。
中考数学压轴题:二次函数综合、相似三角形存在性问题
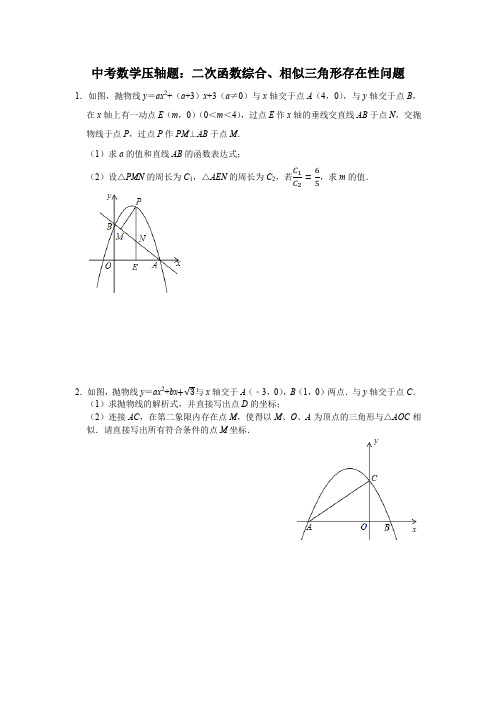
中考数学压轴题:二次函数综合、相似三角形存在性问题1.如图,抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.(1)求a的值和直线AB的函数表达式;(2)设△PMN的周长为C1,△AEN的周长为C2,若C1C2=65,求m的值.2.如图,抛物线y=ax2+bx+√3与x轴交于A(﹣3,0),B(1,0)两点.与y轴交于点C.(1)求抛物线的解析式,并直接写出点D的坐标;(2)连接AC,在第二象限内存在点M,使得以M、O、A为顶点的三角形与△AOC相似.请直接写出所有符合条件的点M坐标.3.如图,二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.(1)求该抛物线的解析式;(2)判断△BCM的形状,并说明理由;(3)探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角形与△BCM相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.4.如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.(1)求抛物线的解析式及点C的坐标;(2)求证:△ABC是直角三角形;(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.5.如图,抛物线y=ax2+bx﹣1(a≠0)经过A(﹣1,0),B(2,0)两点,与y轴交于点C.(1)求抛物线的解析式及顶点D的坐标;(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;(3)点N在抛物线上,点M在抛物线的对称轴上,是否存在以点N为直角顶点的Rt△DNM与Rt△BOC相似?若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由.6.如图,已知抛物线y=13x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP 的面积最大时,求点P的坐标;(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.7.如图,已知抛物线与x轴交于A(﹣1,0),B(4,0),与y轴交于C(0,﹣2).(1)求抛物线的解析式;(2)D是C关于x轴的对称点,P是抛物线上的一点,当△PBD与△AOC相似时,求符合条件的P点的坐标.8.如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连接BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.(1)求抛物线的表达式;(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P 运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;9.如图,已知二次函数y =﹣x 2+bx +c (b ,c 为常数)的图象经过点A (3,1),点C (0,4),顶点为点M ,过点A 作AB ∥x 轴,交y 轴于点D ,交该二次函数图象于点B ,连接BC .(1)求该二次函数的解析式及点M 的坐标;(2)点P 是直线AC 上的动点,若点P ,点C ,点M 所构成的三角形与△BCD 相似,请直接写出所有点P 的坐标.10.如图,抛物线y =ax 2+bx 经过两点A (﹣1,1),B (2,2).过点B 作BC ∥x 轴,交抛物线于点C ,交y 轴于点D .(1)求此抛物线对应的函数表达式及点C 的坐标;(2)若抛物线上存在点M ,使得△BCM 的面积为72,求出点M 的坐标; (3)连接OA 、OB 、OC 、AC ,在坐标平面内,求使得△AOC 与△OBN 相似(边OA 与边OB 对应)的点N 的坐标.11.如图1,抛物线y=ax2+1经过点A(4,﹣3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.(1)求抛物线的解析式,并写出其顶点B的坐标;(2)如图2,设点C(1,﹣2),问是否存在点P,使得以P,O,H为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.。
二次函数-相似三角形存在性问题(一)-含答案

似?若存在,求出点 Q 的坐标;若不存在,请说明理由.
y C
A O
B x
(1)求抛物线的解析式; (2)如图 2,直线 OQ 与线段 BC 相交于点 E,当△OBE 与△ABC 相似时,求点 Q 的坐标.
y
y
A O
B x
C
D
图1
A O
C
B x
E Q
D
图2
第2页,共14页
【分析】
(1)抛物线: y = x2 − 2x − 3;
(2)思路:考虑到△ABC 和△BOE 有一组公共角,公共角必是对应角.
根据线段长度可知∠ABQ 与∠ABC 的两边并不成比例,故(-8,-7)舍掉.
情况二:若∠ABQ=∠BAC,
过点 B 作 AC 平行线,与抛物线交点即为 Q 点.
易得直线 BQ 解析式: y = 3 x − 9 , 42
联立方程:
3 4
x
−
9 2
=
−1 8
x2
+
1 4
x
+
3 ,解得:
x1
=
−10
,
x2
的坐标.
y B
A
C
O
x
第6页,共14页
【分析】 (1) y = 1 x2 − 2x +1 ;
3 (2) tan ABC = 1 ;
2 (3)思路:平行得相等角,构造两边成比例
二次函数与相似三角形综合题
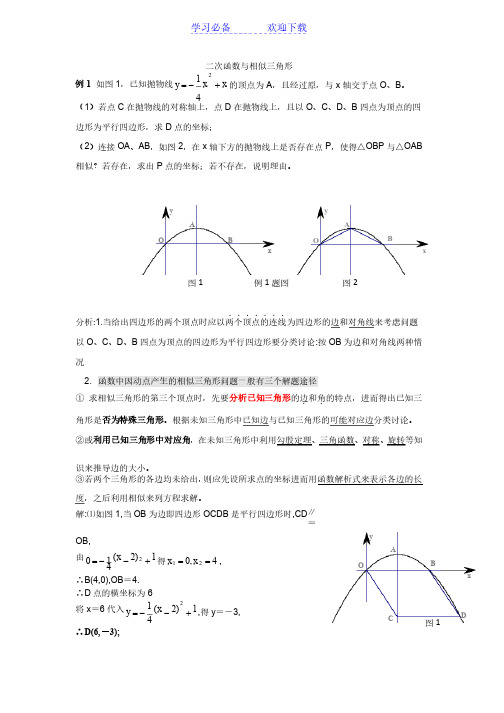
二次函数与相似三角形二次函数与相似三角形例1 如图1,已知抛物线x x 41y 2+-=的顶点为A ,且经过原,与x 轴交于点O 、B 。
(1)若点C 在抛物线的对称轴上,点D 在抛物线上,且以O 、C 、D 、B 四点为顶点的四边形为平行四边形,求D 点的坐标;点的坐标;(2)连接OA 、AB ,如图2,在x 轴下方的抛物线上是否存在点P ,使得△OBP 与△OAB 相似?若存在,求出P 点的坐标;若不存在,说明理由。
点的坐标;若不存在,说明理由。
分析:1.当给出四边形的两个顶点时应以两个顶点的连线.......为四边形的边和对角线来考虑问题以O 、C 、D 、B 四点为顶点的四边形为平行四边形要分类讨论:按OB 为边和对角线两种情况2. . 函数中因动点产生的相似三角形问题一般有三个解题途径函数中因动点产生的相似三角形问题一般有三个解题途径函数中因动点产生的相似三角形问题一般有三个解题途径① 求相似三角形的第三个顶点时,先要分析已知三角形的边.和角.的特点,进而得出已知三角形是否为特殊三角形。
根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、在未知三角形中利用勾股定理、三角函数、三角函数、三角函数、对称、对称、旋转等知识来推导边的大小。
识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解。
度,之后利用相似来列方程求解。
解:⑴如图1,当OB 为边即四边形OCDB 是平行四边形时,CD ∥=OB, 由1)2x (4102+--=得4x ,0x 21==, ∴B(4,0),OB =4. ∴D 点的横坐标为6 将x =6代入1)2x (41y 2+--=,得y =-3, ∴D(6,-3); 例1题图题图 图1 OAByxOAByx图2 COABDyx图1 13E A'OAB Py x图2 (2)先根据A 、C 的坐标,用待定系数法求出直线AC 的解析式,进而根据抛物线和直线AC 的解析式分别表示出点P 、点M 的坐标,即可得到PM 的长;(3)由于∠PFC 和∠AEM 都是直角,F 和E 对应,则若以P 、C 、F 为顶点的三角形和△AEM 相似时,分两种情况进行讨论:①△PFC∽△AEM,②△CFP∽△AEM;可分别用含m 的代数式表示出AE 、EM 、CF 、PF 的长,根据相似三角形对应边的比相等列出比例式,求出m 的值,再根据相似三角形的性质,直角三角形、等腰三角形的判定判断出△PCM 的形状.解答:解:(1)∵抛物线y=ax 2﹣2ax+c (a≠0)经过点A (3,0),点C (0,4), ∴,解得,∴抛物线的解析式为y=﹣x 2+x+4; (2)设直线AC 的解析式为y=kx+b , ∵A(3,0),点C (0,4), ∴,解得,∴直线AC 的解析式为y=﹣43x+4.∵点M 的横坐标为m ,点M 在AC 上,∴M 点的坐标为(m ,﹣43m+4), ∵点P 的横坐标为m ,点P 在抛物线y=﹣x 2+x+4上,∴点P 的坐标为(m ,﹣ m 2+m+4), ∴PM=PE﹣ME=(﹣m 2+m+4)﹣(﹣43m+4)=﹣m 2+73m ,即PM=﹣m 2+73m (0<m <3); (3)在(2)的条件下,连结PC ,在CD 上方的抛物线部分存在这样的点P ,使得以P 、C 、F 为顶点的三角形和△AEM 相似.理由如下:由题意,可得AE=3﹣m ,EM=﹣m+4,CF=m ,PF=﹣m 2+m+4﹣4=﹣m 2+m . 若以P 、C 、F 为顶点的三角形和△AEM 相似,分两种情况:①若△PFC∽△AEM,则PF :AE=FC :EM ,即(﹣m 2+m ):(3﹣m )=m :(﹣ m+4), ∵m≠0且m≠3, ∴m=.∵△PFC∽△AEM,∴∠PCF=∠AME, ∵∠AME=∠CMF,∴∠PCF=∠CMF.在直角△CMF 中,∵∠CMF+∠MCF=90°, ∴∠PCF+∠MCF=90°,即∠PCM=90°, ∴△PCM 为直角三角形;②若△CFP∽△AEM,则CF :AE=PF :EM ,即m :(3﹣m )=(﹣m 2+m ):(﹣m+4), ∵m≠0且m≠3,yxEQP C B OA ∴m=1.∵△CFP∽△AEM,∴∠CPF=∠AME, ∵∠AME=∠CMF,∴∠CPF=∠CMF. ∴CP=CM,∴△PCM 为等腰三角形.综上所述,存在这样的点P 使△PFC 与△AEM 相似.此时m 的值为或1,△PCM 为直角三角形或等腰三角形.点评:此题是二次函数的综合题,其中涉及到运用待定系数法求二次函数、一次函数的解析式,矩形的性质,相似三角形的判定和性质,直角三角形、等腰三角形的判定,难度适中.要注意的是当相似三角形的对应边和对应角不明确时,要分类讨论,以免漏解. 练习1、已知抛物线225333y x x =-+经过53(33)02P E æöç÷ç÷èø,,,及原点(00)O ,. (1)过P 点作平行于x 轴的直线PC 交y 轴于C 点,在抛物线对称轴右侧且位于直线PC 下方的抛物线上,任取一点Q ,过点Q 作直线QA 平行于y 轴交x 轴于A 点,交直线PC 于B 点,直线QA 与直线PC 及两坐标轴围成矩形OABC .是否存在点Q ,使得OPC △与PQB △相似?若存在,求出Q 点的坐标;若不存在,说明理由.点的坐标;若不存在,说明理由.(2)如果符合(2)中的Q 点在x 轴的上方,连结OQ ,矩形OABC 内的四个三角形OPC PQB OQP OQA ,,,△△△△之间存在怎样的关系?为什么?之间存在怎样的关系?为什么?(1)存在.)存在.设Q 点的坐标为()m n ,,则225333n m m =-+, 要使,BQ PB OCP PBQ CP OC =△∽△,则有3333n m --=,即2253333333m m m +--=解之得,12232m m ==,.当123m =时,2n =,即为Q 点,所以得(232)Q ,要使,BQ PB OCP QBP OC CP =△∽△,则有3333n m --=,即2253333333m m m +--=解之得,12333m m ==,,当3m =时,即为P 点,点, 当133m =时,3n =-,所以得(333)Q -,. 故存在两个Q 点使得OCP △与PBQ △相似.相似.Q 点的坐标为(232)(333)-,,,.(2)在Rt OCP △中,因为3tan 3CP COP OC Ð==.所以30COP Ð=. 当Q 点的坐标为(232),时,30BPQ COP Ð=Ð=. 所以90OPQ OCP B QAO Ð=Ð=Ð=Ð=.因此,OPC PQB OPQ OAQ ,,,△△△△都是直角三角形.都是直角三角形.又在Rt OAQ △中,因为3tan 3QA QOA AO Ð==.所以30QOA Ð=. 即有30POQ QOA QPB COP Ð=Ð=Ð=Ð=. 所以OPC PQB OQP OQA △∽△∽△∽△, 又因为QP OP QA OA ,⊥⊥30POQ AOQ Ð=Ð=,所以OQA OQP △≌△.2.在平面直角坐标系xOy 中,已知二次函数223y x x =-++的图象与x 轴交于A B ,两点(点A 在点B 的左边),与y 轴交于点C .(1)若直线:(0)l y kx k =¹与线段BC 交于点D (不与点B C ,重合),则是否存在这样的直线l ,使得以B O D ,,为顶点的三角形与BAC △相似?若存在,求出该直线的函数表达式及点D 的坐标;若不存在,请说明理由;(10)(30),(03)A B C -,,,, (2)若点P 是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较锐角PCO Ð与ACO Ð的大小(不必证明),并写出此时点P 的横坐标p x 的取值范围.的取值范围.(1)假设存在直线:(0)l y kx k =¹与线段BC 交于点D (不与点B C ,重合),使得以B O D ,,为顶点的三角形与BAC △相似.相似.在223y x x =-++中,令0y =,则由2230x x -++=,解得1213x x =-=,(10)(30)A B \-,,,. 令0x =,得3y =.(03)C \,. 设过点O 的直线l 交BC 于点D ,过点D 作DE x ⊥轴于点E .yCl xB A 1x = 练习3图yx B E A OC D1x =l点B的坐标为(30),,点C的坐标为(03),,点A的坐标为(10)-,.4345.AB OB OC OBC\===Ð=,,223332BC\=+=.要使BOD BAC△∽△或BDO BAC△∽△,已有B BÐ=Ð,则只需BD BOBC BA=,①或.BO BDBC BA=②成立.成立.若是①,则有3329244BO BCBDBA´===.而45OBC BE DEÐ=\=,.\在Rt BDE△中,由勾股定理,得222229224BE DE BE BDæö+===ç÷ç÷èø.解得解得94BE DE==(负值舍去).93344OE OB BE\=-=-=.\点D的坐标为3944æöç÷èø,.将点D的坐标代入(0)y kx k=¹中,求得3k=.\满足条件的直线l的函数表达式为3y x=.[或求出直线AC的函数表达式为33y x=+,则与直线AC平行的直线l的函数表达式为3y x=.此时易知BOD BAC△∽△,再求出直线BC的函数表达式为3y x=-+.联立33y x y x==-+,求得点D的坐标为3944æöç÷èø,.]若是②,则有342232BO BABDBC´===.而45OBC BE DEÐ=\=,.\在Rt BDE △中,由勾股定理,得222222(22)BE DE BE BD +===.解得解得2BE DE ==(负值舍去).321OE OB BE \=-=-=.\点D 的坐标为(12),. 将点D 的坐标代入(0)y kx k =¹中,求得2k =.∴满足条件的直线l 的函数表达式为2y x =.\存在直线:3l y x =或2y x =与线段BC 交于点D (不与点B C ,重合),使得以B O D ,,为顶点的三角形与BAC △相似,且点D 的坐标分别为3944æöç÷èø,或(12),.(2)设过点(03)(10)C E ,,,的直线3(0)y kx k =+¹与该二次函数的图象交于点P . 将点(10)E ,的坐标代入3y kx =+中,求得3k =-. \此直线的函数表达式为33y x =-+.设点P 的坐标为(33)x x -+,,并代入223y x x =-++,得250x x -=. 解得1250x x ==,(不合题意,舍去).512x y \==-,.\点P 的坐标为(512)-,.此时,锐角PCO ACO Ð=Ð.又二次函数的对称轴为1x =,\点C 关于对称轴对称的点C ¢的坐标为(23),. \当5px>时,锐角PCO ACO Ð<Ð;当5p x =时,锐角PCO ACO Ð=Ð; 当25p x <<时,锐角PCO ACO Ð>Ð.OxBEA O C1x =PC ¢ ·3.如图所示,已知抛物线21y x =-与x 轴交于A 、B 两点,与y 轴交于点C ,过点A 作AP ∥CB 交抛物线于点P . 在x 轴上方的抛物线上是否存在一点M ,过M 作MG ^x 轴于点G ,使以A 、M 、G 三点为顶点的三角形与D PCA 相似.若存在,请求出M 点的坐标;否则,请说明理由.否则,请说明理由. 解:解: 假设存在假设存在A (1,0)-B (1,0)C (0,1)- ∵ÐPAB=ÐBAC =45 ∴P A ^AC ∵MG ^x 轴于点G , ∴ÐMGA=ÐPAC =90 在Rt △AOC 中,OA=OC=1 ∴AC=2 在Rt △PAE 中,AE=PE=3 ∴AP= 32 设M 点的横坐标为m ,则M 2(,1)m m - ①点M 在y 轴左侧时,则1m <-(ⅰ) 当D AMG ∽D PCA 时,有AG PA =MG CA∵AG=1m --,MG=21m -即211322m m ---=解得11m =-(舍去)(舍去) 223m =(舍去)(舍去)(ⅱ) 当D MAG ∽D PCA 时有AG CA =MGPA即 211232m m ---=解得:1m =-(舍去)(舍去) 22m =- ∴M (2,3)-② 点M 在y 轴右侧时,则1m > (ⅰ) 当D AMG ∽D PCA 时有AG PA =MGCA∵AG=1m +,MG=21m -G M 图3 C B y P A oxG M 图2 C B y P A ox图1 C P B y A ox∴211322m m +-=解得11m =-(舍去)(舍去) 243m =∴M 47(,)39(ⅱ) 当D MAG ∽D PCA 时有AG CA =MGPA即211232m m +-=解得:11m =-(舍去)(舍去) 24m = ∴M (4,15)∴存在点M ,使以A 、M 、G 三点为顶点的三角形与D PCA 相似相似M 点的坐标为(2,3)-,47(,)39,(4,15)4.4.(2013•曲靖压轴题)如图,在平面直角坐标系(2013•曲靖压轴题)如图,在平面直角坐标系xOy 中,直线y=x+4与坐标轴分别交于A 、B 两点,过A 、B 两点的抛物线y=﹣x 2﹣3x+4..点D 为线段AB 上一动点,过点D 作CD⊥x 轴于点C ,交抛物线于点E .(1)当DE=4时,求四边形CAEB 的面积.的面积. (2)连接BE BE,,是否存在点D ,使得△DBE 和△DAC 相似?若存在,求此点D 坐标;若不存在,说明理由.说明理由.考点: 二次函数综合题. 分析: (1)首先求出点A 、B 的坐标,然后利用待定系数法求出抛物线的解析式;(2)设点C 坐标为(m ,0)(m <0),根据已知条件求出点E 坐标为(m ,8+m );由于点E 在抛物线上,则可以列出方程求出m 的值.在计算四边形CAEB 面积时,利用S 四边形CAEB =S △A CE +S 梯形OCEB ﹣S △BCO ,可以简化计算;(3)由于△ACD为等腰直角三角形,而△DBE和△DAC相似,则△DBE必为等腰直角三角形.分两种情况讨论,要点是求出点E的坐标,由于点E在抛物线上,则可以由此列出方程求出未知数.解答:解:(1)在直线解析式y=x+4中,令x=0,得y=4;令y=0,得x=﹣4,∴A(﹣4,0),B(0,4).∵点A(﹣4,0),B(0,4)在抛物线y=﹣x2+bx+c上,∴,解得:b=﹣3,c=4,∴抛物线的解析式为:y=﹣x 2﹣3x+4.(2)设点C坐标为(m,0)(m<0),则OC=﹣m,AC=4+m.∵OA=OB=4,∴∠BAC=45°,∴△ACD为等腰直角三角形,∴CD=AC=4+m,∴CE=CD+DE=4+m+4=8+m,∴点E坐标为(m,8+m).∵点E在抛物线y=﹣x 2﹣3x+4上,∴8+m=﹣m2﹣3m+4,解得m=﹣2.∴C(﹣2,0),AC=OC=2,CE=6,S四边形CAEB=S△ACE+S梯形OCEB﹣S△BCO=×2×6+(6+4)×2﹣×2×4=12.(3)设点C坐标为(m,0)(m<0),则OC=﹣m,CD=AC=4+m,BD=OC=﹣m,则D(m,4+m).∵△ACD为等腰直角三角形,△DBE和△DAC相似∴△DBE必为等腰直角三角形.i)若∠BED=90°,则BE=DE,∵BE=OC=﹣m,∴DE=BE=﹣m,∴CE=4+m﹣m=4,∴E(m,4).∵点E在抛物线y=﹣x2﹣3x+4上,∴4=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣3,∴D(﹣3,1);ii)若∠EBD=90°,则BE=BD=﹣m,在等腰直角三角形EBD中,DE=BD=﹣2m,∴C E=4+m﹣2m=4﹣m,∴E(m,4﹣m).∵点E在抛物线y=﹣x2﹣3x+4上,∴4﹣m=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣2,∴D(﹣2,2).综上所述,存在点D,使得△DBE和△DAC相似,点D的坐标为(﹣3,1)或(﹣2,2).点评:本题考查了二次函数与一次函数的图象与性质、函数图象上点的坐标特征、待定系数法、相似三角形、等腰直角三角形、图象面积计算等重要知识点.第(3)问需要分类讨论,这是本题的难点.5.5.(2013•绍兴压轴题)抛物线(2013•绍兴压轴题)抛物线y=y=((x ﹣3)(x+1x+1))与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C ,点D 为顶点.为顶点.(1)求点B 及点D 的坐标.的坐标.(2)连结BD BD,,CD CD,抛物线的对称轴与,抛物线的对称轴与x 轴交于点E .①若线段BD 上一点P ,使∠DCP=∠BDE,求点P 的坐标.的坐标.②若抛物线上一点M ,作MN⊥CD,交直线CD 于点N ,使∠CMN=∠BDE,求点M 的坐标.的坐标.考点: 二次函数综合题.3718684分析: (1)解方程(x ﹣3)(x+1)=0,求出x=3或﹣1,根据抛物线y=(x ﹣3)(x+1)与x轴交于A ,B 两点(点A 在点B 左侧),确定点B 的坐标为(3,0);将y=(x ﹣3)(x+1)配方,写成顶点式为y=x 2﹣2x ﹣3=(x ﹣1)2﹣4,即可确定顶点D 的坐标;(2)①根据抛物线y=(x ﹣3)(x+1),得到点C 、点E 的坐标.连接BC ,过点C 作CH⊥DE 于H ,由勾股定理得出CD=,CB=3,证明△BCD 为直角三角形.分别延长PC 、DC ,与x 轴相交于点Q ,R .根据两角对应相等的两三角形相似证明△BCD∽△QOC,则==,得出Q 的坐标(﹣9,0),运用待定系数法求出直线CQ 的解析式为y=﹣x ﹣3,直线BD 的解析式为y=2x ﹣6,解方程组,即可求出点P 的坐标;②分两种情况进行讨论:(Ⅰ)当点M 在对称轴右侧时.若点N 在射线CD 上,如备用图1,延长MN交y轴于点F,过点M作MG⊥y轴于点G,先证明△MCN∽△DBE,由相似三角形对应边成比例得出MN=2CN.设CN=a,再证明△CNF,△MGF均为等腰直角三角形,然后用含a的代数式表示点M的坐标,将其代入抛物线y=(x﹣3)(x+1),求出a的值,得到点M的坐标;若点N在射线DC上,同理可求出点M的坐标;(Ⅱ)当点M在对称轴左侧时.由于∠BDE<45°,得到∠CMN<45°,根据直角三角形两锐角互余得出∠MCN>45°,而抛物线左侧任意一点K,都有∠KCN<45°,所以点M不存在.解答:解:(1)∵抛物线y=(x﹣3)(x+1)与x轴交于A,B两点(点A在点B左侧),∴当y=0时,(x﹣3)(x+1)=0,解得x=3或﹣1,∴点B的坐标为(3,0).∵y=(x﹣3)(x+1)=x2﹣2x﹣3=(x﹣1)2﹣4,∴顶点D的坐标为(1,﹣4);(2)①如右图.∵抛物线y=(x﹣3)(x+1)=x2﹣2x﹣3与与y轴交于点C,∴C点坐标为(0,﹣3).∵对称轴为直线x=1,∴点E的坐标为(1,0).连接BC,过点C作CH⊥DE于H,则H点坐标为(1,﹣3),∴CH=DH=1,∴∠CDH=∠BCO=∠BCH=45°,∴CD=,CB=3,△BCD为直角三角形.分别延长PC、DC,与x轴相交于点Q,R.∵∠BDE=∠DCP=∠QCR,∠CDB=∠CDE+∠BDE=45°+∠DCP,∠QCO=∠RCO+∠QCR=45°+∠DCP,∴∠CDB=∠QCO,∴△BCD∽△QOC,∴==,∴OQ=3OC=9,即Q(﹣9,0).∴直线CQ的解析式为y=﹣x﹣3,直线BD的解析式为y=2x﹣6.由方程组,解得.∴点P的坐标为(,﹣);②(Ⅰ)当点M在对称轴右侧时.若点N在射线CD上,如备用图1,延长MN交y轴于点F,过点M作MG⊥y轴于点G.∵∠CMN=∠BDE,∠CNM=∠BED=90°,∴△MCN∽△DBE,∴==,∴MN=2CN.设CN=a,则MN=2a.∵∠CDE=∠DCF=45°,∴△CNF,△MGF均为等腰直角三角形,∴NF=CN=a,CF=a,∴MF=MN+NF=3a,∴MG=FG=a,∴CG=FG﹣FC=a,∴M(a,﹣3+a).代入抛物线y=(x﹣3)(x+1),解得a=,∴M(,﹣);若点N在射线DC上,如备用图2,MN交y轴于点F,过点M作MG⊥y轴于点G.∵∠CMN=∠BDE,∠CNM=∠BED=90°,∴△MCN∽△DBE,∴==,∴MN=2CN.设CN=a,则MN=2a.∵∠CDE=45°,∴△CNF,△MGF均为等腰直角三角形,∴NF=CN=a,CF=a,∴MF=MN﹣NF=a,∴MG=FG=a,点评: 本题是二次函数的综合题型,其中涉及到的知识点有二次函数图象上点的坐标特征,二次函数的性质,运用待定系数法求一次函数、二次函数的解析式,勾股定理,等腰直角三角形、相似三角形的判定与性质,综合性较强,有一定难度.(2)中第②问进行分类讨论及运用数形结合的思想是解题的关键.6.6.(2013•恩施州压轴题)如图所示,直线(2013•恩施州压轴题)如图所示,直线l :y=3x+3与x 轴交于点A ,与y 轴交于点B .把△AOB 沿y 轴翻折,点A 落到点C ,抛物线y=y=x x 2﹣4x+3过点B 、C 和D (3,0). (1)若BD 与抛物线的对称轴交于点M ,点N 在坐标轴上,以点N 、B 、D 为顶点的三角形与△MCD 相似,求所有满足条件的点N 的坐标.的坐标. (2)在抛物线上是否存在点P ,使S △PBD =6=6?若存在,求出点?若存在,求出点P 的坐标;若不存在,说明理由.由.考点: 二次函数综合题.分析: (1)由待定系数法求出直线BD 和抛物线的解析式;(2)首先确定△MCD 为等腰直角三角形,因为△BND 与△MCD 相似,所以△BND 也是等腰直角三角形.如答图1所示,符合条件的点N 有3个;(3)如答图2、答图3所示,解题关键是求出△PBD 面积的表达式,然后根据S △PBD =6的已知条件,列出一元二次方程求解.解答: (1)抛物线的解析式为:y=x 2﹣4x+3=(x ﹣2)2﹣1,∴抛物线的对称轴为直线x=2,顶点坐标为(2,﹣1).直线BD :y=﹣x+3与抛物线的对称轴交于点M ,令x=2,得y=1,∴M(2,1).设对称轴与x 轴交点为点F ,则CF=FD=MN=1,∴△MCD 为等腰直角三角形.∵以点N 、B 、D 为顶点的三角形与△MCD 相似,∴△BND 为等腰直角三角形.如答图1所示:(I )若BD 为斜边,则易知此时直角顶点为原点O ,∴N 1(0,0);(II )若BD 为直角边,B 为直角顶点,则点N 在x 轴负半轴上,∵OB=OD=ON 2=3,∴N 2(﹣3,0);(III)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,∵OB=OD=ON3=3,∴N3(0,﹣3).∴满足条件的点N坐标为:(0,0),(﹣3,0)或(0,﹣3).(2)假设存在点P,使S△PBD=6,设点P坐标为(m,n).(I)当点P位于直线BD上方时,如答图2所示:过点P作PE⊥x轴于点E,则PE=n,DE=m﹣3.S△PBD=S梯形PEOB﹣S△BOD﹣S△PDE=(3+n)•m﹣×3×3﹣(m﹣3)•n=6,化简得:m+n=7 ①,∵P(m,n)在抛物线上,∴n=m2﹣4m+3,代入①式整理得:m2﹣3m﹣4=0,解得:m1=4,m2=﹣1,∴n1=3,n2=8,∴P1(4,3),P2(﹣1,8);(II)当点P位于直线BD下方时,如答图3所示:过点P作PE⊥y轴于点E,则PE=m,OE=﹣n,BE=3﹣n.S△PBD=S梯形PEOD+S△BOD﹣S△PBE=(3+m)•(﹣n)+×3×3﹣(3﹣n)•m=6,化简得:m+n=﹣1 ②,∵P(m,n)在抛物线上,∴n=m 2﹣4m+3,代入②式整理得:m2﹣3m+4=0,△=﹣7<0,此方程无解.故此时点P不存在.综上所述,在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(﹣1,8).点评:本题是中考压轴题,综合考查了二次函数的图象与性质、待定系数法、相似三角形的判定与性质、图形面积计算、解一元二次方程等知识点,考查了数形结合、分类讨论的数学思想.第(2)(3)问均需进行分类讨论,避免漏解.。
初三中考数学专题复习:二次函数综合题(相似三角形问题)含答案

中考数学专题复习:二次函数综合题(相似三角形问题)1.如图①,二次函数y =﹣x 2+bx +c 的图象与x 轴交于点A (﹣1,0)、B (3,0),与y 轴交于点C ,连接BC ,点P 是抛物线上一动点.(1)求二次函数的表达式.(2)当点P 不与点A 、B 重合时,作直线AP ,交直线BC 于点Q ,若①ABQ 的面积是①BPQ 面积的4倍,求点P 的横坐标.(3)如图①,当点P 在第一象限时,连接AP ,交线段BC 于点M ,以AM 为斜边向①ABM 外作等腰直角三角形AMN ,连接BN ,①ABN 的面积是否变化?如果不变,请求出①ABN 的面积;如果变化,请说明理由.2.如图,二次函数2314y x bx =++的图像经过点()8,3A ,交x 轴于点B ,C (点B 在点C 的左侧),与y 轴交于点D .(1)填空:b = ______;(2)点P 是第一象限内抛物线上一点,直线PO 交直线CD 于点Q ,过点P 作x 轴的垂线交直线CD 于点T ,若PQ QT =,求点P 的坐标;(3)在x 轴的正半轴上找一点E ,过点E 作AE 的垂线EF 交y 轴于F ,若AEF 与EFO △相似,求OE 的长.3.如图,已知抛物线2y ax bx c =++与x 轴相交于点()1,0A -,()3,0B ,与y 轴的交点()0,6C .(1)求抛物线的解析式;(2)点(),P m n 在平面直角坐标系第一象限内的抛物线上运动,设PBC 的面积为S ,求S 关于m 的函数表达式(指出自变量m 的取值范围)和S 的最大值;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得①CMN =90°,且∆CMN 与OBC ∆相似,如果存在,请求出点M 和点N 的坐标.4.如图,抛物线L 1:y =ax 2﹣2x +c (a ≠0)与x 轴交于A 、B (3,0)两点,与y 轴交于点C (0,﹣3),抛物线的顶点为D .抛物线L 2与L 1关于x 轴对称.(1)求抛物线L 1与L 2的函数表达式;(2)已知点E 是抛物线L 2的顶点,点M 是抛物线L 2上的动点,且位于其对称轴的右侧,过M 向其对称轴作垂线交对称轴于P ,是否存在这样的点M ,使得以P 、M 、E 为顶点的三角形与△BCD 相似,若存在请求出点M 的坐标,若不存在,请说明理由.5.如图,在平面直角坐标系中,已知直线4y x =+与x 轴、y 轴分别相交于点A 和点C ,抛物线21y x kx k =++-的图象经过点A 和点C ,与x 轴的另一个交点是点B .(1)求出此抛物线的解析式; (2)求出点B 的坐标;(3)若在y 轴的负半轴上存在点D .能使得以A ,C ,D 为顶点的三角形与①ABC 相似,请求出点D 的坐标.6.如图1,已知抛物线23y ax bx =++经过点()1,5D ,且交x 轴于A ,B 两点,交y 轴于点C ,已知点()1,0A -,(),P m n 是抛物线在第一象限内的一个动点,PQ BC ⊥于点Q .(1)求抛物线的解析式;(2)当PQ =m 的值;(3)是否存在点P ,使BPQ 与BOC 相似?若存在,请求出P 点的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,直线y =12x +2与x 轴交于点A ,与y 轴交于点C .抛物线y =ax 2+bx +c的对称轴是x=-32且经过A、C两点,与x轴的另一交点为点B.(1)求二次函数y=ax2+bx+c的表达式;(2)点P为线段AB上的动点,求AP+2PC的最小值;(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A,M,N为顶点的三角形与①ABC 相似?若存在,求出点M的坐标;若不存在,请说明理由.8.如图,抛物线y=−x2+bx+c与x轴相交于A(−1,0),B(3,0)两点,与y轴交于点C,顶点为点D,抛物线的对称轴与BC相交于点E,与x轴相交于点F.(1)求抛物线的函数关系式;(2)连结DA,求sin A的值;(3)若点H线段BC上,BOC与BFH△相似,请直接写出点H的坐标.9.如图,抛物线y=1-2x2+bx+c与x轴交于点A(﹣2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求抛物线的表达式;(2)点P 是第一象限内抛物线上的动点,连接PB ,PC ,当S △PBC =720S △ABC 时,求点P 的坐标; (3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以点M ,N ,E 为顶点的三角形与①OBC 相似?若存在,求点M 的坐标;若不存在,请说明理由.10.如图,抛物线23y ax bx =++与x 轴交于1,0A 、()3,0B -两点,与y 轴交于点C ,设抛物线的顶点为D .(1)求该抛物线的表达式与顶点D 的坐标; (2)试判断BCD △的形状,并说明理由;(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与BCD △相似?若存在,请求出点P 的坐标;若不存在,请说明理由.11.如图,抛物线y =ax 2﹣2ax ﹣3a (a ≠0)与x 轴交于点A ,B .与y 轴交于点C .连接AC ,BC .已知ABC 的面积为2.(1)求抛物线的解析式;(2)平行于x 轴的直线与抛物线从左到右依次交于P ,Q 两点.过P ,Q 向x 轴作垂线,垂足分别为G ,H .若四边形PGHQ 为正方形,求正方形的边长;(3)抛物线上是否存在一点N ,使得①BCN =①CAB ﹣①CBA ,若存在,请求出满足条件N 点的横坐标,若不存在请说明理由.12.如图,二次函数2y x bx c =-++的图像与x 轴交于点A (-1,0),B (2,0),与y 轴相交于点C .(1)求这个二次函数的解析式;(2)若点M 在此抛物线上,且在y 轴的右侧.①M 与y 轴相切,过点M 作MD ①y 轴,垂足为点D .以C ,D ,M 为顶点的三角形与①AOC 相似,求点M 的坐标及①M 的半径长.13.如图,在平面直角坐标系中,抛物线2()0y ax bx c ac =++≠与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C .若线段OA OB OC 、、的长满足2OC OA OB =⋅,则这样的抛物线称为“黄金”抛物线.如图,抛物线22(0)y ax bx a =++≠为“黄金”抛物线,其与x 轴交点为A ,B (其中B 在A 的右侧),与y 轴交于点C .且4OA OB =(1)求抛物线的解析式;(2)若P 为AC 上方抛物线上的动点,过点P 作PD AC ⊥,垂足为D . ①求PD 的最大值;①连接PC ,当PCD 与ACO △相似时,求点P 的坐标.14.如图,在平面直角坐标系xOy 中,已知抛物线2y x bx c =++与x 轴交于点A 、B 两点,其中1,0A ,与y 轴交于点()0,3C .(1)求抛物线解析式;(2)如图1,过点B 作x 轴垂线,在该垂线上取点P ,使得①PBC 与①ABC 相似,请求出点P 坐标;(3)如图2,在线段OB 上取一点M ,连接CM ,请求出12CM BM +最小值.15.如图,抛物线y =ax 2+k (a >0,k <0)与x 轴交于A ,B 两点(点B 在点A 的右侧),其顶点为C ,点P 为线段OC 上一点,且PC =14OC .过点P 作DE ①AB ,分别交抛物线于D ,E 两点(点E 在点D 的右侧),连接OD ,DC .(1)直接写出A ,B ,C 三点的坐标;(用含a ,k 的式子表示) (2)猜想线段DE 与AB 之间的数量关系,并证明你的猜想;(3)若①ODC =90°,k =﹣4,求a 的值.16.如图,抛物线223y x bx c =++与x 轴交于A ,B 两点,与y 轴交于C 点,连接AC ,已知B (﹣1,0),且抛物线经过点D (2,﹣2).(1)求抛物线的表达式;(2)若点E 是抛物线上第四象限内的一点,且2ABES=,求点E 的坐标;(3)若点P 是y 轴上一点,以P ,A ,C 三点为顶点的三角形是等腰三角形,求P 点的坐标.17.如图,在直角坐标系xOy 中,抛物线y =ax 2+bx +2(a ≠0)与x 轴交于点A (﹣1,0)和B (4,0),与y 轴交于点C ,点P 是抛物线上的动点(不与点A ,B ,C 重合).(1)求抛物线的解析式;(2)当点P 在第一象限时,设①ACP 的面积为S 1,①ABP 的面积为S 2,当S 1=S 2时,求点P 的坐标; (3)过点O 作直线l ①BC ,点Q 是直线l 上的动点,当BQ ①PQ ,且①BPQ =①CAB 时,请直接写出点P 的坐标.18.如图,在平面直角坐标系xOy中,直线y=﹣x+3与两坐标轴交于A、B两点,抛物线y=x2+bx+c 过点A和点B,并与x轴交于另一点C,顶点为D.点E在对称轴右侧的抛物线上.(1)求抛物线的函数表达式和顶点D的坐标;(2)若点F在抛物线的对称轴上,且EF①x轴,若以点D,E,F为顶点的三角形与①ABD相似,求出此时点E的坐标;(3)若点P为坐标平面内一动点,满足tan①APB=3,请直接写出①P AB面积最大时点P的坐标及该三角形面积的最大值.19.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B,与y轴交于点C,且OC=2OB=6OA=6,点P是第一象限内抛物线上的动点.(1)求抛物线的解析式;(2)连接BC与OP,交于点D,当S△PCD:S△ODC的值最大时,求点P的坐标;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N.使①CMN=90°,且①CMN与①BOC 相似,若存在,请求出点M、点N的坐标.20.如图,抛物线y=x2+bx+12(b<0)与x轴交于A,B两点(A点在B点左侧),且OB=3OA.(1)请直接写出b=,A点的坐标是,B点的坐标是;(2)如图(1),D点从原点出发,向y轴正方向运动,速度为2个单位长度/秒,直线BD交抛物线于点E,若BE=5DE,求D点运动时间;(3)如图(2),F点是抛物线顶点,过点F作x轴平行线MN,点C是对称轴右侧的抛物线上的一定点,P 点在直线MN上运动.若恰好存在3个P点使得①P AC为直角三角形,请求出C点坐标,并直接写出P点的坐标.答案1.(1)y =﹣x 2+2x +3.(2)P 352或 (3)①ABN 的面积不变,为4.2.(1)2-(2)5⎛ ⎝⎭或5⎛ ⎝⎭(3)4或493.(1)2246y x x =-++(2)S 关于m 的函数表达式为239(03)S m m m =-+<<,S 的最大值是274 (3)存在,M (1,8),N (0,172)或M (74,558),N (0,838)或M (94,398),N (0,38)或M (3,0),N (0,﹣32)4.(1)抛物线L 1:223y x x =--,抛物线L 2:2y x 2x 3=-++;(2)435(,)39M 或(4,5)M -.5.(1)254y x x =++(2)点B 的坐标为(-1,0)(3)点D 的坐标是(0,-203) 6.(1)215322y x x =-++ (2)1或5(3)存在;P (53,529)7.(1)抛物线表达式为:213222y x x =--+;(2)AP +2PC 的最小值是4;(3)存在M(0,2)或(-3,2)或(2,-3)或(5,-18),使得以点A 、M 、N 为顶点的三角形与ABC 相似.8.(1)y =-x 2+2x +3(3)点H 的坐标为(1,2)或(2,1)9.(1)21382y x x =++ (2)P 1(1,10.5),P 2(7,4.5)(3)存在,(3,8)或(3,5或(3,11)30.(1)y =﹣x 2﹣2x +3,(﹣1,4);(2)直角三角形,理由见解析;(3)存在,(0,0)或(0,﹣13)或(-9,0)11.(1)y =﹣13x 2+23x +1(2)﹣6﹣(3)存在,5或11712.(1)22y x x =-++; (2)M 的坐标为(12,94),(32, 54 ),(3,-4),①M 的半径长为12或32或313.(1)213222y x x =--+(2)①PD ①P 坐标为(3,2)-或325()28,-14.(1)243y x x =-+(2)P 点坐标为()3,9或()3,215.(1)点A 、B 、C 的坐标分别为(、、(0,k ) (2)DE =12AB(3)a =1316.(1)224233y x x =--(2)E ,-1)(3)P 点的坐标(0,2)或(02)或(0,﹣2或(0,54)17.(1)213222y x x =-++ (2)点P 的坐标为(103,139)(3)点P 的坐标为(32,﹣2)或(32,﹣2)或(173,﹣509)18.(1)y =x 2﹣4x +3,(2,﹣1)(2)(5,8)或(73,89-)(3)①P AB ,此时P )19.(1)y =﹣2x 2+4x +6 (2)点P 的坐标为(32,152) (3)存在,M 、N 的坐标分别为(3,0)、(0,﹣32)或(94,398)、(0,38)或(1,8)、(0,172)或(74,558)、(0,838)20.(1)﹣8,(2,0),(6,0)(2)3秒或212秒 (3)C 点坐标为(143,﹣329),P 点的坐标为(103,﹣4)或(﹣103,﹣4)或(11027,﹣4)。
二次函数综合(动点)问题——相似三角形存在问题培优教案(横版)

考点/易错点2
相似三角形的性质: (1)相似三角形的对应角相等。 (2)相似三角形的对应边成比例。 (3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。 (4)相似三角形的周长比等于相似比。 (5)相似三角形的面积比等于相似比的平方。
考点/易错点 3 相似三角形模型探究与解题技巧: 1、课堂导入题解 如图,在平面直角坐标系中有两点 A(4,0)、B(0,2),如果点 C 在 x 轴上(C 与 A 不重合),当 点 C 的坐标为_________________时,使得由点 B、O、C 组成的三角形与△AOB 相似(至少找出两个满 足条件的点的坐标).
解:∵点 C 在 x 轴上,∴点 C 的纵坐标是 0,且当∠BOC=90°时,由点 B、O、C 组成的三角形与△AOB 相似,即∠BOC 应该与∠BOA=90°对应,
①当△AOB∽△COB,即 OC 与 OA 相对应时,则 OC=OA=4,C(-4,0); ②当△AOB∽△BOC,即 OC 与 OB 对应,则 OC=1,C(-1,0)或者(1,0). 故答案可以是:(-1,0);(1,0). 解析:分类讨论:①当△AOB∽△COB 时,求点 C 的坐标;②当△AOB∽△BOC 时,求点 C 的坐标; 如果非直角三角形也要分类讨论,对应边不一样就得到不同的结果。
图象
开口 对称轴 顶点坐标 最值
a>0
a<0
当 x=
时,y 有最
当 x= 值是
是
时,y 有最 值
增 在对称轴左侧 y 随 x 的增大而
减 在对称轴右侧 y 随 x 的增大而
性
y 随 x 的增大而 y 随 x 的增大而
(二)梯形的性质:一组对边平行,另一组对边不平行的四边形; 直角梯形的性质:有两个角是直角的梯形; 等腰梯形:两底角相等,两顶角相等,两腰相等,对角线相等的梯形。
【中考数学几何模型】第二十五节:二次函数三角形相似存在性问题

中考数学几何模型第二十五节:二次函数三角形相似存在性问题448.二次函数三角形相似存在性问题(初三)x2+bx+c与x轴交于A,B两点,点A,B分别位于原点的左、右两侧,B0=3A0=3,过点B的直如图,抛物线y=3+36线与y轴正半轴和抛物线的交点分别为C,D,BC=3CD(1)求b,c的值;(2)求直线BD的函数解析式;(3)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上.当△ABD与△BPQ相似时,请直接写出所有满足条件的点Q的坐标.449.二次函数线段最大值三角形相似存在性问题(初三),D 如图,抛物线y=ax2+bx+2与x轴交于A,B两点,且OA=20B,与y轴交于点C,连接BC,抛物线对称轴为直线x=12为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.(1)求抛物线的表达式;(2)当线段DF的长度最大时,求D点的坐标;(3)抛物线上是否存在点D,使得以点0,D,E为顶点的三角形与△BOC相似?若存在,求出m的值;若不存在,请说明理由.450.二次函数铅垂定理面积最大值三角形形似存在性(初三)如图,已知抛物线y=ax2+bx+6经过两点A(―1,0),B(3,0),C是抛物线与y轴的交点.(1)求抛物线的解析式;(2)点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,设△PBC的面积为S,求S关于m的函数表达式(指出自变量m的取值范围)和S的最大值;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N使得∠CMN=90∘,且△CMN与△OBC相似,如果存在,请求出点M和点N的坐标.451.二次函数三角形面积定值三角形相似存在性问题(初三)如图,抛物线y=ax2+bx+8(a≠0)与x轴交于点A(―2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求抛物线的表达式;S△ABC时,求点P的坐标;(2)点P是第一象限内抛物线上的动点,连接PB,PC,当S△PBC=35(3)点N是对称轴1右侧抛物线上的动点,在射线ED上是否存在点M,使得以点M,N,E为顶点的三角形与△OBC相似?若存在,求点M的坐标;若不存在,请说明理由.452.二次函数平行四边形存在性三角形相似存在性问题(初三)如图,二次函数y=ax2+bx+4的图象与x轴交于点A(―1,0),B(4,0),与y轴交于点C,抛物线的顶点为D,其对称轴与线段BC交于点E,垂直于x轴的动直线1分别交抛物线和线段BC于点P和点F,动直线1在抛物线的对称轴的右侧(不含对称轴)沿x轴正方向移动到B点.(1)求出二次函数y=ax2+bx+4和BC所在直线的表达式;(2)在动直线1移动的过程中,试求使四边形DEFP为平行四边形的点P的坐标;(3)连接CP,CD,在动直线1移动的过程中,抛物线上是否存在点P,使得以点P,C,F为顶点的三角形与△DCE相似?如果存在,求出点P的坐标;如果不存在,请说明理由.453.二次函数三角形相似存在性问题(初三)已知抛物线y =ax 2+bx +3与x 轴分别交于A(―3,0),B(1,0)两点,与y 轴交于点C .(1)求抛物线的表达式及顶点D 的坐标;(2)点F 是线段AD 上一个动点.①如图1,设k =AFAD ,当k 为何值时,CF =12AD ?②如图2,以A,F,0为顶点的三角形是否与△ABC 相似?若相似,求出点F 的坐标;若不相似,请说明理由.454.二次函数三角形相似存在性问题(初三)如图1,直线y =―12x +b 与抛物线y =ax 2交于A,B 两点,与y 轴于点C ,其中点A 的坐标为(―4,8).(1)求a,b 的值;(2)将点A 绕点C 逆时针旋转90∘得到点D .①试说明点D 在抛物线上;②如图2,将直线AB 向下平移,交抛物线于E,F 两点(点E 在点F 的左侧),点G 在线段OC 上.若△GEF ∼△DBA (点G,E,F 分别与点D,B,A 对应),求点G 的坐标.455.二次函数三角形存在性问题面积倍分动点问题(初三)如图,已知抛物线y =ax 2+bx(a ≠0)过点A(3,―3)和点B(33,0).过点A 作直线AC//x 轴,交y 轴于点C .(1)求抛物线的解析式;(2)在抛物线上取一点P ,过点P 作直线AC 的垂线,垂足为D .连接OA ,使得以A,D,P 为顶点的三角形与△AOC 相似,求出对应点P 的坐标;(3)抛物线上是否存在点Q ,使得S △AOC =13S △ACQ ?若存在,求出点Q 的坐标;若不存在,请说明理由.答案448.【解】(1)∵BO=3AO=3,∴点B(3,0),点A(-1,0),∴抛物线解析式为:y =3+36(x +1)(x -3)=3+36x 2-3+33x -3+32,∴b =-3+33,c =-3+32;(2)如图1,过点D 作DE ⊥AB 于E,∴CO//DE,∴BCCD =BOOE ,∵BC =3CD,BO =3,∴3=3OE,∴OE =3,∴点D 横坐标为-3,∴点D 坐标为(-3,3+1),设直线BD 的函数解析式为:y =kx +m,把点B(3,0),D(-3,3+1)代入得:{3+1=-3k +m0=3k +m ,解得:{k =-33m =3,∴直线BD 的函数解析式为y =-33x +3;(3)∵点B(3,0),点A(-1,0),点D(-3,3+1),∴AB =4,AD =22,BD =23+2,对称轴为直线x =1,∵直线BD:y =-33x +3与y 轴交于点C,∴点C(0,3),∴OC =3,∵tan ∠CBO =COBO =33,∴∠CBO =30∘,如图1,过点A 作AF ⊥BD 于F,∴AF =12AB =2,BF =3AF =23,BD =2DE =23+2∴DF =BD -BF =23+2-23=2,∴DF =AF,∴∠ADB =45∘,设对称轴与x 轴的交点为N,即点N (1,0),BN =3-1=2,现在分两种情况讨论:第一种情况:若∠CBO =∠PBO =30∘,如图3:∴BN =3PN =2,BP =2PN,∴PN =233,BP =433,(1)当△BAD ∽△BPQ,∴BP BA=BQBD ,∴BQ =2+233,∴点Q1(1-233,0);(2)当△BAD ∽△BQP,∴BPBD=BQAB ,∴BQ =4-433,∴点Q2(-1+433,0);第二种情况:若∠PBO =∠ADB =45∘,如图3:∴BN =PN =2,BP =2BN =22,(3).当△DAB ∽△BPQ,∴BP AD=BQBD ,∴2222=BQ23+2,∴BQ =23+2,∴点Q3(1-23,0);(4).当△BAD ∽△PQB,∴BPBD=BQAD ,∴2223+2=BQ22,∴BQ ==23-2,∴点Q4(5-23,0);综上所述:满足条件的点Q 的坐标为(1-233,0)或(-1+433,0)或(1-23,0)或(5-23,0).449.【解】(1).设OB =t,则OA =2t,则点A 、B 的坐标分别为(2t,0)、(-t,0),则x =12=12(2t -t),解得:t =1,故点A 、B 的坐标分别为(2,0)、(-1,0),则抛物线的表达式为:y =a(x -2)(x +1)=ax 2+bx +2,解得:a =-1,b =1,故抛物线的表达式为:y =-x 2+x +2;(2).对于y =-x 2+x +2,令x =0,则y =2,故点C(0,2),由点A 、C 的坐标得,直线AC 的表达式为:y =-x +2,设点D 的横坐标为m,则点D (m,-m 2+m +2),则点F(m,-m +2),则DF =-m 2+m +2-(-m +2)=-m 2+2m,∵-1<0,故DF 有最大值,DF 最大时m =1,∴点D(1,2);(3)存在,理由如下:点D (m,-m 2+m +2)(m >0),则OE =m,DE =-m 2+m +2,以点O,D,E 为顶点的三角形与△BOC 相似,则DEOE =OBOC 或DEOE =OCOB ,即DOOE =12或DOOE =2,即-m 2+m +2m=12或-m 2+m +2m=2,解得:m =1或-2(舍去)或1+334或1-334(舍去),经检验m =1或1+334是方程的解,且符合题意,故m =1或1+334.450.【解】(1)将A(-1,0)、B(3,0)代入y =ax 2+bx +6,得:{a -b +6=09a +3b +6=0,解得:{a =-2b =4,∴抛物线的解析式为y =-2x 2+4x +6.(2)过点P 作PF ⊥x 轴,交BC 于点F,如图1所示.当x =0时,y =-2x 2+4x +6=6,∴点C 的坐标为(0,6).设直线BC 的解析式为y =kx +c,将B(3,0)、C(0,6)代入y =kx +c,得:{3k +c =0c =6,解得:{k =-2c =6,∴直线BC 的解析式为y =-2x +6.∵点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,∴点P 的坐标为(m,-2m 2+4m +6),则点F 的坐标为(m,-2m +6),∴PF =-2m 2+4m +6-(-2m +6)=-2m 2+6m,∴S =12PF ⋅OB =-3m 2+9m =-3(m -32)2+274,∴当m =32时,△PBC 面积取最大值,最大值为274.∵点P(m,n)在平面直角坐标系第一象限内的抛物线上运动,∴0<m <3.综上所述,S 关于m 的函数表达式为:S =-3m 2+9m(0<m <3),S 的最大值为274.(3)存在点M 、点N 使得∠CMN =90∘,且△CMN 与△OBC 相似.第一种情况:如图2,∠CMN =90∘,当点M 位于点C 上方,过点M 作MD ⊥y 轴于点D,∵∠CDM =∠CMN =90∘,∠DCM =∠NCM,∴△MCD ∼△NCM,若△CMN 与△OBC 相似,则△MCD 与△OBC 相似,设M (a,-2a 2+4a +6),C(0,6),∴DC =-2a 2+4a,DM =a,当DMCD =OBOC =36=12时,△COB ∽△CDM ∽△CMN,∴a-2a 2+4a =12,解得,a =1,∴M(1,8),此时ND =12DM =12,∴N (0,172),当CDDM =OBOC =12时,△COB ∼△MDC ∼△NMC,∴-2a 2+4a a=12,解得a =74,∴M (74,558),∴DN =2DM =72此时N (0,838).第二种情况:如图3,当点M 位于点C 的下方,过点M 作ME ⊥y 轴于点E,设M (a,-2a 2+4a +6),C(0,6),∴EC =2a 2-4a,EM =a,同理可得:2a 2-4aa =12或2a 2-4aa=2,△CMN 与△OBC 相似,解得a =94或a =3,∴M (94,398)或M(3,0),此时N 点坐标为(0,38)或(0,-32).综合以上得,存在M(1,8),N (0,172)或M (74,558),N (0,838)或M (94,398),N (0,38)或M(3,0),N (0,-32),使得∠CMN =90∘,且△CMN 与△OBC 相似.451.【解】(1)∵抛物线y =ax 2+bx +8(a ≠0)过点A (-2,0)和点B(8,0),∴{4a -2b +8=064a +8b +8=0,解得{a =-12b =3.∴拋物线解析式为:y =-12x 2+3x +8;(2)当x =0时,y =8,∴C(0,8),∴直线BC 解析式为:y =-x +8,∵S △ABC =12AB ×OC =12×10×8=40,∴S △PBC =35S △ABC =24,如图1,过点P 作PG ⊥x 轴,交x 轴于点G,交BC 于点F,设p (x,-12x 2+3x +8),∴F(x,-x +8),∴PF =-12x 2+4x,∵S △PBC =12×PF ×OB =24,∴12×(-12x 2+4x )×8=24,∴t 1=2,t 2=6,∴P 1(2,12),P 2(6,8);(3)存在,理由如下:∵C(0,8),B(8,0),∠COB =90∘,∴△OBC 为等腰直角三角形,易知拋物线的对称轴为x =3,∴点E 的横坐标为3,又∵点E 在直线BC 上,∴点E 的纵坐标为5,∴E(3,5),设M(3,m),N (n,-12n 2+3n +8),(1)如图2,当MN =EM,∠EMN =90∘,△NME ∽△COB,则{m -5=n -3-12n 2+3n +8=m ,解得{n =6m =8或{n =-2m =0(舍去),∴此时点M 的坐标为(3,8),(2)如图3,当ME =EN,∠MEN =90∘时,△MEN ∼△COB,则{m -5=n -3-12n 2+3n +8=5,解得:{m =5+15n =3+15或{m =5-15n =3-15(舍去),∴此时点M 的坐标为(3,5+15);(3)如图4,当MN =EN,∠MNE =90∘时,此时△MNE 与△COB 相似,此时的点M 与点E 关于(1)的结果(3,8)对称,设M(3,m),则m -8=8-5,解得m =11,∴M(3,11);此时点M 的坐标为(3,11);故在射线ED 上存在点M,使得以点M,N,E 为顶点的三角形与△OBC 相似,点M 的坐标为:(3,8)或(3,5+15)或(3,11).452.【解】(1)将点A(-1,0),B(4,0),代入y =ax 2+bx +4,得:{0=a -b +40=16a +4b +4,解得:{a =-1b =3,∴次函数的表达式为:y =-x 2+3x +4,当x =0时,y =4,∴C(0,4),设BC 所在直线的表达式为:y =mx +n,将C(0,4)、B(4,0)代入y =mx +n,得:{4=n o =4m +n ,解得:{m =-1n =4,∴BC所在直线的表达式为:y=-x+4;(2)∵DE⊥x轴,PF⊥x轴,∴DE//PF,只要DE=PF,四边形DEFP即为平行四边形,∵y=-x2+3x+4=-(x-32)2+254,∴点D的坐标为:(32,254),将x=32代入y=-x+4,即y=-32+4=52,∴点E的坐标为:(32,52),∴DE=254-52=154,设点P的横坐标为t,则P的坐标为:(t,-t2+3t+4),F的坐标为:(t,-t+4),∴PF=-t2+3t+4-(-t+4)=-t2+4t,由DE=PF得:-t2+4t=154,解得:t1=32(不合题意舍去),t2=52,当t=52时,-t2+3t+4=-(52)2+3×52+4=214,∴点P的坐标为(52,214);(3)存在,理由如下:如下图,连接CD,连接CP:由(2)得:PF//DE,∴∠CED=∠CFP,又∵∠PCF与∠DCE有共同的顶点C,且∠PCF在∠DCE的内部,∴∠PCF≠∠DCE,∴只有∠PCF=∠CDE时,△PCF∼△CDE,∴PFCE =CFDE,∵C(0,4),E(32,52),∴CE=322,由(2)得:DE=154,PF=-t2+4t,F的坐标为:(t,-t+4),∴CF=2t,∴-t2+4t322=2t154,∵t≠0,∴154(-t+4)=3,解得:t =165,当t =165时,-t 2+3t +4=-(165)2+3×165+4=8425,∴点P 的坐标为:(165,8425).453.【解】(1)∵抛物线y =ax 2+bx +3过点A(-3,0),B(1,0),∴{9a -3b +3=0a +b +3=0,解得:{a =-1b =-2,∴拋物线解析式为y =-x 2-2x +3;∵y =-x 2-2x +3=-(x +1)2+4∴顶点D 的坐标为(-1,4);(2)①∵在Rt △AOC 中,OA =3,OC =3,∴AC 2=OA 2+OC 2=18∵D(-1,4),C(0,3),A(-3,0),∴CD 2=12+12=2∴AD 2=22+42=20∴AC 2+CD 2=AD 2∴△ACD 为直角三角形,且∠ACD =90∘.求得直线AD 的解析式为y =2x +6,设F(m,2m +6),∵CF =12AD,∴(2m +6-3)2+m 2=(5)2,解得m =-2或m =-25(舍去),∴F(-2,2),∴F 为AD 的中点,∴AFAD=12,∴k =12.②在Rt △ACD 中,tan ∠CAD =DC AC =232=13,在Rt △OBC 中,tan ∠OCB =OBOC =13,∴∠CAD =∠OCB,∵OA =OC∴∠OAC =∠OCA =45∘,∴∠FAO =∠ACB,若以A,F,O 为顶点的三角形与△ABC 相似,则可分两种情况考虑:第一种情况:当∠AOF =∠ABC 时,△AOF ∼△CBA,∴OF//BC,设直线BC 的解析式为y =kx +b,∴{k +b =0b =3,解得:{k =-3b =3,∴直线BC 的解析式为y =-3x +3,∴直线OF 的解析式为y =-3x,设直线AD 的解析式为y =mx +n,∴{-k +b =4-3k +b =0,解得:{k =2b =6,∴直线AD 的解析式为y =2x +6,联立方程组,并解得:x =-65:,y =185∴F (-65,185).第二种情况:当∠AOF =∠CAB =45∘时,△AOF ∼△CAB,∵∠CAB =45∘,∴OF ⊥AC,即OF 是∠AOC 的角平分线,∴直线OF 的解析式为y =-x,∴联立得:{y =-xy =2x +6,解得:{x =-2y =2,∴F(-2,2).综合以上可得F 点的坐标为F (-65,185)或(-2,2).454.【解】(1)由题意,得{-12×(-4)+b =8(-4)2×a =8,解得{a =12b =6.(2)①如图,分别过点A,D 作AM ⊥y 轴于点M,DN ⊥y 轴于点N.由(1)可知,直线AB 的解析式为y =-12x +6,∴C(0,6),∵∠AMC =∠DNC =∠ACD =90∘,∴∠ACM +∠DCN =90∘,∠DCN +∠CDN =90∘,∴∠ACM =∠CDN∵CA =CD,∴△AMC ≅△CND(SAS)∴AN =AM =4,DN =CM =2,∴D(-2,2),当x =-2时,y =12×22=2,∴点D 在抛物线y =12x 2上.②由{y =-12x +6y =12x 2,解得{x =-4y =8或{x =3y =92,∴点B 的坐标为(3,92),∴直线AD 的解析式为y =-3x -4,直线BD 的解析式为y =12x +3,设E (t,12t 2),∴直线EF 的解析式为y =-12x +12t 2+12t,由{y =-12x +12t 2+12t y =12x 2,解得{y =t y =12t 2或{x =-t -1y =12(t +1)2,∴F (-t -1,12(t +1)2),∵△GEF ∼△DBA,EF//AB,由题意可知,EG//DB,GF//AD,∴直线EG 的解析式为y =12x +12t 2-12t,直线FG 的解析式为y =-3x +12(t +1)2-3(t +1),联立,解得:{x =-37t -57y =12t 2-57t -514,∴G (-37t -57,12t 2-57t -514),令-37t -57=0,解得t =-53,∴G (0,209)455.【解】(1)把A(3,-3)和点B(33,0)代入拋物线得:{3a +3b =-327a +33b =0,解得:a =12,b =-332,则抛物线解析式为y =12x 2-332x;(2)存在,分两种情况讨论:第一种情况:当P 在直线AD 上方时,设P 坐标为(x,12x 2-332x ),则有AD =x -3,PD =12x 2-332x +3,①当△OCA ∽△ADP 时,OCAD =CADP ,即3x -3=312x 2-332x +3,整理得:3x 2-93x +18=23x -6,即3x 2-113x +24=0,解得:x =833或x =3(舍去),此时P(833,-43);②.当△OCA ∽△PDA 时,OCPD =CAAD ,即312x 2-332x +3=3x-3,整理得:3x 2-9x +63=6x -63,即x 2-53x +12=0,解得:x =43或x =3(舍去),此时P(43,6);当点P(0,0)时,也满足△OCA ∽△PDA;第二种情况,当P 在直线AD 下方时,同理可得:P 的坐标为(433,-103),综上所述,P 的坐标为(833,-43)或(43,6)或(433,-103)或(0,0);(3)在Rt △AOC 中,OC =3,AC =3,根据勾股定理得:OA =23,∵12OC ⋅AC =12OA ⋅h,∴h =32,∵S △AOC =13S △AOQ =332,∴△AOQ 边OA 上的高为∴S =12×PM ×OA =12(-x 2-3x )×392,过O 作OM ⊥OA,截取OM =92,过M 作MN//=-32(x +32)2+278.当x =-32时,S 最大=278,OA,交y 轴于点N,如下图所示:在Rt △OMN 中,ON =2OM =9,即N(0,9),过M 作MH ⊥x 轴,在Rt △OMH 中,MH =12OM =94,OH =32OM =934,即M (934,94),设直线MN 解析式为y =kx +9,把M(934,94)代入得:94=934k +9,即k =-3,即y =-3x +9,联立得:{y =-3x +9y =12x 2-332x,解得:{x =33y =0或{x =-23y =15,即Q(33,0)(此时与B 点重合)或(-23,15),则拋物线上存在点Q,使得S △AOC =13S △AOQ ,此时点Q 的坐标为(33,0)或(-23,15).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数与相似三角形的综合问题
宜良八中 陈红
二次函数与相似三角形的综合问题也是上海中考数学试卷中常见的热点问题如:2012年的最后第二题,就是二次函数与相似三角形相结合的综合问题.先来看这个问题:
2012年中考第23题:如图,在平面直角坐标系中,二次函数2
6y ax x c =++的图像经过点()4,0A 、()1,0B -,与y 轴交于点C ,点D 在线段OC 上,=OD t ,点E 在第二象限,∠=90ADE ,1
=
2
tan DAE ∠,EF OD ⊥,垂足为F .
(1)求这个二次函数的解析式;
(2)求线段EF 、OF 的长(用含t 的代数式表示); (3)当∠ECA =∠OAC 时,求t 的值. 解:(1)二次函数c x ax y ++=62
图像经过 点A (4,0),B (-1,0), ∴⎩⎨
⎧=+-=++0602416c a c a ,解得⎩⎨⎧=-=8
2
c a .
∴这个二次函数的解析式为8622
++-=x x y .
(2)易证△ED F ∽△DAO ,∴
DA
ED
AO DF DO EF =
=. 在R t △ADE 中,=90ADE ,∵2
1
tan ==∠AD DE DAE ,
∴21==AO DF DO EF ,即2
1=t EF ,∴t EF 21=. ∵点A 的坐标为(4,0),∴OA =4,DF =2,∴OF =t -2. (3)由(1)得,点C 的坐标为(0,8). 延长CE 交x 轴于点G ,设G 点的坐标为(x ,0),
∵ECA =∠OAC ,∴CG= AG , ∴()22
48-=
+x x ,解得6-=x ,∴GO =6.
由已知,可得点F 在线段OD 上,
又∵OF =t -2,∴FC =OC -OF =10- t ,
∵EF ∥GO ,∴CO CF GO EF =
,∴8
1062t
t
-=,解得6=t . 【点评】本题是利用二次函数图像上的点组成图形与相似形结合,主要是运用了相似三角形中线段的比例关系来解决问题. 难点是角相等这个条件的运用,如何由角的关系转化为边的关系.
下面我们来看解答这类问题的具体方法:
例题1 如图,二次函数图像的顶点为坐标原点O 、且经过点A (3,3),一次函数的图像经过点A 和点B (6,0).
(1)求二次函数与一次函数的解析式;
(2)如果一次函数图像与y 相交于点C ,点D 在线段AC 上,与y 轴平行的直线DE 与二次函数图像相交于点E ,∠DOE =45º,求点D 的坐标.
分析:第(1)小题用待定系数法确定两个函数的解析式;第(2)小题利用△CDO ∽△OED 得比例式,设点D 坐标建立方程解决.
解:(1)设二次函数解析式为2ax y =, ∵点A (3,3)在二次函数图像上,∴a 93=,∴3
1
=
a ,∴二次函数解析式为231x y =.
设一次函数解析式为b kx y +=,∵一次函数的图像经过点A (3,3)和点B (6,0), ∴⎩⎨⎧+=+=,60,33b k b k ∴⎩
⎨⎧=-=6,1b k ∴一次函数解析式为6+-=x y .
(2)∵OC=OB ,∠BOC =90º,∴∠OCB =45º,∵∠DOE =45º,∴∠OCD =∠DOE . 又∵DE//y 轴,∴∠COD =∠ODE ,∴△CDO ∽△OED .∴CO
DO
DO DE =
, ∴CO DE DO ⋅=2.
设点D 的坐标为(6,+-m m ),∴点E 的坐标为(2
31,
m m ). ∴36122)6(2222+-=-+=m m m m OD ,231
6m m DE -+-=.
∵点C (0,6),∴CO =6.∴)31
6(63612222m m m m -+-=+-,
∴2
3,(0,064212==∴=-m ),m m m 舍去不符合题意.∴点D 的坐标为)29
,23(.
【点评】本题以二次函数为载体,结合了一次函数,观察、发现图中的相似三角形,运用相似三角形边的关系建立方程,从而求出点的坐标.
例题2 如图,已知点O 为坐标原点,二次函数)2(22+-+=m x mx y 的图象与x 轴相交于点A 、B ,点C (2,1)在二次函数的图象上,判断∠ACO 与∠CBO 之间的大小关系. 解:∵点C (2,1)在二次函数的图象上,∴,1)2(44=+-+m m ∴.31
-=m ∴函数解析式为3
52312-+-=x x y . 当0=y 时, 03
5
2312=-+-
x x ,.5,121==x x ∴A(1,0), B(5,0).
∴,512,5,122=+===OC OB OA
∴
,515,55
5====OA OC OC OB ∴OA OC
OC OB =, 又∵∠AOC =∠COB ,∴△AOC ∽△COB ,∴∠ACO=∠CBO .
【点评】本题由二次函数图像上的点,确定线段的长度,从而利用边的关系判定三角
形相似,得出角相等,这是函数图像问题中证明角相等常用的方法.
例题3 已知在平面直角坐标系中,O 为坐标原点,二次函数)0(2>+-=b c bx x y 的图像经过点A (-1,b ),与y 轴相交于点B ,且∠ABO 的余切值为3.如果这个函数图像的顶点为C ,求证:∠ACB =∠ABO .
解:根据题意,得b =1+b +c .∴c = -1.∴B (0,-1). 过点A 作AH ⊥y 轴,垂足为点H .∵∠ABO 的余切值为3, ∴3cot ==
∠AH
BH
ABO . 而AH =1,∴BH =3. ∵BO =1,∴HO =2. ∴b =2. ∴所求函数的解析式为122--=x x y .
由2)1(122
2
--=--=x x x y ,得顶点C 的坐标为(1,-2). ∴52=AC ,10=AB ,2=BC ,5=AO ,BO =1. ∴
2===BO
BC
AO AB AB AC . ∴△ABC ∽△AOB . ∴∠ACB =∠ABO .
【点评】本题由于点A 在函数图像上,所以点A 的坐标满足函数解析式,从而求得点B 的坐标,由0>b ,可知点A 在第二象限.由点B 的坐标和∠ABO 的余切值为3,就可以画出线段AB .再过点A 作y 轴的垂线,求出点A 的坐标,由点A 的坐标就可求出这个二次函数的解析式,从而得到顶点C 的坐标.然后与上题类似,利用边的关系得到相似三角形,故问题解决.
例题4 如图,一次函数m x y +-=4
3
的图像与x 轴、y 轴分别相交于点A 和点B ,二次函数64
12
++-
=bx x y 的图像经过A 、B 两点.如果点C 在这个二次函数的图像上,且点C 的横坐标为5,求tan ∠CAB 的值.
解:由题意,得点B 的坐标为(0,6).∴m =6.∴一次函数的解析式为64
3
+-=x y .
解:由题意,得点A 的坐标为(8,0).∴6884
102
++⨯-
=b .
∴4
5=b .
∴二次函数的解析式为64
5412++-=x x y . ∵点C 在这个二次函数的图像上,且点C 的横坐标为5,
∴6654
55412=+⨯+⨯-=y . ∴点C 的坐标为(5,6).
作CH ⊥AB ,垂足为点H .
∵点B 与点C 的纵坐标相等,∴BC ∥x 轴. ∴∠CBH =∠BAO .
又∵∠CHB =∠BOA =90°,∴△CHB ∽△BOA .∴AB
BO
BC CH =
. ∵OB =6,OA =8,∴AB =10. ∴10
6
5=CH .∴CH =3,BH =4,AH =6.
∴2
1
63tan ==∠CAB .
【点评】由于本题二次函数解析式的常数项是确定的,所以直接可以得出它的图像与y 轴的交点坐标.解决本题的关键是利用二次函数的解析式确定点C 坐标,在求三角比时,运用了相似三角形的方法,当然还可以运用面积的方法来解.
【这类问题的解题反思】在解决二次函数与相似三角形的综合问题过程中,主要是运用二次函数的解析式和图形的对称性以及相似三角形相关知识,往往还会涉及方程、距离公式、锐角三角比等相关知识,有时会运用图形运动的相关知识.
在解决问题的过程中,首先要会熟练地用待定系数法、配方法等数学方法.还要会用有关的数学思想,如化归思想、方程思想、函数思想、数形结合思想,特别是分类讨论思想.。
