数据结构课程设计报告(校园导游系统)附有源代码
数据结构(C语言版)实验报告 (校园导游咨询)
《数据结构与算法》实验报告一、需求分析【问题描述】设计一个校园导游程序，为来访的客人提供各种信息查询服务。
【基本要求】(1)设计你所在学校的校园平面图，所含景点不少于10个。
以图中顶点表示校内各景点，存放景点名称、代号、简介等信息；以边表示路径，存放路径长度等相关信息。
(2)为来访客人提供图中任意景点相关信息的查询。
(3)为来访客人提供图中任意景点的问路查询，即查询任意两个景点之间的一个最短的简单路径。
【测试数据】由读者根据实际情况指定。
【实现提示】一般情况下，校园的道路是双向通行的，可设校园平面图是一个无向网。
顶点和边均含有相关信息。
【选作内容】(6)扩充每个景点的邻接景点的方向等信息，使得路径查询结果能提供详尽的导向信息。
二、概要设计1）抽象数据类型定义描述#include<iostream>using namespace std;const int MaxSize=18;const int INFINITY=65535;//最大值无穷class direction;template <class T> class MGraph;template <class T>class VertexNode//定义景点结点，存储景点信息{friend class MGraph<T>;public:int vex;//景点名称T vexname;//景点名称T vexinf;//景点信息direction dir;//存放景点方位信息的direction类的dir。
};class direction{public:int ln;//存放在方向图中的横坐标，表示东西int col;//存放在方向图中的纵坐标，表示南北};template <class T>class MGraph//定义无向图的邻接矩阵{public:MGraph();//构造函数，初始化具有n个顶点的图void printvexname();//显示所有景点及景点代号void printvexinf(int i);//显示代号为i景点的名称及信息void printroad(int i,int j);//显示景点i~j的最短路径方案信息void printdir(int i,int j);//显示景点i到j的方向信息，如“向东100m，向南200m”VertexNode<T> adjlist[MaxSize]; //存放景点全部信息的景点类数组int vertexNum,arcNum; //图的顶点数和边数void Root(int p,int q);//递归寻找pq间的最短路径int Path[MaxSize][MaxSize],Dist[MaxSize][MaxSize];//创建Path和Dist分别存放两点间最短路径的前驱节点，两点间最短路径长度int Line[MaxSize];//Line存放路径int kkk;//在floyed算法中，做Line[]数组的标记private:T vertex[MaxSize]; //存放图中顶点的数组int arc[MaxSize][MaxSize];//存放图中边的数组};2）功能模块设计（如主程序模块设计）int funcchoice()//系统功能选择页面{int choice;cout<<"=============================================================="<<endl;cout<<" 欢迎进入校园导游咨询平台"<<endl;cout<<" 1--显示校园所有景点信息"<<endl;cout<<" 2--查询校园景点信息"<<endl;cout<<" 3--问路查询系统"<<endl;cout<<" 4--退出导游资讯平台"<<endl;cout<<"=============================================================="<<endl;cout<<"请输入要选择的功能号：";cin>>choice;return choice;}3）模块层次调用关系图三、详细设计//程序的头文件#include<iostream>#include<iomanip>#include"guide.h"using namespace std;template <class T>MGraph<T>::MGraph()//a[]为景点代号，b[]为景点名称，c[]为景点信息，d[]为景点方位信息的横坐标，e[]为景点方位信息的纵坐标，s[]为存放景点邻接矩阵信息的一维数组，根据其对称性可以用公式赋值给二维数组arc[][]{i nt s[]={0,1,0,0,2,0,0,0,2,0,0,0,2,3,0,0,0,0,4,2,0,0,0,0,0,2,3,0,0,0,0,0,2,3,1,0,0,0,2,0,2,0,0,2,0,4,0,2,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,2,0,1,0,0,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,3,0,0,2,0,0,0,0,0,0,0,0,0,0,0,0,0,4,4,0,0,2,0};i nt a[]={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17};c har* b[]={"南门","实验楼","南图","大活","睿思楼","大礼堂","南4教","知行楼","国交楼","南3教","南2教","南1教","北图","北3教","北4教","北2教","北1教","北门"};c har* c[]={"南校区正门","物理实验楼","南校区图书馆","大学生活动中心","教师办公楼、医务室及留学生公寓","大礼堂，用于举办各种文艺演出","南校区第4教学楼","实习基地，计算机房等","国际交流中心，教职工餐厅","南校区第3教学楼","南校区第2教学楼","南校区第1教学楼","北校区图书馆","北校区第3教学楼","北校区第4教学楼","北校区第2教学楼","北校区第1教学楼","北校区正门"};i nt d[]={8,6,4,4,1,0,0,1,3,4,6,8,4,3,2,3,5,8};i nt e[]={8,8,8,10,8,10,7,6,6,6,6,6,3,1,0,0,0,2};i nt i,j;v ertexNum=18;a rcNum=30;f or(i=0;i<vertexNum;i++){adjlist[i].vex=a[i];adjlist[i].vexname=b[i];adjlist[i].vexinf=c[i];adjlist[i].dir.ln=d[i];adjlist[i].dir.col=e[i];}f or (i=0; i<vertexNum; i++)//初始化邻接矩阵for (j=0; j<vertexNum; j++)arc[i][j]=arc[j][i]=s[(i*(i+1))/2+j]; //根据s[]的对称性，将一维数组中的数据赋给二维数组arc[][]}template<class T>void MGraph<T>::printvexname(){i nt i;f or(i=0;i<vertexNum;i++)cout<<adjlist[i].vex<<" "<<adjlist[i].vexname<<endl;;}template<class T>void MGraph<T>::printvexinf(int i){c out<<i<<" "<<adjlist[i].vexname<<":"<<adjlist[i].vexinf<<endl;}template<class T>void MGraph<T>::printdir(int i,int j){i nt dx,nb;//临时存放i与j之间的南北东西关系 j在i的哪边？？d x=adjlist[j].dir.col-adjlist[i].dir.col;n b=adjlist[j].dir.ln-adjlist[i].dir.ln;i f(dx>0)//即j在i的东边cout<<"向东"<<dx*100<<"m，";e lsecout<<"向西"<<dx*(0-100)<<"m，";i f(nb>0)//即j在i的南边cout<<"向南"<<nb*100<<"m";e lsecout<<"向北"<<nb*(0-100)<<"m";}template<class T>void MGraph<T>::Root(int p,int q){i f (Path[p][q]>0){Root(p,Path[p][q]);Root(Path[p][q],q);}e lse{Line[kkk]=q;kkk++;}}template<class T>void MGraph<T>::printroad(int i,int j){i nt p,q,m,k,item1,item2;f or(p=0;p<vertexNum;p++)for(q=0;q<vertexNum;q++)Dist[p][q]=arc[p][q];//邻接矩阵赋值f or(k=0;k<vertexNum;k++)for(p=0;p<vertexNum;p++)if (Dist[p][k]>0)for(q=0;q<vertexNum;q++)if (Dist[k][q]>0)if (((Dist[p][q]>Dist[p][k]+Dist[k][q])||(Dist[p][q]==0))&&(p!=q)){Dist[p][q]=Dist[p][k]+Dist[k][q];Path[p][q]=k;}c out<<"\n=====================================================\n";c out<<"从"<<adjlist[i].vexname<<"到"<<adjlist[j].vexname<<"的最短路径为："<<endl;c out<<adjlist[i].vexname;k kk=2;R oot(i,j);i tem2=Line[2];c out<<"-->";p rintdir(i,item2);c out<<"-->"<<adjlist[item2].vexname;f or(m=3;m<=kkk-1;m++){item1=Line[m];cout<<"-->";printdir(item1-1,item1);cout<<"-->"<<adjlist[item1].vexname;}c out<<endl;c out<<"\n=====================================================\n";}========================以下为main.cpp文件中主函数的实现========================== #include<iostream>#include"guide.cpp"using namespace std;int funcchoice()//系统功能选择页面{i nt choice;c out<<"=============================================================="<<endl;c out<<" 欢迎进入校园导游咨询平台"<<endl;c out<<" 1--显示校园所有景点信息"<<endl;c out<<" 2--查询校园景点信息"<<endl;c out<<" 3--问路查询系统"<<endl;c out<<" 4--退出导游资讯平台"<<endl;c out<<"=============================================================="<<endl;c out<<"请输入要选择的功能号：";c in>>choice;r eturn choice;}void main(){M Graph<char*> mg;i nt funcchoice();i nt fc;w hile(1){fc=funcchoice();if(fc==1){int i;for(i=0;i<mg.vertexNum;i++)mg.printvexinf(i);}else if(fc==2){int i;mg.printvexname();cout<<endl<<"请输入所要查询景点代号：";cin>>i;mg.printvexinf(i);}else if(fc==3){int i,j;mg.printvexname();cout<<"请输入两景点代号（我们将把最短路线反馈予您）：";cin>>i>>j;mg.printroad(i,j);}else if(fc==4)break;elsecout<<"输入有误，请重新输入！"<<endl;}}if调试分析遇到的问题及解决的办法：在调试过程中，最常见到的问题有以下几种：1、忘记调用函数类模块template<class T>，有些类中或者函数中涉及函数类模块的调用，但忘记标注会导致编译错误。
西安邮电大学-(数据结构)校园导游系统课程教学设计报告
西安郵電大學数据结构课程设计报告书崔斌专业名称 计算机科学与技术专业计科1106系部名称计算机学院 学生姓名04111185指导教师2012年12月15日 至 间2012年12月21日实验题目：校园导游系统一、实验目的① ：为了让非本校的同学们，家长们能够充分了解本校 ---西安邮电大学。
② ：实践数据结构所学知识。
二、实验内容学校简易的俯视图。
各个景点的简单介绍。
任意两景点之间的所有路径。
任意两景点之间的最少中转景点路径。
任意两景点之间的带权路径长度。
三、需求分析①: ②: ③: ④: ⑤:Init();初始化两个顺序栈Menu();进行选择的模块函数；Intro();景点介绍函数；SearchO;判断是否有此编号的景点；Fin dall path();找路径函数；Fin dallway();找任意两个景点之间的所有路径；(存在栈里面) ShortestwayO;任意两个景点之间中转次数最少的路径；(从栈里面读取出来) NicewayO;任意两个景点之间总权值最小的路径；(从栈里面读取出来) Calculate();(从栈里面读取出来相关数据)，进行分析运算；Byebye();你懂得！四、概要设计1、方案设计对系统进行分析，给出景区图+++++++++++牛++++++++¥++++占-I-ILnJ一戸IJ]一(一恃//思想；递归结合循环，然后，找到终点时还要回溯；两点之间的所有路径void findallway(adjlist *G,int m,int n)//int i,t,k;arcnode *p;p a_th rp;p ush(s,m);G->vertex[m-1].flag=1;if(m==n)rp .sumweight=k=calculate(G);rp .sum=s->t op;rp.num=(y+1);p ush1(&z,r p);printf(" 路径%3d 为(途径%2d 个景点，长度为%3d) : ",y+1,s->top,k);for(i=O;iv=s->t op ;i++)p rintf("->%d",s->elem[i]);p rintf("\n");G->vertex[m-1].flag=1;y++;//外部全局变量二for(p=G->vertex[m-1].firstarc ;p!=NULL ;p=p-> nextarc)t=p->num;if(G->vertex[t-1].flag==0)findallway(G,t,n);G->vertex[s->elem[s->to p]-1].flag=0;// pop s(s);}//从文件里读取数据;错误1 ;不知道此节点有几个邻接点，因为%s 的原因，就会只把第一个节点的相关数据读出来，从第二个节点的相关信息处，开始读出错误(即烫烫烫烫烫烫烫烫烫烫烫)不超过m;错误2 ;读文件时，因为有链表的部分，就按照单链表的创建些写，结果总是此节点的 最后一个邻接点没被读到内存里，究其原因，是最后一个 (不仅我把 p2->nextarc=NULL;还把 free(p1);)void readnet(adjlist *G) {int i,count,m;arcnode *head,* p2,* p1; FILE *fp;fp=fo pen(U,"rt"); if(fp==NULL) {printf(-文件打开失败！ ！ ");exit(0);}for(i=0;i<vnum;i++) {fscanf(fp,"%d %s %s %d %d",&G->vertex[i].num,G->vertex[i].name,G->vertex[i].introduce,&G->vertex[ i].sum,&G->vertex[i].flag);//fprintf()的''后面不加第一个空格也可以。
数据结构校园导航系统课程设计报告
《校园导航系统》课程设计报告姓名：蒋小文学号：110236100123 班级：1班专业：网络工程指导教师：唐轶媛蒋荣萍时间：2012年7月5日信息科学与工程学院目录摘要 (1)1.目的 (2)2.要求 (2)3.题目 (2)4.任务 (2)1).需求分析 (3)2).概要设计 (4)3).详细设计 (5)4).调试分析 (8)5.课设总结 (18)6.附录源代码 (19)1.目的数据结构是计算机专业的核心课程，是一门实践性很强的课程。
课程设计是加强学生实践能力的一个强有力手段，要求学生掌握数据结构的应用、算法的编写、类C语言的算法转换成C （C++）程序并上机调试的基本方法，还要求学生在完成程序设计的同时能够写出比较规范的设计报告。
2.要求2.1 课程设计时间为2周；2.2 设计语言C（C++）不限；2.3 课余时间完成源程序和课程设计报告等文档书写工作，上机时间只能做调试工作。
上机时带上源程序、数据结构教材、C语言教材。
2.4 上机任务（1）选择并定义合适的数据结构；（2）根据程序所要完成的基本要求，设计出完整的算法；（3）设计出主程序（main函数），使其成为完整的程序。
2.5 上机时间：上午8:30--11:30，下午3:00--5:303.题目题目：校园导航系统设计一个校园导游程序，后台操作：3.1、操作员信息管理如修改密码等3.2、能根据学校的规模进行添加景点信息、修改景点信息等功能，3.3、若临时有交通管制，能进行交通管制的设置和撤销（如某某时间段那条路进行那个方向的交通管制等）3.4、前台为来访的客人提供各种信息查询服务：3.4.1、设计学校的校园平面图，所含景点不少于10个。
以图中顶点表示校内各景点，存放景点名称、代号、简介等信息；以边表示路径，存放路径长度等相关信息。
3.4.2、为来访客人提供图中任意景点相关信息的查询。
3.4.3、提供途中任意景点问路查询，即求任意两个景点间的一条最短的简单路径。
c++数据结构课程设计校园导游设计代码
C++数据结构课程设计——校园导游设计代码1. 引言在现代高校教育中，数据结构课程的重要性不言而喻。
而在C++语言中，有关数据结构的课程设计更是相当重要。
本文将探讨如何利用C++语言设计校园导游系统的代码，并给出详细的设计方案和代码实现。
2.设计思路校园导游系统主要包括地图信息的输入、导游路线的规划、用户信息的管理和景点信息的展示。
我们将采用图的数据结构和Dijkstra算法来实现导游路线的规划，采用链表和栈的数据结构来实现用户信息的管理，采用数组和哈希表的数据结构来实现景点信息的展示。
3.系统架构3.1 地图信息的输入为了实现地图信息的输入，我们将采用图的数据结构来描述校园内的各个景点之间的相互关系。
每个景点将作为图的一个节点，而景点之间的路径将作为图的一条边。
我们将设计一个函数来输入景点之间的相互关系，并将其存储在图的邻接矩阵中。
3.2 导游路线的规划为了实现导游路线的规划，我们将采用Dijkstra算法来求解最短路线。
我们将设计一个函数来实现Dijkstra算法，并根据用户的起始点和终点来输出最短路线。
3.3 用户信息的管理为了实现用户信息的管理，我们将采用链表和栈的数据结构来存储用户的历史操作信息。
我们将设计一个函数来实现用户信息的录入和查询，并将其存储在链表和栈中进行管理。
3.4 景点信息的展示为了实现景点信息的展示，我们将采用数组和哈希表的数据结构来存储校园内各个景点的相关信息。
我们将设计一个函数来实现各个景点信息的录入和展示，并将其存储在数组和哈希表中进行管理。
4. 代码实现以下是校园导游系统的C++代码实现：```// TO DO```5. 结语通过以上的设计方案和代码实现，我们成功利用C++语言设计了一个校园导游系统。
该系统能够实现地图信息的输入、导游路线的规划、用户信息的管理和景点信息的展示。
希望本文能够给读者在学习C++数据结构课程设计时提供一定的帮助。
除了以上提到的功能，校园导游系统还可以增加更多的特色功能，比如语音导览、虚拟现实导览、导游路线的可视化展示等。
校园导游系统
西安郵電大学数据结构课程设计报告题目：校园导游系统院系名称：专业名称：班级：学生姓名：学号（8位）：指导教师：设计起止时间：2013年12月16日~2013年12月27日一. 设计目的（1）了解二叉树特性、存储及其操作实现，在计算机领域运用二叉树编译代码实现一件简单实际的操作，熟练掌握二叉树的三种遍历递归与非递归的实现；（2）掌握图的两种遍历深度优先遍历和广度优先遍历，了解两者的区别和优缺点。
学习在计算机中表示和处理图形结构以及绘制简单的地图并输出，熟练掌握图的逻辑结构和存储结构，学习用算法来解决实际问题；（3）掌握邻接链表和邻接矩阵的存储结构，以及这两者的区别，会用邻接链表和邻接数组两种方法来实现数据的存储与读取；（4）巩固文件的存储与读取部分，以便能够加深对文件读写的理解和更好的更熟练的实际应用；（5）学会用计算机解决实际问题，将生活中的问题数据化，然后输入到计算机中以便更快的解决，提高自己的实践能力以及自身的学习能力，加深对课本知识的理解和掌握。
二. 设计内容<1> 设计题目：设计一个校园导游程序，并按各要求进行编程：要求：（1）设计并显示学校的校园平面图，地点（地点名称、地点介绍），路线（公里数）均不少于10个。
（2）提供图中任意地点相关信息的查询。
（3）提供图中任意地点的问路查询：1>任意两个地点之间的一条最短的简单路径；（最短路径长度——中转次数最少）2>任意两个地点之间的一条最佳访问路线；（带权（公里数）最短路径长度）3>任意两个地点之间的所有简单路径。
（4）提供图中所有地点的最佳布网方案；（5）增加新地点和路线、撤销旧地点和路线。
三．概要设计1．功能模块图：2．各个模块详细的功能描述。
该导游系统能为来访者提供包括景点介绍、景点查询、仿真地图、最短路径之类的快捷指导。
最短路径查询和景点概况主要运用了Dijstra算法来实现，其他功能都是通过一些简单的算法来编写的。
数据结构-校园导游程序(附源码)
数据结构-校园导游程序(附源码)简介本文档旨在介绍一个校园导游程序的设计与实现。
该程序使用数据结构来管理校园地点信息，并提供导游功能，供用户查找并导航到目标地点。
文档将依次介绍相关的背景知识、程序设计原理、算法实现以及使用方法。
目录1.背景知识1.校园导游需求2.数据结构概述2.程序设计原理1.数据结构设计2.地点信息管理3.导航算法设计3.算法实现1.数据结构定义2.地点信息管理算法3.导航算法4.使用方法1.程序安装2.数据录入3.导游功能使用5.附录1.附件1：源码文件2.附件2：数据样例1.背景知识1.1 校园导游需求校园导游程序是为了帮助使用者在校园中快速找到目标地点，并提供导航功能，方便出行和参观。
该程序需要管理校园地点的信息，包括名称、位置和介绍等。
使用者可以通过程序查找地点、导航到目标地点。
1.2 数据结构概述数据结构是计算机中用来组织和存储数据的方式。
在校园导游程序中，我们需要选择适合的数据结构来存储和管理地点信息。
常用的数据结构有数组、链表、树、图等。
根据需求分析，我们可以使用图这一数据结构来表示校园地点之间的关系，方便进行导航。
2.程序设计原理2.1 数据结构设计在校园导游程序中，我们使用图这一数据结构来表示校园地点之间的关系。
每个地点可以看作图的一个节点，节点之间的边表示地点之间的连接关系。
通过构建图数据结构，我们可以方便地管理地点信息并进行导航。
2.2 地点信息管理地点信息管理是校园导游程序的核心功能之一。
我们需要设计适合的数据结构来存储地点的信息，包括名称、位置和介绍等。
通过合理的数据结构设计，可以快速地查找和修改地点信息。
2.3 导航算法设计导航算法是实现导游功能的关键。
我们需要设计算法来计算出从起点到目标地点的最短路径，并提供导航指引。
常用的导航算法有Dijkstra算法、A算法等，我们根据需求选择合适的算法进行实现。
3.算法实现3.1 数据结构定义我们使用图这一数据结构来表示校园地点之间的连接关系。
(完整word版)数据结构校园导游系统课程设计
滨江学院《数据结构》课程设计题目校园导游咨询程序设计学号学生姓名院系专业指导教师二Ｏ一二年月日1、题目的内容及要求设计一个校园导游程序，为来访的客人提供各种信息查询服务。
2、需求分析（1）设计你的学校的校园平面图，所含景点不少于10个.以图中顶点表示学校各景点,存放景点名称、代号、简介等信息；以边表示路径，存放路径长度等相关信息。
（2）为来访客人提供图中任意景点的问路查询，即查询任意两个景点之间的一条最短的简单路径。
（3）为来访客人提供图中任意景点相关信息的查询。
3、概要设计1．功能模块图;void CreateUDN();//创建无向网void Search（）;//查询景点信息void Shortestpath（int i)；//计算最短路径void Output（int sight1，int sight2)；//输出函数2．各个模块详细的功能描述。
CreateUDN()；//创建无向网、主要用来保存各景点信息Search（)；//查询景点信息、景点的名称及介绍Shortestpath(int i)；//计算两景点间最短路径Output（int sight1，int sight2）；//输出两景点最短路径及信息3。
模块图4、详细设计一、图的储存结构#define Max 30000#define NUM 10typedef struct ArcCell｛int adj; /＊相邻接的景点之间的路程＊/ ｝ArcCell; /* 定义边的类型＊/ typedef struct VertexType｛int number；/＊景点编号＊/char ＊sight; /＊景点名称＊/char ＊description;/＊景点描述 */｝VertexType; /＊定义顶点的类型 */typedef struct｛VertexType vex［NUM]； /＊图中的顶点，即为景点＊/ ArcCell arcs［NUM][NUM］；/* 图中的边，即为景点间的距离 */ int vexnum，arcnum；/* 顶点数，边数＊/｝MGraph； /* 定义图的类型二、算法1.主程序void main(){int v0，v1；char ck;CreateUDN(NUM,11);do{ck=Menu（）；switch（ck){case ’1’：system("cls”);// narrate();printf（"\n\n\t\t\t请选择起点景点（0～9）：”）；scanf（”%d",＆v0）;printf（”\t\t\t请选择终点景点（0~9）：”）;scanf(”％d",＆v1）；ShortestPath（v0); /＊计算两个景点之间的最短路径＊/ output（v0,v1）; /＊计算两个景点之间的最短路径 */ printf("\n\n\t\t\t\t请按任意键继续。
数据结构课程设计——校园导游咨询系统
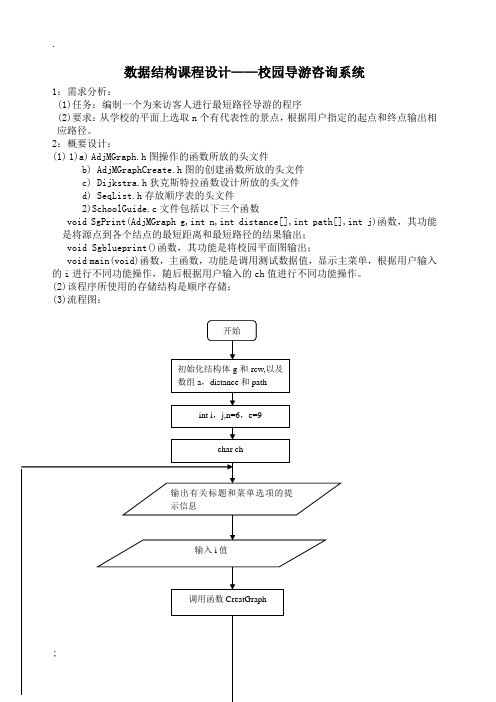
数据结构课程设计——校园导游咨询系统1：需求分析：(1)任务：编制一个为来访客人进行最短路径导游的程序(2)要求：从学校的平面上选取n个有代表性的景点，根据用户指定的起点和终点输出相应路径。
2：概要设计：(1)1)a)AdjMGraph.h图操作的函数所放的头文件b) AdjMGraphCreate.h图的创建函数所放的头文件c) Dijkstra.h狄克斯特拉函数设计所放的头文件d) SeqList.h存放顺序表的头文件2)SchoolGuide.c文件包括以下三个函数void SgPrint(AdjMGraph g,int n,int distance[],int path[],int j)函数，其功能是将源点到各个结点的最短距离和最短路径的结果输出；void Sgblueprint()函数，其功能是将校园平面图输出；void main(void)函数，主函数，功能是调用测试数据值，显示主菜单，根据用户输入的i进行不同功能操作，随后根据用户输入的ch值进行不同功能操作。
(2)该程序所使用的存储结构是顺序存储；(3)流程图：图1-1主函数main()流程图图1-2 SgPrint函数流程图3:详细设计：(1)/*顺序表头文件SeqList.h*/typedef struct{DataType list[MaxSize];int size;}SeqList;void ListInitiate(SeqList *L) /*初始化顺序表L*/ {L->size=0; /*定义初始化数据元素个数*/}int ListLength(SeqList L) /*返回顺序表L的当前数据元素个数*/{return L.size;}int ListInsert(SeqList *L,int i,DataType x)/*在顺序表L的第i(0≤i≤size)个位置前插入数据元素值x*//*插入成功返回1，插入失败返回0*/{int j;if(L->size>=MaxSize){printf("顺序表已满无法插入！\n");return 0;}else if(i<0||i>L->size){printf("参数i不合法！\n");return 0;}else{/*为插入做准备*/for(j=L->size;j>i;j--)L->list[j]=L->list[j-1];L->list[i]=x;/*插入x*/L->size++;/*元素个数加1*/return 1;}}int ListDelete(SeqList *L,int i,DataType *x){/*删除顺序表L中位置为i(0≤i≤size-1)的数据元素并存放到x中*/ /*删除成功返回1，删除失败返回0*/int j;if(L->size<=0){printf("顺序表已空无数据元素可删！\n");return 0;}else if(i<0||i>L->size-1){printf("参数i不合法");return 0;}else{*x=L->list[i]; /*保存删除的元素到x中*//*依次前移*/for(j=i+1;j<=L->size-1;j++)L->list[j-1]=L->list[j];L->size--;return 1;}}int ListGet(SeqList L,int i,DataType *x)/*取顺序表L中第i个数据元素存于x中，成功返回1.失败返回0*/ {if(i<0||i>L.size-1){printf("参数i不合法！\n");return 0;}else{*x=L.list[i];return 1;}}(2)/*AdjMGraph.h图操作的函数所放的头文件*/#include"Seqlist.h"/*包含顺序表头文件*/typedef struct{SeqList Vertices;/*存放结点的顺序表*/int edge[MaxVertices][MaxVertices];/*存放边的邻接矩阵*/ int numOfEdges;/*边的条数*/}AdjMGraph;/*图的结构体定义*/void Initiate(AdjMGraph *G,int n)/*初始化*/{int i,j;for(i=0;i<n;i++)for(j=0;j<n;j++){if(i==j) G->edge[i][j]=0;else G->edge[i][j]=MaxWeight;}G->numOfEdges=0;/*边的条数置为0*/ListInitiate(&G->Vertices);/*顺序表初始化*/}void InsertVertex(AdjMGraph *G,DataType vertex)/*在图G中插入结点vertex*/{ListInsert(&G->Vertices,G->Vertices.size,vertex);/*顺序表尾插入*/}void InsertEdge(AdjMGraph *G,int v1,int v2,int weight)/*在图G中插入边<v1,v2>,边<v1,v2>的权为weight*/if(v1<0||v1>G->Vertices.size||v2<0||v2>G->Vertices.size){printf("参数v1或v2越界出错！\n");exit(1);}G->edge[v1][v2]=weight;G->numOfEdges++;}void DeleteEdge(AdjMGraph *G,int v1,int v2)/*在图G中删除边<v1,v2>*/{if(v1<0||v1>G->Vertices.size||v2<0||v2>G->Vertices.size){printf("参数v1或v2越界出错！\n");exit(1);}G->edge[v1][v2]=MaxWeight;G->numOfEdges--;}void DeleteVerten(AdjMGraph *G,int v)/*删除结点V*/{int n=ListLength(G->Vertices),i,j;DataType x;for(i=0;i<n;i++)/*计算删除后的边数*/for(j=0;j<n;j++)if((i==v||j==v)&&G->edge[i][j]>0&&G->edge[i][j]<MaxWeight) G->numOfEdges--;/*计算被删除边*/for(i=v;i<n;i++) /*删除第v行*/for(j=0;j<n;j++)G->edge[i][j]=G->edge[i+1][j];for(i=0;i<n;i++) /*删除第v列*/for(j=v;j<n;j++)G->edge[i][j]=G->edge[i][j+1];ListDelete(&G->Vertices,v,&x);/*删除结点v*/}int GetFirstVex(AdjMGraph G,int v)/*在图G中寻找序号为v的结点的第一个邻接结点*//*如果这样的邻接结点存在，返回该邻接结点的序号；否则，返回-1*/int col;if(v<0||v>G.Vertices.size){printf("参数v越界出错\n");exit(1);}for(col=0;col<G.Vertices.size;col++)if(G.edge[v][col]>0&&G.edge[v][col]<MaxWeight)return col;return -1;}int GetNextVex(AdjMGraph G,int v1,int v2)/*在图G中寻找v1结点的邻接结点v2的下一个邻接结点*//*如果这样的邻接结点存在，返回该邻接结点的序号；否则，返回-1*//*v1和v2都是相应结点的序号*/{int col;if(v1<0||v1>G.Vertices.size||v2<0||v2>G.Vertices.size){printf("参数v1或v2越界出错！\n");exit(1);}for(col=v2+1;col<G.Vertices.size;col++)if(G.edge[v1][col]>0&&G.edge[v1][col]<MaxWeight) return col;return -1;}(3)/*AdjMGraphCreate.h图的创建函数所放的头文件*/typedef struct{int row;/*行下标*/int col;/*列下标*/int weight;/*权值*/}RowColWeight;/*边信息结构体定义*/void CreatGraph(AdjMGraph *G,DataType V[],int n,RowColWeight E[],int e) /*在图G中插入n个结点信息V和e条边信息E*/{int i,k;Initiate(G,n);/*结点顺序表初始化*/for(i=0;i<n;i++)InsertVertex(G,V[i]);/*结点插入*/for(k=0;k<e;k++)InsertEdge(G,E[k].row,E[k].col,E[k].weight);/*边插入*/}(4)/* Dijkstra.h狄克斯特拉函数设计所放的头文件*/void Dijkstra(AdjMGraph G,int v0,int distance[],int path[])/*带权图G从下标v0结点到其他结点的最短距离distance*//*和最短路径下标path*/{int n=G.Vertices.size;int *s=(int *)malloc(sizeof(int)*n);int minDis,i,j,u;/*初始化*/for(i=0;i<n;i++){distance[i]=G.edge[v0][i];s[i]=0;if(i!=v0&&distance[i]<MaxWeight) path[i]=v0;else path[i]=-1;}s[v0]=1;/*标记结点v0已从集合T加入到集合S中*//*在当前还未到最短路径的结点集中选取具有最短距离的结点u*/for(i=1;i<n;i++){minDis=MaxWeight;for(j=0;j<n;j++)if(s[j]==0&&distance[j]<minDis){u=j;minDis=distance[j];}/*当已不再存在最短路径时算法结束；此语句对非连通图是必须的*/if(minDis==MaxWeight)return;s[u]=1;/*标记结点u已从集合T加入到集合S中*//*修改从v0到其他结点的最短距离和最短路径*/for(j=0;j<n;j++)if(s[j]==0&&G.edge[u][j]<MaxWeight&&distance[u]+G.edge[u][j]<distance[j]) {/*结点v0经结点u到其他结点的最短距离和最短路径*/distance[j]=distance[u]+G.edge[u][j];path[j]=u;}}}(5)/*SchoolGuide.c文件*/#include<stdio.h>#include<stdlib.h>#include<malloc.h>typedef char DataType;#define MaxSize 100#define MaxVertices 10#define MaxWeight 10000#include"AdjMGraph.h"#include"AdjMGraphCreate.h"#include"Dijkstra.h"void SgPrint(AdjMGraph g,int n,int distance[],int path[],int j){ /*输出源点到其他各结点的最短距离和最短路径*/int i;/*从源结点到其他各结点的最短路径及其距离分别为：*/printf("从该结点%c到其他各结点的最短路径及其距离分别为：\n",g.Vertices.list[j]);printf("\n");//输出换行符for(i=0;i<n;i++){ /*从源结点到当前结点的最短路径为*/printf("从结点%c到结点%c的最短路径为:",g.Vertices.list[j],g.Vertices.list[i]);printf("(");//输出左括号if(path[i]!=-1)//源点到其他结点的最短路径的前一结点判断{ if(path[path[i]]!=-1)//该前一结点的前一结点进行判断{if(path[path[path[i]]]!=-1)//该前一结点的前一结点的前一结点进行判断{printf("%c,",g.Vertices.list[path[path[path[i]]]]);//输出相应存在的前一结点}printf("%c,",g.Vertices.list[path[path[i]]]);//输出应存在的前一结点}printf("%c,",g.Vertices.list[path[i]]);//输出应存在的前一结点}printf("%c",g.Vertices.list[i]);//输出当前结点printf(")");//输出换行符右括号printf("，其最短距离为%d；\n",distance[i]);//输出源点到其他结点的最短距离printf("\n");//输出换行符}}void Sgblueprint(){/*显示校园平面图*/printf(" ——————校园平面图——————\n");printf(" B(学生宿舍)———————————————————E(商业街)\n");printf(" / \\ / | \n");printf(" / \\ / | \n");printf(" / \\(B到D) /| \n");printf(" / \\ / | \n");printf(" / \\ / | \n");printf("A(校门口) ———————————————————D(学校食堂和 | \n");printf("| 学校田径场(学校田径场在学校食堂后面)) \\ | \n");printf("| \\(D到F)| \n");printf("| \\| \n");printf("C(第一、第二教学楼和校办) ———————————————————F(第三教学楼和实验楼)\n");}void main(void){AdjMGraph g;char a[]={'A','B','C','D','E','F'};RowColWeightrcw[]={{0,2,5},{0,3,30},{1,0,2},{1,4,8},{2,1,15},{2,5,7},{4,3,4},{5,3,10},{5,4,18}};int i,j,n=6,e=9;//i为控制控制菜单项的数值，j为选取源点的数值char ch;int distance[6],path[6];printf(" 校园导游咨询系统------您身边的导游 \n");printf("\n");printf("\n");printf("\n");/*菜单选项*/printf(" 1:请求校园导游帮组(即咨询校园各景点最短路径)\n");printf(" 2:显示校园平面图\n");printf(" 3:退出校园导游咨询系统\n");printf("请输入你所想进行的功能选项：\n");scanf("%d",&i); //输入控制控制菜单项的数值i的值CreatGraph(&g,a,n,rcw,e);//创建图switch(i){ //选择菜单项的操作case 1:system("cls");/*调用输出校园平面图函数并输出校园平面图*/Sgblueprint();/*提示用户输入起点的序列号*/printf("请输入你所在地或起点的序列号(A-F的序列号为依次0，1,2,3,4，5)：\n");scanf("%d",&j);//用户输入起点的序列号i的值/*调用狄克斯特拉函数计算源点的其他各结点的最短路径及其距离*/Dijkstra(g,j,distance,path);/*提示用户参照校园平面图以了解各景点的代号的含义*/printf("提示：下列A、B、C等均是各景点的代号，如有问题，请参考上面的校园平面图\n");/*调用输出源点到其他各结点的最短距离和最短路径函数并输出相应的最短路径和最短距离*/SgPrint(g,n,distance,path,j);break;case 2:system("cls");Sgblueprint();//调用输出校园平面图函数并输出校园平面图break;case 3:exit(1);break;//退出程序}while(3)//判断程序是否继续运行{printf("\n您是否还想进行其他操作(y/n):\n");//提示用户是否还需继续进行其他操作scanf("%s",&ch);//用户输入y/n以选择是否仍需进行其他操作if(ch=='Y'||ch=='y')//判断用户所输入的ch值是否为y/Y，以判断用户是否进行其他操作{system("cls");printf(" 校园导游咨询系统------您身边的导游 \n");printf("\n");printf("\n");printf("\n");/*菜单选项*/printf(" 1:请求校园导游帮组(即咨询校园各景点最短路径)\n");printf(" 2:显示校园平面图\n");printf(" 3:退出校园导游咨询系统\n");printf("请输入你所想进行的功能选项：\n");scanf("%d",&i);switch(i){ //选择菜单项的操作case 1:system("cls");/*调用输出校园平面图函数并输出校园平面图*/Sgblueprint();/*提示用户输入起点的序列号*/printf("请输入你所在地或起点的序列号(A-F的序列号为依次0，1,2,3,4，5)：\n");scanf("%d",&j);//用户输入起点的序列号i的值/*调用狄克斯特拉函数计算源点的其他各结点的最短路径及其距离*/Dijkstra(g,j,distance,path);/*提示用户参照校园平面图以了解各景点的代号的含义*/printf("提示：下列A、B、C等均是各景点的代号，如有问题，请参考上面的校园平面图\n");/*调用输出源点到其他各结点的最短距离和最短路径函数并输出相应的最短路径和最短距离*/SgPrint(g,n,distance,path,j);break;case 2:system("cls");Sgblueprint();//调用输出校园平面图函数并输出校园平面图break;case 3:exit(1);break;//退出程序}}else return;//退出程序}}4：调试分析：（1）a)测试数据：char a[]={'A','B','C','D','E','F'};RowColWeightrcw[]={{0,2,5},{0,3,30},{1,0,2},{1,4,8},{2,1,15},{2,5,7},{4,3,4},{5,3,10},{5,4,18}}; int n=6,e=9;b)测试结果：(2)所遇到的问题：1）SgPrint函数中的形参如何设置，通过仔细分析图的操作等头文件和主函数，最终分析函数SgPrint中应加入形参AdjMGraph g,int n,int distance[],int path[],int j；2）Sgblueprint函数中输出语句中想输出’\’，直接键入’\’发现不能输出’\’，最终查看消息窗口的提示信息和联系C语言中有关转义字符的相关知识，知道了如果相输出转义字符’\’本身就必须书写成’\\这样的格式；3)在进行菜单项操作时，如何做到清除原有屏幕的操作，通过上网查资料了解到，只需加入“system(“cls”);”该语句即可；4)SgPrint函数中如何实现输出如“从结点A到结点B的最短路径为：（A，C，B），其最短距离为20；”格式，通过分析Dijkstra.h和主函数，最终想到只需添加“if(path[i]!=-1){ if(path[path[i]]!=-1){if(path[path[path[i]]]!=-1){printf("%c,",g.Vertices.list[path[path[path[i]]]]);}printf("%c,",g.Vertices.list[path[path[i]]]);}printf("%c,",g.Vertices.list[path[i]]);}”这些代码，对源点到其他结点的最短路径的前一结点以及该前一结点的前一结点进行判断，并将这些结点输出，就能够解决上述问题。
数据结构校园导游课程设计报告
淮 海 工 学 院 计算机工程学院课程设计报告设计名称： 选题名称： 姓 名： 专业班级： 系 （院）： 设计时间： 设计地点：数据结构课程设计校园导游学 号：软件工程软件 091计算机工程学院2010.12.20~2010.12.31 软件工程实验室、教室指导教师评语：成绩：签名：年月日数据结构课程设计报告第 1 页，共 页1．课程设计目的1、训练学生灵活应用所学数据结构知识，独立完成问题分析，结合数据结构理论知识，编写程序求 解指定问题。
2.初步掌握软件开发过程的问题分析、系统设计、程序编码、测试等基本方法和技能； 3.提高综合运用所学的理论知识和方法独立分析和解决问题的能力； 4.训练用系统的观点和软件开发一般规范进行软件开发，巩固、深化学生的理论知识，提高编程水平， 并在此过程中培养他们严谨的科学态度和良好的工作作风。
2．课程设计任务与要求：任务 根据教材《数据结构-C 语言描述》（耿国华主编）和参考书《数据结构题集（C 语言版）》（严蔚敏、 吴伟民主编）选择课程设计题目，要求通过设计，在数据结构的逻辑特性和物理表示、数据结构的选择应 用、算法的设计及其实现等方面加深对课程基本内容的理解和综合运用。
设计题目从任务书所列选题表中选取，每班每题不得超过 2 人。
学生自选课题 学生原则上可以结合个人爱好自选课题，要求课题有一定的深度与难度，有一定的算法复杂性，能够 巩固数据结构课程所学的知识。
学生自选课题需在 18 周前报课程设计指导教师批准方可生效。
要求： 1、在处理每个题目时，要求从分析题目的需求入手，按设计抽象数据类型、构思算法、通过设计实 现抽象数据类型、编制上机程序和上机调试等若干步骤完成题目，最终写出完整的分析报告。
前期准备工 作完备与否直接影响到后序上机调试工作的效率。
在程序设计阶段应尽量利用已有的标准函数，加大代码 的重用率。
2、.设计的题目要求达到一定工作量（300 行以上代码），并具有一定的深度和难度。
数据结构-校园导游系统
课程设计论文（附有代码！）题目：校园导游咨询学院：计算机科学与工程学院专业：计算机科学与技术姓名：学号：指导教师：2014年9月22日摘要桂林众山环绕，风景优美，加之近年来校园环境也得到不断地改善，来访校园的游客逐渐增加，为了方便众多游客对校园景点的参观，需要给来访人士提供校园导游咨询服务，利用计算机建立一个便利的咨询系统可以很好地解决这个问题。
在本设计实验中，我所采用的是邻接矩阵作为数据的存储结构，用不同的功能模块对两地距离和校园道路信息进行编辑。
当游客来访时，系统能根据用户输入的景点代号查询景点信息，提供任意两个景点间的最短路径查询，并能查询校园内的交通信息，方便游客访问。
工作人员还可以为校园更新景点以及路径信息。
本文将简单介绍该系统的开发背景，详细介绍系统的主要设计思路，函数的建立和使用过程，该系统功能的实现方式和实现结果，以及对所遇到问题的分析解决，最后对该系统进行总结描述。
关键词：校园导游咨询；C++；数据结构；最短路径；查询；目录引言 (1)1系统概述 (1)2需求分析 (1)2.1 系统需求 (1)2.2 开发环境 (2)3详细设计 (3)3.1 系统结构 (3)3.2 数据结构设计以及数据的初始化 (4)3.2.1 图结构设计 (4)3.2.2 数据的初始化 (4)3.3 查询模块的详细设计 (5)3.3.1 查询模块功能子函数设计 (5)3.4 更新功能模块详细设计 (7)3.4.1 更新模块功能子函数设计 (8)4所遇到的问题和分析解决 (10)5系统特色及关键 (11)6结论 (12)参考文献 (13)引言随着计算机科学技术的不断提高，计算机依靠其强大的功能已经成为人们生活中不可缺少的一部分，计算机能解决人类生活中的大部分问题，为人类文明和社会进步做出了巨大贡献。
桂林是一个全世界著名的旅游城市，近几年来旅游业得到了飞速的发展，来自各个国家各个城市的游客给城市带来了巨大的经济效益。
大数据结构课程设计报告材料(校园导游系统)附有源代码
课程论文（设计）2011-2012 学年第2学期课程名称：数据结构课程设计课程性质：实践课专业班级：考核方式：考查学生：学号：学时：1周教师：目录1. 作业容 (1)2. 基本思路 (1)2.1 本校10个景点 (1)2.2 图的初始化 (2)2.3 图的遍历 (2)2.4 求最短路径 (3)3.系统流程 (4)3.1 系统的简单说明 (4)3.2 系统流程图 (5)4. 系统运行效果图 (5)4.1 校园导游界面 (5)4.2 华农校园地图 (6)4.3 景点的相关信息查询 (6)4.4 任意两个景点间的最短路径 (7)4.5 退出校园导游系统 (8)5.总结 (9)6.参考文献 (10)1. 作业容设计一个校园导游程序，为来访客人提供各种信息查询任务。
基本要求：（1）设计你所在学校的校园平面图，所含景点不少于10个。
以图中顶点表示校各景点，存放景点名称、代号、简介信息，以边表示路权，存放路径长度等相关信息。
（2）为来访客人提供图中任意景点相关信息的查询（3）为来访客人提供图中任意景点的问路查询，即查询任意两个景点之间的一条最短的简单路径。
2. 基本思路要完成对整个导游图系统的功能实现，需要对的每一项功能都有清楚的设想和认识，了解并明确每一项功能的实现需要解决的问题，选择正确并且高效的算法把问题逐个解决，最终实现程序的正确调试运行。
有以下设计思路：（1）.结合本校的实际情况，选出10个景点；（2）.人为手工为选出的10个景点赋上相关信息（名称、代号、简介信息、以及路权等等）；（3）.根据选出来的10个景点用邻接矩阵存储校园图。
（4）.依照景点的相关信息创建校园图。
（5）.把纸质上的容，利用C++编程语言编写查找景点相关信息的程序。
（6).根据人为赋值的路权，迪杰斯特拉算法计算任意两点之间的最短路径。
（7）.综上所诉，用一个主函数把这些板块合成，生产一个菜单界面呈现在用户面前。
为此，可把系统分为以下几个核心：图的初始化、图的遍历、求最佳路线。
C++数据结构课程设计-校园导游咨询系统
数据结构（C++）课程设计题目: 校园导游咨询*姓名：学号：院系：专业年级：2014年7月8日目录一、设计题目 (2)二、需求分析 (2)三、概要设计 (6)四、详细设计 (11)五、调试分析 (14)六、测试结果 (14)七、附录：程序设计源代码 (21)一、设计题目校园导游咨询*二、需求分析1)运行环境（软、硬件环境）电脑型号X64 兼容台式电脑处理器英特尔第二代酷睿***************四核主板华硕P8H61-M LX (英特尔H61 芯片组)内存8 GB ( 威刚DDR3 1333MHz )主硬盘西数WDC WD10EALX-009BA0 ( 1 TB / 7200 转/分)显卡ATI Radeon HD 6700 Series ( 512 MB / ATI )显示器SGW5600 PL2208HD ( 21.7 英寸)光驱华硕DRW-24D1ST a DVD刻录机声卡瑞昱ALC887 @ 英特尔 6 Series Chipset 高保真音频网卡瑞昱RTL8168E PCI-E Gigabit Ethernet NIC / 华硕操作系统：Windows 7 Ultimate (x86) sp1编程环境：Microsoft Visual Studio 20122)输入的形式和输入值的范围内容形式范围景点代号int 自然数景点名称string 所有字符景点简介string 所有字符X坐标int 正整数Y坐标int 正整数3)输出的形式描述内容形式范围景点代号int 自然数景点名称string 所有字符景点简介string 所有字符X坐标int 正整数Y坐标int 正整数最短路径图像jpg4)功能描述以我校南汇校区部分景点、进行抽象化，生成了具有15个顶点、18条边的图，以邻接表与邻接矩阵复合形式储存在内存中，主要有以下功能：a.查询景点的信息，包括基本信息和拓展的周围节点信息；b.景点导航，给出起点、终点，规划出最短路径和风景最佳路径；c.修改景点，道路信息，包括添加景点、添加道路、修改景点功能；d.开发人员工具，包括邻接表、邻接矩阵的查看DFS深度优先遍历、BFS广度优先遍历e.显示地图，打开预制的地图文件查看5)测试数据初始地图信息：景点景点名称景点介绍X坐标Y坐标编号0 北校门学校的北入口 2 141 北图书馆学校北侧图书馆12 142 崇德楼经管学院楼26 143 奋进楼公共机房12 2826 284 北运动场具有足球场、篮球场、健身房等12 325 行政楼计算机学院楼及其他行政办公12 396 教师活动中心又称H楼，具有桌球、乒乓球、会议室、舞厅等7 雕塑校园雕塑26 398 南校门学校南入口 2 509 至诚楼办理学生事务处12 5026 5010 大礼堂学校大型文艺演出、讲座场所11 南图书馆学校南侧的图书馆12 52团委、学生会、社联所在处12 1212 大学生文化活动中心13 风帆广场绿地广场，景色优美26 5812 7014 南运动场具有足球场、篮球场、羽毛球场等距离邻接矩阵：三、概要设计1)抽象数据类型定义描述（对各类的成员及成员函数进行抽象描述，参见书或ppt及实验）Site类Data：编号Code景点名称SiteName景点介绍Introduction景点X坐标景点Y坐标Operation：构造函数输入：编号，名称，介绍，X坐标，Y坐标前置条件：无动作：初始化Site类元素输出：无后置条件：无SetSite输入：编号，名称，介绍，X坐标，Y坐标前置条件：无动作：赋值Site类元素输出：无后置条件：无ArcNode类Data ：邻接点下标值Adjvx指向下一个边结点的指针*nextarc;风景等级sceneLevel;距离distance;Operation：构造函数输入：Adjvx, *nextarc, sceneLevel;前置条件：无动作：初始化ArcNode类输出：无后置条件：无VertexNode类Data ：节点内容vex节点首指针*firstarcOperation：无Road类Data ：Site型节点1，节点2距离Distance风景等级Bool型是否是机动车道carAviliable;Operation：SetRoad构造函数输入：节点1，节点2，风景等级前置条件：存在Site对象动作：初始化Road类输出：无后置条件：无BGraph 类Data ：邻接表adjlist[]Int 距离矩阵Int 风景值矩阵Operation：构造函数输入：前置条件：动作：输出：后置条件：无addSite函数输入：景点名称，景点信息，景点X坐标，景点Y坐标前置条件：顶点表已建立动作：添加邻接表顶点、修改邻接矩阵输出：无后置条件：无addRoad函数输入：景点1名称，景点2名称，风景等级前置条件：顶点表已建立动作：添加邻接表的边表，修改邻接矩阵输出：无后置条件：无ShowInfo函数输入：无前置条件：函数已初始化动作：输出当前图信息输出：顶点数、边数后置条件：无pGraph函数输入：无前置条件：函数已初始化动作：输出邻接表输出：邻接表后置条件：无pMatrix输入：无前置条件：函数已初始化动作：输出邻接矩阵输出：邻接矩阵后置条件：无searchByName输入：景点名称前置条件：图已初始化动作：搜索符合名称的节点输出：节点site型后置条件：无DFSTraverse函数输入：无前置条件：图已初始化动作：深度优先遍历输出：遍历路径后置条件：无BFSTraverse函数输入：无前置条件：图已初始化动作：广度优先遍历输出：遍历路径后置条件：无FindPath函数输入：节点1，节点2前置条件：图已初始化动作：计算最短路径输出：路径经过点、路径产长度、每一步的方向后置条件：无2)功能模块设计（如主程序模块设计）1.主程序模块：连接各种功能子模块，使用循环等待用户操作，完成程序的基本操作实现功能。
校园导游咨询系统源代码
typedef struct//用来定义一个图 {
infotype vexs[10]; Ad arcs; int vexnum,arcnum; }MGraph; MGraph b;
MGraph InitGraph()//初始化图形 {
MGraph G;
int i;
int j;
G.vexnum=10; G.arcnum=10;
printf(" \n"); printf( 车结束):"
}
4.查看各景点信息 5.退出系统
"诚心为你服务-请选择(输入编号.回 );
//查看各 v;
printf("\n");
printf("编号.景点名称.简介 \n");
#include<stdlib.h>//standard library 标准库头文件
#include<stdio.h>//标注输入输出函数头文件
#include<string.h>//字符函数头文件
#define MAX 10000 //定义路程最远距离符号常量无穷大
#define MAX_VERTEX_NUM 10//定义的景点/顶点数量符号常量 最大顶点数 10 个
for(i=0;i<G.vexnum;i++) for(j=0;j<G.vexnum;j++) G.arcs[j][i].adj=G.arcs[i][j].adj; return G; }
//菜单
void Menu()
{ printf("\n *************************** **************************\n");
数据结构课程设计报告(校园导游系统)附有源代码(20191123003227)
图 4.3.1 景点 2 红满堂信息查询
图 4.3.2 景点 7 竹园信息查询 4.4 任意两个景点间地最短路径
根据用户地需求 , 在用户输入了起点和终点后计算出最短路径是哪一条路径 . 以下举两个例子 . 第一个例子地起点是 5 东区运动场 , 终点是 1 校史馆 . 第二个例 子地起点是 2 红满堂 , 终点是 10 黑山运动场 . 运行结果如图 4.4.1 和图 4.4.2 所 示 . 83lcPA59W9
图 4.1 校园导游节目图 4.2 华农校园地图
校园地图地查看是通过抽象化 10 个景点来用 printf( > 输入选择 1 之后弹出地界面 , 运行结果如图 4.2. HbmVN777sL
函数输出地图 , 在
图 4.2 抽象化地华南农业大学校园导游地图 4.3 景点地相关信息查询
景点地相关信息查询是通过 information( > 函数来调用输出地 , 在主菜单 那输入 2 之后 , 拿第 2 个景点红满堂和第 7 个景点竹园来当例子 , 第运行结果如 图 4.3.1 和图 4.3.2. V7l4jRB8Hs
2.2 输出 dist[j] 和 path[j] ；
2.3 修改数组 dist 和 path 。
2.4 将顶点 vk 添加到数组 s 中；
3. 系统流程
3.1 系统地简单说明 1. 创建校园图： <1）先手工画好华农地 10 个景点地草图 , 再用 C++语言输出抽象化地校园
地图 . <2）再用 C++语言定义节点个数 N,编写函数 name( >为景点赋值各类信息
为空串 . 1nowfTG4KI
数组 s[n] ：存放源点和已经生成地终点 <即集合 S）, 初态为只有一个源点 v.
校园导游系统课程设计报告
南京航空航天大学《数据结构》课程设计报告校园导游系统目录一、需求分析 (2)二、程序的主要功能 (2)三、程序运行平台 (2)四、数据结构 (2)五、算法设计思想及时间复杂度 (2)六、测试用例及结果 (5)七、存在的不足与对策及编程体会 (6)八、程序源代码 (6)一、需求分析南航学生家长及入学新生很需要一个导游程序，来引领他们参观和了解南航。
二、程序的主要功能1、查询各景点的相关信息2、查询任意两景点间的所有路径3、查询任意两景点间的最短路径 1、增加景点4、推荐参观路线 2、删除景点5、更新导游信息（操作需管理员密码） 3、更新道路信息6、对景点联通性的浏览（2阶矩阵表示）4、更新景点信息7、学校全景一览 5、修改管理员密码三、程序运行平台Microsoft Visual C++ 6.0四、数据结构图的邻接矩阵存储表示，栈的顺序存储表示五、算法设计思想及时间复杂度主要函数介绍：1、求两点间的所有路径：a)相关函数：void dfs(MGraph G,SqStack path,int *used,int u,int w);//深度优先遍历b)主要算法思想：栈的相关操作+深度优先搜索创建一个空栈保存路径，一个空数组保存已标记节点，首先让起点进栈，并标记为已访问，然后调用深度优先搜索，如果该顶点的相邻顶点（即与其有直接通路的顶点）未被访问过就标记为已访问，进栈，然后对它调用深度优先搜索，依次类推，直到获得所有到指定终点的路径。
c)时间复杂度：O（VE），其中V为图的顶点数目，E为图中边的数目。
2、求两点间的最短路径：a)相关函数：void ShortestPath(MGraph G,int v0,int P[][Nmax],int *D);//查询任意两景点间的最短路径void PrintShortest(MGraph G,int v1,int v2,int P[][Nmax],int *D); //输出最短路径b)主要算法思想：迪杰斯特拉算法假设起点为v0，S为已找到的从v0出发的最短路径的终点的集合，其初始状态为空集。
数据结构课程设计报告 (附有完整可运行出来的代码)
课程设计报告设计题目：公园导游图一、流程图二、程序代码#include<iostream>using namespace std;#include<stdio.h>typedef struct //定义图结构{int n; /* 图的顶点个数*/char v[100]; /* 顶点信息*/int e[100][100]; /* 边信息*/int shor; /* 最短路径信息*/}park;park *luru(park *x){int j,k;cout<<"请输入公园景点个数"<<endl;cin>>x->n;if(x->n<=0){cout<<"个数输入错误，请重新输入"<<endl;cin>>x->n;}cout<<"请输入景点名称,每个名称只允许一个字符代替"<<endl;for(j=0;j<x->n;j++)cin>>x->v[j];cout<<"请输入景点之间的路径长度,只允许整数型数值，无路径长度的输入0"<<endl;for(j=0;j<x->n;j++)for(k=0;k<x->n;k++){cout<<"请输入第"<<j+1<<"行"<<"第"<<k+1<<"列的路径长度"<<endl;cin>>x->e[j][k];}return x;}int search(park *x){char start,end,temp;int i=0,j=0,temp_1,temp1=10000;cout<<"请输入要查找的起始景点名称"<<endl;cin>>start;while(i<x->n && start!=x->v[i])i++;if(i==x->n){cout<<"没有找到该景点，按任意键返回"<<endl;return 0;}}cout<<"请输入要查找的终点景点名称"<<endl;cin>>end;while(j<x->n && end!=x->v[j]){j++;if(j==x->n){cout<<"没有找到该景点，按任意键返回"<<endl;return 0;}}x->shor=x->e[i][j];temp_1=x->e[i][j];for (int k=0;k<x->n;k++)//两个顶点最小权值判断{if (x->e[i][k]==0||x->e[k][j]==0 )continue;if(x->shor > x->e[i][k] + x->e[k][j]){x->shor = x->e[i][k] + x->e[k][j];temp=x->v[k];}}if(x->shor==0){cout<<"这两个节点中没有连通路，按任意键返回"<<endl;return 0;}if(x->shor==temp_1){cout<<"最短路径信息: "<<start<<"->"<<end<<endl<<"最小路径长度："<<x->shor<<endl;x->shor=10000;getchar();return 1;if(x->shor<temp_1 && x->shor<=temp1){cout<<"最短路径信息: "<<start<<"->"<<temp<<"->"<<end<<endl<<"最小路径长度："<<x->shor<<endl;x->shor=10000;getchar();return 1;}cout<<"查找失败，按任意键返回"<<endl;getchar();return 0;}int main(){park x;int i=1;luru(&x);do{search(&x);cout<<"是否继续？"<<endl<<"1.继续"<<endl<<"0.退出"<<endl;cin>>i;}while(i!=0);return 0;}三、运行结果。
校园导航系统源代码
数据结构-校园导航系统简介:本系统采用C语言编写,运行环境为Dev-C++;内容以西安电子科技大学南校区为例;主要功能有:1.查询景点信息;2.查询两景点间最短距离;3.查询两景点间所有路线;4.查询西电校园地图;5.修改景点和路径信息.注意事项:在进行修改景点和路径信息操作前,请在可执行文件目录下用记事本创建”super User.CODE”文件来存放用户名与密码(中间以空格隔开),否则无法进入.源代码:#include <string.h>#include <stdio.h>#include <conio.h>#include <stdlib.h>#include <ctype.h>#define Max 20000typedef struct ArcCell{int adj; //两个景点间的距离}ArcCell;typedef struct VertexType{int number; //景点编号char sight[100]; //景点名称char description[1000]; //景点简介char particular1[1000];char particular2[1000];char particular3[1000]; //景点详情}VertexType;typedef struct{VertexType vex[20]; //最多存放20个景点信息ArcCell arcs[20][20]; //两个景点间的距离int vexnum,arcnum;}MGraph;MGraph G;char nameofschool[100]; //学校名称int NUM=9;int P[20][20];int p[20];int visited[20];int a=0;long int D[20];int x[20]={0};//函数声明void CreateUDN(int v,int a);void narrate();void ShortestPath(int num);void output(int sight1,int sight2);char Menu();void search();char SearchMenu();void HaMiTonian(int);void Searchpath1(MGraph g);void disppath(MGraph g,int i,int j);void path(MGraph g,int i,int j,int k);void NextValue(int);void display();int Addnewsight(int n);int Deletesight(int n);void Changesight();char Changemenu();char Sightmenu();int Maintain(void);int VerificatianIdentity(void);void map();//主函数int main(){int v0,v1;int MaintainFlag;char ck;system("color 0F");CreateUDN(NUM,11);do{ck=Menu();switch(ck){case '1':search();break;case '2':system("cls");narrate();printf("\n\n\t\t\t请选择起点景点（0～%d）：",NUM-1);scanf("%d",&v0);printf("\t\t\t请选择终点景点（0～%d）：",NUM-1);scanf("%d",&v1);ShortestPath(v0);output(v0,v1);printf("\n\n\t\t\t\t请按任意键继续...\n");getchar();getchar();break;case'3':system("cls");narrate();x[0]=1;Searchpath1(G);printf("\n\n\t\t\t\t请按任意键继续...\n");getchar();getchar();break;case'4':system("cls");map();printf("\n\n\t\t\t\t\t请按任意键继续...\n");getchar();getchar();break;case'5':system("cls");narrate();MaintainFlag = Maintain();switch(MaintainFlag){case'1':system("cls");narrate();NUM=Addnewsight(NUM);system("cls");narrate();break;case'2':NUM=Deletesight(NUM);break;case'3':Changesight();break;}break;};}while(ck!='e');return 0;}//主菜单char Menu(){char c;int flag;do{flag=1;system("cls");narrate();printf("\n\t\t\t┏━━━━━━━━━━━━━━━┑\n");printf("\t\t\t┃ ┃\n");printf("\t\t\t┃ 1、查询景点信息┃\n");printf("\t\t\t┃ 2、查询两景点间最短路径┃\n");printf("\t\t\t┃ 3、查询两景点间所有路线┃\n");printf("\t\t\t┃ 4、查看西电校园地图┃\n");printf("\t\t\t┃ 5、修改景点和路径信息┃\n");printf("\t\t\t┃ e、退出┃\n");printf("\t\t\t┃ ┃\n");printf("\t\t\t┗━━━━━━━━━━━━━━━┛\n");printf("\t\t\t\t请输入您的选择：");scanf("%c",&c);if(c=='1'||c=='2'||c=='3'||c=='4'||c=='5'||c=='e')flag=0;}while(flag);return c;}//查询菜单char SearchMenu(){char c;int flag;do{flag=1;system("cls");narrate();printf("\n\t\t\t┏━━━━━━━━━━━━━━━┑\n");printf("\t\t\t┃ ┃\n");printf("\t\t\t┃ 1、按照景点编号查询┃\n");printf("\t\t\t┃ 2、按照景点名称查询┃\n");printf("\t\t\t┃ e、返回┃\n");printf("\t\t\t┃ ┃\n");printf("\t\t\t┗━━━━━━━━━━━━━━━┛\n");printf("\t\t\t\t请输入您的选择：");scanf("%c",&c);if(c=='1'||c=='2'||c=='e')flag=0;}while(flag);return c;}//查询信息void search(){int num;int i;char c;char name[20];do{system("cls");c=SearchMenu();switch (c){case '1':system("cls");narrate();printf("\n\n\t\t请输入您要查找的景点编号：");scanf("%d",&num);for(i=0;i<NUM;i++){if(num==G.vex[i].number){printf("\n\t\t您要查找景点信息如下:");printf("\n\t\t(%d)%-5s:%-25s\n\n",i,G.vex[i].sight,G.vex[i].description);printf("\t\t\t\t\t详情介绍:\n\t\t%-s\n",G.vex[i].particular1);printf("\t\t%-s\n",G.vex[i].particular2);printf("\t\t%-s\n",G.vex[i].particular3);printf("\n\t\t按任意键返回...");getchar();getchar();break;}}if(i==NUM){printf("\n\n\t\t\t没有找到！");printf("\n\n\t\t\t按任意键返回...");getchar();getchar();}break;case '2':system("cls");narrate();printf("\n\n\t\t请输入您要查找的景点名称：");scanf("%s",name);for(i=0;i<NUM;i++){if(!strcmp(name,G.vex[i].sight)){printf("\n\t\t您要查找景点信息如下:");printf("\n\t\t(%d)%-5s:%-25s\n\n",i,G.vex[i].sight,G.vex[i].description);printf("\t\t\t\t\t详情介绍:\n\t\t%-s\n",G.vex[i].particular1);printf("\t\t%-s\n",G.vex[i].particular2);printf("\t\t%-s\n",G.vex[i].particular3);printf("\n\t\t按任意键返回...");getchar();getchar();break;}}if(i==NUM){printf("\n\n\t\t\t没有找到！");printf("\n\n\t\t\t按任意键返回...");getchar();getchar();}break;}}while(c!='e');}//构造图形void CreateUDN(int v,int a) {int i,j;strcpy(nameofschool,"西安电子科技大学");G.vexnum=v;G.arcnum=a;for(i=0;i<20;++i) G.vex[i].number=i;strcpy(G.vex[0].sight,"东门");strcpy(G.vex[0].description,"学校正门,可乘坐公交车,出租车等交通工具. ");strcpy(G.vex[0].particular1," 作为学校的正门,门外的交通系统非常发达,常年有出租车"); strcpy(G.vex[0].particular2,"经过,还有916路,173路等众多公交车线路在此设立站牌,所以"); strcpy(G.vex[0].particular3,"完全没必要担心坐不到车,出行非常方便!");strcpy(G.vex[1].sight,"图书馆");strcpy(G.vex[1].description,"馆藏文纸质献约270万余册,种类丰富,环境优美. ");strcpy(G.vex[1].particular1," 南校区图书馆2005年7月1日奠基,主要服务于新校区2万余"); strcpy(G.vex[1].particular2,"名本科生.地上建筑面积4万平方米,总框架五层,地下一层,地面"); strcpy(G.vex[1].particular3,"四层.拥有先进的设施、优雅温馨的阅读环境.");strcpy(G.vex[2].sight,"北门");strcpy(G.vex[2].description,"西电南校区的另外一个出入口,备有一个停车场. ");strcpy(G.vex[2].particular1," 北门日常的人流量不亚于东门,在这里有一个停车场,而且"); strcpy(G.vex[2].particular2,"这里还是西电的快递接收点,可以供广大师生在此寄取快递,非"); strcpy(G.vex[2].particular3,"常方便.而且临近综合楼,较为繁华.");strcpy(G.vex[3].sight,"海棠区");strcpy(G.vex[3].description,"2017级大一萌新即将入住的宿舍区. >o< ");strcpy(G.vex[3].particular1," 海棠宿舍位于学校西北面,所以距离北操,新综,北门较近,"); strcpy(G.vex[3].particular2,"准大一的学弟学妹们将会主要居住在5.6号楼(还有一部分会在"); strcpy(G.vex[3].particular3,"9.10号楼).海棠宿舍为两室一厅,每室各四人.");strcpy(G.vex[4].sight,"大活");strcpy(G.vex[4].description,"大学生活动中心的简称,小剧场就在这里. ");strcpy(G.vex[4].particular1," 大活建设在学校人工湖旁边,里面有实验室、舞蹈室等专用"); strcpy(G.vex[4].particular2,"教室,也是学校举办室内大型活动的常用地点,曾经陈一冰,周鸿"); strcpy(G.vex[4].particular3,"祎,黄晓明等人在此与同学们见面.");strcpy(G.vex[5].sight,"北操");strcpy(G.vex[5].description,"跑步踢球狼人杀...等等有趣的活动,超热闹. ");strcpy(G.vex[5].particular1," 北操基础设施齐全,有足球场跑道观众台羽毛球场等,是"); strcpy(G.vex[5].particular2,"学校举行大型体育赛事的场地,例如:运动会足球赛等.每天晚上"); strcpy(G.vex[5].particular3,"也会有许多同学在此运动玩耍,非常有趣.");strcpy(G.vex[6].sight,"观光塔");strcpy(G.vex[6].description,"南校区最显眼的建筑物,可以俯视整个校园. ");strcpy(G.vex[6].particular1," 观光塔是西电南校区最负盛名的建筑物,位处南校区最为中"); strcpy(G.vex[6].particular2,"间的位置,走在校园里,总是能够看到观光塔,到了晚上塔上的时"); strcpy(G.vex[6].particular3,"钟会亮起,很远都能看到,在月光下特别的漂亮.");strcpy(G.vex[7].sight,"体育馆");strcpy(G.vex[7].description,"今年刚刚建成,外观融合了\"天圆地方\"的思想. ");strcpy(G.vex[7].particular1," 考虑到学校的所在地西安是十三朝古都,亦应融入中国传统"); strcpy(G.vex[7].particular2,"文化的理念,以及体育馆主馆和训练馆的功能需求,最终决定以中"); strcpy(G.vex[7].particular3,"国传统文化的\"天圆地方\"为设计思路.美观大气.");strcpy(G.vex[8].sight,"行政楼");strcpy(G.vex[8].description,"可以进行盖章,补办一卡通等众多操作. ");strcpy(G.vex[8].particular1," 从东门进入学校,左手边的那栋楼就是行政楼,往后稍小一点"); strcpy(G.vex[8].particular2,"的就是行政辅楼.教务处、学工处、电院办公室在行政楼,一卡通"); strcpy(G.vex[8].particular3,"中心、户籍管理、财务处、一些学院的办公室在行政辅楼.");for(i=0;i<20;++i)for(j=0;j<20;++j)G.arcs[i][j].adj=Max;G.arcs[0][8].adj=G.arcs[8][0].adj=150;G.arcs[0][1].adj=G.arcs[1][0].adj=600;G.arcs[1][7].adj=G.arcs[7][1].adj=800;G.arcs[1][6].adj=G.arcs[6][1].adj=50;G.arcs[1][4].adj=G.arcs[4][1].adj=600;G.arcs[3][2].adj=G.arcs[2][3].adj=300;G.arcs[6][2].adj=G.arcs[2][6].adj=350;G.arcs[3][5].adj=G.arcs[5][3].adj=300;G.arcs[4][5].adj=G.arcs[5][4].adj=400;G.arcs[8][7].adj=G.arcs[7][8].adj=250;}//导图模块void narrate(){int i,k=0;printf("\n\t******************欢迎使用%s校园导游程序*****************\n\n",nameofschool);printf("\t━━━━━━━━━━|━━━━━━━━━━━━━━━━━━━━━━━━\n");printf("\t* 景点名称|\t\t\t景点描述\t\t *\n");printf("\t━━━━━━━━━━|━━━━━━━━━━━━━━━━━━━━━━━━\n");for(i=0;i<NUM;i++){printf("\t* (%d)%-15s|\t%-43s *\n",i,G.vex[i].sight,G.vex[i].description);k=k+1;}printf("\t━━━━━━━━━━|━━━━━━━━━━━━━━━━━━━━━━━━\n"); }//迪杰斯特拉算法void ShortestPath(int num){int v,w,i,t;int final[20];int min;for(v=0;v<NUM;v++){final[v]=0;D[v]=G.arcs[num][v].adj;for(w=0;w<NUM;w++)P[v][w]=0;if(D[v]<20000){P[v][num]=1;P[v][v]=1;}}D[num]=0;final[num]=1;for(i=0;i<NUM;++i){min=Max;for(w=0;w<NUM;++w)if(!final[w])if(D[w]<min){v=w;min=D[w];}final[v]=1;for(w=0;w<NUM;++w)if(!final[w]&&((min+G.arcs[v][w].adj)<D[w])){D[w]=min+G.arcs[v][w].adj;for(t=0;t<NUM;t++)P[w][t]=P[v][t];P[w][w]=1;}}}//输出函数void output(int sight1,int sight2){int a,b,c,d,q=0;a=sight2;if(a!=sight1){printf("\n\t\t从%s到%s的最短路径是",G.vex[sight1].sight,G.vex[sight2].sight);printf("(最短距离为%dm.)\n\n\t",D[a]);printf("\t\t%s",G.vex[sight1].sight);d=sight1;for(c=0;c<NUM;++c){gate:;P[a][sight1]=0;for(b=0;b<NUM;b++){if(G.arcs[d][b].adj<20000&&P[a][b]){printf("-->%s",G.vex[b].sight);q=q+1;P[a][b]=0;d=b;if(q%8==0) printf("\n");goto gate;}}。
校园导游实验报告——数据结构
校园导游实验报告——数据结构
校园导游实验报告——数据结构
1.引言
- 简要介绍实验的目的和背景
- 阐述校园导游系统的重要性和应用价值
2.需求分析
- 分析校园导游系统的功能需求和性能要求
- 确定系统的基本模块，如地图显示、导航功能等
3.系统设计
3.1 数据结构设计
- 介绍选择的数据结构，如图、树、队列等的原因和优劣势
- 描述数据结构的组织方式和关键操作
3.2 界面设计
- 展示校园导游系统的用户界面设计
- 解释界面设计的考虑因素，如易用性、用户体验等
4.算法设计与实现
4.1 寻路算法设计
- 探讨常见的寻路算法，如Dijkstra算法、A算法等 - 选择适合校园导游系统的寻路算法，并解释原因
4.2 数据存储与交互
- 描述数据的存储方式，如数据库、文件等
- 分析数据的交互方式，如文件读写、网络传输等5.实验结果与分析
- 展示校园导游系统的功能演示和性能测试结果
- 对实验结果进行详细分析和解释
6.总结与展望
- 总结实验的目标是否达到，解决了哪些问题
- 展望校园导游系统的未来发展方向和改进空间
附件：
附件1：校园导游系统源代码
附件2：校园地图数据文件
附件3：实验中使用的测试数据集
法律名词及注释：
1.版权：指对作品享有的法律保护，包括复制权、发行权等。
2.私下使用：指在非商业、非公开场合下个人使用作品。
3.公共领域：指没有版权保护的作品，可供任何人使用。
4.许可证：指被授权人可以在指定条件下使用作品的文件或证明。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课程论文（设计）2011-2012学年第2学期课程名称：数据结构课程设计课程性质：实践课专业班级：考核方式：考查学生姓名：学号：学时：1周教师姓名：自评分：95分评语及评分目录1. 作业内容 (1)2. 基本思路 (1)2.1 本校10个景点 (1)2.2 图的初始化 (2)2.3 图的遍历 (2)2.4 求最短路径 (3)3.系统流程 (4)3.1 系统的简单说明 (4)3.2 系统流程图 (5)4. 系统运行效果图 (5)4.1 校园导游界面 (5)4.2 华农校园地图 (6)4.3 景点的相关信息查询 (6)4.4 任意两个景点间的最短路径 (7)4.5 退出校园导游系统 (8)5.总结 (9)6.参考文献 (10)1. 作业内容设计一个校园导游程序，为来访客人提供各种信息查询任务。
基本要求：（1）设计你所在学校的校园平面图，所含景点不少于10个。
以图中顶点表示校内各景点，存放景点名称、代号、简介信息，以边表示路权，存放路径长度等相关信息。
（2）为来访客人提供图中任意景点相关信息的查询（3）为来访客人提供图中任意景点的问路查询，即查询任意两个景点之间的一条最短的简单路径。
2. 基本思路要完成对整个导游图系统的功能实现，需要对的每一项功能都有清楚的设想和认识，了解并明确每一项功能的实现需要解决的问题，选择正确并且高效的算法把问题逐个解决，最终实现程序的正确调试运行。
有以下设计思路：（1）.结合本校的实际情况，选出10个景点；（2）.人为手工为选出的10个景点赋上相关信息（名称、代号、简介信息、以及路权等等）；（3）.根据选出来的10个景点用邻接矩阵存储校园图。
（4）.依照景点的相关信息创建校园图。
（5）.把纸质上的内容，利用C++编程语言编写查找景点相关信息的程序。
（6).根据人为赋值的路权，迪杰斯特拉算法计算任意两点之间的最短路径。
（7）.综上所诉，用一个主函数把这些板块合成，生产一个菜单界面呈现在用户面前。
为此，可把系统分为以下几个核心：图的初始化、图的遍历、求最佳路线。
2.1 选出本校10个景点结合华南农业大学实际情况，我选出以下10个景点，从1到10编号：编号名称编号名称编号名称编号名称1 校史馆 2 红满堂 3 行政楼 4 西园5 东区运动场 6 树木园7 竹园8 新校门9 老校门10 黑山运动场2.2 图的初始化由于邻接矩阵特殊的存储方式，它非常便于快速的查找两个顶点之间的边上的权值。
所以，图采用带权的邻接矩阵存储。
决定了图的存储方式后，以华南农业大学10个景点的游览地图作为蓝本，把校园地图抽象化成顶点与边构成的图形式，如图2.2所示，途中数字代表线的权值。
2.3 图的遍历图的遍历是图中最基本的操作。
图的遍历是指从图中某一顶点出发，对图中所有顶点访问一次且仅访问一次。
导游图需要把每条路径的信息都向游客展示，就需要读取每两个顶点间的路径信息。
由于采用了带权的邻接矩阵存储结构进行存储，所以需要针对这一存储结构对路线进行遍历操作。
其遍历算法如图2.3所示。
2.4 求最短路径基于本程序中图的存储是邻接矩阵结构存储的图结构，因而采用适合该存储结构的迪杰斯特拉算法用于解决求最短路径的问题。
迪杰斯特拉提出了一个按路径长度递增的持续产生最短路径的算法，其基本思想是：设置一个集合S 存放已经找到最短路径的顶点，S 的初始状态只包含源点v ，对于v i ∈V-S ，假设从源点v 到v i 的有向边为最短路径。
以后每求得一条最短路径v ，…，v k ，就将v k 加入集合S 中，并将路径v ，…，v k ，v i ，与原来的假设相比较，取路径长度较小者为最短路径。
重复上述过程，直到集合V 中全部顶点加入到集合S 中。
如图2.4所示。
选择图片控件For 循环语句（i=0；i<顶点数；i++）NFor 循环语句(j=0;j<i;j++)YY NY开始 结束如果路径存在输出该路径信息N图2.3 遍历算法示意图图2.4 图的遍历算法执行效果示意图辅助数组dist[n]：元素dist[i]表示当前找到的从源点到终点v i 的最短路径的长度。
初态为:若从v 到v i 有弧，则dist[i]为弧上的权值；否则置dist[i]为∞。
若当前求得的终点为v k ,则根据下式进行迭代：dist[i]=min{dist[i],dist[k]+arc[k][i]} 1≦i ≦n辅助数组path[n]:元素path[i]是一个串，表示当前所找到的从源点到终点v i 的最短路径。
初态为：若从v 到v i 有弧，则path[i]为“vv k ”，否则置path[i]为空串。
数组s[n]：存放源点和已经生成的终点（即集合S ），初态为只有一个源点v 。
算法的伪代码描述是：1.初始化数组dist 、path 和s ；2.while （s 中的元素个数<n ） 2.1 在dist[n]中求最小值，其下标为k （则v k 为正在生成的终点）； 2.2 输出dist[j]和path[j]； 2.3 修改数组dist 和path;2.4 将顶点v k 添加到数组s 中；3.系统流程3.1 系统的简单说明1.创建校园图：（1）先手工画好华农的10个景点的草图，再用C++语言输出抽象化的校园地图。
（2）再用C++语言定义节点个数N ，编写函数name( )为景点赋值各类信息集合S集合V-SVV kV i项，函数information( )，输入各个景点的简介。
（3）读入道路的起始点，为邻接矩阵的边赋相应的值。
2．利用函数travgraph 来查找景点信息。
3．创建一个校园图creat(Matrix_Graph *G)，然后为相应的边赋上现实意义上的权值。
4．用path( )函数来求任意两景点之间的最短路径。
5.如果不查询则调用exit( )函数退出。
5．用main 函数来输出导游界面。
3.2 系统流程图4.系统运行效果图4.1 校园导游界面程序运行，后台对图结构进行初始化，运行结果如图4.1。
开始Main 函数界面菜单输出华农地图调用查询景点函数travgraph( )是否再次查询？调用查询最短距离函数path( )YESNO是否再次查询？ YES NO输入1输入2输入3 调用函数exit( ) 输入4 结束返 回 界面菜单图4.1 校园导游节目图4.2 华农校园地图校园地图的查看是通过抽象化10个景点来用printf( )函数输出地图，在输入选择1之后弹出的界面，运行结果如图4.2。
图4.2 抽象化的华南农业大学校园导游地图4.3 景点的相关信息查询景点的相关信息查询是通过information( )函数来调用输出的，在主菜单那输入2之后，拿第2个景点红满堂和第7个景点竹园来当例子，第运行结果如图4.3.1和图4.3.2。
图4.3.1 景点2红满堂信息查询图4.3.2 景点7竹园信息查询4.4 任意两个景点间的最短路径根据用户的需求，在用户输入了起点和终点后计算出最短路径是哪一条路径。
以下举两个例子。
第一个例子的起点是5东区运动场，终点是1校史馆。
第二个例子的起点是2红满堂，终点是10黑山运动场。
运行结果如图4.4.1和图4.4.2所示。
图4.4.1 从东区运动场到校史馆的最短路径图4.4.2 从红满堂到黑山运动场的最短路径根据截图可知，在现实生活中的最短路径也是如此。
证明了程序的正确性。
4.5 退出校园导游系统用户满足了需求之后，只要在界面菜单处输入4便可退出此次校园导游系统。
运行结果如图4.5。
图4.5 退出校园导游系统5.总结由于设计者水平有限，本导游图系统的功能还比较简单，还有一些好的设想没有实现：比如添加管理模式，使得公园管理人员能够同样方便的更改导游图，因此更改这一导游图还必须在程序员的帮助下进行。
另外，本导游图系统还有一定的局限性，如果存在只有一条通路的景点，导游图将无法求得最佳旅游路径。
公园的导游图系统的这些不足请老师多多谅解。
通过这次的课程设计左右，让我对数据结构中定义无向图和创建无向图的理解更加深刻，不断提升认识，提高编程技巧，借以不断地提高程序设计水平，了解数据结构在编写比较复杂的程序的重要作用；理解了迪杰斯特拉算法的原理，但对于其算法的程序编写还是不太明白；学会了在编写几百行程序时如何查找错误，如何改错误等等。
总而言之，这次的课程设计很好地锻炼自己实际操作能力！参考文献[1]严蔚敏，吴伟民.数据结构（C语言版）.清华大学出版社.1997.[2]李春葆，尹为民，李蓉蓉.数据结构教程（第3版）上机实验指导.清华大学出版社.2009.[3]滕国文.数据结构课程设计.清华大学出版社.2010.218-223.[4]蒋盛益.数据结构学习指导与训练.中国水利水电出版社.2003.//程序名称：校园导游系统//程序员：//编写时间：2012年6月#define N 10#define MAX 25#define MAXedg 30#include <stdio.h>#include <string.h>#include <stdlib.h>#include <conio.h>void clrscr(){system("cls");}typedef int AdjMatrix[MAX][MAX];typedef struct{int vexs[MAX];AdjMatrix arcs;}Matrix_Graph;typedef struct{char name[10];char information[100];struct edgenode *link; }vexnode;typedef struct edgenode{int adjvex;int length;char info[10];char info2[100];struct edgenode *next;}edgenode, *Node ;typedef struct Edge{int lengh;int ivex, jvex;struct Edge *next;} EdgeType;typedef struct{int num;char name[10];} vertex;typedef struct{vertex vexs[MAX];int edges[MAX][MAX];}adjmax;void Name(int i){switch(i){case 1:printf("1:校史馆\n\n");break;case 2:printf("2:红满堂 \n\n");break;case 3:printf("3:行政楼\n\n");break;case 4:printf("4:西园\n\n");break;case 5:printf("5:东区运动场\n\n");break;case 6:printf("6:树木园\n\n");break;case 7:printf("7:竹园\n\n");break;case 8:printf("8:新校门\n\n");break;case 9:printf("9:老校门\n\n");break;case 10:printf("10:黑山运动场\n\n");break;default:printf("景点编号输入错误！请输入1-10的数字编号！\n\n"); break;}void Information(int i)/*景点介绍*/{switch(i){case 1:printf("校史馆:华农校史档案保存的地方。