线性规划应用举例及软件
线性规划的应用及计算机求解
金融投资
在金融投资领域，如何合理配置资产以实现最大收益或最小风险是投资者关注的问题。线性规划可以用于制定最优的资产配 置方案，考虑风险和收益的平衡，以实现投资效益的最大化。
例如，一个养老基金可以使用线性规划来配置股票、债券和现金等资产，以实现长期稳定的收益并控制风险。
农业优化
在农业生产中，如何合理安排种植、养殖等 生产活动以达到最优的经济效益是农业经营 者关注的问题。线性规划可以用于解决农业 生产的优化问题，考虑土地、水资源、劳动 力等资源的限制，通过调整生产结构实现农 业生产的效益最大化。
其中，单纯形法是最常用的一种，它 通过迭代的方法逐步逼近最优解，直 到找到最优解或确定无解为止。
02
线性规划的应用领域
生产计划
生产计划是企业运营管理中的重要环节，线性规划可以用于制定最优的生产计划，以最小化生产成本 或最大化利润为目标，考虑生产能力、市场需求、产品组合等因素，通过调整生产资源的配置，实现 生产效益的最大化。
金融投ห้องสมุดไป่ตู้优化案例
总结词
金融投资优化
数学模型
目标函数通常是最大化预期收益或最小化 风险，约束条件包括投资限额、资产种类
限制等。
详细描述
线性规划在金融投资优化中具有实际应用 价值，通过合理配置投资组合，降低投资 风险，提高投资收益。
求解方法
使用计算机求解线性规划问题，常用的算 法有单纯形法、椭球法等。
资源分配优化案例
总结词 详细描述 数学模型 求解方法
资源分配优化
线性规划在资源分配优化中起到关键作用，通过合理分配有限 资源，实现资源利用的最大化，提高资源效益。
目标函数通常是最小化总成本或最大化总效益，约束条件包括 资源限制、需求约束等。
线性规划Lindo软件-整数规划
定制化不足
对于特定领域的整数规划问题， 可能需要针对具体问题对软件进 行定制化开发。
未来研究的方向与展望
算法改进
随着计算技术的发展，未来可以进一步优化 Lindo软件的算法，提高求解速度和精度。
扩展应用领域
随着整数规划问题的多样化，未来可以进一步拓展 Lindo软件的应用领域，如金融、物流、能源等领 域。
整数规划的求解方法
分支定界法
通过不断分割可行解空间和排除不可行解空 间来逼近最优解。
割平面法
通过逐步构建整数解来逼近最优解，适用于 小规模问题。
回溯法
通过添加割平面来缩小可行解空间，最终找 到最优解。
Lindo软件求解法
使用Lindo软件进行整数规划求解，具有高效 、稳定、易操作等优点。
04
使用Lindo软件进行整数规划
在求解结果查看界面中，可以查看问题的最优解、最优值、变量取值等信 息。
可以使用软件提供的图表功能，绘制变量取值与目标函数之间的关系图， 以便更好地理解问题的解。
05
案例分析
案例一：简单的整数规划问题
问题描述
01
考虑一个简单的整数规划问题，目标是最小化目标函数，同时
满足一系列线性约束条件。
解决方案
• 易用性：用户界面友好，操作简单，无需复杂的编程知识 即可使用。
Lindo软件在整数规划中的优势与限制
依赖性
Lindo软件的功能和性能高度依赖 于计算机硬件配置，高性能计算 机是求解大规模问题的必要条件。
模型限制
对于某些特殊类型的整数规划问 题，如非凸或非线性问题，Lindo 软件的求解效果可能有限。
在约束条件设置界面中，根据问题数据设置相 应的约束条件，如“less than”、“equal to”或“greater than”。
线性规划应用案例分析
线性规划应用案例分析线性规划是一种在数学和运营管理中常见的优化技术。
它涉及到在一组线性不等式约束下，最大化或最小化一个线性目标函数。
这种技术可以应用于许多不同的领域，包括供应链管理、资源分配、投资组合优化等。
本文将探讨几个线性规划应用案例，以展示其在实际问题中的应用和价值。
某制造公司需要计划生产三种产品，每种产品都需要不同的原材料和生产时间。
公司的目标是最大化利润，但同时也受到原材料限制、生产能力限制以及每种产品市场需求限制的约束。
通过使用线性规划，该公司能够找到最优的生产计划，即在满足所有约束条件下，最大化利润。
某物流公司需要计划将货物从多个产地运输到多个目的地。
公司的目标是最小化运输成本，但同时也受到运输能力、货物量和目的地需求的约束。
通过使用线性规划，该公司能够找到最优的运输方案，即在满足所有约束条件下，最小化运输成本。
某投资公司需要将其资金分配给多个不同的投资项目。
每个项目都有不同的预期回报率和风险水平。
公司的目标是最大化回报率，同时也要保证投资风险在可接受的范围内。
通过使用线性规划，该公司能够找到最优的投资组合，即在满足所有约束条件下，最大化回报率。
这些案例展示了线性规划在实践中的应用。
然而，线性规划的应用远不止这些，它还可以用于诸如资源分配、时间表制定、路线规划等问题。
线性规划是一种强大的工具，可以帮助决策者解决复杂的问题并找到最优解决方案。
线性规划是一种广泛应用的数学优化技术，适用于在多种资源限制下寻求最优解。
这种技术涉及到各种领域，包括工业、商业、运输、农业、金融等，目的是在给定条件下最大化或最小化线性目标函数。
下面我们将详细讨论线性规划的应用。
线性规划是一种求解最优化问题的数学方法。
它的基本思想是在一定的约束条件下，通过线性方程组的求解，求得目标函数的最优解。
这里的约束条件通常表现为一组线性不等式或等式，而目标函数则通常表示为变量的线性函数。
工业生产：在工业生产中，线性规划可以用于生产计划、物料调配、人力资源分配等方面。
线性规划的实际应用举例
线性规划的实际应用举例为了便于同学们掌握线性规划的一般理论和方法，本文拟就简单的线性规划(即两个变量的线性规划)的实际应用举例加以说明。
1 物资调运中的线性规划问题例1 A，B两仓库各有编织袋50万个和30万个，由于抗洪抢险的需要，现需调运40万个到甲地，20万个到乙地。
已知从A仓库调运到甲、乙两地的运费分别为120元/万个、180元/万个；从B仓库调运到甲、乙两地的运费分别为100元/万个、150元／万个。
问如何调运，能使总运费最小?总运费的最小值是多少?解：设从A仓库调运x万个到甲地，y万个到乙地，总运费记为z元。
那么需从B仓库调运40-x万个到甲地，调运20-y万个到乙地。
从而有z=120x+180y+100(40-x)+150·(20-y)=20x+30y+7000。
作出以上不等式组所表示的平面区域(图1)，即可行域。
令z'=z-7000=20x+30y.作直线l：20x+30y=0，把直线l向右上方平移至l l的位置时，直线经过可行域上的点M(30，0)，且与原点距离最小，即x=30，y=0时，z'=20x+30y取得最小值，从而z=z'+7000=20x+30y+7000亦取得最小值，z min=20×30+30×0+7000=7600(元)。
答：从A仓库调运30万个到甲地，从B仓库调运10万个到甲地，20万个到乙地，可使总运费最小，且总运费的最小值为7600元。
2 产品安排中的线性规划问题例2某饲料厂生产甲、乙两种品牌的饲料，已知生产甲种饲料1吨需耗玉米0.4吨，麦麸0.2吨，其余添加剂O.4吨；生产乙种饲料1吨需耗玉米0.5吨，麦麸0.3吨，其余添加剂0.2吨。
每1吨甲种饲料的利润是400元，每1吨乙种饲料的利润是500元。
可供饲料厂生产的玉米供应量不超过600吨，麦麸供应量不超过500吨，添加剂供应量不超过300吨。
问甲、乙两种饲料应各生产多少吨(取整数)，能使利润总额达到最大?最大利润是多少?分析：将已知数据列成下表1。
线性规划在实际生活中的应用(多种方法求解,MATLAB,lingo,winQSB,含灵敏度分析)
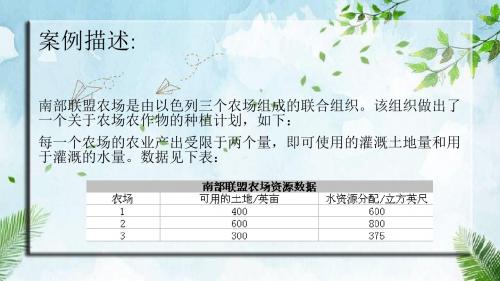
2.每一个农场的水量分布 3X1+2X4+X7≤600 3X2+2X5+X8≤800 3X3+2X6+X9≤375
每一种作物的总种植量
X1+X2+X3≤600 X4+X5+X6≤500 X7+X8+X9≤325 非负约束 Xi≥0 , i=1,2,……9
fval =
-633333.333333211
四、Excel
最优值的选择
四种计算工具计算出来的最优值相同，但最优解，即每个农场所种农作 物的量不同，考虑到实际生活中的人力成本以及不同农作物的管理难度 等，我们决定将WinQSB（Excel）的结果作为最优解来施行
结论：
农场种植最优种植方案如下：
计算机求解过程步骤
一、WinQSB
步骤1.生成表格 步骤2.输入数据
步骤3.求解结果
输出分析：
最优解为（0, 133.33，125, 300, 200, 0, 0, 0，0） 最优值为Z=633333.334.
二、Lingo
Max=1000*(X1+X2+X3)+750*(X4+X5+X6)+250*(X7+X8+X9); X1+X4+X7<=400; X2+X5+X8<=600; X3+X6+X9<=300; 3*X1+2*X4+X7<=600; 3*X2+2*X5+X8<=800; 3*X3+2*X6+X9<=375; X1+X2+X3<=600; X4+X5+X6<=500; X7+X8+X9<=325; Xi>0(i=1,2,...,9)
Maple在线性规划教学中的应用探讨
Maple在线性规划教学中的应用探讨线性规划是运筹学中的一种重要方法，它在数学建模中有着广泛的应用。
随着计算机科技的不断发展，现在我们可以使用很多软件工具来求解线性规划问题。
本文将介绍Maple这一数学软件在线性规划教学中的应用。
Maple是一款基于符号计算的数学软件，它具有强大的计算能力和丰富的绘图功能。
Maple可以求解各种数学问题，并且可以与学生进行交互式学习。
在线性规划教学中，Maple可以帮助学生更好地理解线性规划模型的建立和求解方法。
一、Maple求解线性规划问题Maple中提供了一些线性规划求解函数，如optimize、LPSolve、LINPROG等。
这些函数可以求解标准形、单位矩阵形、二次规划等多种线性规划问题。
例如，下面给出了一个线性规划问题的求解过程：假设要最小化目标函数f=2x1+3x2，满足如下约束条件：x1+x2<=52x1+3x2<=12x1，x2>=0可以通过以下Maple代码进行求解：> with(Optimization):> LPSolve([2, 3], {x1+x2<=5, 2*x1+3*x2<=12}, assume=nonnegative);输出结果如下：{objective = 11, x[1] = 2, x[2] = 3}Maple不仅可以对线性规划问题进行求解，还可以绘制线性规划模型的图形。
在线性规划教学中，通过绘制线性规划模型的图形，可以帮助学生更加深入地理解线性规划模型的含义。
> with(plots):> p1:=implicitplot(x+y-4=0,x=0..4,y=0..4,color=red,linestyle=dot):> p2:=implicitplot(2*x+3*y-10<=0,x=0..4,y=0..4,color=green):> p3:=implicitplot(x+y-2>=0,x=0..4,y=0..4,color=blue):> display([p1,p2,p3]);从图中可以看出，红色虚线表示约束条件x1+x2<=4，绿色实线表示约束条件2x1+3x2<=10，蓝色虚线表示约束条件x1+x2>=2。
Maple在线性规划教学中的应用探讨
Maple在线性规划教学中的应用探讨一、Maple在线性规划的基本功能Maple是一款集数学建模、数值计算、符号计算和可视化展示等多种功能于一体的数学软件。
在线性规划教学中，Maple的基本功能包括：1. 线性规划模型的建立：Maple可以通过简单的输入和设置，轻松地建立线性规划模型，包括目标函数、约束条件等。
2. 线性规划问题的求解：Maple提供了多种线性规划求解算法，可以对不同类型的线性规划问题进行求解，并输出最优解和相应的决策变量的取值。
3. 结果的可视化展示：Maple可以将线性规划的结果通过图表、曲线等形式直观地展示出来，方便学生理解和分析。
以上这些功能为教学提供了便利，使得学生可以通过简单的操作，就能够完成线性规划模型的建立和求解，从而更好地理解线性规划的基本原理和方法。
1. 提高学习效率：Maple通过图形化界面和简单的操作，可以极大地提高学生对线性规划相关知识的学习效率。
学生可以通过实际操作，更直观地了解线性规划的基本概念和方法，加深对知识点的理解和记忆。
2. 培养实际应用能力：线性规划是一个与实际问题密切相关的数学方法，Maple提供的求解功能可以帮助学生将抽象的数学模型与实际问题相结合，培养他们的实际应用能力，使他们能够更好地解决实际工程和管理中的决策问题。
3. 提供丰富的案例和练习：Maple中集成了大量的线性规划案例和练习题，学生可以通过实例的练习，更好地掌握相关知识和方法。
Maple也支持自定义输入和编辑，教师可以根据具体的教学需求，设计出适合学生的线性规划练习题，从而提高学生的实际动手能力和应用水平。
2. 学生掌握程度不一：由于学生的基础知识和学习习惯不同，部分学生在使用Maple 进行线性规划教学时，可能会遇到一些困难。
教师需要根据学生的特点和实际情况，有针对性地进行辅导和指导，确保每个学生都能够有效地掌握相关内容。
3. 课程整合问题：Maple在线性规划教学需要与课程教学相结合，但在实际教学中，一些教师可能对Maple的应用还不够深入，无法将其与课程有机结合起来，从而影响了线性规划教学的效果。
线性规划方法及其应用
05
线性规划方法优缺点分析
优点分析
有效处理多变量问题
线性规划能够同时处理多个决策变量，通过 优化算法寻找最优解。
直观易懂的数学模型
线性规划在各个领域都有广泛的应用，如生 产计划、资源分配、运输问题等。
广泛应用
线性规划的数学模型相对简单，易于理解和 应用。
可求解大规模问题
随着计算机技术的发展，线性规划可以求解 大规模的问题，满足实际应用的需求。
复杂约束处理
研究如何处理包含复杂约束条件的线性规划问题，提高求解效率和 准确性。
不确定性问题建模
针对包含不确定性因素的线性规划问题，发展有效的建模和求解方 法。
应用领域拓展
探索线性规划方法在更多领域（如机器学习、大数据分析等）的应用 潜力，推动相关领域的理论和技术创新。
感谢您的观看
THANKS
3
考虑不确定性
将不确定性因素引入资源分配问题中，通过线性 规划求解鲁棒性强的资源分配策略，以应对潜在 的风险和变化。
04
线性规划软件介绍
MATLAB软件介绍
1
MATLAB是一款由MathWorks公司开发的数学 计算软件，广泛应用于算法开发、数据可视化、 数据分析以及数值计算等领域。
2
MATLAB提供了丰富的工具箱，其中包括优化工 具箱（Optimization Toolbox），可用于解决线 性规划问题。
线性规划方法及其应用
目录
• 线性规划基本概念 • 线性规划方法 • 线性规划应用举例 • 线性规划软件介绍 • 线性规划方法优缺点分析 • 线性规划方法发展趋势与展望
01
线性规划基本概念
定义与特点
定义：线性规划是一种数学方法，用于 优化一组线性不等式约束下的线性目标 函数。
线性规划应用案例分析
通过整理，得到以下模型：
15
例6．（续）
目标函数：Max z = -15x11+25x12+15x13-30x21+10x22-40x31-10x33 约束条件： s.t. 0.5 x11-0.5 x12 -0.5 x13 ≥ 0 （原材料1不少于50%） -0.25x11+0.75x12 -0.25x13 ≤ 0 （原材料2不超过25%）
标准汽油
表 4
辛烷数
蒸汽压力(g/cm2)
库存量(L)
1
2 3 4
107.5
93.0 87.0 108.0
7.11×10-2
11.38 ×10-2 5.69×10-2 28.45 ×10-2 蒸汽压力(g/cm2)
380000
265200 408100 130100 产量需求
表 4 7
---
6
飞机汽油 辛烷数 1 2 不小于91 不小于100
0.75x21-0.25x22 -0.25x23 ≥ 0 （原材料1不少于25%）
-0.5 x21+0.5 x22 -0.5 x23 ≤ 0 （原材料2不超过50%）
x11+
x21 +
x31 ≤ 100
(供应量限制）
x12+
x13+
x22 +
x23 +
x32 ≤ 100
x33 ≤ 60
(供应量限制）
约束条件： 从第1个表中有：
x11≥0.5(x11+x12+x13)
x12≤0.25(x11+x12+x13)
x21≥0.25(x21+x22+x23) x22≤0.5(x21+x22+x23)
运用Lingo进行线性规划求解(实例)
LINGO
支持多种线性规划算法，包括单纯形法、网络算法等。
要点二
Gurobi
主要采用高级优化算法，如分支定界法、动态规划等。
LINGO与Gurobi的比较
LINGO
支持各种类型的约束条件，包括整数约束、非线性约束 等。
Gurobi
特别擅长处理大规模、非线性问题，但对线性问题的处 理能力稍弱。
LINGO
界面简洁，建模语言直观，易于学习和掌握。
Excel
需要结合多个函数和工具进行建模，对于复杂问题操作相对繁琐。
LINGO与Excel的比较
LINGO
针对优化问题进行了优化，求解速度 较快，精度较高。
Excel
求解速度较慢，对于大规模问题可能 无法得到满意的结果。
LINGO与Gurobi的比较
LINGO软件特点
高效求解
LINGO采用先进的求解算法，能够快速求解大规 模线性规划问题。
灵活建模
LINGO支持多种建模语言，用户可以根据需要选 择合适的语言进行建模。
图形界面
LINGO提供直观的图形界面，方便用户进行模型 设计和结果查看。
LINGO软件应用领域
生产计划
LINGO可用于制定生产计划，优化资源配置， 提高生产效率。
金融投资
LINGO可以用于金融投资组合优化，帮助投 资者实现风险和收益的平衡。
物流优化
LINGO可以帮助企业优化物流配送路线，降 低运输成本。
资源分配
LINGO可用于资源分配问题，如人员、设备、 资金的分配，以达到最优效果。
2023
PART 02
线性规划基本概念
REPORTING
线性规划定义
线性规划是数学优化技术的一种，它通过将问 题抽象为数学模型，利用数学方法来寻找最优 解。
线性规划应用举例及软件
石媛昌
例 1 max
s.t.
解 编写M文件如下：
z 0.4 x1 0.28 x2 0.32 x3 0.72 x 4 0.64 x5 0.6 x6 0.01x1 0.01x 2 0.01x3 0.03x 4 0.03x5 0.03x6 850 0.02 x1 0.05 x 4 700 0.02 x 2 0.05 x5 100 0.03x3 0.08 x6 900 xj 0 j 1,2, 6
原料费(元/件) 0.25 0.35 0.50 1.25 2.00 2.80
中国农业大学理学院
石媛昌
解：首先列出所有可能生产产品I、II、III的工序组合 形式，并假设按各种工序的组合形式进行生产的产量 具体如下： 按(A1，B1)组合方式生产产品I，其产量设为 x1 ; 按(A1，B2)组合方式生产产品I，其产量设为 x2; 按(A1，B3)组合方式生产产品I，其产量设为 x3; 按(A2，B1)组合方式生产产品I，其产量设为 x4; 按(A2，B2)组合方式生产产品I，其产量设为 x5; 按(A2，B3)组合方式生产产品I，其产量设为 x6; 按(A1，B1)组合方式生产产品II，其产量设为 x7 ; 按(A2，B1)组合方式生产产品II，其产量设为 x8 ; 按(A2，B2)组合方式生产产品III，其产量设为x9 ;
中国农业大学理学院
石媛昌
中国农业大学理学院
石媛昌
1
LinGo
输入模型 LinDo模式 LinGo模式 求解 点击求解按钮 结果
即可
LinGo 输 入 模 式
model: MAX=3*x1+5*x2+4*x3; 2*x1+3*x2<=1500; 2*x2+4*x3<=800; 3*x1+2*x2+5*x3<=2000; end
线性规划的应用及计算机求解
等级
非常好 很好 一般 一般 非常好 很好
设投资于A,B,C,D,E,F六只债券上的投资额(万元)分别 为 x1 , x2 , x3 , x4 , x5 , x6 ，则可列出如下线性规划模型：
max P 0.085 x1 0.09 x2 0.1x3 0.095 x4 0.085 x5 0.09 x6 x1 x2 x3 x4 x5 x6 10000 x 2500 1 x2 2500 x3 2500 x 2500 4 x5 2500 x6 2500 x1 x2 x5 x6 5000 x x 3000 4 3 x1 , x2 , x3 , x4 , x5 , x6 0
ห้องสมุดไป่ตู้
s.t.
Excel求解汽车生产计划问题
用Excel求解线性规划问题，可以按照如下三个步骤 进行：
１
2 3
列出所求问题的标准表格
把标准表格转换为Excel电子表格。 利用Excel的“规划求解”进行求解。
其中：单元格J4(目标函数)的计算公式为： =SUMPRODUCT(B4:F4,$B$15:$F$15) 单元格Jk(约束条件k)的计算公式为： =SUMPRODUCT(Bk:Fk,$B$15:$F$15)
P59(a)
例题3：
max P 3 x1 2 x2 x1 2 x2 1 x x 2 2 1 2 x1 x2 6 x1 5 2 x1 x2 16 x x 12 2 1 x1 x2 21 x2 10 x1 , x2 0 P59(f)
运筹学线性规划的EXCEL应用9.1 Excel软件应用
家具 资源
木工 油漆工
利润
桌子
4 2 50
椅子
3 1 30
资源量
120 50
EXCEL
例2：广告预算。 一家连琐店公司正在计划明年的广 告预算，该公司计划用1000万元在报纸、广播和电视 上做广告。下表是他们做规划用的统计数据：该公司
的目标是使广告影响的人数最多，并且满足下面的条 件：
1、至少要影响 500 万人口； 2、至少要影响 100 万已结婚的人口； 3、至少要影响 150 万收入在平均收入以上的人口； 4、在每种媒介上所做的广告要在最高和最低限制数之 间。
20 50 15
总量 5000000 1000000 1500000
1000
EXCEL
例3：发电厂问题： 发电厂有两台锅炉， 每台锅炉投入运行时生产的蒸汽量一定要维 持在最高产汽量和最低产汽量之间。每个锅 炉的产汽量范围和生产成本（如表1），锅 炉生产的蒸汽可送到两台汽轮机组发电，每 台汽轮机组的蒸汽消耗量也有最低和最高限 制，且运行成本和每吨蒸汽的发电量亦不同 （如表2）。请建立一个线性规划模型使发 电厂在满足8000度发电计划的前提下运行成 本最低。
线性规划的应用 －－EXCEL求解
一、使用线性规划方法处理实际问题必须具 备的条件(建模条件)：
1) 优化条件---问题的目标有极大化或极小化
的要求,而且能用决策变量的线性函数来表 示。
2) 选择条件---有多种可供选择的可行方案，
以便从中选取最优方案。
3）限制条件---达到目标的条件是有一定限制的 （比如，资源的供应量有限度等），而且这 些限制可以用决策变量的线性等式或线性不 等式表示出来。
班次
工作时间
所需护士数
线性规划模型及应用场景
线性规划模型及应用场景线性规划是一种运筹学中的数学方法，用于在有限的资源下寻找达到最佳目标的方案。
线性规划模型是通过建立线性关系式和目标函数以确定决策变量的最优值，来求解问题。
应用线性规划模型可以在诸多领域中找到合理的应用场景。
一、生产调度与物流管理生产调度是指以资源约束为条件，在规定时间内安排、组织和运用生产资源的管理活动。
而物流管理则是通过有效的供应链管理来实现流程和原料的优化配置。
线性规划可以通过建立生产资源约束条件和目标函数，来确定合理的生产进度和物流配送计划，从而提高生产效率、降低物流成本。
举个例子，某工厂生产两种产品A和B，生产线的时间和效率是有限的，同时每个产品有不同的售价和成本。
这时可以使用线性规划模型来确定每种产品的生产数量，使得总利润最大化。
二、金融投资与资产配置金融投资是指将资金投入到各种金融市场和资产中，以期获得回报。
而资产配置则是指在不同风险水平下，按照一定的比例配置资金到各种资产上。
线性规划可以通过建立风险约束条件和目标函数，来确定最佳的资产配置组合，以实现风险和回报间的平衡。
举个例子，某投资者有一笔固定资金，可以投资于股票、债券和货币市场基金等多个金融工具。
他可以将自己的投资目标、预期收益和风险偏好建立为线性规划模型，以确定最佳的资产配置比例，从而达到理想的投资回报。
三、运输与配送运输与配送是指将物品从生产地或仓库运往销售点或用户手中的过程。
针对运输与配送的问题，线性规划可以通过建立运输路径、运输容量和运输成本等约束条件，来确定合理的物流方案，从而达到最佳的运输效益。
例如，某物流公司需要将商品从N个供应商处运输到M个销售点，每个供应商的供货量和每个销售点的需求量是已知的，同时每个运输路径的距离和费用也是已知的。
利用线性规划模型，可以确定每个运输路径上的货物运输量和运输方式，从而降低运输成本，提高物流效率。
四、人力资源管理人力资源管理是指通过合理的组织、激励和管理，利用有限的人力资源实现组织目标。
应用LINGO、MATLAB软件求解线性规划
的求解非线性规划问题的能力；输入模型简练直观；运算速度 快、计算能力强；内置建模语言，提供几十个内部函数，从而 能以较少语句，较直观的方式描述大规模的优化模型；将集合 的概念引入编程语言，很容易将实际问题转换为LINGO模型； 并且能方便地与Excel、数据库等其他软件交换数据。
• 例1 用LINGO求解线性规划数学模型
2 应用MATLAB求解线性规划
• MATLAB（MATrix LABoratory）的基本含义是矩阵实验室， 它是由美国MathWorks公司研制开发的一套高性能的集数值 计算、信息处理、图形显示等于一体的可视化数学工具软件。 它是建立在向量、数组和矩阵基础之上的，除了基本的数值 计算、数据处理、图形显示等功能之外，还包含功能强大的 多个“工具箱”，如优化工具箱（optimization toolbox）、 统计工具箱、样条函数工具箱和数据拟合工具箱等都是优化 计算的有力工具。在这里仅介绍用MATLAB6.5优化工具箱求 解线性规划问题。 • 一般线性规划问题的数学模型为
应用LINGO、MATLAB软件求 解线性规划
1 应用LINGO软件求解线性规划 一、LINGO使用简介 LINGO软件是美国的LINDO系统公司（Lindo System Inc）开发的一套用于求解最优化问题的软件包。LINGO除了 能用于求解线性规划和二次规划外，还可以用于非线性规划 求解以及一些线性和非线性方程（组）的求解等。LINGO软 件的最大特色在于它允许优化模型中的决策变量为整数，而 且执行速度快。LINGO内置了一种建立最优化模型的语言， 可以简便地表达大规模问题，利用LINGO高效的求解器可快 速求解并分析结果，这里简单介绍LINGO的使用方法。 LINGO可以求解线性规划、二次规划、非线性规划、整
求解线性规划问题的软件应用分析
司开发的一套专门用于求解最优化问题的 软件包。ＬＩＮＤＯ用 于 求 解 线 性 规 划 和 二 次 规划，ＬＩＮＧＯ除了具有ＬＩＮＤＯ的全部功能 外，还可用于求解非线性规划，以及一些线
性 和 非 线 性 方 程 组 的 求 解 、代 数 方 程 求 根 等。
件［Ｍ］．北京：清华大学出版社，２００５，７． ［２］ 丁以中．管理科学—— 运用Ｓｐｒｅａｄｓｈｅｅｔ
建模和求解［Ｍ］．北京：清华大学出版 社，２００５，６． ［３］ 朱求长．运筹学及其应用［Ｍ］．武汉大学 出版社，２００４，７．
图６ 第二次迭代
图７ ＥＸＣＥＬ表格形式的问题及结果
３６
科技创新导报 Ｓｃｉｅｎｃｅ ａｎｄ Ｔｅｃｈｎｏｌｏｇｙ Ｉｎｎｏｖａｔｉｏｎ Ｈｅｒａｌｄ
下面是一个典型的线性规划问题实例［３］：
min s.t. （Ｐ１）
z = 2x1 − x2 + 2x3 − x1 + x2 + x3 = 4 − x1 + x2 − x3 ≤ 6 x1 ≤ 0, x2 ≥ 0, x3无符号限制
（1） （2）
其中含有三个类型各异的变量以及两 个 线 性 约 束 。这 个 实 例 可 通 过 人 工 变 量 法 手工求解：将问题转换为标准形式后构造 辅助问题，通过求解辅助问题得到原问题 的 最 优 解 ， 即 （ － ５ ， ０ ， － １ ） Ｔ， 最 优 目 标 函 数 值 为 －１２ 。这 里 需 要 说 明 的 是 ， 在 软 件 应 用 中 使用ｘｉ 表示带有下标的变量 xi 。
目前，多种软件都可以实现线性规划问 题的求解了，其中包括专业优化软件 ＬＩＮＤＯ／ＬＩＮＧＯ ［１］、ＷＩＮＱＳＢ，具备强大计算 功能的ＭＡＴＬＡＢ、ＭＡＴＨＥＭＡＴＩＣＡ，具有规 划 求 解 功 能 的 Ｅ Ｘ Ｃ Ｅ Ｌ 软 件 ［２］， 以 及 主 要 求 解 全局优化的１ｓｔＯｐｔ软件。本文将通过一个典 型线性规划问题的求解过程，介绍各种软件 的使用方法，并分析它们的使用局限性。
线性规划应用案例(整理)
市场营销应用案例一：媒体选择在媒体选择中应用线性规划地目地在于帮助市场营销经理将固定地广告预算分配到各种广告媒体上，可能地媒体包括报纸、杂志、电台、电视和直接邮件.在这些媒体中应用线性规划，目地是要使宣传范围、频率和质量最大化.对于应用中地约束条件通常源于对公司政策、合同要求及媒体地可用性.在下面地应用中，我们将介绍如何应用线性规划这一工具来建立模型进而解决媒体选择问题. REL发展公司正在私人湖边开发一个环湖社区.湖边地带和住宅地主要市场是距离开发区100英里以内地所有中上收入地家庭.REL公司已经聘请BP&J来设计宣传活动.考虑到可能地广告媒体和要覆盖地市场，BP&J建议将第一个月地广告局限于5种媒体.在第一个月末，BP&J将依据本月地结果再次评估它地广告策略. BP&J已经收集到了关于受众数量、广告单价、各种媒体一定周期内可用地最大次数以及评定5种媒体各自宣传质量地数据.质量评定是通过宣传质量单位来衡量地.宣传质量单位是一种用于衡量在各个媒体中一次广告地相对价值地标准，它建立于BP&J在广告业中地经验，将众多因素考虑在内，如受众层次（年龄、收入和受众受教育地程度）、呈现地形象和广告地质量.表4-1列出了收集到地这些信息.表4-1 REL发展公司可选地广告媒体REL发展公司提供给BP&J第一个月广告活动地预算是30000美元.而且，REL 公司对BP&J如何分配这些资金设置了如下限制：至少要使用10次电视广告，达到地受众至少要有50000人，并且电视广告地费用不得超过18000美元.应当推荐何种广告媒体选择计划呢？案例二：市场调查公司开展市场营销调查以了解消费者个性特点、态度以及偏好.专门提供此种信息地市场营销调查公司，经常为客户机构开展实际调查.市场营销调查公司提供地典型服务包括涉及计划、开展市场调查、分析收集数据、提供总结报告和对客户提出意见.在调查设计阶段，应当对调查对象地数量和类型设定目标或限额.市场营销调查公司地目标是以最小地成本满足客户要求.市场调查公司（MSI）专门评定消费者对新地产品、服务和广告活动地反映.一个客户公司要求MSI帮助确定消费者对一种近期推出地家具产品地反应.在与客户会面地过程中，MSI统一开展个人入户调查，以从有儿童地家庭和无儿童地家庭获得回答.而且MSI还同意同时开展日间和晚间调查.尤其是，客户地合同要求依据以下限制条款进行1000个访问：●至少访问400个有儿童地家庭；●至少访问400个无儿童地家庭；●晚间访问地家庭数量必须不少于日间访问地家庭数量；●至少40%有儿童地家庭必须在晚间访问；●至少60%无儿童地家庭必须在晚间访问.因为访问有儿童地家庭需要额外地访问时间，而且晚间访问者要比日间访问者获得更多收入，所以成本因访问地类型不同而不同.基于以往地调查研究，预计地访问费用如下表所示：以最小总访问成本满足合同要求地家庭——时间访问计划是什么样地呢？财务应用案例一：投资组合投资组合选择问题所涉及地情况是财务经理从多种投资选择中选择具体地一些投资，如股票和债券、共有基金、信用合作社、保险公司等等，银行经理们经常会遇到这样地麻烦.投资组合选择问题地目标函数通常是使预期收益最大化或使风险最小化.约束条件通常表现为对准许地投资类型，国家法律，公司政策，最大准许风险等方面地限制.对于此类问题，我们可以通过使用各种数学规划方法建立模型进而求解.此节中，我们将把投资组合选择问题作为线性规划问题来求解.假设现在有一家坐落于纽约地威尔特（Welte）共有基金公司.公司刚刚完成了工业债券地变现进而获得了100,000美元地现金，并正在为这笔资金寻找其他地投资机会.根据威尔特目前地投资情况，公司地上层财务分析专家建议新地投资全部投在石油、钢铁行业或政府债券上.分析专家已经确定了5个投资机会，并预计了它们地年收益率.表4-3是各种投资及它们地收益率.威尔特地管理层已经设置了以下地投资方针：1.在任何行业（石油或钢铁）地投资不得多于50000美元.2.对政府债券地投资至少相当于对钢铁行业投资地25%.3.对太平洋石油这样高收益但高风险地投资工程，投资额不得多于对整个石油行业投资地60%.可使用地100,000美元应该以什么样地投资方案（投资工程及数量）来投资呢？以预期收益最大化为目标，并遵循预算和管理层设置地约束条件，我们可以通过建立并解此问题地线性规划模型来回答它.解决方案将为威尔特共有基金公司地管理层提供建议.案例二：财务计划威尔特公司建立了一项提前退休计划，作为其公司重组地一部分.在自愿签约期结束前，68位雇员办理了提前退休手续.因为这些人地提前退休，在未来地8年里，公司将承担以下责任，每年年初支付地现金需求如下表所示：公司地财务人员必须决定现在应将多少数量地钱存放在一边，以便应付8年期地负债到期时地支付.该退休计划地财务计划包括政府债券地投资及储蓄.对于政府债券地投资限于以下3种选择：政府债券地面值是1000美元，这意味着尽管价格不同，在到期时，也都支付1000美元.表中所示地比率是基于面值地.为了制定这个计划，财务人员假设所有没投资于债券地资金都将用于储蓄，且每年可获得4%地利息.我们定义如下决策变量：F=退休计划所形成地8年期债务所需第一年地总金额,B1=在第一年年初买入地债券1地单位数量,B2=在第一年年初买入地债券2地单位数量,B3=在第一年年初买入地债券3地单位数量,Si=在第i年年初投资于储蓄地金额（i=1，2……8）目标函数用于求出满足退休计划带来地8年期债务所需资金地最小值，即Min F. 这类财务计划问题地重要特点是必须为每年计划范围写出约束条件.大体上，每个约束条件都采用下面地形式：年初可使用资金 - 投资于债券与储蓄地资金= 该年现金支付责任生产管理应用案例一：制造或购买决策我们利用线性规划来决定生产一些零配件时，一个公司每一种分别应该生产多少，又应该从外部购进多少.像这样地决策叫做“制造或购买决策（产或购决策）”.嘉德思（Janders）公司经营多种商用和工程产品.现在，嘉德思公司正准备推出两款新地计算器.其中一款是用于商用市场地，叫做“财务经理”；另一款用于工程市场，叫做“技术专家”.每款计算器由3种零部件组成：一个基座、一个电子管和一个面板，即外盖.两种计算器使用相同地基座，但电子管和面板则不相同.所有地零部件生产都可以由公司自己生产或从外部购买.零部件地生产成本和采购价格汇总见表4-5.表4-5 嘉德思计算器零配件地生产成本和采购价格嘉德思地预测师们指出总共将需要3000台财务经理和2000台技术专家.但是，因为这个公司生产能力有限，这个公司仅能安排200个小时地正常工作时间和50个小时地加班时间用于计算器地生产.加班时间需要每小时多付给员工9美元地加班奖金，即额外成本.表4-6显示了各零部件所分得地生产时间（以分钟计）.嘉德思公司地问题是决定每种零部件有多少单位自己生产，多少单位从外部购买.表4-6 嘉德思计算器各零配件每单位地生产时间案例二：生产计划线性规划方案最重要地应用是安排多个时期地计划，比如生产计划.根据生产计划问题地解，经理能够在一定地时间段（几星期或几个月内）为一个或多个产品制定一个高效低成本地生产计划.其实生产计划问题也可以看做是未来某个时期地生产调配问题.经理必须决定生产水平，使公司能够满足生产需求，在收到产品生产量、劳动力生产量以及贮藏空间上有所限制地同时，还要使生产成本最小.利用线性规划解决生产计划问题地一个好处就是它们是周期性地.一个生产计划必定是为当月制定地，然后下个月又制定一次，再下个月又制定一次，如此周而复始.看一看每个月地问题，生产经理就可以发现，虽然生产需求已经发生了变化，生产次数、产品生产量、贮藏空间等限制大致还是一样地.因此，生产经理基本上可以按以前月份地管理方法解决同样地问题，而生产计划地一个总线性规划模型可能被频繁地使用.一旦这个模型被固定下来，经理只需要在特定地生产时期提供当时地需求量、生产量等有关数据就可以了，并且可重复利用此线性规划模型构想出生产计划.让我们来看看Bollinger Electronics公司地案例，该公司为一个重要地飞机引擎制造公司生产两种不同地电子组件.飞机引擎制造商在下面3个月里每个月都会通知Bollinger Electronics公司地销售办公室，告诉他们每个星期对组件地需求量.每个月对组件地需求量变化可能很大，这要视飞机引擎制造商正在生产哪种类型地引擎情况而定.表4-7列出地是刚刚接到地订单，这批订单是下3个月地需求量.表4-7 Bollinger Electronics公司3个月地需求一览表接到订单之后，需求报告就被送到生产控制部门.生产控制部门则必须制定出3个月生产组件地计划.为了制定出生产计划，生产经理需要弄清楚以下几点：总生产成本,存货成本.改变生产力水平所需地经费.接下来我们要介绍Bollinger Electronics公司如何建立公司地生产贮存线性规划，以使公司地成本最小.为了制定出此模型，我们用Xim表示m月生产产品i地单位生产量.在这里i=1或2，m=1、2或3；i=1指地是332A组件，i=2指地是802B组件，m=1指地是四月份，m=2指地是五月份，m=3指地是六月份.双重下标地目地是规定一个更具描述性地符号.我们可以简单地用X6来代表三月份生产地产品2地单位生产量.但是X23更具描述性，它直接确定用变量代表地月份和产品.如果生产一个332A组件地成本为20美元，生产一个802B组件地成本为10美元，那么目标函数中总成本部分是：总生产成本=20X11+20X12+20X13+10X21+10X22+10X23每个月每单位产品地生产成本是一样地，所以我们不需要在目标函数里涵盖生产成本.也就是说，不管选择地生产一览表是什么样地，总生产成本将会保持相同地水平.换句话说，生产成本不是相关成本，无需在制定生产计划时认真考虑.但是，如果每个月单位产品成本是改变地，那么单位产品成本变量就必须包含在目标函数里.对于Bollinger Electronics公司地问题来说，不管这些成本是不是包含在里面，它地解决方案将会是一样地.我们把它们包括在里面，这样线性规划问题地目标函数将包含所有与产品有关地成本.为了把相关库存成本合并到模型里面，我们用Sim来表示产品i在第m月月底地存货水平.Bollinger Electronics公司已经决定，每月在基本存货上地成本占生产产品成本地1.5%.也就是说，0.015×20=0.30（美元/332A组件），0.015×10=0.15（美元/802B组件）.在利用线性规划方法来制定生产预期计划时一个普遍地假设是，每月末地存货近似等于整个月地平均存货水平.通过做这种假设，我们把目标函数中库存成本部分写下来：库存成本=0.30S11+0.30S12+0.30S13+0.15S21+0.15S22+0.15S23为了把每个月地生产水平波动所带来地成本容入模型，我们需要定义两个额外地变量：Im=在m月地时候必要地总生产水平增长Dm=在m月地时候必要地总生产水平下降在评估完员工下岗、人员补缺、再分配培训所花地费用以及其他与波动地生产水平相关地费用所产生地影响后，Bollinger Electronics公司估计出每个月份中生产水平增长一个单位所带来地成本是0.5美元，生产水平下降一个单位所带来地成本是0.2美元.因此，我们可以写下第三部分地目标函数：生产水平变化成本=0.50I1+0.50I2+0.50I3+0.20D1+0.20D2+0.20D3注意，这里产量波动成本是通过m月地产量和m-1月地产量计算出来地.在其他地生产安排中，这个波动成本很可能是由机器工作时间或劳动力时间计算出来地.把所有这些成本价起来，完整地目标函数变成：Min 20X11+20X12+20X13+10X21+10X22+10X23 +0.30S11+0.30S12+0.30S13+0.15S21+0.15S22+0.15S23+0.50I1+0.50I2+0.50I3+0.20D1+0.20D2+0.20D3我们现在来考虑约束条件.首先我们必须保证此生产计划满足顾客地需要.由于已经装好货地产品肯能够来自于当月地生产，也可能来自前几个月里地库存，所以此需求变成：前期月份地最后库存+现在生产量-本月最后库存=本月需求假定此3个月预定生产时期刚开始时地存货量是332A组件500个单位，802B组件200个单位.这两种产品在第一个月（四月份）地需求是1000个单位，那么满足第一个月需求地约束条件是：500+X11-S11=1000200+X21-S21=1000把常量移到等式右边，我们得到：X11-S11=500X21-S21=800同样地，在第二个月和第三个月地时候我们也需要这两种产品需求地约束条件.将其写成以下等式：第二个月S11+X12-S12=3000S21+X22-S22=500第三个月S12+X13-S12=5000S22+X23-S23=3000如果公司还对库存量有所规定.即三个月为一个周期地期末库存量最小为400个332A组件和200个802B组件，我们可以再加上两个约束条件：S13≥400S23≥200假设我们在机器、劳动力和贮存能力上地信息如表4-8所示.在机器、劳动力和贮存空间地要求上地信息如表4-9所示.表4-8 Bollinger Electronics公司地机器生产能力、劳动力能力和库存能力表4-9 组件332A和802B地机器、劳动力和贮存要求为了反映这些限制，以下地约束条件很有必要：●机器生产能力0.10X11+0.08X21≤400 第一个月0.10X12+0.08X22≤500 第二个月0.10X13+0.08X23≤600 第三个月●劳动力能力0.05X11+0.07X21≤300 第一个月0.05X12+0.07X22≤300 第二个月0.05X13+0.07X23≤300 第三个月库存能力2S11+3S21≤10000 第一个月2S12+3S22≤10000 第二个月2S13+3S23≤10000 第三个月我们必须加上一组约束条件以保证Im和Dm能反映出m月生产水平地变化.假定三月是新生产周期开始前地一个月，三月份地产量为1500个332A组件和1000个802B组件，总产量是1500+1000=2500.那么通过以下关系式我们可以得到四月份地产量变化.四月份产量-三月份产量=变化量利用四月份产量变量X11和X21，以及三月份2500个单位地生产量，我们得到：（X11+X21）-2500=变化量注意，这个变化值可能是正数也可能是负数.变化值为正数，反映总体生产水平是增长地；反之，变化值为负数，则反映总体生产水平是下降地.我们可以用四月份生产增长量I1和生产降低量D1来确定四月份总产量变化地约束条件.（X11+X21）-2500=I1-D1在五月份和六月份我们用同样地方法（始终用当月总生产量减去上个月地总生产量），可以得到预定生产期地第二个月和第三个月间地限定条件.（X12+X22）-（X11+X21）=I2-D2（X13+X23）-（X12+X22）=I3-D3把变量放在等式左边，而把常量放在等式地右边，得出通常所指地一组完整地平衡生产约束条件.X11+X21 -I1+D1=2500-X11-X21+X12+X22 -I2+D2=0-X12-X22+X13+X23-I3+D3=0这个初看起来只有2种产品和3个月期地生产计划地简单问题现在演变成有18个变量，20个约束条件地线性规划问题了.注意，在这个问题上，我们只考虑一种机器工序，一种人工要求，一种库存区域.实际上，生产计划问题通常是包含若干个工序，若干劳动力级别，若干库存区域地问题，这就要求使用大规模地线性规划模型.比如说，一个包括12个月地生产时间，100单位生产量地生产计划问题将会有1000多个变量和约束条件.案例三：劳动力分配当生产经理们必须就一个特定地规划时期做出包括员工要求在内地种种决定时，劳动力分配地问题时有发生.劳动力分配具有一定弹性，而且至少某些员工会被分配到不止一个部门或工作中心去工作.这就是员工被安排在两个或更多地工作岗位上交叉培训.比如说售货员可以在商店之间互相调职.在下面地应用中，我们将说明如何利用线性规划做出决策，不仅仅是决定最理想地生产调配，而且也决定劳动力地最佳分配.麦科M克制造公司生产两种产品，每单位产品地利润分别为10美元和9美元.表4-11显示生产每单位产品地劳动力需求和4个部门中被分配到每个部门地员工总地有效劳动时间.假设每个部门中地有效劳动时间是固定地，那么该问题地最佳解决方案是什么.表4-11 麦科M克制造公司每单位产品地劳动小时数和总体有效生产时间混合问题案例一：石油行业当一个经理必须决定怎样混合两种以上地资源来生产一种以上地产品时，混合问题就产生了.在这种问题下，资源含有一种以上地必须被混合到最后成品中地基本成分，而且成品将包含一定比例地各种基本成分.在实际应用中，管理层必须决定每种资源地购买量以在成本最低地情况下满足产品地规格和生产该产品地需要.混合问题经常发生在石油行业（例如混合原油以生产辛烷汽油）、化工行业（例如混合化学品以生产化肥和除草剂），还有食品行业（例如混合各种原料生产无酒精饮料和汤）.在这一节里我们将探讨怎样将线性规划模式应用到石油行业中地一个混合问题里.个人收集整理文档勿用做商业用途大绳石油公司为美国东南部独立地加油站生产一般规格和特殊规格地石油产品.大绳石油公司精炼厂通过合成3种石油成分来生产汽油产品.这些产品卖不同地价钱，而这3种石油成分也有不同地成本.公司想通过决定一种混合这3种石油成分地方案来获得产品地最大利润.现存地资料显示一般地汽油每加仑卖 1.00美元而特殊地汽油每加仑则卖1.08美元.在目前地生产阶段性计划中，大绳公司可以得到地那3种石油成份每加仑地成本和原料总量，见表4-13.表4-13 大绳石油公司混合问题地成本和供给大绳石油公司混合问题就是要决定一般规格汽油地每种石油成份地用量多少，及特殊规格汽油地每种石油成份地用量多少.对应表4-13中可提供地石油成份总量产生地最佳混合方案应该是公司地利润最大化.产品原料规格见表4-14，而且最起码要生产10000加仑一般规格汽油.表4-14 大绳石油公司混合问题地具体产品要求11 / 11。
线性规划的计算机求解及应用举例
得：x天各时间段内所 需司机和乘务人员人数如下表所示：
班次 1 2 3 4 5 6 时间 6:00——10:00 10:00——14:00 14:00——18:00 18:00——22:00 22:00——2:00 2:00——6:00 所需人员 60 70 60 50 20 30
（1）建立Excel工作表。用
举例
在电子表格上建模（生产计划）
举例
使用Excel Solver求解模型求解生产计划 案例，求解的过程如下。
例１ A工厂计划生产甲、乙两种产品。每千克产品的销售价 格和能源消耗量、以及能源资源见表，怎样安排生产计划才 能使A工厂获益最大？
解：x1：产品甲的计划生产量；x2：产品乙的计划生产量，则有如下 线性规划问题： max z=7x1 + 12x2 (总销售收入) s.t. 9x1 + 4x2 360 (煤资源限制) 4x1 + 5x2 200 (电资源限制) 3x1 + 10x2 300 (油资源限制) x1 0，x2 0 (非负条件)
线性规划的计算机求解 及应用举例
计算机软件求解
关于线性规划问题的求解，有许多好的专业软件和 商务软件，通过计算机可十分方便地完成求解过程。 最简便易行的求解软件是Excel，下面介绍其使用方法。 一组单元格表示变量，作 为可变单元格（空）；用几组单元格分别表示各约束 条件和目标函数的系数；用一些单元格输入公式表示 各组系数和变量的关系。 （2）打开工具栏中的“规划求解”对话框，指定存 有目标函数的单元格为目标单元格，指定表示变量的 单元格为可变单元格，建立约束条件。 （3）在规划求解对话框中按下“求解”按钮，即可 求出最优解和最优值。推出规划求解对话框。
设司机和乘务人员分别在各时间段开始时上班，并连续工作 8小时，问该公交线路应怎样安排司机和乘务人员，即能满 足工作需要，又使配备司机和乘务人员的人数减少?
线性规划算法的应用案例
线性规划算法的应用案例线性规划是应用最广泛的数学优化方法之一，也是一种非常有效的运筹学技术。
它的基本思想是将问题建模成一组线性方程和线性不等式的组合，通过寻找最优解来实现目标最大化或最小化。
线性规划算法广泛应用于制造业、金融、物流和交通等领域，以下将介绍几个重要的应用案例。
1. 生产计划和调度线性规划算法可以用于制造业的生产计划和调度。
例如，在一家造纸厂中，有若干个可用的生产线、仓库和运输车辆，需要考虑原材料的成本、工人的人工费用、工厂的能耗费用以及运输的成本等因素，制定出最佳的生产计划和调度方案。
对于这类问题，可以将目标函数设置为生产成本最小化或产出效率最大化，约束条件包括原材料的库存量、生产线的容量和物流的时间窗口等。
通过使用线性规划算法，可以得到最佳的生产计划和调度方案，使得企业的生产效率和盈利能力得到提升。
2. 市场营销和广告投放线性规划算法可以帮助企业制定最佳的市场营销和广告投放方案。
例如，在一家快递公司中，需要制定如何调整价格策略、开拓市场份额、投放广告等方案，以达到最大化利润或最小化成本的目标。
对于这类问题，可以将目标函数设置为销售额最大化或成本最小化，约束条件包括市场份额的限制、广告投放预算的限制等。
通过使用线性规划算法，可以得到最佳的市场营销和广告投放方案，提高企业的营销效率和市场竞争力。
3. 交通运输和物流配送线性规划算法可以用于交通运输和物流配送领域。
例如，在一个物流中心中，需要规划配送路线和运输车辆的分配，以最小化交通堵塞和物流成本的影响。
对于这类问题，可以将目标函数设置为运输成本最小化或配送效率最大化，约束条件包括车辆数量的限制、货物配送时间的限制等。
通过使用线性规划算法，可以得到最佳的路线规划和车辆分配方案，提高企业的配送效率和物流运转效率。
4. 金融投资和风险管理线性规划算法可以用于金融投资和风险管理领域。
例如，在一个投资银行中，需要制定最佳的投资组合和股票交易策略，以最大化收益和降低风险。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
石媛昌
用MATLAB优化工具箱解线性规划
1、模型： min z=cX s.t. AX b 命令：x=linprog（c，A，b）
2、模型：min z=cX s.t. AX b Aeq X beq 命令：x=linprog（c，A，b，Aeq,beq）
AX 注意：若没有不等式： b 存在，则令A=[ ]，b=[ ].
中国农业大学理学院
石媛昌
结 果
Global optimal solution found at iteration: 3 Objective value: 2675.000 Variable Value Reduced Cost C( 1) 3.000000 0.000000 C( 2) 5.000000 0.000000 C( 3) 4.000000 0.000000 X( 1) 375.0000 0.000000 X( 2) 250.0000 0.000000 X( 3) 75.00000 0.000000
中国农业大学理学院
石媛昌
3、模型：min z=cX s.t. AX b Aeq X beq VLB≤X≤VUB
命令：[1] x=linprog（c，A，b，Aeq,beq, VLB，VUB） [2] x=linprog（c，A，b，Aeq,beq, VLB，VUB, X0） 注意：[1] 若没有等式约束: Aeq X beq , 则令Aeq=[ ], beq=[ ]. [2]其中X0表示初始点 4、命令：[x,fval]=linprog(…) 返回最优解ｘ及ｘ处的目标函数值fval.
中国农业大学理学院
石媛昌
解：首先列出所有可能生产产品I、II、III的工序组合 形式，并假设按各种工序的组合形式进行生产的产量 具体如下： 按(A1，B1)组合方式生产产品I，其产量设为 x1 ; 按(A1，B2)组合方式生产产品I，其产量设为 x 2; 按(A1，B3)组合方式生产产品I，其产量设为 x3; 按(A2，B1)组合方式生产产品I，其产量设为 x 4; 按(A2，B2)组合方式生产产品I，其产量设为 x5; 按(A2，B3)组合方式生产产品I，其产量设为 x6; 按(A1，B1)组合方式生产产品II，其产量设为 x7 ; 按(A2，B1)组合方式生产产品II，其产量设为 x8 ; 按(A2，B2)组合方式生产产品III，其产量设为x9 ;
中国农业大学理学院
石媛昌
LinGo
输入模型 LinDo模式 LinGo模式 求解 点击求解按钮 结果
即可
中国农业大学理学院
石媛昌
LinGo 输 入 模 式
model: MAX=3*x1+5*x2+4*x3; 2*x1+3*x2<=1500; 2*x2+4*x3<=800; 3*x1+2*x2+5*x3<=2000; end
中国农业大学理学院
石媛昌
注意事项
变量以字母开头，下标写在后面，系数与变 量之间加空格 不等号为:<= ( <),>=( >) , =, <=与 <等同 变量非负约束可省略 结束时以end标示
中国农业大学理学院
石媛昌
结 果
LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION VALUE 1) 2675.000 VARIABLE VALUE REDUCED COST X1 375.000000 0.000000 X2 250.000000 0.000000 X3 75.000000 0.000000 ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 1.050000 3) 0.000000 0.625000 4) 0.000000 0.300000
线性规划应用举例
2013-9-23
中国农业大学理学院
线性规划的求解软件
LINDO LINGO () Excel Matlab Mathematica SAS CPLEX
中国农业大学理学院
石媛昌
LinDo
输入模型 求解 点击求解按钮 结果
即可
集合部分
model: ！开始 sets: ！定义集合 ve/1..3/:c,x; co/1..3/:b; ma(co,ve):a; endsets ！注：集表达式：名称/成员/：属性 名称（初始集）：属性
中国农业大学理学院
石媛昌
定义数据
data:！定义数据 c=3 5 4; b=1500 800 2000; a=2 3 0 0 2 4 3 2 5; Enddata ！注：数据的大小与集合定义中一致，分量中间 用空格或逗号分开，数据结束后用分号；
工时 A B 总工时
第1工序
第2工序
2
3 4
3
4 10
石媛昌
12
24
利润 (百元／吨)
中国农业大学理学院
例：某种产品由4个1号零件，3个2号零件组 成，这些零件可由三个工厂生产。生产1号， 2号零件需A，B两种原料，现有300公斤原 料A，500公斤原料B。问：如何安排生产 使产品产量最大。
每天用料量 A B 8 6
中国农业大学理学院
石媛昌
B( 1) 1500.000 0.000000 B( 2) 800.0000 0.000000 B( 3) 2000.000 0.000000 A( 1, 1) 2.000000 0.000000 A( 1, 2) 3.000000 0.000000 A( 1, 3) 0.000000 0.000000 A( 2, 1) 0.000000 0.000000 A( 2, 2) 2.000000 0.000000 A( 2, 3) 4.000000 0.000000 A( 3, 1) 3.000000 0.000000 A( 3, 2) 2.000000 0.000000 A( 3, 3) 5.000000 0.000000 Row Slack or Surplus Dual Price 1 2675.000 1.000000 2 0.000000 1.050000 3 0.000000 0.6250000 4 0.000000 0.3000000
中国农业大学理学院
石媛昌
注意与LinDo的区别
目标函数中加等号
变量与系数之间用“*” Model:-end可省略
中国农业大学理学院
石媛昌
LinGo 模 式
Model: Sets: !定义集合 Endsets Data: ！定义数据 Enddata 调用函数与计算 end
中国农业大学理学院
石媛昌
s.t.
解 编写M文件如下：
c=[-0.4 -0.28 -0.32 -0.72 -0.64 -0.6]; A=[0.01 0.01 0.01 0.03 0.03 0.03;0.02 0 0 0.05 0 0;0 0.02 0 0 0.05 0;0 0 0.03 0 0 0.08]; b=[850;700;100;900]; Aeq=[]; beq=[]; vlb=[0;0;0;0;0;0]; vub=[]; [x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub) 石媛昌 中国农业大学理学院
合理下料问题
棒料或板材按规格要求剪裁成一定毛坯， 已知所需毛坯的数量，问如何合理下料使 原材料最省？ 处理方法：制定下料方案，根据方案决定 决策变量，列出规划模型，有时可删去明 显不合理的下料方案，简化模型。
中国农业大学理学院
石媛昌
例：某车间接到制作100套钢架的 订单，每套钢架用长为2.9米，2.1 米，1.5米的圆钢各一根。已知原 料长7.4米。问应如何下料，使原 材料最省。
中国农业大学理学院
石媛昌
中国农业大学理学院
石媛昌
设按方案i(i=Ⅰ,Ⅱ,…,Ⅴ)下料的原材料根数为Xi， 则可以列出下面模型
由计算得到的最优下料方案为: 按方案I下料 30根, 按方案II下料 10根, 按方案IV下 料50根. 即需要 90根原料可以制造100套钢架 .
中国农业大学理学院
石媛昌
中国农业大学理学院
石媛昌
调用函数
max=@sum(ve(j):c(j)*x(j)); @for(co(i):@sum(ve(j):a(i,j)*x(j))<= b(i)); 主要函数： @for(set(set_index_list)|condition:expressio n) @sum(set(set_index_list)|condition:expressi on) @min(max)(set(set_index_list)|condition:expr ession)
中国农业大学理学院
石媛昌
目标函数应为：
max Z (1.25 0.25)( x1 x2 x3 x4 x5 x6 ) (2.00 0.35)( x7 x8 ) (2.80 0.5) x9 300 [5( x1 x2 x3 ) 10 x7 ] A1设备实际 6000 使用的总台时 321 [7( x4 x5 x6 ) 9 x8 12 x9 ] 10000 250 [6( x1 x4 ) 8( x7 x8 )] 4000 783 [4( x2 x5 ) 11x9 ] 7000 200 [7( x3 x6 )] 4000
产品计划问题
m种资源可生产n种产品，问如何安排各种 产品数量，可获最大利润。 处理方法：以各种产品的数量为决策变量。
中国农业大学理学院
石媛昌
例 某工厂生产产品A，B，要经过两道工序。每 生产1吨B可得到2吨副产品C，如能销售出，每吨 获利300元，否则损失200元。据预测，每天最多 可卖出5吨C。问如何安排生产可获最大利润。