求函数的单调区间
单调区间的求法步骤

单调区间的求法步骤
《单调区间的求法步骤单调区间的求法步骤》
嘿,亲爱的小伙伴们!今天咱们来聊聊单调区间的求法步骤。
这可是数学里挺重要的一块儿知识哦,别怕别怕,咱们一起轻松拿下它!
咱们先来说说第一步哈,那就是求函数的定义域。
这就好比你要去一个好玩的地方,得先知道能去的范围嘛。
比如说一个分式函数,分母不能等于零,不然就没意义啦。
这定义域就是咱们玩耍的场地,可不能搞错喽!
然后呀,咱们令导数等于零,求出导函数的零点。
这零点可重要啦,就像是路上的转折点。
找到它们,咱们就能更好地搞清楚函数的走势。
再然后呢,咱们以这些零点为分界点,把定义域分成几个小段。
这就像是把咱们的大场地分成了几个小区域。
接着,在每个小段里,咱们选一个数,代入导函数,看看是正还是负。
如果是正的,那这一段函数就是单调递增的;要是负的呢,这一段就是单调递减的。
这就好像是在每个小区域里探探路,看看是上坡还是下坡。
比如说,选个 1 代进去,发现导函数是正的,那这一段就是递增的,是不是挺有趣?
还有哦,咱们把单调递增和单调递减的区间都写出来,这可就算大功告成啦!
怎么样,小伙伴们,单调区间的求法步骤是不是也没有那么可怕呀?多练练,多琢磨琢磨,咱们就能轻松掌握,数学的世界也能变得好玩起来哟!加油加油,相信你们都能行!。
高中数学讲义:求函数的单调区间

函数的单调区间单调性是函数的一个重要性质,对函数作图起到决定性的作用,而导数是分析函数单调区间的一个便利工具。
求一个已知函数的单调区间是每一个学生的必备本领,在求解的过程中也要学会一些方法和技巧。
一、基础知识:1、函数的单调性:设()f x 的定义域为D ,区间I D Í,若对于1212,,x x I x x "Î<,有()()12f x f x <,则称()f x 在I 上单调递增,I 称为单调递增区间。
若对于1212,,x x I x x "Î<,有()()12f x f x >,则称()f x 在I 上单调递减,I 称为单调递减区间。
2、导数与单调区间的联系(1)函数()f x 在(),a b 可导,那么()f x 在(),a b 上单调递增()',()0x a b f x Þ"γ, 此结论可以这样理解:对于递增的函数,其图像有三种类型: ,无论是哪种图形,其上面任意一点的切线斜率均大于零。
等号成立的情况:一是单调区间分界点导数有可能为零,例如:()2f x x =的单调递增区间为[)0+¥,,而()'00f =,另一种是位于单调区间内但导数值等于零的点,典型的一个例子为()3f x x =在0x =处的导数为0,但是()0,0位于单调区间内。
(2)函数()f x 在(),a b 可导,则()f x 在(),a b 上单调递减()',()0x a b f x Þ"Σ,(3)前面我们发现了函数的单调性可以决定其导数的符号,那么由()',()x a b f x "Î,的符号能否推出()f x 在(),a b 的单调性呢?如果()f x 不是常值函数,那么便可由导数的符号对应推出函数的单调性。
求单调区间的方法

求单调区间的方法在数学中,单调区间是指函数在某个区间上是单调递增或者单调递减的区间。
在实际问题中,我们经常需要求解函数的单调区间,以便更好地理解函数的性质和行为。
本文将介绍几种常用的方法来求解单调区间。
一、导数法。
导数法是求解单调区间的常用方法之一。
对于给定函数$f(x)$,我们可以通过求解其导数$f'(x)$的符号来确定函数的单调性。
具体步骤如下:1. 求解函数的导数$f'(x)$;2. 找出导数$f'(x)$的零点,即解方程$f'(x)=0$;3. 将零点所在的区间进行划分,并在每个区间内取一个测试点$x_0$;4. 计算测试点$x_0$对应的导数值$f'(x_0)$,根据导数值的正负确定函数在该区间上的单调性。
二、二阶导数法。
在某些情况下,我们可以通过求解函数的二阶导数$f''(x)$来确定函数的单调区间。
具体步骤如下:1. 求解函数的二阶导数$f''(x)$;2. 找出二阶导数$f''(x)$的零点,即解方程$f''(x)=0$;3. 将零点所在的区间进行划分,并在每个区间内取一个测试点$x_0$;4. 计算测试点$x_0$对应的二阶导数值$f''(x_0)$,根据二阶导数值的正负确定函数在该区间上的凹凸性;5. 根据函数的凹凸性和一阶导数的符号确定函数的单调区间。
三、图像法。
图像法是一种直观的方法,通过观察函数的图像来确定其单调区间。
具体步骤如下:1. 绘制函数$f(x)$的图像;2. 通过观察函数图像,找出函数的上升区间和下降区间;3. 根据图像上升和下降的趋势确定函数的单调区间。
四、综合运用。
在实际问题中,我们通常需要综合运用以上方法来确定函数的单调区间。
例如,对于一个复杂的函数,我们可以先通过导数法找出函数的增减点,然后通过二阶导数法确定函数的凹凸性,最后通过图像法直观地确认函数的单调区间。
求函数单调区间的方法及几个常用结论

求函数单调区间的方法及几个常用结论要确定一个函数的单调区间,可以通过以下几种方法:1.分析函数的导数:如果一个函数在一些区间上的导数恒为正(负),则这个函数在该区间上是严格递增(递减)的。
通过求解函数的导数,可以确定函数的单调性。
对于可导函数,我们可以通过求导数的零点来确定函数的单调区间。
导数为正的区间是函数递增的区间,导数为负的区间是函数递减的区间。
2.分析函数的二阶导数:二阶导数表示函数的导数的导数。
如果一个函数在一些区间上的二阶导数恒为正(负),则该函数在这个区间上是凹的(凸的)。
通过求解函数的二阶导数,可以确定函数的拐点。
拐点可以将函数的区间分为凹和凸的两个部分,函数在凹部分是严格递增的,在凸部分是严格递减的。
3.利用函数的性质或图像:对于一些特定形式的函数,可以直接利用函数的性质或图像来判断函数的单调区间。
例如,对于多项式函数而言,函数的次数决定了函数的单调性。
如果一个多项式函数的次数为奇数,则函数是整个实数轴上的单调函数;如果一个多项式函数的次数为偶数,则函数是在一些区间上单调递增或单调递减。
4. 利用数学不等式:当函数定义域为实数时,我们可以通过利用一些数学不等式来判断函数的单调性。
例如,对于二次函数$f(x) = ax^2 + bx + c$,如果$a > 0$,则函数是开口向上的,函数的单调区间为$(-\infty,+\infty)$;如果$a < 0$,则函数是开口向下的,函数的单调区间为$(+\infty,-\infty)$。
在实际应用中,经常会用到以下几个常用结论:1.定义:如果函数$f$在开区间$(a,b)$上单调递增,且在$x=a$和$x=b$处的极限分别存在,则$f$在闭区间$[a,b]$上连续。
2.定理1:如果函数$f$在闭区间$[a,b]$上连续,在开区间$(a,b)$上可导,且在开区间$(a,b)$上导数恒为零,则$f$在闭区间$[a,b]$上的函数值都相等。
函数的单调区间怎么求

函数的单调区间怎么求
一:函数单调区间的求法:
(1)图像法
对于能作出图像的函数,我们可以通过观察图像确定函数的单调区间,即第一步作出函数图像,二是由单调性的几何意义划分增减区间,最后一步写出单调区间。
注意:当函数递增或递减区间由几个区间组成时,一般情况下不能取它们的并集,而应该用“和”、“或”连接。
(2)定义法
有些函数如果不能作出函数图像来观察出单调区间,可以用定义法来求其单调区间,即首先可以设X1、X2为该区间内任意的两个值,且X1小于X2,其次作差,令F(X1)-F(X2),并通过因式分解、配方、有理化等方法,向有利于判断差值符号的方向变形。
(3)直接法
对于我们所熟知的一次函数、二次函数、反比例函数等,可以根据它们的特征,直接求出单调区间
(4)复合函数单调性的确定
二:求函数最值的方法
(1)函数的最值
(2)利用函数图像求最值
利用函数图像是函数求最值的常用方法,其步骤如下:
(3)利用函数单调性求最值
函数的最值与单调性的关系:
若函数在区间[a,b]上是减函数,则f(x)在[a,b]上的最大值为f(a),最小值为f(b);若函数在区间[a,b]上是增函数,则f(x)在[a,b]上的最大值为f(b),最小值为f(a).。
求复合函数的单调区间

c g ( x1 ) g ( x 2 ) b
又y f (u)在(c, d )上为增函数
即c u1 u2 d
即f [ g ( x1 )] f [ g ( x2 )] y f [ g ( x)]在(a, b)上为增函数
f (u1 ) f (u2 )
例1: 已知函数f (x)在R上是增函数,g(x)在[a,b]上是减 函数,求证:f [g(x)]在[a,b]上是减函数.
0 0.4 1
f ( x) log
0.4
y log 0.4 t是减区间。
x
2
4 x 3的单调递增区间为 2,3 ,
单调递减区间为1, 2 。
拓展1:判断函数f ( x) log
2
拓展2:判断函数f ( x) log
a
x
x 2 4 x 3 的单调性。
y u是定义域内是的单调递增函数。
又u x 2 1在 2,3 上是减函数。
2
y x 2 4 x 3在 2,3 上是减函数。
故函数y x 2 4 x 3的单调递减区间为 2,3。
问 你 求 函 : 能 出 数
y x 2 4 x 3的 调 增 吗 单 递 区 ?
函数,记为y=f(u),u 又是x 的函数,记为u=g(x),且g(x)的值域与f(u)的 定义域的交集不空,则确定了一个y关于x 的函y=f[g(x)],这时y叫x的复合函数,其中 u叫中间变量,y=f(u)叫外层函数,u=g(x) 叫内层函数。x
u
y
y ax2 bx c(a 0)
O
x
b 2a
x
正弦函数的单调区间公式

正弦函数的单调区间公式首先要记住f(x)=sinx的单调增区间是x∈[2kπ-π/2,2kπ+π/2],单调减区间是x∈[2kπ+π/2,2kπ+3π/2],k∈Zf(x)=cosx的单调增区间是x∈[2kπ-π,2kπ],单调减区间是x∈[2kπ,2kπ+π],k∈Z遇到复合函数时,把ωx+φ看作一个整体,以余弦函数为例,函数简化为f(x)=Asin α由于单调区间和A没有关系,所以单调增区间为α∈[2kπ-π,2kπ],k∈Z这时把α=ωx+φ带回,有ωx+φ∈[2kπ-π,2kπ],k∈Z解得单调增区间为x∈[(2kπ-π-φ)/ω,(2kπ-φ)/ω],k∈Z举个例子:求f(x)=5sin(2x+π/4)的单调增区间f(x)的单调增区间为2x+π/4∈[2kπ-π/2,2kπ+π/2],k∈Z则2x∈[2kπ-3π/4,2kπ+π/4],k∈Z即x∈[kπ-3π/8,kπ+π/8],k∈Z扩展资料:单调区间是指函数在某一区间内的函数值y,随自变量x的值增大而增大(或减小)恒成立。
若函数y=f(x)在某个区间是增函数或减函数,则就说函数在这一区间具有(严格的)单调性,这一区间叫做函数的单调区间。
此时也说函数是这一区间上的单调函数。
若函数y=f(x)在某个区间是增函数或减函数,则就说函数在这一区间具有(严格的)单调性,这一区间叫做函数的单调区间。
此时也说函数是这一区间上的单调函数。
注:在单调性中有如下性质。
图例:↑(增函数)↓(减函数)↑+↑=↑两个增函数之和仍为增函数↑-↓=↑增函数减去减函数为增函数↓+↓=↓两个减函数之和仍为减函数↓-↑=↓减函数减去增函数为减函数一般地,设函数f(x)的定义域为I:如果对于属于I内某个区间上的任意两个自变量的值x1、x2,当x1<x2时都有f(x1)<f(x2)。
那么就说f(x)在这个区间上是增函数。
相反地,如果对于属于I内某个区间上的任意两个自变量的值x1、x2,当x1<x2时都有f(x1)>f(x2),那么f(x)在这个区间上是减函数。
函数的单调性及单调区间
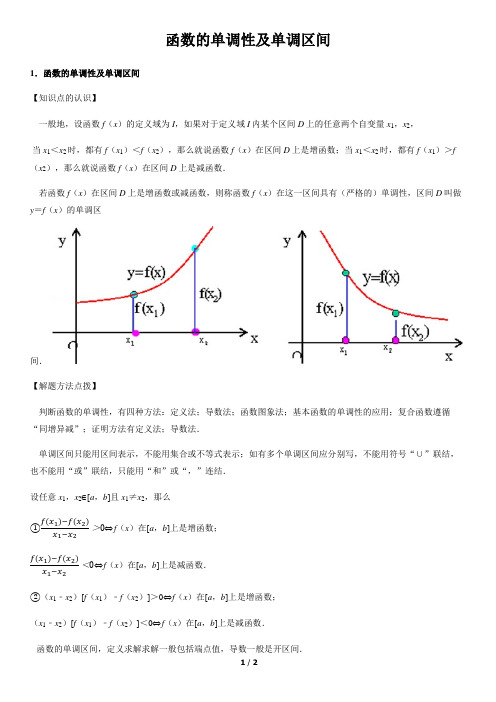
函数的单调性及单调区间1.函数的单调性及单调区间【知识点的认识】一般地,设函数f (x )的定义域为I ,如果对于定义域I 内某个区间D 上的任意两个自变量x 1,x 2, 当x 1<x 2时,都有f (x 1)<f (x 2),那么就说函数f (x )在区间D 上是增函数;当x 1<x 2时,都有f (x 1)>f (x 2),那么就说函数f (x )在区间D 上是减函数.若函数f (x )在区间D 上是增函数或减函数,则称函数f (x )在这一区间具有(严格的)单调性,区间D 叫做y =f (x )的单调区间.【解题方法点拨】判断函数的单调性,有四种方法:定义法;导数法;函数图象法;基本函数的单调性的应用;复合函数遵循“同增异减”;证明方法有定义法;导数法.单调区间只能用区间表示,不能用集合或不等式表示;如有多个单调区间应分别写,不能用符号“∪”联结,也不能用“或”联结,只能用“和”或“,”连结.设任意x 1,x 2∈[a ,b ]且x 1≠x 2,那么①f(x 1)−f(x 2)x 1−x 2>0⇔f (x )在[a ,b ]上是增函数;f(x 1)−f(x 2)x 1−x 2<0⇔f (x )在[a ,b ]上是减函数.②(x 1﹣x 2)[f (x 1)﹣f (x 2)]>0⇔f (x )在[a ,b ]上是增函数;(x 1﹣x 2)[f (x 1)﹣f (x 2)]<0⇔f (x )在[a ,b ]上是减函数.函数的单调区间,定义求解求解一般包括端点值,导数一般是开区间.【命题方向】函数的单调性及单调区间.是高考的重点内容,一般是压轴题,常与函数的导数相结合,课改地区单调性定义证明考查大题的可能性比较小.从近三年的高考试题来看,函数单调性的判断和应用以及函数的最值问题是高考的热点,题型既有选择题、填空题,又有解答题,难度中等偏高;客观题主要考查函数的单调性、最值的灵活确定与简单应用,主观题在考查基本概念、重要方法的基础上,又注重考查函数方程、等价转化、数形结合、分类讨论的思想方法.预测明年高考仍将以利用导数求函数的单调区间,研究单调性及利用单调性求最值或求参数的取值范围为主要考点,重点考查转化与化归思想及逻辑推理能力.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数的单调区间单调性是函数的一个重要性质,对函数作图起到决定性的作用,而导数是分析函数单调区间的一个便利工具。
求一个已知函数的单调区间是每一个学生的必备本领,在求解的过程中也要学会一些方法和技巧。
一、基础知识:1、函数的单调性:设()f x 的定义域为D ,区间I D ⊆,若对于1212,,x x I x x ∀∈<,有()()12f x f x <,则称()f x 在I 上单调递增,I 称为单调递增区间。
若对于1212,,x x I x x ∀∈<,有()()12f x f x >,则称()f x 在I 上单调递减,I 称为单调递减区间。
2、导数与单调区间的联系(1)函数()f x 在(),a b 可导,那么()f x 在(),a b 上单调递增()',()0x a b f x ⇒∀∈≥,此结论可以这样理解:对于递增的函数,其图像有三种类型: ,无论是哪种图形,其上面任意一点的切线斜率均大于零。
等号成立的情况:一是单调区间分界点导数有可能为零,例如:()2f x x =的单调递增区间为[)0+∞,,而()'00f =,另一种是位于单调区间内但导数值等于零的点,典型的一个例子为()3f x x =在0x =处的导数为0,但是()0,0位于单调区间内。
(2)函数()f x 在(),a b 可导,则()f x 在(),a b 上单调递减()',()0x a b f x ⇒∀∈≤,(3)前面我们发现了函数的单调性可以决定其导数的符号,那么由()'f x在(),a b的单调性呢?如果()f x不x a b f x∀∈,的符号能否推出(),()是常值函数,那么便可由导数的符号对应推出函数的单调性。
(这也是求函数单调区间的理论基础)3、利用导数求函数单调区间的步骤(1)确定函数的定义域(2)求出()f x的导函数'()f x(3)令'()0f x的单调增(或减)f x>(或0<),求出x的解集,即为()区间(4)列出表格4、求单调区间的一些技巧(1)强调先求定义域,一方面定义域对单调区间有限制作用(单调区间为定义域的子集)。
另一方面通过定义域对x取值的限制,对解不等式有时会起到简化的作用,方便单调区间的求解(2)在求单调区间时优先处理恒正恒负的因式,以简化不等式(3)一般可令'()0f x>,这样解出的解集就是单调增区间(方便记忆),若()f x不存在常值函数部分,那么求减区间只需要取增区间在定义域上的补集即可(简化求解的步骤)(4)若'()0f x是定义域上的增函数,f x>的解集为定义域,那么说明()若'()0f x>的解集为∅,那么说明没有一个点切线斜率大于零,那么()f x是定义域上的减函数(5)导数只是求单调区间的一个有力工具,并不是唯一方法,以前学过的一些单调性判断方法也依然好用,例如:增+增→增,减+减→减,()1-⨯增→减,复合函数单调性同增异减等。
如果能够通过结论直接判断,那么就无需用导数来判定。
5、求单调区间的一些注意事项(1)单调区间可以用开区间来进行表示,如果用闭区间那么必须保证边界值在定义域内。
例如函数1y x =的单调减区间为()()0,,,0+∞-∞,若写成[)0,+∞就出错了(0不在定义域内)(2)如果增(或减)区间有多个,那么在书写时用逗号隔开,一定不要用并集的符号。
有些同学觉得不等式的解集是多个部分时用“”连接,那么区间也一样,这个观点是错误的。
并集是指将两个集合的元素合并到一起成为一个集合,用在单调区间上会出现问题。
依然以1y x =为例,如果写成()()0,,0+∞-∞,那么就意味着从合并在一起的集合中任取两个变量,满足单调减的条件。
由1y x =性质可知,如果在()()0,,,0+∞-∞两个区间里各取一个,是不满足单调减的性质的。
6、二阶导函数的作用:①几何意义:导数的符号决定原函数的单调性,对于()"f x 而言,决定的是()'f x 的单调性。
当()''0f x >时,()'f x 单调递增,意味着()'f x 随x 的增大而增大,由于导数的几何意义为切线斜率,故切线斜率k 随x 的增大而增大;同理,当()''0f x <时,()'f x 单调递减,则切线斜率k 随x 的增大而减少。
那么在图像上起到什么作用呢?单调增有三种: 其不同之处在于切线斜率随自变量变大的变化不同,所以如果说()'f x 是决定函数单调性的,那么()''f x 在已知单调性的前提下,能够告诉我们是怎样增,怎样减的,进而对作图的精细化提供帮助。
(1)当()"0f x >,其图像特点为: 我们称这样的函数为下凸函数(2)当()"0f x <,其图像特点为: 我们称这样的函数为上凸函数②代数意义:当通过()'f x 无法直接判断符号时,可通过二阶导函数先确定一阶导函数的单调性,再看能否利用条件判断符号。
二、典型例题:例1:下列函数中,在()0,+∞上为增函数的是( )A. ()sin2f x x =B. ()x f x xe =C. ()3f x x x =-D. ()ln f x x x =-+思路:本题只需分析各个函数在()0,+∞上的单调性即可。
A 选项()sin2f x x =通过其图像可知显然在()0,+∞不单调;B 选项()()'1x x x f x e xe x e =+=+,当()0,x ∈+∞时,()'0f x >,所以()f x 在()0,+∞单调递增;C 选项()231=3f x x x x ⎛=--+ ⎝⎭⎝⎭‘可得()f x 在⎛ ⎝⎭单调递减,在3⎛⎫+∞ ⎪⎝⎭单调递增;D 选项()'111x f x x x -=-+=,可得()f x 在()0,1单调递增,在()1,+∞单调递减。
综上,B 符合条件答案:B例2:函数()()212log 4f x x =-的单调递增区间是( )A. ()0,+∞B. (),0-∞C. ()2,+∞D.(),2-∞-思路:先分析()f x 的定义域:()()240,22,x x ->⇒∈-∞-+∞,再观察解析式可得()f x 可视为函数212log ,4y t t x ==-的复合函数,根据复合函数单调性同增异减的特点,可分别分析两个函数的单调性,对于12log y t=而言,y 对t 是减函数。
所以如要求得增区间,则24t x =-中t 对x 也应为减函数。
结合定义域可得()f x 的单调增区间为(),2-∞- 答案:D例3:求函数()()32333x f x x x x e -=+--的单调区间(2009宁夏,21题(1)) 思路:第一步:先确定定义域,()f x 定义域为R ,第二步:求导:()()'232()363333x x f x x x e x x x e --=+--+-- ()()()3933x x x x e x x x e --=--=--+,第三步:令'()0f x >,即()()330x x x x e ---+>第四步:处理恒正恒负的因式,可得()()330x x x -+<第五步:求解()()3,03,x ∈-+∞,列出表格例4:求函数()()ln ln 2f x x x x =+-+的单调区间解:定义域()0,2x ∈()()()()(()2'221121=2222x x x x x x x f x x x x x x x x x -+-++--=++==----()0,2x ∈20,0x x ∴-<+>∴令导数()'0f x >解得:0x x -<⇒<式的过程)∴例5:求函数()2f x =的单调区间 解:()()122'32112ln ln ln 4ln 122x x x x x x f x x x -⋅-==⋅ 令()'0f x >,即解不等式()ln ln 40x x -<,解得40ln 41x x e <<⇒<< ()f x ∴的单调区间为例6:求函数()1ln f x x x =--的单调区间思路:函数还有绝对值,从而考虑先通过分类讨论去掉绝对值,在求导进行单调性分析解:()1ln ,11ln ,01x x x f x x x x -->⎧=⎨--<<⎩,当()0,1x ∈时,()1ln f x x x =--为减函数 当()1,x ∈+∞时,()'111x f x x x -=-=1x > ()'0f x ∴> ()f x ∴在()1,+∞单调递增综上所述:()f x 在()0,1单调递减,在()1,+∞单调递增小炼有话说:(1)对于含绝对值的函数,可通过对绝对值内表达式的符号进行分类讨论可去掉绝对值,从而将函数转变为一个分段函数。
(2)本题在()0,1x ∈时,利用之前所学知识可直接判断出()f x 单调递减,从而简化步骤。
导数只是分析函数单调性的一个工具,若能运用以前所学知识判断单调性,则直接判断更为简便例7:(1)若函数()()()1ln 10,01x f x ax x a x -=++≥>+在区间[)1,+∞单调递增,则a 的取值集合是__________(2)若函数()()()1ln 10,01x f x ax x a x-=++≥>+的递增区间是[)1,+∞,则a 的取值集合是___________解:(1)思路:()()()()2'22221111a ax a f x ax x ax x +-=-=++++,由()f x 在[)1,+∞单调递增可得:1x ∀≥,()()()()2'22201211ax a f x a x ax x +-=≥⇒+≥++。
2max211a x ⎛⎫∴≥= ⎪+⎝⎭ 1a ∴≥(2)思路:()f x 的递增区间为[)1,+∞,即()f x 仅在[)1,+∞单调递增。
令()'222020a f x ax a x a->⇒+->⇒>,若1a >,则()f x 单调递增区间为()0,+∞不符题意,若01a <≤,则x >时,()'0f x >。
所以11a =⇒= 答案:(1)1a ≥,(2)1a =小炼有话说:注意两问的不同之处,在(1)中,只是说明()f x 在区间[)1,+∞单调递增,那么()f x 也可以在其他区间单调递增,即[)1,+∞是增区间的子集。
