制造弯形管道时,经常要先按中心线计算展直长度
弧长的计算

弧长的计算1.已知一条圆弧所在圆的半径为24,所对的圆心角为60°,则这条弧长为()A.4 B.4πC.8 D.8π【变式1】120°的圆心角对的弧长是6π,则此弧所在圆的半径是()A.3 B.4 C.9 D.18【变式2】已知一弧长为L的弧所对的圆心角为120°,那么它所对的弦长为()A.L B.L C.L D.L【变式3】如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为()A.()°B.()°C.()°D.()°【变式4】有一段弧的长度占它所在圆周长的,那么这段弧所对的圆心角是度.【变式5】如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为()A.πB.πC.πD.π2.如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则的长为()A.πB. C.2πD.3π【变式1】如图,▱ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则的长为()A.πB.πC.πD.π【变式2】如图,在扇形AOB中,AC为弦,∠AOB=140°,∠CAO=60°,OA=6,则的长为()A.πB.πC.2πD.2π【变式3】如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,则与的长度之和为()A. B. C. D.π【变式4】已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则的长为()A.2πB.3πC.4πD.5π【变式5】边长为1的等边△ABC在直线l上,按如图所示的方式进行两次旋转,在两次旋转过程中,点C经过的路径长为()A.πB.πC.πD.π3.如图,以O为圆心的圆与直线y=﹣x+交于A、B两点,若△OAB恰为等边三角形,则弧AB的长度为()A.πB.πC.π D.π【变式1】如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2016圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为()A.(4032π+1.0)B.(4032π+1.1)C.(4032π﹣1.0) D.(4032π﹣1.1)【变式2】.制造弯形管道时,经常要先按中心线计算“展直长度”,再下料.右图是一段弯形管道,其中∠O=∠O’=90°,中心线的两条弧的半径都是1000mm,这段变形管道的展直长度约为(取π3.14)()A.9280mm B.6280mm C.6140mm D.457mm【变式3】如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了()A.5πcm B.3πcm C.2πcm D.πcm【变式4】如图,△ABC是等腰直角三角形,且∠ACB=90°.曲线CDEF…叫做“等腰直角三角形的渐开线”,其中弧CD,弧DE,弧EF,…的圆心依次按A、B、C循环.如果AC=1,那么曲线CDEF的长度为()A.B.C.D.π【变式5】如图,若弧AB半径PA为18,圆心角为120°,半径为2的⊙O,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙O自转的周数是()A.5周B.6周C.7周D.8周【变式6】图中的粗线CD表示某条公路的一段,其中AmB是一段圆弧,AC、BD是线段,且AC、BD分别与圆弧相切于点A、B,线段AB=180m,∠ABD=150度.(1)画出圆弧的圆心O;(2)求A到B这段弧形公路的长.4.如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.(1)求证:EB=ED.(2)若AO=6,求的长.【变式1】.如图,在△ABC中,以BC为直径的⊙O交AB于M,弦MN∥AC且MN交BC于点E,ME=1,BM=2,BE=.(1)求证AC是⊙O的切线;(2)求弧NC的长度.【变式2】如图,BM是⊙O的直径,四边形ABMN是矩形,D是⊙O上的点,DC⊥AN,与AN交于点C,已知AC=15,⊙O的半径为30,求的长.【变式3】如图,在△ABC中,AB=AC.分别以B、C为圆心,BC长为半径,BC下方画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD、BD、CD.若BC=6,∠BAC=50°,求弧ED,弧FD的长度之和(结果保留π).【变式4】.如图,菱形ABCD的边长为6,∠BAD=60°,AC为对角线.将△ACD绕点A逆时针旋转60°得到△AC′D′,连接DC′.(1)求证:△ADC≌△ADC′;(2)求在旋转过程中点C扫过路径的长.(结果保留π)【变式5】如图,△ABC中,∠C是直角,∠A=30°,BC=2,以点C为圆心,CB为半径画圆,交AC于点D,交AB于点E.(1)求的长度;(2)过点E作EF⊥BC交圆于F点,写出EF与AC的关系,并证明你写出的关系.【变式6】在10×10的网格纸上建立平面直角坐标系如图所示,在Rt△ABC中,∠OAB=90°,且点B的坐标为(3,4).(1)画出△OAB向左平移3个单位后的△O1A1B1,写出点B1的坐标;(2)画出△OAB绕点O顺时针旋转90°后的△OA2B2,并求点B旋转到点B2时,点B经过的路线长(结果保留π).【课后练习】1.(海淀区期中)若扇形的圆心角为60°,半径为6,则该扇形的弧长为()A.πB.2πC.3πD.4π2.(西城区期末)若一个扇形的半径是18cm,且它的弧长是12π cm,则此扇形的圆心角等于()A.30°B.60°C.90°D.120°3.(通州区期末)如果弧长为6π的弧所对的圆心角为60°,那么这条弧所在的圆的半径是()A.18 B.12 C.36 D.64.(顺义区模拟)如图,小正方形方格的边长为1cm,则的长为cm.5.(门头沟期末)如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置.若BC=1,AC=,则顶点A运动到点A″的位置时,点A两次运动所经过的路程.(计算结果不取近似值)6.(大兴区期末)如图所示,长为4cm,宽为3cm的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板上点A位置变化为A→A1→A2,由A1翻滚到A2时被桌面上一小木块挡住,此时长方形木板的边A2C与桌面成30°角,则点A 翻滚到A2位置时所经过的路径总长度为cm.7.(门头沟区一模)如图,每个多边形的边长都大于2,分别以多边形的各顶点为圆心,1为半径画弧(弧的端点分别在多边形的相邻两边上),则第6个图形中所有弧的弧长的和是,第n个图形中所有弧的弧长的和是(n 为正整数).8.(清华附统练)如图1,在⊙O中,AB为⊙O的直径,AC是弦,OC=4,∠OAC=60度.(1)求∠AOC的度数;(2)在图1中,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;(3)如图2,一动点M从A点出发,在⊙O上按逆时针方向运动,当S△MAO=S△CAO时,求动点M所经过的弧长.9.(海淀区期中)已知:如图,网格中每个小正方形的边长为1,△ABC是格点三角形.(1)画出△ABC绕A点逆时针旋转90°后图形△AB′C′;(2)旋转过程中,点C所经过的路线长为.10.(密云期末)如图,AB是⊙O的直径,弦BC=5,∠BOC=50°,OE⊥AC,垂足为E.(1)求OE的长;(2)求劣弧AC的长.(结果精确到0.1)11.(石景山期末)某校研究性学习小组在研究相似图形时,发现相似三角形的定义、判定及其性质,可以拓展到扇形的相似中去.例如,可以定义:“圆心角相等且半径和弧长对应成比例的两个扇形叫做相似扇形”;相似扇形有性质:弧长比等于半径比、面积比等于半径比的平方….请你协助他们探索这个问题.(1)写出判定扇形相似的一种方法:若,则两个扇形相似;(2)有两个圆心角相等的扇形,其中一个半径为a、弧长为m,另一个半径为2a,则它的弧长为;(3)如图1是一完全打开的纸扇,外侧两竹条AB和AC的夹角为120°,AB为30cm,现要做一个和它形状相同、面积是它一半的纸扇(如图2),求新做纸扇(扇形)的圆心角和半径.12.(昌平二模)如图,在一个横截面为Rt△ABC的物体中,∠CAB=30°,BC=1米.工人师傅把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1B1C1的位置(BC1在l上),最后沿BC1的方向移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).(1)请直接写出AB、AC的长;(2)画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米).。
制造弯形管道时,要先按中心线计算展直长度,再下料,

A 700mm 100 C O
B R=900mm 700mm
D
思考:(1)圆周可以看作是多少度的弧长? (2)1°的圆心角所对弧长是多少? (3)n°的圆心角所对弧长是多少?
nR l 180
cm A.
2 2
C. 2cm
3 2 cm B. 3
D.
3cm
2
B
O D C
2.如图,正六边形内接于圆O, 圆O的半径为10,
100 150 _ 3. 则圆中阴影部分的面积为_____
O
6、(13长春)如图,方格纸中4个 小正方形的边长均为1,则图中阴影部分三个 3 小扇形的面积和为 (结果保留 π). 8
不学 1、配套练习册P100-102页 亦而 24.4弧长和扇形面积第一课时 乐 时 乎习 2、预习下节课,准备一个 !之 , 120°的纸片小扇形。
②当弓形面积大于半圆时 S弓形= S扇形+S△
C
3. 已知等边三角形ABC的边长为a,分别以A、
a B、C为圆心,以 2为半径的圆相切于点D、 E、
F,求图中阴影部分的面积S.
A
F
B D
E C
1.如图,等边△ABC 的边长为12cm, 内切⊙O 切 边BC于D点,则图中阴影部分的 A 面积为( C)
nR 1.弧长公式: l 180 2 1 nR lR 2.扇形面积公式: S扇形 2 360
注意: (1)两个公式的联系和区别; (2)两个公式的逆向应用。
组合图形的面积: (1)割补法 (2)组合法 其中: ①当弓形面积小于半圆时 S弓形= S扇形-S△ ②当弓形面积大于半圆时 S弓形= S扇形+S△
制造弯形管道时-经常要先按中心线计算展直长度

思考:扇形的面积公式与弧长公式有联系吗?
如果扇形的半径为R的圆中,圆心角为no ,那么扇 形面积的计算公式为:
ቤተ መጻሕፍቲ ባይዱ
s n r 2 nr r 1 lr
360
180 2 2
扇形的弧长与扇形面积的关系为:
S扇形
1 lR 2
想一想:扇形的面积公式与什么公式类似?
1则、这已个知扇半形径的为面2积cm,的S扇扇形= ,34其弧.长为
在Rt△OAD中,OA=0.6,利用勾股定理可得:AD=0.3√3
在Rt△ OAD中,∵OD=1/2OA ∴∠ OAD=30° ∴∠A OD=60°, ∠ AOB=120°
有水部分的面积
变式:如图、水平放置的圆柱形排水管道的截
面半径是0.6cm,其中水面高0.9cm,求截面 上有水部分的面积。(精确到0.01cm)。
制造弯形管道时,经常要先按中心线 计算“展直长度”(图中虚线的长度), 再下料,这就涉及到计算弧长的问题
复习
1、已知⊙O半径为R,⊙O的周长C是多少?
C = 2πR
2、已知⊙O半径为R,⊙O的面积S是多少?
S=πR2
问题:已知⊙O半径为R,求n°圆心角所对弧长.
(1)半径为R的圆,周长是多少?C=2πR
A
皮带轮模型
4.如图,两个皮带轮的中心的距离为2.1m,直径分别 为0.65m和0.24m。(1)求皮带长(保留三个有效 数字);(2)如果小轮每分钟750转,求大轮每分 钟约多少转?
如果两个轮是等圆呢?
3.如图所示,把边长为2的正方形ABCD的一边放 在定直线L上,按顺时针方向绕点D旋转到如图 的位置,则点B运动到点B′所经过的路线长度为
A B O
2. 已知矩形ABCD的长AB=4,宽AD=3,按如图放置在
制造弯形管道时经常要先按中心线计算展直长度ppt

04
与传统计算方法的优势比较
传统计算方法的劣势
传统计算方法需要手动测量和计算 ,效率低下,易出错。
VS
传统方法主要依赖经验,难以保证 管道安装的精确性和可靠性。
按中心线计算展直长度的优势
提高测量精度
01
按照中心线计算展直长度可以减少人为误差,提高测量精度,
使管道安装更加精确。
提高效率
02
这种方法可以在计算机上自动计算,提高计算效率,缩短管道
展直长度计算的应用
• 展直长度计算在弯形管道制作和加工中有着广泛的应用。例如,在制 造弯形管道时需要用到各种不同半径和中心角的弯头,这些弯头的制 作就需要用到展直长度计算。另外,在加工弯形管道时也需要用到展 直长度计算来确定加工的长度和形状,以确保管道的质量和使用效果 。
03
按中心线计算展直长度的技巧
领域中不可或缺的一项技术。
06
总结与展望
总结
弯形管道制造过程中的关键步骤 中心线展直长度计算的重要性 计算方法的优缺点分析
该方法的前景展望
发展方向和趋势 应用领域的拓展
对未来研究和应用的建议
该方法存在的不足之处及改进建议
计算精度限制 适用范围的局限性
对计算效率和可靠性的改进建议
THANK YOU.
展直长度计算在其他领域的应用
展直长度计算不仅在管道制造和设计中有着 广泛的应用,在其他领域也有着广泛的应用 。
展直长度计算在其他领域也有着广泛的应用 ,例如在造船、建筑结构、金属加工等领域 。通过对展直长度进行精确计算,可以确保 结构或构件在加工、制造、安装过程中的准 确性和稳定性。因此,展直长度计算是多个
制造和安装周期。
降低成本
03
2019年北京市各区九年级上册期末试卷分类汇编:圆基础(有答案)-(数学)
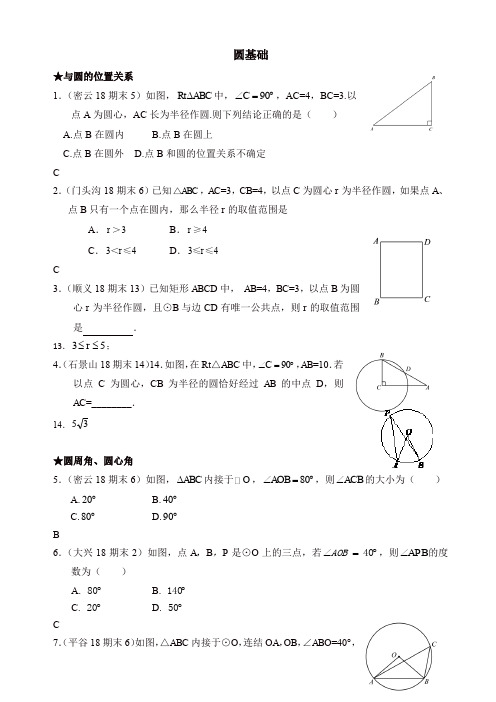
圆基础★与圆的位置关系1.(密云18期末5)如图,Rt ABC ∆中,90C ∠=︒,AC=4,BC=3.以点A 为圆心,AC 长为半径作圆.则下列结论正确的是( ) A.点B 在圆内B.点B 在圆上C.点B 在圆外 D .点B 和圆的位置关系不确定 C2.(门头沟18期末6)已知ABC △,AC =3,CB =4,以点C 为圆心r 为半径作圆,如果点A 、点B 只有一个点在圆内,那么半径r 的取值范围是A .3r >B .4r ≥C .34r <≤D .34r ≤≤C3.(顺义18期末13)已知矩形ABCD 中, AB =4,BC =3,以点B 为圆心r 为半径作圆,且⊙B 与边CD 有唯一公共点,则r 的取值范围是 .13.35r ≤≤;4.(石景山18期末14)14.如图,在Rt △ABC 中,︒=∠90C ,AB =10.若以点C 为圆心,CB 为半径的圆恰好经过AB 的中点D ,则AC =________.14.35★圆周角、圆心角5.(密云18期末6)如图,ABC ∆内接于O ,80AOB ∠=︒,则ACB ∠的大小为( )A.20︒B.40︒C.80︒D.90︒B6.(大兴18期末2)如图,点A ,B ,P 是⊙O 上的三点,若︒=∠40AOB ,则APB ∠的度数为( )A. ︒80B. ︒140C. ︒20D. ︒50 C7.(平谷18期末6)如图,△ABC 内接于⊙O ,连结OA ,OB ,∠ABO =40°,则∠C的度数是()A.100°B.80°C.50°D40°C8.(昌平18期末4)如图,⊙O是△ABC的外接圆,∠A =50︒,则∠BOC的大小为()A.40°B.30°C.80°D.100°D9.(门头沟18期末3)如图,DCE∠是圆内接四边形ABCD的一个外角,如果75∠的度数是()DCE∠=︒,那么BADA.65︒B.75︒C.85︒D.105︒B10.(朝阳18期末6)如图,AB为⊙O的直径,C,D为⊙O上的两点,若AB=14,BC=7.则∠BDC的度数是()A.15°B.30°C.45°D.60°B11.(石景山18期末3)如图,AB是⊙O的直径,点C、D在⊙O上.若∠的度数为()∠25ACD,则BOD︒=A.︒120100B.︒C.︒150130D.︒C12.(西城18期末5)如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=34°,那么∠BAD等于().A.34° B.46°C.56°D.66°C13.(丰台18期末7)如图,A,B是⊙O上的两点,C是⊙O上不与A,B重合的任意一点. 如果∠AOB=140°,那么∠ACB的度数为()A.70°B.110°C .140°D .70°或110°D14.(怀柔18期末5)如图,⊙O 是△ABC 的外接圆,∠BOC =100°,则∠A 的大小为 ( ) A . B . C .D .B15.(通州18期末4)如图,AB 是⊙O 的直径,点C ,D 在⊙O 上.若︒=∠55ABD ,则BCD ∠的度数为( ) A .︒25 B .︒30 C .︒35 D .︒40C16.(燕山18期末3)3.如图,圆心角 ∠ AOB=25°,将 AB 旋转n°得到 CD ,则∠ COD 等于( ) A .25° B .25°+ n° C .50°D .50°+ n° 17.(燕山18期末13)如图,量角器的直径与直角三角尺 ABC 的斜边 AB 重合,其中量角器 0 刻度线的端点 N 与点 A 重合,射线 CP 从 CA 处出发沿顺时针方向以每秒 3°的速度旋转,CP 与量角器的半圆弧交于点 E ,则第 20 秒点 E 在量角器上对应的读数是 °13.120°18.(通州18期末15)⊙O 的半径为1,其内接ABC △的边2=AB ,则C ∠的度数为________.19.(东城18期末14)⊙O 是四边形ABCD 的外接圆,AC 平分∠BAD ,则正确结论的序号是.①AB=AD ;②BC=CD ;③AB AD =;④∠BCA=∠DCA ; ⑤ BC CD =.40︒50︒80︒100︒20.(丰台18期末14)在平面直角坐标系中,过三点A (0,0),B (2,2),C (4,0)的圆的圆心坐标为 .14.(2,0);21.(西城18期末16)如图,⊙O 的半径为3,A ,P 两点在⊙O 上,点B 在⊙O 内,4tan 3APB ∠=,AB AP ⊥.如果OB ⊥OP ,那么OB 的长为 . 1★垂径定理22.(顺义18期末6)如图,已知⊙O 的半径为6,弦AB 的长为8,则圆心O 到AB 的距离为( )A B .C .D .10B23.(石景山18期末4)如图,在⊙O 中,弦AB 垂直平分半径OC .若⊙O 的半径为4,则弦AB 的长为( ) A .32B .34C .52D .54B24.(通州18期末6)如图,⊙O 的半径为4.将⊙O 的一部分沿着弦AB翻折,劣弧恰好经过圆心O .则折痕AB 的长为( ) A. 3B. 32C. 6D. 34 D25.(怀柔18期末7)某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O ,再任意找出圆O 的一条直径标记为AB (如图1),测量出AB =4分米;②将圆环进行翻折使点B 落在圆心O 的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C 、D (如图2);③用一细橡胶棒连接C 、D 两点(如图3); ④计算出橡胶棒CD 的长度.小明计算橡胶棒CD 的长度为( ) A .22分米 B .23分米 C .32分米 D .33分米B26.(门头沟18期末13)如图,在△ABC 中,∠A =60°,⊙O 为△ABC的外接圆.如果BC=,那么⊙O 的半径为________. 227.(西城18期末13)如图,⊙O 的半径等于4,如果弦AB 所对的圆心角等于120 ,那么圆心O 到弦AB 的距离等于 . 228.(大兴18期末13)如图,在半径为5cm 的⊙O 中,如果弦AB 的长为8cm ,OC ⊥AB ,垂足为C ,那么OC 的长为 cm .329.(东城18期末12)如图,AB 是⊙O 的弦,C 是AB 的中点,连接OC 并延长交⊙O 于点D .若CD =1,AB =4,则⊙O 的半径是_______.12、5230.(燕山18期末11)如图,AB 、AC 是⊙O 的弦,OM ⊥ AB ,ON ⊥ AC ,垂足分别为 M 、N .如果 MN =2.5,那么BC =_______5★正多边形31.(东城18期末2)边长为2的正方形内接于M,则M的半径是()A.B.2C D.C32.(丰台18期末12)如图,等边三角形ABC的外接圆⊙O的半径OA的长为2,则其内切圆半径的长为.133.(通州18期末13)如图,AD,AE是正六边形的两条对角线.在不添加任何其他线段的情况下,请写出两个关于图中角度的正确结论:(1)__________________________;(2)______________________.34.(昌平18期末13)如图,⊙O的半径为3,正六边形ABCDEF 内接于⊙O,则劣弧AB的长为.35.(朝阳18期末9)如图,正六边形ABCDEF内接于⊙O,⊙O的半径为3,则正六边形ABCDEF的边长为.36.(平谷18期末13)“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”这是我国古代著名数学家刘徽在《九章算术注》中提到的“如何求圆的周长和面积”的方法,即“割圆术”.“割圆术”的主要意思是用圆内接正多边形去逐步逼近圆.刘徽从圆内接正六边形出发,将边数逐次加倍,并逐次得到正多边形的周长和面积.如图,AB 是圆内接正六边形的一条边,半径OB =1,OC ⊥AB 于点D ,则圆内接正十二边形的边BC 的长是 (结果不取近似值).13=★弧长、扇形面积37.(西城18期末4)圆心角为60︒,且半径为12的扇形的面积等于( ).A.48πB.24πC.4πD.2πB38.(东城18期末5)A ,B 是O 上的两点,OA =1, AB 的长是1π3,则∠AOB 的度数是( )A .30°B .60°C .90°D .120°B39.(大兴18期末4)在半径为12cm 的圆中,长为4πcm 的弧所对的圆心角的度数为( )A. ︒10B. ︒60C. ︒90D. ︒120B40.(通州18期末2)已知一个扇形的半径是1,圆心角是120°,则这个扇形的弧长是( )A .6πB .πC .3πD .32πD41.(海淀18期末13)若一个扇形的圆心角为60°,面积为6π,则这个扇形的半径为_______. 642.(丰台18期末10)半径为2的圆中,60°的圆心角所对的弧的弧长为_______.10.2π343.(大兴18期末14)圆心角为160°的扇形的半径为9cm ,则这个扇形的面积是_______cm 2.14. 36 π .44.(密云18期末12)扇形半径为3cm ,弧长为πcm ,则扇形圆心角的度数为__________.12.60︒45.(平谷18期末10)圆心角为120°,半径为6cm 的扇形的弧长是cm (结果不取近似值).10.4π46.(朝阳18期末7)如图,在△ABC 中,∠BAC =90°,AB =AC =4,以点C 为中心,把△ABC 逆时针旋转45°,得到△A’B’C ,则图中阴影部分的面积为( )A .2B .2πC .4D .4πB47.(石景山18期末11)如图,扇形的圆心角︒=∠60AOB ,半径为3cm .若点C 、D 是 的三等分点,则图中所有阴影部分的面积之和是________cm 2.11.2π48.(怀柔18期末15)在学校的花园里有一如图所示的花坛,它是由一个正三角形和圆心分别在正三角形顶点、半径为1米的三个等圆组成,现在要在花坛正三角形以外的区域(图中阴影部分)种植草皮.草皮种植面积为 米2.π2549.(顺义18期末20)制造弯形管道时,经常要先按中心线计算“展直长度”,再备料.下图是一段管道,其中直管道部分AB 的长为3 000mm ,弯形管道部分BC ,CD 弧的半径都是1 000mm ,∠O =∠O ’=90°,计算图中中心虚线的长度.20. 901000500180180n r l πππ⨯===…………………………….…….……….3分 中心虚线的长度为 30005002300010ππ+⨯=+…………………4分=30001000 3.14=6140+⨯……………………………………………..…5分。
专题12 弧长和扇形面积(解析版) -2021-2022学年九年级数学之专攻圆各种类型题的解法
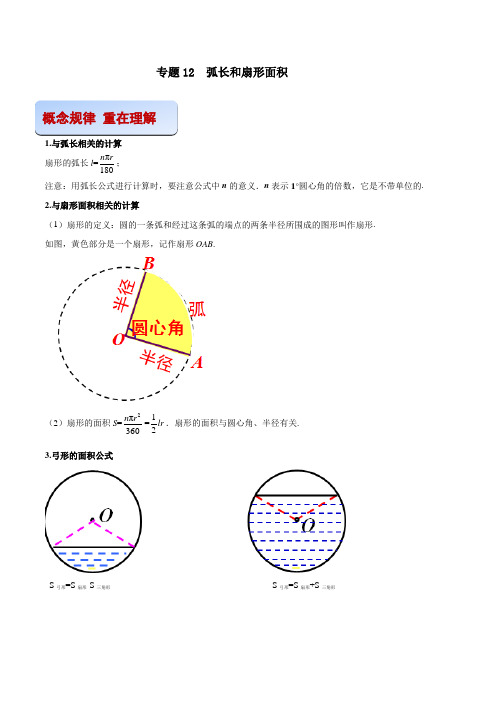
专题12 弧长和扇形面积1.与弧长相关的计算扇形的弧长l=π180n r;注意:用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.2.与扇形面积相关的计算(1)扇形的定义:圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.如图,黄色部分是一个扇形,记作扇形OAB.(2)扇形的面积S=2π360n r=12lr.扇形的面积与圆心角、半径有关.3.弓形的面积公式S弓形=S扇形-S三角形S弓形=S扇形+S三角形概念规律重在理解典例解析掌握方法【例题1】(2021甘肃威武定西平凉)如图,从一块直径为4dm的圆形铁皮上剪出一圆心角为90°的扇形,则此扇形的面积为dm2.【答案】2π.【解析】连接AC,根据圆周角定理得出AC为圆的直径,解直角三角形求出AB,根据扇形面积公式求出即可.连接AC,∵从一块直径为4dm的圆形铁皮上剪出一个圆心角为90°的扇形,即∠ABC=90°,∴AC为直径,即AC=4dm,AB=BC(扇形的半径相等),∵AB2+BC2=22,∴AB=BC=2dm,∴阴影部分的面积是=2π(dm2).【例题2】制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度l.(单位:mm,精确到1mm)【答案】管道的展直长度为2970mm.【解析】由弧长公式,可得弧AB的长因此所要求的展直长度l=2×700+1570=2970(mm).【例题3】如图,圆心角为60°的扇形的半径为10cm.求这个扇形的面积和周长.(精确到0.01cm2和0.01cm)【答案】见解析.【解析】∵n=60,r=10cm,∴扇形的面积为扇形的周长为【例题4】如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.【答案】见解析.【解析】 ()22=24010.60.30.6336020.240.0930.91cm .OABS S ππ+=⨯+⨯⨯=+≈△弓形扇形S一、选择题1.(2021贵州毕节)某小区内的消防车道有一段弯道,如图,弯道的内外边缘均为圆弧,,所在圆的圆心为O ,点C ,D 分别在OA ,OB 上.已知消防车道半径OC =12m ,消防车道宽AC =4m ,∠AOB =120°,则弯道外边缘的长为( )A .8πmB .4πmC .πmD .πm【答案】C各种题型 强化训练【解析】根据线段的和差得到OA=OC+AC,然后根据弧长公式即可得到结论.∵OC=12m,AC=4m,∴OA=OC+AC=12+4=16(m),∵∠AOB=120°,∴弯道外边缘的长为:=(m).2.(2021成都)如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为()A.4πB.6πC.8πD.12π【答案】D【解析】首先确定扇形的圆心角的度数,然后利用扇形的面积公式计算即可.∵正六边形的外角和为360°,∴每一个外角的度数为360°÷6=60°,∴正六边形的每个内角为180°﹣60°=120°,∵正六边形的边长为6,∴S阴影==12π.3.如图,⊙O的直径AB=2,C是弧AB的中点,AE,BE分别平分∠BAC和∠ABC,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为()A.﹣4 B.7﹣4 C.6﹣D.【答案】A【解析】∵⊙O的直径AB=2,∴∠C=90°,∵C是弧AB的中点,∴,∴AC=BC,∴∠CAB=∠CBA=45°,∵AE,BE分别平分∠BAC和∠ABC,∴∠EAB=∠EBA=22.5°,∴∠AEB=180°﹣(∠BAC+∠CBA)=135°,连接EO,∵∠EAB=∠EBA,∴EA=EB,∵OA=OB,∴EO⊥AB,∴EO为Rt△ABC内切圆半径,∴S△ABC=(AB+AC+BC)•EO=AC•BC,∴EO=﹣1,∴AE2=AO2+EO2=12+(﹣1)2=4﹣2,∴扇形EAB的面积==(2﹣),△ABE的面积=AB•EO=﹣1,∴弓形AB的面积=扇形EAB的面积﹣△ABE的面积=,∴阴影部分的面积=⊙O的面积﹣弓形AB的面积=﹣(﹣)=﹣4.4.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为()A.B.C.+D.【答案】C【解析】连接OE、AE,∵点C为OA的中点,∴∠CEO=30°,∠EOC=60°,∴△AEO为等边三角形,∴S==π,扇形AOE∴S=S扇形AOB﹣S扇形COD﹣(S扇形AOE﹣S△COE)阴影=﹣﹣(π﹣×1×)=π﹣π+=+.5.如图,在扇形AOB中,∠AOB=90°,=,点D在OB上,点E在OB的延长线上,当正方形CDEF 的边长为2时,则阴影部分的面积为()A.2π﹣4 B.4π﹣8 C.2π﹣8 D.4π﹣4【答案】A【解析】连接OC,如图所示:∵在扇形AOB 中∠AOB =90°,=, ∴∠COD =45°,∴OD =CD ,∴OC ==4,∴阴影部分的面积=扇形BOC 的面积﹣△ODC 的面积 =﹣×(2)2=2π﹣4.6.中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到12AC BD cm ==,C ,D 两点之间的距离为4cm ,圆心角为60︒,则图中摆盘的面积是( )A .280cm πB .240cm πC .224cm πD .22cm π【答案】B 【解析】先证明COD △是等边三角形,求解,OC OD ,利用摆盘的面积等于两个扇形面积的差可得答案.如图,连接CD ,,60,OC OD COD =∠=︒ COD ∴是等边三角形,4,CD = 4,OC OD ∴==12,AC BD == 16,OA OB ∴==所以则图中摆盘的面积 222601660440.360360AOB CODS S cm πππ⨯⨯-=-=扇形扇形. 二、填空题 1.(2021湖北荆门)如图,正方形ABCD 的边长为2,分别以B ,C 为圆心,以正方形的边长为半径的圆相交于点P ,那么图中阴影部分的面积为 .【答案】2﹣.【解析】连接PB 、PC ,作PF ⊥BC 于F ,根据等边三角形的性质得到∠PBC =60°,解直角三角形求出BF 、PF ,根据扇形面积公式、三角形的面积公式计算,得到答案.解:连接PB 、PC ,作PF ⊥BC 于F ,∵PB =PC =BC , ∴△PBC 为等边三角形, ∴∠PBC =60°,∠PBA =30°,∴BF =PB •cos60°=PB =1,PF =PB •sin60°=,则图中阴影部分的面积=[扇形ABP 的面积﹣(扇形BPC 的面积﹣△BPC 的面积)]×2=[﹣(﹣×2×)]×2=2﹣,故答案为:2﹣.2.(2021湖北宜昌)“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以边长为2厘米的等边三角形ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就是“莱洛三角形”,该“莱洛三角形”的面积为平方厘米.(圆周率用π表示)【答案】(2π﹣2).【解析】图中三角形的面积是由三块相同的扇形叠加而成,其面积等于三块扇形的面积相加,再减去两个等边三角形的面积,分别求出即可.过A作AD⊥BC于D,∵AB=AC=BC=2厘米,∠BAC=∠ABC=∠ACB=60°,∵AD⊥BC,∴BD=CD=1厘米,AD=BD=厘米,∴△ABC的面积为BC•AD=(厘米2),S扇形BAC==π(厘米2),∴莱洛三角形的面积S=3×π﹣2×=(2π﹣2)厘米2.3.(2021湖南怀化)如图,在⊙O中,OA=3,∠C=45°,则图中阴影部分的面积是.(结果保留π)【答案】π﹣.【解析】由∠C=45°根据圆周角定理得出∠AOB=90°,根据S阴影=S扇形AOB﹣S△AOB可得出结论.∵∠C=45°,∴∠AOB=90°,∴S阴影=S扇形AOB﹣S△AOB==π﹣.4.(2021四川凉山)如图,将△ABC绕点C顺时针旋转120°得到△A'B'C,已知AC=3,则线段AB扫过的图形(阴影部分)的面积为.【答案】。
人教版弧长和扇形面积(2)
l为 ,则 l n R
180 A
B
(4)140°圆心角所对的
弧长是多少?
n°
O
l 140R 7R
180
9
1.已知弧所对的圆心角为900,半径是4,则弧 长为______
2. (2006,随州市)已知一条弧的半径为9,
弧长为8 ,那么这条弧所对的圆心角为_____。
3. (2006,枣庄)钟表的轴心到分针针端的长为 5cm ,那么经过40分钟,分针针端转过的弧长 是( )
有水部分的面积 = S扇- S△
0
A
D
B
C
练习:1.如图、水平放置的圆柱形排水管道的
截面半径是0.6cm,其中水面高0.9cm,求截
面上有水部分的面积。(结果保留 )
D
有水部分的面积 = S扇+ S△
A
E
B
0
C
2. (2006,武汉)如图,⊙A、⊙B、⊙C、⊙D 相互外离,它们的半径都是1,顺次连接四个圆心得 到四边形ABCD,则图形中四个扇形(空白部分)的 面积之和是___________.
B A
D
C
3.(2007,山东)如图所示,分别以n边形 的顶点为圆心,以单位1为半径画圆,则图中阴 影部分的面积之和为 个平方单位.
4. 已知等边三角形ABC的边
长为a,分别以A、B、C为圆心,
以
a 2
为半径的圆相切于点D、 E、
F,求图中阴影部分的面积S.
圆心角所对的扇形面积为S,
则
S扇形
nR2
360
A
O
B
1、已知扇形的圆心角为120°,半径为2,
则这个扇形的面积S扇形=
人教版数学 第二十四章 圆 之 弧长的计算
人教版数学 第二十四章 圆 之 弧长的计算一、选择题1. 一个钢管放在V 形架内,如图是其截面图,测得P 点与钢管的最短距离PB =25 cm ,最长距离PA =75 cm.若钢管的厚度忽略不计,则劣弧⌒MN的长为( ) A .503π cm B . 50π cm C .506π cm D . 50√3π cm 2. 一个挂钟分针的长为10厘米,当分针转过225°时,这个分针的针尖转过的弧长是( )A .25π2厘米 B . 15π厘米 C .75π2厘米 D . 75π厘米3. 已知一条圆弧的度数为60°,弧长为10π,则此圆弧的半径为( )A . 15B . 30C .√30D . 15π4. 如图,矩形ABCD 的外接圆O 与水平地面相切于点A ,已知圆O 的半径为4,且⌒BC =2⌒AB.若在没有滑动的情况下,将圆O 向右滚动,使得O 点向右移动了66π,则此时与地面相切的弧为( )A .⌒AB B .⌒BC C .⌒CD D .⌒AD5.若一个扇形的半径是18 cm ,且它的弧长是12π cm ,则此扇形的圆心角等于( )A . 30°B . 60°C . 90°D . 120°6. 如图,△ABC 中,∠A =30°,∠C =90°,⊙O 是△ABC 的外接圆,若⌒AB的长为6π cm ,则AC 的长是( )A . 6 cmB . 8 cmC . 9 cmD . 6√3cm7. 制造弯形管道时,经常要先按中心线计算“展直长度”,再下料.下图是一段弯形管道,其中∠O =∠O ′=90°,中心线的两条弧的半径都是1000 mm ,这段变形管道的展直长度约为(π取3.14)( )A . 9280 mmB . 6280 mmC . 6140 mmD . 457 mm8. 如图,用一个半径为5 cm 的定滑轮带动重物上升,滑轮上一点A 旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )A.5π cm B.3π cm C.2π cm D.π cm二、填空题9. 如图,有一半圆形桥拱,拱的跨度AB=40 m,那么桥拱的弧长为________ m.(结果精确到0.1 m)10. 琪琪坐在爸爸驾驶的小汽车上去外婆家玩,已知小汽车车轮的直径为56 cm,当车轮转动270°时,琪琪在水平方向上平移了________ cm.11. 如图,水平地面有一个面积为120π cm2的灰色扇形OAB,其中OA的长度为12 cm,且OA与地面垂直.若在没有滑动的情况下,将图最左边的扇形向右滚动至点A再一次接触地面时,则O点移动的路径长为______.12. 如图,琪琪做实验时发现,当三角板中30°角的顶点A在⊙O上移动,三角板的两边与⊙O相交于点P、Q时,⌒PQ的长度不变.若⊙O的半径为9,则⌒PQ的长等于________.三、解答题13. 已知扇形的弧长是12π cm,其圆心角是60°,则扇形的半径是多少厘米?14. 如图,一根木棒AB长为2a,斜靠在与地面OM垂直的墙ON上,与地面的倾斜角∠ABO为60°,若木棒A端沿直线ON下滑,且B端沿直线OM向右滑行(NO⊥OM),于是木棒的中点P也随之运动,已知A 端下滑到A′时,AA′=(√3-√2)a,求木棒中点P随之运动到P′时经过的路线长.15. 制弯制管道时,先按中心线计算“展直长度”再下料.如图所示,求管道的展直长度L(单位:mm,精确到10 mm).16. 如图,在半径为r 的⊙O 中,直径AB 与弦CD 相交于点P ,连接AC.若⌒AD的长为29πr ,求∠ACD 的度数.17.一段圆弧形公路弯道,圆弧的半径为2 km ,弯道所对圆心角为10°,一辆汽车从此弯道上驶过,用时20 s ,弯道有一块限速警示牌,限速为40 km/h ,问这辆汽车经过弯道时有没有超速?(π取3)18.如图是某学校田径体育场一部分的示意图,跑道的长度是以该跑道的中心线来计算,第一条跑道每圈为400米,跑道分直道和弯道,直道为长相等的平行线段,弯道为同心的半圆型,弯道与直道相连接,已知直道BC 的长86.96米,跑道的宽为1米.(π=3.14,结果精确到0.01)(1)求第一条跑道的弯道部分⌒AB的半径. (2)求一圈中第二条跑道比第一条跑道长多少米?(3)若进行200米比赛,求第六道的起点F 与圆心O 的连线FO 与OA 的夹角∠FOA 的度数.。
制造弯形管道时经常要先按中心线计算展直长度图
S扇形
nR2 360
.
O· 1°
n° R
例1 如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面 高0.3m,求截面上有水部分的面积(精确到0.01m2).
O
D A
解:如图,连接OA、OB,作弦AB的 垂直平分线,垂足为D,交 »AB 于点C.
∵OC=0.6,DC=0.3,
B
∴OD=OC-DC=0.3.
4. n°的圆心角呢?
半径为R圆的周长为 C 2R
可以看作是360°圆心角所对的弧长
O· 1°
n°
1°的圆心角所对弧长是 1 2R
R
360
n°的圆心角所对的弧长 l 1 2R n nR
360
180
你能根据算出本节开头的弧长吗?
A
700mm
B
100°R=900mm
700mm
a
2.如图,正三角形ABC的边长为a,分别以A、B、 C 为圆心,以
为半径的圆相切于点D、E、F,求图中阴影部分的面积.
ቤተ መጻሕፍቲ ባይዱ
2
解:连接AD,则
AD BC 垂足为D
根据勾股定理,得
AD
AB2 BD2
a2
a 2
2
3a . 2
SVABC 1 BCgAD 1 ag 3a 3a2 .
A
O ·n°
R
B
1. 你还记得圆面积公式吗?
2. 圆面积可以看作是多少度的圆心角所对的扇形的面积? 3. 1°的圆心角所对的扇形面积是多少? 4. n°的圆心角呢?
圆的面积公式: S R2,
360°的圆心角所对的扇形的面积,
制造弯形管道时要先按中心线计算展直长度再下料
制造弯形管道时要先按中心线计算展直长度再下料1.设计:首先需要根据实际需求设计弯形管道的形状、角度和尺寸。
这需要考虑管道的材料、厚度、工作环境以及应力分布等因素。
2.选择材料:根据设计要求选择合适的材料,例如钢、铜、铝等。
材料的选择应考虑到管道的应力和工作温度等因素。
3.计算展直长度:展直长度是指在管道弯曲之前,管道在展开状态下的长度。
计算展直长度的目的是为了通过下料制作出合适大小的弯形管道。
下面将介绍计算展直长度的方法。
计算展直长度的方法:-方法一:格尔库奇公式格尔库奇公式是计算展直长度的一种常用方法。
该方法适用于常见的弯头,其计算公式为:展直长度=(Π/180)×弯头角度×R其中,Π为圆周率,弯头角度为管道弯曲的角度,R为弯头半径。
-方法二:三角函数法三角函数法是另一种计算展直长度的方法。
该方法适用于各种弯曲形状,但需要进行角度的三角函数计算。
展直长度 = 弯头角度× R / tan(弯头角度/2)其中,tan为正切函数,弯头角度为管道弯曲的角度,R为弯头半径。
4.下料制作:根据计算得到的展直长度,将材料切割成相应的长度。
为了方便下料制作,可以使用模板或者专业的下料设备来确保切割的准确性。
5.弯曲:将下料得到的管道加热至一定温度,然后用弯管机器或者手工工具进行弯曲。
在弯曲过程中要注意管道的变形和应力分布,确保弯曲后的形状符合设计要求。
6.合并和焊接:将弯曲后的管道进行合并和焊接,使之成为一个整体。
7.检查和测试:对制作好的弯形管道进行检查和测试,确保其质量符合要求。
常见的检查和测试方法包括可视检查、超声波检测、液压试验等。
总结:制造弯形管道需要先计算展直长度确定下料长度,然后根据设计要求进行下料、弯曲、合并和检查等步骤。
正确计算展直长度是制作弯形管道的关键,可以使用格尔库奇公式或者三角函数法进行计算。
制造弯形管道需要专业的知识和技术,并且在操作过程中要注意安全和质量控制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l
(1)在应用弧长公式
n R 180
, 进行计算时,
要注意公式中n的意义.n表示1°圆心角的倍数,
它是不带单位的;
(2)区分弧、弧的度数、弧长三概念.度数相等的弧, 弧长不一定相等,弧长相等的弧也不一定是等孤,而只有 在同圆或等圆中,才可能是等弧.
例1、制造弯形管道时,要先按中心线计算“展直 长度”,再下料,试计算图所示管道的展直长度 L(单位:mm,精确到1mm)
B
B
O
A
O
C
A
正方形的边长为2,求阴影的面积。
D
C
D
C
A
B A B
C B
O
A
一、弧长的计算公式
l
n 360
2r
nr 180
二、扇形面积计算公式
s
n 360
r
2
或s
1 2
lr
1、有一把折扇,已知折扇的骨柄长为30cm,折扇扇 面宽度是骨柄长的一半,折扇张开的角度为120度, 若要改用一把圆扇,则圆扇的半径应是多少才能得到 与折扇面积一样的风景。
A B O
2. 已知矩形ABCD的长AB=4,宽AD=3,按如图放置在 直线AP上,然后不滑动地转动,当它转动一周时( A A/), 顶点A所经过的路线长等于 。(04年中考题)
D
C
A
B
A/
P
3.如图,某传送带的一个转动轮的半径为10cm, (1)转动轮一周,传送带上的物品被传送多少厘米?
(2)转动轮转1o,传送带上的物品A被传送多少厘米?
B A
D
C
2Hale Waihona Puke 已知正三角形ABC的边长为a,分 别以A、B、C为圆心,以a/2为半径 的圆相切于点D 、 E 、 F , 求图中阴影 部分的面积S.
例3、已知正三角形的边长为a,求它的 内切圆与外接圆组成的圆环的面积.
解:设正三角形的外接圆、内切 圆的半径分别为R,r,面积为 S1、S2.
S=
2 2
1、已知扇形的圆心角为120°,半径为2,则这个 扇形的面积,S扇= 4 .
3
2、已知扇形面积为 5 ,圆心角为50°,则这个 扇形的半径R=____. 6 3、已知半径为2的扇形,面积为 的圆心角的度数为
4 3
,则它
120° .
思考:扇形的面积公式与弧长公式有联系吗?
如果扇形的半径为R的圆中,圆心角为no ,那么扇 形面积的计算公式为:
制造弯形管道时,经常要先按中心线 计算“展直长度”(图中虚线的长度), 再下料,这就涉及到计算弧长的问题
复习
1、已知⊙O半径为R,⊙O的周长C是多少?
C = 2πR
2、已知⊙O半径为R,⊙O的面积S是多少?
S=π R2
问题:已知⊙O半径为R,求n°圆心角所对弧长.
(1)半径为R的圆,周长是多少?C=2π R
O R r
2 2
S1 S 2 R r (R r )
R
2
.
2
∵
r
2
( ) 2 4
2
a
a,
2
∴S=
4
a .
1.如图几7-4-10,已知P、Q分别是半径为 1的半圆圆周上的两个三等分点,AB是 直径,则阴影部分的面积等于 。
2、如图几7-4-3,A是半径为1的圆O外一点, 且OA=2,AB是⊙O的切线,BC//OA,连结AC, 则阴影部分面积等于 。
例2、如图,水平放置的圆柱形排水管道 的截面半径是0.6m,其中水面高0.3m.求截 面上有水部分的面积(精确到0.01m2)
弓形的面积 = S扇- S△
解:如图,连接OA、OB,作弦AB的垂直平分线,垂足为D, 交弧AB于点C. ∵OC=0.6,DC=0.3 ∴OD=OC—DC=0.3
在Rt△OAD中,OA=0.6,利用勾股定理可得:AD=0.3√3
s
n 360
r
2
nr 180
r 2
1 2
lr
扇形的弧长与扇形面积的关系为:
S 扇形
1 2
lR
想一想:扇形的面积公式与什么公式类似?
1、已知半径为2cm的扇形,其弧长为 4 . 则这个扇形的面积,S扇=
3
4 3
,
2、一扇形的弧长是 20 cm ,面积为 240 cm 2 那么扇形的圆心角为 150度 .
(2)1°圆心角所对弧长是多少?
2R
R
360 180 (3)n°圆心角所对的弧长是1° 圆心角所对的弧长的多少倍?
O
n倍
(4)n°圆心角所对弧长是多少?
n° A B
l
nR 180
弧长公式
若设⊙O半径为R, n°的圆心角所对 的弧长为 l ,则
O n°
注意:
l
l
n R 180
A
B
B/
4.如图所示,实数部分是 半径为9m的两条等弧组成 的游泳池,若每条弧所在的 圆都经过另一个圆的圆心, 则游泳池的周长为________
A
D
C/
L
1.扇形OAB的半径为10,∠AOB=900,OA.OB 为两半圆的直径,求图中阴影部分的面积。 变式:如果把图形改为下图,AC是直径,两 个半圆外切,求图中阴影部分的面积。
在Rt△ OAD中,∵OD=1/2OA
∴∠ OAD=30° ∴∠A OD=60°, ∠ AOB=120° 有水部分的面积
变式:如图、水平放置的圆柱形排水管道的截 面半径是0.6cm,其中水面高0.9cm,求截面 上有水部分的面积。(精确到0.01cm)。
D
弓形的面积 = S扇+ S△
A
E
B
0
C
1、如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半 径都是2cm,求图中阴影部分的面积。
2、有一段弯道是圆弧形的,道 o, 长是12m,弧所对的圆心角是81 求这段圆弧的半径R(精确到 0.1m)
图中阴影部分的图形叫什么呢?
扇形
扇形的定义是什么?
A
O
B
由组成圆心角的两条半径和圆心角所 对的弧围成的图形叫做扇形.
问题:已知⊙O半径为R,如何求圆心角n°的扇形的 面积? (1)半径为R的圆,面积是多少? S=π R2
R
2
(2)圆心角为1°的扇形的面积是多少?
360
(3)圆心角为n°的扇形的面积是圆心角为1°的 扇形的面积的多少倍? n倍 (4)圆心角为n°的扇形的面积是多少?
nR
2
360
扇形面积公式 若设⊙O半径为R,圆心角为n°的扇形的面积S扇形, 则
注意:
S 扇形
nR
2
O
360
A
nR
2
B
(1)在应用扇形的面积公式S扇形= 进行计算时, 360 要注意公式中n的意义.n表示1°圆心角的倍数,它 是不带单位的; (2)公式可以理解记忆(即按照上面推导过程记忆).
(3)转动轮转no,传送带上的物品A被传送多少厘米?
A
皮带轮模型
4.如图,两个皮带轮的中心的距离为2.1m,直径分别 为0.65m和0.24m。(1)求皮带长(保留三个有效 数字);(2)如果小轮每分钟750转,求大轮每分 钟约多少转?
如果两个轮是等圆呢?
3.如图所示,把边长为2的正方形ABCD的一边放 在定直线L上,按顺时针方向绕点D旋转到如图 的位置,则点B运动到点B′所经过的路线长度为 ________ B C (A/)
解:由弧长公式,可得弧AB 的长
l 100 900 180 5 0 0 1 5 7 0 (mm)
因此所要求的展直长度 L
2 700 1570 2970(mm)
答:管道的展直长度为2970mm.
1、制作弯形管道时,先按中心线计 算“展直长度”,再下料。试计算图 中所示的管道的展直长度L(即弧AB 的长)。(单位:mm)
