2018-2019学年北京市石景山区八年级(下)期末数学试卷
北京市石景山区八年级下册期末数学试题有答案
CBA石景山区第二学期初二期末试卷数学学校 姓名 准考证号考生须知1．本试卷共6页，共三道大题，26道小题．满分100分，考试时间100分钟． 2．在试卷和答题卡上准确填写学校名称、姓名和考号． 3．试卷答案一律填涂或书写在答题卡上，在试卷上作答无效．在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答．4．考试结束，将本试卷和答题卡一并交回． 一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1．在平面直角坐标系xOy 中，点P （-3,5）关于y 轴对称的点的坐标是（ ）A ．（-3,-5）B ．（3,-5）C ．（3,5）D ．（5,-3）2．下列图形中，既是中心对称图形又是轴对称图形的是（ ）3．一个多边形的内角和为540°，则这个多边形的边数是（ ）A ．4B ．5C ．6D ．74．菱形ABCD 的边长为4，有一个内角为120°，则较长的对角线的长为（ ）A ．43B ．4C ．23D ．25．如图，利用平面直角坐标系画出的正方形网格中，若A （0,2），B （1,1），则点C 的坐标为（ ） A ．（1,-2） C ．（2,1） B ．（1,-1） D ．（2,-1）6．如图，D ，E 为△ABC 的边AB ，AC 上的点，DE ∥BC ，若:1:3AD DB ，AE =2，则AC 的长是（ ） A ．10 B ．8A ．B ．C ．D ．EDA BC ．6D ．47．关于x 的一元二次方程2210mx x -+=有两个实数根，则m 的取值范围是（ ）A ．1m ≤ C ．1m <且0m ≠B ．1m <D ．1m ≤且0m ≠8．如图，将边长为3cm 的等边△ABC 沿着边BC 向右平移2cm ，得到△DEF ，则四边形ABFD 的周长为（ ）A ．15cmB ．14cmC ．13cmD ．12cm9．园林队在某公园进行绿化，中间休息了一段时间．绿化面积S （单位：平方米）与工作时间t （单位：小时）的函数关系的图象如图所示，则休息后园林队每小时绿化面积为（ ） A ．40平方米B ．50平方米C ．80平方米D ．100平方米10．如右图，矩形ABCD 中，AB =2，BC =4，P 为矩形边上的一个动点，运动路线是A →B →C →D →A ，设P 点 经过的路程为x ，以A ，P ，B 为顶点的三角形面积为y ， 则下列图象能大致反映y 与x 的函数关系的是（ ）二、填空题（本题共18分，每小题3分）11．如图，点D ，E 分别为△ABC 的边AB ，BC 的中点，A. B. C. D.若DE =3cm ，则AC = cm .12．已知一次函数2()y m x m =++，若y 随x 的增大而增大，则m 的取值范围是 ．13．如图，在△ABC 中，D 是AB 边上的一点，连接CD ，请添加一个适当的条件 ，使△ACD ∽△ABC （只填一个即可）．14．如中，BC =5，AB =3，BE 平分∠ABC 交AD 于点E ，交对角 线AC 于点F ，则AEFCBF S S △△=．15．如图，矩形ABCD 中，AB =8，AD =10，点E 为DC 边上的一点，将△ADE 沿直线AE 折叠，点D 刚好落在 BC 边上的点F 处，则CE 的长是 .16．如图，在平面直角坐标系xOy 中，一次函数y =x +1与x 、y 轴分别交于点A 、B ， 在直线 AB 上截取BB 1=AB ，过点B 1分别 作x 、y 轴的垂线，垂足分别为点A 1、C 1， 得到矩形OA 1B 1C 1；在直线 AB 上截取B 1B 2= BB 1，过点B 2分别 作x 、y 轴的垂线，垂足分别为点A 2 、C 2， 得到矩形OA 2B 2C 2；在直线AB 上截取B 2B 3= B 1B 2，过点B 3分别 作x 、y 轴的垂线，垂足分别为点A 3、C 3， 得到矩形OA 3B 3C 3；……；则点B 1的坐标是 ；第3个矩形OA 3B 3C 3的面积是 ； 第n 个矩形OA n B n C n 的面积是 （用含n 的式子表示，n 是正整数）．x+1三、解答题（本题共52分，第17-24题，每小题5分；第25-26题，每小题6分）解答应写出文字说明，演算步骤或证明过程. 17．用适当的方法解方程：2610x x --=．18．如图，在□ABCD 中，E ，F 是对角线BD上的两点且BE =DF ，联结AE ，CF ． 求证：AE =CF ．19．一次函数1y kx b =+的图象与正比例函数2y mx =交于点A （-1，2），与y 轴交于点B （0，3）． （1）求这两个函数的表达式；（2）求这两个函数图象与x 轴所围成的三角形的面积．20．如图，在矩形ABCD 中，E 为AD 边上的一点， 过C 点作CF ⊥CE 交AB 的延长线于点F ． （1）求证：△CDE ∽△CBF ；（2）若B 为AF 的中点，CB =3，DE =1，求CD 的长.21．已知关于x 的一元二次方程2(32)60mx m x -++=(0)m ≠． （1）求证：方程总有两个实数根；（2）若方程的两个实数根都是整数，求正整数m 的值.22．如图，Rt △ABC 中，90ACB ∠=︒，CD 是斜边AB 上的中线，分别过点A ，C 作AE ∥DC ，CE ∥AB ， 两线交于点E ．（1）求证：四边形AECD 是菱形；（2）若602B BC ∠=︒=，，求四边形AECD 的面积．23．列方程解应用题：某地区2013年的快递业务量为2亿件，受益于经济的快速增长及电子商务发展等多重因素，快递业务迅猛发展，2015年的快递业务量达到3.92亿件.求该地区这两年快递业务量的年平均增长率.24．某市为了鼓励居民节约用电，采用分段计费的方法按月计算每户家庭的电费，分两档收费：第一档是当月用电量不超过240度时实行“基础电价”；第二档是当用电量超过240度时，其中的240度仍按照“基础电价”计费，超过的部分按照 “提高电价”收费.设每个家庭月用电量为x 度时，应交电费为y 元.具体收费情况如折线图所示，请根据图象回答下列问题：（1）“基础电价”是_________元/度； （2）求出当x ＞240时，y 与x 的函数表达式； （3）小石家六月份缴纳电费132元， 求小石家这个月用电量为多少度？25．已知正方形ABCD 中，点M 是边CB （或CB 的延长线）上任意一点， AN 平分∠MAD ，交射线DC 于点N . （1）如图1，若点M 在线段CB 上 ①依题意补全图1；②用等式表示线段AM ，BM ，DN 之间的数量关系，并证明； （2）如图2，若点M 在线段CB 的延长线上，请直接写出线段AM ，BM ，DN 之间的数量关系.A(元)(度)26别作x （1）H 1（1,2）, H 2（4,-4）, H 3（-2,5）这三个点中的“和谐点”为 ； （2）点C (-1,4)与点P （m ，n ）都在直线y x b =-+上，且点P 是“和谐点”. 若m ＞0，求点P 的坐标．——————————————草 稿 纸——————————————初二数学 试卷答案及评分参考阅卷须知：为便于阅卷，解答题中的推导步骤写得较为详细，阅卷时，只要考生将主要过程正确写出即可．若考生的解法与给出的解法不同，正确者可参照评分参考给分．评分参考中所注分数，表示考生正确做到此步应得的累加分数． 一、 选择题（本题共30分，每小题3分） 11．6 12．2m >- 13．ACD B ∠=∠（或ADC ACB ∠=∠或AD ACAC AB=） 14．925 15． 3 16．（1，2）；12(1)n n +；或2n n +（每空1分）三、解答题（本题共52分，第17-24题，每小题5分；第25-26题，每小题DC6分）1718∵四边形ABCD 是平行四边形 ∴OA ＝OC ，OB ＝OD ⋯⋯⋯⋯⋯2分 又∵BE ＝DF∴OE ＝OF ⋯⋯⋯⋯⋯3分 ∴四边形AECF 是平行四边形 ⋯⋯4分 ∴AE ＝CF ⋯⋯⋯⋯⋯5分证明二：∵四边形ABCD 是平行四边形∴AB ＝CD ，AB ∥CD ⋯⋯⋯⋯⋯1分 ∴∠1＝∠2⋯⋯⋯⋯⋯2分在△ABE 和△CDF 中12 AB CD BE DF =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CDF （SAS ） ⋯⋯⋯⋯⋯4分∴AE CF = ⋯⋯⋯⋯⋯5分 19．解：（1）∵2y mx =过点A （-1，2）∴-m ＝2 ∴m ＝-2 ⋯⋯⋯⋯⋯1分 ∵点A （-1，2）和点B （0，3）在直线1y kx b =+上2133k b k b b -+==⎧⎧∴∴⎨⎨==⎩⎩⋯⋯⋯⋯⋯3分∴这两个函数的表达式为：13y x =+和2-2y x=⋯⋯⋯⋯⋯3分解法二：2=-△(6)6402±622x ±∴=（2）过点A 作AD ⊥x 轴于点D ，则AD ＝2∵13y x =+交x 轴于点C （-3,0） ⋯⋯4分∴1=2AOC S OC AD⨯⨯△ 1=322⨯⨯ =3 ⋯⋯5分即这两个函数图象与x 轴所围成的三角形的面积是3.20．（1）证明：∵四边形ABCD 是矩形∴∠D=∠1=∠2+∠3=90° ⋯⋯⋯⋯⋯1分 ∵CF ⊥CE ∴∠4+∠3=90°∴∠2=∠4∴△CDE ∽△CBF（2） 解：∵四边形ABCD 是矩形∴CD =AB ∵B 为AF 的中点∴BF =AB ∴设CD=BF= x ⋯⋯⋯3分∵△CDE ∽△CBF 21．（1）证明：∵0m ≠ ∴2(32)6mx m x -++∵2[(32)]46m m =-+-⨯△ ⋯⋯⋯⋯⋯1分2912424m m m =++- 29-124m m =+23-20m =()≥ ⋯⋯⋯⋯⋯2分∴此方程总有两个实数根. ⋯⋯⋯⋯⋯3分（2） 解：∵(3)(2)0x mx --=∴1223,x x m ==⋯⋯⋯⋯⋯4分∵方程的两个实数根都是整数，且m 是正整数∴m =1或 m =2 ⋯⋯⋯⋯⋯5分22．（1）证明：∵AE ∥DC ，CE ∥AB∴四边形AECD 是平行四边形 ⋯⋯⋯⋯⋯1分 ∵Rt △ABC 中，90ACB ∠=︒，CD 是斜边AB 上的中线 ∴CD =AD∴四边形AECD 是菱形 ⋯⋯⋯⋯⋯2分（2） 解：联结DE .∵90ACB ∠=︒，60B ∠=︒∴30BAC ∠=︒∴4A AB C ==, ⋯⋯⋯⋯⋯3分∵四边形AECD 是菱形 ∴EC =AD =DB 又∵EC ∥DB ∴四边形ECBD 是平行四边形∴ED = CB =2⋯⋯⋯⋯⋯4分∴2AECD AC ED S ⨯===菱形 ⋯⋯⋯⋯⋯5分23． 解：设该地区这两年快递业务量的年平均增长率为x . 根据题意，得 ⋯⋯1分 22(1) 3.92x += ⋯⋯⋯⋯⋯3分解得120.4, 2.4x x ==-（不合题意，舍去） ⋯⋯⋯⋯⋯4分 ∴0.440x ==%答：该地区这两年快递业务量的年平均增长率为40%. ⋯⋯⋯⋯⋯5分24．（1）0.5 ⋯⋯⋯⋯⋯ 1分 （2）解：当x ＞240时，设y =kx+b ，由图象可得：2401200.6 40021624k b k k b b +==⎧⎧∴⎨⎨+==-⎩⎩ ⋯⋯⋯⋯⋯2分 ∴0.624(240)y x x =-> ⋯⋯⋯⋯⋯3分（3）解：∵132120y =>∴令0.624=132x -， ⋯⋯⋯⋯⋯4分 得：=260x ⋯⋯⋯⋯⋯5分∴小石家这个月用电量为260度.25．（1）①补全图形，如右图所示. ⋯⋯⋯⋯⋯1分 ②数量关系：AM BM DN =+ ⋯⋯⋯⋯⋯2分 证明：在CD 的延长线上截取DE ＝BM ，联结AE .∵四边形ABCD 是正方形∴190B ∠=∠=︒，AD AB =，AB CD ∥ ∴6BAN ∠=∠ 在△ADE 和△ABM 中1 AD AB B DE BM =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△ABM （SAS ） ∴AE AM =，32∠=∠ ⋯⋯⋯⋯⋯⋯3分又∵54∠=∠ ∴EAN BAN ∠=∠ 又∵6BAN ∠=∠ ∴6EAN ∠=∠∴AE NE = ⋯⋯⋯⋯⋯4分 又∵AE AM =，NE DE DN BM DN +=+=∴AM BM DN =+ ⋯⋯⋯⋯⋯5分（证法二：在CB 的延长线上截取BF ＝DN ，联结AF ） （2）数量关系：AM DN BM =- ⋯⋯⋯⋯⋯6分26．（1）H 2 ⋯⋯⋯⋯⋯1分 （2）解：∵点C (-1,4)在直线y x b =-+上∴14b += ∴3b =∴3y x =-+ ⋯⋯⋯⋯⋯2分 ∴3y x =-+与x 轴，y 轴的交点为N （3， 0），M （0，3） ∵点P （m ，n ）在直线3y x =-+上 ∴点P （m ，-m +3）过点P 分别作x 轴，y 轴的垂线，垂足为D ，E ∵m ＞0∴点P 可能在第一象限或第四象限（解法一） ① 若点P 在第一象限，如图1，则,3OD m PD n m +=== -∴3)6PEOD C m m ++==2(-矩形3)PEOD S m m +=(-矩形∵点P 是“和谐点”∴3)6m m +(-= ⋯⋯⋯3分 260m m +-3=2(-3)460=-⨯△＜∴此方程无实根∴第一象限的直线上的点不可能是“和谐点”. ⋯⋯⋯⋯⋯4分② 若点P 在第四象限，如图2，则,3)3OD m PD n m m -=+=-== --( ∴3)46PEOD C m m m +=-=2(-矩形3)PEOD S m m =(-矩形∵点P 是“和谐点”∴3)46m m m -(-= ⋯⋯5分 260m m +-7=1261m m ==，∵点P （m ，-m +3）在第四象限 ∴3m ＞ ∴6m =∴点P （6，-3） ⋯⋯⋯⋯⋯6分综上所述，满足条件的点P 的坐标为P （6，-3）.（解法二）① 若点P 在第一象限，如图1，则,3OD m PD n m +=== - ∴3)6PEOD C m m ++==2(-矩形∵133 4.52MON S ⨯⨯==△ ⋯⋯⋯3分而MONPEOD S S <△矩形 ∴PEOD PEOD C S 矩形矩形≠∴第一象限的直线上的点不可能是“和谐点”. ⋯⋯⋯⋯⋯4分 ② 若点P 在第四象限，如图2，则,OD m PD n == -∴)PEOD C m n =2(-矩形m +3)y yPEOD S mn =-矩形∵点P 是“和谐点”∴2)m n mn (-=- ⋯⋯⋯⋯⋯5分 ∴22mn m =-∵点P （m ，n ）在直线3y x =-+上 ∴3n m =-+ ∴232mm m =-+- 260m m +-7= 1261m m ==，经检验，1261m m ==，是方程232mm m=-+-的解 ∵点P （m ，-m +3）在第四象限 ∴3m ＞ ∴6m =∴点P （6，-3） ⋯⋯⋯⋯⋯6分 综上所述，满足条件的点P 的坐标为P （6，-3）.m +3)。
2018-2019北京期八年级下期末试卷分类汇编八下期末数学试卷分类-几何综合【含答案】
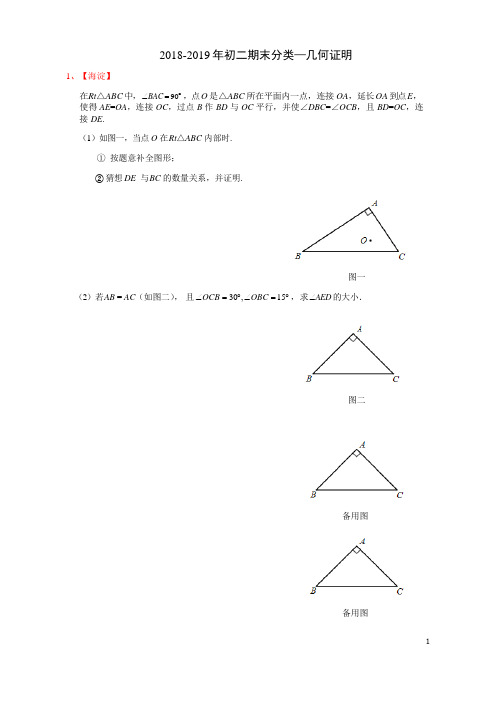
2018-2019年初二期末分类—几何证明1、【海淀】在Rt△ABC 中，∠BAC = 90︒，点O 是△ABC 所在平面内一点，连接OA，延长OA 到点E，使得AE=OA，连接OC，过点B 作BD 与OC 平行，并使∠DBC=∠OCB，且BD=OC，连接DE.（1）如图一，当点O 在Rt△ABC 内部时.① 按题意补全图形；②猜想DE 与BC 的数量关系，并证明.图一（2）若A B = AC（如图二），且∠OCB = 30︒, ∠OBC = 15︒，求∠AED的大小．图二备用图备用图26．四边形ABCD是正方形，AC是对角线，E是平面内一点，且CE<BC．过点C作FC⊥CE，且CF=CE．连接AE，AF．M是AF的中点，作射线DM交AE于点N．（1）如图1，若点E，F分别在BC，CD边上．求证：①∠BAE＝∠DAF；②DN⊥AE；（2）如图2，若点E在四边形ABCD内，点F在直线BC的上方．求∠EAC与∠ADN的和的度数．图1 图227.在正方形ABCD中，点E是射线AC上一点，点F是正方形ABCD外角平分线CM上一点，且CF=AE，连接BE,EF．（1）如图1，当E是线段AC的中点时，直接写出BE与EF的数量关系;（2）当点E不是线段AC的中点，其它条件不变时，请你在图2中补全图形，判断（1）中的结论是否成立，并证明你的结论；的度数. （直接写出结果即可）（3）当点B，E，F在一条直线上时，求CBE27．已知，点E在正方形ABCD的AB边上（不与点A，B重合），BD是对角线，延长AB 到点F，使BF=AE，过点E作BD的垂线，垂足为M，连接AM，CF．（1）根据题意补全图形，并证明MB=ME；（2）①用等式表示线段AM与CF的数量关系，并证明；②用等式表示线段AM，BM，DM之间的数量关系(直接写出即可)．C27．正方形ABCD 中，点P 是直线AC 上的一个动点，连接BP ，将线段BP 绕点B 顺时针旋转90°得到线段BE ，连接CE ．（1）如图1，若点P 在线段AC 上， ①直接写出ACE ∠的度数为 °； ②求证：2222PA PC PB +=；（2）如图2，若点P 在CA 的延长线上，1PA =，PB = ①依题意补全图2；②直接写出线段AC 的长度为 ．图1 图2CE正方形ABCD 中，点M 是直线BC 上的一个动点（不与点B 、C 重合），作射线DM ，过点B 作BN ⊥DM 于点N ，连接CN 。
2019年北京市石景山区初二(下学期)期末数学试卷及答案
2019北京石景山区初二（下）期末数 学学校 姓名 准考证号下面各题均有四个选项，符合题意的选项只有．．一个． 1．若35(0)x y y =≠，则下列各式成立的是A ．35x y = B ．53yx =C ．53yx =D ．53x y = 2．在下列图案中，既是轴对称图形，又是中心对称图形的是A B C D3．若一个多边形的内角和为720°，则这个多边形的边数是A ．4B ．5C ．6D ．7 4．下列函数的图象不经过第三象限，且y 随x 的增大而减小的是A ．31y x =-+B ．31y x =--C ．31y x =+D ．31y x =-5．《孙子算经》是我国古代重要的数学著作，其下卷有题如下：“今有竿不知长短，度 其影得一丈五尺．别立一表，长一尺五寸，影得五寸．问竿长几何？”译文：“有一根竹竿不知道它的长短，量出它在太阳下的影子长一丈五尺．同时立一根一尺五寸的小标杆，它的影长是五寸，则这根竹竿的长度为多少尺？”可得这根竹竿的长度为 （提示：1丈10=尺，1尺10=寸）A ．五丈B ．四丈五尺C ．五尺D ．四尺五寸标杆竹竿6．甲、乙两名同学骑自行车从A 地出发沿同一条路前往B 地，他们离A 地的距离s （km ）与甲离开A 地的时间t （h ）之间的函数关系的图象如图所示，根据图象提供的信息，有下列说法：① 甲、乙同学都骑行了18km ② 甲、乙同学同时到达B 地 ③ 甲停留前、后的骑行速度相同 ④ 乙的骑行速度是12km /h 其中正确的说法是A ．①③B ．①④C ．②④D ．②③7．某校以“我和我的祖国”为主题的演讲比赛中，共有10位评委分别给出某选手的原始评分，在评定该选手成绩时，则从10个原始评分中去掉1个最高分和1个最低分，得到8个有效评分. 8个有效评分与10个原始评分相比，不变的是A ．平均数B ．极差C ．中位数D ．方差8．下面的统计图反映了我国邮电业务（含邮政业务与电信业务）总量的情况．（以上数据来源于国家统计局）根据统计图提供的信息，下列有关我国邮电业务总量推断不合理．．．的是 A ．2018年，电信业务总量比邮政业务总量的5倍还多B ．2011—2018年，邮政业务总量与电信业务总量都是逐年增长的C ．与2017年相比，2018年邮政业务总量的增长率超过20%D ．2011—2018年，电信业务总量年增长的平均值大于邮政业务总量年增长的平均值二、填空题（本题共16分，每小题2分）9．如图，在□ABCD 中，BC =7，AB =4，BE 平分∠ABC 交AD 于点E ，则DE 的长为 .2011-2018年我国邮电业务总量统计图10．直线6y x =-向上平移2个单位长度，则所得新直线的函数表达式为 . 11．菱形ABCD 中，2AB =，120BAD ∠=°，则菱形ABCD 的面积为 . 12．如图，A ，B 两地被池塘隔开，小石通过下面的方法测出A ，B 间的距离：先在AB外选一点C ，然后通过测量找到AC ，BC 的中点D ，E ，并测量出DE 的长为20m ， 由此他就知道了A ，B 间的距离为 m ，小石的依据是 ．13．如图，ADE △和ABC △中，12∠=∠，请添加一个适当的条件 ， 使ADE △∽ABC △（只填一个即可）．14．如图，在ABC △中，点D ，E 分别是边AB ，AC 上的点，DE BC ∥，2BD AD =，若ADE △的面积是1，则四边形DBCE 的面积为 ．15．如右图，矩形ABCD 中，6AB =，8BC =，E 是 BC 边上一点，将ABE △沿AE 翻折，点B 恰好落 在对角线AC 上的点F 处，则BE 的长为 ．16．某林场要考察一种幼树在一定条件下的移植成活率， 在移植过程中的统计结果如下表所示： 移植的幼树n /棵 500 1000 2000 4000 7000 10000 12000 15000 成活的幼树m /棵42386817143456602085801030812915EDCB AFEDCBADE CB A第12题图 第13题图 第14题图ED CBA 21EDCBA在此条件下，估计该种幼树移植成活的概率为 （精确到0.01）；若该林场欲使成活的幼树达到4.3万棵，则估计需要移植该种幼树 万棵.三、解答题（本题共68分，第17-18题每题5分，第19题6分，第20-23题每题5分，第24题7分，第25题5分，第26题6分，第27-28题每题7分）17．如图，菱形ABCD 中，过点D 作DE BA ⊥交BA 的延长线于点E ，DF BC ⊥交BC 的延长线于点F .求证：DE DF =.18．在平面直角坐标系xOy 中，一次函数(0)y kx b k =+≠ 的图象平行于直线12y x =，并且经过点(2,3)A --.（1）求此一次函数的表达式，并画出它的图象；（2）此一次函数的图象与x 轴交于点B ，求AOB △的面积.19．某综合实践小组的同学对本校八年级学生课外阅读最喜爱的图书种类进行了调查. （1）该综合实践小组设计了下列的调查方式，比较合理的是 （填写序号即可） A ．对八年级各班的数学课代表进行问卷调查 B ．对八年级（1）班的全班同学进行问卷调查FE DBAC ．对八年级各班学号为4的倍数的同学进行问卷调查（2）小组同学根据问卷调查（每个被调查的学生只能选择其中一项）的结果绘制了如下两幅统计图（不完整）： 根据以上信息，回答下列问题：①这次被调查的学生共有 人； ②请将图1补充完整并在图上标出数据；③图2中，m = ，“科普类”部分扇形的圆心角是 °； ④若该校八年级共有学生320人，根据调查结果估计此年级最喜欢“文学类” 图书的学生约有 人．20．如图，在ABC △中，点D 是边AB 上一点且ACD B ∠=∠． （1）求证：ACD △∽ABC △； （2）若6AB =，2AD =，求AC 的长．21．如图，在147⨯的正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点 叫做格点．的顶点都在格点上．按照要求完成下列画图（只在此147⨯的 网格中完成且所画各点都是格点，所画的点可以与已知点重合）．DCBA Rt ACB △1220其它艺体类文学类3228322412201684最喜爱的图书类别人数统计图0人数/人最喜爱的图书类别 人数分布统计图其它科普类 25%艺体类 m %文学类 40%图1 图2（1）将ACB △绕点A 逆时针旋转90°，得到AC B ''△；（2）画出所有点D ，使得以A ，B ，C ，D 为顶点的四边形是平行四边形； （3）画出一个与ACB △相似（但不全等）的三角形AEF △，且AEF △与ACB △有 公共点A （画出一个三角形即可）．22．如图，四边形ABCD 中，AD BC ∥，90ABC ∠=°， DB DC =，E 是BC 的中点，连接DE . （1）求证：四边形ABED 是矩形；（2）连接AC ，若30ABD ∠=°，2DC =，求AC 的长.23．如图，在平面直角坐标系xOy 中，过点(0,4)A 的直线1l 与直线2l ：1y x =+相交于点(,2)B m .（1）求直线1l 的表达式；（2）过动点(,0)P n 且垂直于x 轴的直线与1l ，2l 的交点分别为M ，N ，当点M 位于点N 上 方时，请直接写出n 的取值范围是 .EDCBA表1 图124．某农科所甲、乙试验田各有水稻3万个，为了考察水稻穗长的情况，于同一天在这两块试验田里分别随机抽取了50个稻穗进行测量，获得了它们的长度x （单位：cm ），并对数据（穗长）进行了整理、描述和分析.下面给出了部分信息.a .甲试验田．．．．穗长的频数分布统计表如表1所示（不完整）：b .乙试验田．．．．穗长的频数分布直方图如图1所示：甲试验田穗长频数分布表乙试验田穗长的频数分布直方图c .乙试验田穗长在6 6.5x <≤这一组的是：6.3 6.4 6.3 6.3 6.2 6.2 6.1 6.2 6.4d .甲、乙试验田穗长的平均数、中位数、众数、方差如下（表2）：根据以上信息，回答下列问题：（1）表1中m 的值为 ，n 的值为 ； （2）表2中w 的值为 ；（3）在此次考察中，穗长为5.9cm 的稻穗，穗长排名（从长到短排序）更靠前的试验田是 ；稻穗生长（长度）较稳定的试验田是 ；A ．甲B ．乙C ．无法推断（4）若穗长在5.57x <≤范围内的稻穗为“良好”，请估计甲试验田所有“良好”的水稻约为 万个．25．某长途汽车客运公司规定旅客可免费携带一定质量的行李，当行李质量超过规定时，则需要购买行李票，行李票费用y （单位：元）与所携带的行李质量x （单位：kg ）之间的关系如图所示． （1）当行李的质量超过规定时，求y 与x 之间的函数表达式； （2）旅客最多可免费携带多少千克的行李？26．在平面直角坐标系xOy 中，点(1,)A m -是直线2y x =-+上一点，点A 向右平移4个单位长度得到点B ． （1）求点A ，B 的坐标；（2）若直线:2(0)l y kx k =-≠与线段AB 有公共点，结合函数的图象，求k 的取值范围．27．正方形ABCD 中，点P 是直线AC 上的一个动点，连接BP ，将线段BP 绕点B 顺时针旋转90°得到线段BE ，连接CE ．（1）如图1，若点P 在线段AC 上，①直接写出ACE ∠的度数为 °； ②求证：2222PA PC PB +=；（2）如图2，若点P 在CA 的延长线上，1PA =，13PB =， ①依题意补全图2；②直接写出线段AC 的长度为 ．图1 图2DBAPPE28．在平面直角坐标系xOy中，若P，Q为某个矩形不相邻的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P，Q的“相关矩形”．图1为点P，Q的“相关矩形”的示意图．已知点A的坐标为(1,2)．（1）如图2，点B的坐标为(,0)b．①若2b=-，则点A，B的“相关矩形”的面积是；②若点A，B的“相关矩形”的面积是8，则b的值为．（2）如图3，点C在直线1y=-上，若点A，C的“相关矩形”是正方形，求直线AC的表达式；（3）如图4，等边DEF△的边DE在x轴上，顶点F在y轴的正半轴上，点D的坐标为(1,0)．点M的坐标为(,2)m，若在DEF△的边上存在一点N，使得点M，N的“相关矩形”为正方形，请直接写出m的取值范围．yxO–1–21234–1–212345QP图1图2 图3yx12345123456–1–2–3–4–5–6O–1–2Ayx12345123456–1–2–3–4–5–6O–1–2A2019北京石景山区初二（下）期末数学参考答案一、选择题（本题共16分，每小题2分）9．310．62y x =-+11．12．40，三角形中位线定理13．答案不唯一，如：D B ∠=∠或E C ∠=∠或AD AE ABAC=14．815．316．0.86，5三、解答题（本题共68分，第17-18题每题5分，第19题6分，第20-23题每题5分， 第24题7分，第25题5分，第26题6分，第27-28题每题7分） 17．证法一：连接BD ，如图1． ∵四边形ABCD 是菱形，∴12∠=∠． ………………………… 2分 ∵DE BA ⊥，DF BC ⊥，∴DE DF =. ………………………… 5分 证法二：如图2．∵四边形ABCD 是菱形，∴AB BC =． ………………………… 2分 ∵DE BA ⊥，DF BC ⊥，∴ABCD S AB DE =⨯菱形，ABCD S BC DF =⨯菱形． ∴DE DF =． ………………………… 5分 证法三：如图2．∵四边形ABCD 是菱形， ∴DA DC =，12∠=∠．∴34∠=∠． ………………………… 2分 ∵DE BA ⊥，DF BC ⊥，∴90E F ∠=∠=°． ………………………… 3分∴AED △≌CFD △（AAS ）． ………………………… 4分 ∴DE DF =． ………………………… 5分21FE DCBA3421FE DCBA 图1 图218．解：（1）∵一次函数(0)y kx b k =+≠的图象平行于直线12y x =，∴12k =． (1)∵函数图象经过点(2,3)A --，∴1(2)32b ⨯-+=-．∴2b =-．∴一次函数的表达式为122y x =-．… 2分图象如右图所示． ………………………… 3分 （2）过点(2,3)A --作AC x ⊥轴于点C ， ∴3AC =． ∵直线122y x =-与x 轴的交点B 的坐标是(4,0)， ……………… 4分∴1143622AOB S OB AC =⨯=⨯⨯=△． ………………………… 5分19．（1）C ． ……… 1分 （2）①80． ……… 2分 ②如右图所示． ……… 3分 ③20m =；90． ……… 5分 ④128． ……… 6分 20．（1）证明：∵1B ∠=∠，A A ∠=∠，∴ACD △∽ABC △． ………………………… 2分 （2）解： ∵ACD △∽ABC △， ∴AC AD ABAC=． ………… 4分∴26212AC =⨯=． ∵0AC >，∴AC =． ………………………… 5分 21．（1）如图1所示． ………………………… 2分 （2）如图1所示． ………………………… 4分1DCBA（3）如图2所示（未全画出；画出一个三角形即可）． ………………………… 5分22．（1）证明：∵AD BC ∥，90ABC ∠=°，∴90BAD ∠=°． ……… 1分∵DB DC =，E 是BC 的中点， ∴90DEB ∠=°．∴四边形ABED 是矩形． ……… 2分 （2）解： ∵90ABC ∠=°，130∠=°， ∴260∠=°． ∵DB DC =，∴DBC △是等边三角形． ………………………… 3分 ∴2BD BC DC ===． ∵Rt BAD △中，130∠=°，∴1AD =，AB = ………………………… 4分 ∴在Rt ABC △中，AC =． ………………… 5分23．解：（1）设直线1l 的表达式为(0)y kx b k =+≠.…… 1分 ∵直线2l ：1y x =+过点(,2)B m ，∴1m =．∵直线1l 过点(0,4)A 和点(1,2)B ， ∴4, 2.b k b =+=⎧⎨⎩ 解得2,4.k b =-=⎧⎨⎩∴直线1l 的表达式为24y x =-+． …… 4分 （2）1n <． …… 5分24．（1）10；0.28． ………………………… 2分 （2）6.15． ………………………… 3分 （3）A ； ………………………… 5分 A ． ………………………… 6分21EDCBA2图1图24（4）2.1． ………………………… 7分 25．解：（1）设当行李的质量超过规定时，y 与x 之间的函数表达式为(0)y kx b k =+≠. 由图象可知，当30x =时，2y =；当60x =时，8y =，∴302,608.k b k b +=+=⎧⎨⎩ 解得1,54.k b ==-⎧⎪⎨⎪⎩ ………………………… 2分∴当行李的质量超过规定时，y 与x 之间的函数表达式 为14(20)5y x x =-≥． ………………………… 3分 （2）令0y =，得1405x -=，解得20x =．∴旅客最多可免费携带20千克的行李． ………………………… 5分 26．解：（1）∵点(1,)A m -是直线2y x =-+上一点， ∴3m =．∴点A 的坐标为(1,3)-． ………………………… 1分 ∴点(1,3)A -向右平移4个单位长度得到点B 的坐标为(3,3)． …… 2分 （2）当直线:2l y kx =-过点(1,3)A -时，得5k =-． ………………………… 3分 当直线:2l y kx =-过点(3,3)B 时，得53k =． ………… 4分结合函数图象可得b 的取值范围是 5k ≤-或53k ≥． ………… 6分27．（1）①90． ………… 1分 ②证明：连接PE ，如图1． ∵四边形ABCD 是正方形，∴CB AB =，1245∠=∠=°，3490∠+∠=°． ∵将线段BP 绕点B 顺时针旋转90°得到线段BE ， ∴BE BP =，5490∠+∠=°．∴PE =，53∠=∠．∴CBE △≌ABP △（SAS ）． ………………………… 3分 ∴EC PA =，6145∠=∠=°． ∴2690PCE ∠=∠+∠=°．在Rt PCE △中，由勾股定理，得222EC PC PE +=． ……… 4分 ∵EC PA =，PE =，∴2222PA PC PB +=． ………………………… 5分（2分 ②4． ………………………… 7分 28．（1）①6． ………………………… 1分 ②5或3-． ………………………… 3分 （2）解：过点(1,2)A 作直线1y =-的垂线，垂足为点G ，可得3AG =． ∵点C 在直线1y =-上，点A ，C的“相关矩形”AGCH 是正方形， ∴正方形AGCH 的边长为3．如图1，当点C 在直线1x =右侧时，3CG =，可得(4,1)C -．∴直线AC 的表达式为3y x =-+． ………………………… 4分 如图2，当点C 在直线1x =左侧时，3CG =，可得(2,1)C --． ∴直线AC 的表达式为1y x =+．综上所述，直线AC 的表达式为3y x =-+或1y x =+． ………… 5分（3）32m --≤≤。
2018年北京石景山小学八年级数学期末试题word版含答案
2018年北京石景山小学八年级数学期末试题一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1．小元设计了一个关于实数运算的程序，按此程序，输入一个数后，输出的数比输入的数的算术平方根大1，若输入9，则输出的结果为（ ） A ．4B ．4或-2C ．19D ．822．下列表示我国古代窗棂样式结构的图形中,不是轴对称图形的是（ ）A ．B ．C ．D ．3．下列事件中，属于必然事件的是（ ） A ．投掷一枚均匀的硬币，正面朝上； B ．2017年的春节小长假北京将下雪； C ．中国男子足球队在下届世界杯获出线权；D ．投掷两枚均匀的骰子，朝上一面的点数之和大于或等于2． 4有意义，则x 的取值范围是（ ） A ．x ≥2-B ．2x >-C ．2x ≠-D ．x ≤2-5．在一个不透明的盒子中装有m 个球,其中有红球5个，这些球除了颜色外无其他差别.若从中随机摸出一个红球的可能性为13，则m 是（ ）A ．6B ．9C ．10D ．156．下列计算，正确的是（ ）A ．5335=-B ．a a a 26225=+C ．ab b a =+D ．b a b a +=+227．已知，Rt △ABC 中，∠C =90°，BC ＝1，AC ＝2，CD 是AB 边上的高线，则CD 的长为（ ）A. 3B. 5C.332 D. 552 8．计算222)(b a bb b a -⋅-的结果是（ ） A ．b1 B ．2bab ba +- C ．ba ba +- D ．)(1b a b +9．如图，OP 平分AOB ∠，PH OA ⊥于点H ，PH =3，若点Q 是射线OB 上的一个动点，则PQ 的最小值为（ ） A ．2B ．3C ．4D ．5第9题图 第10题图10．如图，△ABC 中，80A ∠=︒，剪去80︒角后，得到一个四边形，则12∠+∠的度数为（ ）A ．100︒B ．160︒C ．260︒D ．280︒二、填空题（本题共18分，每小题3分） 11．当x ＝______时，分式622-+x x 的值为0． 12．比较53和25的大小：53_______25(用“>”或“<”连接)． 13．对于任意不相等的两个实数a 、b ，定义运算★如下：a ★b =ba ba -+， 如3★=4★8=_________． 14．如图，△ABC 中，在中线AD 及其延长线上分别取点E 、F ，连接CE 、BF ．请你添加一个条件，可证 得△BDF ≌△CDE ．你添加的条件是:____________________________________________． （不添加辅助线，只写出一条既可）．15．阅读下面材料：在数学课上，老师提出如下问题：80°21CBA第14题图小涛的作图步骤如下：老师说：“小涛的作图步骤正确”．请回答：得到△ABC是等腰三角形的依据是：①___________________________________________________________________：②___________________________________________________________________．16．有一张直角边为a的等腰直角三角形纸片（如图1），小芹沿它的对称轴折叠1次后得到一个等腰直角三角形（如图2），则图2中的等腰直角三角形的一条腰长为________；再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形（如图3），……，同上操作，若小芹连续将图1的等腰直角三角形折叠n次,则所得到的等腰直角三角形（如图n+1）的腰长为____________．折叠1次折叠2次……折叠n次图1 图2 图3 图n+1三、解答题（本题共52分，第17-24每小题5分；第25-26题，每小题6分）解答应写出文字说明，演算步骤或证明过程.17．18．计算：()32m n m nm nm++--÷．19．解方程：22345525x x x -=+--．20．如图，△ABC 与△DCB 中，AC 与BD 交于点E ，且∠ABD =∠DCA ，AB =DC ． （1）求证：△ABE ≌△DCE ；（2）当∠AEB =100°，求∠EBC 的度数．21．先化简，再求值：222244(2)22y x xy y xy y x y xy-+÷-⋅-，其中x =22．如图，在44⨯的正方形方格中，阴影部分是涂黑5个小正方形所形成的图案．（1）若将方格内空白的两个小正方形涂黑，使得到的新图案成为一个轴对称图形，涂法共有___________种．（2）请在下面的备用图中至少画出具有不同对称轴的三个方案，并画出对称轴．23. 如图是一个转盘,转盘分成8个相同的扇形,颜色分为红、绿、黄、蓝四种．指针的位置固定，转动转盘后任其自由停止，其中的某个扇形会恰好停在指针所指的位置（指针指向两个扇形的交线时，重新转动转盘）．求下列事件发生的可能性大小． （1）指针指向红色； （2）指针指向黄色或蓝色．EDCBA24．列方程解应用题：某工程队准备修建一条长1800m 的道路，由于采用新的施工方式，实际每天修建道路的速度比原计划快20%，结果提前3天完成任务．求原计划修建道路的速度．25．如图1，等边△ABC 中，AD 是BC 边上的中线，E 为AD 上一点（点E 与点A 不重合），以CE 为一边且在CE 下方作等边△CEF ，连接BF ．（1）猜想线段AE ，BF 的数量关系：________________________（不必证明）； （2）当点E 为AD 延长线上一点时，其它条件不变． ① 请你在图2中补全图形；②（1）中结论成立吗？若成立，请证明；若不成立，请说明理由． 图1 图226．如图，已知△ABC 中，∠ABC =15°，ABBC =2，以AB 为直角边向外作等腰直角△BAD 、以BC 为斜边向外作等腰直角△BEC ，连接DE ，请你写出求DE 长的思路．FE D CB A DCBA2018年北京石景山小学八年级数学期末试题答案及评分参考阅卷须知：为便于阅卷，解答题中的推导步骤写得较为详细，阅卷时，只要考生将主要过程正确写出即可．若考生的解法与给出的解法不同，正确者可参照评分参考给分．评分参考中所注分数，表示考生正确做到此步应得的累加分数． 一、 选择题（本题共30分，每小题3分）二、填空题（本题共18分，每小题3分） 11．2-． 12．<． 13．14．DF DE =或FBD ECD ∠=∠或BFD CED ∠=∠.15；a n . 16．①线段垂直平分线上的点到线段两个端点的距离相等；②有两条边相等的三角形是等腰三角形.三、解答题（本题共52分，第17-24题，每小题5分；第26-27题，每小题6分） 17．解：原式32=+……………………………3分3= ……………………………5分 18．解：原式22()3m n m n m m n m n +=⋅-+⋅++ ……………………………3分 223m =-…………………………… 5分 19．解：去分母，得2(5)3(5)4x x --+= …………………………… 2分2103154x x ---=29x -=29x =- (4)分经检验，原方程的解是29x =-． …………………………… 5分 20．（1）证明：在△ABE 和△DCE 中，12,34,,AB DC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△DCE （AAS ）……… 3分（2）解：∵△ABE ≌△DCE∴EB EC = ……………………………4分 ∴56∠=∠又∵56100AEB ∠=∠+∠=︒∴550∠=︒ ……………………………5分21．解：原式221(2)2(2)2y x y x y y x y xy -=⋅⋅-- ……………………………3分 12x =…………………………… 4分当x原式==……………………………5分22．解：（1）6 ……………………………1分（2）……………………………5分说明：上列三类情况中，各选一种为正确答案。
北京市石景山区2017-2018学年八年级下期末质量数学试题含参考答案
石景山区2017—2018学年第二学期初二期末试卷数 学学校姓名 准考证号考生须知1．本试卷共6页，共三道大题，28道小题．满分100分，考试时间100分钟．2．在试卷和答题卡上准确填写学校名称、姓名和考号．3．试卷答案一律填涂或书写在答题卡上，在试卷上作答无效．在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答．4．考试结束，将本试卷和答题卡一并交回．一、选择题（本题共16分，每小题2分）下面各题均有四个选项，其中只有一个是符合题意的．1．在平面直角坐标系中,点关于轴对称的点的坐标为()1,2-A x A ．()12,B ．()12,-C ．()21,D ．()12,--2．下列志愿者标识中是中心对称图形的是A ．B ．C ．D ．3．右图是外周边缘为正八边形的木花窗挂件，则这个八边形的每个内角为 4.如图，在菱形中，分别是的中点，若ABCD E F ，AB AC ， ，则菱形的周长为2EF =ABCD 5. 右图是天安门广场周围的景点分布示意图的一部分，若表示“王府井”的点的坐标为（4，1），表示“人民大会堂”A ．45︒B．100︒C ．120︒D ．135︒A ．4B ．8C ．16D ．20F EDC BA的点的坐标为（0，-1），则表示“天安门”的点的坐标为 A ．（0，0）C ．（-1，0）B ．（1，0） D ．（1，1）6． 关于的方程有两个不相等的实数根，则实数的值可能为x 220x x a -+-=a A ．2B ．2.5C ．3D ．3.57． 把直线向上平移后得到直线，若直线经过点，且2y x =-AB AB ()，m n ，则直线的表达式为28m n +=AB A ． 24y x =-+B ． 28y x =-+C ． 24y x =--D ．28y x =--8．某林业部门要考察某种幼树在一定条件下的移植成活率，下图是这种幼树在移植过程中成活情况的一组数据统计结果.下面三个推断：①当移植棵数是1500时，该幼树移植成活的棵数是1356，所以“移植成活”的概率是0.904；②随着移植棵数的增加，“移植成活”的频率总在0.880附近摆动，显示出一定的稳定性，可以估计这种幼树“移植成活”的概率是0.880；③若这种幼树“移植成活”的频率的平均值是0.875，则“移植成活”的概率是0.875.其中合理的是A ．①③B ．②③C ．①D ．②二、填空题（本题共16分，每小题2分）9．若，则 （填“是”或“不是”）的函数．)0y x =>y x 10．若菱形的两条对角线长分别是6cm ，8cm ，则它的面积为__________cm 2．11．请写出一个一元二次方程，使它的其中一个根为2 ，则此方程可以为 .12．为了了解A 、B 两种玉米种子的相关情况，农科院各用5块100m 2的自然条件相同的试验田进行试验，得到各试验田的产量（单位：kg ）如下：A ： 95 94 100 96 90; B ： 94 99 86 96 100从玉米的产量和产量的稳定性两方面进行选择，你认为该选择 种玉米种子，理1314)m n ，其中，若以，，，为顶点的四边形是平0m >O A B C 行四边形，则点的坐标为 . C 15．已知一次函数，当时，对应的()0y kx b k =+<02x ≤≤函数的取值范围是，的值为 .y 24y -≤≤b 16．已知：线段.a 求作：菱形，使得且.ABCD AB a =60A ∠=︒以下是小丁同学的作法：①作线段 ；AB a =②分别以点，为圆心，线段A B a 两弧交于点；D ③再分别以点，为圆心，线段的长为半径作弧，两弧交于点；D B a C ④连接，，.AD DC BC 则四边形即为所求作的菱形.（如图1）ABCD 老师说小丁同学的作图正确.则小丁同学的作图依据是： .三、解答题（本题共68分，第17-23题，每题5分；第24题6分；第25题5分；26、27题，每题7分；第28题8分）解答应写出文字说明，演算步骤或证明过程.17．用适当的方法解方程： ．2610x x -+=18．如图，在ABCD 中，E ，F 是对角线AC 上的两点，且AF =CE .求证： DE ∥BF .19．如图，在△ABC 中，∠ACB =90°，D ，E 分别为AB ，ACF C的中点，延长DE 到F ，使得EF =DE ，连接AF ，CF ． （1）求证：四边形ADCF 是菱形；（2）请给△ABC 添加一个条件，使得四边形ADCF 是正方形，则添加的条件为 ．20．已知关于的方程.x 2(31)30mx m x +++=（1）求证：不论取何值，方程都有实数根；m （2）若方程有两个整数根，求整数的值.m 21．如图，在△ABC 中，∠ACB =90°，将△ABC 沿BC 方向平移，得到△DEF . （1）写出由条件 “△ABC 沿BC 方向平移，得到△DEF ”直接得到的两个结论，且至少有一个结论是线段间的关系；（2）判断四边形ACFD 的形状，并证明.22．列方程或方程组解应用题：随着生活水平的提高，人们越来越关注健康的生活环境，家庭及办公场所对空气净化器的需求量逐月增多．经调查，某品牌的空气净化器今年三月份的销售量为8万台，五月份的销售量为9.68万台，求销售量的月平均增长率．23．平面直角坐标系中，直线与直线交于点，与轴交于xOy 32y x b =+12y x =(),1A m y 点.B （1）求的值和点的坐标；m B （2）若点在轴上，且△的面积是1，请直接写出点的坐标．C y ABC C 24．如图，点，在矩形的边，上，点与点关于直线对称．设点E F ABCD AD BC B D EF 关于直线的对称点为．A EF G （1）画出四边形关于直线对称的图形；ABFE EF （2）若，直接写出的度数为；16FDC ∠=︒GEF ∠（3）若，，写出求线段长的思路． 4BC =3CD =EF25．近日，某高校举办了一次以“中国梦 青春梦”为主题的诗歌朗诵比赛，共有800名学生参加．为了更好地了解本次比赛成绩的分布情况，随机抽取了其中若干名学生的成绩作为样本，绘制的频数分布表与频数分布直方图的一部分如下（每组分数段中的分数包括最低分，不包括最高分）：请根据所给信息，解答下列问题：（1）a =，b =， c =；（2）请补全频数分布直方图；（3）若成绩在80分及以上均为“优秀”，请你根据抽取的样本数据，估计参加这次比赛的800名学生中成绩优秀的有多少名？26．小泽和小帅两同学分别从甲地出发，骑自行车沿同一条路到乙地参加社会实践活动．如图折线和线段分别表示小泽和小帅离甲地的距离（单位：千米）与时间OAB CD y （单位：小时）之间函数关系的图象．根据图中提供的信息，解答下列问题：x （1）小帅的骑车速度为千米/小时；点的坐标为；C （2）求线段对应的函数表达式；AB （3）当小帅到达乙地时，小泽距乙地还有多远？样本成绩频数分布直方图27．在正方形中，点是直线BC 上一点，连接，将线段绕点顺时针旋ABCD P AP PA P 转，得到线段，连接．90︒PE CE （1）如图1，若点在线段CB 的延长线上．过点作于，与对角线P E EF BC ⊥H 交于点．AC F ①请根据题意补全图形；②求证：．EH FH =（2）若点在射线BC 上，直接写出CE ，CP ，CD 三条线段的数量关系为 .P28．对于平面直角坐标系中的点与图形，给出如下的定义：在点与图形上xOy P W P W 各点连接的所有线段中，最短线段的长度称为点与图形的距离，特别的，当点P W 在图形上时，点与图形的距离为零. 如图1，点，.P W P W ()13A ，()53B ，（1）点与线段的距离为 ；点与线段的距离为 ；()01E ，AB ()51F ，AB （2）若直线上的点与线段的距离为2，求出点的坐标；2y x =-P AB P （3）如图2，将线段沿轴向上平移2个单位，得到线段，连接，，AB y DC AD BC 若直线上存在点，使得点与四边形的距离小于或等于1，y x b =+P P ABCD 请直接写出的取值范围为.b图1图2石景山区2017-2018学年第二学期初二期末数学试卷答案及评分参考阅卷须知：为了阅卷方便，解答题中的推导步骤写得较为详细，考生只要写明主要过程即可。
2019初二下册期末试卷石景山数学
A．①③
B．①④
C．②④
D．②③
7．某校以“我和我的祖国”为主题的演讲比赛中，共有10 位评委分别给出某选手的原始评分，在评定该选手成 绩时，则从10 个原始评分中去掉1个最高分和1个最低分，得到 8 个有效评分. 8 个有效评分与10 个原始评分相比， 不变的是
A．平均数
B．极差
C．中位数
D．方差
17．如图，菱形 ABCD 中，过点 D 作 DE BA 交 BA 的
3 / 15
延长线于点 E ， DF BC 交 BC 的延长线于点 F . 求证： DE DF .
18．在平面直角坐标系 xOy 中，一次函数 y kx b (k 0) 的图象平行于直线 y 1 x ，并且经过点 A(2, 3) . 2 （1）求此一次函数的表达式，并画出它的图象； （2）此一次函数的图象与 x 轴交于点 B ，求 △AOB 的面积.
D．四尺五寸
6．甲、乙两名同学骑自行车从 A 地出发沿同一条路前往 B 地，他们离 A 地的距离 s（km）与甲离开 A 地的时间 t （h）之间的函数关系的图象如图所示，根据图象提供的信息，有下列说法：
1 甲、乙同学都骑行了 18km 2 甲、乙同学同时到达 B 地 3 甲停留前、后的骑行速度相同 4 乙的骑行速度是12km / h 其中正确的说法是
（4）若穗长在 5.5≤ x 7 范围内的稻穗为“良好”，请估计甲试验田所有“良好”
的水稻约为
万个．
25．某长途汽车客运公司规定旅客可免费携带一定质量的行李，当行李质量超过规定时，则需要购买行李票，行 李票费用 y （单位：元）与所携带的行李质量 x （单位： kg ）之间的关系如图所示．
（1）当行李的质量超过规定时，求 y 与 x 之间的函数表达式；
北京市石景山区2019学年八年级下学期期末考试数学试卷【含答案及解析】
北京市石景山区2019学年八年级下学期期末考试数学试卷【含答案及解析】姓名____________ 班级_______________ 分数____________ 题号-二二三四五总分得分、单选题1.在平面直角坐标系中,点，所在的象限是（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.剪纸是中国古老的汉族传统民间艺术之一.下面是制作剪纸的简单流程，展开后的剪纸图案从对称性来判断（ A.是轴对称图形但不是中心对称图形B. 是中心对称图形但不是轴对称图形C. 既是轴对称图形也是中心对称图形D. 既不是轴对称图形也不是中心对称图形3. 如果一个n边形的内角和与外角和相等，那么这个n边形是（）A.四边形B. 五边形C. 六边形D. 七边形4. 如图，在口应疔玄中，八是… 边的中点，「是对角线.的中点，若-，则二.的长为（）A. 2.5B. 5C. 10D. 155.在下列图形性质中，平行四边形不一定具备的是（）A •对角线相等 B. 两组对边分别平行 C.两组对边分别相等D. 对角线互相平分关于的一次函数y = kx + k2 + 1的图象可能是（）、填空题10. 把直线p =-/■■■■ 向上平移•个单位后，与直线的交点在第一象限，则 的取值范围是（ ） A.；广-B. 厂、Q C.丨—芦■■- '/ D. :: !三、单选题11. 一列快车以100千米/小时的速度从甲地驶往乙地，一列特快车以 150千米/小时的速度从乙地驶往甲地，甲、乙两地之间的距离为1000千米•两车同时出发，则大致表示两车之间的距离y （千米）与快车行驶时间t （小时）之间的函数图象是（ ）四、填空题12. ________________________________________ 点P （-3, 2）到咒轴的距离是 •6. F 表记录了甲、乙、 丙、丁四名跳咼运动员最近几次选拔赛成绩的平均数与方差:7. 甲乙丙丁平均数（cm ) 182182182182 方差 5.73.57.18.6td 8.二次方程•' - L-.- I..'有两个实数根，则 _ C. _ 且「 D.m 的取值范围是（）A.9.关于x 的一元 A. - B.B.D.13. 函数卩=亠中，自变量咒的取值范围是___________________14•请写出一个图象过点| '，且函数值1随自变量的增大而减小的一次函数的表达式：（填上一个答案即可）.15.已知一次函数&二海-八-九与-轴，轴分别交于点.，点打，若:1 ., 则片的值是.16•如图1,将正方形芒扎二置于平面直角坐标系中，其中：】边在：轴上，其余各边均与坐标轴平行•直线沿轴的负方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形 .宀：的边所截得的线段长为，平移的时间为r（秒），*与,的函数图象如图2所示，则图1中的点卫的坐标为_____________ ，图2中b的值为團117. 已知：线段：.：，■：，― - | •求作：矩形止匚壬•以下是甲、乙两同学的作业：甲：① 以点f为圆心，：「长为半径作弧；②以点.为圆心，一长为半径作弧；③两弧在J上方交于点厂，连接：* , :'.四边形.即为所求矩形•（如图）乙：① 连接v，作线段一丹r的垂直平分线，交抚二于点I ；Ji. C②连接」.并延长，在延长线上取一点,，使一应2d何，连接「, ' •四边形..即为所求矩形•（如图）老师说甲、乙同学的作图都正确•则甲的作图依据是：_______________________________________________________ ;乙的作图依据是：_______________________________________________________ .五、解答题18. 用适当的方法解方程：.'-■- -J .J19•如图，矩形畧「，-为射线...上一点，连接为?上一点，，交于点「，.求证：•匸m20. 如图，在口 :;.中，过点.作丄于点「，止歹丄，丄于点，,AE = AF求证：四边形心：3是菱形.21. 已知关于的方程• I、i ' 1 1.(1)求证：方程总有两个不相等的实数根；(2)若方程的两个实数根都是整数，求整数的值•22. 如图，四边形ABCD为平行四边形，/ B的角平分线AF交CD于点E,交BC的延长线于点F.(1)求证：BF=CD(2)连接BE, 若BEX AF,Z F=60°,闿£ = 2 ，求討B 的长.23. 列方程或方程组解应用题：某项工程，甲队单独完成所需时间比乙队单独完成所需的时间多5个月，并且两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的6倍•求甲、乙两队单独完成这项工程各需几个月？24. 为进一步加强中小学生近视眼的防控工作，某地区教育主管部门对初二年级学生的视力进行了一次抽样调查，经数据分组整理，绘制的频数分布表与频数分布直方图的一部分如下（每组含前一个边界值，不含后一个边界值）：某地区严二宇生视力抽獰调查频率10 C.024. 2^4.4150.034.4^4-6750.154. 6/x/4_8a0.124.3—5-0go風0〜乩2150b5. 2〜氐41000.20合计*c 1.00某地区甸二疟生視力站忑询查请根据以上信息解答下列问题：（1）表中的•二，.一;（2）在图中补全频数分布直方图；（3）若视力在|以上（含J均属正常，根据抽样调查数据，估计该地区6200名初二年级学生视力正常的有人.25. 一个装有进水管和出水管的容器，从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，接着关闭进水管直到容器内的水放完•假设每分钟的进水量和出水量是两个常数，容器内的水量y （单位：升）与时间x （单位：分钟）之间的部分关系如图象所示•求从关闭进水管起需要多少分钟该容器内的水恰好放完.-'-与直线：i I 相交于点A (2, 4)，直线•与x轴交于点B (6, 0).4(1)分别求直线和・的表达式；(2)过动点P(0，n)且垂直于.轴的直线与•，•的交点分别为C, D,当点C位于点D左方时，请直接写出n的取值范围.1?，DC = 8，点F是边上一点，过点F作f，交射线一于点，.，交射线，：于点〕-.(1)如图1,若 n"，则一..- ；(2)当以，；，；•，〔为顶点的三角形是等边三角形时，依题意在图2中补全图形并求的长；(3)过点」.作「-//：■交射线于点.1，请探究：当「为何值时，以；，二, ,:为顶点的四边形是平行四边形.£ 才.............. 涉C备用團参考答案及解析第1题【答案】蟲黠符号特尬第一象限£十八第二謨限（「十八,由此可得点巧）在第二象限，故选B.第2题【答案】M SSL展幵后陋纸图案既罡轴对称图形也是中心对称图机故醪轴翊和中心对称彫的第3题【答案】第8题【答案】【解析】6、解得“4,故选丸第4题【答案】C【解析】 已知E 罡BC 边的中員，虚AC 的中 包EF=5,根据三角形的中位线走理可得AB=10.根据平行四边形的性质可得匚故选匚第5题【答案】駡骗边分別相等，对甬线互相平分」但对甬线不-定相等，故蛊丁四边形的两组对边分别平行第6题【答案】 第7题【答案】C【ft?析】令*0,则函数茫如『+ 1的團慕与我交于点（0 r k a -Fl> ，因It" A Ch 所CA 團象与yffl 的交点在第由的正辛轴上・故选匚.由题意可得（1-2 ） x 1 &0*=360 越稳定，乙的方差最小，所以应该派乙去，故选圧在平均数一样的情况下，方養越小B【解析】一元二次方程mH 十比十仁0有两个实数根』所以rri±D , i=23+4rri£：0j 解得mk-1 i 故选区第9题【答案】B【解析】把直线=5%再向上平移ni 个单位后7FJ — 1= 2 Jr 4- 47得1如二-5好强E 联立方程得：｛ c ,•解得百因为交点在第一象限■V = --------------7冋辭查了一次働的运用，即一次IS 黴那的作迭，在此题中作图关键是联系实第11题【答案】 2【解析】点P ( -3 ( -2〕到鞭的即离是解，③. I遇；D小达i1距至车地目 f J②地 ;乙 I好大着S--I段•可121=2.第12题【答案】尹【解析】根拐分式有倉义，分母不为0可得解得E,第13题【答案】答案不唯一，如严(t<0)【解析】一次国数函数值灘目变童孟的増大而减卜根据二次醐的性馬可得衣0,文因过啟o , 1) F可得函数的解析式为尸如1 ( 儿所以答案不唯一：如y—K + 1 ( k<0 H第14题【答案】2或-2【解析】一次函数丫=kx+2(k^ 0百薜由的交点B的坐槪为(0r2) r fWB=2.因OB = 2OA，可得OA=n当点A的坐标为(1小)吋，代入即可求得“0当点册坐标为C-1 r Q>时，代入艮网求得匕2「所以曲值是或-2 .第15题【答案】(1- 0) 5^2【解析】令直线沪解得扫亦即可得直线尸心与触的交点坐标为O, o> -根掳團少可期开始平移姑后直g舞q达点州所以点嶺坐标为显e所以点些标汾(1, 0)；由團象2可知，直线尸-抨移曲寸，正好经过点G止时平移后的直线忌轴交点的横坐标为(S),所以点虚號个交点的距宮加山即可得鹉丸很据勾股定理求得心/ ,当Y*平移到BD的位制寸頂最大，即m最大为,所以已血・点睛：本西主要考查了一次的数图偉的平移』根据sao取信息杲解决本題的关键.第16题【答案】勰I寵騎翼燿S麟舷瀨踏平行四边嗨形对角线互相平分的四A^CD r BC=AD f根抿两组对边分别相等的四边形录平行四边形即酸釐盟平行四边形丿又因山肚北叫根1S有一个角是直角的平行四边形是矩形即可判定平行四边形ABB为矩形；由乙的怅图方法可知= , BM = DM.根擔对相平幷的四边形是平行四边瑚呵尹症四边形/3匚励平行四边册，又因Z A BC=90°，根據有一个角是宜角的平行四边形是拒影即可判走平行四边形匚D为矩形,第17题【答案】延二T + 祚‘毛二_2 f 鸟，试題分■析：用公式法解方程艮呵.【解析】试題库析：解：＞^4x-l = 0一/ +4re= 1,r -^4r+4 = l+4（尤 + 2）； =5X^T 2 —±-V?西=一2 + 巫=七=-2-^ .第18题【答案】证明见解析【解析】试题分析:已知独二陌匚根握等腥三角形的'性质可得Z2=Z1J再由Z E^90°-Z2JZ4=9O°-Z3,可得ZE=Z4,所以FEhCZ!试题解析：t.*^A=FGl/.Z2=Z1LJVZ3-Z13・*z^2=^3G丁四边形朋淀矩形，/.Z4DC=90Q C/>ZE=W-Z 2 L Z4=90g -Z3 C.'*Z^F=z^4 Z____ B第伯题【答案】证明见解析【解析】试题分析：方法一：连接AC,由E1BCCAF丄可得Z2=Z1,再由平行线的性质和等腰三角形的判走可证得DA=DC,即可得= ABCD是菱形；方法二：根据已知杀件易证AE琢△AFDj可得AB=AD,所以oABCD是菱形；方法三：由A平行四边形的面积肛BCHE二CUAF,即可证得BC二CD,所以cABCD是菱形.趣解析：连接M ,如團.V AE丄PC C 肿丄DC C AE^AF ,:.Z2 = Z1 ・•.•四边形肋CD杲平行四边形，:,ADWBC ・/.ZZ)JC = Z 1 ・.\ZDJC = Z2 ・DA = DC ..•.d招CD是菱形.证法二•.•四边形肋CD是平行四边形，如图2.= ZD .J FE丄BC C肿丄DC f・・・ZAEB = ZAFD=9Q。
201907评标：石景山八下数学期末答案及评分参考
石景山区2018—2019学年第二学期初二期末数学试卷答案及评分参考阅卷须知：1．为便于阅卷，本试卷答案中有关解答题的推导步骤写得较为详细，阅卷时，只要考生将主要过程正确写出即可．2．若考生的解法与给出的解法不同，正确者可参照评分参考相应给分. 3．评分参考中所注分数，表示考生正确做到此步应得的累加分数． 一、选择题（本题共16分，每小题2分）二、填空题（本题共16分，每小题2分） 9．310．62y x =-+11．12．40，三角形中位线定理13．答案不唯一，如：D B ∠=∠或E C ∠=∠或AD AE ABAC=14．8 15．316．0.86，5三、解答题（本题共68分，第17-18题每题5分，第19题6分，第20-23题每题5分， 第24题7分，第25题5分，第26题6分，第27-28题每题7分） 17．证法一：连接BD ，如图1． ∵四边形ABCD 是菱形，∴12∠=∠． ………………………… 2分 ∵DE BA ⊥，DF BC ⊥，∴DE DF =. ………………………… 5分 证法二：如图2．∵四边形ABCD 是菱形，∴AB BC =． ………………………… 2分 ∵DE BA ⊥，DF BC ⊥，∴ABCD S AB DE =⨯菱形，ABCD S BC DF =⨯菱形． ∴DE DF =． ………………………… 5分21FE DCBA3421FE DBA 图1证法三：如图2．∵四边形ABCD 是菱形， ∴DA DC =，12∠=∠．∴34∠=∠． ………………………… 2分 ∵DE BA ⊥，DF BC ⊥，∴90E F ∠=∠=°． ………………………… 3分∴AED △≌CFD △（AAS ）． ………………………… 4分 ∴DE DF =． ………………………… 5分18．解：（1）∵一次函数(0)y kx b k =+≠的图象平行于直线12y x =，∴12k =． (1)∵函数图象经过点(2,3)A --， ∴1(2)32b ⨯-+=-．∴2b =-．∴一次函数的表达式为122y x =-． (2)图象如右图所示． ………………………… 3分 （2）过点(2,3)A --作AC x ⊥轴于点C ，∴3AC =．∵直线122y x =-与x 轴的交点B 的坐标是(4,0)， ……………… 4分∴1143622AOB S OB AC =⨯=⨯⨯=△． ………………………… 5分19．（1）C ． ……… 1分 （2）①80． ……… 2分 ②如右图所示． ……… 3分 ③20m =；90． ……… 5分 ④128． ……… 6分20．（1）证明：∵1B ∠=∠，A A ∠=∠，∴ACD △∽ABC △． ………………………… 2分 （2）解： ∵ACD △∽ABC △，∴AC ADAB AC =． ………… 4分 ∴26212AC =⨯=． ∵0AC >，∴AC = ………………………… 5分21．（1）如图1所示． ………………………… 2分 （2）如图1所示． ………………………… 4分 （3）如图2所示（未全画出；画出一个三角形即可）． ………………………… 5分22．（1）证明：∵AD BC ∥，90ABC ∠=°，∴90BAD ∠=°． ……… 1分 ∵DB DC =，E 是BC 的中点， ∴90DEB ∠=°．∴四边形ABED 是矩形． ……… 2分 （2）解： ∵90ABC ∠=°，130∠=°， ∴260∠=°． ∵DB DC =，∴DBC △是等边三角形． ………………………… 3分 ∴2BD BC DC ===． ∵Rt BAD △中，130∠=°，∴1AD =，AB =． ………………………… 4分 ∴在Rt ABC △中，AC ==． ………………… 5分1DCBA 图1 图221EDCBA2423．解：（1）设直线1l 的表达式为(0)y kx b k =+≠.∵直线2l ：1y x =+过点(,2)B m ，∴1m =． ∵直线1l 过点(0,4)A 和点(1,2)B ，∴4, 2.b k b =+=⎧⎨⎩ 解得2,4.k b =-=⎧⎨⎩∴直线1l 的表达式为24y x =-+． （2）1n <． …… 5分24．（1）10；0.28． ………………………… 2分 （2）6.15． ………………………… 3分 （3）A ； ………………………… 5分 A ． ………………………… 6分 （4）2.1． ………………………… 7分25．解：（1）设当行李的质量超过规定时，y 与x 之间的函数表达式为(0)y kx b k =+≠. 由图象可知，当30x =时，2y =；当60x =时，8y =，∴302,608.k b k b +=+=⎧⎨⎩ 解得1,54.k b ==-⎧⎪⎨⎪⎩ …………………………2分 ∴当行李的质量超过规定时，y 与x 之间的函数表达式为14(20)5y x x =-≥． …………………………3分 （2）令0y =，得1405x -=，解得20x =．∴旅客最多可免费携带20千克的行李． ………………………… 5分26．解：（1）∵点(1,)A m -是直线2y x =-+上一点，∴3m =．∴点A 的坐标为(1,3)-． ………………………… 1分 ∴点(1,3)A -向右平移4个单位长度得到点B 的坐标为(3,3)． …… 2分 （2）当直线:2l y kx =-过点(1,3)A -时，得5k =-． ………………………… 3分当直线:2l y kx =-过点(3,3)B 时，得53k =． ………… 4分结合函数图象可得b 的取值范围是5k ≤-或53k ≥ ． ………… 6分27．（1）①90． ………… 1分②证明：连接PE ，如图1． ∵四边形ABCD 是正方形，∴CB AB =，1245∠=∠=°，3490∠+∠=°． ∵将线段BP 绕点B 顺时针旋转90°得到线段BE ， ∴BE BP =，5490∠+∠=°． ∴PE =，53∠=∠．∴CBE △≌ABP △（SAS ）． ………………………… 3分 ∴EC PA =，6145∠=∠=°． ∴2690PCE ∠=∠+∠=°．在Rt PCE △中，由勾股定理，得222EC PC PE +=． ……… 4分 ∵EC PA =，PE =，∴2222PA PC PB +=． ………………………… 5分（2）①补全的图形如图2所示． ………………………… 6分 ②4． ………………………… 7分654321EPDCBA图1 图228．（1）①6． ………………………… 1分 ②5或3-． ………………………… 3分 （2）解：过点(1,2)A 作直线1y =-的垂线，垂足为点G ，可得3AG =． ∵点C 在直线1y =-上，点A ，C 的“相关矩形”AGCH 是正方形， ∴正方形AGCH 的边长为3．如图1，当点C 在直线1x =右侧时，3CG =，可得(4,1)C -．∴直线AC 的表达式为3y x =-+． ………………………… 4分 如图2，当点C 在直线1x =左侧时，3CG =，可得(2,1)C --． ∴直线AC 的表达式为1y x =+．综上所述，直线AC 的表达式为3y x =-+或1y x =+． ………… 5分（3）32m --+≤≤23m -≤． ………………………… 7分。
北京市石景山区2018—2019学年第二学期初二数学期末试卷-含详细解答
石景山区2018—2019学年第二学期初二期末试卷数 学学校 姓名 准考证号一、选择题（本题共16分，每小题2分）下面各题均有四个选项，符合题意的选项只有．．一个． 1．若35(0)x y y =≠，则下列各式成立的是A ．35x y= B ．53y x = C ．53y x =D ．53x y= 2．在下列图案中，既是轴对称图形，又是中心对称图形的是ABCD3．若一个多边形的内角和为720°，则这个多边形的边数是A ．4B ．5C ．6D ．74．下列函数的图象不经过第三象限，且y 随x 的增大而减小的是A ．31y x =-+B ．31y x =--C ．31y x =+D ．31y x =-5．《孙子算经》是我国古代重要的数学著作，其下卷有题如下：“今有竿不知长短，度 其影得一丈五尺．别立一表，长一尺五寸，影得五寸．问竿长几何？” 译文：“有一根竹竿不知道它的长短，量出它在太阳 下的影子长一丈五尺．同时立一根一尺五寸的小标 杆，它的影长是五寸，则这根竹竿的长度为多少尺？”可得这根竹竿的长度为（提示：1丈10=尺，1尺10=寸）A ．五丈B ．四丈五尺C ．五尺D．四尺五寸标杆竹竿6．甲、乙两名同学骑自行车从A 地出发沿同一条路前往B 地，他们离A 地的 距离s （km ）与甲离开A 地的时间t （h ）之间的函数关系的图象如图所示， 根据图象提供的信息，有下列说法：① 甲、乙同学都骑行了18km ② 甲、乙同学同时到达B 地 ③ 甲停留前、后的骑行速度相同 ④ 乙的骑行速度是12km/h 其中正确的说法是 A ．①③B ．①④C ．②④D ．②③7．某校以“我和我的祖国”为主题的演讲比赛中，共有10位评委分别给出某选手的原 始评分，在评定该选手成绩时，则从10个原始评分中去掉1个最高分和1个最低分， 得到8个有效评分. 8个有效评分与10个原始评分相比，不变的是A ．平均数B ．极差C ．中位数D ．方差8．下面的统计图反映了我国邮电业务（含邮政业务与电信业务）总量的情况．（以上数据来源于国家统计局）根据统计图提供的信息，下列有关我国邮电业务总量推断不合理．．．的是 A ．2018年，电信业务总量比邮政业务总量的5倍还多B ．2011—2018年，邮政业务总量与电信业务总量都是逐年增长的C ．与2017年相比，2018年邮政业务总量的增长率超过20%D ．2011—2018年，电信业务总量年增长的平均值大于邮政业务总量年增长的平均值2011-2018年我国邮电业务总量统计图二、填空题（本题共16分，每小题2分）9．如图，在□ABCD 中，BC =7，AB =4，BE 平分∠ABC 交AD 于点E ，则DE 的长为 .10．直线6y x =-向上平移2个单位长度，则所得新直线的函数表达式为 . 11．菱形ABCD 中，2AB =，120BAD ∠=°，则菱形ABCD 的面积为 . 12．如图，A ，B 两地被池塘隔开，小石通过下面的方法测出A ，B 间的距离：先在AB外选一点C ，然后通过测量找到AC ，BC 的中点D ，E ，并测量出DE 的长为20m ， 由此他就知道了A ，B 间的距离为 m ，小石的依据是 ．13．如图，ADE △和ABC △中，12∠=∠，请添加一个适当的条件 ， 使ADE △∽ABC △（只填一个即可）．14．如图，在ABC △中，点D ，E 分别是边AB ，AC 上的点，DE BC ∥，2BD AD =， 若ADE △的面积是1，则四边形DBCE 的面积为 ． 15．如右图，矩形ABCD 中，6AB =，8BC =，E 是 BC 边上一点，将ABE △沿AE 翻折，点B 恰好落 在对角线AC 上的点F 处，则BE 的长为 ． 16．某林场要考察一种幼树在一定条件下的移植成活率， 在移植过程中的统计结果如下表所示：在此条件下，估计该种幼树移植成活的概率为 （精确到0.01）；若该林场欲使成活的幼树达到4.3万棵，则估计需要移植该种幼树 万棵.FEDCBAEDCBA第12题图 第13题图 第14题图ED CBA 21EDCBA三、解答题（本题共68分，第17-18题每题5分，第19题6分，第20-23题每题5分， 第24题7分，第25题5分，第26题6分，第27-28题每题7分） 17．如图，菱形ABCD 中，过点D 作DE BA ⊥交BA 的延长线于点E ，DF BC ⊥交BC 的延长线于点F . 求证：DE DF =.18．在平面直角坐标系xOy 中，一次函数(0)y kx b k =+≠ 的图象平行于直线12y x =，并且经过点(2,3)A --.（1）求此一次函数的表达式，并画出它的图象；（2）此一次函数的图象与x 轴交于点B ，求AOB △的面积.19．某综合实践小组的同学对本校八年级学生课外阅读最喜爱的图书种类进行了调查. （1）该综合实践小组设计了下列的调查方式，比较合理的是 （填写序号即可） A ．对八年级各班的数学课代表进行问卷调查 B ．对八年级（1）班的全班同学进行问卷调查 C ．对八年级各班学号为4的倍数的同学进行问卷调查（2）小组同学根据问卷调查（每个被调查的学生只能选择其中一项）的结果绘制了如下两幅统计图（不完整）：根据以上信息，回答下列问题：①这次被调查的学生共有 人； ②请将图1补充完整并在图上标出数据；③图2中，m = ，“科普类”部分扇形的圆心角是 °； ④若该校八年级共有学生320人，根据调查结果估计此年级最喜欢“文学类” 图书的学生约有 人．FEDBA最喜爱的图书类别 人数分布统计图其它科普类 25%艺体类 m %文学类 40%图1 图220．如图，在ABC △中，点D 是边AB 上一点且ACD B ∠=∠． （1）求证：ACD △∽ABC △； （2）若6AB =，2AD =，求AC 的长．21．如图，在147⨯的正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点 叫做格点．Rt ACB △的顶点都在格点上．按照要求完成下列画图（只在此147⨯的 网格中完成且所画各点都是格点，所画的点可以与已知点重合）．（1）将ACB △绕点A 逆时针旋转90°，得到AC B ''△；（2）画出所有点D ，使得以A ，B ，C ，D 为顶点的四边形是平行四边形； （3）画出一个与ACB △相似（但不全等）的三角形AEF △，且AEF △与ACB △有 公共点A （画出一个三角形即可）．22．如图，四边形ABCD 中，AD BC ∥，90ABC ∠=°， DB DC =，E 是BC 的中点，连接DE . （1）求证：四边形ABED 是矩形；（2）连接AC ，若30ABD ∠=°，2DC =，求AC 的长.23．如图，在平面直角坐标系xOy 中，过点(0,4)A 的直线1l 与直线2l ：1y x =+相交于点(,2)B m . （1）求直线1l 的表达式；（2）过动点(,0)P n 且垂直于x 轴的直线与1l ，2l 的交点分别为M ，N ，当点M 位于点N 上 方时，请直接写出n 的取值范围是 .DCB A EDCBA表1 图124．某农科所甲、乙试验田各有水稻3万个，为了考察水稻穗长的情况，于同一天在这两块试验田里分别随机抽取了50个稻穗进行测量，获得了它们的长度x （单位：cm ），并对数据（穗长）进行了整理、描述和分析.下面给出了部分信息. a .甲试验田．．．．穗长的频数分布统计表如表1所示（不完整）： b .乙试验田．．．．穗长的频数分布直方图如图1所示：c .乙试验田穗长在6 6.5x <≤这一组的是：6.3 6.4 6.3 6.3 6.2 6.2 6.1 6.2 6.4 d .甲、乙试验田穗长的平均数、中位数、众数、方差如下（表2）：根据以上信息，回答下列问题：（1）表1中m 的值为 ，n 的值为 ； （2）表2中w 的值为 ；（3）在此次考察中，穗长为5.9cm 的稻穗，穗长排名（从长到短排序）更靠前的试验田是 ；稻穗生长（长度）较稳定的试验田是 ； A ．甲B ．乙C ．无法推断（4）若穗长在5.57x <≤范围内的稻穗为“良好”，请估计甲试验田所有“良好”的水稻约为 万个．乙试验田穗长的频数分布直方图4.5 55.5 66.5 77.5 稻穗长度/cm25．某长途汽车客运公司规定旅客可免费携带一定质量的行李，当行李质量超过规定时，则需要购买行李票，行李票费用y （单位：元）与所携带的行李质量x （单位：kg ）之间的关系如图所示．（1）当行李的质量超过规定时，求y 与x 之间的函数表达式；（2）旅客最多可免费携带多少千克的行李？26．在平面直角坐标系xOy 中，点(1,)A m -是直线2y x =-+上一点，点A 向右平移4个单位长度得到点B ． （1）求点A ，B 的坐标；（2）若直线:2(0)l y kx k =-≠与线段AB 有公共点，结合函数的图象， 求k 的取值范围．27．正方形ABCD 中，点P 是直线AC 上的一个动点，连接BP ，将线段BP 绕点B 顺时针旋转90°得到线段BE ，连接CE ．（1）如图1，若点P 在线段AC 上，①直接写出ACE ∠的度数为 °； ②求证：2222PA PC PB +=；（2）如图2，若点P 在CA 的延长线上，1PA =，PB ①依题意补全图2；②直接写出线段AC 的长度为 ．图1 图2CE28．在平面直角坐标系xOy 中，若P ，Q 为某个矩形不相邻的两个顶点，且该矩形的边均与某条坐标轴垂 直，则称该矩形为点P ，Q 的“相关矩形”． 图1为点P ，Q 的“相关矩形”的示意图． 已知点A 的坐标为(1,2)． （1）如图2，点B 的坐标为(,0)b ．①若2b =-，则点A ，B 的“相关矩形”的面积是 ； ②若点A ，B 的“相关矩形”的面积是8，则b 的值为 ．（2）如图3，点C 在直线1y =-上，若点A ，C 的“相关矩形”是正方形，求直线AC 的表达式；（3）如图4，等边DEF △的边DE 在x 轴上，顶点F 在y 轴的正半轴上，点D 的 坐标为(1,0)．点M 的坐标为(,2)m ，若在DEF △的边上存在一点N ，使得 点M ，N 的“相关矩形”为正方形，请直接写出m 的取值范围．图2 图3图4石景山区2018—2019学年第二学期初二期末数学试卷答案及评分参考阅卷须知：1．为便于阅卷，本试卷答案中有关解答题的推导步骤写得较为详细，阅卷时，只要考生将主要过程正确写出即可．2．若考生的解法与给出的解法不同，正确者可参照评分参考相应给分. 3．评分参考中所注分数，表示考生正确做到此步应得的累加分数． 一、选择题（本题共16分，每小题2分）二、填空题（本题共16分，每小题2分） 9．310．62y x =-+11．12．40，三角形中位线定理13．答案不唯一，如：D B ∠=∠或E C ∠=∠或AD AE ABAC=14．8 15．316．0.86，5三、解答题（本题共68分，第17-18题每题5分，第19题6分，第20-23题每题5分， 第24题7分，第25题5分，第26题6分，第27-28题每题7分） 17．证法一：连接BD ，如图1． ∵四边形ABCD 是菱形，∴12∠=∠． ………………………… 2分 ∵DE BA ⊥，DF BC ⊥，∴DE DF =. ………………………… 5分 证法二：如图2．∵四边形ABCD 是菱形，∴AB BC =． ………………………… 2分 ∵DE BA ⊥，DF BC ⊥，∴ABCD S AB DE =⨯菱形，ABCD S BC DF =⨯菱形． ∴DE DF =． ………………………… 5分21FE DCBA3421FE DBA 图1图2证法三：如图2．∵四边形ABCD 是菱形， ∴DA DC =，12∠=∠．∴34∠=∠． ………………………… 2分 ∵DE BA ⊥，DF BC ⊥，∴90E F ∠=∠=°． ………………………… 3分∴AED △≌CFD △（AAS ）． ………………………… 4分 ∴DE DF =． ………………………… 5分18．解：（1）∵一次函数(0)y kx b k =+≠的图象平行于直线12y x =，∴12k =． (1)∵函数图象经过点(2,3)A --， ∴1(2)32b ⨯-+=-．∴2b =-．∴一次函数的表达式为122y x =-． (2)图象如右图所示． ………………………… 3分 （2）过点(2,3)A --作AC x ⊥轴于点C ，∴3AC =．∵直线122y x =-与x 轴的交点B 的坐标是(4,0)， ……………… 4分∴1143622AOB S OB AC =⨯=⨯⨯=△． ………………………… 5分19．（1）C ． ……… 1分 （2）①80． ……… 2分 ②如右图所示． ……… 3分 ③20m =；90． ……… 5分 ④128． ……… 6分20．（1）证明：∵1B ∠=∠，A A ∠=∠，∴ACD △∽ABC △． (2)分（2）解： ∵ACD △∽ABC △，∴AC ADAB AC =． ………… 4分 ∴26212AC =⨯=． ∵0AC >，∴AC = ………………………… 5分21．（1）如图1所示． ………………………… 2分 （2）如图1所示． ………………………… 4分 （3）如图2所示（未全画出；画出一个三角形即可）． ………………………… 5分22．（1）证明：∵AD BC ∥，90ABC ∠=°，∴90BAD ∠=°． ……… 1分 ∵DB DC =，E 是BC 的中点， ∴90DEB ∠=°．∴四边形ABED 是矩形． ……… 2分 （2）解： ∵90ABC ∠=°，130∠=°， ∴260∠=°． ∵DB DC =，∴DBC △是等边三角形． ………………………… 3分 ∴2BD BC DC ===． ∵Rt BAD △中，130∠=°，∴1AD =，AB =． ………………………… 4分1DCBA 图1 图221EDCBA24∴在Rt ABC △中，AC =． ………………… 5分23．解：（1）设直线1l 的表达式为(0)y kx b k =+≠.∵直线2l ：1y x =+过点(,2)B m ，∴1m =． ∵直线1l 过点(0,4)A 和点(1,2)B ， ∴4, 2.b k b =+=⎧⎨⎩ 解得2,4.k b =-=⎧⎨⎩∴直线1l 的表达式为24y x =-+． …… （2）1n <． …… 5分24．（1）10；0.28． ………………………… 2分 （2）6.15． ………………………… 3分 （3）A ； ………………………… 5分 A ． ………………………… 6分 （4）2.1． ………………………… 7分25．解：（1）设当行李的质量超过规定时，y 与x 之间的函数表达式为(0)y kx b k =+≠. 由图象可知，当30x =时，2y =；当60x =时，8y =，∴302,608.k b k b +=+=⎧⎨⎩ 解得1,54.k b ==-⎧⎪⎨⎪⎩ (2)分∴当行李的质量超过规定时，y 与x 之间的函数表达式为14(20)5y x x =-≥． ………………………… 3分 （2）令0y =，得1405x -=，解得20x =．∴旅客最多可免费携带20千克的行李． ………………………… 5分26．解：（1）∵点(1,)A m -是直线2y x =-+上一点，∴3m =．∴点A 的坐标为(1,3)-． ………………………… 1分 ∴点(1,3)A -向右平移4个单位长度得到点B 的坐标为(3,3)． …… 2分（2）当直线:2l y kx =-过点(1,3)A -时， 得5k =-． ………………………… 3分当直线:2l y kx =-过点(3,3)B 时， 得53k =． ………… 4分结合函数图象可得b 的取值范围是5k ≤-或53k ≥ ． ………… 6分27．（1）①90． ………… 1分 ②证明：连接PE ，如图1． ∵四边形ABCD 是正方形，∴CB AB =，1245∠=∠=°，3490∠+∠=°． ∵将线段BP 绕点B 顺时针旋转90°得到线段BE ， ∴BE BP =，5490∠+∠=°．∴PE =，53∠=∠．∴CBE △≌ABP △（SAS ）． ………………………… 3分 ∴EC PA =，6145∠=∠=°． ∴2690PCE ∠=∠+∠=°．在Rt PCE △中，由勾股定理，得222EC PC PE +=． ……… 4分 ∵EC PA =，PE =，∴2222PA PC PB +=． ………………………… 5分654321EPDCBA（2）①补全的图形如图2所示． ………………………… 6分 ②4． ………………………… 7分28．（1）①6． ………………………… 1分 ②5或3-． ………………………… 3分 （2）解：过点(1,2)A 作直线1y =-的垂线，垂足为点G ，可得3AG =． ∵点C 在直线1y =-上，点A ，C 的“相关矩形”AGCH 是正方形， ∴正方形AGCH 的边长为3．如图1，当点C 在直线1x =右侧时，3CG =，可得(4,1)C -．∴直线AC 的表达式为3y x =-+． ………………………… 4分 如图2，当点C 在直线1x =左侧时，3CG =，可得(2,1)C --． ∴直线AC 的表达式为1y x =+．综上所述，直线AC 的表达式为3y x =-+或1y x =+． ………… 5分（3）32m --≤≤23m -≤． ………………………… 7分图1 图2。
京改版2018--2019学年度第二学期八年级期末考试数学试卷
绝密★启用前京改版2018--2019学年度第二学期八年级期末考试数学试卷注意事项：1．做卷时间100分钟，满分120分 2．做题要仔细，不要漏做 一、单选题(计30分）1．（本题3分）在▱ABCD 中，对角线AC ，BD 相交于点O ，若△AOB 的面积为3，则▱ABCD 的面积为( )A ．6B ．9C ．12D ．182．（本题3分）如图，点A 的坐标是（1，1），若点B 在x 轴上，且△ABO 是等腰三角形，则点B 的坐标不可能是（ ）A ．（2，0）B ．（21，0） C ．（2，0） D ．（1，0） 3．（本题3分）已知点（-4，1y ），（2，2y ）都在直线12+-=x y 上，则1y ，2y 的大小关系是（ ）A ．21y y >B ．21y y <C ．21y y =D ．不能比较 4．（本题3分）关于的一元二次方程，有一个根是，则A ．B ．C ．或D ．或5．（本题3分）两瓶酒精，甲瓶有升，浓度未知；乙瓶有升，浓度，从甲瓶中倒入乙瓶升酒精，摇匀后倒回一部分给甲瓶，此时甲瓶浓度为，乙瓶浓度为，此时乙瓶中有酒精（ ）升．6．（本题3分）矩形的对角线一定具有的性质是（ ） A ．互相垂直 B ．互相垂直且相等 C ．相等D ．互相垂直平分7．（本题3分）为了了解某校学生的课外阅读情况，随机抽查了10学生周阅读用时数，结果如下表： 小时 学生人数则关于这10名学生周阅读所用时间，下列说法正确的是A ．中位数是B ．众数是12C ．平均数是D ．方差是68．（本题3分）在已知点M （3，﹣4），在x 轴上有一点与M 的距离为5，则该点的坐标为（ ）A ．（6，0）B ．（0，1）C ．（0，﹣8）D ．（6，0）或（0，0） 9．（本题3分）下列四边形中，对角线一定相等的是（ ） A ．菱形B ．矩形C ．平行四边形D ．梯形10．（本题3分）若等腰三角形的两边分别是一元二次方程x 2﹣7x +12＝0的两根，则等腰三角形的周长为（ ）A ．10B ．11C ．10或11D ．以上都不对 二、填空题（计30分）11．（本题4分）一组数据，，，，的极差是，那么的值是 . 12．（本题4分）一次函数b kx y +=的图象经过点（0，2），且与直线x y 21=平行，则该一次函数的关系式为 ．13．（本题4分）如图，直线AB 对应的函数解析式是________．14．（本题4分）如图，□ABCD 的对角线AC 、BD 交于点O ，点E 是AD 的中点，△BCD 的周长为18，则△DEO 的周长是_______．15．（本题4分）已知关于x 的函数y=（m ﹣5） +1是一次函数，则m=________.16．（本题4分）一次数学测试后，某班50名学生的成绩被分为5组，第1～4组的频数分别为12、10、6、8，则第5组的频率是_____________．17．（本题4分）一次函数y=－4x+12的图象与x 轴交点坐标是_________，与y 轴交点坐标是_______，图象与坐标轴所围成的三角形面积是 ________．18．（本题4分）如图，在△ABC 中，点D 、E 、F 分别是边AB 、BC 、CA 上的中点，且AB=6cm ，AC=8cm ，则四边形ADEF 的周长等于 cm ．三、解答题（计58分）19．（本题7分）解下列方程：(1)(2x －1)2＝9； (2)x 2＋3x －4＝0.20．（本题7分）一元一次方程的应用:某商场开展优惠促销活动，将甲种商品六折岀售，乙种商品八折出售.已知甲、乙两种商品的原销售单价之和为1400元,某顾客参加活动购买甲、乙各一件,共付1000元。
201807石景山区八下数学期末考试参考评分标准
……………………1 分 ………………………2 分
O
12
B
FC
图 24-1
a．连接 BD 交 EF 于点O ． b．在 Rt△ DFC 中，设 FC x ，则 FD 4 x ，由勾股定理，求得 FD 长；
c．Rt△ BDC 中，勾股可得 BD 5 ，由点 B 与点 D 的对称性可得OD 的长；
1. m
…………………… 4 分
∵方程有两个整数根且 m 是整数，
∴ m 1或 m 1．
…………………… 5 分
初二数பைடு நூலகம்试卷答案及评分参考
第 2 页（共 5 页）
21．解：（1）① AD∥ BE 或 AD BE ； ┈┈┈┈┈┈┈┈┈1 分
② B DEF ；(答案不唯一)
┈┈┈2 分
G
AE3
D
c．可证 DE DF BF 或△ DFC ≌△ DEG ，可证 CF GE AE BH ，可得 FH 的长；
d．在 Rt△ EHF 中，勾股可求 EF 的长．…………6 分
BH
12 FC
25．解：（1）0.05，14，0.30． ………3 分
（2）如右图所示：
………4 分
………………………2 分
（2）设线段 AB 对应的函数表达式为 y kx b(k 0) ．
∵ A 0.5,8 ， B 2.5,24 ，
0.5k b 8 ∴ 2.5k b 24
…………………3 分
k 8 解得： b 4 ．
……………………5 分
2
∴x
64 2
2
⋯⋯⋯⋯⋯4 分
∴
3 2 2 ⋯⋯5 分
x 32 2 ，x
石景山区初二数学期末试卷
1. 下列各数中，是负数的是（）A. -5B. 0C. 5D. -3.52. 下列各数中，有理数是（）A. √16B. √-9C. πD. 2/33. 已知 a > b，则下列不等式中正确的是（）A. a + b > b + aB. a - b < b - aC. ab > baD. a/b < b/a4. 下列代数式中，同类项是（）A. 3x^2yB. 5xy^2C. 2x^2yD. 4x^25. 下列函数中，是二次函数的是（）A. y = 2x + 3B. y = x^2 + 2x + 1C. y = 3x^3 + 4x^2 + 5D. y = 2/x6. 下列图形中，是轴对称图形的是（）A. 矩形B. 正方形C. 三角形D. 梯形7. 已知一个长方形的长是8cm，宽是5cm，那么它的周长是（）A. 20cmB. 22cmC. 24cmD. 26cm8. 下列各数中，能被3整除的是（）A. 123B. 124C. 125D. 1269. 下列各数中，能被4整除的是（）A. 14B. 15C. 16D. 1710. 下列各数中，能被5整除的是（）A. 20B. 21C. 22D. 2311. 若 a = 2，b = -3，则 a + b 的值为 _______。
12. 已知 a^2 = 25，则 a 的值为 _______。
13. 下列函数中，自变量的取值范围是 _______。
14. 下列各数中，绝对值最大的是 _______。
15. 下列图形中，面积最大的是 _______。
三、解答题（共45分）16. （15分）解下列方程：(1) 3x - 5 = 14(2) 2(x + 3) = 4x - 817. （15分）已知长方形的长是6cm，宽是4cm，求它的对角线长度。
18. （15分）已知一次函数 y = kx + b 的图象经过点 (2, 5) 和 (3, 4)，求该函数的解析式。
2018年-2019年北京初二数学试卷下学期期末汇编：数与式及答案
2018-2019北京初二数学下学期期末汇编：数与式一．选择题（共4小题）1．（2018春•西城区期末）使二次根式有意义的x的取值范围是（）A．x＜3B．x≥3C．x≥0D．x≠32．（2018春•北京期末）下列各式中，运算正确的是（）A．a2+a2＝2a4B．a3﹣a2＝a C．a6÷a2＝a3D．（a2）3＝a63．（2018春•北京期末）点A，B，C，D在数轴上的位置如图所示，则实数﹣2对应的点可能是（）A．点A B．点B C．点C D．点D4．（2018春•北京期末）的相反数是（）A．B．﹣C．±D．二．填空题（共6小题）5．（2018春•朝阳区期末）如图，在数轴上点A表示的实数是．6．（2018春•西城区期末）计算：3﹣×＝．7．（2019春•朝阳区期末）如图，在数轴上点A表示的实数是．8．（2019春•怀柔区期末）如图，正方形ABCD和正方形BEFG的边长分别为1和3，点C在边BG上，连接DE，DG，EG，则△DEG的面积为．9．（2019春•海淀区校级期末）（tan73°）2019×（﹣2tan17°）2019+（）﹣1＝．10．（2019春•朝阳区期末）已知每购进100克巧克力糖的成本为4.8元．某超市开展促销活动，对巧克力糖采用两种包装进行销售，其包装费、销售价格如下表所示：对于该超市而言，卖相同重量的巧克力糖，盈利更多的是．（填“精致装”或豪华装”）三．解答题（共9小题）11．（2018春•海淀区期末）已知x＝2﹣，y＝2+，求：x2+xy+y2的值．12．（2018春•海淀区期末）计算：（﹣）×．13．（2018春•房山区期末）计算：﹣（π﹣1）0+|﹣1|+（﹣）﹣214．（2018春•朝阳区期末）已知a＝+1，求代数式a2﹣2a+7的值．15．（2018春•北京期末）已知x＝，y＝，求代数式（3xy2﹣2xy）÷xy+（2x）2+3的值．16．（2018春•北京期末）阅读下列材料并解答问题：数学中有很多恒等式可以用图形的面积来得到．例如，图1中阴影部分的面积可表示为a2﹣b2；若将阴影部分剪下来，重新拼成一个矩形（如图2），它的长，宽分别是a+b，a﹣b，由图1，图2中阴影部分的面积相等，可得恒等式（a+b）（a﹣b）＝a2﹣b2．（1）观察图3，根据图形，写出一个代数恒等式：；（2）现有若干块长方形和正方形硬纸片如图4所示．请你仿照图3，用拼图的方法推出恒等式（a+b）2＝a2+2ab+b2，画出你的拼图并标出相关数据；（3）利用前面推出的恒等式（a+b）（a﹣b）＝a2﹣b2和（a+b）2＝a2+2ab+b2计算：①（）（）；②（x+2）2．17．（2018春•北京期末）计算：|1﹣|﹣+．18．（2019春•怀柔区期末）已知a2+4a+2＝0．求代数式a（a+8）﹣（a+3）（a﹣3）+（a﹣2）2的值．19．（2019春•西城区期末）计算﹣÷2018-2019北京初二数学下学期期末汇编：数与式参考答案与试题解析一．选择题（共4小题）1．（2018春•西城区期末）使二次根式有意义的x的取值范围是（）A．x＜3B．x≥3C．x≥0D．x≠3【分析】直接利用二次根式有意义的条件进而分析得出答案．【解答】解：二次根式有意义的x的取值范围是：x≥3．故选：B．【点评】此题主要考查了二次根式有意义的条件，正确把握定义是解题关键．2．（2018春•北京期末）下列各式中，运算正确的是（）A．a2+a2＝2a4B．a3﹣a2＝a C．a6÷a2＝a3D．（a2）3＝a6【分析】根据合并同类项法则、同底数幂的除法、幂的乘方逐一计算可得．【解答】解：A、a2+a2＝2a2，错误；B、a3、a2不是同类项，不能合并，错误；C、a6÷a2＝a4，错误；D、（a2）3＝a6，正确；故选：D．【点评】本题主要考查幂的运算，解题的关键是掌握合并同类项法则、同底数幂的除法、幂的乘方的运算法则．3．（2018春•北京期末）点A，B，C，D在数轴上的位置如图所示，则实数﹣2对应的点可能是（）A．点A B．点B C．点C D．点D【分析】根据被开方数越大算术平方根越大，可得，根据数的大小，可得答案．【解答】解：∵2＜＜3，0＜﹣2＜1，∴实数﹣2对应的点可能是B点，故选：B．【点评】本题考查了实数与数轴，利用被开方数越大算术平方根越大得出2＜＜3是解题关键．4．（2018春•北京期末）的相反数是（）A．B．﹣C．±D．【分析】根据相反数的意义，可得答案．【解答】解：的相反数是﹣，故选：B．【点评】本题考查了实数的性质，在一个数的前面加上负号就是这个数的相反数．二．填空题（共6小题）5．（2018春•朝阳区期末）如图，在数轴上点A表示的实数是﹣．【分析】根据勾股定理，可得圆的半径，根据圆的性质，可得答案．【解答】解：如图，由勾股定理，得OB＝＝＝，由圆的性质，得OA＝OB＝，∴点A表示的实数是﹣，故答案为：﹣．【点评】本题考查了实数与数轴，利用勾股定理得出OB的长是解题关键．6．（2018春•西城区期末）计算：3﹣×＝．【分析】先进行二次根式的乘法运算，然后化简后合并即可．【解答】解：原式＝3﹣＝3﹣2＝．故答案为．【点评】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．7．（2019春•朝阳区期末）如图，在数轴上点A表示的实数是．【分析】根据勾股定理，可得斜线的长，根据圆的性质，可得答案．【解答】解：由勾股定理，得斜线的长为＝，由圆的性质，得点A表示的数为，故答案为：．【点评】本题考查了实数与数轴，利用勾股定理得出斜线的长是解题关键．8．（2019春•怀柔区期末）如图，正方形ABCD和正方形BEFG的边长分别为1和3，点C在边BG上，连接DE，DG，EG，则△DEG的面积为．【分析】根据题意列出算式，计算即可求出值．【解答】解：根据题意得：12+32+×1×（3﹣1）﹣×1×（1+3）﹣×32＝1+9+1﹣2﹣＝，故答案为：【点评】此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．9．（2019春•海淀区校级期末）（tan73°）2019×（﹣2tan17°）2019+（）﹣1＝1．【分析】根据互余的两个锐角的正切的乘积等于1以及负整数指数幂的公式计算即可．【解答】解：（73°）2019×（﹣2tan17°）2019+（）﹣1＝＝（﹣1）2019+2＝﹣1+2＝1．故答案为：1【点评】此题主要考查了实数运算，正确化简各数是解题关键．10．（2019春•朝阳区期末）已知每购进100克巧克力糖的成本为4.8元．某超市开展促销活动，对巧克力糖采用两种包装进行销售，其包装费、销售价格如下表所示：对于该超市而言，卖相同重量的巧克力糖，盈利更多的是精致装．（填“精致装”或豪华装”）【分析】根据“利润＝售价﹣成本价”，分别得出两种包装卖出500克巧克力糖的利润，再比较即可．【解答】解：精致装卖出500克巧克力糖的利润为：5×（8﹣0.8﹣4.8）＝12（元）；豪华装卖出500克巧克力糖的利润为：36﹣4.8×5﹣1.5＝10.5（元）．∵12＞10.5，∴对于该超市而言，卖相同重量的巧克力糖，盈利更多的是精致装．故答案为：精致装．【点评】本题考查了利润，成本，售价的关系．读懂题目信息，从表格中获取有关信息是解题的关键．三．解答题（共9小题）11．（2018春•海淀区期末）已知x＝2﹣，y＝2+，求：x2+xy+y2的值．【分析】将x2+xy+y2变形为x2+2xy+y2﹣xy，得到原式＝（x+y）2﹣xy，再把x＝2﹣，y＝2+代入计算即可求解．【解答】解：∵x＝2﹣，y＝2+，∴x2+xy+y2＝x2+2xy+y2﹣xy＝（x+y）2﹣xy＝（2﹣+2+）2﹣（2﹣）（2+）＝16﹣4+3＝15．【点评】考查了分母有理化，熟练掌握平方差公式是解答问题的关键．12．（2018春•海淀区期末）计算：（﹣）×．【分析】利用二次根式的乘法法则运算．【解答】解：原式＝﹣＝2﹣1＝1．【点评】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．13．（2018春•房山区期末）计算：﹣（π﹣1）0+|﹣1|+（﹣）﹣2【分析】原式利用二次根式性质，零指数幂、负整数指数幂法则，以及绝对值的代数意义计算即可求出值．【解答】解：原式＝2﹣1+﹣1+4＝3+2．【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．14．（2018春•朝阳区期末）已知a＝+1，求代数式a2﹣2a+7的值．【分析】将a的值代入a2﹣2a+7＝（a﹣1）2+6计算可得．【解答】解：a2﹣2a+7＝（a﹣1）2+6，当时，原式＝（+1﹣1）2+6＝5+6＝11．【点评】本题主要考查二次根式的化简求值，解题的关键是掌握二次根式的混合运算顺序和运算法则及完全平方公式．15．（2018春•北京期末）已知x＝，y＝，求代数式（3xy2﹣2xy）÷xy+（2x）2+3的值．【分析】根据多项式除以单项式和积的乘方可以化简题目中的式子，然后将x、y的值代入化简后的式子即可解答本题．【解答】解：（3xy2﹣2xy）÷xy+（2x）2+3＝3y﹣2+4x2+3＝4x2+3y+1．当x＝，y＝时，原式＝＝22．【点评】本题考查整式的混合运算﹣化简求值，解答本题的关键是明确整式化简求值的方法．16．（2018春•北京期末）阅读下列材料并解答问题：数学中有很多恒等式可以用图形的面积来得到．例如，图1中阴影部分的面积可表示为a2﹣b2；若将阴影部分剪下来，重新拼成一个矩形（如图2），它的长，宽分别是a+b，a﹣b，由图1，图2中阴影部分的面积相等，可得恒等式（a+b）（a﹣b）＝a2﹣b2．（1）观察图3，根据图形，写出一个代数恒等式：（a+b）（2a+b）＝2a2+3ab+b2；（2）现有若干块长方形和正方形硬纸片如图4所示．请你仿照图3，用拼图的方法推出恒等式（a+b）2＝a2+2ab+b2，画出你的拼图并标出相关数据；（3）利用前面推出的恒等式（a+b）（a﹣b）＝a2﹣b2和（a+b）2＝a2+2ab+b2计算：①（）（）；②（x+2）2．【分析】（1）根据面积的两种表达方式得到图3所表示的代数恒等式；（2）作边长为a+b的正方形即可得；（3）套用所得公式计算可得．【解答】解：（1）由图3知，等式为：（a+b）（2a+b）＝2a2+3ab+b2，故答案为：（a+b）（2a+b）＝2a2+3ab+b2；（2）如图所示：由图可得（a+b）2＝a2+2ab+b2；（3）①原式＝（）2﹣（）2＝3﹣2＝1；②（x+2）2＝x2+2×x×2+22＝x2+4x+4．【点评】本题考查了完全平方公式的几何背景，根据矩形的面积公式分整体与部分两种思路表示出面积，然后再根据同一个图形的面积相等即可解答．17．（2018春•北京期末）计算：|1﹣|﹣+．【分析】直接利用立方根以及算术平方根的定义化简进而得出答案．【解答】解：原式＝﹣1﹣3﹣2＝﹣6．【点评】此题主要考查了实数运算，正确化简各数是解题关键．18．（2019春•怀柔区期末）已知a2+4a+2＝0．求代数式a（a+8）﹣（a+3）（a﹣3）+（a﹣2）2的值．【分析】先算乘法，再合并同类项，最后代入求出即可．【解答】解：a（a+8）﹣（a+3）（a﹣3）+（a﹣2）2＝a2+8a﹣a2+9+a2﹣4a+4＝a2+4a+13，∵a2+4a+2＝0，∴a2+4a＝﹣2，∴原式＝﹣2+13＝11．【点评】本题考查了整式的混合运算和求值，能正确根据整式的运算法则进行化简是解此题的关键．19．（2019春•西城区期末）计算﹣÷【分析】直接利用二次根式的混合运算法则分别化简得出答案．【解答】解：原式＝2﹣＝．【点评】此题主要考查了二次根式的混合运算，正确掌握运算法则是解题关键．11 / 11。
北京石景山区18-19学度初二下年末试卷-数学
北京石景山区18-19学度初二下年末试卷-数学初二数学【一】选择题〔此题共24分，每题3分〕在每个小题给出的四个备选答案中，只有一个是正确的,请将所选答案前的字母填写在各小题后的括号内、1、在平面直角坐标系中，点P (2，-3)关于x 轴对称的点的坐标是〔〕 A.(-2，-3)B.(2，3) C.(-2，3)D.(2，-3)2、一次函数y x b =+的图像经过【一】【二】三象限，那么b 的值可以是〔〕 A.-2B.-1C.0D.23.顺次连结任意四边形各边中点所得到的四边形一定是〔〕A.平行四边形B.菱形C.矩形D.正方形4.下面每个选项中给出了某个变化过程中的两个变量x 和y ， 其中y 不是．．x 的函数的选项是〔〕A 、y ：正方形的面积，x ：这个正方形的周长B 、y ：某班学生的身高，x ：这个班学生的学号C 、y ：圆的面积，x ：这个圆的直径D 、y ：一个正数的平方根，x ：这个正数5、1x =是方程220x bx +-=的一个根，那么方程的另一个根是〔〕A.1B.2C.-2D.-16.关于x 的方程2210x kx k ++-=的根的情况描述正确的选项是〔〕A.k 为任何实数，方程都没有实数根B.k 为任何实数，方程都有两个不相等的实数根C.k 为任何实数，方程都有两个相等的实数根D.根据k 的取值不同，方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种7、如图，在周长为20cm 的□ABCD 中，AB ≠AD ，AC 、BD 相交于点O ，OE ⊥BD 交AD 于E ，那么△ABE 的周长为〔〕 A 、4cmB 、6cmC 、8cmD 、10cm 8、四边形ABCD 为矩形纸片、把纸片ABCD 折叠，使点B 恰A 、34B 、33C 、24D 、８【二】填空题〔此题共15分，每题3分〕 9、请写出一个两根异号的一元二次方程、10、截止至2018年6月4日，今年110米栏世界前10个最好成绩〔单位：秒〕如下： 这组数据的极差是____________、11、如果一个多边形的每个内角都相等，它的一个外角等于一个内角的三分之二，这个正多边形的边数是__________、 12、将一张等腰直角三角形纸片沿中位线剪开可以拼成不同形状的四边形，请写出其中一种四边形的名称 、第12题图第13题图 13、一次函数1y kx b =+与2y x a =+的图象如图，有以下结12y y <，其中所论：①0k <；②0a >；③当3x <时，有正确结论的序号是________________、【三】解答题〔本大题共5个小题，每题5分，共25分〕14、解方程：2450x x +-=解：15、解方程：273(7)0x x x ---=（） 解：16、要在一个8cm ⨯12cm 相片外侧的四周镶上宽度相同的银边，并且要使银边的面积和相片的面积相等，那么银边的宽度应该是多少？ 解：17、一个一次函数的图像经过点3,7-（），且和坐标轴相交，当与坐标轴围成的直角三角形的两腰相等时，求这个一次函数的解析式、 解：18、看图说故事、如图，设计一个问题情境，使情境中出现的一对变量满足图示的函数关系、结合图象，说出这对变量的变化过程的实际意义、 解：【四】解答题〔本大题共6个小题，每题6分，共36分〕 19、如图，在等腰梯形ABCD 中，AD ∥BC ，AD =2，BC =4，高解：20、在△ABC 中，点O 是AC 边上的一个动点，过点O 作直线分线于点E ，交∠BCA 的外角平分线于点F 、〔1〕求证：EO =FO ；〔2〕当点O 运动到何处时，四边形AECF 是矩形？ 并证明你的结论、 证明：21、甲和乙上山游玩，甲乘坐缆车，乙步行，两人相约在山顶的缆车终点会合、乙行走到缆车终点的路程是缆车到山顶的线路长的2倍，甲在乙出发后50min 才乘上缆车，缆车的平均速度为180m/min 、设乙出发x min 后行走的路程为y m 、图中的折线表示乙在整个ab +B C EF M N O AD行走过程中y 与x 的函数关系、 〔1〕乙行走的总路程是___________m ，他途中休息了________min 、 函数关系〔2〕①当50≤x ≤80时，求y 与x 的式；②当甲到达缆车终点时，乙离缆车终点的路程 是多少？22、阅读材料：如果1x ，2x 是一元二次方程20a x b x c ++=的两根，那么有1212,bcx x x x aa+=-=. 这是一元二次方程根与系数的关系，我们利用它可以用来解题，例12,x x 是方程2630x x +-=的两根，求2212x x +的值.解法可以这样：126x x +=-，123x x =-，那么222212112()2x x x x x x +=+-=2(6)2(3)42--⨯-=. 请你根据以上解法解答下题：12,x x 是方程2420x x -+=的两根，求： 〔1〕1211x x +的值；〔2〕212()x x -的值. 解：23、为了进一步了解八年级学生的身体素质情况，体育老师对八年级〔1〕班50位学生进行一分钟跳绳次数测试，以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图、如下所示：〔1〕表中的a =；〔2〕请把频数分布直方图补充完整； 〔3〕这个样本数据的中位数落在第组；〔4〕假设八年级学生一分钟跳绳次数〔x 〕达标要求是：120x <不合格；120140x ≤<为合格；140160x ≤<为良；160x ≥为优、假设该年级共有400名学生，请根据以上信息，估算该年级跳绳达到优的人数、24、将一张直角三角形纸片ABC 折叠，使点A 与点C 重合，这时DE 为折痕，△CBE 为等腰三角形；再继续将纸片沿△CBE 的对称轴EF 折叠，这时得到了两个完全重合的矩形〔其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形〕，我们称这样两个矩形为“叠加矩形”、请完成以下问题：9跳绳次数305019503600 80 x/min y/m O〔1〕如图②，正方形网格中的△ABC 能折叠成“叠加矩形”吗？如果能，请在图②中画出折痕；〔2〕如图③，在正方形网格中，以给定的BC 为一边，画出一个斜△ABC ，使其顶点A 格点上，且△ABC 折成的“叠加矩形”为正方形；〔3〕如果一个三角形所折成的“叠加矩形”为正方形，那么它必须满足的条件是、石景山区2017—2017学年度第二学期期末考试初二数学参考答案【一】选择题〔此题共8个小题，每题3分，共24分〕1 2 3 4 5 6 7 8 BD A D C B D A【二】填空题〔此题共5个小题，每题3分，共15分〕9、21x =〔答案不唯一〕10、0.2611、512、平行四边形、矩形、等腰梯形〔三种中任选一种均给总分值〕13、①〔多项选择不得分〕【三】解答题〔此题共25分，每题5分〕 14.解：〔其它解法酌情给分〕2(2)9x +=………………………………2分 23x +=±…………………………………3分 ∴11x =；25x =-…………………………5分15.解：(7)(73)0x x x --+=…………………………………………2分(7)(47)0x x --=…………………………………………4分∴17x =，274x =……………………………………5分16、解：设银边的宽度为x cm ，由题意列方程(122)(82)2812x x ++=⨯⨯……………………2分210240x x +-=解之122,12x x ==-…………………………………4分 其中212x =-不符合题意，舍去，所以2x = 答：银边的宽度为2cm …………………………5分17、解：设一次函数解析式为y kx b =+，由题意0b ≠…………………1分图象与两轴交点分别为(,0),(0)b b k -，bb k-=，解得1k =±………………………………3分把点3,7-（）代入解析式，当1k =时10b =；当1k =-时4b =……4分 所以，函数解析式为10y x =+或4y x =-+…………………5分18、学生可以设计多种情境、比如，把这个图看成“小王骑车的s-t 图”：小王以400米/分钟的速度匀速骑了5分钟，在原地休息了6分钟，然后以500米/分钟的速度匀速骑回出发地、………………………………………5分 【四】计算与证明题〔此题共36分，每题6分〕19、解：过D 作DE ∥AB 交BC 于点E ，那么四边形ABED 是平行四边形、…………1分DE=AB=DC ，BE=AD.在等腰三角形DEC 中，………………………………………2分 EC=BC-BE=BC-AD=4-2=2，CF=12EC=1，……………………4分DC ∴=………………………………6分 20.证明：CE 是BAC ∠的平分线,OCE ECB ∴∠=∠//,,MN BC OEC BCE ∴∠=∠ ,OEC OCE OE OC ∴∠=∠∴=同理可证OF OC =,OF OE ∴=………………………………3分当O 为中点时，四边形AECF 是矩形、………………………………4分 由OF OE OA OC ==，可知四边形AECF 是平行四边形、 由CE 、CF 分别为∠BCA 的内外角平分线可知∠ECF 为直角， 所以四边形AECF 是矩形、……………………………………6分 21、解：⑴3600，20、……………………………………2分 ⑵①当5080x ≤≤时，设y 与x 的函数关系式为y kx b =+、 根据题意，当50x =时，1950y =；当80x =，3600y =、所以，y 与x 的函数关系式为55800y x =-……………………………4分 ②缆车到山顶的路线长为3600÷2=1800〔m 〕， 缆车到达终点所需时间为1800÷180＝10〔min 〕、 甲到达缆车终点时，乙行走的时间为10＋50＝60〔min 〕、 把60x =代入55800y x =-，得y=55×60—800=2500、所以，当甲到达缆车终点时，乙离缆车终点的路程是3600-2500=1100〔m 〕、……………………………6分 22、解：由，121242x x x x +==，………………………………2分 〔1〕121212114 2.2x x x x x x ++===………………………………………4分〔2〕222121212()()44428.x x x x x x -=+-=-⨯=………………………………………6分23、解：〔1〕a 12；……………1分〔2〕画图答案如下图：……………2分〔3〕中位数落在第3组；……………4分〔4〕48、……………6分24、解：〔1〕………………………………………………2分〕〔2〕……………………………………4分答案不惟一，所画三角形的一边长与该〕〔3〕三角形的一边长与该边上的高相等………………………………………6分。
北京市石景山区八年级下期末数学试题有答案
C B A石景山区第二学期初二期末试卷 数 学学校 姓名 准考证号 考 生 须 知 1．本试卷共6页，共三道大题，26道小题．满分100分，考试时间100分钟．2．在试卷和答题卡上准确填写学校名称、姓名和考号．3．试卷答案一律填涂或书写在答题卡上，在试卷上作答无效．在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答．4．考试结束，将本试卷和答题卡一并交回．下面各题均有四个选项，其中只有一个．．是符合题意的． 1．在平面直角坐标系xOy 中，点P （-3,5）关于y 轴对称的点的坐标是（ ）A ．（-3,-5）B ．（3,-5）C ．（3,5）D ．（5,-3）2．下列图形中，既是中心对称图形又是轴对称图形的是（ ）3．一个多边形的内角和为540°，则这个多边形的边数是（ ）A ．4B ．5C ．6D ．74．菱形ABCD 的边长为4，有一个内角为120°，则较长的对角线的长为（ ）A ．43B ．4C ．23D ．25．如图，利用平面直角坐标系画出的正方形网格中，若A （0,2），B （1,1），则点C 的坐标为（ ）A ．（1,-2）C ．（2,1）B ．（1,-1） D ．（2,-1）6．如图，D ，E 为△ABC 的边AB ，AC 上的点，DE ∥BC ， A ． B ． C ． D ．若:1:3AD DB =，AE =2，则AC 的长是（ ）A ．10C ．6 B ．8D ．47．关于x 的一元二次方程2210mxx -+=有两个实数根，则m 的取值范围是（ ） A ．1m ≤C ．1m <且0m ≠ B ．1m <D ．1m ≤且0m ≠8．如图，将边长为3cm 的等边△ABC 沿着边BC 向右平移2cm ，得到△DEF ，则四边形ABFD 的周长为（ ）A ．15cmB ．14cmC ．13cmD ．12cm 9．园林队在某公园进行绿化，中间休息了一段时间．绿化面积S （单位：平方米）与工作时间t （单位：小时）的函数关系的图象如图所示，则休息后园林队每小时绿化面积为（ ）A ．40平方米B ．50平方米C ．80平方米D ．100平方米10．如右图，矩形ABCD 中，AB =2，BC =4，P 为矩形边上的一个动点，运动路线是A →B →C →D →A ，设P 点经过的路程为x ，以A ，P ，B 为顶点的三角形面积为y ，则下列图象能大致反映y 与x 的函数关系的是（ ）二、填空题（本题共18分，每小题3分）第13题图 第14题图第15题图11．如图，点D ，E 分别为△ABC 的边AB ，BC 的中点，若DE =3cm ，则AC = cm.12．已知一次函数2()y m x m =++，若y 随x 的增大而增大，则m 的取值范围是 ．13．如图，在△ABC 中，D 是AB 边上的一点，连接CD ，请添加一个适当的条件 ，使△ACD ∽△ABC （只填一个即可）．14．如图，在□ABCD 中，BC =5，AB =3，BE 平分∠ABC 交AD 于点E ，交对角线AC 于点F ，则AEFCBF S S △△= ．15．如图，矩形ABCD 中，AB =8，AD =10，点E 为DC 边上的一点，将△ADE 沿直线AE 折叠，点D 刚好落在 BC 边上的点F 处，则CE 的长是 . 16．如图，在平面直角坐标系xOy 中，一次函数y =x +1与x 、y 轴分别交于点A 、B ，在直线 AB 上截取BB 1=AB ，过点B 1分别作x 、y 轴的垂线，垂足分别为点A 1、C 1， 得到矩形OA 1B 1C 1； 在直线 AB 上截取B 1B 2= BB 1，过点B 2分别 作x 、y 轴的垂线，垂足分别为点A 2 、C 2，得到矩形OA 2B 2C 2；在直线AB 上截取B 2B 3= B 1B 2，过点B 3分别x+1EF CB作x 、y 轴的垂线，垂足分别为点A 3、C 3，得到矩形OA 3B 3C 3；……；则点B 1的坐标是 ；第3个矩形OA 3B 3C 3的面积是 ；第n 个矩形OA n B n C n 的面积是 （用含n 的式子表示，n 是正整数）．三、解答题（本题共52分，第17-24题，每小题5分；第25-26题，每小题6分）解答应写出文字说明，演算步骤或证明过程.17．用适当的方法解方程：2610x x --=．18．如图，在□ABCD 中，E ，F 是对角线BD 上的两点且BE =DF ，联结AE ，CF ． 求证：AE =CF ．19．一次函数1y kx b =+的图象与正比例函数2y mx =交于点A （-1，2），与y 轴交于点B （0，3）．（1）求这两个函数的表达式；（2）求这两个函数图象与x 轴所围成的三角形的面积．20．如图，在矩形ABCD 中，E 为AD 边上的一点， 过C 点作CF ⊥CE 交AB 的延长线于点F ．（1）求证：△CDE ∽△CBF ； （2）若B 为AF 的中点，CB =3，DE =1，求CD 的长.21．已知关于x 的一元二次方程2(32)60mx m x -++=(0)m ≠．（1）求证：方程总有两个实数根；（2）若方程的两个实数根都是整数，求正整数m 的值.22．如图，Rt △ABC 中，90ACB ∠=︒，CD 是斜边AB上的中线，分别过点A ，C 作AE ∥DC ，CE ∥AB ，两线交于点E ．（1）求证：四边形AECD 是菱形；（2）若602B BC ∠=︒=，，求四边形AECD 的面积．23．列方程解应用题：某地区2013年的快递业务量为2亿件，受益于经济的快速增长及电子商务发展等多重因素，快递业务迅猛发展，2015年的快递业务量达到3.92亿件.求该地区这两年快递业务量的年平均增长率.24．某市为了鼓励居民节约用电，采用分段计费的方法按月计算每户家庭的电费，分两档收费：第一档是当月用电量不超过240度时实行“基础电价”；第二档是当用电量超过240度时，其中的240度仍按照“基础电价”计费，超过的部分按照 “提高电价”收费.设每个家庭月用电量为x 度时，应交电费为y 元.具体收费情况如折线图所示，请根据图象回答下列问题：（1）“基础电价”是_________元/度；（2）求出当x ＞240时，y 与x 的函数表达式；（3）小石家六月份缴纳电费132元，求小石家这个月用电量为多少度？25．已知正方形ABCD 中，点M 是边CB （或CB 的延长线）上任意一点，(元)(度)AN平分∠MAD，交射线DC于点N.（1）如图1，若点M在线段CB上①依题意补全图1；②用等式表示线段AM，BM，DN之间的数量关系，并证明；（2）如图2，若点M在线段CB的延长线上，请直接写出线段AM，BM，DN之间的数26别作A的周长与面积相等，则点H （3,6）是“和谐点”.（1）H 1（1,2）, H 2（4,-4）, H 3（-2,5）这三个点中的“和谐点”为 ；（2）点C (-1,4)与点P （m ，n ）都在直线y x b =-+上，且点P 是“和谐点”. 若m ＞0，求点P 的坐标．——————————————草 稿 纸——————————————初二数学 试卷答案及评分参考阅卷须知：为便于阅卷，解答题中的推导步骤写得较为详细，阅卷时，只要考生将主要过程正确写出即可．若考生的解法与给出的解法不同，正确者可参照评分参考给分．评分参考中所注分数，表示考生正确做到此步应得的累加分数．一、 选择题（本题共30分，每小题3分）11．6 12．2m >- 13．ACD B ∠=∠（或ADC ACB ∠=∠或AD AC AC AB=） 14．925 15．3 16．（1，2）；12(1)n n +；或2n n +（每空1分） 三、解答题（本题共52分，第17-24题，每小题5分；第25-26题，每小题6分）解法二： 2=-△(6)640±18．证明一：联结AF ，CE ，联结AC 交BD 于点O.∵四边形ABCD 是平行四边形 ∴OA ＝OC ，OB ＝OD ⋯⋯⋯⋯⋯2分 又∵BE ＝DF ∴OE ＝OF ⋯⋯⋯⋯⋯3分 ∴四边形AECF 是平行四边形 ⋯⋯4分∴AE ＝CF ⋯⋯⋯⋯⋯5分证明二：∵四边形ABCD 是平行四边形∴AB ＝CD ，AB ∥CD ⋯⋯⋯⋯⋯1分∴∠1＝∠2 ⋯⋯⋯⋯⋯2分在△ABE 和△CDF 中 12 ABCD BE DF =⎧⎪∠=∠⎨⎪=⎩ ∴△ABE ≌△CDF （SAS ） ⋯⋯⋯⋯⋯4分∴AE CF = ⋯⋯⋯⋯⋯5分19．解：（1）∵2y mx =过点A （-1，2）∴-m ＝2 ∴m ＝-2 ⋯⋯⋯⋯⋯1分∵点A （-1，2）和点B （0，3）在直线1y kx b =+上21 33k b k b b -+==⎧⎧∴∴⎨⎨==⎩⎩⋯⋯⋯⋯⋯3分∴这两个函数的表达式为：13y x =+和2-2y x = ⋯⋯⋯⋯⋯3分（2）过点A 作AD ⊥x 轴于点D ，则AD ＝2 ∵13y x =+交x 轴于点C （-3,0） ⋯⋯4分 ∴1=2AOC S OC AD ⨯⨯△1=322⨯⨯=3 ⋯⋯5分即这两个函数图象与x 轴所围成的三角形的面积是3.20．（1）证明：∵四边形ABCD 是矩形 ∴∠D=∠1=∠2+∠3=90° ⋯⋯⋯⋯⋯1分∵CF ⊥CE ∴∠4+∠3=90° ∴∠2=∠4 ∴△CDE ∽△CBF ⋯⋯⋯⋯⋯2分（2） 解：∵四边形ABCD 是矩形 ∴CD =AB ∵B 为AF 的中点 ∴BF =AB ∴设CD=BF= x ⋯⋯⋯3分 ∵△CDE ∽△CBF 21．（1）证明：∵0m ≠ ∴2(32)60mx m x -++=是关于x 的一元二次方程∵2[(32)]46m m =-+-⨯△ ⋯⋯⋯⋯⋯1分2912424m m m =++-29-124m m =+23-20m =()≥ ⋯⋯⋯⋯⋯2分∴此方程总有两个实数根. ⋯⋯⋯⋯⋯3分（2） 解：∵(3)(2)0x mx --= ∴1223,x x m ==⋯⋯⋯⋯⋯4分∵方程的两个实数根都是整数，且m 是正整数∴m =1或 m =2 ⋯⋯⋯⋯⋯5分22．（1）证明：∵AE ∥DC ，CE ∥AB∴四边形AECD 是平行四边形 ⋯⋯⋯⋯⋯1分D∵Rt △ABC 中，90ACB ∠=︒，CD 是斜边AB 上的中线∴CD =AD∴四边形AECD 是菱形 ⋯⋯⋯⋯⋯2分 （2） 解：联结DE .∵90ACB ∠=︒，60B ∠=︒∴30BAC ∠=︒∴4A AB C ==,⋯⋯⋯⋯⋯3分∵四边形AECD 是菱形 ∴EC =AD =DB 又∵EC ∥DB∴四边形ECBD 是平行四边形∴ED = CB =2⋯⋯⋯⋯⋯4分∴2AECD AC ED S ⨯===菱形⋯⋯⋯⋯⋯5分23． 解：设该地区这两年快递业务量的年平均增长率为x . 根据题意，得 ⋯⋯1分 22(1) 3.92x += ⋯⋯⋯⋯⋯3分解得120.4, 2.4x x ==-（不合题意，舍去） ⋯⋯⋯⋯⋯4分∴0.440x ==%答：该地区这两年快递业务量的年平均增长率为40%. ⋯⋯⋯⋯⋯5分24．（1）0.5 ⋯⋯⋯⋯⋯ 1分（2）解：当x ＞240时，设y =kx+b ，由图象可得：2401200.640021624k b k k b b +==⎧⎧∴⎨⎨+==-⎩⎩ ⋯⋯⋯⋯⋯2分∴0.624(240)y x x =-> ⋯⋯⋯⋯⋯3分（3）解：∵132120y =>∴令0.624=132x -， ⋯⋯⋯⋯⋯4分得：=260x ⋯⋯⋯⋯⋯5分∴小石家这个月用电量为260度.25．（1）①补全图形，如右图所示. ⋯⋯⋯⋯⋯1分②数量关系：AM BM DN =+ ⋯⋯⋯⋯⋯2分 证明：在CD 的延长线上截取DE ＝BM ，联结AE .∵四边形ABCD 是正方形∴190B ∠=∠=︒，AD AB =，AB CD ∥ ∴6BAN ∠=∠ 在△ADE 和△ABM 中1 AD AB B DE BM =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△ABM （SAS ）∴AE AM =，32∠=∠ ⋯⋯⋯⋯⋯⋯3分 又∵54∠=∠ ∴EAN BAN ∠=∠ 又∵6BAN ∠=∠ ∴6EAN ∠=∠∴AE NE = ⋯⋯⋯⋯⋯4分 又∵AE AM =，NE DE DN BM DN +=+=∴AM BM DN =+ ⋯⋯⋯⋯⋯5分 （证法二：在CB 的延长线上截取BF ＝DN ，联结AF ） （2）数量关系：AM DN BM =- ⋯⋯⋯⋯⋯6分26．（1）H 2 ⋯⋯⋯⋯⋯1分 （2）解：∵点C (-1,4)在直线y x b =-+上∴14b += ∴3b =∴3y x =-+ ⋯⋯⋯⋯⋯2分 ∴3y x =-+与x 轴，y 轴的交点为N （3， 0），M （0，3） ∵点P （m ，n ）在直线3y x =-+上 ∴点P （m ，-m +3）过点P 分别作x 轴，y 轴的垂线，垂足为D ，E ∵m ＞0∴点P 可能在第一象限或第四象限（解法一） ① 若点P 在第一象限，如图1，则,3OD m PD n m +=== -∴3)6PEOD C m m ++==2(-矩形3)PEOD S m m +=(-矩形∵点P 是“和谐点”∴3)6m m +(-= ⋯⋯⋯3分260m m +-3=2(-3)460=-⨯△＜∴此方程无实根∴第一象限的直线上的点不可能是“和谐点”. ⋯⋯⋯⋯⋯4分② 若点P 在第四象限，如图2，则,3)3OD m PD n m m -=+=-== --( ∴3)46PEOD C m m m +=-=2(-矩形3)PEOD S m m =(-矩形∵点P 是“和谐点”∴3)46m m m -(-= ⋯⋯5分 260m m +-7=1261m m ==，∵点P （m ，-m +3）在第四象限 ∴3m ＞ ∴6m =∴点P （6，-3） ⋯⋯⋯⋯⋯6分综上所述，满足条件的点P 的坐标为P （6，-3）.（解法二）① 若点P 在第一象限，如图1，则,3OD m PD n m +=== - ∴3)6PEOD C m m ++==2(-矩形 ∵133 4.52MON S ⨯⨯==△ ⋯⋯⋯3分 而MONPEOD S S <△矩形m +3)y y 图1∴PEOD PEOD C S 矩形矩形≠∴第一象限的直线上的点不可能是“和谐点”. ⋯⋯⋯⋯⋯4分 ② 若点P 在第四象限，如图2，则,OD m PD n == -∴)PEOD C m n =2(-矩形PEOD S mn =-矩形∵点P 是“和谐点”∴2)m n mn (-=- ⋯⋯⋯⋯⋯5分 ∴22mn m =-∵点P （m ，n ）在直线3y x =-+上 ∴3n m =-+∴232mm m=-+- 260m m +-7=1261m m ==，经检验，1261m m ==，是方程232mm m=-+-的解 ∵点P （m ，-m +3）在第四象限 ∴3m ＞ ∴6m =∴点P （6，-3） ⋯⋯⋯⋯⋯6分 综上所述，满足条件的点P 的坐标为P （6，-3）.m +3)。
北京市石景山区八年级下期末数学试题有答案
石景山区第二学期初二期末试卷数 学学校 姓名 准考证号一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1．在平面直角坐标系xOy 中，点P （-3,5）关于y 轴对称的点的坐标是（ ）A ．（-3,-5）B ．（3,-5）C ．（3,5）D ．（5,-3）2．下列图形中，既是中心对称图形又是轴对称图形的是（ ）3．一个多边形的内角和为540°，则这个多边形的边数是（ ）A ．4B ．5C．6D．74．菱形ABCD 的边长为4，有一个内角为120°，则较长的对角线的长为（ ）A．B ．4C ．D ．25．如图，利用平面直角坐标系画出的正方形网格中， 若A （0,2），B （1,1），则点C 的坐标为（ ） A ．（1,-2） C ．（2,1） B ．（1,-1） D ．（2,-1）6．如图，D ，E 为△ABC 的边AB ，AC 上的点，DE ∥BC ， 若:1:3AD DB ，AE =2，则AC 的长是（ ） A ．10 C ．6 B ．8 D ．4A ．B ．C ．D ．7．关于x 的一元二次方程2210mx x -+=有两个实数根，则m 的取值范围是（ ）A ．1m ≤ C ．1m <且0m ≠B ．1m <D ．1m ≤且0m ≠8．如图，将边长为3cm 的等边△ABC 沿着边BC 向右平移2cm ，得到△DEF ，则四边形ABFD 的周长为（ ）A ．15cmB ．14cmC ．13cmD ．12cm9．园林队在某公园进行绿化，中间休息了一段时间．绿化面积S （单位：平方米）与工作时间t （单位：小时）的函数关系的图象如图所示，则休息后园林队每小时绿化面积为（ ） A ．40平方米B ．50平方米C ．80平方米D ．100平方米10．如右图，矩形ABCD 中，AB =2，BC =4，P 为矩形边上的一个动点，运动路线是A →B →C →D →A ，设P 点 经过的路程为x ，以A ，P ，B 为顶点的三角形面积为y ， 则下列图象能大致反映y 与x 的函数关系的是（ ）二、填空题（本题共18分，每小题3分）11．如图，点D ，E 分别为△ABC 的边AB ，BC 的中点，若DE =3cm ，则AC = cm .12．已知一次函数2()y m x m =++，若y 随x 的增 大而增大，则m 的取值范围是．A. B. C. D.13．如图，在△ABC 中，D 是AB 边上的一点，连接CD ，请添加一个适当的条件 ，使△ACD ∽△ABC （只填一个即可）．14．如中，BC =5，AB =3，BE 平分∠ABC 交AD 于点E ，交对角 线AC 于点F ，则AEFCBF S S △△=．15．如图，矩形ABCD 中，AB =8，AD =10，点E 为DC 边上的一点，将△ADE 沿直线AE 折叠，点D 刚好落在 BC 边上的点F 处，则CE 的长是 .16．如图，在平面直角坐标系xOy 中，一次函数y =x +1与x 、y 轴分别交于点A 、B ， 在直线 AB 上截取BB 1=AB ，过点B 1分别 作x 、y 轴的垂线，垂足分别为点A 1、C 1， 得到矩形OA 1B 1C 1；在直线 AB 上截取B 1B 2= BB 1，过点B 2分别 作x 、y 轴的垂线，垂足分别为点A 2 、C 2， 得到矩形OA 2B 2C 2；在直线AB 上截取B 2B 3= B 1B 2，过点B 3分别 作x 、y 轴的垂线，垂足分别为点A 3、C 3， 得到矩形OA 3B 3C 3；……；则点B 1的坐标是 ；第3个矩形OA 3B 3C 3的面积是 ； 第n 个矩形OA n B n C n 的面积是 （用含n 的式子表示，n 是正整数）．三、解答题（本题共52分，第17-24题，每小题5分；第25-26题，每小题6分）解答应写出文字说明，演算步骤或证明过程. 17．用适当的方法解方程：2610x x --=． x+118．如图，在□ABCD 中，E ，F 是对角线BD上的两点且BE =DF ，联结AE ，CF ． 求证：AE =CF ．19．一次函数1y kx b =+的图象与正比例函数2y mx =交于点A （-1，2），与y 轴交于点B （0，3）． （1）求这两个函数的表达式；（2）求这两个函数图象与x 轴所围成的三角形的面积．20．如图，在矩形ABCD 中，E 为AD 边上的一点， 过C 点作CF ⊥CE 交AB 的延长线于点F ． （1）求证：△CDE ∽△CBF ；（2）若B 为AF 的中点，CB =3，DE =1，求CD 的长.21．已知关于x 的一元二次方程2(32)60mx m x -++=(0)m ≠． （1）求证：方程总有两个实数根；（2）若方程的两个实数根都是整数，求正整数m 的值.22．如图，Rt △ABC 中，90ACB ∠=︒，CD 是斜边AB 上的中线，分别过点A ，C 作AE ∥DC ，CE ∥AB ， 两线交于点E ．（1）求证：四边形AECD 是菱形；（2）若602B BC ∠=︒=，，求四边形AECD 的面积．23．列方程解应用题：某地区2013年的快递业务量为2亿件，受益于经济的快速增长及电子商务发展等多重因素，快递业务迅猛发展，2015年的快递业务量达到3.92亿件.求该地区这两年快递业务量的年平均增长率.24．某市为了鼓励居民节约用电，采用分段计费的方法按月计算每户家庭的电费，分两档收费：第一档是当月用电量不超过240度时实行“基础电价”；第二档是当用电量超过240度时，其中的240度仍按照“基础电价”计费，超过的部分按照 “提高电价”收费.设每个家庭月用电量为x 度时，应交电费为y 元.具体收费情况如折线图所示，请根据图象回答下列问题： （1）“基础电价”是_________元/度； （2）求出当x ＞240时，y 与x 的函数表达式； （3）小石家六月份缴纳电费132元， 求小石家这个月用电量为多少度？ 之间26．A(度)轴的垂线，若与坐标轴围成的矩形的周长与面积相等， 则这个点叫做“和谐点”.如右图，过点H （-3,6）分 别作x 轴，y 轴的垂线，与坐标轴围成的矩形OAHB 的周长与面积相等，则点H （3,6）是“和谐点”.（1）H 1（1,2）, H 2（4,-4）, H 3（-2,5）这三个点中的“和谐点”为 ； （2）点C (-1,4)与点P （m ，n ）都在直线y x b =-+上，且点P 是“和谐点”. 若m ＞0，求点P 的坐标．——————————————草 稿 纸——————————————初二数学 试卷答案及评分参考阅卷须知：为便于阅卷，解答题中的推导步骤写得较为详细，阅卷时，只要考生将主要过程正确写出即可．若考生的解法与给出的解法不同，正确者可参照评分参考给分．评分参考中所注分数，表示考生正确做到此步应得的累加分数． 一、 选择题（本题共30分，每小题3分） 11．6 12．2m >- 13．ACD B ∠=∠（或ADC ACB ∠=∠或AD ACAC AB=） 14．925 15．3 16．（1，2）；12(1)n n +；或2n n +（每空1分）三、解答题（本题共52分，第17-24题，每小题5分；第25-26题，每小题6分）17 2=-△(6)62x ±∴=62±18．证明一：联结AF ，CE ，联结AC 交BD 于点O.∵四边形ABCD 是平行四边形 ∴OA ＝OC ，OB ＝OD ⋯⋯⋯⋯⋯2分 又∵BE ＝DF∴OE ＝OF ⋯⋯⋯⋯⋯3分 ∴四边形AECF 是平行四边形 ⋯⋯4分 ∴AE ＝CF ⋯⋯⋯⋯⋯5分证明二：∵四边形ABCD 是平行四边形∴AB ＝CD ，AB ∥CD ⋯⋯⋯⋯⋯1分 ∴∠1＝∠2⋯⋯⋯⋯⋯2分在△ABE 和△CDF 中12 AB CD BE DF =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CDF （SAS ） ⋯⋯⋯⋯⋯4分∴AE CF = ⋯⋯⋯⋯⋯5分 19．解：（1）∵2y mx =过点A （-1，2）∴-m ＝2 ∴m ＝-2 ⋯⋯⋯⋯⋯1分 ∵点A （-1，2）和点B （0，3）在直线1y kx b =+上2133k b k b b -+==⎧⎧∴∴⎨⎨==⎩⎩⋯⋯⋯⋯⋯3分 ∴这两个函数的表达式为：13y x =+和2-2y x=⋯⋯⋯⋯⋯3分（2）过点A 作AD ⊥x 轴于点D ，则AD ＝2∵13y x =+交x 轴于点C （-3,0） ⋯⋯4分∴1=2AOC S OC AD⨯⨯△ 1=322⨯⨯ =3 ⋯⋯5分即这两个函数图象与x 轴所围成的三角形的面积是3.20．（1）证明：∵四边形ABCD 是矩形∴∠D=∠1=∠2+∠3=90° ⋯⋯⋯⋯⋯1分 ∵CF ⊥CE ∴∠4+∠3=90°∴∠2=∠4∴△CDE ∽△CBF（2） 解：∵四边形ABCD 是矩形∴CD =AB ∵B 为AF 的中点∴BF =AB ∴设CD=BF= x ⋯⋯⋯3分∵△CDE ∽△CBF21．（1）证明：∵0m ≠ ∴2(32)6mx m x -++∵2[(32)]46m m =-+-⨯△ ⋯⋯⋯⋯⋯1分2912424m m m =++- 29-124m m =+23-20m =()≥ ⋯⋯⋯⋯⋯2分∴此方程总有两个实数根. ⋯⋯⋯⋯⋯3分（2） 解：∵(3)(2)0x mx --=∴1223,x x m ==⋯⋯⋯⋯⋯4分∵方程的两个实数根都是整数，且m 是正整数∴m =1或 m =2 ⋯⋯⋯⋯⋯5分22．（1）证明：∵AE ∥DC ，CE ∥AB∴四边形AECD 是平行四边形 ⋯⋯⋯⋯⋯1分 ∵Rt △ABC 中，90ACB ∠=︒，CD 是斜边AB 上的中线 ∴CD =AD∴四边形AECD 是菱形 ⋯⋯⋯⋯⋯2分（2） 解：联结DE .∵90ACB ∠=︒，60B ∠=︒∴30BAC ∠=︒ ∴4A AB C ==, ⋯⋯⋯⋯⋯3分∵四边形AECD 是菱形∴EC =AD =DB 又∵EC ∥DB ∴四边形ECBD 是平行四边形∴ED = CB =2⋯⋯⋯⋯⋯4分∴2AECD AC ED S ⨯===菱形 ⋯⋯⋯⋯⋯5分23． 解：设该地区这两年快递业务量的年平均增长率为x . 根据题意，得 ⋯⋯1分 22(1) 3.92x += ⋯⋯⋯⋯⋯3分解得120.4, 2.4x x ==-（不合题意，舍去） ⋯⋯⋯⋯⋯4分 ∴0.440x ==%答：该地区这两年快递业务量的年平均增长率为40%. ⋯⋯⋯⋯⋯5分24．（1）0.5 ⋯⋯⋯⋯⋯ 1分 （2）解：当x ＞240时，设y =kx+b ，由图象可得：2401200.6 40021624k b k k b b +==⎧⎧∴⎨⎨+==-⎩⎩ ⋯⋯⋯⋯⋯2分 ∴0.624(240)y x x =-> ⋯⋯⋯⋯⋯3分（3）解：∵132120y =>∴令0.624=132x -， ⋯⋯⋯⋯⋯4分 得：=260x ⋯⋯⋯⋯⋯5分 ∴小石家这个月用电量为260度.25．（1）①补全图形，如右图所示. ⋯⋯⋯⋯⋯1分 ②数量关系：AM BM DN =+ ⋯⋯⋯⋯⋯2分 证明：在CD 的延长线上截取DE ＝BM ，联结AE .∵四边形ABCD 是正方形∴190B ∠=∠=︒，AD AB =，AB CD ∥ ∴6BAN ∠=∠ 在△ADE 和△ABM 中 1 AD AB B DE BM =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△ABM （SAS ）∴AE AM =，32∠=∠ ⋯⋯⋯⋯⋯⋯3分 又∵54∠=∠ ∴EAN BAN ∠=∠ 又∵6BAN ∠=∠ ∴6EAN ∠=∠∴AE NE = ⋯⋯⋯⋯⋯4分 又∵AE AM =，NE DE DN BM DN +=+=∴AM BM DN =+ ⋯⋯⋯⋯⋯5分（证法二：在CB 的延长线上截取BF ＝DN ，联结AF ） （2）数量关系：AM DN BM =- ⋯⋯⋯⋯⋯6分26．（1）H 2 ⋯⋯⋯⋯⋯1分 （2）解：∵点C (-1,4)在直线y x b =-+上∴14b += ∴3b =∴3y x =-+ ⋯⋯⋯⋯⋯2分 ∴3y x =-+与x 轴，y 轴的交点为N （3， 0），M （0，3） ∵点P （m ，n ）在直线3y x =-+上 ∴点P （m ，-m +3）过点P 分别作x 轴，y 轴的垂线，垂足为D ，E ∵m ＞0∴点P 可能在第一象限或第四象限（解法一） ① 若点P 在第一象限，如图1，则,3OD m PD n m +=== -∴3)6PEOD C m m ++==2(-矩形3)PEOD S m m +=(-矩形∵点P 是“和谐点”∴3)6m m +(-= ⋯⋯⋯3分 260m m +-3=2(-3)460=-⨯△＜∴此方程无实根∴第一象限的直线上的点不可能是“和谐点”. ⋯⋯⋯⋯⋯4分② 若点P 在第四象限，如图2，则,3)3OD m PD n m m -=+=-== --( ∴3)46PEOD C m m m +=-=2(-矩形y3)PEOD S m m =(-矩形∵点P 是“和谐点”∴3)46m m m -(-= ⋯⋯5分 260m m +-7=1261m m ==，∵点P （m ，-m +3）在第四象限 ∴3m ＞ ∴6m =∴点P （6，-3） ⋯⋯⋯⋯⋯6分综上所述，满足条件的点P 的坐标为P （6，-3）.（解法二）① 若点P 在第一象限，如图1，则,3OD m PD n m +=== - ∴3)6PEOD C m m ++==2(-矩形∵133 4.52MON S ⨯⨯==△ ⋯⋯⋯3分而MONPEOD S S <△矩形 ∴PEOD PEOD C S 矩形矩形≠∴第一象限的直线上的点不可能是“和谐点”. ⋯⋯⋯⋯⋯4分 ② 若点P 在第四象限，如图2，则,OD m PD n == -∴)PEOD C m n =2(-矩形PEOD S mn =-矩形∵点P 是“和谐点”∴2)m n mn (-=- ⋯⋯⋯⋯⋯5分 ∴22mn m =-∵点P （m ，n ）在直线3y x =-+上 ∴3n m =-+ ∴232mm m =-+- 260m m +-7= 1261m m ==，经检验，1261m m ==，是方程22mm-∵点P （m ，-m +3）在第四象限 ∴3m ＞ ∴6m =m +3)y∴点P（6，-3）⋯⋯⋯⋯⋯6分综上所述，满足条件的点P的坐标为P（6，-3）.。
201807石景山区八下数学期末考试参考评分标准
石景山区2018-2019学年第二学期初二期末数学试卷答案及评分参考阅卷须知：为了阅卷方便，解答题中的推导步骤写得较为详细，考生只要写明主要过程即可。
若考生的解法与本解法不同，正确者可参照评分参考给分，解答右端所注分数，表示考生正确做到这一步应得的累加分数 一、选择题（本题共16分，每小题2分）二、填空题（本题共16分，每小题2分）9．不是 10．24 11．()20x x -= （答案不唯一） 12．A ；,A B 两种玉米种子的平均产量相同，A 种玉米产量的方差小，比B 种玉米产量稳定. 13．1x > 14．()5,3或()1,3- 15．416．三边都相等的三角形是等边三角形；等边三角形的每个内角都是60︒；四边都相等的四边形是菱形. 三、解答题（（本题共68分，第17-23题，每小题5分；第24题6分；第25题5分；第26、27题，每小7分；28题8分）解答应写出文字说明，演算步骤或证明过程． 1718．证明：∵四边形ABCD∴AB CD ∥，AB CD =．…………… 2分 ∴∠1=∠2．∵AF CE =，∴△AFB ≌△CED ． ………………3分∴∠3=∠4． …………………4分∴DE BF ∥． …………………5分方法一方法二：连接BD ，交AC 于点O ． ∵四边形ABCD 是平行四边形，∴OA OC =，OB OD =． …………… 2分 ∵AF CE =，∴OF OE =． ………………3分 ∴四边形EBFD 是平行四边形． ⋯ ⋯⋯4分 ∴DE BF ∥ ⋯ ⋯⋯ ⋯⋯5分 19．（1）证明：∵E 为线段AC 的中点， ∴AE =EC ． ∵EF =DE∴四边形ADCF 是平行四边形． ……… 2分 又∵D 为线段AB 的中点，∴ DE BC ∥ ……………… 3分 ∵∠AED =∠ACB =90°，∴AC ⊥FD ．∴平行四边形ADCF 是菱形． ………… 4分（2） CA =CB 或 ∠B =45°(答案不唯一)………… 5分 20．（1）证明：当0=m 时，原方程可化为30x +=，方程有实根3x =- …………………… 1分 当0m ≠时，()23130mx m x +++=是关于x 的一元二次方程. ∵2(31)43m m ∆=+-⨯261129m m m +-=+()2310m =-≥ ……………………2分 ∴此方程总有两个实数根. ……………………3分 综上所述，不论m 取何值，方程都有实数根.（2） 解： ∵()(3)10x mx ++=，∴1213,m x x =-=-.…………………… 4分∵方程有两个整数根且m 是整数，∴1m =-或1m =． …………………… 5分F EDCBA21．解：（1）①AD BE ∥或AD BE =； ┈┈┈┈┈┈┈┈┈1分②B DEF ∠=∠；(答案不唯一) ┈┈┈2分（2）判断：四边形ACFD 是矩形．证明：∵△ABC 沿BC 方向平移，得到△DEF ，∴AD CF ∥且=AD CF ． …………………… 3分∴四边形ACFD 是平行四边形． ……………… 4分 ∵90DFE ACB ∠=∠=︒∴四边形ACFD 是矩形． ………………… 5分22．解：设净化器销售量的月平均增长率为x ． ………1分 根据题意得：()2819.68x +=． ………………3分 解得：10.110%x ==，2 2.1x =-（不合题意舍去）……… 4分 答：净化器销售量的月平均增长率为10%．……………… 5分23．解：（1）∵直线32y x b =+与直线12y x =交于点(),1A m ，∴112m =．∴2m =． ……………………1分∴()21,A ．∴3212b ⨯+=． ……………………2分 ∴2b =-．∴()02,B -． ……………………3分 （2）点()01,C -或()03,C -．……………………5分24．解：（1）如图24-1所示． ……………………1分 （2）127︒． ………………………2分（3）思路1：a ．连接BD 交EF 于点O ．b ．在Rt △DFC 中，设FC x =，则4FD x =-，由勾股定理，求得FD 长；c ．Rt △BDC 中，勾股可得5BD =，由点B 与点D 的对称性可得OD 的长；d ．在Rt △DFO 中，同理可求OF 的长，可证2EF OF =，求得EF 的长．说明：每步1分 ………………………6分注：利用面积或其他方法求解的酌情对应给分！思路2：a ．过点E 作EH BC ⊥于H ；b ．在Rt △DFC 中，设FC x =，则4FD x =-， 由勾股定理，可求FC 的长；c ．可证DE DF BF ==或△DFC ≌△DEG ，可证 C F G E A E B H ===，可得FH 的长；d ．在Rt △EHF 中，勾股可求EF 的长．…………6分25．解：（1）0.05，14，0.30． ………3分 （2）如右图所示： ………4分 （3）141280052040+⨯= ………5分答：估计参加这次比赛的800名学生中成绩优秀的有520名．26．解：（1）小帅的骑车速度：16千米/小时；…………1分()0.50,C ． ………………………2分 （2）设线段AB 对应的函数表达式为(0)y kx b k =+≠． ∵()0.58,A ，()2.524,B ， ∴0.582.524k b k b +=⎧⎨+=⎩…………………3分解得：84k b =⎧⎨=⎩． ……………………5分∴线段AB 对应的函数表达式为()840.5 2.5y x x =+≤≤．（3） 当2x =时，82420y =⨯+=． …………6分 答： 当小帅到达乙地时，小泽距乙地还有4千米． …………7分27．解：（1）①补全图形如右图所示． ………1分 ②证明：∵线段PA 绕点P 顺时针旋转90︒得到线段PE ， ∴PA PE =，90APE ∠=︒． …………………2分 ∵四边形ABCD 是正方形， ∴490ABC ∠=∠=︒，AB BC =． ∵ EF BC ⊥于H ， ∴5904∠=︒=∠．∴2390∠+∠=︒． ∴13∠=∠．∴△APB ≌△PEH ． …………3分 ∴PB EH =，AB PH =． ∴BC PH = ∴PB CH =．∴CH EH =． …………4分 ∵1452ACB BCD ∠=∠︒=∴CH FH =．∴EH FH =． ………………5分（2）当点P 在线段BC上时：)CE CD CP =-． ………………6分当点P 在线段BC的延长线上时：)CE CD CP =+．…………7分28．解： （12． ………………2分 （2）如图1，点()5,3B 在直线2y x =-上． ∵点()13A ，，()53B ，，∴AB 平行于x 轴． 当1y =时，21x -=． ∴3x =．∴()131，P ………………4分 过2P 作2P E AB ⊥交AB 的延长线 于点E ．∵直线2y x =-与坐标轴分别交 于点()()0-2,2,0，C D ， ∴OC OD =．∴可证245P BE ODC ∠=∠=︒． ∵22P B =，∴2P E BE ==∴(25P ． ………………6分 ∴点P 的坐标为()31，或(5+． （3）24b -≤≤ ………………8分。
5.石景山答题卡：201907八下数学期末考试
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效石景山区2018—2019学年第二学期初二期末
数学试卷答题卡
初二数学答题卡第1页（共4页）初二数学答题卡第2页（共4页）
注
意
事
项
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效
初二数学 答题卡 第3页（共4页）
初二数学 答题卡 第4页（共4页）
学 校 姓 名。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2018-2019学年北京市石景山区八年级（下）期末数学试卷一、选择题（本题共16分，每小题2分）下面各题均有四个选项，符合题意的选项只有一个．1．（2分）若3x＝5y（y≠0），则下列各式成立的是（）A．＝B．＝C．D．＝2．（2分）在下列图案中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．3．（2分）一个多边形的内角和是720°，这个多边形的边数是（）A．4B．5C．6D．74．（2分）下列函数的图象不经过第三象限，且y随x的增大而减小的是（）A．y＝﹣3x+1B．y＝﹣3x﹣1C．y＝3x+1D．y＝3x﹣15．（2分）《孙子算经》是我国古代重要的数学著作，其下卷有题如下：“今有竿不知长短，度其影得一丈五尺．别立一表，长一尺五寸，影得五寸．问竿长几何？”译文：“有一根竹竿不知道它的长短，量出它在太阳下的影子长一丈五尺．同时立一根一尺五寸的小标杆，它的影长是五寸，则这根竹竿的长度为多少尺？”可得这根竹竿的长度为（提示：1丈＝10尺，1尺＝10寸）（）A．五丈B．四丈五尺C．五尺D．四尺五寸6．（2分）甲、乙两名同学骑自行车从A地出发沿同一条路前往B地，他们离A地的距离s（km）与甲离开A地的时间t（h）之间的函数关系的图象如图所示，根据图象提供的信息，有下列说法：①甲、乙同学都骑行了18km②甲、乙同学同时到达B地③甲停留前、后的骑行速度相同④乙的骑行速度是12km/h其中正确的说法是（）A．①③B．①④C．②④D．②③7．（2分）某校以“我和我的祖国”为主题的演讲比赛中，共有10位评委分别给出某选手的原始评分，在评定该选手成绩时，则从10个原始评分中去掉1个最高分和1个最低分，得到8个有效评分．8个有效评分与10个原始评分相比，不变的是（）A．平均数B．极差C．中位数D．方差8．（2分）下面的统计图反映了我国邮电业务（含邮政业务与电信业务）总量的情况．根据统计图提供的信息，下列有关我国邮电业务总量推断不合理的是（）A．2018年，电信业务总量比邮政业务总量的5倍还多B．2011﹣2018年，邮政业务总量与电信业务总量都是逐年增长的C．与2017年相比，2018年邮政业务总量的增长率超过20%D．2011﹣2018年，电信业务总量年增长的平均值大于邮政业务总量年增长的平均值二、填空题（本题共16分，每小题2分）9．（2分）如图，在▱ABCD中，BC＝7，AB＝4，BE平分∠ABC交AD于点E，则DE的长为．10．（2分）直线y＝﹣6x向上平移2个单位长度，则所得新直线的函数表达式为．11．（2分）菱形ABCD中，AB＝2，∠BAD＝120°，则菱形ABCD的面积为．12．（2分）如图，A，B两地被池塘隔开，小石通过下面的方法测出A，B间的距离：先在AB外选一点C，然后通过测量找到AC，BC的中点D，E，并测量出DE的长为20m，由此他就知道了A，B间的距离为m，小石的依据是．13．（2分）如图，△ADE和△ABC中，∠1＝∠2，请添加一个适当的条件，使△ADE∽△ABC（只填一个即可）．14．（2分）如图，在△ABC中，点D，E分别是边AB，AC上的点，DE∥BC，BD＝2AD，若△ADE的面积是1，则四边形DBCE的面积为．15．（2分）如图，矩形ABCD中，AB＝6，BC＝8，E是BC边上一点，将△ABE沿AE翻折，点B恰好落在对角线AC上的点F处，则BE的长为．16．（2分）某林场要考察一种幼树在一定条件下的移植成活率，在移植过程中的统计结果如下表所示：移植的幼树n/棵5001000200040007000100001200015000成活的幼树m/棵42386817143456602085801030812915成活的频率0.8460.8680.8570.8640.8600.8580.8590.861在此条件下，估计该种幼树移植成活的概率为（精确到0.01）；若该林场欲使成活的幼树达到4.3万棵，则估计需要移植该种幼树万棵．三、解答题（本题共68分，第17-18题每题5分，第19题6分，第20-23题每题5分，第24题7分，第25题5分，第26题6分，第27-28题每题7分）17．（5分）如图，菱形ABCD中，过点D作DE⊥BA交BA的延长线于点E，DF⊥BC交BC的延长线于点F．求证：DE＝DF．18．（5分）在平面直角坐标系xOy中，一次函数y＝kx+b（k≠0）的图象平行于直线y＝x，并且经过点A（﹣2，﹣3）．（1）求此一次函数的表达式，并画出它的图象；（2）此一次函数的图象与x轴交于点B，求△AOB的面积．19．（6分）某综合实践小组的同学对本校八年级学生课外阅读最喜爱的图书种类进行了调查．（1）该综合实践小组设计了下列的调查方式，比较合理的是（填写序号即可）A．对八年级各班的数学课代表进行问卷调查B．对八年级（1）班的全班同学进行问卷调查C．对八年级各班学号为4的倍数的同学进行问卷调查（2）小组同学根据问卷调查（每个被调查的学生只能选择其中一项）的结果绘制了如下两幅统计图（不完整）：根据以上信息，回答下列问题：①这次被调查的学生共有人；②请将图1补充完整并在图上标出数据；③图2中，m＝，“科普类”部分扇形的圆心角是°；④若该校八年级共有学生320人，根据调查结果估计此年级最喜欢“文学类”图书的学生约有人．20．（5分）如图，在△ABC中，点D是边AB上一点且∠ACD＝∠B．（1）求证：△ACD∽△ABC；（2）若AB＝6，AD＝2，求AC的长．21．（5分）如图，在14×7的正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫做格点．Rt△ACB 的顶点都在格点上．按照要求完成下列画图（只在此14×7的网格中完成且所画各点都是格点，所画的点可以与已知点重合）．（1）将△ACB绕点A逆时针旋转90°，得到△AC′B′；（2）画出所有点D，使得以A，B，C，D为顶点的四边形是平行四边形；（3）画出一个与△ACB相似（但不全等）的三角形△AEF，且△AEF与△ACB有公共点A（画出一个三角形即可）．22．（5分）如图，四边形ABCD中，AD∥BC，∠ABC＝90°，DB＝DC，E是BC的中点，连接DE．（1）求证：四边形ABED是矩形；（2）连接AC，若∠ABD＝30°，DC＝2，求AC的长．23．（5分）如图，在平面直角坐标系xOy中，过点A（0，4）的直线l1与直线l2：y＝x+1相交于点B（m，2）．（1）求直线l1的表达式；（2）过动点P（n，0）且垂直于x轴的直线与l1，l2的交点分别为M，N，当点M位于点N上方时，请直接写出n的取值范围是．24．（7分）某农科所甲、乙试验田各有水稻3万个，为了考察水稻穗长的情况，于同一天在这两块试验田里分别随机抽取了50个稻穗进行测量，获得了它们的长度x（单位：cm），并对数据（穗长）进行了整理、描述和分析．下面给出了部分信息．a．甲试验田穗长的频数分布统计表如表1所示（不完整）：b．乙试验田穗长的频数分布直方图如图1所示：甲试验田穗长频数分布表（表1）分组/cm频数频率4.5≤x＜540.085≤x＜5.590.185.5≤x＜6n6≤x＜6.5110.226.5≤x＜m0.207≤x＜7.52合计50 1.00c．乙试验田穗长在6≤x＜6.5这一组的是：6.3，6.4，6.3，6.3，6.2，6.2，6.1，6.2，6.4d．甲、乙试验田穗长的平均数、中位数、众数、方差如下（表2）：试验田平均数中位数众数方差甲 5.924 5.8 5.80.454乙 5.924w 6.50.608根据以上信息，回答下列问题：（1）表1中m的值为，n的值为；（2）表2中w的值为；（3）在此次考察中，穗长为5.9cm的稻穗，穗长排名（从长到短排序）更靠前的试验田是；稻穗生长（长度）较稳定的试验田是；A．甲B．乙C．无法推断（4）若穗长在5.5≤x＜7范围内的稻穗为“良好”，请估计甲试验田所有“良好”的水稻约为万个．25．（5分）某长途汽车客运公司规定旅客可免费携带一定质量的行李，当行李质量超过规定时，则需要购买行李票，行李票费用y（单位：元）与所携带的行李质量x（单位：kg）之间的关系如图所示．（1）当行李的质量超过规定时，求y与x之间的函数表达式；（2）旅客最多可免费携带多少千克的行李？26．（6分）在平面直角坐标系xOy中，点A（﹣1，m）是直线y＝﹣x+2上一点，点A向右平移4个单位长度得到点B．（1）求点A，B的坐标；（2）若直线l：y＝kx﹣2（k≠0）与线段AB有公共点，结合函数的图象，求k的取值范围．27．（7分）正方形ABCD中，点P是直线AC上的一个动点，连接BP，将线段BP绕点B顺时针旋转90°得到线段BE，连接CE．（1）如图1，若点P在线段AC上，①直接写出∠ACE的度数为°；②求证：P A2+PC2＝2PB2；（2）如图2，若点P在CA的延长线上，P A＝1，PB＝，①依题意补全图2；②直接写出线段AC的长度为．28．（7分）在平面直角坐标系xOy中，若P，Q为某个矩形不相邻的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P，Q的“相关矩形”．图1为点P，Q的“相关矩形”的示意图．已知点A的坐标为（1，2）．（1）如图2，点B的坐标为（b，0）．①若b＝﹣2，则点A，B的“相关矩形”的面积是；②若点A，B的“相关矩形”的面积是8，则b的值为．（2）如图3，点C在直线y＝﹣1上，若点A，C的“相关矩形”是正方形，求直线AC的表达式；（3）如图4，等边△DEF的边DE在x轴上，顶点F在y轴的正半轴上，点D的坐标为（1，0）．点M的坐标为（m，2），若在△DEF的边上存在一点N，使得点M，N的“相关矩形”为正方形，请直接写出m的取值范围．2018-2019学年北京市石景山区八年级（下）期末数学试卷参考答案与试题解析一、选择题（本题共16分，每小题2分）下面各题均有四个选项，符合题意的选项只有一个．1．【解答】解：A、＝，可以化成：xy＝15，故此选项错误；B、＝，可以化成：xy＝15，故此选项错误；C、＝，可以化成：5x＝3y，故此选项错误；D、＝，可以化成：3x＝5y，故此选项正确．故选：D．2．【解答】解：A、既是中心对称图形又是轴对称图形，故本选项正确；B、不是中心对称图形，是轴对称图形，故本选项错误；C、不是中心对称图形，是轴对称图形，故本选项错误；D、是中心对称图形，不是轴对称图形，故本选项错误．故选：A．3．【解答】解：∵多边形的内角和公式为（n﹣2）•180°，∴（n﹣2）×180°＝720°，解得n＝6，∴这个多边形的边数是6．故选：C．4．【解答】解：A、y＝﹣3x+1的图象经过第一、二、四象限，且y随x的增大而减小，故选项正确；B、y＝﹣3x﹣1的图象经过第二、三、四象限，且y随x的增大而减小，故选项错误；C、y＝3x+1的图象经过第一、二、三象限，且y随x的增大而增大，故选项错误；D、y＝3x﹣1的图象经过第一、三、四象限，且y随x的增大而增大，故选项错误；故选：A．5．【解答】解：设竹竿的长度为x尺，∵竹竿的影长＝一丈五尺＝15尺，标杆长＝一尺五寸＝1.5尺，影长五寸＝0.5尺，∴＝，解得x＝45（尺）．45尺合四丈五尺．故选：B．6．【解答】解：由图象可得，甲、乙同学都骑行了18km，故①正确，甲比乙先到达B地，故②错误，甲停留前的速度为：10÷0.5＝20km/h，甲停留后的速度为：（18﹣10）÷（1.5﹣1）＝16km/h，故③错误，乙的骑行速度为：18÷（2﹣0.5）＝12km/h，故④正确，故选：B．7．【解答】解：根据题意，从10个原始评分中去掉1个最高分和1个最低分，得到8个有效评分．8个有效评分与10个原始评分相比，不变的是中位数．故选：C．8．【解答】解：12345×5＝61725＜65557，因此A选项是正确的，电信业务2015﹣2016年，业务总量由23346亿元降至15617亿元，不是一直增长，因此选项B是错误的，（12345﹣9764）÷9764≈26.43%，因此选项C是正确的，从2011年到2018年，电信业务每年都比邮政业务的总量要大，因此D选项是正确的，故选：B．二、填空题（本题共16分，每小题2分）9．【解答】解：∵四边形ABCD为平行四边形，∴AE∥BC，∴∠AEB＝∠EBC，∵BE平分∠ABC，∴∠ABE＝∠EBC，∴∠ABE＝∠AEB，∴AB＝AE，∵BC＝7，CD＝AB＝4，∴DE＝AD﹣AE＝7﹣4＝3．故答案为：3．10．【解答】解：直线y＝﹣6x向上平移2个单位长度，则所得新直线的函数表达式为：y＝﹣6x+2．故答案为：y＝﹣6x+2．11．【解答】解：在菱形ABCD中，∠BAC＝∠BAD＝×120°＝60°又∵在△ABC中，AB＝BC，∴△ABC为等边三角形，∴AC＝AB＝2．在菱形ABCD中，AC⊥BD，∴△AOB为直角三角形，∴∠ABO＝90°﹣∠BAO＝30°∴AO＝AB＝1，∴OB＝＝，∴BD＝2BO＝2，∴菱形ABCD的面积＝AC×BD＝×2×2＝2，故答案为：2．12．【解答】解：∵点D，E是AC，BC的中点，∴AB＝2DE＝40（m），小石的依据是三角形中位线定理，故答案为：40；三角形中位线定理．13．【解答】解：∵∠1＝∠2，∴∠DAE＝∠BAC，∴要使△ADE∽△ABC，则添加的一个条件可以是∠D＝∠B或∠E＝∠C或＝．故答案为：∠D＝∠B或∠E＝∠C或＝．14．【解答】解：∵DE∥BC，∴△ADE∽△ABC，∴＝（）2，∵BD＝2AD，∴，∵△ADE的面积是1，∴△ABC的面积是9，∴四边形DBCE的面积为：8，故答案为：815．【解答】解：∵AB＝6，BC＝8，∠B＝90°∴AC＝＝10∵将△ABE沿AE翻折，点B恰好落在对角线AC上的点F处∴AB＝AF＝6，BE＝EF，∠B＝∠AFE＝90°∴FC＝AC﹣AF＝4，在Rt△EFC中，CE2＝FC2+EF2，∴（8﹣BE）2＝16+BE2，∴BE＝3故答案为：316．【解答】解：概率是大量重复实验的情况下，频率的稳定值可以作为概率的估计值，即次数越多的频率越接近于概率∴这种幼树移植成活率的概率约为0.86．若该林场欲使成活的幼树达到4.3万棵，则估计需要移植该种幼树4.3÷0.86＝5（万棵），故答案为：0.86，5．三、解答题（本题共68分，第17-18题每题5分，第19题6分，第20-23题每题5分，第24题7分，第25题5分，第26题6分，第27-28题每题7分）17．【解答】证法一：连接BD，如图1．∵四边形ABCD是菱形，∴∠1＝∠2，∵DE⊥BA，DF⊥BC，∴DE＝DF．证法二：如图2，∵四边形ABCD是菱形，∴AB＝BC．∵DE⊥BA，DF⊥BC，∴S菱形ABCD＝AB×DE，S菱形ABCD＝CB×DF，∴DE＝DF．证法三：如图2，∵四边形ABCD是菱形，∴DA＝DC，∠1＝∠2，∴∠3＝∠4，∵DE⊥BA，DF⊥BC，∴∠E＝∠F＝90°，在△AED和△CFD中，∵∴△AED≌△CFD（AAS），∴DE＝DF．18．【解答】解：（1）∵一次函数y＝kx+b（k≠0）的图象平行于直线y＝x，∴k＝，∵函数图象经过点A（﹣2，﹣3），∴﹣3＝（﹣2）+b．∴b＝﹣2．∴一次函数的表达式为y＝；图象如图所示：；（2）过点A作AC⊥x轴于点C，∴AC＝3．∵直线y＝﹣2与x轴的交点B的坐标是（4，0），∴S△AOB＝OB•AC＝＝6．19．【解答】解：（1）C．（2）①32÷40%＝80人，故答案为：80．②80﹣32﹣20﹣12＝16人，补全条形统计图如图所示．③＝20%，∴m＝20，360°×25%＝90°，噶答案为：20，90°．④320×40%＝128人，故答案为：128．20．【解答】解：（1）∵∠1＝∠B，∠A＝∠A，∴△ACD∽△ABC；（2）∵△ACD∽△ABC，∴＝，∴AC2＝6×2＝12，∴AC＝2；21．【解答】解：（1）如图1所示．（2）如图1所示．（3）如图2所示（未全画出；画出一个三角形即可）．22．【解答】（1）证明：∵AD∥BC，∠ABC＝90°，∴∠BAD＝90°，∵DB＝DC，E是BC的中点，∴∠DEB＝90°，∴四边形ABED是矩形；（2）解：∵∠ABC＝90°，∠ABD＝30°，∴∠DBE＝60°，∵DB＝DC，∴△DBC是等边三角形，∴BD＝BC＝DC＝2，∵Rt△BAD中，∠ABD＝30°，∴AD＝1，AB＝，∴在Rt△ABC中，AC＝＝．23．【解答】解：（1）∵点B在直线l2上，∴2＝m+1，∴m＝1，点B（1，2）设直线l1的表达式为y＝kx+b，由题意，解得k＝﹣2，b＝4，∴直线l1的表达式为y＝﹣2x+4．（2）由图象可知n＜1，故答案为n＜1．24．【解答】解：（1）m＝50×0.2＝10，7≤x＜7.5这一组的频率为2÷50＝0.04，∴n＝1﹣（0.08+0.18+0.22+0.20+0.04）＝0.28，故答案为：10，0.28；（2）表2中w的值为＝6.15，故答案为：6.15；（3）穗长为5.9cm的稻穗在甲试验田在中位数之前，在乙试验田中在中位数之后，所以穗长排名（从长到短排序）更靠前的试验田是甲，因为甲试验田的稻穗长度的方差小，所以稻穗生长（长度）较稳定的试验田是甲，故答案为：A、A；（4）估计甲试验田所有“良好”的水稻约为3×（0.22+0.2+0.28）＝2.1（万个）．故答案为：2.1．25．【解答】解：（1）设当行李的质量超过规定时，y与x之间的函数表达式为y＝kx+b（k≠0）．由图象可知，当x＝30时，y＝2；当x＝60时，y＝8，∴解得∴当行李的质量超过规定时，y与x之间的函数表达式为y＝（x≥20）．（2）在y＝（x≥20）中令y＝0，得＝0解得x＝20．∴旅客最多可免费携带20千克的行李．26．【解答】解：（1）∵点A（﹣1，m）是直线y＝﹣x+2上一点，∴m＝1+2＝3．∴点A的坐标为（﹣1，3）．∴点（﹣1，3）向右平移4个单位长度得到点B的坐标为（3，3）．（2）当直线l：y＝kx﹣2过点A（﹣1，3）时，得3＝﹣k﹣2，解得k＝﹣5．当直线l：y＝kx﹣2过点B（3，3）时，得3＝3k﹣2，解得k＝．如图，若直线l：y＝kx﹣2（k≠0）与线段AB有公共点，则b的取值范围是k≤﹣5或k≥．27．【解答】解：（1）①如图1中，连接PE．∵四边形ABCD是正方形，∴BA＝BC，∠ABC＝∠BCD＝90°，∠ACB＝∠BAP＝45°，∵∠PBE＝90°，∴∠ABC＝∠PBE，∴∠ABP＝∠CBE，∵BP＝BE，∴△ABP≌△CBE（SAS），∴∠BAP＝∠BCE＝45°，∴∠ACE＝90°故答案为90．②证明：在Rt△PCE中，由勾股定理，得EC2+PC2＝PE2，∵△ABP≌△CBE，∴P A＝EC，∵PE＝PB，∴P A2+PC2＝2PB2．（2）①补全的图形如图2所示．②连接PE，设BE交PC于O．同法可证：△ABP≌△CBE，∴P A＝EC，∠APE＝∠CEB，∵∠BOC＝∠POE，∴∠OBP＝90°，∵PE＝PB＝，∴PC＝＝5，∴AC＝PC＝P A＝4．故答案为4．28．【解答】解：（1）①∵b＝﹣2，∴点B的坐标为（﹣2，0），如图2﹣1所示：∵点A的坐标为（1，2），∴由矩形的性质可得：点A，B的“相关矩形”的面积＝（1+2）×2＝6，故答案为：6；②如图2﹣2所示：由矩形的性质可得：点A，B的“相关矩形”的面积＝|b﹣1|×2＝8，∴|b﹣1|＝4，∴b＝5或b＝﹣3，故答案为：5或﹣3；（2）过点A（1，2）作直线y＝﹣1的垂线，垂足为点G，则AG＝3，∵点C在直线y＝﹣1上，点A，C的“相关矩形”AGCH是正方形，∴正方形AGCH的边长为3，当点C在直线x＝1右侧时，如图3﹣1所示：CG＝3，则C（4，﹣1），设直线AC的表达式为：y＝kx+a，则，解得；，∴直线AC的表达式为：y＝﹣x+3；当点C在直线x＝1左侧时，如图3﹣2所示：CG＝3，则C（﹣2，﹣1），设直线AC的表达式为：y＝k′x+b，则，解得：，∴直线AC的表达式为：y＝x+1，综上所述，直线AC的表达式为：y＝﹣x+3或y＝x+1；（3）∵点M的坐标为（m，2），∴点M在直线y＝2上，∵△DEF是等边三角形，顶点F在y轴的正半轴上，点D的坐标为（1，0），∴OD＝OE＝DE＝1，EF＝DF＝DE＝2，∴OF＝OD＝，分两种情况：如图4所示：①当点N在边EF上时，若点N与E重合，点M，N的“相关矩形”为正方形，则点M的坐标为（﹣3，2）；若点N与F重合，点M，N的“相关矩形”为正方形，则点M的坐标为（﹣2+，2）；∴m的取值范围为﹣3≤m≤﹣2+；②当点N在边DF上时，若点N与D重合，点M，N的“相关矩形”为正方形，则点M的坐标为（3，2）；若点N与F重合，点M，N的“相关矩形”为正方形，则点M的坐标为（2﹣，2）；∴m的取值范围为2﹣≤m≤3；综上所述，m的取值范围为﹣3≤m≤﹣2+或2﹣≤m≤3．。