液态混合物和溶液
合集下载
第四章,液体混合物与溶液

3. 化学势(chemical potential)
(1)
G G G dG dnB dT p dp n T p ,nB B T , n B B T , p , n
C
当组成不变时,
G dG SdT Vdp dnB n B B T , p ,nC
2.单选题: (1)1molA与 nmol B组成的溶液,体积为0.65 dm3 ,当xB = 0.8 时,A的偏摩尔体积VA=0.090dm3· -1,那么B的偏摩尔VB 为: mol (A) 0.140 dm3· -1 ; mol (B) 0.072 dm3· -1 ; mol (C) 0.028 dm3· -1 ; mol (D) 0.010 dm3· -1 。 mol
ΔG TΔS
1
ΔS2 ΔS1 ΔS 56.25J K
1
ΔG2 ΔG1 ΔG 298.15 56.25J 16.77kJ
(5)化学势与温度的关系
B SB,m T p,nB
4. 恒温下理想气体混合物化学势
(1)单组分纯理想气体
RT dGm Vmdp dp p
T Gm RT ln p
Gm RT ln p C
* (Pg) O (g) p RT dp O (g) RT ln( p / p O ) p O p
B
G T p ,nB T , p ,n
S
C
nB T , p ,n
S
B ,m
C
(3) 等温等压下, 系统内发生相变化或化学变化时, 有
2.4 拉乌尔定律、亨利定律
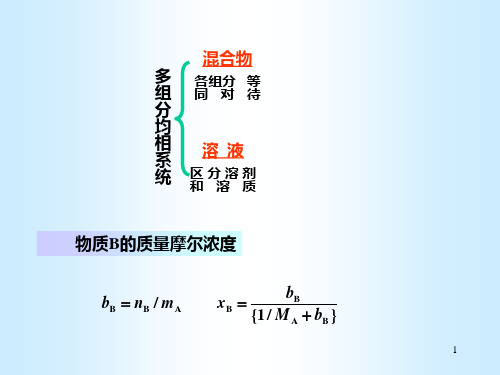
混合物
多 组
各组分 等 同对待
分
均
相 系
溶液
统
区分溶剂 和溶质
物质B的质量摩尔浓度
bB nB / mA
xB
{1 /
bB MA
bB }
1
§2-4 拉乌尔定律、亨利定律
1. 液态混合物和溶液的饱和蒸气 压
设由组分A, B, C……组成液态混 合物或溶液, T一定时, 达到气, 液两相 平衡.
此时, 气态混合物的总压力为p, 则 p 即为温度T下该液态混合物或溶液的 饱和蒸气压.
水(A)和乙酸乙酯(B)不完全混溶, 在37.55℃时两液相呈平衡.
一相中含质量分数为w(B) = 0.0675的酯, 另一相中含w(A) =
0.0379的水, 假定拉乌尔定律对每相中的溶剂都能适用, 已知
37.55℃时, 纯乙酸乙酯的蒸气压力是22.13kPa, 纯水的蒸气
压力是6.399kPa, 试计算:
ln p(s) 3133 27.650 11.99 p(s) 160.3k Pa Pa 200K / K
计算结果表明, 所给过程是恒温恒压不可逆相变化过程, 为
此可根据计算所得的液体及固体CO2在200 K的蒸气压数据, 设
计以下可逆过程进行计算:
8
s, 100kPa, 200K
s, 160.3kPa, 200K G2
(1)计算下述过程Gm :
CO2( s, 100kPa, 200K ) →CO2( l, 100kPa, 200K )
(2)判断在100 kPa下, CO2(l)能否稳定存在?
(1) 200 K时液体及固体CO2的饱和蒸气压:
ln p(l) 2013 22.405 12.34 p(l) 228.7kPa Pa 200K / K
多 组
各组分 等 同对待
分
均
相 系
溶液
统
区分溶剂 和溶质
物质B的质量摩尔浓度
bB nB / mA
xB
{1 /
bB MA
bB }
1
§2-4 拉乌尔定律、亨利定律
1. 液态混合物和溶液的饱和蒸气 压
设由组分A, B, C……组成液态混 合物或溶液, T一定时, 达到气, 液两相 平衡.
此时, 气态混合物的总压力为p, 则 p 即为温度T下该液态混合物或溶液的 饱和蒸气压.
水(A)和乙酸乙酯(B)不完全混溶, 在37.55℃时两液相呈平衡.
一相中含质量分数为w(B) = 0.0675的酯, 另一相中含w(A) =
0.0379的水, 假定拉乌尔定律对每相中的溶剂都能适用, 已知
37.55℃时, 纯乙酸乙酯的蒸气压力是22.13kPa, 纯水的蒸气
压力是6.399kPa, 试计算:
ln p(s) 3133 27.650 11.99 p(s) 160.3k Pa Pa 200K / K
计算结果表明, 所给过程是恒温恒压不可逆相变化过程, 为
此可根据计算所得的液体及固体CO2在200 K的蒸气压数据, 设
计以下可逆过程进行计算:
8
s, 100kPa, 200K
s, 160.3kPa, 200K G2
(1)计算下述过程Gm :
CO2( s, 100kPa, 200K ) →CO2( l, 100kPa, 200K )
(2)判断在100 kPa下, CO2(l)能否稳定存在?
(1) 200 K时液体及固体CO2的饱和蒸气压:
ln p(l) 2013 22.405 12.34 p(l) 228.7kPa Pa 200K / K
物理化学(第三版)第3章 液态混合物和溶夜

B
dnB
B
dnB
...
B dnB
B
B
B
dG
B
dnB
≤0
B
< 自动进行 = 平衡
应用条件:( 恒温、恒压、 W’=0)
化学势在相平衡中的应用
设有物质的量为dn的纯物质A,在恒温恒压无非体积功的 条件下,由液相转移到气相。
A(l) T, p,W'0 A(g)
l
g
dnl dng
dn g
dG
溶液中组成可分为溶质和溶剂。
以物态可分为气态溶液、固态溶液和液态溶液。
3.1 偏摩尔量与化学势
一、偏摩尔量的定义 多组分系统的广度性质X不仅是温度、压力的
函数,还与系统的组成有关,即
X = f(T,p,nB,nC…)
dX
X T
p,nB ,nC L
dT
X p
T ,nB ,nC L
dp
解: (1)NaCl饱和溶液的质量分数:
w(
NaCl)
=
m(
m(NaCl) NaCl) + m(H
2O)
= 3.173 =0.2644 26.44% 12.003
(2)NaCl饱和溶液中
n(NaCl) = m(NaCl) 3.173= 0.0542mol M (NaCl) 58.5
n(H2O)
4.质量摩尔浓度--bB
bB
nB mA
单位:mol·kg-1
【例3-1】 在常温下取NaCl饱和溶液10.00cm3,测得 其质量为12.003g,将溶液蒸干,得NaCl固体3.173g 。求:(1)NaCl饱和溶液的质量分数,(2)饱和 溶液中NaCl和H2O的物质的量分数,(3)物质的量 浓度,(4)质量摩尔浓度。
物理化学(第五版) 演示文稿4-6 真实液态混合物和真实溶液

aA
def
exp
A A
RT
A
def
(
A
A
)
/
RTMA
bB
B
并且
lim bB 0
A
1
B
A
A
RTAM A
bB
(A)
B
A
A
RT
ln
aA
(B)
(A)与(B)比较 ln aA AMA bB
B
因 xA = 1 / (1+ MA bB)
故
ln
aA
A (1
xA
xA )
A
A
RT
ln
aA
A
= 1095Pa/94.7Pa=11.6
Cd,[%] = p´Cd,实 / p´Cd,计算 = 1095Pa/1894Pa=0.587
**本例中, Cd 对拉乌尔定律产生 哪种偏差? 对亨利定律产生 哪种偏差?
比较 理想稀溶液 真实溶液
pB= kx,B xB pB= kx,B aB,x= kx,B xBB,x
(2) 以[%Cd] = 1仍遵守亨利定律时 T、p下的Cd(1) 为 标准态。
解:(1) 当以 T、p 下的纯液体Cd为标准态时, Cd的组成必须为xCd。
所以,当[%Cd] = 20 时, xCd = 0. 316 a Cd,x = p Cd,实测 / pCd*
= 1095Pa/1840Pa=0.592
§4-6 真实液态混合物和真实溶液
一、真实液态混合物中组分 B 的化学势
1、活度与活度因子
一定温度下,各组分的化学势不符合
B
(l)
B, x
(l)
RT
物理化学2.3拉乌尔定律和亨利定律

数学表达式:
pB T一定 (平衡)
xB
pB=kx,BxB
稀溶液的气、液平衡
kx,B 亨系数
pB=kx,BxB
kx,B 亨利系数 当溶质的组成标度用bB 表示时,亨利定律可表示成:
p B k b, B bB
注意:kx,B ,kb,B 的单位是不同的。
Pa
Pa/b
pB=kx,BxB
注意
亨利定律的适用条件及对象是稀溶液中的溶质,既 溶质分子B周围几乎全是溶剂A分子。
pA,p真B,p空C yA, yB, yC
T一定 (平衡)
xAA,,Bx,BC,x…C
多组分系统的气、液平衡
2. 拉乌尔定律
表述为:
平衡时,稀溶液中溶剂A在 气相中的蒸气分压等于同一 温度下,该纯溶剂的饱和蒸 气压p*A与该溶液中溶剂的摩 尔分数xA的乘积。
数学表达式为:
pA
p
* A
x
A
pA,pB1, yA, yB1, xA, xB1,
T一定 (平衡)
稀溶液的气、液平衡
注意
pA
p
* A
x
A
拉乌尔定律的适用条件及对象是:
稀溶液中的溶剂,既溶剂分子A 周围几乎全是 其它的A分子;
理想液态混合物中各组分。
3. 亨利定律
表述为:
一定温度下,稀溶液中挥发 性溶质B在平衡气相中的分压 力pB与该溶质B在平衡液相中 的摩尔分数xB成正比。
第二章 多组分系统热力学
《基础物理化学》 高等教育出版社,2011
§2.4 稀溶液的两个经验定律
—— 拉乌尔定律和亨利定律
1. 液态混合物和溶液的气、液平衡
设图中系统由组分A,B,C……组成液态混合物或溶液,
pB T一定 (平衡)
xB
pB=kx,BxB
稀溶液的气、液平衡
kx,B 亨系数
pB=kx,BxB
kx,B 亨利系数 当溶质的组成标度用bB 表示时,亨利定律可表示成:
p B k b, B bB
注意:kx,B ,kb,B 的单位是不同的。
Pa
Pa/b
pB=kx,BxB
注意
亨利定律的适用条件及对象是稀溶液中的溶质,既 溶质分子B周围几乎全是溶剂A分子。
pA,p真B,p空C yA, yB, yC
T一定 (平衡)
xAA,,Bx,BC,x…C
多组分系统的气、液平衡
2. 拉乌尔定律
表述为:
平衡时,稀溶液中溶剂A在 气相中的蒸气分压等于同一 温度下,该纯溶剂的饱和蒸 气压p*A与该溶液中溶剂的摩 尔分数xA的乘积。
数学表达式为:
pA
p
* A
x
A
pA,pB1, yA, yB1, xA, xB1,
T一定 (平衡)
稀溶液的气、液平衡
注意
pA
p
* A
x
A
拉乌尔定律的适用条件及对象是:
稀溶液中的溶剂,既溶剂分子A 周围几乎全是 其它的A分子;
理想液态混合物中各组分。
3. 亨利定律
表述为:
一定温度下,稀溶液中挥发 性溶质B在平衡气相中的分压 力pB与该溶质B在平衡液相中 的摩尔分数xB成正比。
第二章 多组分系统热力学
《基础物理化学》 高等教育出版社,2011
§2.4 稀溶液的两个经验定律
—— 拉乌尔定律和亨利定律
1. 液态混合物和溶液的气、液平衡
设图中系统由组分A,B,C……组成液态混合物或溶液,
物理化学第四章 溶液

上一内容 下一内容 回主目录
返回
2012-3-17
二、亨利定律
稀溶液上挥发性溶质的分压与溶质的摩尔分数成正 比。但比例常数不为pB*(1803年,Henry): pB=kx,B xB 换算浓度可有:pB=kc,B cB /c (c =1mol/L); pB=kb,B bB/b (b =1mol/kg); pB=k%,B[%B] 等。 k称为亨利系数,其值与T、p、溶剂、溶质以及溶液 组成的表示方法有关。 使用亨利定律要求溶质在气、液两相中的存在形态 相同。如水中NH3、HCl不能用,CO2只可近似应用。
∂∆ G ∆ mix S = − mix = − R ∑ nB ln xB ∂T p B
B
∂∆ mix G = 0 ∆ mixV = ∂p T
上一内容 下一内容 回主目录
∆ mix H = ∆ mix G + T ∆ mix S = 0
返回
2012-3-17
上一内容 下一内容 回主目录
返回
2012-3-17
三、偏摩尔量的的几个重要公式
1、集合公式 、 定T定p定组成条件下:
dZ = ∑ Z BdnB
nk
在保持偏摩尔量不变的情况下,对上式积分
Z = Z1 ∫ dn1 + Z 2 ∫ dn2 + ⋅ ⋅ ⋅ + Z k ∫ dnk
0 0 0 n1 n2
= n1 Z1 + n2 Z 2 + ⋅ ⋅ ⋅ + nk Z k
上一内容 下一内容 回主目录
返回
2012-3-17
三、拉乌尔定律与亨利定律的应用
1、用拉乌尔定律测定非挥发性溶质的摩尔质量M 、用拉乌尔定律测定非挥发性溶质的摩尔质量
返回
2012-3-17
二、亨利定律
稀溶液上挥发性溶质的分压与溶质的摩尔分数成正 比。但比例常数不为pB*(1803年,Henry): pB=kx,B xB 换算浓度可有:pB=kc,B cB /c (c =1mol/L); pB=kb,B bB/b (b =1mol/kg); pB=k%,B[%B] 等。 k称为亨利系数,其值与T、p、溶剂、溶质以及溶液 组成的表示方法有关。 使用亨利定律要求溶质在气、液两相中的存在形态 相同。如水中NH3、HCl不能用,CO2只可近似应用。
∂∆ G ∆ mix S = − mix = − R ∑ nB ln xB ∂T p B
B
∂∆ mix G = 0 ∆ mixV = ∂p T
上一内容 下一内容 回主目录
∆ mix H = ∆ mix G + T ∆ mix S = 0
返回
2012-3-17
上一内容 下一内容 回主目录
返回
2012-3-17
三、偏摩尔量的的几个重要公式
1、集合公式 、 定T定p定组成条件下:
dZ = ∑ Z BdnB
nk
在保持偏摩尔量不变的情况下,对上式积分
Z = Z1 ∫ dn1 + Z 2 ∫ dn2 + ⋅ ⋅ ⋅ + Z k ∫ dnk
0 0 0 n1 n2
= n1 Z1 + n2 Z 2 + ⋅ ⋅ ⋅ + nk Z k
上一内容 下一内容 回主目录
返回
2012-3-17
三、拉乌尔定律与亨利定律的应用
1、用拉乌尔定律测定非挥发性溶质的摩尔质量M 、用拉乌尔定律测定非挥发性溶质的摩尔质量
4-3多组分系统热力学-理想液态混合物与理想稀溶液

物理化学
Physical Chemistry
物理化学(上册)
绪论 第一章 气体 第二章 热力学第一定律 第三章 热力学第二定律 第四章 多组分系统热力学 第五章 化学平衡 第六章 相平衡
第四章 多组分系统热力学
§4-!本章基本要求 §4-1多组分系统热力学概念 §4-2拉乌尔定律与亨利定律 §4-3偏摩尔量 §4-4化学势 §4-5理想液态混合物 §4-6理想稀溶液 §4-7活度活度系数 §4-8化学势小节 §4-$小结与学习指导
d* S*dT V *dp
B
B
B
mixG p
T
B
nBVB
B
nBVB* mixV
2. mixV 0 或 V mix m 0
mix p
G
T
(RT
nB ln xB )
B
p
T
0
§4-5理想液态混合物
四、理想液态混合物混合性质
dG B S B dT VB dp
dG * S * dT V *dp
B
B
6.
mixU mix H P mixV 0
mixU 0 或 mixU m 0
§4-5理想液态混合物
四、理想液态混合物混合性质
小结: 1. mixV=0 , mixU=0 , mixH=0 2. Q=0, W=0 3. mixS=-RnBlnB>0 (绝热 S>0)
mixA=RTnBlnB<0 (恒温恒容W =0 A<0) mixG=RTnBlnB<0 (恒温恒压W =0 G<0)
§4-6理想稀溶液
一、理想稀溶液定义 无限稀溶液,溶质的浓度趋于零的溶液。 对溶剂(A表示)用符合拉乌尔定律
Physical Chemistry
物理化学(上册)
绪论 第一章 气体 第二章 热力学第一定律 第三章 热力学第二定律 第四章 多组分系统热力学 第五章 化学平衡 第六章 相平衡
第四章 多组分系统热力学
§4-!本章基本要求 §4-1多组分系统热力学概念 §4-2拉乌尔定律与亨利定律 §4-3偏摩尔量 §4-4化学势 §4-5理想液态混合物 §4-6理想稀溶液 §4-7活度活度系数 §4-8化学势小节 §4-$小结与学习指导
d* S*dT V *dp
B
B
B
mixG p
T
B
nBVB
B
nBVB* mixV
2. mixV 0 或 V mix m 0
mix p
G
T
(RT
nB ln xB )
B
p
T
0
§4-5理想液态混合物
四、理想液态混合物混合性质
dG B S B dT VB dp
dG * S * dT V *dp
B
B
6.
mixU mix H P mixV 0
mixU 0 或 mixU m 0
§4-5理想液态混合物
四、理想液态混合物混合性质
小结: 1. mixV=0 , mixU=0 , mixH=0 2. Q=0, W=0 3. mixS=-RnBlnB>0 (绝热 S>0)
mixA=RTnBlnB<0 (恒温恒容W =0 A<0) mixG=RTnBlnB<0 (恒温恒压W =0 G<0)
§4-6理想稀溶液
一、理想稀溶液定义 无限稀溶液,溶质的浓度趋于零的溶液。 对溶剂(A表示)用符合拉乌尔定律
《物理化学》(南大第五版)知识点总结

γ γ
W=ΔU= CV dT ;ΔH= Cp dT
不可逆绝热过程:Q=0 ; 利用 CV(T2-T1)=-pe(V2-V1)求出 T2, W=ΔU= CV dT ;ΔH= Cp dT 2、相变化 可逆相变化:ΔH=Q=nΔ_H; W=-p(V2-V1)=-pVg=-nRT ; ΔU=Q+W
B (T , p, sln ) b , B (T ) RT ln a b , B ; ab,B=γb,B bB;
标准态为:同温下 bB=1 且符合
亨利定律的溶质(假想状态) 。
B (T , p, sln ) %, (T ) RT ln a%, B ; a%,B=γ%,B[%B]; B
标准态为:同温下[B%]=1 且
符合亨利定律的溶质(一般为假想状态) 。 三、各种平衡规律 1、液态混合物的气液平衡
* pA=p * A ax,A ; pA=p A ax,A ; p=pA+pB
2、溶液的气液平衡
pA=p * A ax,A;pB=kx,Bax,B=kb,Bab,B=k%,Ba%,B;p=pA+pB
r Gm (T ) RT ln K
[ p( H 2 ) / p ][c( ZnCl 2 )] c2 (H C l )
三、 范特荷夫等温方程
r Gm (T ) r Gm (T ) RT ln J RT ln J / K
四、平衡常数与温度的关系
B f Gm ( B,298)
(4)ΔG 与温度的关系 ΔG=ΔH-TΔS ,设 ΔH、ΔS 不遂温度变化。 五、化学势 1、化学式的定义和物理意义
B (
G ) T , p ,nc ( c B ) ;在 T、p 及其他物质的量保持不变的情况下,增加 1molB 物质引 n B
W=ΔU= CV dT ;ΔH= Cp dT
不可逆绝热过程:Q=0 ; 利用 CV(T2-T1)=-pe(V2-V1)求出 T2, W=ΔU= CV dT ;ΔH= Cp dT 2、相变化 可逆相变化:ΔH=Q=nΔ_H; W=-p(V2-V1)=-pVg=-nRT ; ΔU=Q+W
B (T , p, sln ) b , B (T ) RT ln a b , B ; ab,B=γb,B bB;
标准态为:同温下 bB=1 且符合
亨利定律的溶质(假想状态) 。
B (T , p, sln ) %, (T ) RT ln a%, B ; a%,B=γ%,B[%B]; B
标准态为:同温下[B%]=1 且
符合亨利定律的溶质(一般为假想状态) 。 三、各种平衡规律 1、液态混合物的气液平衡
* pA=p * A ax,A ; pA=p A ax,A ; p=pA+pB
2、溶液的气液平衡
pA=p * A ax,A;pB=kx,Bax,B=kb,Bab,B=k%,Ba%,B;p=pA+pB
r Gm (T ) RT ln K
[ p( H 2 ) / p ][c( ZnCl 2 )] c2 (H C l )
三、 范特荷夫等温方程
r Gm (T ) r Gm (T ) RT ln J RT ln J / K
四、平衡常数与温度的关系
B f Gm ( B,298)
(4)ΔG 与温度的关系 ΔG=ΔH-TΔS ,设 ΔH、ΔS 不遂温度变化。 五、化学势 1、化学式的定义和物理意义
B (
G ) T , p ,nc ( c B ) ;在 T、p 及其他物质的量保持不变的情况下,增加 1molB 物质引 n B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等等。
2.集合公式
若体系发生的过程为等温等压过程,dT=0,dP=0,则
将此式积分,得 ——偏摩尔量的集合公式
它的物理意义——在多组分体系中,广度性质Z等于体系中各组分的偏摩尔量与物质的量之乘积的加和。
例如:
二组分体系,有
与纯物质的摩尔量相似,V = nVm
集合公式是偏摩尔量最主要的性质。另一个性质是吉布斯-杜亥姆公式。
4、系统的组成改变,偏摩尔量也会改变。
xB→1,偏摩尔量→摩尔量。
5、对于均相多组分体系,也只有【T、P、nC】条件下,体系的广度性质X对nB的偏微商才是偏摩尔量。比如 ,而 就不是。
6、 既是化学势,也是偏摩尔吉布斯函数。
7、热力学关系式中的广延性质(U、H、G等),用该广度性质的偏摩尔量来代替也成立,例如
3.吉布斯-杜亥姆公式Gibbs - Duhem’s equation
将集合公式 微分
据
∴ ——吉布斯-杜亥姆公式
将等式左右两边除以物质的总量,得
——吉布斯-杜亥姆公式
此式表明了【T、P】下系统各偏摩尔量之间是联合联系,联合依赖的。
例如:
二组分体系有
n1dV1.m+ n2dV2.m= 0 ;
x1dV1.m+ x2dV2.m= 0 ——→dV1.m= -x2dV2.m/ x1
在【T、P、nC】条件下,
在系统中不断加入组分B,
同时测出相应的体积,
作nB——V图,
则曲线的斜率即为偏摩尔体积。
关于偏摩尔量,要注意几点:图4-1
1、只有广度性质才有对应的偏摩尔量。因为只有广度性质才与体系中物质的量有关。
2、偏摩尔量也是状态函数,是强度性质。
3、只有均相多组分体系才使用偏摩尔量的概念。单组分体系的偏摩尔量等于其摩尔量。
定义——系统中物质B的化学势为:
μB= GB=
物理意义——在恒T、恒P下,除B组分外其它物质的量不变时,加入dnB的物质后系统吉布斯函数发生相应的变化,dGB/dnB的比值称为B组分的化学势。或:在大量物系中加入1molB组分所引起的系统吉布斯函数的改变值。
注意:
(1)化学势是体系的状态函数,强度性质,单位J/mol。
第4章多组分系统热力学
重点:
偏摩尔量的定义,化学势的定义,纯理想气体、理想气体混合物、理想液态混合物和理想稀溶液中各组分化学势的表达式,拉乌尔定律和亨利定律的内容及应用,理想液态混合物的定义以及理想液态混合物的混合性质,理想稀溶液的定义及稀溶液的依数性及其应用条件。
难点:
理想稀溶液中溶质化学势的表达式中标态的规定。
(2)化学势与温度、压力有关。
(3)纯物质的化学势为:μB= GB= = =Gm
(4)化学势的绝对值不能确定,所以不同物质的化学势不能作比较。
(5)化学势总是指某种物质的化学势,没有整个物系的化学势这种概念,另外化学势,如H2O(l)+H2O(g)物系,只有一种物质,有两个相,化学势也有两个。
2.组成可变的多组分系统的热力学基本方程
说明——【T、P】下,系统中某一个或几个组分的量发生变化时,其它各组分的偏摩尔量也要随之变化,而且系统中各组分偏摩尔量随浓度的变化并不是彼此独立的,而是相互联系的。
§4.2化学势Chemical potential
在各偏摩尔量中,以偏摩尔吉布斯函数应用最广泛,有另一个名称——化学势
1.化学势的定义及表示式
设系统中含有k种物质,其物质的量分别为n1、n2、….、nk,则
G = f(T,p,n1,n2,….,nk)
全微分,有
dG = + + + +….
= + +
而等式在多组分物系中仍然适用,就有
= -S = V
代入dG的全微分式,有
dG = -SdT+Vdp+
或者是,
往无限大的体系中加入1摩尔B物质而引起体系广度性质Z的改变量;
例如:
表示水的偏摩尔体积partial molar volume of water,其物理意义是在【T、P】下,往无限大的体系(此体系不一定是由水组成)中加入1mol水,体系体积的变化量;或往有限的体系中加入微量的水(之所以限制微量,是为了保证体系nC不变)而引起该体系体积的变化。
那么,对于单相多组分系统,是否具有这种简单的加和性呢?
一般来说,不论是什么系统,物质的质量(克)和物质的量(摩尔)总是具有加和性的。但是,系统的其他广度性质则不一定具有简单的加和性。
以体积这一广延性质为例,
Vm*(水)= 18.09 cm3/mol,Vm*(乙醇)= 58.35 cm3/mol,
取1mol水和1mol乙醇混合,其体积V≠(18.09+58.35)cm3= 76.44 cm3,而是74.40 cm3。
重要公式
1.
2.
3.
前言
多组分系统——含两个或两个以上组分的系统称为多组分系统。可以是多相的,也可以是单相的。
根据研究方法的差别,多组分单相系统分为混合物和溶液:
混合物mixture——对多组分单相系统中的各组分用相同的方法研究,则称为混合物。
溶液solution——将多组分单相系统分为溶剂和溶质,并用不同的方法研究,则该系统称为溶液。
说明两组分混合前的体积和(V1+V2)与混合后的实际体积并不相等;两者的差值ΔV亦没有简单的规律。【Flash动画4-1】要找出规律,须引入“偏摩尔量”这个新概念。
在多组分(k个组分)的均相混合系统中,某一广度性质X(例如V、U、H、G),是T和P和各物质物质的量n的函数,即
X = f(T, P, n1,n2, … …nk),显然,X的全微分为
式中nC是除B物质以外的所有其他物质物质的量,B不同,nC也要相应变化。现令
称为B物质的某广度性质X的偏摩尔量partial molar quantities。
则上式可写成
从定义式可以看出,
偏摩尔量的物理意义——在等温等压下,其它组分物质的量不变的条件下,在系统中加入微量B物质dnB而引起Z的微小变化dZ与dnB之比。
气态混合物真实混合物
混合物液态混合物混合物
固态混合物理想混合物拉乌尔定律
遵循一定的规律
液态溶液理想稀溶液亨利定律
溶液溶液
固态溶液真实溶液
电解质溶液
溶液
非电解质溶液
§4.1偏摩尔量Partial molar quantities
1.偏摩尔量
对于纯物质,广度性质具有加和性:
V = nVm,U = nUm,S = nSm,等。
2.集合公式
若体系发生的过程为等温等压过程,dT=0,dP=0,则
将此式积分,得 ——偏摩尔量的集合公式
它的物理意义——在多组分体系中,广度性质Z等于体系中各组分的偏摩尔量与物质的量之乘积的加和。
例如:
二组分体系,有
与纯物质的摩尔量相似,V = nVm
集合公式是偏摩尔量最主要的性质。另一个性质是吉布斯-杜亥姆公式。
4、系统的组成改变,偏摩尔量也会改变。
xB→1,偏摩尔量→摩尔量。
5、对于均相多组分体系,也只有【T、P、nC】条件下,体系的广度性质X对nB的偏微商才是偏摩尔量。比如 ,而 就不是。
6、 既是化学势,也是偏摩尔吉布斯函数。
7、热力学关系式中的广延性质(U、H、G等),用该广度性质的偏摩尔量来代替也成立,例如
3.吉布斯-杜亥姆公式Gibbs - Duhem’s equation
将集合公式 微分
据
∴ ——吉布斯-杜亥姆公式
将等式左右两边除以物质的总量,得
——吉布斯-杜亥姆公式
此式表明了【T、P】下系统各偏摩尔量之间是联合联系,联合依赖的。
例如:
二组分体系有
n1dV1.m+ n2dV2.m= 0 ;
x1dV1.m+ x2dV2.m= 0 ——→dV1.m= -x2dV2.m/ x1
在【T、P、nC】条件下,
在系统中不断加入组分B,
同时测出相应的体积,
作nB——V图,
则曲线的斜率即为偏摩尔体积。
关于偏摩尔量,要注意几点:图4-1
1、只有广度性质才有对应的偏摩尔量。因为只有广度性质才与体系中物质的量有关。
2、偏摩尔量也是状态函数,是强度性质。
3、只有均相多组分体系才使用偏摩尔量的概念。单组分体系的偏摩尔量等于其摩尔量。
定义——系统中物质B的化学势为:
μB= GB=
物理意义——在恒T、恒P下,除B组分外其它物质的量不变时,加入dnB的物质后系统吉布斯函数发生相应的变化,dGB/dnB的比值称为B组分的化学势。或:在大量物系中加入1molB组分所引起的系统吉布斯函数的改变值。
注意:
(1)化学势是体系的状态函数,强度性质,单位J/mol。
第4章多组分系统热力学
重点:
偏摩尔量的定义,化学势的定义,纯理想气体、理想气体混合物、理想液态混合物和理想稀溶液中各组分化学势的表达式,拉乌尔定律和亨利定律的内容及应用,理想液态混合物的定义以及理想液态混合物的混合性质,理想稀溶液的定义及稀溶液的依数性及其应用条件。
难点:
理想稀溶液中溶质化学势的表达式中标态的规定。
(2)化学势与温度、压力有关。
(3)纯物质的化学势为:μB= GB= = =Gm
(4)化学势的绝对值不能确定,所以不同物质的化学势不能作比较。
(5)化学势总是指某种物质的化学势,没有整个物系的化学势这种概念,另外化学势,如H2O(l)+H2O(g)物系,只有一种物质,有两个相,化学势也有两个。
2.组成可变的多组分系统的热力学基本方程
说明——【T、P】下,系统中某一个或几个组分的量发生变化时,其它各组分的偏摩尔量也要随之变化,而且系统中各组分偏摩尔量随浓度的变化并不是彼此独立的,而是相互联系的。
§4.2化学势Chemical potential
在各偏摩尔量中,以偏摩尔吉布斯函数应用最广泛,有另一个名称——化学势
1.化学势的定义及表示式
设系统中含有k种物质,其物质的量分别为n1、n2、….、nk,则
G = f(T,p,n1,n2,….,nk)
全微分,有
dG = + + + +….
= + +
而等式在多组分物系中仍然适用,就有
= -S = V
代入dG的全微分式,有
dG = -SdT+Vdp+
或者是,
往无限大的体系中加入1摩尔B物质而引起体系广度性质Z的改变量;
例如:
表示水的偏摩尔体积partial molar volume of water,其物理意义是在【T、P】下,往无限大的体系(此体系不一定是由水组成)中加入1mol水,体系体积的变化量;或往有限的体系中加入微量的水(之所以限制微量,是为了保证体系nC不变)而引起该体系体积的变化。
那么,对于单相多组分系统,是否具有这种简单的加和性呢?
一般来说,不论是什么系统,物质的质量(克)和物质的量(摩尔)总是具有加和性的。但是,系统的其他广度性质则不一定具有简单的加和性。
以体积这一广延性质为例,
Vm*(水)= 18.09 cm3/mol,Vm*(乙醇)= 58.35 cm3/mol,
取1mol水和1mol乙醇混合,其体积V≠(18.09+58.35)cm3= 76.44 cm3,而是74.40 cm3。
重要公式
1.
2.
3.
前言
多组分系统——含两个或两个以上组分的系统称为多组分系统。可以是多相的,也可以是单相的。
根据研究方法的差别,多组分单相系统分为混合物和溶液:
混合物mixture——对多组分单相系统中的各组分用相同的方法研究,则称为混合物。
溶液solution——将多组分单相系统分为溶剂和溶质,并用不同的方法研究,则该系统称为溶液。
说明两组分混合前的体积和(V1+V2)与混合后的实际体积并不相等;两者的差值ΔV亦没有简单的规律。【Flash动画4-1】要找出规律,须引入“偏摩尔量”这个新概念。
在多组分(k个组分)的均相混合系统中,某一广度性质X(例如V、U、H、G),是T和P和各物质物质的量n的函数,即
X = f(T, P, n1,n2, … …nk),显然,X的全微分为
式中nC是除B物质以外的所有其他物质物质的量,B不同,nC也要相应变化。现令
称为B物质的某广度性质X的偏摩尔量partial molar quantities。
则上式可写成
从定义式可以看出,
偏摩尔量的物理意义——在等温等压下,其它组分物质的量不变的条件下,在系统中加入微量B物质dnB而引起Z的微小变化dZ与dnB之比。
气态混合物真实混合物
混合物液态混合物混合物
固态混合物理想混合物拉乌尔定律
遵循一定的规律
液态溶液理想稀溶液亨利定律
溶液溶液
固态溶液真实溶液
电解质溶液
溶液
非电解质溶液
§4.1偏摩尔量Partial molar quantities
1.偏摩尔量
对于纯物质,广度性质具有加和性:
V = nVm,U = nUm,S = nSm,等。
