反证法证明多项式不可约
多项式在有理数域上不可约判定,

第21卷 第1期 湖南理工学院学报(自然科学版) Vol.21 No.12008年3月 Journal of Hunan Institute of Science and Technology (Natural Sciences) Mar. 2008有理数域上的一类不可约多项式张 卫,史滋福(湖南师范大学 数学与计算机科学学院,长沙 410081)摘 要: 首先介绍了判别有理数域上多项式不可约的常用结论,讨论了形如12()()()()()1n f x x x a x a x a ϕ=−−−+"的多项式的性质,并且得到了定理:若,6n >()0x ϕ>且它的次数小于的一半,则n 12()()()()()1n f x x x a x a x a ϕ=−−−+"在Q 上不可约.关键词: 有理数域; 不可约多项式; 次数中图分类号:O151.23 文献标识码:A 文章编号: 1672-5298(2008)01-0005-03A Class Irreducible Polynomials on Rational Number FieldZHANG Wei , SHI Zi-fu(Department of Mathematics, Hunan Normal University, Changsha 410081, China)Abstract: Some common results which used to decide a polynomial on rational number field irreducible are explained in this paper. Some properties of polynomial such as 12()()()()()1n f x x x a x a x a ϕ=−−−+"are discussed and some theorem is obtained if ,6n >()0x ϕ>and the degree of ()x ϕ is less than a half of ,then n ()f x is irreducible on rational number field.Key words: rational number field; irreducible polynomial; degree研究数域上不可约多项式就如研究整数中的素数一样重要. 如果F 是代数闭域,则F 上的不可约多项式就是全体的一次多项式,而在素域F 上的不可约多项式研究却是一个复杂的工作. 在我们熟悉的有理数域Q 上,存在着任意次的不可约多项式. 到目前为止,在有理数域Q 上,判断多项式不可约的方法主要有以下几类:Ⅰ 通过多项式的系数与某素数的整除关系来判定不可约,如Eisenstein 判别法及其推广形式[1][2]. Ⅱ 通过多项式的系数与某素数的大小关系来判定不可约,如命题1[3]设是一个素数,且整数适合p 12,,,n a a a "10nk k a =p <<∑,则多项式212()n n f x p a x a x a x =++++"在Q 上不可约.Ⅲ 将多项式作为函数所得到的一些特殊取值来判定不可约,如命题2[4] 若整系数多项式()f x 对于无限个整数值x ,其函数值()f x 都是素数,那么多项式()f x 在Q 上不可约.Ⅳ 通过辅助多项式的根的取值来判定不可约,如 命题3[5] 设是n 个两两不同的整数,那么多项式12,,,n a a a "1()()1ni i f x x a ==−−∏在Q 上不可约.本文给出一类可以通过的多项式的次数或者多项式在某点的取值来进行判定的不可约多项式.收稿日期:2007-12-20 基金项目: 湖南省自然科学基金项目(04JJ40003) 作者简介:张 卫(1963− ), 男,江西赣州人,博士,湖南师范大学讲师. 主要研究方向: 多项式代数和环论命题4[5]设是n (n ≥2)个两两不同的整数,如果多项式12,,,a a a "n 1()()1ni i f x x a ==−+∏在Q 上可约,则n 是一个偶数.引理1 设是n (n ≥3)个两两不同的整数,若多项式12,,,n a a a "212()()()()1n f x x a x a x a =−−−"+在Q 上可约,则存在整系数多项式h x ,使得()2()()f x h x =.证明 因为n ,对于任何整数3≥0x ,或者()201020()()0n x a x a x a −−="或者−2201020010203()()()()()()n x a x a x a x a x a x a −−−≥−−−"2≥,所以,因此0()0f x ≠()f x 没有一次有理因式.现设()()()f x g x h x =是()f x 的真因式分解,其中()g x 与都是整系数多项式,且()h x ()g x 与的次数都小于,令()h x n ()()()x g x h x ϕ=−,由()1i f a =,()()1i i g a h a ==±,于是()0,1,2,,i a i n ϕ==".如果()0x ϕ≠,则必有deg(())x n ϕ<,这是不可能的,所以()0x ϕ=. 因此()()g x h x =,即有2()()f x h x =. 由引理1立即可得.定理1 设是n (n ≥3)个两两不同的整数,则当是偶数时,多项式12,,,n a a a "n 212()()()()1n f x x a x a x a =−−−"+在Q 上不可约.定理2 设是n (n ≥3)个两两不同的整数,且12,,,n a a a "212()()()()1n f x x a x a x a =−−−+".若存在0x , 使得,则0()0f x <()f x 在Q 上不可约.引理2 设是n (n ≥3)个两两不同的整数,且12,,,n a a a "222121()()()()()()1r r n f x x a x a x a x a x a +=−−−−−+"".若()f x 有真因式()g x ,则()g x 的次数至少是的一半.n 证明 设()()()f x g x h x =,且deg(())g x <[2n],由于()1,1,2,,i f a i n ==",所以, ,于是()1i g a =±1,2,,i n ="()g x 至少在[个点恒取值]deg(())12ng x ≥+1+或者1−,此时()g x 是常数,矛盾.推论1 设是n (n ≥3)个两两不同的整数,若多项式12,,,n a a a "222121()()()()()()1r r n f x x a x a x a x a x a +=−−−−−+""有真因式()g x ,则()g x 的次数deg(())[]2ng x r n ≤+−.引理3 设是n (n ≥3)个两两不同的整数, 12,,,n a a a "[]2nr <,且222121()()()()()()1r r n f x x a x a x a x a x a +=−−−−−+"".如果()f x 在Q 上可约,则一定存在整系数多项式,使得()h x 2()()f x h x =.证明 设()f x 的真因式分解()()()f x g x h x =,(),()g x h x 都是整系数多项式,且次数[]2n deg(()),deg(())g x h x r n ≤≤+−[]2n . 令()()()x g x h x ϕ=−,和引理1相仿,由于也有deg(())x n ϕ<,所以()0x ϕ=,即2()()f x h x =.类似地可以证明引理4设是n (n ≥3)个两两不同的整数,且12,,,n a a a "12()()()()()1n f x x x a x a x a ϕ=−−−"+ 6 湖南理工学院学报(自然科学版) 第21卷.第1期 张 卫等:有理数域上的一类不可约多项式 7如果deg(())[]2nr x ϕ=<,且()f x 在Q 上可约,则一定存在整系数多项式,使得()h x 2()()=f x h x .定理3 设是n (n ≥3)个两两不同的整数,且12,,,n a a a "12()()()()()1n f x x x a x a x a ϕ=−−−"+.如果deg(())[]2nr x ϕ=<,且 deg(())x n ϕ+是奇数,则()f x 在Q 上不可约.定理4 设是n (n ≥3)个两两不同的整数,且12,,,n a a a "12()()()()()1n f x x x a x a x a ϕ=−−−"+.如果deg(())[]2nr x ϕ=<,且存在实数0x ,使得0()0f x <,则()f x 在Q 上不可约.定理5 设是n (n >6)个两两不同的整数,且12,,,n a a a "12()()()()()1n f x x x a x a x a ϕ=−−−"+,如果deg(())[]2nr x ϕ=<,且()0x ϕ=没有有理根,则()f x 在Q 上不可约.证明 不妨设,令12n a a a <<<"012n x a =−,因为0()0x ϕ≠,所以01()2r x ϕ≥,从而0001010()()()()()1ϕ−=−−−+"n n f x x x a x a x a <123311()()()()122222124211()()()(122222−⋅⋅⋅⋅⋅−+<−⋅⋅⋅⋅⋅−+""r r n n =222((2)!122−++−−⋅−+=−+n n r r n n 2)!1>. 因为当n 时,62deg(())[]log (2)!22nr x ,所以n ϕ=<<−−0()0f x <,再由定理4即得定理5.鉴于在定理证明中关于()x ϕ其实只利用了01()2r x ϕ≥,所以有推论2 若, 且,那么212()()()()1n f x x a x a x a =−−−+"6n >()f x 在Q 上不可约.最后提出两个问题作为本文的结束. 问题1 定理5在的时候是否也成立?6n =问题2 推论2中由于()x ϕ的次数仅等于1,是否的条件可以去掉? 6n >参考文献[1] 张海山. Eisenstein 判别法的推广[J]. 首都师范大学学报(自然科学版), 2001,22(3):13~15 [2] 陈 侠. 关于整系数不可约多项式[J]. 沈阳航空工业学院学报, 2004,21(1): 77~78 [3] 冯克勤,余红兵. 整数与多项式[M]. 北京: 高等教育出版社, 1999: 138~142[4] 黎伯堂,刘桂真. 高等代数解题技巧与方法[M]. 济南: 山东科学技术出版社, 1999:154~171 [5] 王品超. 高等代数新方法[M]. 济南: 山东教育出版社, 1989: 11~44李克安教授被评为第三届湖南省“双十佳期刊编辑”为了进一步加强编辑队伍建设,鼓励期刊出版行业出人才,出好人才,繁荣和发展期刊出版事业,中共湖南省委宣传部、湖南省新闻出版局联合组织评选了第三届湖南省“双十佳期刊编辑”。
爱森斯坦判法在判断根时的条件爱森斯坦判别法在判断根时的条件爱森斯坦判别法在判断根时的条件爱森斯坦判

爱森斯坦判别法是目前为止用来判断[]Z x 内一个多项式可约与否的最好结果。
爱森斯坦判别法 设给定n 次本原多项式01()[](1)Z n n f x a a x a x x n =+++∈≥L如果存在一个素数p ,使|(0,1,...,1)i p a i n =-,但20|,|n p a p a //,则()f x 在[]Z x 内不可约。
证明:用反证法。
设()f x 在[]Z x 内可约,即()()()f x g x h x =, 其中0101()[],()[].Z Z m m l l g x b b x b x x h x c c x c x x =+++∈=+++∈L L这里0deg ()deg ()g x f x <<。
为方便计,下面式子中多项式(),(),()f x g x h x 的系数,,i i i a b c 的下标大于其对应多项式的次数时,均认为等于零。
因为n m l a b c =,而|n p a /,故|,|m l p b p c //。
另一方面,0|p a ,而000a b c =,故0|p b 或0|p c ;不妨设0|p b ,此时因20|p a /,故0|p c /。
设|(0,...,1)i p b i r =-,但|(0)r p b r m <</。
此时|r p a ,而 011110()r r r r r a b c b c b c b c --=++++L括号中各项均含有因子p ,故0|r p b c 。
但0|,|r p b p c //,p 为素数,矛盾。
由此,()f x 在[]Z x 内不可约。
爱森斯坦判别法是目前为止用来判断Z[x]内一个多项式可约与否的最好结果。
艾森斯坦判别法是代数的定理,给出了判定整系数多项式不能分解为整系数多项式乘积的充分条件。
由高斯定理,这判别法也是多项式在有理数域不可约的充分条件。
艾森斯坦判别法是说:给出下面的整系数多项式如果存在素数p ,使得p 不整除an ,但整除其他ai ; p^2 不整除a0 , 那么f (x ) 是不可约的。
(完整版)高等代数多项式习题解答
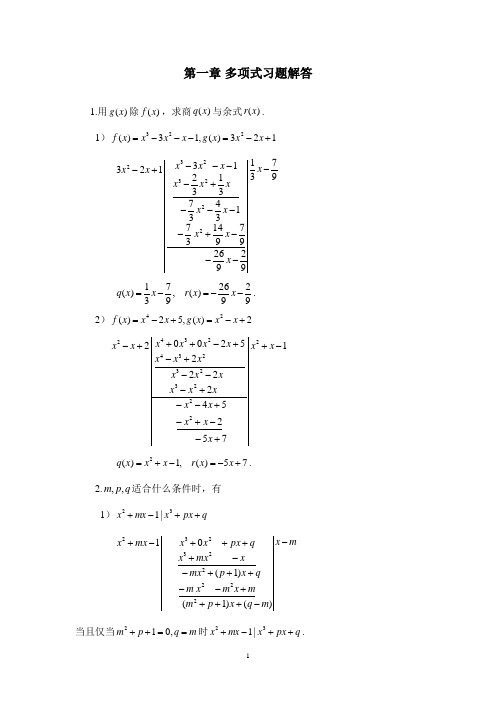
第一章 多项式习题解答1.用)(x g 除)(x f ,求商)(x q 与余式)(x r .1)123)(,13)(223+-=---=x x x g x x x x f9731929269791437134373132131232223232----+----+----+-x x x x x x x x x x x x x x 92926)(,9731)(--=-=x x r x x q . 2)2)(,52)(24+-=+-=x x x g x x x f17525422225200222223232342342-++--+-+--+---+-+-+++-x x x x x x x xx x x x x x x x x x x x x x75)(,1)(2+-=-+=x x r x x x q .2.q p m ,,适合什么条件时,有1)q px x mx x ++-+32|1m x m q x p m mx m x m qx p mx x mx x q px x x mx x --++++--+++--++++-+)()1()1(01222223232 当且仅当m q p m ==++,012时q px x mx x ++-+32|1.本题也可用待定系数法求解.当q px x mx x ++-+32|1时,用12-+mx x 去除q px x ++3,余式为零,比较首项系数及常数项可得其商为q x -.于是有q x mq x q m x mx x q x q px x ++--+=-+-=++)1()()1)((2323.因此有m q p m ==++,012.2)q px x mx x ++++242|1由带余除法可得)1()2()1)(1(2222224m p q x m p m m p mx x mx x q px x --++--++-+-++=++ 当且仅当0)1()2()(22=--++--=m p q x m p m x r 时q px x mx x ++++242|1.即⎩⎨⎧=--+=--010)2(22m p q m p m ,即⎩⎨⎧=+=,1,0p q m 或⎩⎨⎧==+.1,22q m p 本题也可用待定系数法求解.当q px x mx x ++++242|1时,用12++mx x 去除q px x ++24,余式为零,比较首项系数及常数项可得其商可设为q ax x ++2.于是有)1)((2224++++=++mx x q ax x q px x.)()1()(234q x mq a x q ma x a m x ++++++++=比较系数可得.0,1,0=+=++=+mq a p q ma a m 消去a 可得⎩⎨⎧=+=,1,0p q m 或⎩⎨⎧==+.1,22q m p 3.求)(x g 除)(x f 的商)(x q 与余式)(x r .1);3)(,852)(35+=--=x x g x x x x f解:运用综合除法可得327109391362327117083918605023---------商为109391362)(234+-+-=x x x x x q ,余式为.327)(-=x r2)i x x g x x x x f 21)(,)(23+-=--=.解:运用综合除法得:ii ii i i i 892521892421011121+----+-------商为)25(22i ix x +--,余式为i 89+-. 4.把)(x f 表成0x x -的方幂和,即表示成 +-+-+202010)()(x x c x x c c 的形式.1)1,)(05==x x x f ;2);2,32)(024-=+-=x x x x f3).1,73)1(2)(0234-=++-+-+=x i x x i ix x x f分析:假设)(x f 为n 次多项式,令])()()[()()()()(10021000202010--++-+-+=-++-+-+=n n nn x x c x x c c x x c x x c x x c x x c c x f0c 即为0x x -除)(x f 所得的余式,商为10021)()()(--++-+=n n x x c x x c c x q .类似可得1c 为0x x -除商)(x q 所得的余式,依次继续即可求得展开式的各项系数.解:1)解法一:应用综合除法得.5110141110416311563143211143211111111111100000115)(x x f =1)1(5)1(10)1(10)1(5)1(2345+-+-+-+-+-=x x x x x .解法二:把x 表示成1)1(+-x ,然后用二项式展开1)1(5)1(10)1(10)1(5)1(]1)1[(234555+-+-+-+-+-=+-=x x x x x x x2)仿上可得812226122412210412112082422128442302012-----------------432)2()2(8)2(22)2(2411)(+++-+++-=x x x x x f . 3)因为i iii i i i i i i i i i ii ii i i 2111510157104141173121-----------+-------+---- .)()(2))(1()(5)57(73)1(2)(432234i x i x i i x i i x i ix x i ix x x f +++-++-+-+=++-+-+=5.求)(x f 与)(x g 的最大公因式1)1)(,143)(23234--+=---+=x x x x g x x x x x f解法一:利用因式分解),13)(1(143)(3234--+=---+=x x x x x x x x f).1()1(1)(223-+=--+=x x x x x x g因此最大公因式为1+x .解法二:运用辗转相除法得)(3438)(01122132)(1434343)(41432112321212314121)(3122123423422223232x q x x q x x x x x x x x r x x x x x x x x x x r x x x x x x x x x x x x q =+=---------=--+---+--=------++--++-= 因此最大公因式为1+x .2)13)(,14)(2334+-=+-=x x x g x x x f .解:运用辗转相除法得(注意缺项系数补零)2564411627)(125627)(2565391649216491633323)(10310031004911916)(920910310132310323110391031)(13221232323423422223232--=--=+-+-+-+--=-++-+-+-++-+++--=+--++--+++-+-=x x q x x r x x x x x x x r x x x x x x x x x x x x x x x x r x x x x x x x x x x x x q .1))(),((=x g x f3).124624)(,110)(23424+++-=+-=x x x x x g x x x f)()()22(24)()(123x r x f x x x x f x g +=---=,),()22)((241)122()22)(22()(21223x r x x r x x x x x x x f ++-=---+--= ,)()122(22)(24122231x x r x x x x x x x r -=--=--=- 因此.122))(),((2--=x x x g x f6.求)(),(x v x u 使:))(),(()()()()(x g x f x g x v x f x u =+1);22)(,242)(234234---+=---+=x x x x x g x x x x x f解:运用辗转相除法得:)()(1022)(222422)(222221)(3133123423422323242342x q x x q x x xx x r x x x x x x x x x x r xx x x x x x x x x x x x q ==--=---+---+-=--+----++= 因此2)())(),((22-==x x r x g x f .且有 )()()()(11x r x q x g x f +=,),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=..2)()(1)(,1)()(212+=+=--=-=x x q x q x v x x q x u2);452)(,951624)(23234+--=++--=x x x x g x x x x x f解:运用辗转相除法得:)(96)(20999966936)(810249516241)(32422324523131)(3122123423422223232x q x x q x x x xx x x x r xx x x x x x x x x r x x x x x x x x x x x x q =+=+-+-+-+--=+--++--+-=+--+---++--+-= 因此1)())(),((2-=-=x x r x g x f .且有)()()()(11x r x q x g x f +=,),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=..13232)3131(21)()(1)(,3131)()(2212--=+---=--=+-==x x x x x q x q x v x x q x u 3).1)(,144)(2234--=++--=x x x g x x x x x f解:运用辗转相除法得:)(32)(3331431441)(21211)(121222342342222x q x x x r x x x x x x x x x x x x r x x xx x x x x q =--=++-++---++--=-----+= 因此.1)())(),((2==x r x g x f 且有)()()()(11x r x q x g x f +=,),()()()(221x r x q x r x g +=).()()(321x q x r x r =于是)()]()()([)()()()()(21212x q x q x g x f x g x q x r x g x r --=-=)()]()(1[)()(212x g x q x q x f x q ++-=..23)1)(3(1)()(1)(,1)()(232212--+=+-+=+=--=-=x x x x x x q x q x v x x q x u7.设u tx x x g u x x t x x f ++=++++=323)(,22)1()(的最大公因式是一个二次多项式,求u t ,的值.解:运用带余除法有),()()2()1(1)(22)1()(12323x r x g u x t x t u tx x u x x t x x f +=+--++⋅++=++++= 由题意可得,)(1x r 即为)(),(x g x f 的最大公因式.因此有01≠+t .进一步),(])1(211)[()(221x r t t x t x r x g ++-++= ])1(21[)1()2()1()1()(22222t t u x t t t u t t x r +--++-++-+=. 要使)(1x r 为)(),(x g x f 的最大公因式的充要条件是.0)(2=x r 即⎩⎨⎧=--+=-++-+,0)]2()1[(,0)2()1()1(222t t u t t u t t 解得⎪⎩⎪⎨⎧--=+-=⎪⎩⎪⎨⎧+-=--=⎪⎩⎪⎨⎧±==⎩⎨⎧-==.2111,117;2111,117;231,0;4,0i t i u i t i u i t u t u 8.证明:如果),(|)(),(|)(x g x d x f x d 且)(x d 为)(x f 与)(x g 的一个组合,那么)(x d 是)(x f 与)(x g 的一个最大公因式.证明:由)(|)(),(|)(x g x d x f x d 可知)(x d 是)(x f 与)(x g 的一个公因式.下证)(x f 与)(x g 的任意一个公因式是)(x d 的因式.由)(x d 为)(x f 与)(x g 的一个组合可知,存在多项式)(),(x v x u ,使得)()()()()(x g x v x f x u x d +=.设)(x ϕ是)(x f 与)(x g 的任意一个公因式,则)(|)(),(|)(x g x x f x ϕϕ.故)()()()(|)(x g x v x f x u x +ϕ即).(|)(x d x ϕ因此)(x d 是)(x f 与)(x g 的一个最大公因式.9.证明:)()(())(),(())()(),()((x h x h x g x f x h x g x h x f =的首项系数为1). 证明:存在多项式)(),(x v x u ,使得)()()()())(),((x g x v x f x u x g x f +=.所以有)()()()()()()())(),((x h x g x v x h x f x u x h x g x f +=.即)())(),((x h x g x f 是 )()(x h x f 与)()(x h x g 的一个组合.显然有)(|))(),((),(|))(),((x g x g x f x f x g x f .从而)()(|)())(),((),()(|)())(),((x h x g x h x g x f x h x f x h x g x f .由第8题结果)())(),((x h x g x f 是)()(x h x f 与)()(x h x g 的一个最大公因式.又)(x h 是首项系数为1的,因此).())(),(())()(),()((x h x g x f x h x g x h x f =10.如果)(x f ,)(x g 不全为零,证明1))(),(()(,)(),(()((=x g x f x g x g x f x f . 证明:由)(x f ,)(x g 不全为零可得其最大公因式不为零多项式,即.0))(),((≠x g x f 又存在多项式)(),(x v x u ,使得)()()()())(),((x g x v x f x u x g x f +=.于是))(),(()()())(),(()()(1x g x f x g x v x g x f x f x u +=. 因此1))(),(()(,)(),(()((=x g x f x g x g x f x f . 11.如果)(x f ,)(x g 不全为零,且))(),(()()()()(x g x f x g x v x f x u =+,那么1))(),((=x v x u .证明:由)(x f ,)(x g 不全为零可得.0))(),((≠x g x f 由))(),(()()()()(x g x f x g x v x f x u =+有.1))(),(()()())(),(()()(=+x g x f x g x v x g x f x f x u 于是1))(),((=x v x u .12.证明:如果,1))(),((,1))(),((==x h x f x g x f 那么.1))()(),((=x h x g x f 证法一、由条件1))(),((,1))(),((==x h x f x g x f 可得存在多项式)(),(11x v x u ; )(),(22x v x u 使得1)()()()(11=+x g x v x f x u ,1)()()()(22=+x h x v x f x u .两式相乘得1)()()()()()]()()()()()()()()([21211221=+++x h x g x v x v x f x h x v x u x g x v x u x f x u x u . 因此有.1))()(),((=x h x g x f证法二、反证法证明.显然.0))()(),((≠x h x g x f 若,1))()(),((≠x h x g x f 则存在不可约多项式)(x p ,使得)(x p 为)(x f 与)()(x h x g 的公因式.因此有)(|)(x f x p 且)()(|)(x h x g x p .由)(x p 的不可约性有)(|)(x g x p 或)(|)(x h x p .若)(|)(x g x p ,则)(x p 为)(x f 与)(x g 的一个公因式,与1))(),((=x g x f 相矛盾.若)(|)(x h x p ,则)(x p 为)(x f 与)(x h 的一个公因式,与1))(),((=x h x f 相矛盾.因此1))()(),((≠x h x g x f 不成立,即有.1))()(),((=x h x g x f13.设)(),(),(),(,),(),(2121x g x g x g x f x f x f n m 都是多项式,而且).,,2,1;,,2,1(,1))(),((n j m i x g x f j i ===求证:1))()()(),()()((2121=x g x g x g x f x f x f n m .证明:由),,2,1(1))(),((1n j x g x f j ==,反复利用第12题结果可得1))()()(),((211=x g x g x g x f n .类似可得.,,2,1))()()(),((21m i x g x g x g x f n i ==再反复利用12题结果可得1))()()(),()()((2121=x g x g x g x f x f x f n m .14.证明:如果,1))(),((=x g x f 那么.1))()(),()((=+x g x f x g x f 证明:方法一.由,1))(),((=x g x f 存在多项式)(),(x v x u 使得1)()()()(=+x g x v x f x u .从而有,1)())()(())()()((,1))()()(()())()((111111=+-++=++-x g x v x u x g x f x u x g x f x v x f x v x u 因此有.1))()(),((,1))()(),((=+=+x g x f x g x g x f x f 由12题结果结论成立.方法二:用反证法.若.1))()(),()((≠+x g x f x g x f 则存在不可约多项式)(x p ,使得)(x p 为)()(x g x f 与)()(x g x f +的公因式.即)()(|)(x g x f x p 且)()(|)(x g x f x p +.由)(x p 的不可约性及)()(|)(x g x f x p ,有)(|)(x f x p 或)(|)(x g x p .若)(|)(x f x p ,又)()(|)(x g x f x p +,因此有)]())()([(|)(x f x g x f x p -+,即)(|)(x g x p ,也即)(x p 为)(x f 与)(x g 的一个公因式,与1))(),((=x g x f 相矛盾.类似可得当)(|)(x g x p 时也与已知1))(),((=x g x f 矛盾.所以.1))()(),()((=+x g x f x g x f15.求下列多项式的公共根:.12)(;122)(23423++++=+++=x x x x x g x x x x f解法一:利用因式分解可得);1)(1(122)(223+++=+++=x x x x x x x f ).1)(1(12)(22234+++=++++=x x x x x x x x g因此1))(),((2++=x x x g x f .)(x f 与)(x g 的公共根为.2321i ±- 解法二:运用辗转相除法求出)(x f 与)(x g 的最大公因式,最大公因式的根即为所求的公共根.),1(2)1)(()(2++--=x x x x f x g ).1)(1()(2+++=x x x x f因此1))(),((2++=x x x g x f .)(x f 与)(x g 的公共根为.2321i ±- 16.判别下列多项式有无重因式: 1);84275)(2345-+-+-=x x x x x x f 解:,4421205)('234+-+-=x x x x x f运用辗转相除法可得.)2(44))('),((22-=+-=x x x x f x f 因此2-x 为)(x f 的三重因式.解法二:试根可得2为)(x f 的根)1()2()2()2()43)(2()(23232234++-=----=++--=x x x x x x x x x x x x f .因此2-x 为)(x f 的三重因式. 2).344)(24--+=x x x x f解:).12(4484)('33-+=-+=x x x x x f 1))('),((=x f x f .故)(x f 无重因式. 17.求t 值使13)(23-+-=tx x x x f 有重根.解法一:要使)(x f 有重根,则1))('),((≠x f x f ..63)('2t x x x f +-=),12(33)(')3131(13)(23+-+-=-+-=x t x f x tx x x x f .415)41523)(12(63)('2++-+=+-=t x x t x x x f当,033=-t 即3=t 时),(|)(',)1(3363)('22x f x f x x x x f -=+-=2)1())('),((-=x x f x f ,因此1为)(x f 的三重根. 当0415=+t ,即415-=t 时,21))('),((+=x x f x f ,21-为)(x f 的二重根.解法二:设b a x ab a x b a x b x a x x f 22232)2()2()()()(-+++-=--=. 因此有⎪⎩⎪⎨⎧==+=+.1,2,3222b a t ab a b a 由第一个方程有a b 26-=,代人第三个方程有,0132,1)23(232=+-=-a a a a 即0)12()1(2=+-a a .因此有⎪⎩⎪⎨⎧===,3,1,1t b a 或⎪⎪⎩⎪⎪⎨⎧-==-=.415,4,21t b a即当3=t 时1为)(x f 的三重根;当415-=t 时,21-为)(x f 的二重根.18.求多项式q px x ++3有重根的条件.解:令q px x x f ++=3)(.显然当0==q p 时,0为)(x f 的三重根.当0≠p 时, p x x f +=23)(',q x px xf q px x x f ++=++=32)('31)(3,)427()42729)(32()('222p q p p q x p q x p x f ++-+=. 要使)(x f 有重根,则1))('),((≠x f x f .即,042722=+pq p 即.027423=+q p 显然 0==q p 也满足.027423=+q p 因此)(x f 有重根的条件是.027423=+q p19.如果,1|)1(242++-Bx Ax x 求.,B A解法一:利用整除判定方法,1|)1(242++-Bx Ax x 的充要条件是用2)1(-x 除124++Bx Ax ,余式为零.)31()42()32()1(12224B A x A B A B Ax Ax x Bx Ax --++++++-=++.因此有0)31()42(=--++B A x A B ,即⎩⎨⎧-==⎩⎨⎧=--=+.2,1.031,042B A B A A B 解法二:要使1|)1(242++-Bx Ax x 成立,则1至少是124++Bx Ax 的二重根.因此1既是124++Bx Ax 的根,也是其导数的根.而Bx Ax Bx Ax 24)'1(324+=++.故有⎩⎨⎧-==⎩⎨⎧=+=++.2,1.024,01B A B A B A 解法三:利用待定系数法.令Dx D C x D C A x A C Ax D Cx Ax x Bx Ax +-++-+-+=++-=++)2()2()2()()1(12342224因此有⎪⎪⎩⎪⎪⎨⎧==-=+-=-.1,02,2,02D D C B D C A A C 解得⎪⎪⎩⎪⎪⎨⎧==-==.1,2,2,1D C B A 20.证明:!!212n x x x n++++ 不能有重根.证明:令,!!21)(2n x x x x f n++++= 则,)!1(!21)('12-++++=-n x x x x f n因此有,!)(')(n x x f x f n +=从而有)!),('())('),((n x x f x f x f n =.!n x n因式只有)0(≠c c 及)1,0(n k c cx k ≤≤≠.而)1,0(n k c cx k ≤≤≠显然不是)('x f 的因式.因此有1)!),('())('),((==n x x f x f x f n.所以)(x f 没有重根.21.如果a 是)('''x f 的一个k 重根,证明a 是)()()](')('[2)(a f x f a f x f ax x g +-+-=的一个3+k 重根. 证明:)],(')('[21)(''2)(')(''2)](')('[21)('a f x f x f a x x f x f a x a f x f x g ---=--++=).('''2)(''21)('''2)(''21)(''x f ax x f x f a x x f x g -=--+=显然有0)(")(')(===a g a g a g .由a 是)('''x f 的一个k 重根可得a 是)(''x g 的一个1+k 重根,设a 是)(x g 的s 重根,则3,12+=+=-k s k s .本题常见错误证法.错误证法一:由a 是)('''x f 的一个k 重根就得出a 是)(''x f 的一个1+k 重根,a 是)('x f 的一个2+k 重根,a 是)(x f 的一个3+k 重根,于是)(2)()()()](')('[2)(3x h a x a f x f a f x f a x x g k +-=+-+-=从而a 是)(x g 的3+k 重根.事实上,由a 是)('''x f 的一个k 重根推不出a 是)(''x f 的一个1+k 重根,a 是)('x f 的一个2+k 重根,a 是)(x f 的一个3+k 重根. 如3)()()()(23+-+-+-=+a x a x a x x f k ,则1)(2))(3()('2+-+-+=+a x a x k x f k ,2))(2)(3()(''1+-++=+k a x k k x f .a 既不是)(x f 的根,也不是)('x f 与)(''x f 的根.错误证法二:由)],(')('[21)(''2)(')(''2)](')('[21)('a f x f x f a x x f x f a x a f x f x g ---=--++=)('''2)(''21)('''2)(''21)(''x f ax x f x f a x x f x g -=--+=得出a 是)(''x g 的1+k 重根,直接得出a 是)(x g 的3+k 重根,缺了a 是)(x g 与)('x g 的根验证.22.证明:0x 是)(x f 的k 重根的充分必要条件是,0)()(')(0)1(00====-x f x f x f k 而.0)(0)(≠x f k证明:必要性.设0x 是)(x f 的k 重根,从而0x x -是)(x f 的k 重因式,从而是)('x f 的1-k 重因式,是)(''x f 的2-k 重因式,...,是)()1(x f k -的单因式,而不是)()(x f k 的因式.因此0x 是)(x f ,)('x f ,)(''x f ,...,)()1(x f k -的根,而不是)()(x f k 的根.故有,0)()(')(0)1(00====-x f x f x f k 而.0)(0)(≠x f k充分性.由,0)()(')(0)1(00====-x f x f x f k 而0)(0)(≠x f k 可知0x 是)(x f ,)('x f ,)(''x f ,...,)()1(x f k -的根,而不是)()(x f k 的根.因此0x 是)()1(x f k -的单根,是)()2(x f k -二重根,依此类推,是)(x f 的k 重根.23.举例说明断语“如果α是)('x f 的m 重根,那么α是)(x f 的1+m 重根”是不对的.解:例如2)()(1+-=+m x x f α,m x m x f ))(1()('α-+=.α是)('x f 的m 重根,但α不是)(x f 的根.24.证明:如果),(|)1(n x f x -那么)(|)1(n n x f x -.证明:由)(|)1(n x f x -可得)()1()(x g x x f n -=.从而.0)1(=f 因此有),()1()(x h x x f -=从而有).()1()(n n n x h x x f -=即)(|)1(n n x f x -.证法二:要证)(|)1(n n x f x -,只要证1-n x 在复数域上的各个根都是)(n x f 的根.1-n x 的根为.1,,2,1,0,2sin 2cos-=+=n k nk i n k x k ππ由)(|)1(n x f x -可得)()1()(x g x x f n -=.从而.0)1(=f 从而0)1()(==f x f nk .即,2sin 2cos nk i n k x k ππ+=1,,2,1,0-=n k 都是)(n x f 的根.因此有)(|)1(n n x f x -.25.证明:如果)()(|)1(32312x xf x f x x +++,那么).(|)1(),(|)1(21x f x x f x --证明:要证)(|)1(),(|)1(21x f x x f x --成立,只要证1是)(1x f 和)(2x f 的根.12++x x 的两个根为231,23121ii --=+-=εε.由)()(|)1(32312x xf x f x x +++可得)()1()()(23231x g x x x xf x f ++=+.于是,0)()1()()(,0)()1()()(2223222321112312131121=++=+=++=+εεεεεεεεεεεεg f f g f f即0)1(231)1(,0)1(231)1(2121=+-=--f if f i f .故有.0)1()1(21==f f 所以 )(|)1(),(|)1(21x f x x f x --.26.求多项式1-n x 在复数范围内和在实数范围内的因式分解. 解:1-n x 的根为.1,,2,1,0,2sin 2cos -=+=n k nk i n k k ππε故在复数范围内的分解式为)())()(1(112-----=-n n x x x x x εεε .在实数范围内,因k n k -=εε,)0(n k <<.当n 为奇数时,1-n x 的根中一个为实根,其余为虚根,其分解式为]1)([]1)(][1)()[1(12121222212++-++-++--=-+---x x x x x x x x n n n n nεεεεεε .当n 为偶数时,1-n x 的根中二个为实根,即,1±其余为虚根,其分解式为].1)([]1)(][1)()[1)(1(11212222212++-++-++-+-=-+---x x x x x x x x x n n n n nεεεεεε27.求下列多项式的有理根. 1);1415623-+-x x x解:多项式可能的有理根为.14,7,2,1±±±±由系数取值可知,x 取负数时,多项式的值均为负的,故该多项式没有负根.检验得2为其根,进一步运用综合除法可得074114821415612-----即)74)(2(14156223+--=-+-x x x x x x ,显然742+-x x 没有有理根.因此1415623-+-x x x 仅有一个有理根2,且为单根.2);157424---x x x解:多项式可能的有理根为.41,21,1±±±444222026242113121570421------------因此有)1()12()444()21(1574222224--+=--+=---x x x x x x x x x ,显然12--x x 没有有理根.因此21-为157424---x x x 的二重根.3).3111462345----+x x x x x解:多项式可能的有理根为.3,1±±检验得1-为其根,进一步运用综合除法可得1213630351133511038601138601311146111--------------故)3()1()12)(3()1(3111464222345-+=++-+=----+x x x x x x x x x x x .即1-为其四重跟,3为单根.28.下列多项式在有理数域上是否可约? 1);12+x解:显然12+x 无有理根,又为二次的,故在有理数域上不可约. 2);2128234++-x x x解:取素数2=p ,满足艾森斯坦判别法的条件,因此在有理数域上不可约. 3);136++x x 解:令,1+=y x).(3918211561)1()1(1)(234563636y g y y y y y y y y x x x f =++++++=++++=++=取素数,3=p )(y g 满足艾森斯坦判别法条件,因此在有理数域上不可约,从而)(x f 在有理数域上不可约.4)p px x p ,1++为奇素数;解:令1-=y x ,由p 为奇数可得1)1()1(1)(+-+-=++=y p y px x x f p p).()(1222211y g p y p C y C y C yC y p p p p p p p p p =-++--+-=---- 由组合数定义)11(-≤≤p k C kp 均为整数,且12)1()1()1(⋅-+--= k k k p p p C k p,分子中有因子p ,分母个各数均小于p ,又p 为素数,因此约分时p 不会被约去,因此有kpC p |,取素数为p ,)(y g 满足艾森斯坦判别式条件,因此)(y g 在有理数域上不可约,从而)(x f 在有理数域上不可约. 5)k kx x ,144++为整数. 解:令,1+=y x 则有).(2)1(4641)1(4)1(1423444y g y k y y y y k y kx x =+++++=++++=++取素数,2=p )(y g 满足艾森斯坦判别法条件,因此在有理数域上不可约,从而)(x f 在有理数域上不可约.。
关于多项式不可约性的定理

关于多项式不可约性的定理
多项式不可约性定理(Irreducibility Theorem)是数论中
一个重要的定理,它可以用来判断一个多项式是否可以被约分,从而可以帮助数学家们更好地求解多项式的根。
多项式不可约性定理的形式很简单:任何一个非负整数的多项式,只要它的系数不全为
0,就是不可约的。
这个定理的证明是由古典数论中的结论——“欧拉定理”推导而来的。
欧拉定理宣称:任何一个大于1的正整数都可以表示为质数的乘积。
通过把多项式的系数转换为质数的乘积,可以把多项式分解为该质数的乘积,从而证明多项式不可约性定理。
多项式不可约性定理有着重要的应用价值。
它可以用来确定一个多项式是否可以被约分,以及求解多项式的根。
例如,如果一个多项式的系数都是质数,那么它就是不可约的,而且可以求出它的根;如果一个多项式的系数不全是质数,那么它就是可约的,可以用约分的方法求解。
多项式不可约性定理的另一个重要的应用是,它可以用来证明另外一个重要的定理,即“欧拉定理”。
例如,如果一个正整数大于
1,它可以表示为质数的乘积,那么它就是不可约的,而
且可以用多项式不可约性定理来证明。
总之,多项式不可约性定理是数论中一个重要的定理,它可以用来判断一个多项式是否可以被约分,从而可以帮助数学家们更好地求解多项式的根,也可以用来证明欧拉定理。
因此,它对数论的研究有着重要的意义。
三个多项式不可约性的证明

三个多项式(不)可约性的证明1(浙大1993(16分)).证明f(x)=(x−a1)(x−a2)···(x−a n)−1在Q上不可约,其中a1,a2,···,a n是互异的整数.证明:(证法1)若不然,假设f(x)=φ1(x)φ2(x),由于f(x)是整系数多项式,所以可设φ1(x)和φ2(x)均为整系数多项式,且∂[φ1(x)]<∂[f(x)],∂[φ2(x)]<∂[f(x)].f(a i)=φ1(a i)φ2(a i)=−1,考虑到它们均为整系数多项式,所以有φ1(a i)=±1,φ2(a i)=∓1.令g(x)=φ1(x)+φ2(x),则g(a i)=0,i=1,2,...,n.而∂[g(x)]≤∂φ1(x)<n,∂[g(x)]≤∂φ2(x)<n,得g(x)=0,φ1(x)=−φ2(x),所以f(x)=−φ2(x).1于是对任意的实数c,f(c)=−(φ1(c))2≤0.但再由条件:f(x)=(x−a1)(x−a2)···(x−a n)−1,取c=max{a1,a2,...,a n}+3,则f(c)≥3n−1>0,矛盾.于是假设错误,所以f(x)在Q上不可约.(证法2)由于φ1(a i)=−φ2(a i),i=1,2,...,n且∂[φk(x)]<∂[f(x)]≤n,k=1,2.,所以f(x)=−[φ1(x)]2.由于φ1(x)和φ2(x)都是整系数多项式,所以−φ21(x)的首系数为负数,而f(x)的首系数为+1,矛盾.例2.设a1,a2,···,a n是互异的整数,证明f(x)=(x+a1)(x+a2)···(x+a n)+1在Q上可约的充要条件是f(x)=g2(x),g(x)∈Z[x].证明:充分性显然成立.必要性.若f(x)在Q上可约,因为f(x)∈Z[x],可设f(x)=g(x)h(x),g(x),h(x)∈Z[x].又因为f(a i)=1,所以g(a i)和h(a i)同时为1或−1,即g(a i)=h(a i),i=1,2,...,n.又∂[g(x)]<∂[f(x)]≤n,∂[h(x)]<∂[f(x)]≤n,得g(x)=h(x),所以f(x)=[g(x)]2.例3.设a1,a2,···,a n是互异的整数,证明f(x)=(x−a1)2(x−a2)2···(x−a n)2+1在Q上不可约.证明:若f(x)在Q上可约,设f(x)=g(x)h(x),g(x),h(x)∈Z[x].又对任意的c∈R(实数),f(c)=(c−a1)2(c−a2)2···(c−a n)2+1>0,所以f(x)无实根.考虑f(a i)=g(a i)h(a i)=1,g(x)和h(x)均为整系数多项式,所以g(a i)=1且h(a i)=1或g(a i)=−1且h(a i)=−1.不妨假设存在a k使得g(a k)=1,则由于g(x)也无实根,所以必有g(a i)=1,i= 1,2,...,n.再考虑到若g(x)的次数小于n,得g(x)≡1,这是不可能的.所以∂[g(x)]=∂[h(x)]=n.由于g(a i)−h(a i)=0,且g(x)和h(x)都是首系数为1的n次多项式,所以g(x)−h(x)的次数小于n,且有n个互异的根a1,a2,...,a n,因而g(x)≡h(x),得f(x)=(x−a1)2(x−a2)2···(x−a n)2+1=[g(x)]2.令l(x)=(x−a1)(x−a2)···(x−a n),则[l(x)]2+1=[g(x)]2,(g(x)−l(x))(g(x)+l(x))=1.对任意的a∈Z,(g(a)−l(a))(g(a)+l(a))=1(两个整数的乘积为1),g(a)−l(a)=g(a)+l(a)=1或(−1).得l(a)≡0,矛盾.所以f(x)不可约.。
不可约多项式的和仍是不可约多项式

不可约多项式的和仍是不可约多项式不可约多项式的和仍然是不可约多项式,这是多项式理论中的一个重要性质。
在这篇文章中,我们将解释什么是不可约多项式,为什么它们的和仍然是不可约的,并提供一些具体的示例来说明这个结论。
首先,我们需要明确什么是多项式和什么是不可约多项式。
一个多项式是由常数项、一次项、二次项等有限项的代数和构成的数学表达式。
每个项由一个系数乘以一个变量的幂次。
例如,多项式P(x)=2x^3-3x+1就是一个多项式,其中2、-3和1是系数,x^3、x和1是项,3、1和0是幂次。
不可约多项式是指不能再被其他多项式整除的多项式。
换句话说,如果一个多项式P(x)不可以被另一个多项式Q(x)整除,那么P(x)就是一个不可约多项式。
例如,多项式P(x)=x^2-3x+2是不可约的,因为它不能被任何其他一次或更低次数的多项式整除。
现在我们来证明不可约多项式的和仍然是不可约的。
假设P(x)和Q(x)是两个不可约多项式,我们要证明它们的和P(x)+Q(x)仍然是不可约的。
为了证明这个结论,我们使用反证法。
假设P(x)+Q(x)是可约的,则存在一个多项式R(x)使得P(x)+Q(x)=R(x),其中R(x)不是常数。
由于P(x)和Q(x)是不可约的,我们可以假设R(x)的次数大于等于P(x)和Q(x)的次数,即deg(R) ≥ deg(P)、deg(R) ≥ deg(Q)。
然后,我们可以将P(x)和Q(x)表示为如下形式:P(x) =a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0,Q(x) = b_mx^m+b_{m-1}x^{m-1}+...+b_1x+b_0。
其中a_n、a_{n-1}、...、a_1、a_0是P(x)的系数,b_m、b_{m-1}、...、b_1、b_0是Q(x)的系数。
根据多项式的加法,我们有P(x)+Q(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0+b_mx^m+b_{m-1}x^{m-1}+...+b_1x+b_0=R(x)。
有理数域上多项式不可约的判定论文

有理数域上多项式不可约的判定论文毕业设计(论文)有理数域上多项式不可约的判定系别:数学与物理系专业(班级):数学与应用数学2012级2班作者(学号):赵伟(51205012006)指导教师:刘晓敏(讲师)完成日期: 2016年4月22日蚌埠学院教务处制目 录中文摘要 ........................................................................ 1 英文摘要 (2)1 引言 (3)1.1 本课题的作用,意义 (3)1.2 国内外的发展趋向和发展趋势以及尚待研究的问题 ........................ 3 2 有理数域上的多项式 (4)2.1 不可约多项式的概念 (4)2.2 本原多项式 (4)2.3 有理数域上多项式的等价 ................................................... 5 3 有理数域上多项式不可约的判别方法 . (6)3.1 有理根判别法 (6)3.2 因式分解唯一性判别方法 (6)3.3 艾森斯坦因(Eisenstein)判别法及推广 (7)3.3.1艾森斯坦因(Eisenstein)直接判别法 (7)3.3.2艾森斯坦因(Eisenstein)间接判法 (8)3.3.3通过艾森斯坦因(Eisenstein)判别法派生出的一种判别法 (9)3.3.4艾森斯坦因判别法的推广 (11)3.4 反证法 (11)3.5 克朗奈克判别法 (12)3.6 综合法 .................................................................... 13 4 其他特殊多项式不可约的判别方法 . (14)4.1 奇次多项式的判定方法 ................................................... 14 4.2 形如2ax bx c ++的判定方法 ............................................ 14 5 结论 ....................................................................... 16 谢辞 ........................................................................... 17 参考文献 . (18)有理数域上多项式不可约的判定摘要:对于判断有理数域上的不可约多项式的问题,最终都等价地转化为判断整数域上不可约多项式的问题.对于判断整系数不可约多项式,有经典的艾森斯坦因判别法,但这个判别法只是判别多项式不可约的一个充分条件,这就限制了它的使用范围,同时还存在着大量的多项式不能用艾森斯坦因判别法判别.本文主要把前人研究整系数不可约多项式所得的成果进行总结和归纳,在此基础上做了一些研究和探讨,给出了有理根判别法、反证法以及克朗奈克等判别方法,拓宽了判别多项式不可约的范围,同时使多项式不可约的判定更加系统化.关键词:有理数域;多项式;不可约;判别法The Judgement of Irreducible Polynomials onRational FieldAbstract:For judgment irreducible rational polynomial problem domain,eventually equivalently transformed into irreducible polynomials judgment on the issueinteger field for the entire judgment coefficient irreducible classic Eisensteindiscrimination law, but this discrimination discrimination law is a sufficientcondition for a polynomial irreducible, which limits the scope of its use, butthere are still a lot of discrimination because of polynomial method can notdistinguish by Eisenstein. in this paper, the whole previous studies irreduciblepolynomial coefficients obtained review and summarize achievements, on thisbasis, do some research and discussion, given the rational root discriminationlaw, as well as discrimination method reductio ad absurdum kroner Naik et al.,to broaden the scope of discrimination irreducible polynomial, while thepolynomials Irreducibility more systematic.Key words:Rational Field; polynomial; irreducible; discrimination law1 引言1.1 本课题的作用,意义随着经济的不断深入发展,以及改革开放带来的机遇与挑战,当代社会迎来一个快速发展的机遇.在互联网大数据的时代背景下,数字在人们工作和学习中扮演着重要的角色.在多项式中又以其不可约的判定方式最为重要.然而一个多项式在数系定义在不同的不同数域情况下得到的有关可约性的性质是有差异的(在后文中会给出相关的介绍).本课题在探讨多项式可约性的的判定方式时,是放在有理数域上进行研究的.我们将探讨总结几种定义判定方式,使我们更好地更迅速地解决遇到有关多项式的问题.1.2 国内外的发展趋向和发展趋势以及尚待研究的问题艾森斯坦因法,有理根判别法,奇次多项式判别法等等都可为判定定义在有理数域上的多项式是否可约.其中艾森斯坦因判别法最为经典.但是国内外研究发现,艾森斯坦因判别法,有着自身不足的地方,当满足判别法的质数p不存在时,我们不能判断这个多项式是否可约.这时须要我们总结更多的关于多项式在有理数域上不可约的判定方法.需要通过我们归纳总结以后,得到一个较为全面的解决多项式不可约的方法,使得在理数域上多项式不可约的判定更加系统化.在遇到特殊的有理数系上的不可约多项式时,可以找到对应的判定方法快捷准确滴解决多项式不可约的判定问题.2 有理数域上的多项式在介绍和总结多项式在有理数域上不可约的相关判别方式之前,我们需要先了解一下相关概念等知识.2.1 不可约多项式的概念过去我们都知道一个多项式可进行因式分解,即分解成几个因式乘积的形式,其实我们仅仅是在有理数域上考虑这个多项式是否能进行因式分解,却并没有进一步讨论和研究这个问题,也没有严格地讨论和证明它们是否真的不可再分.其实不可再分的概念,是相对的,是相对于系数的的数域而言的,并非绝对.用以下例子加以说明对94-x 进行分解,可分解为 )3)(3(9224+-=-x x x正如上面所说的那样,我们考虑94-x 这个多项式所在的数系仅仅是而是有理数域,但是若是将94-x 放在实数域上,则还可以因式分解为为)3)(3)(3924-++=-x x x x (并且在复数域上,还可以再进一步因式分解为)3)(3)(3)(3(94+-+-=-x x i x i x x由上述分析可以得出结论,必须在给定的数域进行分析,所谓的不可再分只是相对的的,只有明确系数域后,才有确切的涵义.所以多项式是否可约与数域紧密相关.将数域p 作为选定一个系数域,][x p 作为多项环,则关于多项环][x p 在数域p 上的多项式的因式分解的不可约定义如下:定义[]1数域p 上的次数大于或等于1的多项式)(x p 称为域)(x p 上的不可约多项式,如果它不能表示成数域p 上两个次数比)(x p 的次数低的多项式的乘积.2.2 本原多项式设()011a x a x a x f n n n n +++=-- 是有理数域上的一个多项式,取一整数b ,前提条件是()x bf 总是一个系数为整数的多项式式,若()x bf 的每一项系数都有公因子,那么公因子可以提出来,得到()()x cg x bf =,也就是()()x g bc x f =,其中()x g 是有理数域上的一整系数多项式,而且()x g 的每一项系数都只有1±这样的公约数,例如一多项式()x x x x x x 3155152522322424--=--.定义[]22 若一个系数非0且为整数的多项式()011a x a x a x f n n n n +++=-- ,该多项式的系数01,,,a a a n n -除了1±没有其他的公因子,即该多项式的所有系数都是互质的,则该多项式被称作为一个本原多项式.2.3 有理数域上多项式的等价设()x f 是有理数域上的任意一个非0的有理系数多项式,通过上述分析可知,()x f 都可以写成()()x cg x f =,其中c 为有理数域上任意一个数,()g x 是一个本原多项式,那么称()x f 与()g x 等价,即讨论有理数域上任意一个系数非0的多项式()x f 的问题最终都等价地转换为讨论该多项式的一个本原多项式的问题.3 有理数域上多项式不可约的判别方法3.1 有理根判别法利用是否有有理根的判别方式判定多项式在有理数域上不可约其实很简单,其前提条件是针对次数小于或者等于三次的多项式.有理根判别法顾名思义只需验证该多项式是否有有理根,如果有有理根,则在有理数域上可约.例1 判别多项式()227f x x x =++在Q 上不可约.解 ()x f 的最高次项的次数是2,所以可以运用有理根判别法.由有理根判别法,若)(x f 可约,则一定有有理根,又)(x f 的可能有理根是:士1,士7.因为()01≠±f ,()07≠±f ,所以士1、士7均不是)(x f 的有理根,故)(x f 在有Q 上不可约.例[]32 证明()107-1919223x x x x f +-=在有理数域上不可约.解 ()x f 的最高次项的次数是3,所以可以运用有理根判别法.又士1、士107是()x f 可能存在的有理根,而()01≠±f ,()0107≠±f ,所以士1、士107都不是()x f 的有理根,故()x f 在Q 上不可约.当然有理数域上多项式的次数大于3,不能用上述判定方式.例2 设()x f 是有理数域上的一个多项式,()14424++=x x x f ,试证明()x f 在有Q 上不可约.解 我们通过前面关于有理根的相关分析和研究,知道士1、士4是()x f 可能存在的有理根,但是()01≠±f ,()04≠±f .所以运用有理根判别法,我们会得出()14424++=x x x f 在Q 上是不可约的结论.但是()x f 是有理数域上可约的多项式,因为()()2212+=x x f .因此针对次数大于或者等于4的整系数多项式,有理根判别法不适用,这就需要给出其他的判别方法进行判定. 3.2因式分解唯一性判别方法定理[]41.3 因式分解的唯一性定理定理 数域p 上每一个次数1≥的多项式()x f 都可以唯一地分解成数域p 上一些不可约多项式的乘积.把多项式分解成实数域上次数比它小的几个不可约的因式乘积的形式,而将有理数域看做成实数域上的一部分.如果该多项式不可约的因式全都是有理数,由因式分解的唯一性定理确定了关于该多项式的不可约因式是唯一的的,可以得知,该多项式在Q 上必然可约.例4 证明441x +在有理数域上不可约.解 ()()1212214224+-++=+x x x x x ,结合因式分解的唯一性定理可以知道,若144+x 在有理数域上具有可约性,必须是该等式,但由于上述等式右边系数不都是有理数,故144+x 在有理数域上不可约.例5 证明425x -在有理数域上不可约.解 )(42255x x x x -=+,结合因式分解的唯一性定理可以知道,若254-x 在有理数域上具有可约性,必须该等式,但由于上述等式右边系数不都是有理数,故254-x 在有理数域上不可约.3.3 艾森斯坦因(Eisenstein)判别法及推广3.3.1 艾森斯坦因(Eisenstein)直接判别法定理[]52.3 设()1110...n n n n f x a x a x a x a --=++++是一个整系数多项式,若有一个素数p 使得(1)p 不整除最高次项的系数n a ; (2)p 整除其他各项的系数; (3)2p 不整除常数项0a .那么多项式()f x 在有理数域上不可约.证明 反证法 假设)(x f 是有理数域上的一个非0的多项式,那么)(x f 就可以写成如下形式:)......)(......()(011011c x c x c b x b x b x f m m m m l l l l +++++=---- ),,(n m l n m l =+<所以m l n c b a =,000c b a =.()都为整数n n c b ,由0a 被p 整除,得到0b 或0c 能被p 整除.可是0a 不能被2p 整除,故0b 和0c 不能被p 同时整除.所以不妨假设0b 不能被p 能整除,但0c 不能被p 整除.另一方面,因为n a 不能被p 不整除,所以l b 不能被p 整除,假定0b ,1b ,……,l b 中首先不能被p 整除的是k b .比较一下)(x f 中k x 的系数,得出等式k k k k c b c b c b a 0110......+++=-式中p 能整除k a ,1-k b ,……o b ,故p 必须整除0c b k .可是p 是一个质数,故p 至少能整除k b 与0c 中一个.这是与前面所述矛盾.所以)(x f 在有理数域上是不可约.例6 证明()663++=x x x f n 在Q 上不可约. 证明 若取6=p ,则有: (1)3=n a 不能被p 整除;(2)0......221====--a a a n n ,61=a ,60=a 可以被p 整除; (3)60=a 不能被2p 整除.故)(x f 在有理数域上不可约.例7 在任意的n 情况下,证明3+n x 在有理数域上不可约. 解 取3=p ,则有: (1) 1=n a 不能被p 整除;(2) 0......221====--a a a n n ,01=a ,20=a 不能被p 整除; (3) 30=a 不能被2p 整除. 故()3+=n x x f 在有理数域上不可约.3.3.2艾森斯坦因(Eisenstein)间接判别法有一类Q 上的多项式不适合用艾森斯坦来判别,因为有些p 并不能满足定理的条件,所以想到多项式的等价替换,我们可以尝试对其做适当替换,给出艾森斯坦因间接判别法.定理[]63.3 有理系数多项式)(x f 在有理数域上不可约的充分必要条件是:对于任意有理数0≠a 和b ,多项式)()(b ax f x g +=在有理数域上不可约.证明 (充分性) 反证法.已知)()(b ax f x g +=在Q 上不可约.若)(x f 在Q 上可约,那么可以设)()()(21x f x f x f =,()()(21x f x f 为Q 上多项式),于是)()()()(21b ax f b ax f b ax f x g ++=+=,这与)(x g 不可约矛盾,故)(x f 在有理数域上不可约.(必要性) 反证法.已知)(x f 不可约.如果在Q 上)(x g 可约,即)()()()(21x g x g b ax f x g =+=()()(21x g x g 是Q 上多项式.) 在上式中用abx a -1代替x ,有)1()1()(21a bx a g a b x a g x f --=,这说明在有理数域上)(x f 是可约的,与已给条件矛盾.所以)(x g 在Q 上不可约.所以对于一些在有理数域上的多项式,当不能直接用艾森斯坦因判别方式判定该多项式可约性时,可通过适当的替换b ay x +=后,再用艾森斯坦因判别方式来判断.例8 证明()24+=x x f 在有理数域上不可约.证明 ()()34642112344++++=++=+x x x x x x f取3=p ,则有1不被p 整除,4,6,3能被p 整除1,4,6,3不被2p 整除.这些都符合前面给出的艾森斯坦因判定方式的几个条件,故通过前面的分析我们可得出结论()()34642112344++++=++=+x x x x x x f 在有理数域上不可约,故()24+=x x f 在有理数域上不可约.例9 证明()15245++=x x x f 在有理数域不可约.证明 令5=p ,24=a ,显然1p ≠,倘若()f x 在Q 上不可约,则没有有理根,令1x y =+,代入()f x则()()1+=x f y g ()()115240151452353254155++++++++=y y C y C y C y C y C y30125120240120242345+++++=y y y y y由于(1) 5整除120,240,125,3; (2) 5不整除24; (3) 2552即不整除30故由艾森斯坦因间接判别方式可以证明出()g y 在有理数域上不可约,故()f x 在有理数域上不可约.艾森斯坦因(Eisenstein)直接判别法和间接判别法是判定多项式在Q 上非常常用的方法,但是,这种方法是有局限性的,因为不一定每次都能找到适合的数字p ,a ,b ,使得)()(b ax f x g +=成立,故我们给出如下的一种判别式.3.3.3 通过艾森斯坦因(Eisenstein)判别法派生出的一种判别法定理[]74.3 设有理数域上()1110...n n n n f x a x a x a x a --=++++是一个整系数多项式.若存在一个质数p ,使得(1)p 不整除常数项0a ; (2)p 整除其他各项的系数; (3)2p 不整除最高次项系数n a . 则()f x 在有理数域上不可约.证明 若)(x f 可约,那么)(x f 可以写成:)()()(x h x g x f =.设k k x b x b x b b x g ++++=......)(2210l l x c x c x c c x f ++++=......)(2210 其中 n l k n l n k =+<<,,. 于是 000,c b a c b a l k n ==.因n a p ,而n a 不能被2p 整除.k b 和l c 其中的一个能被p 整除.可以假设k b 能被p 整除而l c 不能被p 整除.可以说)(x g 的所有系数不能被p 整除,否则会与 (1)矛盾.设p 不能整除)(x g 的最后一个系数为s b )(k s <.参考等式011......c b c b c b a l s l s l s l s +-+++++= 通过假设l s s l s b b a p +++,......,,1 )1(≥l 因此l s c b p ,从而s b p ,或l c p ,这与假设矛盾.例10 证明()261293345++++=x x x x x f 在有理数域上不可约.证明 不可以用艾森斯坦因(Eisenstein)来判定()x f ,因为无法找到一个质数p 使得(1) 最高次项的系数被p 整除; (2) 其他各项的系数都能被p 整除; (3) 常数项不被2p 整除.三个条件都满足.但存在质数3=p ,满足(1) 2不能被3整除; (2) 3,9,12,6能被3整除; (3) 3不能被23整除. 故)(x f 在有理数域上不可约.例11 证明()466123346++++=x x x x x f 在有理数域上不可约. 证明 不可以用艾森斯坦因判别方式,因为无法找到一个质数p 使得 (1) 最高次项的系数被p 整除; (2) 其他各项的系数都能被p 整除; (3) 常数项不被2p 整除.三个条件都满足.但存在质数3=p ,满足(1) 4不能被3整除; (2) 3,12,6能被3 整除; (3) 3不能被23整除. 故)(x f 在有理数域上不可约.一类特殊的多项式并满足用上述判定方式的判别条件,但是这类的多项式也可能是不可约的.同样的情况也适用于直接判别法和派生出的判别法.针对这类情况,引出艾森斯坦因(Eisenstein)推广法的推广.3.3.4艾森斯坦因判别法的推广定理[]84.3 设整系数多项式nn x a x a x a a x f ++++=......)(2210,假如有质数p 使得:(1) p 不能整除daj )0(n j <<;(2) p 整除dad a d a d a d a n j j ,......,,......,1110+-;(3) 2p 不能整除d ad a n ,0;(4) p 不能整除b d a j -,其中b 整除20daa n ,且20d a ab n ≠,),......,(10n a a a d =,故)(x f 在有理数域上不可约.例12 证明多项式20820)(35++=x x x f 在Q 上不可约.证明 因为4)20,0,0,8,0,20(),,,,,(012345===a a a a a a d ,取5=p ,则有:(1) 2483==d a 不能被5整除;(2) 542005===d a d a 被5整除,040124====d a d a d a 被5整除; (3) 542005===d a d a 不能被25整除; (4).5,1,2±±±=-b b b d a不能被25整除.故20820)(35++=x x x f 在Q 上不可约.上面的几种判别方式都有局限性的,下面我们将给出其他方法用于判定.3.4 反证法我们在没有找到艾森斯坦因判别法中质数p 时,经常运用反证法来证明.例13 证明()()()()121----=n b x b x b x x f 在Q 上不可约,其中11,,b b b n n -是n 个整数.证明 反证法,若多项式()f x 在Q 上可约,则一定存在系数为整数的多项式()x f 1,()x f 2,有()()()x f x f x f 21=.()()()()x f x f 010∂<∂,()()()()x f x f 020∂<∂,由()1-=i b f ,可得:()11=x f ,()12-=x f 或者()11-=x f ,()12=x f ,则()()x f x f 21+是等于0,()()x f x f 21-=,()()x f x f 21-=,此时()f x 首项系数为1-,与题设条件矛盾,故()f x 在Q 上不可约.3.5 克朗奈克判别法定理[]95.3 设()[]x Q x f ∈,则在有限步下()x f 能分解成不可约多项式的乘积 克朗奈克判别法.(只考虑()x f 是系数定义在整系数域上的多项式.)证明 令()[]x Z x f ∈,且n f =deg .下面对n 用第二数学归纳法证.当1=n 时定理显然成立.假设定理对于小于n 的整系数多项式已经成立).那么对于n 次整系数多项式()x f ,若()x f 可分解,设其为()()()x f x f x f 21=,则必有一个次数2n≤的因式,所以考虑在有限步下作出()x f 的次数2n≤的因式的方法.对此,设⎥⎦⎤⎢⎣⎡=2n s ,取1+s 个互不相同的整数n a a a ,,,10 并计算它们的函数值再将()i a f 析因,s i ,,1,0 =,各取其中的一个因数,记作()()()n a g a g a g ,,10.这样得到了1+s 个数对()s i a g a i i ,,1,0,, =.根据拉格朗日插值公式,它们唯一地确定了一个次数不超过s 的多项式()x g .因为()i a g 不全为0.显然它可以是整系数的.作出这样的多项式()x g 并用它去除()x f .由于()i a f 的因数个数是有限的,设它为i k ,那么这样的不同的()x g 至多是∏=ni i k 0个.因此上述所构造的()x g 及用()x g 除()x f 的步骤是有限的.若对于所有这样的()x g 都有()x g 不整除()x f 则断言()x f 是不可约的.因为若不然,则有()()()x q x h x f =,其中不妨设2deg nh ≤.这时,()i a h 整除()s i a f i ,,1,0, =,因而()x h 由n a a a ,,,10 ()i a f 的1+s 因数()()s i a h i ,,1,0 =唯一决定,与我们的假设相矛盾,故这时定理成立.又若有某个()x g 整除()x f ,则得()()()x l x g x f =,其中n l n g <≤deg ,deg .因而由归纳假定,也存在着一种方法(在一般情况下就是前面所述的求()x g 的方法).在有限步下把它们分解为不可约多项式的乘积,故这时定理也真.因此,根据第二归纳法原理,定理成立.显然,以上证明不仅给出了将次数大于1的整系数多项式分解为Q 上的不可约多项式的乘积的一般方法,而且这种做法包括了Q 上不可约多项式的判别.例14 证明()15+=x x f 在有理数域上不可约.证明 252<=s ,取1,0,1110==-=a a a ,则()01=-f ,()10=f ,()21=f ,从而()1-f 的因子是0,()0f 的因子是1()1f 的因子是1,2.令()01=-g ,()10=g ,()11=g ;()01=-g ;()10=g ()21=g应用插值多项式知:()()()()()()()()()()221011101101011021--=-+-++-+-++=x x x x x x x g ;()()()()()()()()()1011101210101102+=-+-++-+-++=x x x x x x g 由带余除法可知,()x g 1不整除()x f ,()x g 2不整除()x f ,从而()x f 在Q 上不可约.但是,由于这种做法比较麻烦,其实用价值依赖于计算机技术.3.6 综合法在遇到一些特殊的多项式时,如果发现用前面所给的一种方法判定较为复杂时,可以同时使用前面方法中的几种方法来判定多项式不可约的问题.例15 证明()144++=kx x x f 在有理数域上不可约.证明 ()x f 的有理根只有两个,分别是1-和1+,但是()01≠±f ,所以()x f 没有一次因式,所以若()x f 可约,则()x f 只能表示成两个因式乘积的形式.令()()()1122-+-+=bx x ax x x f ,其中a 和b 都为整数. ()()()12234+++++++=x b a x ab x b a x比较等式两边的系数,得0=+b a ,02=+ab ,k b a 4=+.即22=a ,则2±=a ,与a 为整数矛盾.故()x f 在有理数域上不可约.4 其他特殊多项式不可约的判别方法4.1 奇次多项式的判定方法定理[]101.4 对于整系数多项式()2122212210...n n n n f x a x a x a x a x a ++=+++++若存在素数p 使(1) p |122...,,,;n n n a a a ++(2) 2p |01...,,,;n a a a(3) p 21n a +;(4)3p 0a .那么,()f x 在有理数域上不可约.例16 证明()61647323+++=x x x x f 在有理数域上不可约.证明 不可以用艾森斯坦因(Eisenstein)来判定()x f 在有理数域上是否可约,因为无法找到一个质数p 使得(1) 最高次项的系数被p 整除; (2) 其他各项的系数都能被p 整除; (3) 常数项不被2p 整除三个条件都满足. 但可找到素数2p =,满足定理4.1的四个条件,(1) 4能被2整除;(2) 16能被2整除,6能被2整除; (3) 73不能被2整除; (4) 6不能被32整除.故()61647323+++=x x x x f 在有理数域上不可约.需要注意的是奇次的判定方法有局限性,而不是必要条件.当某一多项式不适合上述判定法时,我们需要转换其他的判定法进行可约性验证.4.2 形如2ax bx c ++的判定方法有一些多项式很特别,我们可以不用前面介绍的判定法,就可以对这类多项式在有理数域上的可约性进行快速判定.给出下面一种判定方式,更简单地更快速地判定一类定义在Q 上多项式不可约的相关问题定理[]112.4 对于整系数多项式2()f x ax bx c =++,如果abc 为奇数,则()f x 在有理数域上不可约.证明 假设()f x 可约,则存在整数1122,,,a b a b ,使得1122()()()f x a x b a x b =++212122112()a a x a b a b x b b =+++即有 12122112,,a a a b a b a b c b b ==+=由abc 为奇数,可得,,,a b c 为奇数故1122,,,a b a b 为奇数从而1221,a b a b 为奇数,进而1221a b a b +为偶数,这与1221b a b a b =+为奇数矛盾.得证.例17 证明()3532++=x x x f 在Q 上不可约.证明 因3=a ,5=b ,3=c ,45353=**=abc 为奇数,故()3532++=x x x f 在有理数域上不可约.当abc 的乘积不为奇数的时候,不能用这种方式判定多项式在Q 上可约性. 例18 证明多项式()722++=x x x f 在有理数域上不可约.解 1=a 2=b .由于1=a ,2=b ,7=c ,14721=**=abc ,14是偶数,故用上面给出的判定方法无法知道()x f 在有理数域上是否可约.其实很简单,运用前面给出的有理根判别方法,()x f 的最高次项的次数是2,所以可以运用有理根判别法.由有理根判别法,若)(x f 可约,则一定有有理根,又)(x f 的可能有理根是: -1、1、-7、7.因为()01≠±f ,()07≠±f ,所以-1、1、-7、7均不是)(x f 的有理根,故)(x f 在有理数域上不可约.5 结论对于系域定义在有理数域上的多项式,其不可约的判定方法有多种,本文给出了其中的几种判定方式.可是其中几种判别方式有着一些不足的地方.但是通过我们归纳总结以后,得到一个较为全面的解决多项式不可约的方式,几种判定方法之间形成互补关系,使得定义在有理数域上的多项式可约性的相关判定越发全面准确,在遇到特殊的定义在有理数域上的不可约多项式时,找到对应的判定方式,便于快捷准确地解决多项式不可约的判定问题.谢辞时光荏苒,美好的大学四年时间过得飞快,眼看着到了和母校说再见的时候,无论我在社会上去的怎样的成就,我都不会忘记我的母校,忘不了我生活了四年的母校——蚌埠学院.我十分感谢母校四年来对我的栽培,让我健康成长;四年来为我提供了优质的生活学习环境,为我们走入社会打下坚定地基础.再此我也向学校的领导和主任报以衷心的感谢,感谢四年来你们对我们广大学子的关心,多次操心于开展各种活动促进我们德智体美全面发展,再次我想说你们辛苦了!其次,特别感谢我的指导刘晓敏老师.在毕业论文的设计的过程中,她渊博的知识开阔了我的视野,在此我表示衷心的感谢感谢的敬意!当然还要感谢被我作为参考文献的这些作者们,谢谢你们,让我丰富了自己的知识,让我更好更快的完成这篇论文,谢谢你们!此时,更不应忘记的还有我的父母,是他们含辛茹苦将我培养成才,是他们无微不至的关心使我顺利完成了学业.衷心祝福他们健康!参考文献[1] 乔世东.多项式在有理数域上不可约的几种证明[J].雁北师院学报,1996,12(6):31-32.[2] 王骁力,夏云青.利用同态关系讨论有理数域上多项式的可约性判定[J].中州大学学报,2010,27(3):99-102.[3] 陈林,田应智.有理数域上的不可约多项式[J].伊犁师范学院学报,自然科学版,2009,(2):13-16.[4]张卫,史滋福.有理数域上的一类不可约多项式[J].湖南理工学院学报(自然科学版),2008,21(1):5-7.[5] 陈丽. 有理数域上多项式不可约的判定[J]. 安庆师范学院学报: 自然科学版,2009,15(3): 80-82.[6]刘中良.有理数域上多项式不可约的判定[J].科技信息,2009,(1):77-79.[7] 黄宗文.有理数域上整系数奇次多项式不可约的一个判别法[J].广西教育学院学报,2002,(4): 77-79.[8] 兰春霞.整系数多项式在有理数域上不可约的几个判定定理[J]..丽水学院学报,2005,27(2):13-14.[9]巩娟.整系数多项式在有理数域上不可约判别法[J].遼寧師專學報(自然科學版).2009,11(3): 36-44.[10] 马正义.整系数多项式在有理数域上的不可约性[J].丽水师范专科学校学报,2002,24(5):12-13.[11]Franois Anton,Darka Mioc,Marcelo Santos.Exact Computation of the Topologyand Geometric Invariants of the Voronoi Diagram of Spheres in 3D[J] .Journal of Computer Science & Technology, 2013,12(9): 83-86.。
整系数多项式不可约的判别法

在高 等代 数 中介 绍 了艾 森施 坦 白 ( i n Es — e
s i) 别法 , tn 判 e 它是 判 别整 系数 多项式 为 不可 约 多
维普资讯
第2卷~ 期 6 第1
20 0 8年 8月
’
江
西
科
学
Vo . 6 No 4 12 . Au . 0 g 2 08
JANG S I I XI C ENC E
文 章 编 号 :0 1 6 9 20 )4— 5 9一O 10 —3 7 (0 8 0 0 1 2
项式的一个非常有用 的判别法 , 但这个方法使用 时有其 局 限性 , 文介 绍 另为 2个方 法 , 本 使用 它可
以判断 一 些 无 法 使 用 艾 森施 坦 白 ( i ntn 判 Es s i) e e 别 法判 断 的整 系数 多项式 的可 约性 。 定 理 1设 )=a +ax+… +ax 是 一 个 : 0 l n 整 系数 多项 式 , f ) 有 有理 根 , 能 找 到 一 若 ( 没 并
P使 :1a , , ( )。a 中至少有—个不能被 P整除 ;2 a( ()
收稿 日期 :0 7— 1— 7 修订 日期 :0 8— —2 20 1 2 ; 20 0 4 8
作者简介 : 杨明顺 (9 4一) 16 陕西渭南人 , 副教授 , 研究 方向 : 数论 。 基金项 目: 国家 自然科学基金资助项 目(0 7 15 , 16 15 ) 陕西基 础教育科研项 目( JY 0 3 2 , 南师范学 院基金资助 SJ B 6 0 ) 渭
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反证法证明多项式不可约
在有理数域上,直接判别一个多项式是否不可约,是一件及其困难和复杂的事情,此时我们可以利用反证法来判别.
例 1 已知)(x p 是次数大于零的多项式,若对于任意两个多项式)(x f 和)(x g ,由)()(|)(x g x f x p 可以推出)(|)(x f x p 或)(|)(x g x p ,则)(x p 是不可约多项式.
证明 假设)(x p 可约,则必存在次数小于))((x p ∂的多项式)(x f 与)(x g ,使得)()()(x g x f x p =,即)()(|)(x g x f x p ,又由已知条件,知)(|)(x f x p ,)(|)(x g x p ,但))(())((x p x f ∂<∂,))(())((x p x g ∂<∂,所以不可能实现,从而)(x p 必不为可约多项式.
例2 次数大于1的整系数多项式)(x f 对于任意整数的函数值都是素数,则)(x f 为有理数域Q 上的不可约多项式.
证明 假设)(x f 不是有理数域Q 上的不可约多项式,因为1))((>∂x f ,所以)(x f 在整数环Z 上也可约,即有整系数多项式)(1x f 与)(2x f ,使得)()()(21x f x f x f =,其中))(())((x f x f i ∂<∂,2,1=i .
由已知条件知,若a 为一个整数,则)(a f 为素数,即)()()(21a f a f a f =为素数,所以1)(1±=a f 或1)(2±=a f ,再由a 的无限性,知1)(1=a f ,1)(1-=a f 或1)(2=a f ,1)(2-=a f 四个式子中至少有一个式子对无限个a 成立,即)(1x f 与)(2x f 中有一个为零次多项式,这与已知条件矛盾,所以结论成立. 例3 设011)(a x a x a x f n n n n +++=-- 是一个整系数多项式,如果有一个素
数p ,使得
(1)n a p |/
; (2)021,,,|a a a p n n --;
(3)02|a p /
, 那么()f x 在有理数域上是不可约的.
证明 假设)(x f 在有理数域上可约,那么)(x f 可以分解成两个次数较低的整系数多项式的乘积,即
))(()(011011c x c x c b x b x b x f m m m m l l l l ++++++=---- ),,(n m l n m n l =+<<,
因此m l n c b a =,000c b a =.
因为0|a p ,所以p 能整除0b 或0c .又因为02|a p /
,所以p 不能同时整除0b 及0c ,因此不妨假定0|b p ,但0|c p /
.另一方面,因为n a p |/,所以l b p |/.假设在l b b b ,,,10 中第一个不能被p 整除的是k b ,比较)(x f 中k x 的系数,得等式
k k k k c b c b c b a 0110+++=- ,
式中01,,,b b a k k -都能被p 整除,所以0c b k 也必能被p 整除,但因p 是一个素数,所以k b 与0c 中至少有一个被p 整除,这是一个矛盾,故)(x f 在有理数域上是不可约的.
对于一些关于不可约多项式定理的逆定理,均可尝试用反证法来证明,在否定结论之后,利用已知条件推出了矛盾,从而使命题得证.。
