MATLAB 数据库
利用MATLAB进行数据库连接和操作

利用MATLAB进行数据库连接和操作引言随着信息技术的飞速发展,数据库的使用在各个领域中变得越来越重要。
而MATLAB作为一种功能强大的数值计算和数据分析工具,提供了方便的数据库连接和操作功能。
本文将介绍如何利用MATLAB进行数据库连接和操作,以及一些常见的应用场景。
一、数据库连接在使用MATLAB进行数据库操作之前,首先需要进行数据库连接。
MATLAB 中可以通过调用数据库驱动程序实现与各种类型的数据库的连接。
1. JDBC连接JDBC(Java Database Connectivity)是一种用于执行SQL语句的Java API。
在MATLAB中,我们可以使用JDBC来实现与支持JDBC连接的数据库的通信。
首先,我们需要下载适当的JDBC驱动程序,并将其添加到MATLAB的Java类路径中。
之后,我们可以使用MATLAB提供的“database”函数来实现数据库的连接。
例如,我们可以使用如下的代码来连接一个MySQL数据库:```matlaburl = 'jdbc:mysql://localhost:3306/database_name';username = 'username';password = 'password';conn = database(url, username, password);```2. ODBC连接ODBC(Open Database Connectivity)是一种用于连接各种类型的数据库的标准接口。
在MATLAB中,我们可以通过ODBC来连接支持ODBC连接的数据库。
首先,我们需要在系统中配置好ODBC数据源。
之后,我们可以使用MATLAB提供的“odbc”函数来实现数据库的连接。
例如,我们可以使用如下的代码来连接一个MS Access数据库:```matlabdatasource = 'Microsoft Access Driver (*.mdb, *.accdb)';databasefile = 'C:\path\to\database.accdb';username = 'username';password = 'password';conn = odbc(datasource, username, password, 'db_file', databasefile);```二、数据库操作数据库连接成功后,我们就可以利用MATLAB进行各种数据库操作了。
基于Matlab和数据库的3-PRS串并联机构位置正解

越性 , 因而广泛 应用 于 独 立机 构 、 节 机 构 、 关 机床 工作
台、 工件定位、 微动机构等领域 J 。但位置正解非常
复杂 , 响 了并 联机 构 的深入研 究 、 展 。研 究位 置正 影 发 解 的 目的在 于 : 解决 诸 如 如何 用 最 小 的机 构 尺 寸 获得 曲线 。
维普资讯
基 于 Malb和 数据 库 的 3一P S串并联 t a R 机 构 位 置 正 解
房 勋 黄俊杰 赵俊伟
( 河南理 工大 学 , 南 焦 作 4 4 0 ) 河 500
摘
要 : 于大 多数并联 机构 。 对 位置 正解 都 是 一 个难 题 。 利用 Mal t b软件 卓 越 的 数学 计 算 功 能 。 易 地 求 a 容
5 结语
通过上述工作得出如下结论 : 在影响机床定位精 度的众多因素中, 机床导轨直线度与机床定位精度之
间具有 直接 的联 系 , 而且 也 是 导致 定 位 精度 超 差 的最 主要 因素 。通过 一 系列 措施 改 善 导 轨 直线 度 , 可 以 就
p r Ba e n t a ,t e Ac e sd tb s ewe n t e o t u a a tra d t ea ie i p tp r me e e. s d o h t h c s aa a e b t e h u p tp r me e n her lt n u aa tr v
数值法和解析法。数值法数学模型简单 , 适应于大多
数并联 机构 , 但是 不能求 得机 构 的所 有位 置解 ; 解析法
能够求得 全部 的解 , 输入输出的误差效应可 以定量地
2 贺振 明. 数控机床位置精度 的补偿. 机电一体化 ,9 8 3 :4— 6 19 ( ) 3 3
matlab数据库编程

在MATLAB中,可以使用内置的Database Toolbox进行数据库编程。
以下是一些基本步骤,以帮助您开始使用MATLAB进行数据库编程。
1. 连接到数据库使用Database Toolbox提供的函数,可以连接到各种类型的数据库,例如MySQL、Oracle、SQL Server等。
例如,要连接到MySQL 数据库,可以使用以下代码:```matlabconn = database('username','password','database_name','host_name','port');```其中,username和password是数据库的用户名和密码,database_name是数据库的名称,host_name是数据库的主机名,port 是数据库的端口号。
2. 执行SQL查询连接到数据库后,可以使用SQL查询语句执行各种操作,例如SELECT、INSERT、UPDATE、DELETE等。
例如,要查询一个名为table_name的表中的所有数据,可以使用以下代码:```matlabsql_query = 'SELECT * FROM table_name';result = exec(conn, sql_query);```其中,exec函数执行SQL查询并返回结果。
3. 处理查询结果查询结果可以以表格或元数据的形式返回。
可以使用MATLAB 内置的函数处理查询结果,例如将结果保存到变量中、显示结果等。
例如,要将查询结果保存到名为result的变量中,可以使用以下代码:```matlabresult = fetch(result);```其中,fetch函数将查询结果保存到变量中。
4. 关闭连接在完成所有操作后,应该关闭与数据库的连接。
可以使用close 函数关闭连接,例如:```matlabclose(conn);```以上是MATLAB数据库编程的基本步骤。
Matlab数据库编程入门

M atlab数据库编程入门Matlab与数据库链接有三种方法,本文只讲述其中以ODBC的方式进行链接。
1.配置数据源(1).“控制面板”----“管理工具”——“数据源(ODBC)”——“添加”——“创建数据源名称和选择数据库文件”。
(2).采用修改注册表,自动配置数据源。
DB_path='D:\Program Files\MATLAB71\work\StuSystem.mdb';DB_sourcename='Godman';LinkDB(DB_path,DB_sourcename,1);(LinkDB为自编函数)2.建立链接对象——database调用格式:conna=database(‘datasourcename’,’username’,’password’);如conna=database('SampleDB','','');其中SampleDB为上文中创建的数据源名称,当默认情况下,数据库文件的username和password为空。
3.建立并打开游标——exec调用格式:curs=exec(conna,'sqlquery');如curs=exec(conna,'select*from database')其中conna为上文中链接对象,select*from database表示从表database中选择所有的数据.4.把数据库中的数据读取到Matlab中——fetch调用格式:curs=fetch(curs,RowLimit);Data=curs.Data;%把读取到的数据用变量Data保存.如curs=fetch(curs);把所有的数据一次全部读取到Matlab中,RowLimit为每次读取的数据参数的行数,默认为全部读取,但是全部读取会很费时间(和计算机性能很大关系)。
Matlab中的数据库连接与查询技巧

Matlab中的数据库连接与查询技巧简介:Matlab是一种强大的数学计算软件,除了在数值计算和科学工程领域得到广泛应用外,它也具备与数据库连接和查询的功能。
本文将介绍在Matlab中如何实现与数据库的连接和查询,并提供一些应用技巧和最佳实践。
一、数据库连接技巧在Matlab中,可以使用不同的方法来建立与数据库的连接。
首先,需要安装Matlab的Database Toolbox以获得数据库相关的功能。
具体的安装方法可以参考Matlab官方文档。
1. 直接连接最简单的方法是使用Matlab中提供的直接连接函数。
这些函数允许用户直接指定数据库的连接参数,例如数据库类型、主机地址、端口号等。
一旦成功连接,就可以执行查询和更新操作。
2. 使用ODBC连接另一种常用的方法是使用ODBC(Open Database Connectivity)驱动来连接数据库。
ODBC提供了一个统一的接口,使得可以使用通用的SQL语句来操作不同类型的数据库。
在Matlab中,可以使用database函数来创建一个ODBC连接对象并指定相应的数据源和驱动。
3. 使用JDBC连接JDBC(Java Database Connectivity)是一种Java语言的接口标准,用于连接不同数据库并执行相关操作。
Matlab中可以通过创建java对象的方式来调用JDBC功能。
这种方法可以轻松地连接不同类型的数据库,并且还可以利用Java的强大功能来处理复杂的查询和数据处理任务。
二、数据库查询技巧一旦成功建立了与数据库的连接,接下来就可以进行查询操作了。
本节将介绍一些常用的数据库查询技巧,包括基本查询、条件查询、排序、分组和连接查询。
1. 基本查询基本查询是指从数据库中检索记录的最简单形式。
在Matlab中,可以使用SQL语句来执行基本查询操作。
例如,通过使用SELECT语句和FROM子句,可以从指定的表中检索所有记录或指定列的数据。
然后,使用WHERE子句可以添加条件来进一步筛选结果。
Matlab数据库编程指南-Godman

Matlab数据库编程指南-GodmanMatlab与数据库链接有三种方法,本文只讲述其中以ODBC的方式进行链接。
本文件包含四部分,其中第三部分为我自己写的一些数据库函数操作的函数,第四部分为网上的一些资料。
如有疑问可以邮件联系**************Godman 2009.3.30 晚Good Luck!第一部分:读取数据其相关信息查看1.配置数据源(1).“控制面板”----“管理工具”——“数据源(ODBC)”——“添加”——“创建数据源名称和选择数据库文件”。
具体操作见“配置数据源.gif”(2).采用修改注册表,自动配置数据源。
DB_path='D:\Program Files\MATLAB71\work\StuSystem.mdb';DB_sourcename='Godman';LinkDB(DB_path,DB_sourcename,1);(LinkDB为自编函数)2.建立链接对象——database调用格式:conna=database(‘datasourcename’,’username’,’password’);如conna=database('SampleDB','','');其中SampleDB为上文中创建的数据源名称,当默认情况下,数据库文件的username和password为空。
3.建立并打开游标——exec调用格式:curs=exec(conna,'sqlquery');如curs=exec(conna,'select * from database')其中conna为上文中链接对象,select * from database表示从表database中选择所有的数据.4.把数据库中的数据读取到Matlab中——fetch调用格式:curs=fetch(curs,RowLimit);Data=curs.Data;%把读取到的数据用变量Data保存.如curs=fetch(curs);把所有的数据一次全部读取到Matlab中,RowLimit为每次读取的数据参数的行数,默认为全部读取,但是全部读取会很费时间(和计算机性能很大关系)。
matlab database

clearwarnings清除数据连接的警告信息close关闭数据库连接commit提交数据库修改exec执行SQL 语句并打开游标get获取database 对象的属性insert将MATLAB 的元胞数组导insconnection入数据库表isreadonly检查数据库连接是否有效ping检查数据库连接是否为只读rollback获取数据库连接的状态信息set撤销数据库修改sql2native设置数据库连接属性update将JDBC SQL 语法转化成为bestrowid获取数据库表唯一行标识columnprivileges获取数据库列权限columns获取数据库表列名称crossreference获取主键和外部键值信息dmd构建数据库元数据对象exportedkeys获取输出外部键信息get获取数据库元数据属性importedkeys获取输入外部键信息indexinfo获取数据库表的索引和统计信息primarykeys获取数据表或者Schema的主键信息procedurecolumns获取catalog的存储过程的参数procedures和结果列supports获取catalog的存储过程tableprivileges检查某属性是否被数据库元tables数据支持versioncolumns获取数据库表权限列表attr获取数据集中列的属性close关闭游标clos获取数据集中列的个数columnnames获取数据集中列的名称fetch将数据导入MATLAB 的元胞get数组querytimeout获取游标对象的属性rows数据库查询超时时间set获取数据集的行数width设置游标获取数据的行数驱动函数结果集函数Driver 构建数据库驱动对象clearwarnings 清除结果集警告Get 获取数据库驱动属性close 关闭结果集对象Isdriver 检查驱动是否为有效的JDBC get 获取结果集属性驱动对象isnullcolumn 检查结果集中最后一条记录isjdbc 检查驱动是否JDBC 兼容是否为空isurl 检查URL是否为有效URL namecolumn 将结果集列名映射到结果集register 加载数据库驱动程序列索引unregister 卸载数据库驱动程序resultset 构建结果集对象驱动管理函数drivermanager 构建数据库驱动管理对象get 获取数据库驱动管理对象属性set 设置数据库驱动管理对象属性结果集元数据函数rsmd 构建结果集元数据对象get 获取结果集元数据属性可视化工具函数(ViusalQueryBuilder)confds 配置数据源(UNIX 平台)querybuilder 启动可视化工具通用函数logintimout 设置或获取建立数据库连接的超时时间参数setdbprefs 设置处理空值时数据库的行为参数。
matlab gui 数据管理系统
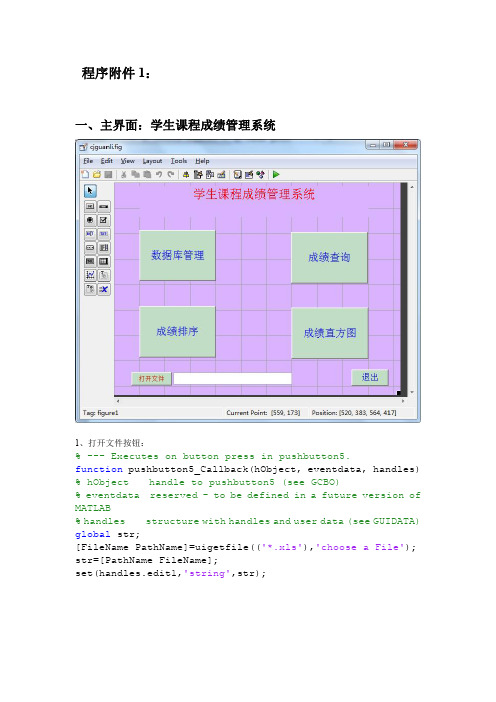
2、数据库管理按扭:
% --- Executes on button press in pushbutton1. function pushbutton1_Callback(hObject, eventdata, handles) % hObject handle to pushbutton1 (see GCBO) % eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) %shujukuguanli(); global str; setappdata(shujukuguanli(),'str',str);
xlswrite(str1,handles.xingming,1,'A2');
xlswrite(str1,handles.xuehao,1,'B2');
xlswrite(str1,handles.chengji,1,'C2');
end
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基MATLAB 数据库linspace(a,b,c)均匀生成介于a到b的c个值,c默认为100如linspace(0,100,5)即[0 25 50 75 100]linspace(-1.3,1.3)就是生成介于-1.3到1.3的100个值meshgrid是生成网格的函数,一般是生成二维网格矩阵数据,但这里生成的是三维网格矩阵数据。
先以二维数据为例,比如要绘制函数z=f(x,y)的图像x方向在[1,2,3,4,5]五个点上采样,即x=1:5y 方向在[10 20 30 40]四个点上采样,即y=10:10:40那么就一共有5*4=20个采样点。
分别为(1,10) (2,10) (3,10) (4,10) (5,10)(1,20) (2,20) (3,20) (4,20) (5,20)(1,30) (2,30) (3,30) (4,30) (5,30)(1,40) (2,40) (3,40) (4,40) (5,40)命令[X,Y]=meshgrid(x,y)生成的X就是这20个采样点的横坐标,Y既是其纵坐标,即X=1 2 3 4 51 2 3 4 51 2 3 4 51 2 3 4 5Y=10 10 10 10 1020 20 20 20 2030 30 30 30 3040 40 40 40 40然后再对这20个采样点计算z的值,即Z=f(X,Y),最后用mesh(X,Y,Z)即可绘制图像三维网格数据与此类似,现在xyz三个方向都是取-1.3到1.3的100个数据,总共就是100^3即一百万个采样点,[x,y,z]=meshgrid(linspace(-1.3,1.3));中的x,y和z就分别是这一百万个采样点的三个维度上的坐标。
而s=(x.^2 + (9/4)*y.^2 + z.^2 - 1).^3 - x.^2.*z.^3 - (1/9)*y.^2.*z.^3;就得到了函数s=f(x,y,z)=(x.^2 + (9/4)*y.^2 + z.^2 - 1).^3 - x.^2.*z.^3 - (1/9)*y.^2.*z.^3在这一百万个采样点中的值size():获取矩阵的行数和列数(1)s=size(A),当只有一个输出参数时,返回一个行向量,该行向量的第一个元素时矩阵的行数,第二个元素是矩阵的列数。
(2)[r,c]=size(A),当有两个输出参数时,size函数将矩阵的行数返回到第一个输出变量r,将矩阵的列数返回到第二个输出变量c。
(3)size(A,n)如果在size函数的输入参数中再添加一项n,并用1或2为n赋值,则size将返回矩阵的行数或列数。
其中r=size(A,1)该语句返回的时矩阵A的行数,c=size(A,2) 该语句返回的时矩阵A 的列数。
Input() 数据输入Disp() 输出项既可以是字符串也可以是矩阵矩阵运算w=gallery('cauchy',1000); %产生一个1000×1000的柯西矩阵t1=clock; % 获取系统时间w_norm=norm(w) %计算范数t2=clock; %获取系统时间t_norm=etime(t2,t1) %计算范数的耗时t3=clock; %获取系统时间w_normest=normest(w); %估计范数t4=clock; %获取系统时间t_normest=etime(t4,t3) %估计范数的耗时特殊矩阵的创建Zeros(m,n) 生成m*n个全零矩阵Eye(m,n) 生成m*n个单位矩阵One(m,n) 生成m*n个全1矩阵Rand(m,n) 生成m*n个随机矩阵Randn(m,n)生成m*n个标准正态分布随机矩阵linspace(a,b,c)均匀生成介于a到b的c个值,c 默认为100magic(n) 产生n阶魔方矩阵矩阵求值det(A) A为一个矩阵矩阵求秩rank(A)矩阵求迹trace(A) 即求对角线元素和也等于特征值之和a必须为方阵矩阵的逆inv(A)矩阵的伪逆pinv(A) 也称广义矩阵矩阵特征值和特征向量[VB,DB]=eig(B).多项式poly2sym([1 3 2]) 创建多项式ans =x^2 + 3*x + 2p=polyder(P,Q) 求多项式P与多项式Q乘积的导函数多项式[p,q]=polyder(P,Q)求多项式P与多项式Q相除的导函数求多项式的根r=roots(c)C=poly(r): r为多项式的根,c为多项式的系数向量1 求导syms a x %定义符号变量a和xf=sin(a*x) %创建函数fdfx=diff(f,x) %对x求导dfa=diff(f,a) %对a求导2积分syms x %定义符号变量xf=x*log(1+x) %创建函数fint1=int(f,x) %对x积分int2=int(f,x,0,1) %求[0,1]区间上的积分3 复数函数x1=-1+x %直接构造法,实部虚部形式x2=sqrt(2)*exp(i*(3*pi/4)) %直接构造法,复指数形式%符号函数法的构造,实部虚部的形式syms a b real; %声明a,b为实数型x3=a+b*i %实部虚部形式复数的符号表达subs(x3,{a,b},{-1,1}) %带入集体数值%符号函数构造法,复指数形式syms r ct real; %声明 r ct 为实数型x4=r*exp(ct*i); %复数形式的复数表达式subs(x4,{r,ct},{sqrt(2),3*pi/4}) %带入具体值3.1复数函数绘图t=0:0.01:2*pi;y=t+i*t.*sin(t); % 直角坐标表示r=abs(y);bdelta=angle(y); %极坐标表示subplot(2,1,1) %绘制直角坐标图plot(y)title('直角坐标图');subplot(2,1,2) %绘制极坐标polar(delta,r)title('极坐标图') 4 三维绘图t=0:0.01:2*pi;y=t+i*t.*sin(t); % 直角坐标表示r=abs(y);bdelta=angle(y); %极坐标表示subplot(2,1,1) %绘制直角坐标图plot(y)title('直角坐标图');subplot(2,1,2) %绘制极坐标polar(delta,r)title('极坐标图')function ex0303()t=0:pi/50:6*pi;xt=exp(-0.1*t).*cos(t);yt=exp(-0.1*t).*sin(t); %拆分窗口为2*2subplot(2,2,1),plot3(xt,yt,t),grid ontitle('(xt,yt,t)三维图a');subplot(2,2,2),plot3(xt,yt,t),grid on, view([0 0 1]); title('在(0,0,1)观察a的图a1')subplot(2,2,3),plot3(xt,yt,t), grid ontitle('(t,xt,yt)的三维图b');subplot(2,2,4),plot3(t,xt,yt),grid on,view([0 -4 0]) title('在(0,-4,0)观察b的图b1');4.1 图形处理x=randn(500,1); y=randn(500,3); %定义想x,y为正态分布随机数subplot(3,1,2); hist(x); %绘制x为变量的分布图subplot(3,1,3); hist(x,100); %绘制概率分布图subplot(3,1,1); hist(y,25); %绘制分布图t= x*pi/180; %设置x为正态分布随机数,设置函数关系rose(t); set(findobj('Type','line'),'LineWidth',1.5) %绘制玫瑰图4.1.1 柱状图x=randn(1000,1)*100;x=[5 2 1;4 2 7;3 6 9;5 1 7;6 2 5]; %定义x取值subplot(1,2,2); bar(x); %绘制柱状图subplot(1,2,1); barh(x,'stack'); %绘制水平的柱状图z=[15,35,10;20,10,30] %设置坐标轴范围subplot(2,2,1); h1=bar3(z,'detached');set(h1,'FaceColor','w'); title('分离式柱状图')subplot(2,2,2); h2=bar3(z,'grouped');set(h2,'FaceColor','w'); title('分组式柱状图'); subplot(2,2,3);h3=bar3(z,'stacked');set(h3,'FaceColor','w'); title('叠加式柱状图'); subplot(2,2,4); h4=bar3h(z);set(h4,'FaceColor','W'); title('水平放置的三维柱状图');4.1.2面积图part1=[4 6 7 9 2 3]'; part2=[2 1 3 7 9 8]'; %定义part1、part2取值area([part1 part2]) %绘制part1、part2面积图gtext('total=part1+part2') %添加图形标注4.1.3饼图1)x=rand(1,5); y=[0.2 0.3,0.1]; %定义x取值为正态分布随机数,定义y取值subplot(1,2,1); pie(x); %绘制以x为变量的饼图subplot(1,2,2); pie(y); %绘制以y为变量的饼图4.1.4火柴杆图stemt=0:0.2:10; y=exp(-0.5*t).*sin(7*t); %定义t的范围及刻度,y与t的函数subplot(2,1,1); stem(t,y); hold on; %绘制火柴杆图形plot(t,y); plot(t,y,'r');xlabel('X'); ylabel('Y');subplot(2,1,2); stem(t,y,'-.dg','fill');xlabel('X');ylabel('Y');2)t=0:pi/10:6*pi; x=exp(-t/10).*cos(t);y=2*exp(-t/10).*sin(t);stem3(x,y,t,'filled'); %绘制三维火柴杆图hold on; plot3(x,y,t);xlabel('X');ylabel('Y');zlabel('Z');-1-0.50.51-2-1125101520XYZ三维火柴杆图4.1.5阶梯图contourz=peaks; %绘制peaks图形subplot(2,1,1); contour(z); %绘制peaks图形等高线图subplot(2,1,2); contour(z,[3.8 1.5]); clabel(c,h); %标注figure %新建Figure窗口subplot(2,1,1); [c,h]=contour(z,4); clabel(c,h) %标注等高线图中的函数值subplot(2,1,2); contourf(z,4)4.1.5圆柱体图cylindersubplot(1,2,1);[X,Y,Z]=cylinder;mesh(X,Y,Z);title('单位圆柱体')subplot(1,2,2);t=1:10;r(t)=t.*t; [X,Y,Z]=cylinder(r,40); mesh(X,Y,Z); title('一般圆柱体')四单元1.1 二元插值函数[x,y]=meshgrid(-4:4); %产生已知数据栅格点z=peaks(x,y); %产生已知点上的函数值[x1,y1]=meshgrid(-4:0.25:4); %产生更精细的插值栅格点z1=interp2(x,y,z,x1,y1,'nearest');surf(x1,y1,z1) %画基于最邻近法插值的三维表面图z2=interp2(x,y,z,x1,y1,'linear');surf(x1,y1,z2) %画基于二维的分段线插值的三维表面图z3=interp2(x,y,z,x1,y1,'cubic');surf(x1,y1,z3) %画基于二维三次多项式插值的三维表面图1.2 interp函数对正弦函数插值x=0:2*pi;y=sin(x);z=interpft(y,15);xx=linspace(0,2*pi,15); %生成从0到2π之间的15个线性等分点的行向量plot(x,y,'-o',xx,z,':o')1.3x=-3:3;y=[-1 -1 -1 0 1 1 1]; %产生已知点t=-3:.01:3; %产生细密插值点的横坐标p=pchip(x,y,t); %用'cubic'方法对已知点进行细密插值ppol=spline(x,y) %先用已知点进行分段样条插值s=ppval(ppol,t); %再用插值后的样条函数求插值点的y值plot(x,y,'o',t,p,'-',t,s,'-.') % 圆圈代表已知点构成的曲线,%短横线代表用‘cubic’方法进行细密插值后的曲线, %点画线代表先分段插值在细密插值后的曲线-3-2-10123-1.5-1-0.50.511.5102030405060data1data2data3例1 求 f = 2 在0<x<8中的最小值与最大值f='2*exp(-x).*sin(x)';fplot(f,[0,8]); %制图语句[xmin,ymin]=fminbnd(f,0,8)f1='-2*exp(-x).*sin(x)';[xmax,ymax]=fminbnd(f1,0,8)例1 66,11)(2≤≤-+=xxxg用分段线性插值法求插值,并观察插值误差.1.在[-6,6]中平均选取5个点作插值x=linspace(-6,6,100);y=1./(x.^2+1);x1=linspace(-6,6,5);y1=1./(x1.^2+1);plot(x,y,x1,y1,x1,y1,'o','LineWidth',1 .5),gtext('n=4'),2.在[-6,6]中平均选取11个点作插值x=linspace(-6,6,100);y=1./(x.^2+1);x1=linspace(-6,6,11);y1=1./(x1.^2+1);plot(x,y,x1,y1,x1,y1,'o','LineWidth',1 .5),gtext('n=10'),拉格朗日调用函数function f=language(x,y,x0) %求已知数据点的拉格朗日差值多项式%已知数据点的x 坐标向量:x%已知数据点的y 坐标向量:y%插值点的x坐标:x0%求得的拉格朗日差值多项式或在x0处的差值:fsyms t l;if(length(x)==length(y))n=length(x);elsedisp('x和y的维数步相等!');return; %检错endh=sym(0);for(i=1:n)l=sym(y(i));for(j=1:i-1)l=l*(t-x(i))/(x(i)-x(j));end;for(j=i+1:n)l=l*(t-x(j))/(x(i)-x(j));end;h=h+l; endsimplify(h);if(nargin==3)f=sub(h,'t',x0); %计算插值点的函数值elsef=collect(h);f=vpa(f,6); %将插值多项式的系数化成6位精度的小数end拉格朗日图像function y=lagrange(x0,y0,x);n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;end主窗口输入>> x=[-5:5];>> y=1./(1+x.^2);>> x0=[-5:0.001:5];>> y0=lagrange(x,y,x0);>> y1=1./(1+x0.^2);>> plot(x0,y0,'r')>> hold on>> plot(x0,y1,'g')>> gtext('n=10的图像')>>-5-4-3-2-112345-0.500.511.52n=10的图像.用多项式拟合的命令x=0:0.1:1;y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2]; A=polyfit(x,y,2) z=polyval(A,x);plot(x,y,'k+',x,z,'r')13.7.1一元多项式回归 %ex1327.m 多项式拟合 %%%输入数据 x0=17:2:29; x0=[x0,x0];y0=[20.48,25.13,26.15,30.0,26.1,20.3,19.35... 24.35,28.11,26.3,31.4,26.92,25.7,21.3]; %%%%多项式系数拟合,得系数p [p,s]=polyfit(x0,y0,2); p%%%%%y 的拟合值及预测值y 的置信半径delta [y,delta]=polyconf(p,x0,s); y%%%%%交互式画图 polytool(x0,y0,2)182022242628101520253035%加载自带的汽车数据,识别预测功率和汽车自身重量,作为里程相应 load carsmall x1=Weight;x2=Horsepower; %包括NaN 数据 y=MPG;%计算一下线性模型回归系数 X=[ones(size(x1)) x1 x2 x1.*x2];b=regress(y,X) %剔除NaN 数据 %对数据和模型进行绘图 scatter3(x1,x2,y,'filled') hold onx1fit=min(x1):100:max(x1); x2fit=min(x2):10:max(x2);[X1FIT,X2FIT]=meshgrid(x1fit,x2fit);YFIT=b(1)+b(2)*X1FIT+b(3)*X2FIT+b(4)*X1FIT.*X2FIT;mesh(X1FIT,X2FIT,YFIT) xlabel('重量') ylabel('马力') zlabel('耗油量')view(50,10) %调整图形视角效果1000200030004000500005010015020025051015202530354045马力重量耗油量本文采用SPCE061A 单片机为核心处理器,应用基于隐马尔可夫模型的语音识别方法,进行了车载灯光语音识别系统的软硬件设计开发,实验证明本系统能够实现语音识别和控制功能。
