2020名校冲刺卷(二)
2020冲刺高考理科数学精选高分压轴试卷第二卷答案解析(10页)
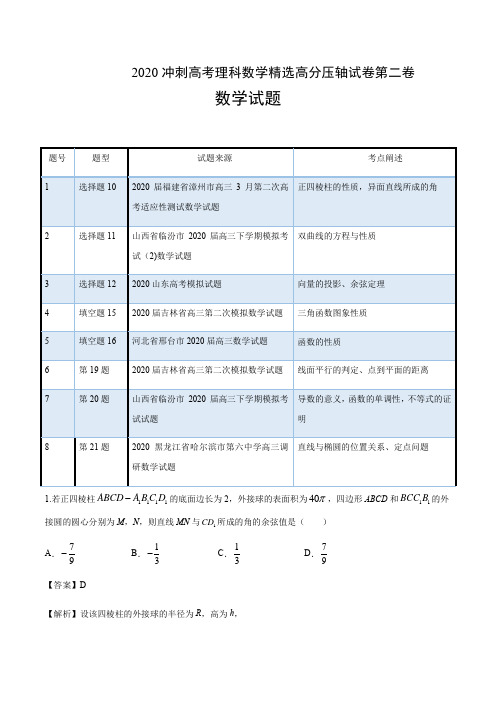
2020冲刺高考理科数学精选高分压轴试卷第二卷数学试题1.若正四棱柱1111ABCD A B C D -的底面边长为2,外接球的表面积为40π,四边形ABCD 和11BCC B 的外接圆的圆心分别为M ,N ,则直线MN 与1CD 所成的角的余弦值是( ) A .79-B .13-C .13D .79【答案】D【解析】设该四棱柱的外接球的半径为R ,高为h ,由2440S R ππ==,得=R ,由==R h =所以112,6,3=====CD CC C D DE EC .因为四边形ABCD 和11BCC B 的外接圆的圆心分别为M ,N ,所以M ,N 分别为BD 和1BC 的中点,所以1//MN DC ,所以DEC ∠为直线MN 与1CD 所成的角或其补角,又9947cos 2339+-∠==⨯⨯DEC ,所以直线MN 与1CD 所成的角的余弦值为79,故选:D.2.已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为12,F F ,点M 在双曲线的右支上,点N 为2F M 的中点,O 为坐标原点,22ON NF b -=,260ONF ∠=︒,12F MF △的面积为( )A .22142x y -=B .22144x y -=C .22182y x -=D .22184x y -=【答案】C【解析】由N 为2MF 的中点,所以1//ON MF ,且11||||2ON MF =,故1260F MF ∠=︒,2121||||(||||)2ON NF MF MF a -=-=,故2a b =,设双曲线的焦距为2c ,在12MF F △中,由余弦定理可得22212124||||2||||cos60c MF MF MF MF =+-⋅︒,21212(||||)||||MF MF MF MF =-+⋅2124||||a MF MF =+⋅, 22212||||444MF MF c a b ∴⋅=-=,12F MF ∴△的面积为2121||||sin 602MF MF ⋅⋅︒=2222,48b a b ∴===,双曲线的方程为22182y x -=.故选:C3.在ABC ∆中,3AC =,向量AB u u u v 在AC u u u v上的投影的数量为2,3ABC S ∆-=,则BC =( )A.5 B .C D .【答案】C【解析】∵向量AB u u u v在AC u u u v 上的投影的数量为2-,∴||cos 2AB A =-u u u r.①∵3ABC S ∆=,∴13||||sin ||sin 322AB AC A AB A ==u u u r u u u r u u ur , ∴||sin 2AB A =u u u r.② 由①②得tan 1A =-,∵A为ABC∆的内角,∴34Aπ=,∴2||3sin4 ABπ== u u u r在ABC∆中,由余弦定理得2222232cos323(2942BC AB AC AB ACπ=+-⋅⋅⋅=+-⨯⨯-=,∴BC=故选C.4.函数()sin()8cos22xf x xπ=--的最小值为_______.【答案】7-【解析】由()sin()8cos22xf x xπ=--所以2()cos8cos2cos18cos222x x xf x x=-=--即2()2cos8cos122x xf x=--,由1cos12x-≤≤令cos2xt=,[]1,1t∈-则2281y t t=--,对称轴为2t=所以2281y t t=--在[]1,1-递减当1t=,即cos12x=时,有min()7f x=-故答案为:7-5.函数()f x 在[0,)+∞上单调递增,且()f x 为奇函数.当0x >时,(2)2()1f x f x =-,且(2)3f =,则满足()5272xf -<-<的x 的取值范围是___________. 【答案】()2log 3,3【解析】根据题意,因为当0x >时,(2)2()1f x f x =-,且(2)3f =()()22113f f ∴=-=, 所以()12f =.又()()42215f f =-=, 所以()()445f f -=-=-,5(27)2x f -<-<Q()()()4271x f f f ∴-<-<.因为()f x 在[0,)+∞上单调递增,且()f x 为奇函数, 所以()f x 在(,)-∞+∞上单调递增.所以()()()4271xf f f ∴-<-<,4271x ∴-<-<,328x ∴<<,2log 33x ∴<<即()2log 3,3x ∈,故答案为:()2log 3,3.6.如图,四棱锥P -ABCD 的底面是正方形,E 为AB 的中点,,1,3,PD CE AE PD PC ⊥===(1)证明:AD ⊥平面PCD .(2)求DA 与平面PCE 所成角的正弦值. 【解析】(1)证明:因为E 为AB 的中点,1AE =, 所以2CD AB ==,所以222CD PD PC +=,从而PD CD ⊥. 又PD CE ⊥,CD CE C =I ,所以PD ⊥底面ABCD ,所以PD AD ⊥. 因为四边形ABCD 是正方形,所以AD CD ⊥. 又CD PD D =I ,所以AD ⊥平面PCD.(2)解:以D 为坐标原点,建立空间直角坐标系D xyz -,如图所示, 则()2,0,0A ,()0,0,3P ,()2,1,0E ,()0,2,0C ,所以()2,1,3PE =-u u u r ,()2,1,0EC =-u u u r ,()2,0,0DA =u u u r. 设平面PCE 的法向量为(),,n x y z =r, 则0PE n EC n ⋅=⋅=u u u r r u u u r r ,即23020x y z x y +-=⎧⎨-+=⎩,令3x =,得()3,6,4n =r .cos ,||||n DA n DA n DA ⋅==r u u u rr u u u r r u u u r ,故DA 与平面PCE7.已知函数()ln(21)(21)1f x x m x =---+.(1)若()y f x =在2x =处的切线与直线320170x y -+=垂直,求()y f x =的极值; (2)若函数()y f x =的图象恒在直线1y =的下方. ①求实数m 的取值范围;②求证:对任意正整数1n >,都有4(1)ln[(2)!]5n n n +<. 【解析】(1)由()ln(21)(21)1f x x m x =---+可得2'()221f x m x =--, 所以21'(2)233f m =-=-,即12m =. 则3()ln (21)2f x x x =--+,2(23)'()1=2121x f x x x --=---1()2x >, 令'()0f x =可得32x =, 当32x >时,'()<0f x ,当1322x <<时,'()>0f x . ∴()f x 在3(,+)2∞上单调递减,在13(,)22上单调递增,∴()f x 的极大值为333()ln 2ln 2222f =-+=,无极小值. (2)①由条件可知:只需()1f x <,即ln(21)(21)0x m x ---<在1(,+)2∞上恒成立.即(21)ln(21)m x x ->-,而12x >,∴210x ->,∴ln(21)21x m x ->-恒成立.令ln(21)()21x g x x -=-,则222ln(21)'()(21)x g x x --=-, 令'()0g x =可得12e x +=. 当1122e x +<<时'()0g x >,当12e x +>时,)'(0g x <,∴()g x 在11(,)22e +上单调递增,在1(,)2e ++∞上单调递减, 故()g x 的最大值为11()2e g e+=,∴1m e>, 即实数m 的取值范围是1(,)e+∞.②由①可知,25m =时,ln(21)2<215x x --,即2(21)ln(21)5x x --<对任意的12x >恒成立. 令21()k x k *=-∈N ,则2ln 5kk <,2ln1ln 2ln3ln(2)12325n n ++++<++++()L L , 即212ln1ln 2ln3ln(2)5n n n +++++<()L , ∴2(21)4(1)ln[(2)!]55n n n n n ++<<. 8.设曲线E 是焦点在x 轴上的椭圆,两个焦点分别是是1F ,2F ,且122F F =,M 是曲线上的任意一点,且点M 到两个焦点距离之和为4.(1)求E 的标准方程;(2)设E 的左顶点为D ,若直线l :y kx m =+与曲线E 交于两点A ,B (A ,B 不是左右顶点),且满足DA DB DA DB +=-u u u v u u u v u u u v u u u v,求证:直线l 恒过定点,并求出该定点的坐标.【解析】(1)设椭圆方程为22221(0)x y a b a b+=>>,由题意2422a c =⎧⎨=⎩,即21a c =⎧⎨=⎩,∴b ==∴椭圆E 的方程是22143x y +=.(2)由(1)可知()2,0D -,设()11,A x y ,()22,B x y ,联立22143y kx mx y =+⎧⎪⎨+=⎪⎩,得()()222348430k x mkx m +++-=,()()()22222(8)4344121612390mk k m k m ∆=-+-=-+>,即22340k m +->,∴122834mk x x k -+=+,()21224334m x x k-=+, 又()()()2212121212y y kx m kx m k x x mk x x m =++=+++22231234m k k -=+,∵DA DB DA DB +=-u u u r u u u r u u u r u u u r ,∴DA DB ⊥u u u r u u u r,即0DA DB ⋅=u u u r u u u r ,即()()()11221212122,2,240x y x y x x x x y y +⋅+=++++=,∴2222224128312240343434m mk m k k k k---+⨯++=+++,∴2271640m mk k -+=, 解得12m k =,227m k =,且均满足即22340k m +->, 当12m k =时,l 的方程为()22y kx k k x =+=+,直线恒过()2,0-,与已知矛盾;当22 7m k=,l的方程为2277y kx k k x⎛⎫=+=+⎪⎝⎭,直线恒过2,07⎛⎫- ⎪⎝⎭.。
【精品高考数学】2020年高考数学金榜冲刺卷(北京专版)(二)+答案

2020年高考数学金榜冲刺卷(二)注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.4.测试范围:高中全部内容.一、选择题共10题,每题4分,共40分.在每题列出的四个选项中,选出符合题目要求的一项. 1.已知集合{|(1)(3)0}A x x x =--<,{|24}B x x =<<,则A B =I ( )A .()1,3B .()1,4C .()2,3D .()2,42.sin390︒的值为( )A .12B .12-C .2-D .23.已知复数21i z i =-,则z 的虚部为( ) A .-1 B .i - C .1 D .i4.设0.7log 0.8a =,11log 0.9b =,0.91.1c =,那么( )A .a b c <<B .a c b <<C .b a c <<D .c a b <<5.84(1)(1)x y ++的展开式中22x y 的系数是( )A .56B .84C .112D .1686.如图,长方体1111ABCD A B C D -中,12AA AB ==,1AD =,点,,E F G 分别是1DD , AB ,1CC 的中点,则异面直线1A E 与GF 所成的角是A .90oB .60oC .45oD .30o7.已知两条直线260x a y ++=和(2)320a x ay a -++=互相平行,则a 等于( )A .0或3或-1B .0或3C .3或-1D .0或-18.已知底面是等腰直角三角形的三棱锥P -ABC 的三视图如图所示,俯视图中的两个小三角形全等,则()A .P A ,PB ,PC 两两垂直 B .三棱锥P -ABC 的体积为83C .||||||PA PB PC ===D .三棱锥P -ABC 的侧面积为9.已知P ,Q 是边长为1的正方形ABCD 边上的两个动点,则AP CQ BP DQ ⋅-⋅u u u r u u u r u u u r u u u r 的取值范围为( )A .[]1,1-B .[]1,2-C .⎡⎤⎣⎦D .⎡⎣10.已知函数()32e ,0461,0x x f x x x x ⎧<=⎨-+≥⎩,其中e 为自然对数的底数,则函数 ()()()2310g x f x f x ⎡⎤=-⎣⎦3+的零点个数为( )A .4B .5C .6D .3 二、填空题共5题,每题5分,共25分. 11.已知双曲线221y x m -=的一条渐近线方程为2x y =,则m =__________. 12.函数())0,2f x x πωϕϕϕπ⎛⎫=+><< ⎪⎝⎭的图像如图所示,则该函数的最小正周期为________.13.已知函数()221x f x x =-,数列{}n a 的通项公式为()2019n n a f n N ⎛⎫=∈* ⎪⎝⎭,则2019a =____.此数列前2019项的和为____.14.已知函数()()()()1231,1log 1,1x x f x x x +⎧-<⎪=⎨+≥⎪⎩,若()2f m =,则()2f m -=______. 15.设,a b 是两个实数,给出下列条件:①1a b +>;②2a b +=;③2a b +>;④222a b +>;⑤1ab >.其中能推出:“,a b 中至少有一个大于1”的条件是____________.三、解答题共6题,共85分.解答应写出文字说明,演算步骤或证明过程.16.(本小题14分)在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,8a =,2b c -=,1cos 4A =-. (1)求sinB 的值;(2)求cos(2)6A π+的值.17.(本小题14分)如图,在四棱柱ABCD −A 1B 1C 1D 1中,底面ABCD 和侧面BCC 1B 1都是矩形,E 是CD 的中点,D 1E ⊥CD ,AB =2BC =2.(Ⅰ)求证:BC ⊥D 1E .(Ⅱ)求证:BC ∥平面BED 1.(Ⅲ)若平面BCC 1B 1与平面BED 1所成的锐二面角的大小为π3,求线段D 1E 的长度.18.(本小题14分)改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪80年代的153万件提升到2018年的507.1亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于1kg )收费10元,续重5元/kg (不足1kg 按1kg 算). (如:一个包裹重量为2.5,kg 则需支付首付10元,续重10元,一共20元快递费用)(1)若你有三件礼物,,A B C 重量分别为0.4 1.2 1.9kg kg kg ,,,要将三个礼物分成两个包裹寄出(如:,A B 合为一个包裹,C 一个包裹),那么如何分配礼物,使得你花费的快递费最少?(2)为了解该快递点2019年的揽件情况,在2019年内随机抽查了30天的日揽收包裹数(单位:件),得到如下表格:现用这30天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取4天,记这4天中日揽收包裹数超过200件的天数为随机变量,X 求X 的分布列和期望19.(本小题15分)已知函数()ln f x ax x =+()a R ∈.(1)若2a =,求曲线()y f x =在1x =处切线的斜率;(2)求()f x 的单调区间;(3)设2()22g x x x =-+,若对任意1(0,)x ∈+∞,均存在[]20,1x ∈,使得12()()f x g x <,求a 的取值范围.20.(本小题14分)在平面直角坐标系xOy 中,已知点(1,0)F ,动点Q 到点F 的距离比到直线2x =-的距离小1个单位长度(1)求动点Q 的轨迹方程C ;(2)若过点F 的直线l 与曲线C 交于,A B 两点,8FA FB ⋅=-u u u v u u u v,求直线l 的方程.21.(本小题14分)定义:给定整数i ,如果非空集合满足如下3个条件:①A N *⊆;②{}1A ≠;③,x y N *∀∈,若x y A +∈,则xy i A -∈. 则称集合A 为“减i 集”(1){}1,2P =是否为“减0集”?是否为“减1集”?(2)证明:不存在“减2集”;(3)是否存在“减1集”?如果存在,求出所有“减1集”;如果不存在,说明理由.2020年高考数学金榜冲刺卷(二)注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.4.测试范围:高中全部内容.一、选择题共10题,每题4分,共40分.在每题列出的四个选项中,选出符合题目要求的一项. 1.已知集合{|(1)(3)0}A x x x =--<,{|24}B x x =<<,则A B =I ( ) A .()1,3B .()1,4C .()2,3D .()2,4【答案】C【解析】根据题意,{|13}A x x =<<,则{|23}(2,3)A B x x ⋂=<<=. 故本题正确答案为C.2.sin390︒的值为( )A .12B .12-C .2-D .2【答案】A【解析】试题分析: 因为()()0000000sin 600sin 360240sin 240sin 18060sin 60=+==+=-=故选择C3.已知复数21i z i =-,则z 的虚部为( ) A .-1B .i -C .1D .i【答案】A 【解析】2i 2i(i 1)22i 1i i 1(i 1)(i+1)2z +-+====----,故z 的虚部为1-. 故选:A.4.设0.7log 0.8a =,11log 0.9b =,0.91.1c =,那么() A .a b c << B .a c b <<C .b a c <<D .c a b<<【答案】C【解析】【分析】利用指数函数和对数函数的单调性得出结论.【详解】解:Q 0.70.70.7log 1log 0.8log 0.7<<,∴0.7log 00.81<<Q 1111log 0.9log 1<∴11log 0.90<Q 0.901.1 1.1>∴0.91.11>综上,c a b >>.故选:C.5.84(1)(1)x y ++的展开式中22x y 的系数是( )A .56B .84C .112D .168 【答案】D【解析】因为8(1)x +的展开式中2x 的系数为28C ,4(1)y +的展开式中2y 的系数为24C ,所以22x y 的系数为2284168C C =.故选D.6.如图,长方体1111ABCD A B C D -中,12AA AB ==,1AD =,点,,E F G 分别是1DD , AB ,1CC 的中点,则异面直线1A E 与GF 所成的角是A .90oB .60oC .45oD .30o【答案】A 【解析】由题意:ABCD ﹣A 1B 1C 1D 1是长方体,E ,F ,G 分别是DD 1,AB ,CC 1的中点,连接B 1G , ∵A 1E ∥B 1G ,∴∠FGB 1为异面直线A 1E 与GF 所成的角或其补角.连接FB 1,在三角形FB 1G 中,AA 1=AB =2,AD =1,B 1F ==B 1G ==,FG ==B 1F 2=B 1G 2+FG 2.∴∠FGB 1=90°,即异面直线A 1E 与GF 所成的角为90°.故选A .7.已知两条直线260x a y ++=和(2)320a x ay a -++=互相平行,则a 等于( ) A .0或3或-1 B .0或3 C .3或-1 D .0或-1【答案】D【解析】Q 两条直线260x a y ++=和()2320a x ay a -++=互相平行 216232a a a a -∴=≠--,或121k a =-和223a k a -=-同时不存在解得:1a =-或0a =本题正确选项:D8.已知底面是等腰直角三角形的三棱锥P -ABC 的三视图如图所示,俯视图中的两个小三角形全等,则( )A .P A ,PB ,PC 两两垂直 B .三棱锥P -ABC 的体积为83C .||||||PA PB PC ===D .三棱锥P -ABC 的侧面积为【答案】C 【解析】根据三视图,可得三棱锥P -ABC 的直观图如图所示,其中D 为AB 的中点,PD ⊥底面AB C.所以三棱锥P -ABC 的体积为114222323⨯⨯⨯⨯=,2AC BC PD ∴===,AB ∴==,||||||DA DB DC ∴===||||||PA PB PC ∴==== 222PA PB AB +≠Q ,PA ∴、PB 不可能垂直,即,PA ,PB PC 不可能两两垂直,122PBA S ∆=⨯=Q 122PBC PAC S S ∆∆===Q∴三棱锥P -ABC 的侧面积为故正确的为C.故选:C.9.已知P ,Q 是边长为1的正方形ABCD 边上的两个动点,则AP CQ BP DQ ⋅-⋅u u u r u u u r u u u r u u u r 的取值范围为( )A .[]1,1-B .[]1,2-C .⎡⎤⎣⎦D .⎡⎣【答案】A【解析】以点A 为原点,建立直角坐标系,如图所示:则()0,0A ,()10B ,,()1,1C ,()0,1D ,设点()11,P x y ,()22,Q x y ,∴()11,AP x y =u u u r ,()221,1CQ x y =--u u u r ,()111,BP x y =-u u u r ,()22,1DQ x y =-u u u r,∴()()()()12122112211111AP CQ BP DQ x x y y x x y y x x ⋅-⋅=-+-----=-u u u r u u u r u u u r u u u r ,又∵P ,Q 是边长为1的正方形ABCD 边上的两个动点,则101x ≤≤,201x ≤≤,∴2111x x -≤-≤.10.已知函数()32e ,0461,0x x f x x x x ⎧<=⎨-+≥⎩,其中e 为自然对数的底数,则函数 ()()()2310g x f x f x ⎡⎤=-⎣⎦3+的零点个数为( )A .4B .5C .6D .3 【答案】A【解析】当x ≥0时,f (x )=4x 3﹣6x 2+1的导数为f ′(x )=12x 2﹣12x ,当0<x <1时,f (x )递减,x >1时,f (x )递增,可得f (x )在x =1处取得最小值,也为最小值﹣1,且f (0)=1,作出函数f (x )的图象,g (x )=()()23103f x f x ⎡⎤-+⎣⎦,可令g (x )=0,t =f (x ), 可得3t 2﹣10t +3=0,解得t =3或13, 当t 13=,即f (x )13=,g (x )有三个零点; 当t =3,可得f (x )=3有一个实根,综上g (x )共有四个零点;二、填空题共5题,每题5分,共25分.11.已知双曲线221y x m -=的一条渐近线方程为2x y =,则m =__________. 【答案】14【解析】因为渐近线方程为2x y =,且双曲线焦点在x 轴上,故可得102b m a ==>,解得14m =.故答案为:14.12.函数())0,2f x x πωϕϕϕπ⎛⎫=+><< ⎪⎝⎭的图像如图所示,则该函数的最小正周期为________.【答案】8【解析】由(0)f ϕ=,得sin 2ϕ=, Q 2ϕπ<<π,34πϕ∴=,则3())4f x x πω=+,Q ()3104f πω⎛⎫=+= ⎪⎝⎭, 34πωπ∴+=,即4πω=,则函数的最小正周期2284T πππω===,故答案为:813.已知函数()221x f x x =-,数列{}n a 的通项公式为()2019n n a f n N ⎛⎫=∈* ⎪⎝⎭,则2019a =____.此数列前2019项的和为____.【答案】20192a = 2020 【解析】由题可知,2220192019120192201922019212019n nn n a f n n n ⋅⎛⎫====+ ⎪--⎝⎭⋅- 则2019201912220192019a =+=⨯- 201920192019201911 (12201942019220192019)S =++++++--⨯- 即()()()20191201822017100910102019...S a a a a a a a =+++++++2100922020=⨯+=故答案为:20192a = 202014.已知函数()()()()1231,1log 1,1x x f x x x +⎧-<⎪=⎨+≥⎪⎩,若()2f m =,则()2f m -=______. 【答案】23-或1 【解析】()112312m m f m +<⎧=⇒⎨-=⎩或()210log 12m m m ≥⎧⇒=⎨+=⎩或3m =, ∴22m -=-或21m -=,∴()()2223f m f -=-=-或()()211f m f -==. 故答案为:23-或1 15.设,a b 是两个实数,给出下列条件:①1a b +>;②2a b +=;③2a b +>;④222a b +>;⑤1ab >.其中能推出:“,a b 中至少有一个大于1”的条件是____________.【答案】③. 【解析】若12,23a b ==,则1a b +>,但1,1a b <<,故①推不出; 若1a b ==,则2a b +=,故②推不出;若2,3a b =-=-,则222a b +>,故④推不出;若2,3a b =-=-,则1ab >,故⑤推不出;对于③,即2a b +>,则,a b 中至少有一个大于1,反证法:假设1a ≤且1b ≤,则2a b +≤与2a b +>矛盾,因此假设不成立,,a b 中至少有一个大于1.故答案为:③.三、解答题共6题,共85分.解答应写出文字说明,演算步骤或证明过程.16.(本小题14分)在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,8a =,2b c -=,1cos 4A =-. (1)求sinB 的值;(2)求cos(2)6A π+的值.【答案】(1;(2.【解析】(1)Q 由1cos 4A =-,可得sin A = ∴由22642cos 2b c bc A b c ⎧=+-⎨-=⎩,可得:64b c =⎧⎨=⎩,∴由sin sin b a B A=得sin B =;(2)Q 27cos22cos 1,sin 22sin cos 8A A A A A =-=-==71cos(2)cos 2cos sin 2sin 66682A A A πππ⎛∴+=-=-⨯ ⎝⎭=.17.(本小题14分)如图,在四棱柱ABCD −A 1B 1C 1D 1中,底面ABCD 和侧面BCC 1B 1都是矩形,E 是CD 的中点,D 1E ⊥CD ,AB =2BC =2.(Ⅰ)求证:BC ⊥D 1E .(Ⅱ)求证:BC ∥平面BED 1.(Ⅲ)若平面BCC 1B 1与平面BED 1所成的锐二面角的大小为π3,求线段D 1E 的长度.【答案】(1)证明过程详见解析;(2)D 1E =1.【解析】(1)证明:∵底面和侧面是矩形,∴,又∵∴平面3分∵平面∴BC⊥D1E.6分(2)解法1:延长,交于,连结,则平面ADD1A1平面BED1底面ABCD是矩形,E是CD的中点,,∴连结,则又由(1)可知BC⊥D1E又∵D1E⊥CD,∴底面ABCD,∴D1E⊥AE∴平面BED19过E作于,连结,则是平面ADD1A1与平面BED1即平面BCC1B1与平面BED1所成锐二面角的平面角,所以又,∴又易得,,从而由,求得D 1E =1. 12分解法2:由(1)可知BC ⊥D 1E又∵D 1E ⊥CD ,∴底面ABCD 7分设为的中点,以E 为原点,以,,所在直线分别为轴,建立空间直角坐标系如图. 8分设,则,,,,设平面的一个法向量∵,由,得令,得9分设平面BCC 1B 1法向量为m ⃗⃗ =(x 1,y 1,z 1),因为CB ⃗⃗⃗⃗⃗ =(1,0,0),CB 1⃗⃗⃗⃗⃗⃗⃗ =(1,1,a),由{m ⃗⃗ ⋅CB ⃗⃗⃗⃗⃗ =0m ⃗⃗ ⋅CB 1⃗⃗⃗⃗⃗⃗⃗ =0得{x 1=0,x 1+y 1+az 1=0. 令z 1=−1,得m ⃗⃗ =(0,a,−1). 10分由平面BCC 1B 1与平面BED 1所成的锐二面角的大小为π3, 得|cos <m ⃗⃗ ,n ⃗ >|=|m ⃗⃗⃗ ⋅n ⃗ ||m ⃗⃗⃗ ||n ⃗ |=a √2⋅√a 2+1=cos π3,解得a =1. 即线段D 1E 的长度为.18.(本小题14分)改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪80年代的153万件提升到2018年的507.1亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于1kg )收费10元,续重5元/kg (不足1kg 按1kg 算). (如:一个包裹重量为2.5,kg 则需支付首付10元,续重10元,一共20元快递费用)(1)若你有三件礼物,,A B C 重量分别为0.4 1.2 1.9kg kg kg ,,,要将三个礼物分成两个包裹寄出(如:,A B 合为一个包裹,C 一个包裹),那么如何分配礼物,使得你花费的快递费最少?(2)为了解该快递点2019年的揽件情况,在2019年内随机抽查了30天的日揽收包裹数(单位:件),得到如下表格:现用这30天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取4天,记这4天中日揽收包裹数超过200件的天数为随机变量,X 求X 的分布列和期望【答案】(1), A B 一个包裹,C 一个包裹时花费的运费最少,为30元;(2)详见解析.【解析】(1) ,A B 一个包裹,C 一个包裹时,需花费151530+=(元), A C ,一个包裹,B 一个包裹时,需花费201535+=(元),B C ,一个包裹,A 一个包裹时,需花费251035+=(元),综上,, A B 一个包裹,C 一个包裹时花费的运费最少,为30元.(2)由题意知,每日揽包裹数超过200件的概率为13X 可取10,1,2,3,4,4,3X B ⎛⎫ ⎪⎝⎭:,()()44120,1,23,3,,43k kkP X k C k -⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝=⎭== 则X 的分布列为()14433E X =⨯=所以这4天中日揽收包裹数超过200件的天数期望为43.19.(本小题15分)已知函数()ln f x ax x =+()a R ∈. (1)若2a =,求曲线()y f x =在1x =处切线的斜率; (2)求()f x 的单调区间;(3)设2()22g x x x =-+,若对任意1(0,)x ∈+∞,均存在[]20,1x ∈,使得12()()f x g x <,求a 的取值范围. 【答案】(Ⅰ).(Ⅱ)当0a ≥时,()f x 的单调递增区间为(0,)+∞当0a <时,函数()f x 的单调递增区间为1(0,)a -,单调递减区间为1(,)a-+∞ (Ⅲ)31a e <-. 【解析】(Ⅰ)由已知1()2(0)f x x x=+>',(1)213f '=+=.曲线()y f x =在1x =处切线的斜率为. (Ⅱ)11'()(0)ax f x a x x x+=+=>. ①当0a ≥时,由于0x >,故10ax +>,'()0f x > 所以,()f x 的单调递增区间为(0,)+∞. ②当0a <时,由'()0f x =,得1x a=-. 在区间1(0,)a-上,()0f x '>,在区间1(,)a-+∞上()0f x '<, 所以,函数()f x 的单调递增区间为1(0,)a-,单调递减区间为1(,)a-+∞. (Ⅲ)由已知,转化为max max ()()f x g x <.max ()2g x =由(Ⅱ)知,当0a ≥时,()f x 在(0,)+∞上单调递增,值域为R ,故不符合题意. (或者举出反例:存在33()32f e ae =+>,故不符合题意.)当0a <时,()f x 在1(0,)a -上单调递增,在1(,)a-+∞上单调递减, 故()f x 的极大值即为最大值,11()1ln()1ln()f a aa-=-+=----, 所以21ln()a >---,解得31a e <-.20.(本小题14分)在平面直角坐标系xOy 中,已知点(1,0)F ,动点Q 到点F 的距离比到直线2x =-的距离小1个单位长度(1)求动点Q 的轨迹方程C ;(2)若过点F 的直线l 与曲线C 交于,A B 两点,8FA FB ⋅=-u u u v u u u v,求直线l 的方程.【答案】(1)24y x =(2)1y x =-或1y x =-+【解析】(1)根据抛物线的定义,知动点Q 的轨迹是以(1,0)F 为焦点,以1x =-为准线的抛物线, 所以动点Q 的轨迹方程C 为:24y x =;(2)①当l 的斜率不存在时,可知48FA FB ⋅=-≠-u u u r u u u r,不符合条件; ②当l 的斜率存在且不为0时,设l :(1)y kx =-,则2(1)4y k x y x=-⎧⎨=⎩,联立可得()2222240k x k x k -++=, 设()()1122,,,A x y B x y ,则21212224,1k x x x x k ++=⋅=.因为向量,FA FB u u u r u u u r方向相反,所以()()()12121224||||11148FA FB FA FB x x x x x x k ⎛⎫⋅=-=-++=-+++=-+=- ⎪⎝⎭u u u r u u u r u u u r u u u r ,所以21k =,即1k =±,所以直线l 的方程为1y x =-或1y x =-+.21.(本小题14分)定义:给定整数i ,如果非空集合满足如下3个条件:①A N *⊆;②{}1A ≠;③,x y N *∀∈,若x y A +∈,则xy i A -∈.则称集合A 为“减i 集”(1){}1,2P =是否为“减0集”?是否为“减1集”? (2)证明:不存在“减2集”;(3)是否存在“减1集”?如果存在,求出所有“减1集”;如果不存在,说明理由.【答案】(1)是“减0集”;不是“减1集”(2)证明见解析;(3)存在;{1,3},{1,3,5},{1,3,5,7},⋯⋯{1,3,5,⋯⋯,21n -,}⋯⋯,*()n N ∈【解析】(1)*P N ⊆Q ,{1}P ≠,112P +=∈,110P ⨯-∈,P ∴是“减0集”同理,*P N ⊆Q ,{1}P ≠,112P +=∈,111P ⨯-∉,P ∴不是“减1集”.(2)假设存在A 是“减2集”,则若x y A +∈, 那么2xy A -∈,当2x y xy +=-时,有(1)(1)3x y --=, 则x ,y 一个为2,一个为4,所以集合A 中有元素6,但是33A +∈,332A ⨯-∉,与A 是“减2集”,矛盾,故不存在“减2集” (3)存在“减1集”A .{1}A ≠.①假设1A ∈,则A 中除了元素1以外,必然还含有其它元素. 假设2A ∈,11A +∈,而111A ⨯-∉,因此2A ∉. 假设3A ∈,12A +∈,而121A ⨯-∈,因此3A ∈. 因此可以有{1A =,3}.假设4A ∈,13A +∈,而131A ⨯-∉,因此4A ∉.假设5A ∈,14A +∈,141A ⨯-∈,235+=,231A ⨯-∈,因此5A ∈.因此可以有{1A =,3,5}.以此类推可得:{1A =,3,5,⋯⋯,21n -,}⋯⋯,*()n N ∈, 以及A 的满足以下条件的非空子集:{1,3},{1,3,5},{1,3,5,7},⋯⋯。
2020年高考语文临考冲刺卷浙江卷(二)

2020 年高考语文临考冲刺卷浙江卷(二)1. 下列各句中,没有错别字且加粗字的注音全部正确的一项是( )A. 先知往往是寂寞的,他最先看到问题的所在;但先知的伟大就在于能够忍受寂寞,并在寂寞中,踽(yǔ踽)独行,不因他人的漫骂和攻讦(ji )é而隐瞒或改变自己的观点。
B. “嫦娥”四号的成功是国际合作的成果:13台载(z ǎ荷i) (h è)中4台是与德国等国家合作的,与俄罗斯合作的同位素热源则保障了它安全渡过月夜。
C. 当你面临无法逃遁(d ùn)的困惑时,网络上千篇一律的爆款“鸡汤”并不能帮你解决问题,但文学能揭穿黑暗,迎接光明,使你抛弃卑鄙(b ǐ和)浅薄,趋向高尚和精深。
D. 个人史是汇入正史河流的涓涓细流,哪怕只是一个少年只(zh ī言)片语的勾沉,也是重建被遗忘与被毁坏的偌(nu ò)大历史的一砖一瓦。
2. 阅读下面的文字,完成下列各题。
一直以来,人们都认为祝融是根正苗红的炎黄后裔。
然而翻看更多的史料,就会发现高贵的祝融其实是个官名。
【甲】《国语》有此记载: “黎为高辛氏火正,以淳耀敦大,天明地德,光照四海,故命之曰‘祝融'其功大矣。
”可见“祝融”是官职,负责掌管用火事宜。
这在《汉书?五行志上》中得到了印证:“古之火正,谓火官也,掌祭火星,行火政。
”【乙】由字可知, “祝”在甲骨文中如人跪在神前祷告; “融”的形态则是炊烟自一种叫“鬲” 的烹饪器具旁边如虫般蠕动而出。
祝融成为“火”的代言,众望所归!火的使用在人类社会发展的进程中意义重大。
对于尚在蒙昧状态下的古代先民来说,火是防御野兽的工具、抵御严寒的利器、烹饪美食的神物。
即便是燧人明了钻木取火,火不必再靠天赐予,但如何保留火种、如何将火的使用极大化,依然是个难题。
在这一点上祝融绝对功德无量,否则也做不了火官。
而且在那一时期火之威力堪比如今的武器,身为火官,必然会在现实生活中参与部落战争,并担负重任。
人教版2020年名校小升初语文冲刺试卷(二)(II )卷

人教版2020年名校小升初语文冲刺试卷(二)(II )卷姓名:________ 班级:________ 成绩:________小朋友,带上你一段时间的学习成果,一起来做个自我检测吧,相信你一定是最棒的!一、积累运用 (共9题;共39分)1. (5分)写出两个带有下面偏旁的字(至少写两个)。
匚:________、________ 宀:________、________土:________、________ 立:________、________2. (5分)读课文古诗两首《小儿垂钓》,把能搭配的词语用线连起来。
蓬头________ 莓苔侧坐 ________ 借问路人 ________ 稚子3. (5分)比一比,再组词。
径________ 霜________ 犹________ 橙________ 促________经________ 雪________ 忧________ 澄________ 捉________4. (8分)写出下列词语的反义词容易—________ 悲伤—________ 丑陋—________5. (2分)下面一段话,修改完全正确的一项是()在综合实践课上,老师让小华到前面讲“阿凡提斗财主”的故事。
虽然小华嗓子哑了,但是讲得很认真,很生动,我们全班同学都把他吸引了。
A . “虽然……但是…”改为“因为……所以……”;“我们全班同学都把他吸引了”改为“我们都被他讲的故事吸引了”。
B . “阿凡提斗财主”改为《阿凡提斗财主》;“我们全班同学都把他吸引了”改为“我们都被他讲的故事吸引了”。
C . “阿凡提斗财主”改为《阿凡提斗财主》;“虽然……但是……”改为“因为……所以……”。
6. (1分)写出下列词语的近义词。
坚强——________ 牢靠——________经常——________ 发现——________7. (5分)用加横线的词语造句。
①大家脸上露出笑容,情不自禁地鼓起掌来。
2020届名校学术联盟新高考原创冲刺模拟试卷(二)文科数学

2020届名校学术联盟新高考原创冲刺模拟试卷(二)文科数学★祝考试顺利★ 注意事项:1、考试范围:高考范围。
2、试题卷启封下发后,如果试题卷有缺页、漏印、重印、损坏或者个别字句印刷模糊不清等情况,应当立马报告监考老师,否则一切后果自负。
3、答题卡启封下发后,如果发现答题卡上出现字迹模糊、行列歪斜或缺印等现象,应当马上报告监考老师,否则一切后果自负。
4、答题前,请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
5、选择题的作答:每个小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。
6、主观题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。
如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
7、保持答题卡卡面清洁,不折叠,不破损,不得使用涂改液、胶带纸、修正带等。
8、考试结束后,请将本试题卷、答题卡、草稿纸一并依序排列上交。
第I 卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每个小题所给出的四个选项中,只 有一项是符合题目要求的,把正确选项的代号填在答题卡的指定位置.)1.设集合1|02x A x x +⎧⎫=≥⎨⎬-⎩⎭,{}1,0,1,2B =-,则A B = A .{}1,0,1-B .{}0,1,2C .{}1,0,1,2-D .{}1,22.设复数z 满足i z 32-=,则=z A .3B .13C .2D .133.“1x <”是“ln(1)0x +<”的 A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件4.在ABC ∆中,1a =,30A =,60B =,则b 等于A B .12C D .25.若某空间几何体的三视图如图所示,则该几何体的体积是A .2B .1C .D .6.若椭圆2221x y a +=经过点1,3P ⎛⎫ ⎪ ⎪⎝⎭,则椭圆的离心率e =A .2B 1C .3D .37.设数列{}n a 满足32111232n n a a a a n +++=-,则n a = A .112n -B .312n -C .12nD .2n n 8.已知α满足972cos =α,则cos cos 44ππαα⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭A. 718B. 2518C. 718-D. 2518-9.如果123,,,P P P 是抛物线2:4C y x =上的点,它们的横坐标123,,,x x x ,F 是抛物线C的焦点,若12201820x x x +++=,则122018PF P F P F +++=A .2028B .2038C .4046D .405610.已知()f x 是定义在R 上的奇函数,且在(),-∞+∞上是减函数,()12f =-,则满足()232f x -<的实数x 的取值范围是A .()1,1-B .()2,0-C .()2,2-D .()0,211.一个圆锥SC 的高和底面直径相等,且这个圆锥SC 和圆柱OM 的底面半径及体积也都相等,则圆锥SC 和圆柱OM 的侧面积的比值为 A.2BCD12.已知函数(1)2y f x =+-是奇函数,21()1x g x x -=-,且()f x 与()g x 的图像的交点为11(,)x y ,22(,)x y ,,66(,)x y ,则126126x x x y y y +++++++=A .0B .6C .12D .18第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每小题5分,满分20分)13.双曲线2212516y x -=的渐近线方程为_____________14.设x ,y 满足约束条件⎪⎩⎪⎨⎧≤-+≥+-≥+0530101y x y x y ,则y x z +-=2的最小值为 .15.设,a b ∈R ,222a b +=,则221411a b +++的最小值为______. 16.若两曲线21y x =-与ln 1y a x =-存在公切线,则正实数a 的取值范围是 . 三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤,第17 ~ 21题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答.) 17.(12分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c2cos Asin C-=. (1)求角A 的大小; (2)若cos(B +6π)=14,求cosC 的值.18.(12分)2019年10月28日至10月31日,中国共产党第十九届四中全会在北京召开。
2020年高考英语临考冲刺卷 浙江卷(二)

2020年高考英语临考冲刺卷浙江卷(二)Thirteen-year-old Madison Williams was studying in her bedroom when Leigh Williams, her mother, told her that a little boy fell into a septic tank(化粪池) and no one could reach him.Madison and Leigh ran to a neighbor’s yard, where they found the boy’s worried mother and other adults surrounding the tank opening. It stuck out a few inches above the ground and was 11 inches in width — slightly wider than a basketball — with a hatch(盖子) that had been moved unnoticed. The two-year-old boy had slipped in and was drowning(溺水) in four feet of waste water inside the eight-feet-deep tank.Madison surveyed the situation. She was the only one who could fit through the small hole. Without hesitation, she told the adults, “Lower me in.” Inside, the tank was dark, and the air was smelly. In the process, she jammed her left wrist against a hidden pole, injuring the muscles in her wrist so severely that the hand was left useless.Rather than tending to her injury, Madison tried to feel the underwater boy. Minutes went by before she saw the outline of his foot. Madison shot her good hand out and grasped the foot tightly. “Pull me up!” she shouted. Then, ten minutes after Madison had entered the tank, she and the boy were lifted out.Bu t the boy wasn’t out of trouble. He had lacked oxygen long enough that he wasn’t breathing. He was placed on his side, and an adult hit him hard on the back. It was only when Madison heard him cry that she knew he was all right. It took Madison longer to recover than the boy, who was taken to hospital and left hospital that same night. She, however, experienced months of painful treatment, for the injury that she had postponed tending was more severe, which, says neighbor Mary Holley, made the girl’s action s all the more impressive.1.What most likely caused the boy to fall into the septic tank?A.The tank was very hard to be noticed.B.The boy was curious about the unknown.C.The hatch was not in the correct position.D.The tank opening stood out on the ground.2.Which of the following can be used to best describe Madison?A.ModestB.Optimistic.C.Determined.D.Hard-working.3.What is the text mainly about?A.A lucky little boy.B.A terrible drowning accident.C.A hidden septic tank.D.An admirable teen hero.On a bright early summer morning, many young swimmers gather at a local swimming pool in the state of Maryland.They are members of a competitive summer swim team, and that's a regular part of their daily life. As they train and cut seconds off their times, which makes them closer to the championship in the following large-scale(大规模的) competitions, they are getting lots of physical exercise and vitamin D from the sun. However, the benefits of belonging to a sports team are not just honor or health related. You can learn useful life skills.Paul Waas, coach of the swim team, explains, "The discipline(自制力) comes into play when you're talking about concentrating on the details that your coaches are saying as it makes you faster rather than just going up and down the pool the same way you have every time. When you focus on what you're doing right and what you can do better, then you'll see the improvement."Besides, there is also responsibility, goals and workings within a group. Again, here is Coach Waas. "It's really great! It's so fun to watch from year to year. I've had kids who as 7-year-olds on the team could barely pay attention in practice and were only interested in who was going first. Now they've come back as 8-year-olds, having set some goals and having things that they want to achieve. These skills can help them a lot."But playing the sports is not without harm. Some can be hard on the body. Young athletes suffer serious injuries that follow them into adulthood. Coach Waas says that in fact, swimming is different from most others. First, it poses a lower risk of injury. The second one relates to how swim teams are structured. Actually t children are not the only ones who can benefit. Adults can also benefit from team sports.1. Why do the swimmers gather at a swimming pool in the early morning?A. To obtain vitamin D from the sun.B. To build practical skills for future.C. To join in a large-scale competition.D. To carry out their routine practice.2. What do Paul Waas' words imply in paragraph 2?A. Swimmers should concentrate on details.B. Members get disciplined and focused in the team.C. Coaches play a key role in players' improvement.D. Most swimmers enjoy swimming in the same way.3. What does the author want to convey in the text?A. Exercise benefits everyone.B. Swimming is better than other sports.C. Team sports teach life lessons.D. Physical exercise should be a habit.From ancient stories to modern researches, the label(标签) attached to being left-handed is undeniable. Left-handed people, or “lefties” as they are often called, are generally believed to be good at art — Leonardo da Vinci, Picasso and Michelangelo are all left-handed.Our brain is divided into two parts: the left hemisphere(大脑半球) and the right hemisphere. The left hemisphere, linked to logic and analysis, is responsible for the right side of the body. The right hemisphere, linked to creativity and imagination, controls the left side of the body. So, people tend to believe lefties are controlled by the right side of the brain, and are more creative than right-handers. Some also think that lefties may not be as good as right-handers in mathematics and problem-solving skills.However, a recent study carried out by scientists from the University of Liverpool in the UK and the University of Milan in Italy proved this theory wrong. The study involved(涉及) more than 2,300 students in Italy aged between 6 and 17 years old. They were asked to complete several mathematical tasks of different levels. It turned out the left-handers outperformed the others when the tasks involved difficult problem-solving. This pattern was particularly clear in male adolescents. However, when it came to simple arithmetic, there was no difference betweenleft-handers and right-handers.It was also discovered that those who are "severely" right-handed performed less well in all the experiments compared to “medium” right-handers and left-handers.“Taken together, these findings show that handedness does influence abilities to some degree," the study’s authors wrote. However, “handedness is just an indirect expression of brain function," wrote psychology professor Giovanni Sala from the University of Liverpool in the UK, the lead author of the study. Sala also noted that only one third of people with a highly-developed right side of the brain are left-handed. It means that there are lots of right-handed people with a similar brain function as left-handers.1.The author begins the text by ____________.A.telling some ancient storiesB.giving examples of artworksC.introducing a modern researchD.presenting conventional wisdom2.What is the main focus of paragraph 2?A.Skills of solving problems.B.Ways of becoming creative.C.People's opinions of left-handers.D.The functions of two hemispheres.3.What can we learn from the recent study led by Giovanni Sala?A.Handedness doesn’t have any association with brain function.B.People with a highly-developed right hemisphere are most likely lefties.C.The “severely” right-handed are far better at simple arithmetic than lefties.D.Right-handers didn’t perform as well as lefties when handling tough problems.4.The text is most probably taken from ____________.A.a medical reportB.a science magazineC.a biology textbookD.an education essayWith the ever-increasing cost of living, one's salary is sometimes not enough for anything beyond putting food on the table. ①________ Consequently, finding the perfect work-life balance is a struggle for most of us, especially those who are living with pets. If you're one of those people, here's what you can do.◎Exercise with your pet.If your free time is not adequate for both exercising and bonding with your pet, you can combine the two for an even better outcome. ②________ Or try to fit in a hike on the weekend. Your bond will grow even stronger. Taking part in these activities helps you and your pet live a healthy life.◎Don't forget about your family.③________ So, as you make the necessary lifestyle changes with your pet, extend the changes as far as your family is concerned. For instance, bring your kids along on walks with your pet and use the opportunity to get up to date with their lives. If you have the means and the time, you can also organize outings as a great way to bring the whole family, including the four-legged members.◎④________Some pets require lots of activities while others can do just fine with minimal(极少的) exercise. It is, therefore, necessary that you consider both your lifestyle and an animal's personality. For instance, if you have no free time on weekdays, keep off dogs like terriers as they need lots of activities to stay healthy. ⑤________ For example, if your kids are below 5 years of age, avoid dogs like poodles as they're known to be too nervous around small kids.A.Choose a pet that fits your lifestyle.B.Consider switching your existing lifestyle.C.The number of kids you have and their ages should also be considered.D.Take your pet friend for a walk around the neighborhood every evening.E.The next step is to change the relationships between your pet and family.F.This is why most people often have to work long hours and even weekends.G.Your family needs your love and presence just as much as your four-legged friend.阅读下面短文,从短文后各题所给的A、B、C和D四个选项中,选出可以填入空白处的最佳选项。
2020年高考全国名校联考冲刺金卷全国Ⅱ卷 语文(二) Word版含答案

2020届百校联考高考百日冲刺金卷全国II卷·语文(二)注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置。
2.全部答案写在答题卡上,写在本试卷上无效。
3.本试卷满分150分,测试时间150分钟。
4.考试范围:高考全部内容。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
政府是公共治理体系的重要组成部分,政府承担着管理政治、经济、文化、社会、环境生态等方面事务的职能,而大数据技术为政府更好履职提供了更加有利的条件。
首先,更多指标印证宏观经济形势。
宏观经济变量如增长、投资和消费等,与许多实物指标、运行指标等确实存在某种相关性,如用电量、货运量等。
现在,大数据技术提供了更多能够利用的指标,如工程机械制造企业能够通过物联网得知全球各地用户设备的实时使用状况,并能够与投资、工程建设、房地产建设等指标及时有效地相互验证。
再如居民消费价格指数(CPI)是重要的调控指标,现在一些平台性网络企业也发布与之高度相关的指数,例如“1号店快速消费品价格指数”“阿里巴巴网购价格指数”(aSPI)和“阿里巴巴网购核心商品价格指数”(aSPI-core)等。
由于这些指数直接从网络产生的海量实时数据中挖掘产生,真实性、实效性都较好,为政府相关决策提供了有效的信息。
这方面的研究国内外有许多,例如利用网络搜索指数或其它大数据技术对就业形势、增长率、通胀预期、房价趋势投资指数等问题所做的研究,均取得了有意义的结果。
其次,结构性数据呈现行业特点。
互联网、物联网的广泛应用,能够反映出许多产业、企业、产品的生产、销售和运转情况。
例如各种原材料的市场价格、各种产品的出厂价格,各种设备的开工情况、各种商品的销售情况等等,这些信息更加实时、定向和颗粒化,而不仅仅是CPI、PPI(生产价格指数)、开工率这种汇总指标。
因此,政府在继续实施总量调控的同时,有可能更多地采用结构式、分布式政策,在差异化调控的基础上实现总量目标。
2020年中考数学冲刺卷 【2】含答案解析

2020年中考数学冲刺卷一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(3分)如图,直线a∥b,∠1=70°,那么∠2的度数是()A.50°B.60°C.70°D.80°2.(3分)实数√38的值在()A.5和6之间B.6和7之间C.7和8之间D.8和9之间3.(3分)党的十八大以来,积极践行“绿水青山就是金山银山”的发展理念,大力开展植树造林,到2018年底,全国森林面积达到32.2亿亩,森林覆盖率达到22.35%,32.2亿用科学记数法表示为()A.32.2×108B.32.2×109C.3.22×108D.3.22×1094.(3分)如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于()A.60m B.40m C.30m D.20m5.(3分)用配方法解关于x的一元二次方程x2﹣2x﹣3=0,配方后的方程可以是()A.(x﹣1)2=4 B.(x+1)2=4 C.(x﹣1)2=16 D.(x+1)2=16 6.(3分)为了解某班学生双休户外活动情况,对部分学生参加户外活动的时间进行抽样调查,结果如下表:户外活动的时间(小时)1 2 3 6学生人数(人) 2 2 4 2则关于“户外活动时间”这组数据的众数、中位数、平均数分别是()A.3、3、3 B.6、2、3 C.3、3、2 D.3、2、37.(3分)如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA、OB于点E、F,那么第二步的作图痕迹②的作法是()A.以点F为圆心,OE长为半径画弧B.以点F为圆心,EF长为半径画弧C.以点E为圆心,OE长为半径画弧D.以点E为圆心,EF长为半径画弧8.(3分)《九章算术》勾股章有一“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深,葭长各几何.”意思是:如示意图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度和芦苇的长度分别是多少?备注:1丈=10尺.设芦苇长x尺,则可列方程为()A.x2+102=(x+1)2B.(x﹣1)2+52=x2C.x2+52=(x﹣1)2D.x2+12=(x﹣1)29.(3分)如图,是一组按照某种规律摆放成的图案,则图6中三角形的个数是()A.18 B.19 C.20 D.2110.(3分)如图,矩形ABCD中,AB=4,AD=3,P是边CD上一点,将△ADP沿直线AP对折,得到△APQ.当射线BQ交线段CD于点F时,DF的最大值是()A.3 B.2 C.4−√7D.4−√5二、填空题(每题5分,满分30分,将答案填在答题纸上)11.(5分)计算:(√2+1)(√2−1)=.12.(5分)若点P(1﹣2a,a﹣2)关于原点的对称点在第一象限内,a为整数,则a的值为.13.(5分)如图,已知斜坡BQ的坡度i=1:2.4,坡长BQ=13米,在斜坡BQ上有一棵银杏树PQ,小李在A处测得树顶P的仰角为α,测得水平距离AB=8米.若tanα=0.75,点A,B,P,Q在同一平面上,PQ⊥AB于点C,则银杏树PQ的高度为米.14.(5分)如图是一个上下底密封纸盒的三视图(图中尺寸单位:cm),请你根据图中数据,计算这个密封纸盒的表面积为cm2.(结果可保留根号)15.(5分)若关于x的方程x2﹣2mx+9=0有两个相等实数根,则方程2x−m =3x的解为.16.(5分)已知:y关于x的函数y=k2x2﹣(2k+1)x+1的图象与坐标轴只有两个不同的交点A、B,P点坐标为(4,2),则△PAB的面积为.三、解答题:本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤. 17.若实数x,y满足√2018−x+|x+y−4037|=0,求代数式x2﹣2xy+y2的值.18.先化简,再求值:2a−1÷(2a−1−2a+1a−1),其中a=√116+(−2)−2+2sin60°−(π−3)°.19.如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.(1)求证:△AFE≌△CDE;(2)若AB=4,BC=8,求图中阴影部分的面积.20.“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下:(1)本次比赛参赛选手共有人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为;(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.21.对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足﹣M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值,例如,如下图中的函数,它的最大值是12,最小值是﹣1,它也是有界函数,其边界值是1.(1)分别判断函数y=1x(1≤x≤5)和y=x+1(x>0)是不是有界函数?若是有界函数,求其边界值;(2)若函数y=﹣2x﹣1(a≤x≤b,a<b)的边界值是3,且这个函数的最大值也是3,求a的值及b的取值范围.22.如图,已知Rt△EBC中,∠B=90°,A为BE边上一点,以边AC上的点O为圆心、OA 为半径的圆O与EC相切,D为切点,AD∥BC.(1)求证:∠E=∠ACB.(2)若AD=1,tan∠DAC=√22,求BC的长.23.某厂家欲将n件产品运往A,B,C三地销售,运费分别为30元/件,8元/件,25元/件,且要求运往C地的件数是运往A地件数的2倍,设安排x件产品运往A地.(1)当n=200时,①根据信息填表:A地B地C地产品件数(件)x2x运费(元)30x②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?(2)若总运费为5800元,求n的最小值.24.如图1,抛物线W:y=12x2−2的顶点为点A,与x轴的负半轴交于点D,直线AB交抛物线W于另一点C,点B的坐标为(1,0).(1)求直线AB的解析式;(2)求tan∠BDC的值;(3)将抛物线W向下平移m(m>0)个单位得到抛物线W1,如图2,记抛物线W1的顶点为A1,与x轴负半轴的交点为D1,与射线BC的交点为C1.问:在平移的过程中,tan∠D1C1B是否恒为定值?若是,请求出tan∠D1C1B的值;若不是,请说明理由.2020年中考数学冲刺卷参考答案一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.C ; 2.B ; 3.D ; 4.B ; 5.A ; 6.A ; 7.D ; 8.B ; 9.C ; 10.C ;二、填空题(每题5分,满分30分,将答案填在答题纸上) 11.1; 12.1; 13.10;14.12+2√3; 15.±9; 16.52或4;三、解答题:本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤. 17.1; 18.原式=2a +2=2√3+1;19.阴影部分的面积=S △ACF ﹣S △AEF =12×4×8−12×4×3=10; 20.50;30%; 21.1;﹣2<b ≤122.略;23.221;24.直线AB 的解析式为y =2x ﹣2; tan ∠BDC =1;tan ∠D 1C 1B。
