2015佛山一模 广东省佛山市普通高中2015届高三教学质量检测(一)数学文试卷及答案
广东省佛山市第一中学2015届高三10月月考数学(文)试题 Word版含答案
佛山一中2015届10月考（文科）数学试题2014-10-12一、选择题：本大题共10小题，每小题5分，共50分．1．设集合A ＝{x |y ＝3x －x 2}，B ＝{y |y ＝2x ，x >1}，则A ∩B 为( )A ．B ．(2,3]C ． 2．已知f (x )＝⎩⎪⎨⎪⎧ln 1x x >01x x <0，则f (x )>－1的解集为( )A ．(－∞，－1)∪(0，e )B ．(－∞，－1)∪(e ，＋∞)C ．(－1,0)∪(e ，＋∞)D ．(－1,0)∪(0，e )3．已知R x ∈，则“4|2||1|>-++x x ”是“2-<x ”的（ ） A . 充分而不必要条件 B .必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 4．设a ＝⎝ ⎛⎭⎪⎫120.5，b ＝0.30.5，c ＝log 0.30.2，则a 、b 、c 的大小关系是( )A ．a >b >cB ．a <b <cC ．b <a <cD ．a <c <b5．已知f (x )＝(x －a )(x －b )－2 (a <b )，并且α、β是方程f (x )＝0的两个根(α<β)，则实数a 、b 、α、β的大小关系可能是( )A ．α<a <b <βB ．a <α<β<bC ．a <α<b <βD ．α<a <β<b 6．在ABC ∆中, 已知向量)72cos ,18(cos 00=AB , )27cos 2,63cos 2(00=AC , 则BAC ∠cos 的值为 A ．0 B ．21 C ．22 D ．23 7.若f (x )＝x 3－6ax 的单调递减区间是(－2,2)，则a 的取值范围是( )A ．(－∞，0]B ．C ．{2}D ．∪[43，83] B ．(－13，1]∪∪∪[12，43)∪[43，3)9．函数x x y cos +=的大致图象是 （ ）A ．B ．C ．D ．10．已知命题“x ∃∈R ，12x a x -++≤”是假命题，则实数a 的取值范围是 A.)1,3(- B. ]1,3[- C. ),1()3,(+∞--∞ D. ),1[]3,(+∞--∞ 二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分． （一）必做题（11－13题）11．若函数f (x )＝⎩⎪⎨⎪⎧(a －2)x ，x ≥2⎝ ⎛⎭⎪⎫12x －1，x <2是R 上的单调减函数，则实数a 的取值范围是12．已知函数)2(+x f 是定义在),(∞+∞-上的奇函数. 当)2,(∞-∈x 时，4)(x x x f -=，则 当),2(∞+∈x 时，=)(x f13．设函数()y f x =是定义域为R 的奇函数，且满足(2)()f x f x -=-对一切x ∈R 恒成立，当-1≤x ≤1时，3()f x x =．则下列四个命题：①()f x 是以4为周期的周期函数； ②()f x 在上的解析式为3()(2)f x x =-；③()f x 在33(,())22f 处的切线方程为3450x y +-=；④()f x 的图像的对称轴中有x =±1.其中正确的命题是（二）选做题（14－15题，考生只能从中选做一题）14.(坐标系与参数方程选做题)已知直线l :132x ty t =+⎧⎨=-⎩（t 为参数且t R ∈）与曲线C :22x cos y cos αα=⎧⎨=+⎩(α是参数且[)02,απ∈)，则直线l 与曲线C 的交点坐标为 .15.（几何证明选讲选做）如图(4)，AB 是半圆的直径，C 是AB 延长线上一点，CD 切半圆于点D ，CD =2，DE ⊥AB ，垂足为E ，且E 是OB 的中点，则BC 的长为 ．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）已知函数)2||,0,0)(sin()(πϕωϕω<>>+=A x A x f 的 图象的一部分如下图所示.(1)求函数)(x f 的解析式;(2)当]32,6[--∈x 时,求函数)2()(++=x f x f y 的最大值与最小值及相应的x 的值.17. （本小题满分12分）近年空气质量逐步恶化，雾霾天气现象出现增多，大气污染危害加重．大气污染可引起心悸、呼吸困难等心肺疾病．为了解某市心肺疾病是否与性别有关，在某医院随机的对入院50人进行了问卷调查得到了如下的列联表：患心肺疾病 不患心肺疾病 合计 男 5 女 10 合计 50已知在全部50人中随机抽取1人，抽到患心肺疾病的人的概率为35．（Ⅰ）请将上面的列联表补充完整；（Ⅱ）是否有99.5%的把握认为患心肺疾病与性别有关？说明你的理由；（Ⅲ）已知在不患心肺疾病的5位男性中，有3位又患胃病．现在从不患心肺疾病的5位男性中，任意选出3位进行其他方面的排查，求恰好有一位患胃病的概率．下面的临界值表供参考：2()P K k ≥0.15 0.10 0.05 0.025 0.010 0.005 0.001 k2.0722.7063.8415.0246.63 57.87910.828（参考公式22()()()()()n ad bc K a b c d a c b d -=++++ 其中n a b c d =+++）yOx12 －13 5 －218．（本小题满分14分）如图，1AA 、1BB 为圆柱1OO 的母线，BC 是底面圆O 的直径，D 、E 分别是1AA 、1CB 的中点．（I ）证明：DE //平面ABC ；（II ）若21==BC BB ，求三棱锥BC A A 1-的体积的最大值。
2015年佛山市普通高中高三教学质量检测(一)文科综合(历史)(试题+答案)
2015年佛山市普通高中高三教学质量检测（一）文科综合（历史）能力试题2015.1本试卷共12页，满分150分，考试时间150分钟.注意事项:1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考号填写在答题卡上．用2B铅笔将答题卡试卷类型（A）填涂在答题卡上，并在答题卡右上角的“试室号”和“座位号”栏填写试室号、座位号，将相应的试室号、座位号信息点涂黑．2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案答在试题卷上无效．3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答卷上各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。
不按以上要求作答的答案无效．4．考试结束后，将答卷和答题卡一并交回．第一部分 选择题 （共140分）一、单项选择题：本题共35小题，每小题4分，共140分．在每小题给出的四个选项中，只有一个选项符合题目要求，选对的得4分，错选、不选得0分．12．公元前817年鲁武公带着长子姬括、次子姬戏拜见周天予，周天子格外喜欢姬戏，故硬性作主，立姬戏为鲁国太子。
待鲁武公病逝，姬戏即位，是为懿公。
这说明A．宗法制已经崩溃 B．姬括足鲁国的小宗C．地方官员由中央任命 D．天子好恶是立储君的唯一标准13．有学者认为，我国历史上的第一次社会政治大转型，发自商鞅，极盛于始皇，而完成于汉武。
与该转型描述相符的是A．“兼并天下，建皇帝之号，立百官之职，收天下之权，尽归于中央” B．“诏知府公事并须长吏、通判签议连书，方许行下”C．“设行中书省……统郡县，镇边鄙，与都省为表里”D．“革中书省，归其政于六部，置殿阁大学士”14．据史料记载，隋文帝开皇四年，智贾租得常田一亩，交与田租银钱五文，租田人不负担田赋；灌田水渠破而水溢，田主不负责。
据此可知A．均田制已经瓦解 B．租佃制在全国范围推广C．土地私有制开始确立 D．经济生活中存在契约意识15．近代以来不同中国人对美国的政治看法不一。
【解析】广东省佛山市2015届高三第一次教学质量检测(一模)数学文试题Word版含解析
2015年广东省佛山市高考数学一模试卷（文科）一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）复数等于（）A．1+2i B．1﹣2i C．2﹣i D．2+i【考点】：复数代数形式的乘除运算．【专题】：数系的扩充和复数．【分析】：利用复数的运算法则即可得出．【解析】：解：原式===2﹣i，故选：C．【点评】：本题考查了复数的运算法则，属于基础题．2．（5分）已知集合M={x∈R|0＜x＜2}，N={x∈R|x＞1}，则M∩（∁R N）=（）A．[1，2）B．（1，2）C．[0，1）D．（0，1]【考点】：交、并、补集的混合运算．【专题】：集合．【分析】：求出N的补集，从而求出其与M的交集．【解析】：解：∵集合M={x∈R|0＜x＜2}=（0，2），N={x∈R|x＞1}=（1，+∞）∴∁R N=（﹣∞，1]∴M∩∁R N=（（0，2）∩[1，+∞）=（0，1]故选：D．【点评】：本题考查了集合的运算，是一道基础题．3．（5分）若函数y=的图象关于原点对称，则实数a等于（）A．﹣2 B．﹣1 C．1 D． 2【考点】：函数奇偶性的性质；函数的图象．【专题】：函数的性质及应用．【分析】：根据函数y=的图象关于原点对称，得到函数y=f（x）是R上的奇函数，根据奇函数的定义求出a的值即可．【解析】：解：令y=f（x），∵函数y=的图象关于原点对称，∴函数y=f（x）是R上的奇函数，∴f（﹣x）====﹣=﹣f（x）=﹣，∴a=﹣1，故选：B．【点评】：本题考查了函数的奇偶性，是一道基础题．4．（5分）已知x，y满足不等式组，则目标函数z=3x+y的最大值为（）A．12 B．24 C．8 D．【考点】：简单线性规划．【专题】：不等式的解法及应用．【分析】：作出题中不等式组表示的平面区域，得如图的四边形OABC及其内部，再将目标函数z=2x+y对应的直线进行平移，可得当x=4，y=0时，z=3x+y取得最大值为12．【解析】：解：作出不等式组表示的平面区域，得到如图的四边形OABC及其内部，其中O（0，0），A（4，0），B（，），C（0，8）设z=F（x，y）=3x+y，将直线l：z=3x+y进行平移，当l经过点A时，目标函数z达到最大值∴z最大值=F（4，0）=12故选：A．【点评】：本题给出二元一次不等式组，求目标函数z=3x+y的最大值，着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，属于基础题．5．（5分）已知两个单位向量的夹角为45°，且满足⊥（λ﹣），则实数λ的值为（）A．1 B．C．D．2【考点】：平面向量数量积的运算．【专题】：计算题；平面向量及应用．【分析】：运用向量的数量积的定义，可得两个单位向量的数量积，再由向量垂直的条件：数量积为0，计算即可得到所求值．【解析】：解：由单位向量的夹角为45°，则•=1×1×cos45°=，由⊥（λ﹣），可得，•（λ﹣）=0，即λ﹣=0，则﹣1=0，解得λ=．故选B．【点评】：本题考查平面向量的数量积的坐标定义和性质，考查向量垂直的条件，考查运算能力，属于基础题．6．（5分）在空间中，有如下四个命题：①平行于同一个平面的两条直线是平行直线；②垂直于同一条直线的两个平面是平行平面；③若平面α内有不共线的三个点到平面β距离相等，则α∥β；④过平面α的一条斜线有且只有一个平面与平面α垂直．其中正确的两个命题是（）A．①、③ B．②、④ C．①、④ D．②、③【考点】：平面与平面之间的位置关系；空间中直线与直线之间的位置关系．【专题】：作图题．【分析】：我们可以从正方体去观察理解，①从空间两条直线的位置关系判断．②由线面垂直的性质定理判断；③从两平面的位置关系判断；④由射影的条数判断．【解析】：解：①平行于同一个平面的两条直线，可能平行，相交或异面．不正确；②垂直于同一条直线的两个平面是平行平面，由线面垂直的性质定理知正确；③若平面α内有不共线的三个点到平面β距离相等，可能平行，也可能相交，不正确；④过平面α的一条斜线有且只有一个平面与平面α垂直．正确，因为一条斜线只有一条射影，只能确定一个平面．故选B【点评】：本题主要考查了两直线的位置关系，两平面的位置关系及线面垂直的性质定理，斜线，垂线，射影等概念，作为客观题要多借助空间几何体来判断．7．（5分）某校高三年级学生会主席团有共有5名同学组成，其中有3名同学来自同一班级，另外两名同学来自另两个不同班级．现从中随机选出两名同学参加会议，则两名选出的同学来自不同班级的概率为（）A．0.35 B．0.4 C．0.6 D．0.7【考点】：互斥事件的概率加法公式；相互独立事件的概率乘法公式．【专题】：概率与统计．【分析】：分别计算出从5名学生中选出2名学生进入学生会的基本事件总数和满足这两名选出的同学来自不同班级的基本事件个数，代入古典概型概率计算公式，可得答案【解析】：解：来自同一班级的3名同学，用1，2，3表示，来自另两个不同班级2名同学用，A，B表示，从中随机选出两名同学参加会议，共有12，13，1A，1B，23，2A，2B，3A，3B，AB共10种，这两名选出的同学来自不同班级，共有1A，1B，23，2A，2B，3A，3B共7种，故这两名选出的同学来自不同班级概率P==0.7故选：D【点评】：本题考查的知识点是古典概型概率计算公式，其中熟练掌握利用古典概型概率计算公式求概率的步骤，是解答的关键．8．（5分）已知双曲线﹣=1的左、右焦点分别为F1，F2，过F2的直线与该双曲线的右支交于A、B两点，若|AB|=5，则△ABF1的周长为（）A．16 B．20 C．21 D．26【考点】：双曲线的简单性质．【专题】：计算题；圆锥曲线的定义、性质与方程．【分析】：根据双曲线的定义和性质，即可求出三角形的周长．【解析】：解：由双曲线的方程可知a=4，则|AF1|﹣|AF2|=8，|BF1|﹣|BF2|=8，则|AF1|+|BF1|﹣（|BF2|+|AF2|）=16，即|AF1|+|BF1|=|BF2|+|AF2|+16=|AB|+16=5+16=21，则△ABF1的周长为|AF1|+|BF1|+|AB|=21+5=26，故选D．【点评】：本题主要考查双曲线的定义，根据双曲线的定义得到A，B到两焦点距离之差是个常数是解决本题的关键．9．（5分）已知f（x）=x﹣x2，且a，b∈R，则“a＞b＞1”是“f（a）＜f（b）”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【考点】：必要条件、充分条件与充要条件的判断．【专题】：简易逻辑．【分析】：根据二次函数的性质分别判断其充分性和必要性．【解析】：解：画出函数f（x）=x﹣x2的图象，如图示：，由图象得：f（x）在（，+∞）递减，∴a＞b＞1时，f（a）＜f（b），是充分条件，反之不成立，如f（0）=0＜f（）=1，不是必要条件，故选：A．【点评】：本题考查了二次函数的性质，考查了充分必要条件，是一道基础题．10．（5分）有10个乒乓球，将它们任意分成两堆，求出这两堆乒乓球个数的乘积，再将每堆乒乓球任意分成两堆并求出这两堆乒乓球个数的乘积，如此下去，直到不能再分为止，则所有乘积的和为（）A．45 B．55 C．90 D．100【考点】：归纳推理．【专题】：等差数列与等比数列；推理和证明．【分析】：用特殊值法，假设每次分出一个，分别求出每一次的乘积，然后等差数列的性质相加可得答案．【解析】：解：假设每次分堆时都是分出1个球，第一次分完后应该一堆是1个球，另一堆n﹣1个，则乘积为1×（n﹣1）=n﹣1；第二次分完后应该一堆是1个球，另一堆n﹣2个，则乘积为1×（n﹣2）=n﹣2；依此类推最后一次应该是应该一堆是1个球，另一堆1个，则乘积为1×1=1；设乘积的和为T n，则T n=1+2+…+（n﹣1）=n（n﹣1）当n=10时，T10=×10×（10﹣1）=45故选：A【点评】：本题主要考查等差数列的求和．属基础题．在解答选择填空题时，特殊值法是常用方法之一．解决本题的关键在于特殊值法的应用．二、填空题：本大共3小题，考生作答4小题，每小题5分，满分15分．（一）必做题（11～13题）11．（5分）如果f（x）=，那么f[f（2）]=1．【考点】：函数的值．【专题】：计算题；函数的性质及应用．【分析】：根据x的范围，分别求出相对应的函数值，从而得到答案．【解析】：解：∵f（2）=0，∴f（0）=1，即f[f（2）]=1，故答案为：1．【点评】：本题考查了分段函数问题，考查了函数求值问题，是一道基础题．12．（5分）已知点A（﹣2，0），B（0，4）到直线l：x+my﹣1=0的距离相等，则m的值为或1．【考点】：点到直线的距离公式．【专题】：直线与圆．【分析】：利用点到直线的距离公式即可得出．【解析】：解：由点到直线的距离公式可得=，即|4m﹣1|=3，解得m=或1．故答案为：或1．【点评】：本题考查了点到直线的距离公式，属于基础题．13．（5分）如图，为了测量河对岸A、B两点之间的距离，观察者找到一个点C，从C点可以观察到点A、B；找到一个点D，从D点可以观察到点A、C；找到一个点E，从E点可以观察到点B、C；并测量得到一些数据：CD=2，CE=2，∠D=45°，∠ACD=105°，∠ACB=48.19°，∠BCE=75°，∠E=60°，则A、B两点之间的距离为．（其中cos48.19°取近似值）【考点】：解三角形的实际应用．【专题】：应用题；解三角形．【分析】：求出AC，通过正弦定理求出BC，然后利用余弦定理求出AB．【解析】：解：依题意知，在△ACD中，∠A=30°由正弦定理得AC==2在△BCE中，∠CBE=45°，由正弦定理得BC==3在△ABC中，由余弦定理AB2=AC2+BC2﹣2AC•BCcos∠ACB=10∴AB=．故答案为：．【点评】：本题考查三角形的面积的求法，正弦定理与余弦定理的应用，考查计算能力．三、几何证明选讲14．（5分）如图，P是圆O外一点，PA，PB是圆O的两条切线，切点分别为A，B，PA中点为M，过M作圆O的一条割线交圆O于C，D两点，若PB=2，MC=1，则CD=2．【考点】：与圆有关的比例线段．【专题】：几何证明．【分析】：由切割线定理，得MA2=MC•MD，由此能求出CD．【解析】：解：由已知得MA=，∵MA是切线，MCD是割线，∴MA2=MC•MD，∵MC=1，∴3=1×（1+CD），解得CD=2．故答案为：2．【点评】：本题考查与圆有关的线段长的求法，是基础题，解题时要认真审题，注意切割线定理的合理运用．四、坐标系与参数方程15．（2012•湖南）在极坐标系中，曲线C1：ρ（cosθ+sinθ）=1与曲线C2：ρ=a（a＞0）的一个交点在极轴上，则a=．【考点】：简单曲线的极坐标方程．【专题】：计算题．【分析】：根据ρcosθ=x，ρsinθ=y，ρ2=x2+y2将极坐标方程化成普通方程，利用交点在极轴上进行建立等式关系，从而求出a的值．【解析】：解：∵曲线C1的极坐标方程为：ρ（cosθ+sinθ）=1，∴曲线C1的普通方程是x+y﹣1=0，∵曲线C2的极坐标方程为ρ=a（a＞0）∴曲线C2的普通方程是x2+y2=a2∵曲线C1：ρ（cosθ+sinθ）=1与曲线C2：ρ=a（a＞0）的一个交点在极轴上∴令y=0则x=，点（，0）在圆x2+y2=a2上解得a=故答案为：【点评】：本题主要考查了简单曲线的极坐标方程与普通方程的转化，同时考查了计算能力和分析问题的能力，属于基础题．三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤．16．（12分）已知函数f（x）=sin（ωx﹣）（ω＞0，x∈R）的最小正周期为π．（1）求f（）．（2）在图3给定的平面直角坐标系中，画出函数y=f（x）在区间[﹣，]上的图象，并根据图象写出其在（﹣，）上的单调递减区间．【考点】：五点法作函数y=Asin（ωx+φ）的图象；正弦函数的图象．【专题】：作图题；三角函数的图像与性质．【分析】：（1）依题意先解得ω=2，可得解析式f（x）=sin（2x﹣），从而可求f（）的值．（2）先求范围2x﹣∈[﹣，]，列表，描点，连线即可五点法作图象，并根据图象写出其在（﹣，）上的单调递减区间．【解析】：解：（1）依题意得=π，解得ω=2，∴f（x）=sin（2x﹣），…2分∴f（）=sin（）=sin cos﹣cos sin==…4分（2）∵x∈[﹣，]∴2x﹣∈[﹣，]，列表如下：2x﹣﹣﹣π﹣0x ﹣﹣﹣f（x）0 ﹣1 0 1画出函数y=f（x）在区间[﹣，]上的图象如下：由图象可知函数y=f（x）在（﹣，）上的单调递减区间为（﹣，﹣），（，） (12)分【点评】：本题主要考察了五点法作函数y=Asin（ωx+φ）的图象，三角函数的图象与性质，属于基础题．17．（12分）某地区“腾笼换鸟”的政策促进了区内环境改善和产业转型，空气质量也有所改观，现从当地天气网站上收集该地区近两年11月份（30天）的空气质量指数（AQI）（单位：μg/m3）资料如下：（图1和表1）2014年11月份AQI数据日期1 2 3 4 5 6 7 8 9 10AQI 89 55 52 87 124 72 65 26 46 48日期11 12 13 14 15 16 17 18 19 20AQI 58 36 63 78 89 97 74 78 90 117日期21 22 23 24 25 26 27 28 29 30AQI 137 139 77 63 63 77 64 65 55 45表12014年11月份AQI数据频率分布表分组频数频率[20，40）[40，60）[60，80）[80，100）[100，120）[120，140]表2（Ⅰ）请填好2014年11月份AQI数据的频率分布表（表2）并完成频率分布直方图（图2）；（Ⅱ）该地区环保部门2014年12月1日发布的11月份环评报告中声称该地区“比去年同期空气质量的优良率提高了20多个百分点”（当AQI＜100时，空气质量为优良）．试问此人收集到的资料信息是否支持该观点？【考点】：频率分布直方图．【专题】：概率与统计．【分析】：（Ⅰ）根据题意，填写2014年11月份AQI数据的频率分布表，画出频率分布直方图；（Ⅱ）利用数据计算2013年与2014年的11月优良率是多少，比较数据信息得出结论．【解析】：解：（Ⅰ）根据题意，填写2014年11月份AQI数据的频率分布表，如下；分组频数频率[20，40）2[40，60）7[60，80）12[80，100）5[100，120） 1[120，140] 3（3分）；根据频率分布表，画出频率分布直方图如下；（6分）（Ⅱ）支持，理由如下：2013年11月的优良率为：，…（8分）2014年11月的优良率为：，…（9分）∴；…（11分）∴利用数据信息得出“比去年同期空气质量的优良率提高了20多个百分点”．…（12分）【点评】：本题考查了频率分布表与频率分布直方图的应用问题，是基础题目．18．（14分）如图，四棱锥P﹣ABCD，侧面PAD是边长为2的正三角形，且与底面垂直，底面ABCD是∠ABC=60°的菱形，M为PC的中点．（Ⅰ）求证：PC⊥AD；（Ⅱ）在棱PB上是否存在一点Q，使得A，Q，M，D四点共面？若存在，指出点Q的位置并证明；若不存在，请说明理由；（Ⅲ）求点D到平面PAM的距离．【考点】：点、线、面间的距离计算；空间中直线与直线之间的位置关系．【专题】：空间位置关系与距离．【分析】：（Ⅰ）法一：取AD中点O，连结OP，OC，AC，依题意可知△PAD，△ACD均为正三角形，从而AD⊥平面POC，由此能证明PC⊥AD．法二：连结AC，依题意可知△PAD，△ACD均为正三角形，从而AM⊥PC，DM⊥PC，由此能证明PC⊥AD．（Ⅱ）当点Q为棱PB的中点时，A，Q，M，D四点共面．取棱PB的中点Q，连结QM，QA，由已知得QM∥BC，由此能证明A，Q，M，D四点共面．（Ⅲ）点D到平面PAM的距离即点D到平面PAC的距离，由已知得得PO为三棱锥P﹣ACD 的体高，由V D﹣PAC=V P﹣ACD，能求出点D到平面PAM的距离．【解析】：（Ⅰ）证法一：取AD中点O，连结OP，OC，AC，依题意可知△PAD，△ACD均为正三角形，所以OC⊥AD，OP⊥AD，又OC∩OP=O，OC⊂平面POC，OP⊂平面POC，所以AD⊥平面POC，又PC⊂平面POC，所以PC⊥AD．…（4分）证法二：连结AC，依题意可知△PAD，△ACD均为正三角形，又M为PC的中点，所以AM⊥PC，DM⊥PC，又AM∩DM=M，AM⊂平面AMD，DM⊂平面AMD，所以PC⊥平面AMD，又AD⊂平面AMD，所以PC⊥AD．…（4分）（Ⅱ）解：当点Q为棱PB的中点时，A，Q，M，D四点共面，证明如下：…（6分）取棱PB的中点Q，连结QM，QA，又M为PC的中点，所以QM∥BC，在菱形ABCD中AD∥BC，所以QM∥AD，所以A，Q，M，D四点共面．…（8分）（Ⅲ）解：点D到平面PAM的距离即点D到平面PAC的距离，由（Ⅰ）可知PO⊥AD，又平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，PO⊂平面PAD，所以PO⊥平面ABCD，即PO为三棱锥P﹣ACD的体高．…（9分）在Rt△POC中，，，在△PAC中，PA=AC=2，，边PC上的高AM=，所以△PAC的面积，…（10分）设点D到平面PAC的距离为h，由V D﹣PAC=V P﹣ACD得…（11分），又，所以，…（13分）解得，所以点D到平面PAM的距离为．…（14分）【点评】：本题考查异面直线垂直的证明，考查四点共面的判断与求法，考查点到平面的距离的求法，解题时要注意空间思维能力的培养．19．（14分）已知数列{a n}的前n项和为S n，若4S n=（2n﹣1）a n+1+1（n∈N），且a1=1．（1）求证：数列{a n}为等差数列；（2）设bn=，数列{b n}的前n项和为T n，证明：T n＜（n∈N）．【考点】：数列的求和；数列递推式．【专题】：等差数列与等比数列．【分析】：（1）由已知得4a n=（2n﹣1）a n+1﹣（2n﹣3）a n，从而=，由此能证明数列{a n}是首项为1，公差为2的等差数列．（2）由a n=2n﹣1，S n=n+=n2，得bn===，由此利用裂项求和法能证明T n ＜（n∈N）．【解析】：（1）证明：∵4S n=（2n﹣1）a n+1+1，①∴n≥2时，4S n﹣1=（2n﹣3）a n+1，②①﹣②，得4a n=（2n﹣1）a n+1﹣（2n﹣3）a n，n≥2∴（2n+1）a n=（2n﹣1）a n+1，∴=，∴a n==1×=2n﹣1，∴a n﹣a n﹣1=（2n﹣1）﹣（2n﹣3）=2，∴数列{a n}是首项为1，公差为2的等差数列．（2）解：∵数列{a n}是首项为1，公差为2的等差数列，∴a n=2n﹣1，S n=n+=n2，∴bn====，n≥2∴T n＜（1+++…+）=．∴T n＜（n∈N）．【点评】：本题考查数列{a n}为等差数列的证明，考查不等式的证明，解题时要认真审题，注意累乘法和裂项求和法的合理运用．20．（14分）已知点M（2，1），N（﹣2，1），直线MP，NP相交于点P，且直线MP的斜率减直线NP的斜率的差为1．设点P的轨迹为曲线E．（Ⅰ）求E的方程；（Ⅱ）已知点A（0，1），点C是曲线E上异于原点的任意一点，若以A为圆心，线段AC 为半径的圆交y轴负半轴于点B，试判断直线BC与曲线E的位置关系，并证明你的结论．【考点】：圆与圆锥曲线的综合．【专题】：圆锥曲线的定义、性质与方程．【分析】：（Ⅰ）设出P点坐标，依题意得列关于P点坐标的方程，化简后得答案；（Ⅱ）证法一、设出C点坐标，把c的坐标代入E的轨迹方程，再求出圆A的方程，求出点B的坐标，进一步求出直线BC的方程，和抛物线方程联立后由判别式等于0可证直线BC与曲线E相切．证法二：设出C点坐标，把c的坐标代入E的轨迹方程，再求出圆A的方程，求出点B的坐标，进一步求得直线BC的斜率，然后利用导数求出抛物线在过C点的切线的斜率，可得直线BC与曲线x2=4y过点C的切线重合，即说明直线BC与曲线E相切．【解析】：解：（Ⅰ）设P（x，y），依题意得，化简得x2=4y（x≠±2），∴曲线E的方程为x2=4y（x≠±2）；（Ⅱ）结论：直线BC与曲线E相切．证法一：设C（x0，y0），则，圆A的方程为，令x=0，则，∵y0＞0，y＜0，∴y=﹣y0，点B的坐标为（0，﹣y0），直线BC的斜率为，直线BC的方程为，即，代入x2=4y得，，即，，∴直线BC与曲线E相切．证法二：设C（x0，y0），则，圆A的方程为，令x=0，则，∵y0＞0，y＜0，∴y=﹣y0，点B的坐标为（0，﹣y0），直线BC的斜率为，由x2=4y得，得，，过点C的切线的斜率为，而，∴k=k1，∴直线BC与曲线x2=4y过点C的切线重合，即直线BC与曲线E相切．【点评】：本题考查了曲线方程的求法，考查了圆与圆锥曲线的综合，考查了直线与圆的位置关系，对于（Ⅱ）的第二种证明方法，运用了利用导数研究过曲线上某点的切线的斜率，体现了导数在解题中的广泛应用，该题属中高档题．21．（14分）设函数f（x）=的导函数为f'（x）（a为常数，e=2.71828…是自然对数的底数）．（Ⅰ）讨论函数f（x）的单调性；（Ⅱ）求实数a，使曲线y=f（x）在点（a+2，f（a+2））处的切线斜率为﹣；（Ⅲ）当x≠a时，若不等式||+k|x﹣a|≥1恒成立，求实数k的取值范围．【考点】：利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．【专题】：导数的综合应用．【分析】：（Ⅰ）根据导数和函数的单调性的关系即可求出单调区间；（Ⅱ）根据导数的几何意义，令a+2=t，则有e t+t3﹣1=0，构造函数，利用导数求出即可；（Ⅲ）原不等式可化为，在分类讨论，继而求出实数k的取值范围．【解析】：解：（Ⅰ）函数f（x）的定义域是（﹣∞，a）∪（a，+∞），…（1分）对f（x）求导得：，…（2分）由f'（x）＞0得x＞a+1；由f'（x）＜0得x＜a或a＜x＜a+1，…（4分）所以f（x）在（﹣∞，a），（a，a+1）上单调递减，在（a+1，+∞）上单调递增．…（5分）（Ⅱ）由（Ⅰ）得…（6分）令得e a+2+a3+6a2+12a+7=0…①令a+2=t，则有e t+t3﹣1=0，…（8分）令h（t）=e t+t3﹣1，则h'（t）=e t+3t2＞0，…（9分）故h（t）是R上的增函数，又h（0）=0，因此0是h（t）的唯一零点，即﹣2是方程①的唯一实数解，故存在唯一实数a=﹣2满足题设条件．…（10分）（Ⅲ）因为，故不等式可化为，令x﹣a=t，则t≠0，…（11分）且有…（12分）①若t＜0，则，即，此时k≥0；②若0＜t≤1，则，即，此时k≥1；③若t＞1，则，即，此时k≥1．故使不等式恒成立的k的取值范围是[1，+∞）．…（14分）【点评】：本题考查了导数和函数单调性的关系，以及导数的几何意义，以及不等式恒成立的问题，培养了学生的转化能力，属于中档题。
2015届高三教学质量一模数学试题(理)及答案
2015年高三教学质量检测（1）数学试题（理科）第Ⅰ卷一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1、已知集合{1,0,1},{||10}A B x x =-=+>，那么AB =A ．{1,0,1}-B ．{0,1}C ．(1,)-+∞D ．[)1,-+∞ 2、已知复数1z i =+，则21z-= A ．i - B ．1 C ．i D ．-13、沿一个正方体三个面的对角线截得的几何体如图所示，则该几何体的左视图为4、已知程序框图如图所示，则该程序框图的功能是A ．求11112310++++的值 B ．求111124620+++的值 C ．求11112311++++的值 D ．求111124622+++的值 5、已知平面向量,a b 满足11,(2)()2a b a b a b ==+-=-，则与a 与b 的夹角为 A ．6π B ．3π C ．23π D ．56π6、在正项等比数列{}n a 中，232629log log log 3a a a ++=，则111a a 的值是 A ．16 B ．8 C ．4 D ．27、在二项式251()x x-的展开式中，含7x 的项的系数为A ．-10B ．10C ．-5D ．58、某城市对机动车单双号限行进行了调查，在参加调查的2548名有车人中有1560名持反对意见，2452名无车人中有1200名持反对意见，在运用这些数据说明“拥有车辆”与“反对机动车单双号限行”是否有关系时，用什么方法最有说服力A ．平均数与方差B ．回归直线方程C ．独立性检验D ．概率9、焦点在y 轴上的双曲线G 的下焦点为F ，上顶点为A ，若线段FA 的中垂线与双曲线G 有公共点，则双曲线G 的离心率的取值范围是（ ）A ．()1,3B ．(]1,3C ．()3,+∞D ．[)3,+∞ 10、已知()[)[]211,010,1x x f x x x ⎧+∈-⎪=⎨+∈⎪⎩，则下列函数的图象正确的是A ．()1f x +的图象B ．()f x 的图象C ．()fx 的图象 D ．()f x 的图象11、若直线20(0,0)ax by a b -+=>>过圆22:2410C x y x y ++-+=的圆心，则11a b+的最小值为（ ） A ．14 B．32+．32+ 12、定义域为R 的偶函数()f x 满足对任意x R ∈，有()()()21f x f x f +=-，且当[]2,3x ∈时，()221218f x x x =-+-，若函数()log (1)a y f x x =-+在()0,+∞上恰有三个零点，则a 的取值范围是（ ） A． B． C． D．第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上。
金山中学、广雅中学、佛山一中2015届高三联考文科数学试题
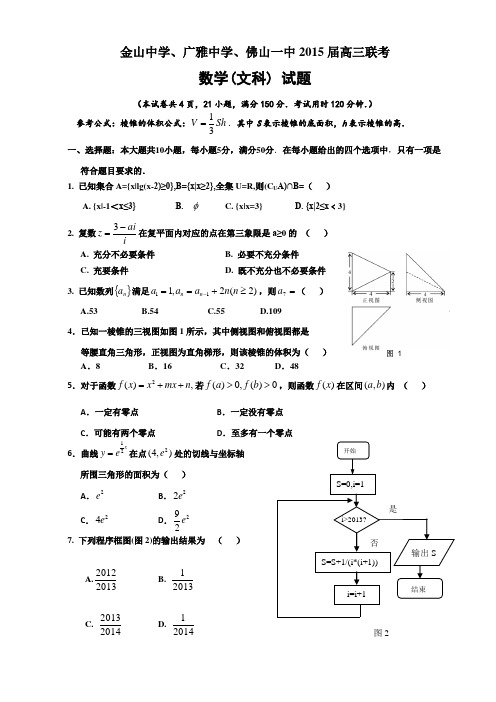
图 1金山中学、广雅中学、佛山一中2015届高三联考数学(文科) 试题（本试卷共4页，21小题，满分150分．考试用时120分钟．）参考公式：棱锥的体积公式：13V Sh =．其中S 表示棱锥的底面积，h 表示棱锥的高． 一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知集合A={x|lg(x-2)≥0},B={x|x≥2},全集U=R,则(C U A)∩B=（ ）A. {x|-1＜x≤3}B. φC. {x|x=3}D. {x|2≤x ﹤3}2. 复数iaiz -=3在复平面内对应的点在第三象限是a≥0的 （ ） A. 充分不必要条件 B. 必要不充分条件 C. 充要条件D. 既不充分也不必要条件3. 已知数列{}n a 满足)2(2,111≥+==-n n a a a n n ，则=7a （ ） A.53 B.54C.55D.1094．已知一棱锥的三视图如图1所示，其中侧视图和俯视图都是 等腰直角三角形，正视图为直角梯形，则该棱锥的体积为（ ） A ．8 B ．16 C ．32 D ．485．对于函数2(),f x x mx n =++若()0,()0f a f b >>，则函数()f x 在区间(,)a b 内 （ ）A ．一定有零点B ．一定没有零点C ．可能有两个零点D ．至多有一个零点 6．曲线12x y e=在点2(4,)e 处的切线与坐标轴所围三角形的面积为（ ）A ．2e B ．22eC ．24e D ．292e7. 下列程序框图(图2)的输出结果为 （ ）A.20132012B. 20131C.20142013 D. 20141图2图 38. 设,22ππθ⎛⎫∈- ⎪⎝⎭，则关于θ的方程1cos 2tan θθ-=的解的个数为（ ）A ．0B ．1C ．2D ．39. 点P 到图形E 上每一个点的距离的最小值称为点P 到图形E 的距离.已知点(1,0)A ,圆C :2220x x y ++=,那么平面内到圆C 的距离与到点A 的距离之差为1的点的轨迹是（ ）A. 双曲线的一支B. 椭圆C. 抛物线D. 射线 10．定义两种运算：a b ⊕=a b ⊗2()(2)2xf x x ⊕=⊗-为( )A ．奇函数B ．偶函数C ．奇函数且为偶函数D ．非奇函数且非偶函数二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分． （一）必做题（11－13题）11．（a →+b →）与a →垂直，且⎥b →⎢=2⎥a →⎢，则a →与b →的夹角为 12. 若等比数列{a n }的前项n 和为S n ，且S 4S 2 = 5，则S 8S 4 =13．已知函数21()(2),()(1,2)1x x x f x x g x a a x x -+==>-≥≥．①若[)02,x ∃∈+∞，使0()f x m =成立，则实数m 的取值范围为 ；②若[)12,x ∀∈+∞，[)22,x ∃∈+∞使得12()()f x g x =，则实数a 的取值范围为 ．（二）选做题（14－15题，考生只能从中选做一题）14.（坐标系与参数方程选做题）在极坐标系中，过点3π4,2A ⎛⎫⎪⎝⎭引圆4sin ρθ=的一条切线，则切线长为 ．15．（几何证明选讲选做题）如图3，PA 是圆O 的切线，切点为A ，PO 交圆O 于,B C 两点，且2,1,PA PB ==则AB 的长为 .三．解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）如图4,在直角坐标系xOy 中,角α的顶点是原点,始边与x 轴正半轴重合,终边交单位圆于点A ,且⎪⎭⎫⎝⎛∈2,3ππα.将角α的终边按 逆时针方向旋转6π,交单位圆于点B .记),(),,(2211y x B y x A . (Ⅰ)若411=x ,求2x ; (Ⅱ)分别过,A B 作x 轴的垂线,垂足依次为,C D .记△AOC 的 面积为1S ,△BOD 的面积为2S .若21S S =,求角α的值.17.（本小题满分12分）从某校高三年级800名学生中随机抽取50名测量身高．据测量，被抽取的学生的身高全部介于155cm 和195cm 之间，将测量结果分成八组得到的频率分布直方图如图5：（1）试估计这所学校高三年级800名学生中身高在180cm 以上（含180cm ）的人数为多少； （2）在样本中，若学校决定身高在185cm 以上的学生中随机抽取2名学生接受某军校考官 进行面试，求：身高在190cm 以上的学生中至少有一名学生接受面试的概率．18．（本小题满分14分）如图6，已知三棱柱ABC —A 1B 1C 1的侧棱与底面垂直，且∠ACB ＝90°，∠BAC ＝30°，BC ＝1，AA 1＝6，点P 、 M 、N 分别为BC 1、CC 1、AB 1的中点． （1）求证：PN//平面ABC ； （2）求证：A 1M ⊥平面AB 1C 1；（3）求点M 到平面AA 1B 1的距离．cm ）图5 图6图419（本题满分14分）已知数列{}n a 满足1331(,2)n n n a a n N n *-=+-∈≥且395a =。
佛山市2015届普通高中高三教学质量检测(二)(文数)
佛山市2015届普通高中高三教学质量检测（二）数学（文科）本试卷共4页，21小题，满分150分，考试用时120分钟. 注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。
3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4．考生必须保持答题卡的整洁．考试结束后，将答题卡一并交回。
一、选择题：本大题共10小题，每小题5分，满分50分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．集合{|11}x Z x ∈-≤≤的子集个数为（ ）A ．3B ．4C ．7D ．82．若复数z 满足(1)i z i -=，其中i 为虚数单位，则在复平面上复数z 对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 3．已知向量(1,0)a =-，13(,2b =，则向量a 与b 的夹角为（ ） A ．6π B ． 3π C ．23π D ． 56π4．由不等式组22024010x y x y x --≥⎧⎪-+≥⎨⎪-≤⎩确定的平面区域记为M ，若直线320x y a -+=与M 有公共点，则a 的最大值为（ ）A ．3-B ．1C ．2D ．4 5．某班有49位同学玩“数字接龙”游戏，具体规则按如图所示 的程序框图执行（其中a 为座位号），并以输出的值作为下一个 输入的值。
若第一次输入的值为8，则第三次输出的值为（A ． 8B ．15C ． 29D ．366．不可能以直线12y x b =+作为切线的曲线是（ ） A ．sin y x = B ．1y x= C ．ln y x = D ． xy e =7．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若)cos cos b A a B -=，则A=（ ）A ．12π B ． 6π C ． 4π D ．3π8．已知函数()()(2)f x x a bx a =++，(,)a b R ∈，则“0a =”是“()f x 为偶函数”的 A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件9．已知a ，b ，c 均为直线，α，β为平面，下面关于直线与平面关系的命题：（1）任意给定一条直线a 与一个平面α，则平面α内必存在与a 垂直的直线； （2）a ∥β，β内必存在与a 相交的直线；（3）α∥β，a ⊂α，b ⊂β，必存在与a ，b 都垂直的直线； （4）α⊥β，c αβ=，a ⊂α，b ⊂β，若a 不垂直c ，则a 不垂直b 。
广东省佛山市2015届普通高中高三教学质量检测(一)数学【文】试题及答案
广东省佛山市2015届普通高中高三教学质量检测（一）数学（文）试题一．选择题:本大题共8小题,每小题5分,满分40分．1．复数31i i ++等于（ ）． A ．12i + B ．12i - C ．2i - D ．2i +2．已知集合{}{}|02,|1M x R x N x R x =∈<<=∈>,则()R M N =I ð（ ）． A ．[)1,2 B ．()1,2 C ．(]0,1 D ．[)0,1 3．若函数的图象关于原点对称，则实数a 等于 A ．-2 B ．-1 C ．1 D ．24．已知,a b R ∈,则“1a b >>”是“log 1a b <”的（ ）．A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 5．已知,x y 满足不等式组，则目标函数的最大值为 A ．12 B ．24 C ．8 D ．6．在空间，有如下四个命题：其中正确的两个命题是A ．①②B ．②④C ．①④D ．②③7．某校高三年级学生全主席团共有5名同学组成，其中有3名同学来自同一班级，另外两名同学来自另两个不同班级，现从中随机选出两名同学参加会议，则两名选出的同学来自不同班级的概率为A ．0.35B ．0.4C ．0.6D ．0.78．已知双曲线的左、右焦点分别为F 1，F 2，过F 2的直线与该双曲线的右支交于A 、B 两点，若的周长为 A ．16 B ．20 C ．21 D ．269．已知的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件10．有10个乒乓球，将它们任意分成两堆，求出这两堆乒乓球个数的乘积，再将每堆乒乓球任意分成两堆并求出两堆乒乓球个数的乘积，如此下去，直到不能再分为止，则所有乘积的和为A ．45B ．55C ．90D ．100二．填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分．（一）必做题（9～13题）11．如果()11sin 1x f x x x ⎧≤⎪=⎨>⎪⎩,那么()2f f =⎡⎤⎣⎦____________． 12．已知点()()2,0,0,4A B -到直线:10l x my +-=的距离相等,则m 的值为____________．13．如图1,为了测量河对岸,A B 两点之间的距离,观察者找到一个点C ,从C 点可以观察到点,A B ,找到一个点D ,从D 点可以观察到点,A C ,找到一个点E ,从E 点可以观察到点,B C ,并测量得到一些数据:2,45,105,48.19,75,CD CE D ACD ACB BCE ==∠=∠=∠=∠=o o o o E ∠=60o ,则,A B 两点之间的距离为____________．（其中cos 48.19o 取近似值23）．（二）必做题（14～15题,考生只能从中选做一题）14．（几何证明选讲）如图2,P 是圆O 外一点,,PA PB 是圆O 的两条切线,切点分别为,,A B PA 中点为M ,过M 作圆O 的一条割线交圆O 于,C D 两点,若1PB MC ==,则CD =_________．15．（坐标系与参数方程）在极坐标系中,曲线)1:sin 1C ρθθ+=与曲线()2:0C a a ρ=>的一个交点在极轴上,则a =__________．三．解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤．16．（本小题满分12分）已知函数()()sin 0,4f x x x R πωω⎛⎫=->∈ ⎪⎝⎭的最小正周期为π． （1）求6f π⎛⎫ ⎪⎝⎭． （2）在图3给定的平面直角坐标系中,画出函数()y f x =在区间,22ππ⎡⎤-⎢⎥⎣⎦上的图象,并根据图象写出其在,22ππ⎛⎫- ⎪⎝⎭上的单调递减区间．17．（本小题满分12分）某地区“腾笼换鸟”的政策促进了区内环境改善和产业转型,空气质量也有所改观,现从当地天气网站上收集该地区近两年11月份（30天）的空气质量指数（AQI ）（单位:3/g m μ）资料如下:（1）请填好2014年11月份AQI 数据的平率分布表并完成频率分布直方图．（2）该地区环保部门2014年12月1日发布的11月份环评报告中声称该地区“比去年同期空气质量的优良率提高了20多个百分点”（当100AQI <时,空气质量为优良）．试问此人收集到的资料信息是否支持该观点?18．（本小题满分14分）如图6,四棱锥P ABCD -,侧面PAD 是边长为2的正三角形,且与底面垂直,底面ABCD 是60ABC ∠=o 的菱形,M 为棱PC 上的动点,且[]()0,1PM PC λλ=∈． （1）求证:PBC V 为直角三角形．（2）试确定λ的值,使得二面角P AD M --的平面角余弦值为5．19．（本小题满分14分）数列{}n a 的前n 项和为n S ,已知()()211,12n n a S n a n n n N *==--∈． （1）求23,a a ．（2）求数列{}n a 的通项．（3）设11n n n b S S +=,数列{}n b 的前n 项和为n T ,证明:52n T <()n N *∈．。
广东省佛山市第一中学2015届高三10月段考数学(理)试题 Word版含答案
佛山一中2015届高三上学期数学（理科）段考试题命题人 谭江南 审题人 卢志常2014.10.14本试卷共4页，21小题，满分150分。
考试用时120分钟。
一、选择题：本大题共8小题，每小题5分，满分40分. 在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合A ＝{x|－x 2－3x>0}，B ＝{x|x<－1}，则A ∩B ＝( )A ．{x|－3<x<－1}B ．{x|－3<x<0}C ．{x|x<－1}D ．{x|x>0} 2．函数2cos 1y x =+在下列哪个区间上为增函数A ．π[0, ]2B ．π[, π]2C ．[]0, πD ．[]π, 2π 3．已知幂函数()y f x =的图象过点11(,)28--，则2log (4)f 的值为 A ． 3 B ．4 C ．6 D ．－6 4．已知函数()12sin()cos()2f x x x ππ=++-，则()f x 是A ．周期为π的奇函数B ．周期为π的偶函数C ．周期为2π的奇函数D ．周期为2π的偶函数5．向量a ，b 满足|a |＝1，|a －b |＝32，a 与b 的夹角为60°，则|b |＝A ．12B ．13C ．14D ．156．已知非零向量a 、b ，“函数2()()f x ax b =+为偶函数”是“a b ⊥”的A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分也非必要条件7．在平行四边形ABCD 中，AC 与BD 交于O ，E 是线段OD 的中点，AE 的延长线与CD 交于点F ，若AC →＝a ，BD →＝b ，则AF →等于A ．14a ＋12bB ．23a ＋13bC ．12a ＋14bD ．13a ＋23b8．设()f x 与()g x 是定义在同一区间[,]a b 上的两个函数，若函数()()y f x g x =-在[,]x a b ∈上有两个不同的零点，则称()f x 和()g x 在[,]a b 上是“关联函数”，区间[,]a b 称为“关联区间”．若2()34f x x x =-+与()2g x x m =+在[0,3]上是“关联函数”，则m 的取值范围为A. 9(,2]4-- B.[1,0]- C.(,2]-∞- D.9(,)4-+∞二、填空题：本大共7小题，考生作答6小题，每小题5分，满分30分． (一)必做题(9～13题)9．已知函数f (x )＝(m －2)x 2＋(m 2－4)x ＋m 是偶函数，函数g (x )＝－x 3＋2x 2＋mx ＋5在(－∞，＋∞)内单调递减，则实数m 等于________．10．已知向量a 与b 的夹角为2π3，且|a |＝1，|b |＝4，若(2a ＋λb )⊥a ，则实数λ＝________. 11．有一道解三角形的题目，因纸张破损有一个条件模糊不清，具体如下：“在△ABC 中，已知a =4B π=， ，求b .”若破损处的条件为三角形的一个内角的大小，且答案提示b =试在横线上将条件补充完整.12．若数()f x x a =+-a =__________.13．直线2()y x m m R =+∈和圆122=+y x 交于A 、B 两点,以Ox 为始边,OA ,OB 为终边的角分别为α,β,则)sin(βα+的值为_________.(二)选做题(14～15题，考生只能从中选做一题) 14．（坐标系与参数方程）直角坐标系xoy 中，以原点为极点，x 轴的正半轴为极轴建立极坐标系，设A 、B 分别在曲线C ：⎩⎨⎧+=+=θθsin 23cos 24y x （θ为参数）和曲线21=ρ上，则||AB 的取值范围是_______15．（几何证明选讲）如图，PC 切圆O 于点C ，割线PAB 经过圆心O ，4,8PC PB ==，则OBC S ∆= ．三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤． 16．（本题满分12分）在锐角ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ．已知3cos 24C =-. （Ⅰ）求sin C ；（Ⅱ）当2c a =，且b =a .17．（本题满分12分）为了解甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽出取14件和5件，测量产品中的微量元素x,y 的含量（单位：毫克）．下表是乙厂的5件产品的测量数据：（1）已知甲厂生产的产品共有98件，求乙厂生产的产品数量；（2）当产品中的微量元素x,y 满足x ≥175，且y ≥75时,该产品为优等品。
2015年佛山市普通高中高三教学质量检测(一)理科综合(试题+答案)
2015年佛山市普通高中高三教学质量检测（一）理科综合试题 2015.2本试卷共12页,满分300分，考试时间150分钟注意事项：1、答卷前，考生务必用黑色字迹的钢笔或签字笔将白已的姓名和考号填写在答题卡上．用2B 铅笔将答题卡试卷类型（A 或B ）填涂在答题卡上，并在答题卡右上角的“试室号”和“座位号”栏填写试室号、座位号，将相应的试室号、座位号信涂黑。
2、选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案答在试题卷上无效。
3、非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答卷各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4、考试结束后，将答卷和答题卡一并交回。
第一部分 选择题 （共118分）一、单项选择题：本大题共16小题，每小题4分。
共64分。
在每小题给出的四个选项中，只有一个选项符合题目要求，选对的得4分，选错或不答的得0分。
1．下列有关蛋白质说法正确的是A ．蛋白质不参与生物膜系统的构成B ．抗体蛋白在细胞内液和细胞外液中都起作用C ．人体蛋白类激素都可以起到信息分子的作用D ．蛋白质进出细胞需要载体蛋白的参与2．对非洲爪蟾的精巢切片进行显微观察，绘制以下示意图，有关说法错误．．的是A ．甲、丁细胞均为初级精母细胞B ．乙、丙细胞不含有染色单体C ．丙细胞处于有丝分裂后期D ．乙、丁细胞内的两条染色体都发生了互换3．下图是基因表达过程的示意图，有关说法正确的是甲 乙 丙 丁A．①为单链，不存在碱基互补配对现象B．一条③上可同时结合多个②C．④上的密码子决定了氨基酸种类D．该过程需要解旋酶和DNA聚合酶的参与4．下列符合现代生物进化理论的叙述是A．新物种的形成可以不经过隔离B．进化时基因频率总是变化的C．基因突变产生的有利变异决定生物进化的方向D．一般来说突变频率高的基因所控制的性状更适应环境5．下列关于细胞分化、衰老、癌变和凋亡的叙述，错误．．的是A．高度分化的细胞更适合做植物组织培养的材料B．衰老的细胞内水分减少、代谢减慢C．细胞凋亡是生物体正常的生命活动D．原癌基因或抑癌基因发生的变异累积可导致癌症6．为探究NAA促进插条生根的最适浓度，某兴趣小组进行了预实验，结果如右图。
佛山市普通高中高三教学质量检测
2015年佛山市普通高中高三教学质量检测（一）文科综合试题2015．1本试卷共12页，满分300分。
考试时间150分钟。
注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考号填写在答题卡上。
用2B铅笔将答题卡试卷类型（A）填涂在答题卡上，并在答题卡右上角的“试室号”和“座位号”栏填写试室号、座位号，将相应的试室号、座位号信息点涂黑。
2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案答在试题卷上无效。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答卷上各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4．考试结束后，将答卷和答题卡一并交回。
第一部分选择题（共140分）一、单项选择题：本题共35小题，每小题4分，共140分，在每小题给出的四个选项中，只有一个选项符合题目要求，选对的得4分，错选、不选0分。
2014年12月26日，贵广高铁正式运营，沿途美景吸引游客前往。
读下图回答1—2题。
1．贵广高铁全程的桥隧比达到81%，其主要原因是A．地貌复杂 B．降低成本 C．客流需求 D．气候多变2．游客在桂林看到的峰林景观，其形成的主要外力作用是A．褶皱隆起 B．流水溶蚀 C．风力侵蚀 D．冰川侵蚀3．下图为秦岭2000年的土地利用构成，由图图判断A．秦岭的土地利用以耕地最多 B．北坡自然带的种类要比南坡多C．南坡林地、草地比重人于北坡 D．人类活动对南坡影响比北坡大4．2014年9月24日，美国国家宇航局（NASA）发布的一组卫星图片显示：近年来世界第四大湖“咸海”（内流湖）水域面积明显缩小，2020年或将完全消失。
引起咸海水域变化的人为原因是A．大规模围湖造田 B．流域面积缩小C．流域内用水量大 D．全球气候变暖5．读我国人口和劳动力增长率变化预测图。
2015年佛山市普通高中高三教学质量检测答案
2015年佛山市普通高中高三教学质量检测（一）文科综合试题参考答案及评分标准2015．1一、选择题：本题共35小题，每小题4分，共140分。
在每小题给出的四个选项中，只有一个选项符合题目要求，题号 1 2 3 4 5 6 7 8 9 10 11答案 A B D C A B D C B D C题号12 13 14 15 16 17 18 19 20 21 22 23 答案 B A D B C B C C A B A D 题号24 25 26 27 28 29 30 31 32 33 34 35 答案 B D B B D A A C A C B C二、非选择题：本大题共6小题，满分160分。
36．（26分）（1）①2009年至2014年前三季度我国国内生产总值持续增长，增长速度总体放缓，但仍处于较高水平。
（2分）②这说明我国积极推进经济结构战略性调整，转变经济发展方式取得成效。
（2分）评分说明：①中答到生产总值持续增长可给1分，答到增长速度总体放缓可给1分。
②中答到推进经济结构战略性调整或转变经济发展方式取得成效任何一层意思的即可给2分。
（2）①劳动者是生产过程的主体，在生产力发展中起主导作用；我国实施科教兴国、人才强国战略；发展社会主义市场经济，必须健全生产要素按贡献参与分配的制度。
（4分）②更加尊重市场对资源配置起决定性作用的规律，更好发挥政府的宏观调控作用。
（4分）③收入是消费的基础和前提：提高人民物质文化生活水平，是改革开放和社会主义现代化建设的根本目的；就业是民生之本：以人为本是科学发展观的核心立场；人民生活水平全面提高是全面建成小康社会的新要求。
（4分）评分说明：①中含有3个要点，答对任意1点给2分，2点或以上给4分。
②中含有2个要点，每点2分。
③中含有5个要点，答对任意1点给2分，2点或以上给4分。
（3）①中共中央政治局“定调”体现了中国共产党是中国特色社会主义事业的领导核心，中国共产党对国家和社会事务进行政治领导。
[参考答案]2015年佛山市普通高中高三教学质量检测(一)理科数学试题 (1)
![[参考答案]2015年佛山市普通高中高三教学质量检测(一)理科数学试题 (1)](https://img.taocdn.com/s3/m/ccb54d03ba1aa8114431d975.png)
2015 年佛山市普通高中高三教学质量检测（一）数学试题（理科）参考答案和评分标准一、选择题：本大题共 8 小题，每小题 5 分，满分 40 分． 题号 答案1C2C3B4A5D 11． 或6A7B8A二、填空题：本大共 7 小题，考生作答 6 小题，每小题 5 分，满分 30 分． [必做题] 9．1 [选做题] 14． 2 10． , 2 4, 15．112．96 625(或 0.1536 )13． 101 2 2 2三、解答题：本大题共 6 小题，满分 80 分，解答须写出文字说明、证明过程或演算步骤． 16.【解析】(Ⅰ)依题意得 π ,解得 2 ,所以 f x sin 2 x ,„„„„„„2 分 4 所以 f sin sin cos cos sin 3 2 1 2 6 2 .„„„4 分 3 4 3 4 2 2 2 2 4 6 3 4 5 3 (Ⅱ)因为 x ,所以 2 x ,列表如下:„„„„„„„„6 分 2 2 4 4 4 3 3 x 8 8 2 2 8 8 3 2x 5 0 2 4 4 4 22π2 0 0 1 2 上的图像如图所示! 画出函数 y f x 在区间 , 2 2 y y12 2„„„8 分1 2 3 8 8O1 21 23 82x8x 在 , 由图象可知函数 y f 1„„„10 分 3 上的单调递减区间为 , , , .„„„„12 分 2 2 2 8 8 2 17.【解析】(Ⅰ) 频率分布表(3 分)；频率分布直方图(6 分) (Ⅱ) 支持,理由如下:1 19 2013年 11 月的优良率为: 20 0.005 0.005 0.015 0.010 , „„„„8 分 3 30 26 2014 年 11 月的优良率为: , „„„„9 分 30佛山一模(理科数学) 第 1 页 共 5 页因此26 19 7 23.3% 20% „„„„11 分 30 30 302014 年 11 月份 AQI 数据频率分布表 分组 频数 频率 2014 年 11 月份 AQI 数据频率分布直方图频率 组距所以数据信息可支持“比去年同期空气质量的优良率提高了 20 多个百分点”.„„„„„„„12 分20, 40 40, 60 60, 80 80,100 100,120 120,1402 7 12 5 1 31 15 7 30 2 5 1 6 1 30 1 100.025 0.020 0.015 0.010 0.005 20 40 60 80 100 120 140 A QI18.【解析】(Ⅰ)取 AD 中点 O ,连结 OP, OC, AC ,依题意可知△ PAD ,△ ACD 均为正三角形, 所以 OC AD , OP AD ,又 OC OP O , OC 平面 POC , OP 平面 POC , 所以 AD 平面 POC ,又 PC 平面 POC ,所以 AD PC , 因为 BC // AD ,所以 BC PC ,即 PCB 90,从而△ PBC 为直角三角形.„„„„„„5 分 说明:利用 PC 平面 AMD 证明正确,同样满分! (Ⅱ)[向量法]由(Ⅰ)可知 PO AD ,又平面 PAD 平面 ABCD , 平面 PAD 平面 ABCD AD , PO 平面 PAD ,所以 PO 平面 ABCD .„„„„„„6 分 以 O 为原点,建立空间直角坐标系 O xyz 如图所示,则P zM AP 0, 0, 3 , A 0, 1, 0 , D 0,1, 0 , C O 3, 0,0 , D B C PC 3, 0, 3 „„„„„„7 分 x 3, 0, 3 3 ,„„„„„„9 分 由 PM PC 3, 0, 3 可得点 M 的坐标为 所以 AM 3,1, 3 3 , DM 3, 1, 3 3 , 3x y 3 3 z 0 设平面 MAD 的法向量为 n x, y, z ,则 n AM 0 ,即 3x y 3 3 z 0 n DM 0 1 z x 解得 ,令 z ,得 n 1, 0, ,„„„„„„11 分 y 0 显然平面 PAD 的一个法向量为 OC 3, 0, 0 ,„„„„„„12 分 n OC 3 1 2 5 1 依题意 cos n, OC ,解得 或 1 (舍去), 2 5 3 n OC 2 1 3 y 所以,当 1 3时,二面角 P AD M 的余弦值为2 5 5.„„„„„„14 分佛山一模(理科数学) 第 2 页 共 5 页[传统法]由(Ⅰ)可知 AD 平面 POC ,所以 AD OM , AD OP , 所以 POM 为二面角 P AD M 的平面角, 即 cos POM 2 5 5,„„„„„„8 分P在△ POM 中, sin POM 55 所以 sin PMO sin POM 4 sin POM cos, PO 3 , OPM 4,M A O D,„„„10 分 B C cos POM sin 4 10 PM PO PM 3 6 由正弦定理可得 ,即 ,解得 PM ,„„„„„„12 分 3 sin POM sin PMO 5 3 10 5 10 PM 1 2 2 , 又 PC PO OC 6 ,所以 PC 3 1 2 5 所以,当 时,二面角 P AD M 的余弦值为 .„„„„„„14 分 3 5 5 19.【解析】(Ⅰ)当 n 2 时, S2 4a2 2 ,解得 a2 ； „„„„„„„„„„„„„„1 分 6 11 当 n 3 时, S3 9a3 6 , 解得 a3 ； „„„„„„„„„„„„„„„„2 分 12 2 (Ⅱ)方法一：当 n 2 时， S n S S n(n 1) ，整理得43 10n1 „„„„„„„„„„„„„„„„„5 分 Sn n Sn1 n(n 1) ，即 n 1 n n 1Sn 所以数列 是首项为 1,公差为 1 的等差数列. „„„„„„„„„„„„„„„„„6 分 n n 1Sn n2 所以 n ，即 Sn „„„„„„„„„„„„„„„„„7 分 n 1 n 1 . „„„„„„„„„„„„„„„„„8 分 代入 S n n 2 a n n(n 1) 中可得 an 1 n n 1 1 5 11 1 方法二：由(Ⅰ)知: a1 , a2 , a3 ,猜想 an 1 ,„„„„„„„„„„„„„4 分 2 6 12 n n 1下面用数学归纳法证明: ①当 n 1 时， a 1 nn2 12 n 1Snnn 1nSn1112*1 11，猜想成立；„„„„„„„„„„„„„„„„„5 分②假设 n k k N,猜想也成立,即 ak1 21 ,则 k k 1当 n k 1 时,有 ak 1 Sk 1 S k k 1 a k 1 k 1 k k 2a k k k 1佛山一模(理科数学) 第 3 页 共 5 页整理得 k 2 ak 1 kak 2 ，从而 1 k 2 ak 1 kak 2 k 即 n k 1 时猜想也成立.1112 k 2 ，于是 ak 1 1 k k 1 k 1 k 1 k 2 1 . n n 1„„„„„„„„„„„„„„„„„8 分所以对于任意的正整数 n ,均有 an 1 2 (Ⅲ) 由(Ⅱ)得 Sn n , bn n 1n 2 , n n 12„„„„„„„„„„„„„„„„9 分当 k 2 时，b kk 2k k (k 1) k k (k 1) k (k 1) k 2 k 1 3 5 当 n 1 时, T1 成立； „„„„„„„„„„„„„„„„„„„12 分 2 2 5 1 1 5 2 当 n 2 时,所以 T 3 2 1 1 1 1 n 2 n n 1 2 n 1 2 2 3 3 4 综上所述,命题得证. „„„„„„„„„„„„„„„„„„„„„„„„„„„„„„14 分 20.【解析】(Ⅰ) 因为曲线 E 为双曲线,所以 m m 10 ,解得 0 m 1 , 所以实数 m 的取值范围为 0,1 .„„„„„„„„„„„„„„„„„„„4 分 (Ⅱ)结论: l 与曲线 E 相切.„„„„„„„„„5 分 证明:当 m 4 时,曲线 E 为2k 21k k1221 1 „„„11 分 k k 1 x22 y 1,即 3x2 4 y2 12 , 4 3 2设 P x0 , y0 ,其中 x0 1 y0 16 ,„„„„„„„„„„„„„„6 分 线段 PA 的中点为 Qx0 1 y0 , ,直线 AP 的斜率为 k y0 ,„„„„„„„„„„„„7 分 2 2 x0 1 当 y0 0 时，直线 l 与曲线 E 相切成立. 2 2 y x0 y0 1 x 1 x0 1 x 1 当 y 0 时，直线 l 的方程为 y 0 0 0 x ,„9 分 x ,即 y 0 2 y0 2 y0 2 y0 x0 1 x0 7 2 2 2 2 因为 x 1 y 16 ,所以 x y 1 2 x 14 ,所以 y x ,„„„„„„10 分 0 0 0 0 0 y0 y0 x 1 x 7 代入 3 x 4 y 12 得 3x 4 0 x 0 12 , y0 y0 2 2 2 2 化简得 4 x 1 3 y x 8x 1x 7 x 4 x 7 12 y2 0 ,„„„„12 分 0 0 0 0 0 2 02 2 即 x 7 x 8 x 1x 7 x 16 x 1 0 ,2 2 2 2所以 64 x 1 0020x07 4 x 7 16 1 0 x2 0 00 20 2所以直线 l 与曲线 E 相切.„„„„„„„„„„„„„„„„„„„„14 分 说明:利用参数方程求解正确同等给分!佛山一模(理科数学) 第 4 页 共 5 页21.【解析】(Ⅰ)当 a 1 时,函数 f x 的定义域是 1, 0 0, ,„„„„„„1 分x对fx求导得 f x x 1ln x 1 x2,„„„„„„„„„„„„„„„„„„2 分x ln x 1,只需证: x 0 时, g x0 . x 1 x 1 1 又 g x 0 ,„„„„„„„„„„„„3 分 2 2 x 1 x 1 x 1令 g x 故 g x 是 0, 上的减函数,所以 g x g 0ln1 0 „„„„„„„„„„5 分 所以 f x 0 ,函数 fx是 0, 上的减函数.„„„„„„„„„„„„„„„„„„„6 分(Ⅱ)由题意知, f x x1 1,„„„„„„„„„„„„„„„„7 分a ln 1a 0 „„„„„„„„„„„„„8 分 1 a 1 a a 1 1 0 ,„„„„„„„„„„„„„9 分 令 t a ln 1a , a 1,则 t a 2 1 a 1a 1 a即1ln 1a 1,故 t a 是 ,1 上的增函数,又 t 0 0 ,因此 0 是 t a 的唯一零点,a ln 1a 0 有唯一实根 0 ,所以 a 0 ,„„„„„„„„„„„„„10 分 1 a x [说明]利用两函数 y 与 y ln 1x 图象求出 a 0 (必须画出大致图象),同样给至 10 分. 1 x ln e x 1 1 x ln ex ln e x 11 ln x 1 , 故原不等式等价于 ,„„„11 分 (Ⅲ)因为 x x x x e 1 e 1 e 1 x e 1 ln x 1 由(Ⅰ)知,当 a 1 时, f x 是 0, 上的减函数,„„„„„„„„„„„„„12 分 x x 故要证原不等式成立,只需证明:当 x 0 时, x e 1 , x x 令 h x e x 1 , 则 hx e 1 0 , h x 是 0, 上的增函数,„„„„„„„„„„13 分即方程 所以 h x h 0 0 ,即 x e 1, 故 fx即ln x 1 ln e x 11 x „„„„„„„„„„„„„„„„„„„„„„14 分 x ex 1 ex 1x f e x 1 ,佛山一模(理科数学) 第 5 页 共 5 页。
广东省佛山市高三数学教学质量检测(一)试题 文
2015年佛山市普通高中高三教学质量检测（一）本试卷共4页,21小题,满分150分.考试时间120分钟. 注意事项:1．答卷前,考生务必填写答题卷上的有关项目．2．选择题每小题选出答案后,用2B 铅笔把答案涂在答题卷相应的位置上．3．非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内；如需改动,先划掉原来的答案,然后再写上新的答案；不准使用铅笔和涂改液,不按以上要求作答的答案无效．4．请考生保持答题卷的整洁.考试结束后,将答题卷交回. 参考公式: 锥体的体积公式13V Sh =,其中S 为柱体的底面积,h 为锥体的高. 一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．复数i1i3++等于( ) A ．i 21+ B ．i 21-C．i2-D ．i 2+2．已知集合{}02M x x =∈<<R ,{}1N x x =∈>R ,则()R MN =ð( )A ．[)1,2B ．()1,2C ．[)0,1D ．(]0,13．若函数42x xay +=的图象关于原点对称,则实数a 等于( ) A ．2- B ．1- C ．1 D ．24．已知x ,y 满足不等式组282800x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩,则目标函数3z x y =+的最大值为( )A ．12B ．24C ．8D ．3325．已知两个单位向量12,e e 的夹角为45︒,且满足()121λ⊥-e e e ,则实数λ的值是( )A ．1 BCD ．2 6．在空间中，有如下四个命题： ①平行于同一个平面的两条直线是平行直线； ②垂直于同一条直线的两个平面是平行平面；③若平面α内有不共线的三个点到平面β距离相等，则α∥β；④过平面α的一条斜线有且只有一个平面与平面α垂直. 其中正确的两个命题是( ) A ．①③B ．②④C ．①④D ．②③7．某校高三年级学生会主席团有共有5名同学组成,其中有3名同学来自同一班级,另外两名同学来自另两个不同班级.现从中随机选出两名同学参加会议,则两名选出的同学来自不同班级的概率为( )A ．0.35B ．0.4C ．0.6D ．0.78. 已知双曲线221169x y -=的左、右焦点分别为1F ,2F ,过2F 的直线与该双曲线的右支交于A 、B 两点,若5=AB ,则1ABF ∆的周长为( )A ．16B ．20C ．21D ．26 9．已知()2f x x x =-,且a ,b ∈R ,则“1a b >>”是“()()f a f b <”的( )A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件10．有10个乒乓球,将它们任意分成两堆,求出这两堆乒乓球个数的乘积,再将每堆乒乓球任意分成两堆并求出这两堆乒乓球个数的乘积,如此下去,直到不能再分为止,则所有乘积的和为( )A . 45B . 55C . 90D .100二、填空题：本大共5小题，考生作答4小题，每小题5分，满分20分． (一)必做题(11～13题)11．如果()1,10,1x f x x ì£ïï=íï>ïî,那么()2f f =⎡⎤⎣⎦ . 12．已知点()2,0A -、()0,4B 到直线l :10x my +-=的距离相等,则m 的值为 . 13. 如图1,为了测量河对岸A 、B 两点之间的距离,观察者找到一个点C ,从C 点可以观察到点A 、B ；找到一个点D ,从D 点可以观察到点A 、C ；找到一个点E ,从E 点可以观察到点B、C；并测量得到一些数据:2CD =,CE =45D ∠=︒,105ACD ∠=︒,48.19ACB ∠=︒,75BCE ∠=︒,E ∠=60︒,则A 、B 两点之间的距离为_________.(其中cos 48.19︒取近似值23)C图1O DCAMPB图22013年11月份AQI 数据频率分布直方图(二)选做题(14～15题，考生只能从中选做一题)14.(几何证明选讲)如图2,P 是圆O 外一点,PA 、PB是圆O 的两条切线,切点分别为A 、B ,PA 中点为M ,过M 作圆O 的一条割线交圆O 于C 、D 两点,若PB =1MC =,则CD= .15.(坐标系与参数方程)在极坐标系中,曲线1C :)sin 1ρθθ+=与曲线2C :a ρ=(0a >)的一个交点在极轴上,则a =______.三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤． 16.(本小题满分12分)已知函数()sin 4f x x πω⎛⎫=- ⎪⎝⎭(0ω>),x ∈R 的最小正周期为π.(Ⅰ) 求6f π⎛⎫⎪⎝⎭； (Ⅱ) 在图3给定的平面直角坐标系中,画出函数()y f x =在区间,22ππ⎡⎤-⎢⎥⎣⎦上的图像,并根据图象写出其在2π⎛- ⎝17.(本小题满分12分)某地区“腾笼换鸟”的政策促进了区内环境改善和产业转型,空气质量也有所改观,现从当地天气网站上收集该地区近两年11月份(30天)的空气质量指数(AQI )(单位:3g /m μ)资料如下:图32014年11月份AQI 数据表12014年11月份AQI 数据频率分布表 表2PABC DM图620 40 AQI60 80 100 120 140 图42014年11月份AQI 数据频率分布直方图(Ⅰ) 请填好2014年11月份AQI 数据的频率分布表．．．．．并完成频率分布直方图．．．．．．．；(Ⅱ) 该地区环保部门2014年12月1日发布的11月份环评报告中声称该地区“比去年同期空气质量的优良率提高了20多个百分点”(当AQI 100<时,空气质量为优良).试问此人收集到的资料信息是否支持该观点?18.(本小题满分14分)如图6,四棱锥P ABCD -,侧面PAD 是边长为2的正三角形,且与底面垂直,底面ABCD 是60ABC ∠=︒的菱形,M 为PC 的中点.(Ⅰ) 求证:PC AD ⊥；(Ⅱ) 在棱PB 上是否存在一点Q ,使得,,,A Q M D 四点共面?若存在,指出点Q 的位置并证明；若不存在,请说明理由；(Ⅲ) 求点D 到平面PAM 的距离.19.(本小题满分14分)已知数列{}n a 的前n 项和为n S ,若()14211n n S n a +=-+(*n ∈N ),且11=a .(Ⅰ) 求证：数列{}n a 为等差数列； (Ⅱ) 设n b =数列{}n b 的前n 项和为n T ,证明:32n T <(*n ∈N ).20.(本小题满分14分)已知点()2,1M ,()2,1N -,直线MP ,NP 相交于点P ,且直线MP 的斜率减直线NP 的斜率的差为1.设点P 的轨迹为曲线E . (Ⅰ) 求E 的方程；(Ⅱ) 已知点()0,1A ,点C 是曲线E 上异于原点的任意一点,若以A 为圆心,线段AC 为半径的圆交y 轴负半轴于点B ,试判断直线BC 与曲线E 的位置关系,并证明你的结论.21.(本小题满分14分)设函数()e xf x x a=-的导函数为()f x '(a 为常数,e 2.71828=⋅⋅⋅是自然对数的底数).(Ⅰ) 讨论函数()f x 的单调性； (Ⅱ) 求实数a ,使曲线()y f x =在点()()2,2a f a ++处的切线斜率为3261274a a a +++-；(Ⅲ) 当x a ≠时,若不等式()()1f x k x a f x '+-≥恒成立,求实数k 的取值范围. 2015年佛山市普通高中高三教学质量检测（一） 数学试题（文科）参考答案和评分标准一、选择题：本大题共10小题，每小题5分，满分50分．[必做题] 11．1 12．112-或 13[选做题] 14．2 15三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤． 16.【解析】(Ⅰ)依题意得2ππω=,解得2ω=,所以()sin 24f x x π⎛⎫=- ⎪⎝⎭,………………2分 所以s i63f ππ⎛⎫=-⎪⎝⎭2.………4分 (Ⅱ)因为22x ππ-≤≤,所以532444x πππ-≤-≤,列表如下:……………………6分8π3π2014年11月份AQI 数据频率分布直方图2014年11月份AQI 数据频率分布表画出函数()y f x =在区间,⎡⎤-上的图像如图所示! 由图象可知函数()y f x =在,22⎛⎫-⎪⎝⎭上的单调递减区间为,28ππ⎛⎫-- ⎪⎝⎭,3,82ππ⎛⎫⎪⎝⎭.…………12分 17.【解析】(Ⅰ) 频率分布表(3分)；频率分布直方图(6分) (Ⅱ) 支持,理由如下:2013年11月的优良率为:119200.0050.0050.0150.010330⎛⎫⨯⨯+++= ⎪⎝⎭, …………8分2014年11月的优良率为:3026, …………9分 因此2619723.3%20%303030-=≈> …………11分 所以数据信息可支持“比去年同期空气质量的优良率提高了20多个百分点”.…………………12分………8分PABCDM QO18.【解析】(Ⅰ)方法一:取AD 中点O ,连结,,OP OC AC ,依题意可知△PAD ,△ACD 均为正三角形,所以OC AD ⊥,OP AD ⊥,又OCOP O =,OC ⊂平面POC ,OP ⊂平面POC ,所以AD ⊥平面POC ,又PC ⊂平面POC ,所以PC AD ⊥.………………4分 方法二:连结AC ,依题意可知△PAD ,△ACD 均为正三角形, 又M 为PC 的中点,所以AM PC ⊥,DM PC ⊥, 又AMDM M =,AM ⊂平面AMD ,DM ⊂平面AMD ,所以PC ⊥平面AMD ,又AD ⊂平面AMD ,所以PC AD ⊥.………………4分(Ⅱ)当点Q 为棱PB 的中点时,,,,A Q M D 四点共面,证明如下:………………6分 取棱PB 的中点Q ,连结QM ,QA ,又M 为PC 的中点,所以//QM BC ,在菱形ABCD 中//AD BC ,所以//QM AD ,所以,,,A Q M D 四点共面.………………8分(Ⅲ)点D 到平面PAM 的距离即点D 到平面PAC 的距离, 由(Ⅰ)可知PO AD ⊥,又平面PAD ⊥平面ABCD ,平面PAD 平面ABCD AD =,PO ⊂平面PAD ,所以PO ⊥平面A B C D ,即PO 为三棱锥P ACD -的体高.………………9分在Rt POC ∆中,PO OC =,PC = 在PAC ∆中,2PA AC ==,PC ,边PC 上的高AM ==, 所以PAC ∆的面积1122PAC S PC AM ∆=⋅==,………………10分 设点D 到平面PAC 的距离为h ,由D PAC P ACD V V --=得………………11分1133PAC ACD S h S PO ∆∆⋅=⋅,又22ACD S ∆==,所以11133h =………13分 解得h=, 所以点D 到平面PAM 的距离为5.………………14分 19.【解析】(Ⅰ) 由题设()14211n n S n a +=-+,则21413a S =-=，3234115,a S =-=35a =. 当2n ≥时，()14231n n S n a -=-+, 两式相减得()()12121n n n a n a ++=-, ……………………………………2分方法一：由()()12121n n n a n a ++=-，得12121n n a a n n +=+-，且2131a a=. 则数列21n a n ⎧⎫⎨⎬-⎩⎭是常数列，即1121211n a a n ==-⨯-，也即21n a n =- ……………………………6分所以数列{}n a 是首项为1,公差为2的等差数列 ………………………………………7分方法二：由()()12121n n n a n a ++=-，得()()122321n n n a n a +++=+， 两式相减得212n n n a a a +++=,且1322a a a += ……………………………………6分所以数列{}n a 等差数列. ………………………………………7分 (Ⅱ) 由(Ⅰ)得12-=n a n ,()21212n n n S n +-==,()121n b n n =-,…………9分当1=n 时,1312T =<成立；…………………………………………………10分 当2n ≥时,()()111111*********n b n n n n n n n n ⎛⎫==<=- ⎪---⎛⎫⎝⎭- ⎪⎝⎭…………12分所以1111111122231n T n n ⎡⎤⎛⎫⎛⎫⎛⎫<+-+-++- ⎪ ⎪ ⎪⎢⎥-⎝⎭⎝⎭⎝⎭⎣⎦1113111222n ⎛⎫=+-<+= ⎪⎝⎭综上所述,命题得证.………………………………………………………………………………14分 20.【解析】(Ⅰ)设(),P x y ,依题意得11122y y x x ---=-+, ……………………3分 化简得24x y=(2x ≠±),所以曲线E的方程为24x y =(2x ≠±). …………………5分(Ⅱ) 结论:直线BC 与曲线E 相切. 证法一:设()00,C x y ,则2004x y =,圆A的方程为()()22220011x y x y +-=+-, ……………7分 令0x =,则,()()()2222000111y x y y -=+-=+,因为00,0y y ><,所以y y =-,点B的坐标为()00,y -, ………………………………………9分直线BC 的斜率为002y k x =,直线BC 的方程为0002y y y x x +=,即002y y x y x =-,……………11分 代入24x y =得200024y x x y x ⎛⎫=- ⎪⎝⎭,即20000840x x y x x y -+=,……………13分()22000000064441640y x x y y y x ∆=-⋅=-=,所以,直线BC 与曲线E 相切.……………………………………………………………14分 证法二:设()00,C x y ,则2004x y =,圆A的方程为()()22220011x y x y +-=+-,……………7分令0x =,则,()()()2222000111y x y y -=+-=+,因为00,0y y ><,所以y y =-,点B的坐标为()00,y -,………………………………………9分直线BC 的斜率为02y k x =,…………………………………10分 由24x y =得214y x =得12y x '=,过点C 的切线的斜率为1012k x =,……………12分 而200000122142x y k x x x ⨯===,所以1k k =,……………13分 所以直线BC 与曲线24x y =过点C 的切线重合,即直线BC 与曲线E 相切.…………………………………………………………14分 21.【解析】(Ⅰ)函数()f x 的定义域是()(),,a a -∞+∞,…………………………1分对()f x 求导得:()()()2e 1x x af x x a --'=-,…………………2分由()0f x '>得1x a >+；由()0f x '<得x a <或1a x a <<+,…………………4分 所以()f x 在(),a -∞,(),1a a +上单调递减,在()1,a ++∞上单调递增.…………………5分(Ⅱ)由(Ⅰ)得()2e 24af a +'+=……………………………………6分令232641274a a e a a ++++-=得 32261270a a a a e +++++=………① 令2a t +=,则有310te t +-=,……………………………8分令()31th t e t =+-,则()203th t e t '=+>,……………………………9分故()h t 是R 上的增函数,又()00h =,因此0是()h t 的唯一零点,即2-是方程①的唯一实数解,故存在唯一实数2a =-满足题设条件.…………………………………………………………10分(Ⅲ)因为()()1f x x a f x x a '--=-,故不等式()()1f x k x a f x '+-≥可化为11x a k x a x a--+-≥-,令x a t -=,则0t ≠,……………………………11分 且有111k t t≥-- ………12分 ① 若0t <,则1kt t -≥,即21k t ≥-,此时0k ≥； ② 若01t <≤,则12kt t ≥-,即2221111k t t t ⎛⎫≥-=--+ ⎪⎝⎭,此时1k ≥；③ 若1t >,则1kt t ≥,即21k t≥,此时1k ≥. 故使不等式恒成立的k 的取值范围是[)1,+∞.………………………………………………14分。
【真题】15年广东省佛山一中高三(上)数学期中试卷含答案(文科)
2014-2015学年广东省佛山一中高三（上）期中数学试卷（文科）一、选择题（本大题共10小题，每小题5分，共50分．每小题的4个选项中，只有1项是正确的．请把答案填涂在答题卡上）.1．（5分）设集合A={x|x2﹣3x+2=0}，则满足A∪B={0，1，2}的集合B的个数是（）A．1 B．3 C．4 D．62．（5分）已知复数z满足（3+4i）z=25，则z=（）A．3﹣4i B．3+4i C．﹣3﹣4i D．﹣3+4i3．（5分）函数f（x）=2sin（ωx+φ）（ω＞0，﹣＜φ＜）的部分图象如图所示，则ω，φ的值分别是（）A． B． C． D．4．（5分）设x，y∈R，向量=（x，1）=（1，y），=（2，﹣4）且⊥，∥，则x+y=（）A．0 B．1 C．2 D．﹣25．（5分）已知，则sin2α=（）A．﹣B．﹣C．D．6．（5分）若a=2x，b=log x，则“a＞b”是“x＞1”的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分又不必要条件7．（5分）如图所示的程序框图，它的输出结果是（）A．3 B．4 C．5 D．68．（5分）在区间[0，10]内随机取出两个数，则这两个数的平方和也在区间[0，10]内的概率是（）A．B．C．D．9．（5分）设函数f（x）=﹣，[x]表示不超过x的最大整数，则y=[f（x）]的值域是（）A．{0，1}B．{0，﹣1}C．{﹣1，1}D．{1，1}10．（5分）已知函数f（x）=|2x﹣1|，a＜b＜c，且f（a）＞f（c）＞f（b），则下列结论中成立的是（）A．a＜0，b＜0，c＜0 B．a＜0，b≥0，c＞0 C．2﹣a＜2c D．2a+2c＜2二、填空题（本大题共3小题，其中11、12、13为必做题，14、15为选做题，二选一．每小题5分，共20分．请把正确答案填写在答题卷相应的横线上）. 11．（5分）若f（x）=2x+2﹣x lga是奇函数，则实数a=．12．（5分）已知函数y=f（x）的图象在M（1，f（1））处的切线方程是+2，f（1）+f′（1）=．13．（5分）当k＞0时，两直线kx﹣y=0，2x+ky﹣2=0与x轴围成的三角形面积的最大值为．三、（坐标系与参数方程选做题）14．（5分）在极坐标系中，点A的极坐标为（2，0），直线l的极坐标方程为ρ（cosθ+sinθ）+2=0，则点A到直线l的距离为．四、（几何证明选讲选做题）15．如图所示，过⊙O外一点A作一条直线与⊙O交于C，D两点，AB切⊙O于B，弦MN过CD的中点P．已知AC=4，AB=6，则MP•NP=．五、解答题：本大题共6小题，共80分，解答应写成文字说明、证明过程或演算步骤.16．（12分）在△ABC中，边a、b、c分别是角A、B、C的对边，且满足bcosC=（3a﹣c）cosB．（1）求cosB；（2）若•=4，b=4，求边a，c的值．17．（12分）年龄在60岁（含60岁）以上的人称为老龄人，某小区的老龄人有350人，他们的健康状况如下表：其中健康指数的含义是：2代表“健康”，1代表“基本健康”，0代表“不健康，但生活能够自理”，﹣1代表“生活不能自理”．（Ⅰ）随机访问该小区一位80岁以下的老龄人，该老龄人生活能够自理的概率是多少？（Ⅱ）按健康指数大于0和不大于0进行分层抽样，从该小区的老龄人中抽取5位，并随机地访问其中的3位．求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率．18．（14分）a∈R，解关于x的不等式≥a（x﹣1）．19．（14分）如图，在三棱锥P﹣ABC中，PA⊥底面ABC，∠BCA=90°，AP=AC，点D，E分别在棱PB，PC上，且BC∥平面ADE．（Ⅰ）求证：DE⊥平面PAC；（Ⅱ）若PC⊥AD，且三棱锥P﹣ABC的体积为8，求多面体ABCED的体积．20．（14分）已知各项均为正数的数列{a n}的前n项和为S n，且a2n+a n=2S n（1）求a1（2）求数列{a n}的通项；（3）若b n=（n∈N*），T n=b1+b2+…b n，求证：T n＜．21．（14分）已知函数f（x）=（x2﹣3x+3）•e x的定义域为[﹣2，t]，设f（﹣2）=m，f（t）=n．（1）试确定t的取值范围，使得函数f（x）在[﹣2，t]上为单调函数；（2）求证：m＜n；（3）求证：对于任意的t＞﹣2，总存在x0∈（﹣2，t），满足=（t﹣1）2；又若方程=（t﹣1）2；在（﹣2，t）上有唯一解，请确定t的取值范围．2014-2015学年广东省佛山一中高三（上）期中数学试卷（文科）参考答案与试题解析一、选择题（本大题共10小题，每小题5分，共50分．每小题的4个选项中，只有1项是正确的．请把答案填涂在答题卡上）.1．（5分）设集合A={x|x2﹣3x+2=0}，则满足A∪B={0，1，2}的集合B的个数是（）A．1 B．3 C．4 D．6【解答】解：A={x|x2﹣3x+2=0}={x|x=1或x=2}={1，2}，若A∪B={0，1，2}，则0∈B，则B={0}，{0，2}，{1，0}，{0，1，2}，共4个，故选：C．2．（5分）已知复数z满足（3+4i）z=25，则z=（）A．3﹣4i B．3+4i C．﹣3﹣4i D．﹣3+4i【解答】解：∵复数z满足（3+4i）z=25，则z====3﹣4i，故选：A．3．（5分）函数f（x）=2sin（ωx+φ）（ω＞0，﹣＜φ＜）的部分图象如图所示，则ω，φ的值分别是（）A． B． C． D．【解答】解：∵在同一周期内，函数在x=时取得最大值，x=时取得最小值，∴函数的周期T满足=﹣=，由此可得T==π，解得ω=2，得函数表达式为f（x）=2sin（2x+φ）又∵当x=时取得最大值2，∴2sin（2•+φ）=2，可得+φ=+2kπ（k∈Z）∵，∴取k=0，得φ=﹣故选：A．4．（5分）设x，y∈R，向量=（x，1）=（1，y），=（2，﹣4）且⊥，∥，则x+y=（）A．0 B．1 C．2 D．﹣2【解答】解：∵⊥，∥，∴2x﹣4=0，2y+4=0，解得x=2，y=﹣2．∴x+y=0．故选：A．5．（5分）已知，则sin2α=（）A．﹣B．﹣C．D．【解答】解：将两边平方得，，可得，故选：B．6．（5分）若a=2x，b=log x，则“a＞b”是“x＞1”的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分又不必要条件【解答】解：如图，x=x0时，a=b，∴若a＞b，则得到x＞x0，且x0＜1，∴a＞b 不一定得到x＞1；∴a＞b不是x＞1的充分条件；若x＞1，则由图象得到a＞b，∴a＞b是x＞1的必要条件；∴a＞b是x＞1的必要不充分条件．故选：B．7．（5分）如图所示的程序框图，它的输出结果是（）A．3 B．4 C．5 D．6【解答】解：∵k=0，a=45时，sina=cosa不满足判断框中的条件，k=1，a=90时，sina＞cosa，不满足判断框中的条件，k=2，a=135时，sina＞cosa，不满足判断框中的条件，k=3，a=180时，sina＞cosa，不满足判断框中的条件，k=4，a=225时，sina=cosa，不满足判断框中的条件，k=5，a=270时，sina＜cosa，满足判断框中的条件，即输出的结果为5，故选：C．8．（5分）在区间[0，10]内随机取出两个数，则这两个数的平方和也在区间[0，10]内的概率是（）A．B．C．D．【解答】解：将取出的两个数分别用x，y表示，则x，y∈[0，10]要求这两个数的平方和也在区间[0，10]内，即要求0≤x2+y2≤10，故此题可以转化为求0≤x2+y2≤10在区域内的面积比的问题．即由几何知识可得到概率为；故选：D．9．（5分）设函数f（x）=﹣，[x]表示不超过x的最大整数，则y=[f（x）]的值域是（）A．{0，1}B．{0，﹣1}C．{﹣1，1}D．{1，1}【解答】解：函数f（x）=﹣，[x]表示不超过x的最大整数，∴f（x）=﹣，分析可得，﹣＜f（x）＜，∴[f（x）]={0，﹣1}，故选：B．10．（5分）已知函数f（x）=|2x﹣1|，a＜b＜c，且f（a）＞f（c）＞f（b），则下列结论中成立的是（）A．a＜0，b＜0，c＜0 B．a＜0，b≥0，c＞0 C．2﹣a＜2c D．2a+2c＜2【解答】解：对于A，若a＜0，b＜0，c＜0，因为a＜b＜c，所以a＜b＜c＜0，而函数f（x）=|2x﹣1|在区间（﹣∞，0）上是减函数，故f（a）＞f（b）＞f（c），与题设矛盾，所以A不正确；对于B，若a＜0，b≥0，c＞0，可设a=﹣1，b=2，c=3，此时f（c）=f（3）=7为最大值，与题设矛盾，故B不正确；对于C，取a=0，c=3，同样f（c）=f（3）=7为最大值，与题设矛盾，故C不正确；对于D，因为a＜c，且f（a）＞f（c），说明可能如下情况成立：（i）a、c位于函数的减区间（﹣∞，0），此时a＜b＜c＜0，可得f（a）＞f（b）＞f（c）与题设矛盾；（ii）a、c不在函数的减区间（﹣∞，0），则必有a＜0＜c，所以f（a）=1﹣2a ＞2c﹣1=f（c），化简整理，得2a+2c＜2成立．综上所述，可得只有D正确故选：D．二、填空题（本大题共3小题，其中11、12、13为必做题，14、15为选做题，二选一．每小题5分，共20分．请把正确答案填写在答题卷相应的横线上）.11．（5分）若f（x）=2x+2﹣x lga是奇函数，则实数a=．【解答】解：函数f（x）=2x+2﹣x lga是奇函数∴f（x）+f（﹣x）=0，∴2x+2﹣x lga+2﹣x+2x lga=0，即2x+2﹣x+lga（2x+2﹣x）=0∴lga=﹣1∴a=故答案为：．12．（5分）已知函数y=f（x）的图象在M（1，f（1））处的切线方程是+2，f（1）+f′（1）=3．【解答】解：由已知切点在切线上，所以f（1）=，切点处的导数为切线斜率，所以，所以f（1）+f′（1）=3故答案为：313．（5分）当k＞0时，两直线kx﹣y=0，2x+ky﹣2=0与x轴围成的三角形面积的最大值为．【解答】解：由两直线kx﹣y=0，2x+ky﹣2=0与x轴围成的三角形如图，联立，解得B（）．则=．当且仅当k=，即k=时上式取等号．故答案为：．三、（坐标系与参数方程选做题）14．（5分）在极坐标系中，点A的极坐标为（2，0），直线l的极坐标方程为ρ（cosθ+sinθ）+2=0，则点A到直线l的距离为．【解答】解：由题意得点A（2，0），直线l为ρ（cosθ+sinθ）+2=0，即x+y+2=0，∴点A到直线l的距离为=2，故答案为2．四、（几何证明选讲选做题）15．如图所示，过⊙O外一点A作一条直线与⊙O交于C，D两点，AB切⊙O于B，弦MN过CD的中点P．已知AC=4，AB=6，则MP•NP=．【解答】解：∵AB为⊙O的切线，ACD为⊙O的割线由切割线定理可得：AB2=AC•AD由AC=4，AB=6，故AD=9故CD=5又∵P是弦CD的中点故PC=PD=由相交弦定理得MP•NP=PC•PD=故答案为：五、解答题：本大题共6小题，共80分，解答应写成文字说明、证明过程或演算步骤.16．（12分）在△ABC中，边a、b、c分别是角A、B、C的对边，且满足bcosC=（3a﹣c）cosB．（1）求cosB；（2）若•=4，b=4，求边a，c的值．【解答】解：（1）在△ABC中，∵bcosC=（3a﹣c）cosB，由正弦定理可得sinBcosC=（3sinA﹣sinC）cosB，∴3sinA•cosB﹣sinC•cosB=sinBcosC，化为：3sinA•cosB=sinC•cosB+sinBcosC=sin （B+C）=sinA．∵在△ABC中，sinA≠0，故cosB=．（2）由•=4，b=4，可得，a•c•cosB=4，即ac=12．…①．再由余弦定理可得b2=32=a2+c2﹣2ac•cosB=a2+c2﹣，即a2+c2=40，…②．由①②求得a=2，c=6；或者a=6，c=2．综上可得，，或．17．（12分）年龄在60岁（含60岁）以上的人称为老龄人，某小区的老龄人有350人，他们的健康状况如下表：其中健康指数的含义是：2代表“健康”，1代表“基本健康”，0代表“不健康，但生活能够自理”，﹣1代表“生活不能自理”．（Ⅰ）随机访问该小区一位80岁以下的老龄人，该老龄人生活能够自理的概率是多少？（Ⅱ）按健康指数大于0和不大于0进行分层抽样，从该小区的老龄人中抽取5位，并随机地访问其中的3位．求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率．【解答】解：（Ⅰ）解：该社区80岁以下的老龄人共有120+133+32+15=300人，…（1分）其中生活能够自理的人有120+133+32=285人，…（2分）记“随机访问该小区一位80岁以下的老龄人，该老人生活能够自理”为事件A，则P（A）==．…（4分）（Ⅱ）根据表中数据可知，社区健康指数大于0的老龄人共有280人，不大于0的老龄人共有70人，…（5分）所以，按照分层抽样，被抽取的5位老龄人中，有位为健康指数大于0的，依次记为：a，b，c，d，有一位健康指数不大于0的，记为e．…（7分）从这5人中抽取3人的基本事件有：（a，b，c）（a，b，d）（a，b，e）（a，c，d）（a，c，e）（a，d，e）（b，c，d）（b，c，e）（b，d，e）（c，d，e）共10种，…（9分）其中恰有1位老龄人的健康指数不大于0的事件有：（a，b，e）（a，c，e）（a，d，e）（b，c，e）（b，d，e）（c，d，e）共6种，…（10分）记“被访问的3位老龄人中恰有1位老龄人的健康指数不大于0”为事件B，则P（B）=…（12分）18．（14分）a∈R，解关于x的不等式≥a（x﹣1）．【解答】解：原不等式可转化为≥0（*）．（1）当a=1时，（*）式为≥0，解得x＜0或x≥1．（2）当a≠1时，（*）可式为≥0①若a＜1，则a﹣1＜0，＜0，解得≤x＜0，或x≥1；②若1＜a≤2，则1﹣a＜0，≥1，解得x＜0，或1≤x≤；③若a＞2，则a﹣1＞1，0＜＜1，1﹣a＜0，解得x＜0，或≤x≤1；综上，当a=1时，不等式解集为{x|x＜0或x≥1}当a＜1时，不等式解集为{x|≤x＜0，或x≥1}当1＜a≤2时，不等式解集为{x|x＜0，或1≤x≤}当a＞2时，不等式解集为{x|x＜0，或≤x≤1}．19．（14分）如图，在三棱锥P﹣ABC中，PA⊥底面ABC，∠BCA=90°，AP=AC，点D，E分别在棱PB，PC上，且BC∥平面ADE．（Ⅰ）求证：DE⊥平面PAC；（Ⅱ）若PC⊥AD，且三棱锥P﹣ABC的体积为8，求多面体ABCED的体积．【解答】解：（Ⅰ）∵BC∥平面ADE，BC⊂平面PBC，平面PBC∩平面ADE=DE ∴BC∥ED．∵PA⊥底面ABC，BC⊂底面ABC，∴PA⊥BC．又∠BCA=90°，∴AC⊥BC．∵PA∩AC=A，∴BC⊥平面PAC．∴DE⊥平面PAC．（Ⅱ）由（Ⅰ）知，DE⊥平面PAC，∵PC⊂平面PAC，∴DE⊥PC，又∵PC⊥AD，AD∩DE=D，∴PC⊥平面ADE，∴AE⊥PC，∵AP=AC，∴E是PC的中点，ED是△PBC的中位线．==．∴V ABCED===6．20．（14分）已知各项均为正数的数列{a n}的前n项和为S n，且a2n+a n=2S n （1）求a1（2）求数列{a n}的通项；（3）若b n=（n∈N*），T n=b1+b2+…b n，求证：T n＜．【解答】解：（1）令n=1，得a12+a1=2S1=2a1，∵a1＞0，∴a1=1，（2）又a2n+a n=2S n，有a2n+1+a n+1=2S n+1，两式相减得并整理得（a n+1+a n）（a n+1﹣a n﹣1）=0，∵a n＞0，∴a n+1﹣a n=1，∴数列{a n}是以a1=1，公差为1的等差数列，通项公式为a n=1+（n﹣1）×1=n；（3）n=1时b1=1＜符合…（9分）n≥2时，因为==2（﹣）所以T n=b1+b2+…b n＜1+2（++…+﹣）=1=∴T n＜．21．（14分）已知函数f（x）=（x2﹣3x+3）•e x的定义域为[﹣2，t]，设f（﹣2）=m，f（t）=n．（1）试确定t的取值范围，使得函数f（x）在[﹣2，t]上为单调函数；（2）求证：m＜n；（3）求证：对于任意的t＞﹣2，总存在x0∈（﹣2，t），满足=（t﹣1）2；又若方程=（t﹣1）2；在（﹣2，t）上有唯一解，请确定t的取值范围．【解答】解：（1）∵f′（x）=（2x﹣3）•e x+（x2﹣3x+3）•e x=x（x﹣1）e x，由f′（x）＞0可得，x＞1或x＜0；由f′（x）＞＜0可得，0＜x＜1；∴f（x）在（﹣∞，0），（1，+∞）上递增，在（0，1）上递减，欲f（x）在[﹣2，t]上为单调函数，则﹣2＜t≤0；∴t的取值范围为（﹣2，0]．（2）证明：∵f（x）在（﹣∞，0），（1，+∞）上递增，在（0，1）上递减，∴f（x）在x=1处取得极小值e，又∵f（﹣2）=m=＜e=f（1），∴f（x）在[﹣2，+∞）上的最小值为f（﹣2）．从而当t＞﹣2时，f（﹣2）＜f（t），即m＜n；（3）证明：∵=﹣x0，∴=（t﹣1）2可化为﹣x0=（t﹣1）2，令g（x）=x2﹣x﹣（t﹣1）2，则证明方程x2﹣x﹣（t﹣1）2=0在（﹣2，t）上有解，并讨论解的个数．∵g（﹣2）=6﹣（t﹣1）2=﹣（t+2）（t﹣4），g（t）=t（t﹣1）﹣（t﹣1）2=（t+2）（t﹣1），①当t＞4或﹣2＜t＜1时，g（﹣2）•g（t）＜0，则方程x2﹣x﹣（t﹣1）2=0在（﹣2，t）上有且只有一解；②当1＜t＜4时，g（﹣2）＞0，且g（t）＞0，又∵g（0）=﹣（t﹣1）2＜0，∴方程x2﹣x﹣（t﹣1）2=0在（﹣2，t）上有解，且有两解；③当t=1时，g（x）=x2﹣x=0，从而解得，x=0或x=1，故方程x2﹣x﹣（t﹣1）2=0在（﹣2，t）上有且只有一解；④当t=4时，g（x）=x2﹣x﹣6=0，从而解得，x=﹣2或x=3，故方程x2﹣x﹣（t﹣1）2=0在（﹣2，t）上有且只有一解；综上所述，对于任意的t＞﹣2，总存在x0∈（﹣2，t），满足=（t﹣1）2；当方程=（t﹣1）2在（﹣2，t）上有唯一解时，t的取值范围为（﹣2，1]∪[4，+∞）．赠送—高中数学知识点【1.3.1】单调性与最大（小）值（1）函数的单调性①定义及判定方法②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数．③对于复合函数[()]y f g x=，令()u g x=，若()y f u=为增，()u g x=为增，则[()]y f g x=为增；若()y f u=为减，()u g x=为减，则[()]y f g x=为增；若()y f u=为增，()u g x=为减，则[()]y f g x=为减；若()y f u=为减，()u g x=为增，则[()]y f g x=为减．（2）打“√”函数()(0)af x x ax=+>的图象与性质()f x分别在(,-∞、)+∞上为增函数，分别在[、上为减函数．（3）最大（小）值定义①一般地，设函数()y f x=的定义域为I，如果存在实数yxoM 满足：（1）对于任意的x I ∈，都有()f x M ≤； （2）存在0x I ∈，使得0()f x M =．那么，我们称M 是函数()f x 的最大值，记作max ()f x M =．②一般地，设函数()y f x =的定义域为I ，如果存在实数m 满足：（1）对于任意的x I ∈，都有()f x m ≥；（2）存在0x I ∈，使得0()f x m =．那么，我们称m 是函数()f x 的最小值，记作max ()f x m =．【1.3.2】奇偶性（4）函数的奇偶性①定义及判定方法②若函数()f x 为奇函数，且在0x =处有定义，则(0)0f =．③奇函数在y 轴两侧相对称的区间增减性相同，偶函数在y 轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．。
2015年佛山一模文科数学试题及答案(全word精美)
2015年佛山市普通高中高三教学质量检测（一）数 学（文科） 2015.1本试卷共4页,21小题,满分150分.考试时间120分钟. 注意事项:1．答卷前,考生务必填写答题卷上的有关项目．2．选择题每小题选出答案后,用2B 铅笔把答案涂在答题卷相应的位置上．3．非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内；如需改动,先划掉原来的答案,然后再写上新的答案；不准使用铅笔和涂改液,不按以上要求作答的答案无效．4．请考生保持答题卷的整洁.考试结束后,将答题卷交回. 参考公式: 锥体的体积公式13V Sh =,其中S 为柱体的底面积,h 为锥体的高. 一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．复数i1i3++等于( ) A ．i 21+B ．i 21-C ．i 2-D ．i 2+2．已知集合{}02M x x =∈<<R ,{}1N x x =∈>R ,则()R MN =ð( )A ．[)1,2B ．()1,2C ．[)0,1D ．(]0,13．若函数42x xay +=的图象关于原点对称,则实数a 等于( )A ．2-B ．1-C ．1D ．24．已知x ,y 满足不等式组282800x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩,则目标函数3z x y =+的最大值为( )A ．12B ．24C ．8D ．3325．已知两个单位向量12,e e 的夹角为45︒,且满足()121λ⊥-e e e ,则实数λ的值是( )A ．1 BC．3D ．2 6．在空间中，有如下四个命题： ①平行于同一个平面的两条直线是平行直线； ②垂直于同一条直线的两个平面是平行平面；③若平面α内有不共线的三个点到平面β距离相等，则α∥β； ④过平面α的一条斜线有且只有一个平面与平面α垂直. 其中正确的两个命题是( )A ．①③B ．②④C ．①④D ．②③7．某校高三年级学生会主席团有共有5名同学组成,其中有3名同学来自同一班级,另外两名同学来自另两个不同班级.现从中随机选出两名同学参加会议,则两名选出的同学来自不同班级的概率为( ) A ．0.35 B ．0.4 C ．0.6 D ．0.78. 已知双曲线221169x y -=的左、右焦点分别为1F ,2F ,过2F 的直线与该双曲线的右支交于A 、B 两点,若5=AB ,则1ABF ∆的周长为( )A ．16B ．20C ．21D ．26 9．已知()2f x x x =-,且a ,b ∈R ,则“1a b >>”是“()()f a f b <”的( )A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件10．有10个乒乓球,将它们任意分成两堆,求出这两堆乒乓球个数的乘积,再将每堆乒乓球任意分成两堆并求出这两堆乒乓球个数的乘积,如此下去,直到不能再分为止,则所有乘积的和为( )A . 45B . 55C . 90D . 100 二、填空题：本大共5小题，考生作答4小题，每小题5分，满分20分． (一)必做题(11～13题)11．如果()1,10,1x f x x ì£ïï=íï>ïî,那么()2f f =⎡⎤⎣⎦ . 12．已知点()2,0A -、()0,4B 到直线l :10x my +-=的距离相等,则m 的值为 .13. 如图1,为了测量河对岸A 、B 两点之间的距离,观察者找到一个点C ,从C 点可以观察到点A 、B ；找到一个点D ,从D 点可以观察到点A 、C ；找到一个点E ,从E 点可以观察到点B 、C ；并测量得到一些数据:2CD =,CE =45D ∠=︒,105ACD ∠=︒,48.19ACB ∠=︒,75BCE ∠=︒,E ∠=60︒,则A 、B 两点之间的距离为_________.(其中cos 48.19︒取近似值23)(二)选做题(14～15题，考生只能从中选做一题)14.(几何证明选讲)如图2,P 是圆O 外一点,PA 、PB 是圆O 的两条切线,切点分别为A 、B ,PA 中点为M ,过M 作圆O 的一条割线交圆O 于C 、D 两点,若PB =1MC =,则CD = . 15.(坐标系与参数方程)在极坐标系中,曲线1C:)sin 1ρθθ+=与曲线2C :a ρ=(0a >)的一个交点在极轴上,则a =______.C图1O DCA MB图22014年11月份AQI 数据频率分布表 表22013年11月份AQI 数据频率分布直方图2014年11月份AQI 数据频率分布直方图三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤． 16.(本小题满分12分)已知函数()sin 4f x x πω⎛⎫=- ⎪⎝⎭(0ω>),x ∈R 的最小正周期为π.(Ⅰ) 求6f π⎛⎫⎪⎝⎭； (Ⅱ) 在图3给定的平面直角坐标系中,画出函数()y f x =在区间,22ππ⎡⎤-⎢⎥⎣⎦上的图像,并根据图象写出其在,22ππ⎛⎫- ⎪⎝⎭17.(本小题满分12分)某地区“腾笼换鸟”的政策促进了区内环境改善和产业转型,空气质量也有所改观,现从当地天气网站上收集该地区近两年11月份(30天)的空气质量指数(AQI )(单位:3g /m μ)资料如下:(Ⅰ) 请填好2014年11月份AQI 数据的频率分布表．．．．．并完成频率分布直方图．．．．．．．；(Ⅱ) 该地区环保部门2014年12月1日发布的11月份环评报告中声称该地区“比去年同期空气质量的优良率提高了20多个百分点”(当AQI 100<时,空气质量为优良).试问此人收集到的资料信息是否支持该观点?表1PABC DM图618.(本小题满分14分)如图6,四棱锥P ABCD -,侧面PAD 是边长为2的正三角形,且与底面垂直,底面ABCD 是60ABC ∠=︒的菱形,M 为PC 的中点.(Ⅰ) 求证:PC AD ⊥；(Ⅱ) 在棱PB 上是否存在一点Q ,使得,,,A Q M D 四点共面?若存在,指出点Q 的位置并证明；若不存在,请说明理由；(Ⅲ) 求点D 到平面PAM 的距离.19.(本小题满分14分)已知数列{}n a 的前n 项和为n S ,若()14211n n S n a +=-+(*n ∈N ),且11=a .(Ⅰ) 求证：数列{}n a 为等差数列； (Ⅱ)设n b =,数列{}n b 的前n 项和为n T ,证明:32n T <(*n ∈N ).20.(本小题满分14分)已知点()2,1M ,()2,1N -,直线MP ,NP 相交于点P ,且直线MP 的斜率减直线NP 的斜率的差为1.设点P 的轨迹为曲线E . (Ⅰ) 求E 的方程；(Ⅱ) 已知点()0,1A ,点C 是曲线E 上异于原点的任意一点,若以A 为圆心,线段AC 为半径的圆交y 轴负半轴于点B ,试判断直线BC 与曲线E 的位置关系,并证明你的结论.21.(本小题满分14分)设函数()e xf x x a=-的导函数为()f x '(a 为常数,e 2.71828=⋅⋅⋅是自然对数的底数).(Ⅰ) 讨论函数()f x 的单调性；(Ⅱ) 求实数a ,使曲线()y f x =在点()()2,2a f a ++处的切线斜率为3261274a a a +++-；(Ⅲ) 当x a ≠时,若不等式()()1f x k x a f x '+-≥恒成立,求实数k 的取值范围.8π38π2015年佛山市普通高中高三教学质量检测（一）数学试题（文科）参考答案和评分标准一、选择题：本大题共10小题，每小题5分，满分50分．[必做题] 11．1 12．112-或 13 [选做题] 14．215．2三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤．16.【解析】(Ⅰ)依题意得2ππω=,解得2ω=,所以()sin 24f x x π⎛⎫=- ⎪⎝⎭,………………2分 所以sin sin cos cos sin 6343434f πππππππ⎛⎫⎛⎫=-=-=⎪ ⎪⎝⎭⎝⎭1222-⨯=………4分 (Ⅱ)因为2x ππ-≤≤,所以532x πππ-≤-≤,列表如下:……………………6分画出函数()y f x =在区间,⎡⎤-上的图像如图所示!由图象可知函数()y f x =在,22-⎪⎝⎭上的单调递减区间为,28-- ⎪⎝⎭,,82 ⎪⎝⎭.…………12分 17.【解析】(Ⅰ) 频率分布表(3分)；频率分布直方图(6分) (Ⅱ) 支持,理由如下:2013年11月的优良率为:119200.0050.0050.0150.010330⎛⎫⨯⨯+++= ⎪⎝⎭, …………8分2014年11月的优良率为:3026, …………9分 ………8分2014年11月份AQI 数据频率分布直方图2014年11月份AQI 数据频率分布表PABC DM QO因此2619723.3%20%303030-=≈> …………11分 所以数据信息可支持“比去年同期空气质量的优良率提高了20多个百分点”.…………………12分18.【解析】(Ⅰ)方法一:取AD 中点O ,连结,,OP OC AC ,依题意可知△PAD ,△ACD 均为正三角形,所以OC AD ⊥,OP AD ⊥,又OC OP O =,OC ⊂平面POC ,OP ⊂平面POC , 所以AD ⊥平面POC ,又PC ⊂平面POC ,所以PC AD ⊥.………………4分 方法二:连结AC ,依题意可知△PAD ,△ACD 均为正三角形, 又M 为PC 的中点,所以AM PC ⊥,DM PC ⊥, 又AMDM M =,AM ⊂平面AMD ,DM ⊂平面AMD ,所以PC ⊥平面AMD ,又AD ⊂平面AMD ,所以PC AD ⊥.………………4分(Ⅱ)当点Q 为棱PB的中点时,,,,A Q M D 四点共面,证明如下:………………6分 取棱PB的中点Q ,连结QM ,QA ,又M 为PC 的中点,所以//QM BC ,在菱形ABCD 中//AD BC ,所以//QM AD ,所以,,,A Q M D 四点共面.………………8分 (Ⅲ)点D 到平面PAM 的距离即点D 到平面PAC 的距离, 由(Ⅰ)可知PO AD ⊥,又平面PAD ⊥平面ABCD ,平面PAD 平面ABCD AD =,PO ⊂平面PAD ,所以PO ⊥平面ABCD ,即PO 为三棱锥P ACD -的体高.………………9分在Rt POC ∆中,PO OC ==PC ,在PAC ∆中,2PA AC ==,PC =,边PC上的高AM==, 所以PAC ∆的面积1122PAC S PC AM ∆=⋅==,………………10分 设点D 到平面PAC 的距离为h ,由D PAC P ACD V V --=得………………11分1133PAC ACD S h S PO ∆∆⋅=⋅,又22ACD S ∆==所以1133h =………13分 解得h =, 所以点D 到平面PAM 的距离为5.………………14分19.【解析】(Ⅰ) 由题设()14211n n S n a +=-+,则21413a S =-=，3234115,a S =-=35a =. 当2n ≥时，()14231n n S n a -=-+,两式相减得()()12121n n n a n a ++=-, ……………………………………2分 方法一：由()()12121n n n a n a ++=-，得12121n n a a n n +=+-，且2131a a=. 则数列21n a n ⎧⎫⎨⎬-⎩⎭是常数列，即1121211n a a n ==-⨯-，也即21n a n =- ……………………………6分 所以数列{}n a 是首项为1,公差为2的等差数列 ………………………………………7分 方法二：由()()12121n n n a n a ++=-，得()()122321n n n a n a +++=+，两式相减得212n n n a a a +++=,且1322a a a += ……………………………………6分 所以数列{}n a 等差数列. ………………………………………7分 (Ⅱ) 由(Ⅰ)得12-=n a n ,()21212n n n S n +-==,()121n b n n =-,…………9分当1=n 时,1312T =<成立；…………………………………………………10分 当2n ≥时,()()111111*********n b n n n n n n n n ⎛⎫==<=- ⎪---⎛⎫⎝⎭- ⎪⎝⎭…………12分所以1111111122231n T n n ⎡⎤⎛⎫⎛⎫⎛⎫<+-+-++- ⎪ ⎪ ⎪⎢⎥-⎝⎭⎝⎭⎝⎭⎣⎦1113111222n ⎛⎫=+-<+= ⎪⎝⎭综上所述,命题得证.………………………………………………………………………………14分 20.【解析】(Ⅰ)设(),P x y ,依题意得11122y y x x ---=-+, ……………………3分 化简得24x y =(2x ≠±),所以曲线E 的方程为24x y =(2x ≠±). …………………5分 (Ⅱ) 结论:直线BC 与曲线E 相切.证法一:设()00,C x y ,则2004x y =,圆A 的方程为()()22220011x y x y +-=+-, ……………7分 令0x =,则,()()()2222000111y x y y -=+-=+,因为00,0y y ><,所以0y y =-,点B 的坐标为()00,y -, ………………………………………9分 直线BC 的斜率为002y k x =,直线BC 的方程为0002y y y x x +=,即0002yy x y x =-,……………11分代入24x y =得200024y x x y x ⎛⎫=-⎪⎝⎭,即20000840x x y x x y -+=,……………13分 ()22000000064441640y x x y y y x ∆=-⋅=-=,所以,直线BC 与曲线E 相切.……………………………………………………………14分证法二:设()00,C x y ,则2004x y =,圆A 的方程为()()22220011x y x y +-=+-,……………7分 令0x =,则,()()()2222000111y x y y -=+-=+,因为00,0y y ><,所以0y y =-,点B 的坐标为()00,y -,………………………………………9分 直线BC 的斜率为02y k x =,…………………………………10分 由24x y =得214y x =得12y x '=,过点C 的切线的斜率为1012k x =,……………12分 而200000122142x y k x x x ⨯===,所以1k k =,……………13分 所以直线BC 与曲线24x y =过点C 的切线重合,即直线BC 与曲线E 相切.…………………………………………………………14分 21.【解析】(Ⅰ)函数()f x 的定义域是()(),,a a -∞+∞,…………………………1分对()f x 求导得:()()()2e 1x x af x x a --'=-,…………………2分由()0f x '>得1x a >+；由()0f x '<得x a <或1a x a <<+,…………………4分 所以()f x 在(),a -∞,(),1a a +上单调递减,在()1,a ++∞上单调递增.…………………5分(Ⅱ)由(Ⅰ)得()2e 24af a +'+=……………………………………6分令232641274a a e a a ++++-=得 32261270a a a a e +++++=………① 令2a t +=,则有310te t +-=,……………………………8分令()31th t e t =+-,则()203th t e t '=+>,……………………………9分故()h t 是R 上的增函数,又()00h =,因此0是()h t 的唯一零点,即2-是方程①的唯一实数解, 故存在唯一实数2a =-满足题设条件.…………………………………………………………10分 (Ⅲ)因为()()1f x x a f x x a '--=-,故不等式()()1f x k x a f x '+-≥可化为11x a k x a x a--+-≥-, 令x a t -=,则0t ≠,……………………………11分 且有111k t t≥-- ………12分 ① 若0t <,则1kt t -≥,即21k t ≥-,此时0k ≥； ② 若01t <≤,则12kt t ≥-,即2221111k t t t ⎛⎫≥-=--+ ⎪⎝⎭,此时1k ≥；③ 若1t >,则1kt t ≥,即21k t≥,此时1k ≥. 故使不等式恒成立的k 的取值范围是[)1,+∞.………………………………………………14分。
2015年佛山市普通高中高三教学质量检测
2015年佛山市普通高中高三教学质量检测（2015佛山一模）24．我国推出“八项规定”、“六项禁令”以来，公款消费得到了有效遏制，给某高档白酒厂的发展带来了重大影响。
该影响的合理传导途径是①白酒价格降低 ②生产规模缩小 ③消费需求减少 ④酒厂利润减少A ．①-③-②-④B ．③-①-④-②C ．①-③-④-②D ．③-①-②-④25．几年前我国房价高涨，购房者却络绎不绝，政府通过限购令等来调控楼市；如今多地政府相继取消限购令，房价依然呈下跌趋势，持币观望者大有人在。
对这一现象的合理解释是A ．经济不景气，居民收入下降B ．政策因素影响消费需求C ．楼市价格对需求的影响有限D ．消费受心理预期的影响26．下图是我国国内企业与国外企业在某些产品中存在的成本“剪刀差”。
它给我国国内企业的启示是A ．发挥人力资源比较优势B ．加快发展战略性新兴产业C ．转变对外经济发展方式D ．大力发展劳动密集型产业27．习近平主席在哈萨克斯坦访问时全面阐述中国对中亚国家睦邻友好合作政策，倡导用创新的合作模式，共同建设区域大合作的“丝绸之路经济带”。
“丝绸之路经济带”①是适应世界多极化发展的客观要求②是市场经济发展的内在要求③有利于更好地利用国际国内两个市场、两种资源④有利于把“引进来”和“走出去”更好结合起来A ．①②③B ．②③④C ．①③④D ．①②④28．截至（2014年）11月30日，广东省累计报告登革热确诊病例45053例。
防治登革热，人人有责！以下做法与书本知识对应正确的是①做好家居清洁卫生、灭蚊共作，彻底杜绝传染源——个人利益服从国家利益②协助村（居）委会做好灭蚊宣传工作——参与民主管理③对卫生做得不好的部门提出批评和建议——参与民主监督④对政府相关部门灭蚊行动提出书面建议——参与民主决策A ．①②③B ．①②④C ．①③④D ．②③④29．中国共产党和我国国家机构得组织活动原则都是民主集中制。
我国出台关系国家前途和命运得重大决策通常要经历的法定程序是①全国人大审议通过 ②国务院编制草案稿 ③中共中央召开党外人士座谈会听取意见④全国政协会议讨论 ⑤中国共产党中央委员会全体会议通过决议A ．③-⑤-②-④-①B ．①-②-③-④-⑤C ．⑤-③-④-①-②D ．③-⑤-④-①-②30、2014年APEC 峰会于11月5日至11日在北京召开，此次峰会的主题是：共建面向未来的亚太伙伴关系。
(理科数学)-2015-2016学年佛山市普通高中高三教学质量检测(一)
．
11．宋元时期杰出的数学家朱世杰在其数学巨著《四元玉鉴》卷中“菱草形段”第一个问题“今有菱草六 百八十束，欲令‘落一形’捶（同垛）之，问底子（每层三角形边菱草束数，等价于层数）几何？”中探 讨了“垛积术”中的落一形垛（“落一形”即是指顶上 1 束，下一层 3 束，再下一层 6 束， , 成三角 锥的堆垛，故也称三角垛，如图，表示第二层开始的每层菱草束数），则本问题中三角垛底层菱草总束数 为 ．
轴正半轴为极轴，建立极坐标系． （1）求直线 l 与圆 C 的交点的极坐标； （2）若 P 为圆 C 上的动点，求 P 到直线 l 的距离 d 的最大值． 24．（本小题满分 10 分） 选修 4—5：不等式选讲 已知函数 f ( x ) | x 2 | a ， g ( x ) | x 4 | ， a R． （1）解不等式 f ( x ) g ( x ) a ； （2）任意 x R， f ( x ) g ( x ) a 恒成立，求 a 的取值范围．
C． 45
D． 55 ）
是函数 f ( x ) sin( 2 x ) 的一个极大值点，则 f ( x ) 的一个单调递减区间是（ B． (
2
6 , 3
)
5
3 , 6
)
C． (
2
F1 、F2 分别是双曲线
x2 y2 1（ a 0 ，b 0 ）的左、右两个焦点，若在双曲线上存在点 P ， a2 b2
b ”是“ ln a ln b ”的（
B．必要不充分条件 D．既不充分又不必要条件
x y 10 4．若变量 x ， y 满足 0 x y 20 ，则 2 x 3 y 的最大值为（ 0 y 15
广东省佛山市普通高中2016届高三数学教学质量检测试题(一)文(含解析)
2015～2016学年佛山市普通高中高三教学质量检测（一）数 学（文科）一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若复数z 满足i 1i z =--,则在复平面内,z 所对应的点在（ ）A. 第一象限B. 第二象限C. 第三象限D. 第四象限 【答案】B【解析】1i1i i z --==-+，故选B.2. 已知U =R ,函数ln(1)y x =-的定义域为M ,集合{02}N x x =<<,则U ()MN =（ ）A. (,0]-∞B. (0,1)C. [1,2)D.[2,)+∞【答案】A 【解析】{10}{1}(,1)M x x x x =->=<=-∞，U(,0][2,)N =-∞+∞，∴U (){0}MN x x =≤．3. 在等差数列{}n a 中,13a =,1033a a =,则{}n a 的前12项和12S =（ ）A. 120B. 132C. 144D.168【答案】D 【解析】∵13a =,1033a a =，∴1193(2)a d a d +=+，∴2d =．∴12121112321682S ⨯=⨯+⨯=．4. 曲线C :ln y x x =在点(e,e)M 处的切线方程为（ ）A. e y x =-B. e y x =+C. 2e y x =-D.2e y x =+【答案】C【解析】∵ln y x x =，∴ln 1y x '=+，∴ln 12k e =+=，∴切线方程为2()y e x e -=-，即2e y x =-．5. 设变量,x y 满足10020015x y x y y -≤⎧⎪≤+≤⎨⎪≤≤⎩,则23x y +的最大值为（ ）A. 20B. 35C. 45D. 55 【答案】D6. 已知()sin(2)f x x ϕ=+的图像向右平移12π个单位后得到函数()g x 的图像,则“函数()g x 的图像关于点(,0)6π中心对称”是“6πϕ=-”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件 【答案】B【解析】()sin(2)6g x x πϕ=-+．∵函数()g x 的图像关于点(,0)6π中心对称， ∴266k ππϕπ⨯-+=，k Z ∈．∴6k πϕπ=-，k Z ∈，故选B ．7．已知函数22()ln(e 1)1x f x x x =+-+,()2f a =,则()f a -的值为（ ） A. 1 B. 0 C. 1- D. 2- 【答案】B【解析】2222()()ln(e1)1[ln(e 1)()1]xx f x f x x x x x -+-=+-++-+--+222[ln(e 1)ln(e 1)]22x x x x -=+-+-+22222e 1ln 22ln e 22e 1x x x x x x x -+=-+=-++222222x x =-+=，∴()()2f a f a +-=．∵()2f a =，∴()2()0f a f a -=-=．8．已知sin cos 5θθ+=,则tan()4πθ+=（ ）A. 12B. 2C. 12±D. 2±【答案】D【解析】∵sin cos θθ+=，∴sin()4πθ+=．∴cos()45πθ+==±，∴sin()4tan()24cos()4πθπθπθ++==±+．9．若图的框图所给的程序运行结果为20S =,k （ ）A ．9k =？B ．8k ≤？C ．8k <？D ．8k >？ 【答案】D【解析】由程序框图可知：10.,该几何体的外接球的表面积是（ ）A. 13πB. 16πC. 25πD.27π【答案】C【解析】该几何体为一个长方体，其中底面为正方体，且对角线长为4，高为3，5=． ∴外接球的直径25R =，∴外接球的表面积是2425R ππ=．11. 已知1F ,2F 分别是双曲线C :22221x y a b -=(0,0a b >>)的左右两个焦点,若在双曲线CS 1 11 20 k 109 8侧视图俯视图上存在点P 使1290F PF ∠=︒,且满足12212PF F PF F ∠=∠,那么双曲线C 的离心率为（ ）1 B.2 C. D. 2【答案】A 【解析】设2PF m=，则12PF a m=+．1290F PF ∠=︒,12212PF F PF F ∠=∠，∴1230PF F ∠=，∴21212PF F F c ==，∴12PF a c =+．∵2221212PF PF F F +=，∴222(2)(2)a c c c ++=，∴22220c ac a --=，∴2220e e --=，∴212e +==．12.若函数()2e ln()e 2x x f x x m =++-存在正的零点,则实数m 的取值范围为（ ）A. (-∞B. )+∞C. (,e)-∞D. (e,)+∞ 【答案】A【解析】令2e ln()e 20x x x m ++-=， ∴1111ln()()e 22x xx m e +=-=-.∵11()2x y e =-过点1(0,)2，且单调减函数． ∴0x >时，111()22x y e =-<． 问题等价于1ln()2y x m =+<，0x >恒成立．∵ln()y x m =+在(0,)+∞上为增函数，∴1ln 2m <，m <二、填空题:本大题共4小题,每小题5分,满分20分.13.从某班5位老师中随机选两位老师值班,有女老师被选中的概率为710,则在这5位老师中,女老师有_______人. 【答案】2【解析】假设女老师有1人，则女老师被选中的概率为410，不合题意. 假设女老师有2人，通过列举便知有女老师被选中的概率为710．14.在ABC ∆中,A 、B 、C 的对边分别是c b a ,,,且B b cos 是A c C a cos ,cos 的等差中项,则B 的大小为_______.【答案】3π【解析】∵B b cos 是A c C a cos ,cos 的等差中项， ∴2cos cos cos b B a C c A =+，∴2sin cos sin cos sin cos sin()sin B B A C C A A C B =+=+=，∵0B π<<，∴sin 0B >，∴1cos 2B =，∴3B π=．15.抛物线C :24y x =上到直线l :y x =距离为2的点的个数为________. 【答案】3【解析】设满足条件的点的坐标为2(,)4t t ，∴点2(,)4t t 直线l :y x =2=，∴214t t -=，或214t t -=-．由214t t -=，得2440t t --=，∴2t =±由214t t -=-，得2440t t -+=，∴4t =．16.在等腰直角ABC ∆中,90ABC ∠=︒,2AB BC ==,M 、N 为AC 边上两个动点,且满足MN =则BM BN ⋅的取值范围为________.【答案】3[,2]2【解析】以A 为原点建立直角坐标系，如图则B，设(,0)(0M x x ≤≤，∵MN =(N x +，∴4(1,4)AB AC AP ABAC=+=，即(1,4)P∴((,BM BN x x ⋅=-⋅22x =+23(22x =-+．∵0x ≤≤3[,2]2BM BN ⋅∈．三、解答题:本大题共6小题,共70分,解答须写出必要的文字说明、证明过程或演算步骤. 17.(本小题满分12分) 已知数列{}n a 的前n 项和为nS ,且满足21n n a S =-(*n ∈N ).（1）求证:数列{}n a 为等比数列； （2）若(21)n n b n a =+,求{}n b 的前n 项和nT . 【解析】（1）当1n =时,1112121a S a =-=-,解得11a =. ……1分当2n ≥时,21n n a S =-，1121n n a S --=-，两式相减得12n n na a a --=，∴1n n a a -=-， ……3分∴数列{}n a 是首项为1,公比为1-的等比数列. ……5分（2）由（1）可得1(1)n n a -=-，∴1(21)(1)n n b n -=+⋅-. ……6分01213(1)5(1)7(1)(21)(1)n n T n -=⋅-+⋅-+⋅-+++⋅-1213(1)5(1)(21)(1)(21)(1)n nn T n n --=⋅-+⋅-++-⋅-++⋅-， ……8分两式相减得121232(1)2(1)2(1)(21)(1)n nn T n -=+⋅-+⋅-++⋅--+⋅-……9分1[1(1)]32(21)(1)1(1)n nn ----=+⨯-+⋅---……10分1(22)(1)2n n -=+⋅-+. ……11分∴数列{}n b 的前n 项和n T 1(1)(1)1n n -=+⋅-+. ……12分18.(本小题满分12分)某射击爱好者想提高自己的射击水平,制订了一个训练计划,为了了解训练效果,执行训练计划前射击了10发子弹(每发满分为10.9环),计算出成绩中位数为9.65环,总成绩为95.1环,成绩标准差为1.09环,执行训练计划后也射击了10发子弹,射击成绩茎叶图如图所示: （1）请计算该射击爱好者执行训练计划后射击成绩的中位数、总成绩与标准差； （2）如果仅从已知的前后两次射击的数据分析,你认为训练计划对该射击爱好者射击水平的提高有无帮助？为什么？【解析】（1）训练后成绩中位数为9.69.79.652+=环, (1)分总成绩为7.88.89.09.39.69.79.89.810.410.895+++++++++=环， ……3分 平均成绩为9.49环. ……4分 方差为2222222222( 1.7)(0.7)(0.5)(0.2)0.10.20.30.30.9 1.30.6410-+-+-+-++++++=,标准差为0.8环. ……7分 （2）中位数与总成绩训练前相同,888673408810.9.8.7.>,总成绩训练前都比训练后大,∵95.195而这是衡量一个人平均射击水平的主要指标, ......9分可见训练前的平均水平还比训练后的平均水平要好, (11)分故此训练计划对该射击爱好者射击水平的提高没有帮助. (12)分【答案二】尽管总成绩训练后都比训练前稍小,但相差并不大,并无显著差异, ……9分<,训练后的标准差比训练前的标准差要小很多,而0.8 1.09成绩稳定性显著提高了,说明该射击爱好者心理素质更稳定了,这也是射击水平提高的表现. ……11分故此训练计划对该射击爱好者射击水平的提高有帮助. ……12分19.(本小题满分12分) 如图,三棱柱111ABC A B C -中,侧面11AA C C ⊥侧面11ABB A,1AC AA ==,1160AAC ∠=︒, 1AB AA ⊥,H 为棱1CC 的中点,D 为1BB的中点.（1）求证:1A D ⊥平面1AB H；（2）若AB =,求三棱柱111ABC A B C -的体积.【解析】（1）连结1AC ,∵1ACC ∆为正三角形,H 为棱1CC 的中点,∴1AH CC ⊥,从而1AH AA ⊥,又面11AAC C ⊥平面11ABB A ,面11AAC C平面11ABB A 1AA =,AH ⊂平面11AAC C ,∴AH ⊥平面11ABB A .又1A D ⊂平面11ABB A ,∴AH ⊥1A D①, ……2分设AB =,由1AC AA ==,∴12AC AA a ==,1DB a=,111111DB A B B A AA ==,又111190DB A B A A ∠=∠=︒,∴11A DB ∆∽11AB A ∆,∴1111B AA B A D∠=∠,A 1B 1C 1ACBDHHDBCAC 1B 1A 1M又11190B A D AA D ∠+∠=︒,∴11190B AA AA D ∠+∠=︒,设11AB A D O =,则11A D AB ⊥…②, ……5分由①②及1AB AH A=,可得1A D ⊥平面1AB H. ……6分（2）方法一:取1AA 中点M ,连结1C M ,则1//C M AH,∴1C M ⊥面11ABB A . ……7分∴11111111333C AB A AB A V S C M -∆=⋅==, ……10分∴三棱柱111ABC A B C -的体积为1113C AB A V -= ……12分20.(本小题满分12分)已知椭圆Γ的中心在原点，焦点在x 轴，焦距为2倍. （1）求椭圆Γ的标准方程；（2）设(2,0)P ,过椭圆Γ左焦点F 的直线l 交Γ于A 、B 两点,若对满足条件的任意直线l ,不等式PA PB λ⋅≤(λ∈R )恒成立,求λ的最小值.【解析】（1）依题意,2221a c abc ⎧=⎪=⎨⎪=+⎩, ……1分解得22a =,21b =,∴椭圆Γ的标准方程为2212x y +=. ……3分（2）设1122(,),(,)A x yB x y ,∴11221212(2,)(2,)(2)(2)PA PB x y x y x x y y ⋅=-⋅-=--+,当直线l 垂直于x 轴时,121x x ==-,12y y =-且2112y =,此时1(3,)PA y =-,21(3,)(3,)PB y y =-=--,∴22117(3)2PA PB y ⋅=--=. ……6分当直线l 不垂直于x 轴时,设直线l :(1)y k x =+,由22(1)22y k x x y =+⎧⎨+=⎩,得2222(12)4220k x k x k +++-=, ∴2122412k x x k +=-+,21222212k x x k -=+, ……8分∴21212122()4(1)(1)PA PB x x x x k x x ⋅=-+++++ 2221212(1)(2)()4k x x k x x k =++-+++2222222224(1)(2)41212k k k k k k k -=+⋅--⋅++++2217221k k +==+217131722(21)2k -<+. ……11分 要使不等式PA PB λ⋅≤(λ∈R )恒成立,只需max 17()2PA PB λ≥⋅=,即λ的最小值为172. ……12分21.(本小题满分12分)设常数0a >,函数2()ln 1x f x a xx =-+.（1）当34a =时,求()f x 的最小值；（2）求证：()f x 有唯一的极值点.【解析】（1）222(1)()(1)x x x a f x x x +-'=-+322(2)2(1)x a x ax ax x +---=+， ……2分 当34a =时,322224563(1)(493)()4(1)4(1)x x x x x x f x x x x x +---++'==++， ……4分 由于0x >时,2249304(1)x x x x ++>+,故当01x <<时,()0f x '<,()f x 递减,当1x >时,()0f x '>, ()f x 递增,即当1x =时, ()f x 取极小值即最小值1(1)2f =. ……6分（2）由（1）知322(2)2()(1)x a x ax af x x x +---'=+,令32()(2)2g x x a x ax a =+---, 要证()f x 有唯一的极值点,即证()g x 在(0,)+∞上有唯一的变号零点. ……7分事实上,2()3(42)2g x x a x a '=+--,令()0g x '=,解得1x =,2x =.……9分其中10x <,20x >.∵(0)20g a '=-<,且()g x '的图像是开口向上的抛物线,故在区间2(0,)x 上,()0g x '<,()g x 递减,∴()()200g x g a <=-<,在区间2(,)x +∞上,()0g x '>,()g x 递增,∵32()(2)2g x x a x ax a =+---2()2()x x a x x a a =-+--, ∴22(1)(1)2(1)(1)20g a a a a a a +=+++-=+++>, ∴2()(1)0g x g a ⋅+<,即()g x 在(0,)+∞上有唯一零点.即()f x 在(0,)+∞上有唯一的极值点,且为极小值点. ……12分请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清楚题号.22.(本小题满分10分)选修41-:几何证明选讲如图,四边形ABCD 是圆内接四边形,BA 、CD 的延长线交于点P ,且AB AD =,2BP BC =.（1）求证:2PD AB =；（2）当2BC =,5PC =时,求AB 的长. 【解析】（1）∵四边形ABCD 是圆内接四边形,∴PAD PCB ∠=∠, ……1分 又APD CPB ∠=∠,∴APD ∆∽CPB ∆,PD ADPB CB =, ……3分 而2BP BC =,∴2PD AD =,又AB AD =,∴2PD AB =. ……5分 （2）依题意24BP BC ==,设AB t =,由割线定理得PD PC PA PB ⋅=⋅, ……7分即25(4)4t t ⨯=-⨯,解得87t =,即AB 的长为87. ……10分23.(本小题满分10分)选修44-:坐标系与参数方程选讲已知直线l 的方程为4y x =+,圆C 的参数方程为2cos 22sin x y θθ=⎧⎨=+⎩(θ为参数),以原点为极点,x 轴正半轴为极轴,建立极坐标系. （1）求直线l 与圆C 的交点的极坐标；（2）若P 为圆C 上的动点,求P 到直线l 的距离d 的最大值.【解析】（1）直线l :4y x =+,圆C :22(2)4x y +-=, ……1分 由224(2)4y x x y =+⎧⎨+-=⎩,解得22x y =-⎧⎨=⎩或04x y =⎧⎨=⎩, ……3分 PABCD对应的极坐标分别为3)4π,(4,)2π. ……5分（2）[方法1]设(2cos ,22sin )P θθ+,则)14d πθ==++,当cos()14πθ+=时,d取得最大值2+ ……10分[方法2]圆心(0,2)C 到直线l=,圆的半径为2,∴P 到直线l 的距离d的最大值为2 ……10分24.(本小题满分10分)选修45-:不等式选讲 已知函数()2f x x a =-+,()4g x x =+,其中a ∈R .（1）解不等式()()f x g x a <+；（2）任意x ∈R ,2()()f x g x a +>恒成立,求a 的取值范围.【解析】（1）不等式()()f x g x a <+， 即24x x -<+， ……2分两边平方得2244816x x x x -+<++,解得1x >-, ∴原不等式的解集为()1,-+∞. ……5分（2）不等式2()()f x g x a +>，可化为224a a x x -<-++, ……7分又()()24246x x x x -++≥--+=,∴26a a -<,解得23a -<<,∴a 的取值范围为()2,3-. ……10分。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2015年佛山市普通高中高三教学质量检测（一）数 学（文科） 2015.1本试卷共4页,21小题,满分150分.考试时间120分钟. 注意事项:1．答卷前,考生务必填写答题卷上的有关项目．2．选择题每小题选出答案后,用2B 铅笔把答案涂在答题卷相应的位置上．3．非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内；如需改动,先划掉原来的答案,然后再写上新的答案；不准使用铅笔和涂改液,不按以上要求作答的答案无效．4．请考生保持答题卷的整洁.考试结束后,将答题卷交回. 参考公式: 锥体的体积公式13V Sh =,其中S 为柱体的底面积,h 为锥体的高. 一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．复数i1i3++等于( ) A ．i 21+B ．i 21-C ．i 2-D ．i 2+2．已知集合{}02M x x =∈<<R ,{}1N x x =∈>R ,则()R MN =ð( )A ．[)1,2B ．()1,2C ．[)0,1D ．(]0,13．若函数42x xay +=的图象关于原点对称,则实数a 等于( ) A ．2- B ．1- C ．1 D ．24．已知x ,y 满足不等式组282800x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩,则目标函数3z x y =+的最大值为( )A ．12B ．24C ．8D ．3325．已知两个单位向量12,e e 的夹角为45︒,且满足()121λ⊥-e e e ,则实数λ的值是( )A ．1 BCD ．2 6．在空间中，有如下四个命题： ①平行于同一个平面的两条直线是平行直线；②垂直于同一条直线的两个平面是平行平面；③若平面α内有不共线的三个点到平面β距离相等，则α∥β； ④过平面α的一条斜线有且只有一个平面与平面α垂直. 其中正确的两个命题是( )A ．①③B ．②④C ．①④D ．②③7．某校高三年级学生会主席团有共有5名同学组成,其中有3名同学来自同一班级,另外两名同学来自另两个不同班级.现从中随机选出两名同学参加会议,则两名选出的同学来自不同班级的概率为( )A ．0.35B ．0.4C ．0.6D ．0.78. 已知双曲线221169x y -=的左、右焦点分别为1F ,2F ,过2F 的直线与该双曲线的右支交于A 、B 两点,若5=AB ,则1ABF ∆的周长为( )A ．16B ．20C ．21D ．26 9．已知()2f x x x =-,且a ,b ∈R ,则“1a b >>”是“()()f a f b <”的( )A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件10．有10个乒乓球,将它们任意分成两堆,求出这两堆乒乓球个数的乘积,再将每堆乒乓球任意分成两堆并求出这两堆乒乓球个数的乘积,如此下去,直到不能再分为止,则所有乘积的和为( ) A . 45 B . 55 C . 90 D . 100 二、填空题：本大共5小题，考生作答4小题，每小题5分，满分20分． (一)必做题(11～13题)11．如果()1,10,1x f x x ì£ïï=íï>ïî,那么()2f f =⎡⎤⎣⎦ . 12．已知点()2,0A -、()0,4B 到直线l :10x my +-=的距离相等,则m 的值为 . 13. 如图1,为了测量河对岸A 、B 两点之间的距离,观察者找到一个点C ,从C 点可以观察到点A 、B ；找到一个点D ,从D 点可以观察到点A 、C ；找到一个点E ,从E 点可以观察到点B 、C ；并测量得到一些数据:2CD =,CE =45D ∠=︒,105ACD ∠=︒,48.19ACB ∠=︒,75BCE ∠=︒,E ∠=60︒,则A 、B 两点之间的距离为_________.(其中cos 48.19︒取近似值23)C图1O DCA MP B图22013年11月份AQI 数据频率分布直方图2014年11月份AQI 数据频率分布直方图频率组距(二)选做题(14～15题，考生只能从中选做一题)14.(几何证明选讲)如图2,P 是圆O 外一点,PA 、PB 是圆O 的两条切线,切点分别为A 、B ,PA 中点为M ,过M 作圆O 的一条割线交圆O 于C 、D 两点,若PB =,1MC =,则CD = .15.(坐标系与参数方程)在极坐标系中,曲线1C :)sin 1ρθθ+=与曲线2C :a ρ=(0a >)的一个交点在极轴上,则a =______.三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤． 16.(本小题满分12分)已知函数()sin 4f x x πω⎛⎫=- ⎪⎝⎭(0ω>),x ∈R 的最小正周期为π.(Ⅰ) 求6f π⎛⎫⎪⎝⎭； (Ⅱ) 在图3给定的平面直角坐标系中,画出函数()y f x =在区间,22ππ⎡⎤-⎢⎥⎣⎦上的图像,并根据图象写出其在,22ππ⎛⎫- ⎪⎝⎭17.(本小题满分12分)某地区“腾笼换鸟”的政策促进了区内环境改善和产业转型,空气质量也有所改观,现从当地天气网站上收集该地区近两年11月份(30天)的空气质量指数(AQI )(单位:3g /m μ)资料如下:(Ⅰ) 请填好2014年11月份AQI 数据的频率分布表．．．．．并完成频率分布直方图．．．．．．．； 图3表1PABC DM图6(Ⅱ) 该地区环保部门2014年12月1日发布的11月份环评报告中声称该地区“比去年同期空气质量的优良率提高了20多个百分点”(当AQI 100<时,空气质量为优良).试问此人收集到的资料信息是否支持该观点?18.(本小题满分14分)如图6,四棱锥P ABCD -,侧面PAD 是边长为2的正三角形,且与底面垂直,底面ABCD 是60ABC ∠=︒的菱形,M 为PC 的中点.(Ⅰ) 求证:PC AD ⊥；(Ⅱ) 在棱PB 上是否存在一点Q ,使得,,,A Q M D 四点共面?若存在,指出点Q 的位置并证明；若不存在,请说明理由；(Ⅲ) 求点D 到平面PAM 的距离.19.(本小题满分14分)已知数列{}n a 的前n 项和为n S ,若()14211n n S n a +=-+(*n ∈N ),且11=a .(Ⅰ) 求证：数列{}n a 为等差数列； (Ⅱ) 设n b =数列{}n b 的前n 项和为n T ,证明:32n T <(*n ∈N ).20.(本小题满分14分)已知点()2,1M ,()2,1N -,直线MP ,NP 相交于点P ,且直线MP 的斜率减直线NP 的斜率的差为1.设点P 的轨迹为曲线E . (Ⅰ) 求E 的方程；(Ⅱ) 已知点()0,1A ,点C 是曲线E 上异于原点的任意一点,若以A 为圆心,线段AC 为半径的圆交y 轴负半轴于点B ,试判断直线BC 与曲线E 的位置关系,并证明你的结论.21.(本小题满分14分)设函数()e xf x x a=-的导函数为()f x '(a 为常数,e 2.71828=⋅⋅⋅是自然对数的底数).(Ⅰ) 讨论函数()f x 的单调性；(Ⅱ) 求实数a ,使曲线()y f x =在点()()2,2a f a ++处的切线斜率为3261274a a a +++-；(Ⅲ) 当x a ≠时,若不等式()()1f x k x a f x '+-≥恒成立,求实数k 的取值范围. 2015年佛山市普通高中高三教学质量检测（一）数学试题（文科）参考答案和评分标准一、选择题：本大题共10小题，每小题5分，满分50分．[必做题] 11．1 12．112-或 13[选做题]14．215．三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤． 16.【解析】(Ⅰ)依题意得2ππω=,解得2ω=,所以()sin 24f x x π⎛⎫=- ⎪⎝⎭,………………2分 所以s i63f ππ⎛⎫=-⎪⎝⎭………4分(Ⅱ)因为2x ππ-≤≤,所以532x πππ-≤-≤,列表如下:……………………6分 ………8分8π3π2014年11月份AQI 数据频率分布直方图2014年11月份AQI 数据频率分布表PABCDM QO画出函数()y f x =在区间,ππ⎡⎤-上的图像如图所示! 由图象可知函数()y f x =在,22- ⎪⎝⎭上的单调递减区间为,28-- ⎪⎝⎭,,82 ⎪⎝⎭.…………12分17.【解析】(Ⅰ) 频率分布表(3分)；频率分布直方图(6分) (Ⅱ) 支持,理由如下:2013年11月的优良率为:119200.0050.0050.0150.010330⎛⎫⨯⨯+++= ⎪⎝⎭, …………8分2014年11月的优良率为:3026, …………9分 因此2619723.3%20%303030-=≈> …………11分 所以数据信息可支持“比去年同期空气质量的优良率提高了20多个百分点”.…………………12分18.【解析】(Ⅰ)方法一:取AD 中点O ,连结,,OP OC AC ,依题意可知△PAD ,△ACD 均为正三角形,所以OC AD ⊥,OP AD ⊥,又OCOP O =,OC ⊂平面POC ,OP ⊂平面POC ,所以AD ⊥平面POC ,又PC ⊂平面POC ,所以PC AD ⊥.………………4分 方法二:连结AC ,依题意可知△PAD ,△ACD 均为正三角形, 又M 为PC 的中点,所以AM PC ⊥,DM PC ⊥, 又AMDM M =,AM ⊂平面AMD ,DM ⊂平面AMD ,所以PC ⊥平面AMD ,又AD ⊂平面AMD ,所以PC AD ⊥.………………4分(Ⅱ)当点Q 为棱PB 的中点时,,,,A Q M D 四点共面,证明如下:………………6分 取棱PB 的中点Q ,连结QM ,QA ,又M 为PC 的中点,所以//QM BC ,在菱形ABCD 中//AD BC ,所以//QM AD ,所以,,,A Q M D 四点共面.………………8分 (Ⅲ)点D 到平面PAM 的距离即点D 到平面PAC 的距离, 由(Ⅰ)可知PO AD ⊥,又平面PAD ⊥平面ABCD ,平面PAD 平面ABCD AD =,PO ⊂平面PAD ,所以PO ⊥平面ABCD ,即PO 为三棱锥P ACD -的体高 (9)分在Rt POC ∆中,PO OC ==PC =,在PAC ∆中,2PA AC ==,PC =边PC 上的高AM ==,所以PAC ∆的面积1122PAC S PC AM ∆=⋅==,………………10分 设点D 到平面PAC 的距离为h ,由D PAC P ACD V V --=得………………11分1133PAC ACD S h S PO ∆∆⋅=⋅,又224ACD S ∆==所以11323h ⨯=………13分解得h =,所以点D 到平面PAM ………………14分 19.【解析】(Ⅰ) 由题设()14211n n S n a +=-+,则21413a S =-=，3234115,a S =-=35a =. 当2n ≥时，()14231n n S n a -=-+,两式相减得()()12121n n n a n a ++=-, ……………………………………2分方法一：由()()12121n n n a n a ++=-，得12121n n a a n n +=+-，且2131a a=. 则数列21n a n ⎧⎫⎨⎬-⎩⎭是常数列，即1121211n a a n ==-⨯-，也即21n a n =- ……………………………6分所以数列{}n a 是首项为1,公差为2的等差数列 ………………………………………7分方法二：由()()12121n n n a n a ++=-，得()()122321n n n a n a +++=+， 两式相减得212n n n a a a +++=,且1322a a a += ……………………………………6分所以数列{}n a 等差数列. ………………………………………7分 (Ⅱ) 由(Ⅰ)得12-=n a n ,()21212n n n S n +-==,()121n b n n =-,…………9分当1=n 时,1312T =<成立；…………………………………………………10分 当2n ≥时,()()111111*********n b n n n n n n n n ⎛⎫==<=- ⎪---⎛⎫⎝⎭- ⎪⎝⎭…………12分所以1111111122231n T n n ⎡⎤⎛⎫⎛⎫⎛⎫<+-+-++- ⎪ ⎪ ⎪⎢⎥-⎝⎭⎝⎭⎝⎭⎣⎦1113111222n ⎛⎫=+-<+= ⎪⎝⎭综上所述,命题得证.………………………………………………………………………………14分 20.【解析】(Ⅰ)设(),P x y ,依题意得11122y y x x ---=-+, ……………………3分 化简得24x y=(2x ≠±),所以曲线E的方程为24x y =(2x ≠±). …………………5分(Ⅱ) 结论:直线BC 与曲线E 相切. 证法一:设()00,C x y ,则2004x y =,圆A的方程为()()22220011x y x y +-=+-, ……………7分 令0x =,则,()()()2222000111y x y y -=+-=+,因为00,0y y ><,所以y y =-,点B的坐标为()00,y -, ………………………………………9分直线BC 的斜率为002y k x =,直线BC 的方程为0002y y y x x +=,即0002yy x y x =-,……………11分代入24x y =得200024y x x y x ⎛⎫=-⎪⎝⎭,即20000840x x y x x y -+=,……………13分 ()22000000064441640y x x y y y x ∆=-⋅=-=,所以,直线BC 与曲线E 相切.……………………………………………………………14分证法二:设()00,C x y ,则2004x y =,圆A 的方程为()()22220011x y x y +-=+-,……………7分 令0x =,则,()()()2222000111y x y y -=+-=+,因为00,0y y ><,所以0y y =-,点B 的坐标为()00,y -,………………………………………9分直线BC 的斜率为02y k x =,…………………………………10分由24x y =得214y x =得12y x '=,过点C 的切线的斜率为1012k x =,……………12分 而200000122142x y k x x x ⨯===,所以1k k =,……………13分 所以直线BC 与曲线24x y =过点C 的切线重合,即直线BC 与曲线E 相切.…………………………………………………………14分 21.【解析】(Ⅰ)函数()f x 的定义域是()(),,a a -∞+∞,…………………………1分对()f x 求导得:()()()2e 1x x af x x a --'=-,…………………2分由()0f x '>得1x a >+；由()0f x '<得x a <或1a x a <<+,…………………4分 所以()f x 在(),a -∞,(),1a a +上单调递减,在()1,a ++∞上单调递增.…………………5分(Ⅱ)由(Ⅰ)得()2e 24af a +'+=……………………………………6分令232641274a a e a a ++++-=得 32261270a a a a e +++++=………① 令2a t +=,则有310te t +-=,……………………………8分令()31th t e t =+-,则()203th t e t '=+>,……………………………9分故()h t 是R 上的增函数,又()00h =,因此0是()h t 的唯一零点,即2-是方程①的唯一实数解, 故存在唯一实数2a =-满足题设条件.…………………………………………………………10分(Ⅲ)因为()()1f x x a f x x a '--=-,故不等式()()1f x k x a f x '+-≥可化为11x a k x a x a--+-≥-, 令x a t -=,则0t ≠,……………………………11分 且有111k t t≥-- ………12分 ① 若0t <,则1kt t -≥,即21k t≥-,此时0k ≥； ② 若01t <≤,则12kt t ≥-,即2221111k t t t ⎛⎫≥-=--+ ⎪⎝⎭,此时1k ≥；③ 若1t >,则1kt t ≥,即21k t≥,此时1k ≥. 故使不等式恒成立的k 的取值范围是[)1,+∞.………………………………………………14分。