实验3 多元线性回归模型
《计量经济学》eviews实验报告多元线性回归模型

2013
517.11
1316.34
40321
2014
530.83
1333.4
43910
要求:
(1)试建立二元线性回归销售模型。
(2)考虑北京地区有人口万人,人均年收入为元,试北京市汽车拥有量做出预测。
二、实验目的
掌握多元线性回归模型的原理,多元线性回归模型的建立、估计、检验及预测的方法,以及相应的EViews软件操作方法。
x2t(人均收入)
2000
104.12
1113.53
10349.7
2001
114.47
1127.89
11577.8
2002
133.93
1142.83
12463.9
2003
163.07
1154.06
13882.6
2003
182.42
1167.76
15637.8
2005
182.42
1184.14
17653
三、实验步骤(简要写明实验步骤)
(1)建立二元线性回归销售模型
(2)预测
在上方输入ls y c x3 x4回车得到下图
在回归方程中有Forecast,残差立为yfse,点击ok后自动得到下图
在上方空白处输入ls y c x3 x4---之后点击proc中的forcase中se输入yfse点击ok得到2015预测值
《计量经济学》实验报告多元线性回归模型
一、实验内容
建立2000-2014年北京市民用汽车拥有量模型。
调查北京市民用汽车拥有量数据见表1。观测变量分别是民用汽车拥有量yt(万辆),北京市年末人口数x1t(万人)和城镇人均可支配收入x2t(千元)。
3 多元线性回归模型(经典模型,举一反三)

样本回归函数的矩阵表达:
ˆ ˆ Y Xβ
或
e1 e e 2 e n
ˆ Y Xβ e
其中:
ˆ 0 ˆ ˆ 1 β ˆ k
二、多元线性回归模型的基本假定
假设1,解释变量是非随机的或固定的,且各 X之间互不相关(无多重共线性)。
表示:各变量X值固定时Y的平均响应。
j也被称为偏回归系数,表示在其他解释变
量保持不变的情况下,X j每变化1个单位时,Y的 均值E(Y)的变化; 或者说j给出了X j的单位变化对Y均值的 “直接”或“净”(不含其他变量)影响。
其中
Y Xβ μ
总体回归模型n个随机方程的矩阵表达式为:
1 1 X 1
五、样本容量问题
⒈ 最小样本容量 所谓“最小样本容量”,即从最小二乘原理 和最大或然原理出发,欲得到参数估计量,不管 其质量如何,所要求的样本容量的下限。 样本最小容量必须不少于模型中解释变量 的数目(包括常数项),即 n ≥ k+1
因为,无多重共线性要求:秩(X)=k+1
可求得: ( X X) 于是:
1
0.0003 0.7226 0.0003 1.35 E 07
103 .172 0.7770
ˆ 1 0.7226 0.0003 15674 ˆ β ˆ 2 0.0003 1.35 E 07 39648400
Yi 0 1 X 1i 2 X 2 i k X ki i
也被称为总体回归函数的随机表达形式。它 的 非随机表达式为:
03多元线性回归模型

03多元线性回归模型多元线性回归模型是一种经济学和统计学中广泛使用的模型,用于描述多个自变量与因变量之间的关系。
它是在线性回归模型的基础上发展而来的。
在多元线性回归模型中,因变量是由多个自变量共同决定的。
Y = β0 + β1X1 + β2X2 + β3X3 + … + βkXk + ε其中,Y表示因变量,X1、X2、X3等表示自变量,β0、β1、β2、β3等表示回归系数,ε表示误差项。
回归系数β0、β1、β2、β3等表示自变量对因变量的影响程度。
回归系数的符号和大小反映着自变量与因变量的正相关或负相关程度以及影响的大小。
误差项ε是对影响因变量的所有其他变量的影响程度的度量,它是按照正态分布随机生成的。
在多元线性回归模型中,回归系数和误差项都是未知的,需要根据样本数据进行估计。
通常采用最小二乘法来估计回归系数和误差项。
最小二乘法是一种常用的方法,它通过最小化误差平方和来估计回归系数与误差项。
最小二乘法假设误差为正态分布,且各自变量与误差无关。
因此,通过最小二乘法求解出的回归系数可以用于预测新数据。
多元线性回归模型还需要检验回归系数的显著性。
通常采用F检验和t检验来进行检验。
F检验是用于检验整个多元线性回归模型的显著性,即检验模型中所有自变量是否与因变量有关系。
F检验的原假设是回归方程中所有回归系数都为0,备择假设是至少有一个回归系数不为0。
如果p-value小于显著性水平,就可以拒绝原假设,认为多元线性回归模型显著。
总之,多元线性回归模型利用多个自变量来解释因变量的变化,是一种实用性强的模型。
它的参数估计和显著性检验方法也相对比较成熟,可以用于多个领域的实际问题分析。
3多元线性回归模型参数估计

3多元线性回归模型参数估计多元线性回归是一种用于预测多个自变量与因变量之间关系的统计模型。
其模型形式为:Y=β0+β1X1+β2X2+...+βnXn+ε,其中Y是因变量,X1、X2、..、Xn是自变量,β0、β1、β2、..、βn是模型的参数,ε是误差项。
多元线性回归模型参数的估计可以使用最小二乘法(Ordinary Least Squares,OLS)来进行。
最小二乘法的基本思想是找到一组参数估计值,使得模型预测值与实际观测值之间的平方差最小。
参数估计过程如下:1.根据已有数据收集或实验,获取因变量Y和自变量X1、X2、..、Xn的观测值。
2.假设模型为线性关系,即Y=β0+β1X1+β2X2+...+βnXn+ε。
3.使用最小二乘法,计算参数估计值β0、β1、β2、..、βn:对于任意一组参数估计值β0、β1、β2、..、βn,计算出模型对于所有观测值的预测值Y'=β0+β1X1+β2X2+...+βnXn。
计算观测值Y与预测值Y'之间的平方差的和,即残差平方和(RSS,Residual Sum of Squares)。
寻找使得RSS最小的参数估计值β0、β1、β2、..、βn。
4.使用统计方法计算参数估计值的显著性:计算回归平方和(Total Sum of Squares, TSS)和残差平方和(Residual Sum of Squares, RSS)。
计算决定系数(Coefficient of Determination, R^2):R^2 = (TSS - RSS) / TSS。
计算F统计量:F=(R^2/k)/((1-R^2)/(n-k-1)),其中k为自变量的个数,n为观测值的个数。
根据F统计量的显著性,判断多元线性回归模型是否合理。
多元线性回归模型参数估计的准确性和显著性可以使用统计假设检验来判断。
常见的参数估计的显著性检验方法包括t检验和F检验。
t检验用于判断单个参数是否显著,F检验用于判断整个回归模型是否显著。
实验三_多元线性回归模型及非线性回归(1)

实验三_多元线性回归模型及⾮线性回归(1)实验三多元线性回归模型及⾮线性回归⼀、多元线性回归模型例题3.2.2 建⽴2006年中国城镇居民⼈均消费⽀出的多元线性回归模型。
数据:地区 2006年消费⽀出Y 2006年可⽀配收⼊X12005年消费⽀出X2北京 14825.41 19977.52 13244.2 天津 10548.05 14283.09 9653.3 河北 7343.49 10304.56 6699.7 ⼭西 7170.94 10027.70 6342.6 内蒙古 7666.61 10357.99 6928.6 辽宁 7987.49 10369.61 7369.3 吉林 7352.64 9775.07 6794.7 ⿊龙江 6655.43 9182.31 6178.0 上海 14761.75 20667.91 13773.4 江苏 9628.59 14084.26 8621.8 浙江 13348.51 18265.10 12253.7 安徽7294.73 9771.05 6367.7 福建 9807.71 13753.28 8794.4 江西 6645.54 9551.12 6109.4 ⼭东 8468.40 12192.24 7457.3 河南6685.18 9810.26 6038.0 湖北 7397.32 9802.65 6736.6 湖南 8169.30 10504.67 7505.0 ⼴东 12432.22 16105.58 11809.9 ⼴西 6791.95 9898.75 7032.8 海南 7126.78 9395.13 5928.8 重庆 9398.69 11569.74 8623.3 四川 7524.81 9350.11 6891.3 贵州6848.39 9116.61 6159.3 云南 7379.81 10069.89 6996.9 西藏 6192.57 8941.08 8617.1 陕西 7553.28 9267.70 6656.5 ⽢肃6974.21 8920.59 6529.2 青海 6530.11 9000.35 6245.3 宁夏 7205.57 9177.26 6404.3 新疆 6730.018871.276207.51、建⽴模型01122Y X X βββµ=+++2、估计模型(1)录⼊数据打开EViews6,点“File ”→“New ”→“Workfile ”选择“Unstructured/Undated”,在Observations 后输⼊31,如下所⽰:点“ok”。
多元线性回归模型实验报告
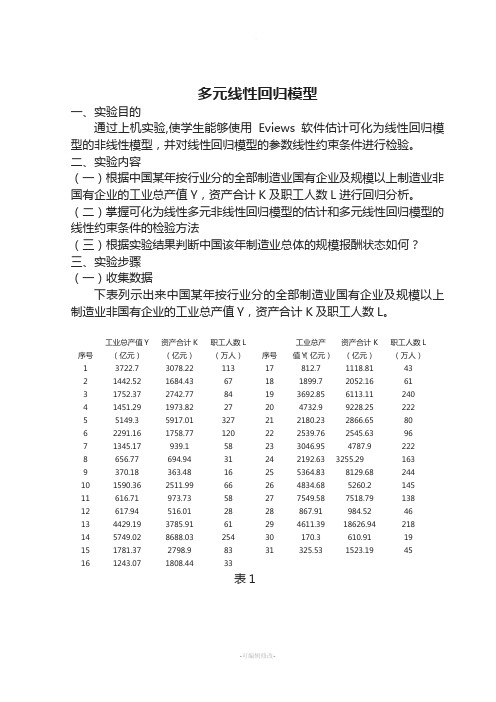
多元线性回归模型一、实验目的通过上机实验,使学生能够使用Eviews 软件估计可化为线性回归模型的非线性模型,并对线性回归模型的参数线性约束条件进行检验。
二、实验内容(一)根据中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y,资产合计K及职工人数L进行回归分析。
(二)掌握可化为线性多元非线性回归模型的估计和多元线性回归模型的线性约束条件的检验方法(三)根据实验结果判断中国该年制造业总体的规模报酬状态如何?三、实验步骤(一)收集数据下表列示出来中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y,资产合计K及职工人数L。
序号工业总产值Y(亿元)资产合计K(亿元)职工人数L(万人)序号工业总产值Y(亿元)资产合计K(亿元)职工人数L(万人)1 3722.7 3078.22 113 17 812.7 1118.81 432 1442.52 1684.43 67 18 1899.7 2052.16 613 1752.37 2742.77 84 19 3692.85 6113.11 2404 1451.29 1973.82 27 20 4732.9 9228.25 2225 5149.3 5917.01 327 21 2180.23 2866.65 806 2291.16 1758.77 120 22 2539.76 2545.63 967 1345.17 939.1 58 23 3046.95 4787.9 2228 656.77 694.94 31 24 2192.63 3255.29 1639 370.18 363.48 16 25 5364.83 8129.68 24410 1590.36 2511.99 66 26 4834.68 5260.2 14511 616.71 973.73 58 27 7549.58 7518.79 13812 617.94 516.01 28 28 867.91 984.52 4613 4429.19 3785.91 61 29 4611.39 18626.94 21814 5749.02 8688.03 254 30 170.3 610.91 1915 1781.37 2798.9 83 31 325.53 1523.19 4516 1243.07 1808.44 33表1(二)创建工作文件(Workfile)。
3多元线性回归模型参数估计

3多元线性回归模型参数估计多元线性回归是一种回归分析方法,用于建立多个自变量和一个因变量之间的关系模型。
多元线性回归模型可以表示为:Y=β0+β1X1+β2X2+…+βnXn+ε其中,Y表示因变量,X1,X2,…,Xn表示自变量,β0,β1,β2,…,βn表示模型参数,ε表示误差项。
多元线性回归模型的目标是估计出模型参数β0,β1,β2,…,βn,使得实际观测值与模型预测值之间的误差最小化。
参数估计的方法有很多,下面介绍两种常用的方法:最小二乘法和梯度下降法。
1. 最小二乘法(Ordinary Least Squares, OLS):最小二乘法是最常用的多元线性回归参数估计方法。
它的基本思想是找到一组参数估计值,使得模型预测值与实际观测值之间的残差平方和最小化。
首先,我们定义残差为每个观测值的实际值与模型预测值之间的差异:εi = Yi - (β0 + β1X1i + β2X2i + … + βnXni)其中,εi表示第i个观测值的残差,Yi表示第i个观测值的实际值,X1i, X2i, …, Xni表示第i个观测值的自变量,β0, β1, β2, …,βn表示参数估计值。
然后,我们定义残差平方和为所有观测值的残差平方的总和:RSS = ∑(Yi - (β0 + β1X1i + β2X2i + … + βnXni))^2我们的目标是找到一组参数估计值β0,β1,β2,…,βn,使得残差平方和最小化。
最小二乘法通过数学推导和求导等方法,可以得到参数估计值的解析解。
2. 梯度下降法(Gradient Descent):梯度下降法是一种迭代优化算法,可以用于估计多元线性回归模型的参数。
它的基本思想是通过迭代调整参数的值,使得目标函数逐渐收敛到最小值。
首先,我们定义目标函数为残差平方和:J(β) = 1/2m∑(Yi - (β0 + β1X1i + β2X2i + … + βnXni))^2其中,m表示样本数量。
多元线性回归模型实验报告

多元线性回归模型实验报告实验报告:多元线性回归模型1.实验目的多元线性回归模型是统计学中一种常用的分析方法,通过建立多个自变量和一个因变量之间的模型,来预测和解释因变量的变化。
本实验的目的是利用多元线性回归模型,分析多个自变量对于因变量的影响,并评估模型的准确性和可靠性。
2.实验原理多元线性回归模型的基本假设是自变量与因变量之间存在线性关系,误差项为服从正态分布的随机变量。
多元线性回归模型的表达形式为:Y=b0+b1X1+b2X2+...+bnXn+ε,其中Y表示因变量,X1、X2、..、Xn表示自变量,b0、b1、b2、..、bn表示回归系数,ε表示误差项。
3.实验步骤(1)数据收集:选择一组与研究对象相关的自变量和一个因变量,并收集相应的数据。
(2)数据预处理:对数据进行清洗和转换,排除异常值、缺失值和重复值等。
(3)模型建立:根据收集到的数据,建立多元线性回归模型,选择适当的自变量和回归系数。
(4)模型评估:通过计算回归方程的拟合优度、残差分析和回归系数的显著性等指标,评估模型的准确性和可靠性。
4.实验结果通过实验,我们建立了一个包含多个自变量的多元线性回归模型,并对该模型进行了评估。
通过计算回归方程的拟合优度,我们得到了一个较高的R方值,说明模型能够很好地拟合观测数据。
同时,通过残差分析,我们检查了模型的合理性,验证了模型中误差项的正态分布假设。
此外,我们还对回归系数进行了显著性检验,确保它们是对因变量有显著影响的。
5.实验结论多元线性回归模型可以通过引入多个自变量,来更全面地解释因变量的变化。
在实验中,我们建立了一个多元线性回归模型,并评估了模型的准确性和可靠性。
通过实验结果,我们得出结论:多元线性回归模型能够很好地解释因变量的变化,并且模型的拟合优度较高,可以用于预测和解释因变量的变异情况。
同时,我们还需注意到,多元线性回归模型的准确性和可靠性受到多个因素的影响,如样本大小、自变量的选择等,需要在实际应用中进行进一步的验证和调整。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验3 多元线性回归模型
一、实验名称:多元线性回归模型.
二、实验目的:掌握多元线性回归模型的建模方法,并会利用Matlab 作统计分析与检验. 三、实验题目:设某公司生产的商品在市场的销售价格为1x (元/件)、用于商品的广告费用为2x (万元)、销售量为y (万件)的连续12个月的统计数据如表.
月份 销售价格1x
广告费用2x
销售量y 1
100 5.50 55 2 90 6.30 70 3 80 7.20 90 4 70 7.00 100 5 70 6.30 90 6 70 7.35 105 7 70 5.60 80 8 65 7.15 110 9 60 7.50 125 10 60 6.90 115 11 55 7.15 130 12
50
6.50
130
四、实验要求:
1、建立销售量y 关于销售价格1x 和广告费用2x 的多元线性回归模型.
1、绘制散点图,可以直观地看出y 与x1,x2分别呈线性关系,所以采用多元线性回归模型:y=β0+β1*x1+β2*x2+ε 源程序: clear
x1=[100;90;80;70;70;70;70;65;60;60;55;50];
x2=[5.50;6.30;7.20;7.00;6.30;7.35;5.60;7.15;7.50;6.90;7.15;6.50]; y=[55;70;90;100;90;105;80;110;125;115;130;130]; X=[ones(size(x1)),x1,x2]; [b,bint,r,rint,stat]=regress(y,X) figure(1)
plot(x1,y,'k+',x2,y,'k*') axis([0,100,50,150])
title ('销售量y 关于销售价格x1和广告费用x2的多元线性回归模型') xlabel ('费用'),ylabel ('销售量')
legend ('+ 销售价格(元)','*广告费用(万元)') figure(2),rcoplot(r,rint) 调试结果:b =
116.1568
-1.3079
11.2459
bint =
60.4045 171.9090
-1.6005 -1.0152
4.9472 17.5446
r =
7.7782
0.7027
-2.4973
-3.3269
-5.4548
-2.2630
-7.5826
-1.5532
2.9714
-0.2811
5.3681
6.1385
rint =
2.0370 1
3.5194
-10.1081 11.5136
-13.0085 8.0138
-14.9338 8.2799
-16.3810 5.4714
-13.3901 8.8641
-14.9658 -0.1995
-13.2859 10.1796
-7.9467 13.8894
-12.0498 11.4877
-5.1699 15.9060
-2.3733 14.6504
stat = 0.9606 109.5892 0.0000 27.6100
有图像分析可知:第一个样本点和第七个样本点出现偏差,则剔除这两个点,重新编程:clear
x1=[100;90;80;70;70;70;70;65;60;60;55;50];
x2=[5.50;6.30;7.20;7.00;6.30;7.35;5.60;7.15;7.50;6.90;7.15;6.50];
y=[55;70;90;100;90;105;80;110;125;115;130;130];
x1(1)=[];x2(1)=[];y(1)=[];
x1(7)=[];x2(7)=[];y(7)=[];
X=[ones(10,1),x1,x2];
[b,bint,r,rint,stat]=regress(y,X)
figure(1)
plot(x1,y,'k+',x2,y,'k*')
axis([0,100,50,150])
title('销售量y关于销售价格x1和广告费用x2的多元线性回归模型')
xlabel('费用'),ylabel('销售量')
legend('+ 销售价格(元)','*广告费用(万元)')
figure(2),rcoplot(r,rint)
调试结果:
b =109.8882
-1.4831
13.8233
bint = 65.4833 154.2930
-1.7529 -1.2133
8.4229 19.2237
stat =0.9730 125.9368 0.0000 15.6544
根据下图图像分析,第一个样本数据还是异点数据,多次调试,重新编程:clear
x1=[100;90;80;70;70;70;70;65;60;60;55;50];
x2=[5.50;6.30;7.20;7.00;6.30;7.35;5.60;7.15;7.50;6.90;7.15;6.50];
y=[55;70;90;100;90;105;80;110;125;115;130;130];
x1(5)=[];x2(5)=[];y(5)=[];
x1(7)=[];x2(7)=[];y(7)=[];
X=[ones(10,1),x1,x2];
[b,bint,r,rint,stat]=regress(y,X)
figure(1)
plot(x1,y,'k+',x2,y,'k*')
axis([0,100,50,150])
title('销售量y关于销售价格x1和广告费用x2的多元线性回归模型') xlabel('费用'),ylabel('销售量')
legend('+ 销售价格(元)','*广告费用(万元)')
figure(2),rcoplot(r,rint)
调试结果:
b =111.1561
-1.4816
13.5915
bint =70.1011 152.2112
-1.7329 -1.2303
8.6470 18.5359
stat = 0.9721 139.1705 0.0000 14.2868
2、2、设第13个月将该商品的销售价格定为80元/件,广告费用为7万元,预计该商品的销售量将是多少?并对其作统计上的误差分析.
答:已知:x1=80,x2=7代入多元线性回归模型:
y=β0+β1*x1+β2*x2+ε
其中由上一小题得出:β0=111.1561,β1=-1.4816,β2=13.5915。
所以:y=111.1561-80*1.4816+13.5915*7= 87.7686(万件)
由上一小题得出:stat = 0.9721 139.1705 0.0000 14.2868
发现:F=139.1705较大,p=0.0000,远小于0.05,所以说明回归模型是显著;
由:bint =[70.1011 152.2112] [-1.7329 -1.2303] [8.6470 18.5359]回归系数的置信区间都不包含0,说明回归模型的自变量和截距两项对因变量的影响显著。
决定系数为0.9721接近1,说明回归模型的拟合精度较高。
3、利用Matlab画出回归曲线的图形.
源程序:
clear
x1=[100;90;80;70;70;70;70;65;60;60;55;50];
x2=[5.50;6.30;7.20;7.00;6.30;7.35;5.60;7.15;7.50;6.90;7.15;6.50];
y=111.1561-1.4816*x1+13.5915*x2;
plot(y,'r--')
title('销售量y回归曲线图形')
ylabel('销售量(万件)')
legend('销售量(万件)')
调试结果:。
