四年级奥数火车过桥问题完整讲课教案
小四奥数火车过桥问题

例3. 一位旅客乘火车以每秒15米的速度前进,他看见对面开来的火车只用2秒钟就从他身边驶过。
如果知道迎面来的火车长70米,求它每小时行驶多少千米?课堂练习:1.一列货车全长240米,每秒行驶15米,全车连续通过一条隧道和一座桥,共用40秒钟,桥长150米,这条隧道长多少米?2.一列火车开过一座长1200米的大桥,需要75秒钟,火车开过路旁的电线杆只需15秒钟,求火车长多少米?3.一列火车通过一座长530米的桥需40秒钟,以同样的速度穿过380米的山洞需30秒钟,求这列火车的速度与车身的长度。
4.在上、下行轨道上,两列火车相对开来,一列火车长182米,每秒行18米,另一列火车每秒行17米,两列火车错车而过用了10秒钟,求另一列火车长多少米?5.有两列火车,一列长140米,每秒行24米,另一列长230米,每秒行13米,现在两车相向而行,求这两列火车错车时从相遇到离开需几秒钟?第三关例1 一列火车行驶的速度是72千米/时,小聪要测量这列火车的长度,在车头到达他身边时他按动秒表,到车尾开离他身边时按停秒表,测得19秒钟,这列火车长多少米?点拨:火车通过的是一个人,这个人的长度忽略不计,设想火车尾部在小聪身旁停下,车头距小聪身旁(即火车尾部)的长度正好是火车19秒钟行的路程,因此用“速度X时间二路程”的关系式解决这个问题。
例2 一列火车以72千米/时的速度全车过一座长738米的桥,行了52秒钟,这列火车长多少米?点拨:由火车行驶速度与时间,可求出行的路程,而这个路程是桥长度与火车长度的和。
例3 一列火车通过一座长1680米的桥时,有1分27秒钟全车都在桥上,已知它每分钟行960米,这列火车长多少米?点拨:火车过桥问题中既有“路程的和”也有“路程的差”。
为了弄清这两者,观察火车的行走可以固定一个标准,即按“头部”或“尾部”所行的路线来确定。
例4 一列火车长700米,从路边的一棵大树旁边通过,用来1.75分钟。
火车过桥问题教案

火车过桥问题教案教案标题:火车过桥问题教案教学目标:1. 理解和应用火车过桥问题的基本概念和原则;2. 培养学生的逻辑思维和问题解决能力;3. 提高学生的合作与沟通能力。
教学重点:1. 理解火车过桥问题的背景和规则;2. 运用逻辑思维解决火车过桥问题;3. 培养学生的合作与沟通能力。
教学准备:1. PowerPoint演示文稿;2. 火车过桥问题的练习题;3. 计时器。
教学过程:Step 1:导入(5分钟)使用一些与火车有关的图片或视频来引起学生对火车的兴趣,并提出以下问题:你们知道火车过桥问题吗?你们认为火车过桥的时候会遇到什么问题?请同学们思考并做出回答。
Step 2:讲解火车过桥问题(10分钟)使用PowerPoint演示文稿向学生介绍火车过桥问题的背景和规则。
解释问题的基本概念,例如桥的承重限制、火车的速度等,并通过具体案例进行说明。
Step 3:小组合作解决问题(15分钟)将学生分成小组,每个小组共同解决一道火车过桥问题。
提供适当的练习题,让学生在小组内合作讨论,找出解决问题的最佳策略。
鼓励学生思考问题的不同角度和可能的解决方案。
Step 4:展示和讨论(10分钟)每个小组派出一名代表,向全班展示他们的解决方案。
在展示过程中,鼓励其他学生提出问题和不同的解决思路。
引导学生进行讨论和比较,分析各种解决方案的优缺点。
Step 5:归纳总结(5分钟)总结学生们在解决火车过桥问题中所采用的不同策略和解决思路,并指出其中的优点和不足之处。
引导学生思考如何更好地解决类似的问题,并鼓励他们运用逻辑思维和创造力。
Step 6:拓展练习(10分钟)提供一些拓展练习题,让学生在课后继续练习和思考。
鼓励学生尝试不同的问题变体,并寻找更高效的解决方法。
Step 7:课堂反思(5分钟)与学生一起回顾课堂内容,让他们分享他们在解决火车过桥问题中的收获和困惑。
鼓励学生提出问题和建议,以便今后的教学改进。
教学扩展:1. 鼓励学生设计自己的火车过桥问题,并与同学们分享。
小学奥数:第7讲四年级数学火车过桥问题教案
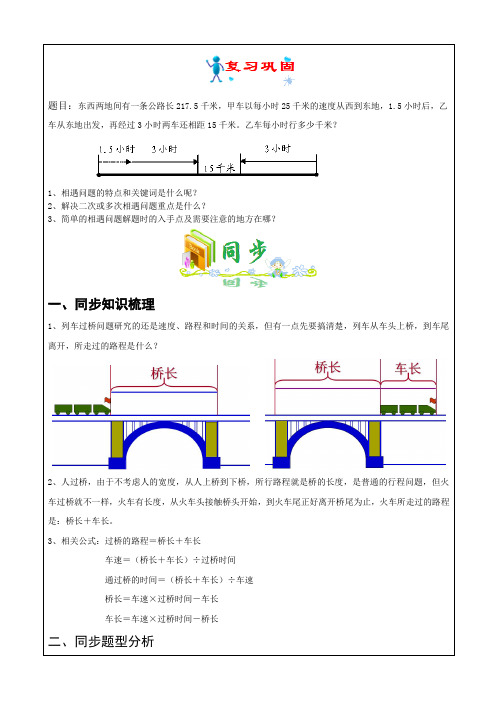
题目:东西两地间有一条公路长217.5千米,甲车以每小时25千米的速度从西到东地,1.5小时后,乙车从东地出发,再经过3小时两车还相距15千米。
乙车每小时行多少千米?1、相遇问题的特点和关键词是什么呢?2、解决二次或多次相遇问题重点是什么?3、简单的相遇问题解题时的入手点及需要注意的地方在哪?一、同步知识梳理1、列车过桥问题研究的还是速度、路程和时间的关系,但有一点先要搞清楚,列车从车头上桥,到车尾离开,所走过的路程是什么?2、人过桥,由于不考虑人的宽度,从人上桥到下桥,所行路程就是桥的长度,是普通的行程问题,但火车过桥就不一样,火车有长度,从火车头接触桥头开始,到火车尾正好离开桥尾为止,火车所走过的路程是:桥长+车长。
3、相关公式:过桥的路程=桥长+车长车速=(桥长+车长)÷过桥时间通过桥的时间=(桥长+车长)÷车速桥长=车速×过桥时间-车长车长=车速×过桥时间-桥长二、同步题型分析题型1、求时间例:一列火车长180米,每秒行20米,这列火车通过320米长的大桥需要多长时间?分析:根据路程÷速度=时间,可以求出列车通过桥梁时用的时间。
列车完全通过桥梁一共走的路程是桥长+车长:180+320=500(米),列车通过这座桥梁要500÷20=25(秒)。
题型2、求速度例1:一列长300米的列车,完全通过一座长450米的桥梁,一共用了2分钟。
这列火车过桥时每分钟行多少米?分析:列车完全通过一座桥梁,行的路程是桥长+车长。
火车完全通过桥梁一共走的路程是300+450=750(米),这列火车过桥时每分钟行750÷2=375(米)。
例2:一列火车通过一座长500米的桥梁用了40秒,用同样的速度通过另一座600米的桥梁用了45秒。
这列火车过桥时每秒钟行多少米?列车通过第一座桥梁:行的路程是500米+车长 40秒列车通过第二座桥梁:行的路程是600米+车长 45秒这列火车(45-40)秒钟行的路程是(600-500)米。
奥数列车过桥问题教案

奥数列车过桥问题教案一、教学目标1. 让学生理解并掌握列车过桥问题的基本概念和原理。
2. 培养学生解决实际问题的能力,提高学生的逻辑思维和数学素养。
3. 引导学生运用数学知识分析和解决生活中的问题,培养学生的应用意识。
二、教学内容1. 列车过桥问题的定义及基本公式。
2. 单列火车、多列火车过桥问题的解法。
3. 实际生活中的列车过桥问题案例分析。
三、教学重点与难点1. 重点:列车过桥问题的基本概念、公式及解法。
2. 难点:如何灵活运用所学知识解决实际问题。
四、教学方法1. 采用问题驱动的教学模式,引导学生主动探究、积极思考。
2. 利用多媒体课件辅助教学,生动形象地展示列车过桥过程。
3. 结合生活中的实际案例,让学生感受数学与生活的紧密联系。
4. 开展小组讨论、同桌交流活动,提高学生的合作与沟通能力。
五、教学安排1. 课时:2课时2. 教学过程:第一课时:a. 引入列车过桥问题,讲解基本概念和公式。
b. 分析单列火车过桥问题的解法。
c. 课堂练习,巩固所学知识。
第二课时:a. 讲解多列火车过桥问题的解法。
b. 分析实际生活中的列车过桥问题案例。
c. 小组讨论,探讨解决实际问题的方法。
六、教学策略1. 案例分析:通过分析典型列车过桥问题案例,让学生理解问题实质,掌握解决方法。
2. 练习设计:设计具有梯度的练习题,让学生在解决实际问题的过程中,巩固知识,提高能力。
3. 互动交流:鼓励学生课堂上积极提问、发表见解,教师及时解答疑问,促进师生互动。
七、教学评价1. 课堂表现:观察学生在课堂上的参与程度、提问回答等情况,了解学生的学习状态。
2. 练习完成情况:检查学生课后练习的完成质量,评估学生对知识的掌握程度。
3. 小组讨论:评价学生在小组讨论中的表现,包括合作意识、沟通能力和解决问题能力。
八、教学资源1. 多媒体课件:制作生动形象的课件,帮助学生更好地理解列车过桥问题。
2. 案例素材:收集生活中的列车过桥问题案例,用于教学实践。
《火车过桥》(教案)四年级上册奥数人教版

《火车过桥》教学目标:1. 让学生掌握火车过桥问题的基本概念和计算方法。
2. 培养学生的逻辑思维能力和解决问题的能力。
3. 培养学生运用数学知识解决实际问题的能力。
教学内容:1. 火车过桥问题的基本概念。
2. 火车过桥问题的计算方法。
教学重点:1. 火车过桥问题的基本概念。
2. 火车过桥问题的计算方法。
教学难点:1. 火车过桥问题的计算方法。
教学准备:1. 教学课件。
2. 火车过桥问题相关练习题。
教学过程:一、导入(5分钟)1. 教师通过图片或实物展示火车过桥的场景,引导学生观察并思考火车过桥时可能会遇到的问题。
2. 学生分享观察到的现象和问题。
二、基本概念(10分钟)1. 教师讲解火车过桥问题的基本概念,包括火车长度、桥长、火车速度等。
2. 学生跟随教师一起总结火车过桥问题的基本概念。
三、计算方法(15分钟)1. 教师讲解火车过桥问题的计算方法,包括如何计算火车过桥所需的时间和距离。
2. 学生跟随教师一起练习火车过桥问题的计算方法。
四、练习题(15分钟)1. 教师给出一些火车过桥问题的练习题,让学生独立完成。
2. 教师对学生的答案进行点评和讲解。
五、总结(5分钟)1. 教师引导学生回顾本节课所学的内容,总结火车过桥问题的基本概念和计算方法。
2. 学生分享学习收获和体会。
教学反思:本节课通过讲解火车过桥问题的基本概念和计算方法,让学生掌握了火车过桥问题的解决方法。
在教学过程中,我注重引导学生观察和思考,让学生通过自己的努力解决问题。
在练习题环节,我及时对学生的答案进行点评和讲解,帮助学生巩固所学知识。
总体来说,本节课达到了预期的教学目标,学生能够较好地理解和掌握火车过桥问题的解决方法。
但在教学过程中,我发现部分学生对火车过桥问题的理解还存在一定的困难,需要在今后的教学中加强指导。
重点关注的细节是“计算方法”,因为这是解决火车过桥问题的关键步骤,也是学生容易感到困惑的部分。
在补充和说明这个重点细节时,需要详细解释火车过桥问题的计算原理,并提供具体的计算步骤和示例,以便学生能够清晰地理解和掌握。
小学数学教案:《火车过桥》微教案

小学数学教案:《火车过桥》微教案一、教学目标:1. 让学生理解火车过桥的问题,掌握火车过桥的基本原理。
2. 培养学生运用数学知识解决实际问题的能力。
3. 培养学生合作学习、积极思考的良好学习习惯。
二、教学内容:1. 火车过桥的基本原理2. 火车过桥的数学模型3. 火车过桥的实际应用三、教学重点与难点:1. 火车过桥的基本原理2. 火车过桥的数学模型的建立与运用四、教学方法:1. 情境教学法:通过设置火车过桥的情境,让学生身临其境,激发学习兴趣。
2. 小组合作学习:培养学生合作学习的能力,共同解决火车过桥问题。
3. 引导发现法:引导学生发现火车过桥的规律,培养学生独立思考的能力。
五、教学准备:1. 教具:火车模型、桥模型、卡片等。
2. 学具:每位学生准备一份火车过桥的练习题。
六、教学过程:1. 导入新课:通过展示火车过桥的图片或视频,引导学生关注火车过桥的现象,激发学生的学习兴趣。
2. 探究火车过桥的基本原理:引导学生思考火车过桥时,车身、桥长和桥宽之间的关系。
通过小组讨论,总结出火车过桥的基本原理。
3. 建立火车过桥的数学模型:引导学生根据火车过桥的基本原理,建立数学模型。
让学生尝试用字母表示火车长度、桥长和桥宽,列出相应的等式。
4. 应用数学模型解决问题:让学生运用刚建立的数学模型,解决实际问题。
例如,火车长度为30米,桥长为120米,桥宽为8米,求火车完全过桥所需的路程。
5. 巩固练习:布置一些有关火车过桥的练习题,让学生独立完成,检验学生对火车过桥数学模型的掌握程度。
七、课堂小结:1. 让学生回顾本节课所学内容,总结火车过桥的基本原理和数学模型。
2. 强调火车过桥问题在实际生活中的应用,提醒学生关注数学与生活的联系。
3. 鼓励学生在课后继续探究类似问题,培养学生的独立思考能力。
八、作业布置:1. 请学生运用火车过桥的数学模型,解决一些实际问题。
2. 让学生收集有关火车过桥的资料,了解火车过桥在实际生活中的九、课后反思:1. 教师应反思本节课的教学目标是否达成,学生对火车过桥的基本原理和数学模型是否掌握。
四年级奥数巧解列车过桥问题教学设计

教案学生姓名:授课教师:所授科目:奥数学生年级:课次:课时:上课时间:教学内容巧解列车过桥问题训练目标“列车过桥”也是行程问题的一种情况,首先要清楚列车通过一段桥是从车头上桥到车尾离桥。
列车运动的总路程是桥长加车长,这是解题的关键,其他问题可以按照行程问题的一般数量关系来解决,我们在学习这个专题时可利用身边现在的东西,如橡皮、铅笔等,根据题意动手演示从而找到解题的线索。
典型例题例题1一辆公共汽车长10米,经过一座大桥,桥长290米,这辆车的速度为每分钟30米,这辆车经过东风桥需要多少分钟?分析与解答;这道题要考虑公共汽车的长度,以车头为参照点,汽车完全通过大桥所走的路程应该是桥长+ 车长,如图,然后根据“路程÷速度= 时间”这个数量关系式就能求出经过大桥所需时间。
解:(290+10)÷30=300÷30=10(分钟)答:这辆车经过东风桥需要10分钟例题2一列高速列车长240米,这列火车全速通过一座高架桥需要10秒钟,这座高架桥全长420米。
求这列火车每秒行多少米。
?分析与解答:从图中看出以车头为参照点,通过的路程为桥长+车长。
因为根据“路程÷速度= 时间”可得。
解:(240+420)÷10=660÷10=66(米/秒)答:这列火车每秒行66米例题3一列火车长360米,这列火车每秒行45米。
从车头进入隧道口,到全车驶出隧道总共用了20秒。
问这个隧道长多少米?分析与解答:如上图:考虑到火车自身的长度,通过隧道所走的路程包括隧道长度和车长,根据“速度×时间= 路程”可得。
解; 20×45-360=900-360=540(米)答:这个隧道长540米例题4 一和谐号列车通过360米长的1号隧道用了24秒,接着通过2号隧道用了16秒,已知2号隧道全长216米。
求这列火车的长度。
分析与解答如图,火车行驶24秒包括隧道长度及车长,同理,行驶16秒也包括隧道长度及车长。
《火车过桥问题》教学设计

《火车过桥问题》教学设计分析与解:火车通过桥,行进的总路程为车长与桥长的和,根据时间=路程÷速度,可以求出火车过桥的时间。
(120+7080)÷40=180(秒)=3(分)答:火车过桥需3分钟。
例2:王芳站在铁路边上,一列货车从她面前开过用了3分钟,已知这列货车长540米,以同样的速度通过一座桥用了25分钟,这座桥长多少米?分析与解:王芳是静止的,货车从她面前开过所行的路程就是车长540米,知道了时间是3分钟,就可以求出货车的速度。
用货车的速度乘通过大桥的25分钟时间,就求出了货车行进的总路程,也就是货车的长度与桥的长度之和,再减去车长,就得到了桥长。
货车的速度: 540÷3=180(米)货车行的总路程:180×25=4500(米)车长+桥长桥长:4500-540=3960(米)答:座桥长3960米。
例3:火车通过长为1286米的铁桥用了64秒,如果火车的速度的速度加快1倍,它通过1910米的隧道用了45秒。
求火车原来的速度和它的长度。
分析与解:如果用原来的速度通过1910米的隧道用了45×2=90(秒)。
先通过铁桥和隧道的长度差和所用时间差,求出这列火车的速度,有了火车的速度,问题也就可以解决了。
如果不提速通过隧道的时间: 45×2=90(秒)火车的速度:(1910-1286)÷(90-64)=24(米)火车的长度:24×64-1286=250(米)答:火车的速度是每秒24米,火车的长度是250米。
例4:有两列火车,一列车长176米,每秒行22米,另一列车长144米,每秒行18米,现在两车相向而行,问从相遇到离开需要几秒钟?分析与解:从两车车头相遇到两车车尾相离,一共要行176+144=320(米),两车每秒共行22+18=40(米),所以,从相遇到相离一共要经过8秒。
(176+144)÷(22+18)=8(秒)答:从相遇到离开需要8秒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级奥数火车过桥
问题完整
火车过桥问题
公式:火车过桥总路程=
过桥时间= 车速=
车长=
桥长=
例1:一列列车长150米,每秒行19米,全车通过420米的大桥,需要多长时间?
练1:一列火车全车400米,以每小时40千米的速度通过一条长2.8千米的隧道,共需多少时间?
例2:一列火车全长450米,每秒行驶16米,全车通过一条隧道需90秒。
求这条隧道长多少米?
练1:一座大桥长2100米,一列火车以每分钟800米的速度通过这座大桥,从车头上桥到车尾离开共用3.1分钟,这列火车长多少米?
例3:一列火车通过180米长的桥用40秒,用同样的速度,穿过300米长的隧道用48秒,求这列火车的速度和列车长度。
练1:一列火车通过199米的桥需要80秒,用同样的速度通过172米的隧道要74秒,求列车的速度和车长。
练2:一列火车长600米,速度为每分1000米,铁路上有两条隧道,火车自车头进入第一隧道到车尾离开第一隧道用了3分钟,用从车头进入第二隧道到车尾离开第二隧道用了4分钟。
从车头进入第一隧道到车尾离开第二隧道共用了9分钟。
问两条隧道之间相距多少米?
例4:少先队员346人排成两路纵队去参观科技成果展览。
队伍行进的速度是每分钟行23米,前后两人都相距1米。
现在队伍需要通过一座长702米的桥,整个队伍从上桥到离桥共需几分钟?
练1:五年级394个学生排成两路纵队去郊游,每两个学生相隔0.5米,队伍以每分钟行61米的速度通过一座207米的大桥,一共需要多长时间?
例5:一列火车长192米,从路边的一根电线杆旁经过用了16秒,这列火车以同样速度通过312米长的桥,需多长时间?
练1:一列火车长800米,从路边的一颗大树旁通过用了1.5分钟,以同样的速度通过一座大桥用了3.5分钟。
求这座大桥的长度。
例6:一座大桥长1000米,一列火车从桥上通过,火车从开始上桥到完全下桥共用120秒,整列火车完全在桥上为80秒。
求火车速度和车长?。
