小学六年级奥数教案-11圆与扇形
小学数学 《圆和扇形》教案

《圆和扇形》教案教学内容教材P1~9页。
教学目标1、通过观察、操作,认识圆,会用圆规画圆。
初步认识扇形。
2、在探索圆的特征、画圆以及设计图案的过程中,进一步发展空间观念。
3、能用有关圆的知识解决一些简单的实际问题,能表达解决问题的过程,并尝试解释所得的结果。
4、对周围环境中与圆有关的事物有好奇心,能主动参与数学活动,获得数学活动经验,感受圆及图案的美。
教学准备多媒体课件。
教学过程一、圆的认识1、例1。
创设了富有童趣的动物汽车设计大赛的问题情境,呈现了小鸭子、米老鼠和小猴子设计的三角形、正方形、圆等三种不同形状车轮的汽车,提出“你喜欢谁的设计”“说说你的理由”,让学生借助生活经验思考、想象并充分表达自己的意见,使学生知道圆形车轮比三角形、正方形车轮易滚动并且平稳,感受车轮设计‘成圆形的道理,初步体会圆的特征,激发学生对圆的兴趣。
接着让学生认识并举出身边的面是圆形的物品,进一步体会圆与现实生活的密切联系。
2、例2。
在认识圆的特征及各部分名称时,教材设计了三个层次的活动。
活动一,用硬币或圆柱体在纸上描圆,并剪下来。
活动二,将圆形纸片按不同方向多次对折并观察对折后的圆形纸片,交流自己的发现。
通过交流,认识圆的轴对称性、圆有无数条对称轴以及所有折痕都相交于一点等。
活动三,认识圆心、直径、半径及其字母表示O。
3、议一议。
设计了两个问题,通过讨论,使学生认识到:同一个圆里,直径、半径有无数条;直径是半径的2倍或半径是直径的一半。
二、图案设计1、例1。
教材安排了三个活动。
活动一,欣赏图案。
教材呈现了四幅利用圆设计成的漂亮图案,让学生欣赏,体会图案的美。
活动二,模仿画图案。
教材以第一个图案为例,用四幅图清晰地介绍了用圆规和直尺设计这个图案的具体过程。
教学中,教师可按照书中的步骤示范画出图案(1)并涂色。
然后,让学生试画图案(2)并把试画的图案让大家欣赏,初步获得成功的体验。
活动三,独立设计图案。
让学生设计两个自己喜欢的图案并把最得意的作品在全班展示,感受成功的乐趣。
小学六年级奥数教案设计-圆与扇形

小学六年级奥数教案—11圆与扇形本教程共30讲圆与扇形五年级已经学习过三角形、矩形、平行四边形、梯形以及由它们形成的组合图形的相关问题,这一讲学习与圆有关的周长、面积等问题。
圆的面积=πr2,圆的周长=2πr,本书中如无特殊说明,圆周率都取π=3.14。
例1如下图所示,200米赛跑的起点和终点都在直跑道上,中间的弯道是一个半圆。
已知每条跑道宽1.22米,那么外道的起点在内道起点前面多少米?(精确到0.01米)分析与解:半径越大,周长越长,所以外道的弯道比内道的弯道长,要保证内、外道的人跑的距离相等,外道的起点就要向前移,移的距离等于外道弯道与内道弯道的长度差。
虽然弯道的各个半径都不知道,然而两条弯道的中心线的半径之差等于一条跑道之宽。
设外弯道中心线的半径为R,内弯道中心线的半径为r,则两个弯道的长度之差为πR-πr=π(R-r)=3.14×1.22≈3.83(米)。
即外道的起点在内道起点前面3.83米。
例2有七根直径5厘米的塑料管,用一根橡皮筋把它们勒紧成一捆(如左下图),此时橡皮筋的长度是多少厘米?分析与解:由右上图知,绳长等于6个线段AB与6个BC弧长之和。
将图中与BC弧类似的6个弧所对的圆心角平移拼补,得到6个角的和是360°,所以BC弧所对的圆心角是60°,6个BC弧等于直径5厘米的圆的周长。
而线段AB等于塑料管的直径,由此知绳长=5×6+5×3.14=45.7(厘米)。
例3左下图中四个圆的半径都是5厘米,求阴影部分的面积。
分析与解:直接套用公式,正方形中间的阴影部分的面积不太好计算。
容易看出,正方形中的空白部分是4个四分之一圆,利用五年级学过的割补法,可以得到右上图。
右上图的阴影部分的面积与原图相同,等于一个正方形与4个半圆(即2个圆)的面积之和,为(2r)2+πr2×2=102+3.14×50≈257(厘米2)。
例4 草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见左下图)。
六年级上册数学教案《圆和扇形》练习课 人教版

六年级上册数学教案《圆和扇形》练习课人教版一、教学目标1.熟练掌握圆的基本概念和性质。
2.能正确理解和计算扇形的面积,掌握计算方法。
3.能够解决与圆和扇形相关的实际问题。
二、教学重点1.圆的相关概念和性质的掌握。
2.扇形面积的计算方法及应用。
三、教学内容1.圆的定义和性质。
2.扇形的定义和性质。
3.扇形面积的计算方法及相关练习。
四、教学准备1.教师:备好课件、黑板、彩色粉笔。
2.学生:准备好练习册和文具。
五、教学过程1. 圆的定义和性质•引导学生快速复习圆的定义,并让学生能够说出圆的直径、半径和周长的计算方法。
•以实例让学生体会圆的性质,例如直径相等的圆的半径也相等等。
2. 扇形的定义和性质•通过图示让学生认识什么是扇形,并引导学生说出扇形的定义。
•讲解扇形的性质,比如圆心角的关系等。
3. 扇形面积的计算方法•教师讲解扇形面积的计算公式,并进行例题讲解。
•让学生自行计算扇形的面积,并帮助他们解决其中的困惑。
4. 综合练习•让学生进行练习册上与圆和扇形相关的练习题,加深对知识点的理解和掌握。
•教师巡视课堂,辅导学生解决问题,及时纠正错误。
六、课堂小结通过本节课的学习,相信大家对圆和扇形有了更深入的认识,掌握了一些重要的计算方法。
希望同学们能够认真复习本节课内容,做好预习工作,以便更好地掌握数学知识。
七、作业布置1.完成练习册上与圆和扇形相关的练习题。
2.思考并记录生活中与圆和扇形相关的实际问题。
以上为本节课的教学内容,请同学们认真学习,做到知识点的牢固掌握。
希望大家在数学学习中取得更加优异的成绩!以上内容为六年级上册数学教案《圆和扇形》练习课人教版的详细内容,请学生们认真复习和备考。
小学六年级奥数教案-圆与扇形

小学六年级奥数教案—11圆与扇形本教程共30讲圆与扇形五年级已经学习过三角形、矩形、平行四边形、梯形以及由它们形成的组合图形的相关问题,这一讲学习与圆有关的周长、面积等问题。
圆的面积=πr2,圆的周长=2πr,本书中如无特殊说明,圆周率都取π=3.14。
例1如下图所示,200米赛跑的起点和终点都在直跑道上,中间的弯道是一个半圆。
已知每条跑道宽1.22米,那么外道的起点在内道起点前面多少米?(精确到0.01米)分析与解:半径越大,周长越长,所以外道的弯道比内道的弯道长,要保证内、外道的人跑的距离相等,外道的起点就要向前移,移的距离等于外道弯道与内道弯道的长度差。
虽然弯道的各个半径都不知道,然而两条弯道的中心线的半径之差等于一条跑道之宽。
设外弯道中心线的半径为R,内弯道中心线的半径为r,则两个弯道的长度之差为πR-πr=π(R-r)=3.14×1.22≈3.83(米)。
即外道的起点在内道起点前面3.83米。
例2有七根直径5厘米的塑料管,用一根橡皮筋把它们勒紧成一捆(如左下图),此时橡皮筋的长度是多少厘米?分析与解:由右上图知,绳长等于6个线段AB与6个BC弧长之和。
将图中与BC弧类似的6个弧所对的圆心角平移拼补,得到6个角的和是360°,所以BC弧所对的圆心角是60°,6个BC弧等于直径5厘米的圆的周长。
而线段AB等于塑料管的直径,由此知绳长=5×6+5×3.14=45.7(厘米)。
例3左下图中四个圆的半径都是5厘米,求阴影部分的面积。
分析与解:直接套用公式,正方形中间的阴影部分的面积不太好计算。
容易看出,正方形中的空白部分是4个四分之一圆,利用五年级学过的割补法,可以得到右上图。
右上图的阴影部分的面积与原图相同,等于一个正方形与4个半圆(即2个圆)的面积之和,为(2r)2+πr2×2=102+3.14×50≈257(厘米2)。
例4 草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见左下图)。
六年级数学-圆和扇形教案
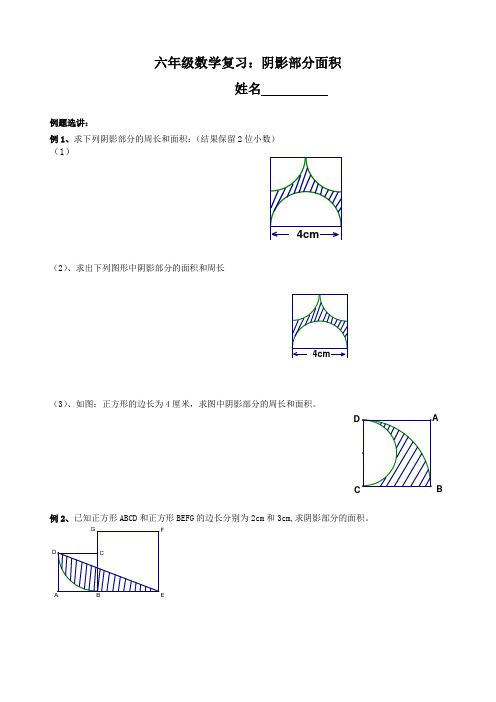
4cm4cm六年级数学复习:阴影部分面积姓名例题选讲:例1、求下列阴影部分的周长和面积:(结果保留2位小数)(1)(2)、求出下列图形中阴影部分的面积和周长(3)、如图:正方形的边长为4厘米,求图中阴影部分的周长和面积。
DB例2、已知正方形ABCD 和正方形BEFG 的边长分别为2cm 和3cm,求阴影部分的面积。
例3、如图,正方形ABCD和正方形CEFG的边长分别为10厘米和12厘米。
B、C、E在一直线上,GE是以C为圆心,CE为半径的一条弧,联结AE、AG,求图中阴影部分的面积。
例4、如图,一个半圆与一个圆心角为45度的扇形重叠在一起,扇形的一条半径与半圆O的直径AB重合,另一条半径BC与半圆弧相交于点D。
已知AB=4cm,OD和AB垂直,求阴影部分的面积。
例5、如如图,正方形的边长是12厘米,分别以四条边为直径画半圆,构成一个四叶图,求这个四叶图的周长和面积。
例6、已知正方形ABCD的边长为4cm求出这个花瓣形状的阴影部分的面积。
cm BC AC AB CAB 2,,90===∠ο【即时检测】1、求出下列图形中空白部分的面积。
2、 求出下列图形中阴影部分的面积(1) (2)(4)3、求阴影部分的周长和面积(精确到0.1cm )4、求下图阴影部分周长与面积(单位:厘米)6cm10cm6【拓展题】1、现在有四根半径为5厘米的圆柱形物件,为了方便运输,准备用绳子捆绑在一起,横截面如图所示,如果要求物品的两端各用一根绳子绕三圈,并留出20厘米长打结,那么需要准备多长的绳子。
2、以4分米为直径的半圆绕点A旋转了45°,如图所示。
求阴影部分的周长。
3、这个问号的面积是多少?3cm3cm3cmDCBA4、 如图,已知正方形ABCD 的边长为6厘米,在这个正方形中有个半径为1厘米的圆沿着它的四条边滚动一周,求圆滚动时扫过的面积。
【回家作业】 一、填空题1.最小的自然数是 .2.分解素因数:36 . 3.写出数轴上的点表示的数:点A 表示的数是: ;点B表示的数是: . 4.化简比:20分钟∶32小时= . 5.已知一个比例的两个外项互为倒数,其中一个内项是123,那么另一个内项是 . 6.王强工作3天得到540元报酬,照这样计算,他工作20天可以得到报酬 元.7.爸爸和妈妈的月收入之比是5:4,如果他们两人每月的总收入是18000元,那么妈妈的月收入为 元.8.一件商品,提价20%后又降价30%,这件商品的现价是原价的 (用百分数表示). 9.按有关规定,进口某种货物需交纳货物价值12%的税。
冀教版小学六年级数学上册《圆和扇形》(扇形的认识)教学设计

学生可能会说:
●扇形都是圆的一部分。
●扇形是由两条半径和圆上的一段曲线围成的图形。
●扇形都有一个角,角的顶点在圆心。
3、教师进行概括,介绍弧和圆心角等的概念,并在圆上标出。
在学生感知扇形特点的基础上,认识有关概念,有利于理解其实际意义。
观察比较中,加深对“扇形”折扇的认识,为认识扇形做准备。
师:再看这把扇子(打开普通的折扇),你发现这把打开的扇子与前面那把有什么不同?
学生可能会说:
●这把扇子打开后不是圆形。
●这把扇子打开后像个半圆。
……
二、认识扇形
1、出示教材中的四幅图,让学生观察,说一说涂色部分,进而引出扇形。
借助学生的生活经验,初步认识扇形,感受圆形与名称的联系。
师:观察得真仔细,说得也很对,扇形都是由两条半径和圆上的一段曲线围成的,如果我们把两条半径与圆上曲线的交点记作A、B,圆上A、B两点之间的去线叫做“弧”,记作“弧AB”。
在图上标出半径、圆心,弧AB
师:每个扇形都有一个角,角的顶点在圆心,这个角就叫做圆心角。
教师在圆上标出圆心角。
三、拓展学习
1、让学生动手测量书中几个扇形的圆心角的度数,并在图上标出圆心和圆心角的度数。
师:很好。同学们看到这样的实物都能想到学过的图形。今天,我们再来认识一种新的平面图形。
出示教材中的四幅图。
师:请同学们观察四个圆中的涂色部分,说一说它们的样子像什么?
学生可能回答:
●涂色部分的图形,一个比一个大,像一把打开的扇子。
……
师:同学们观察得很仔细,图中涂角是180°的扇形面积占圆面积的 ,圆心角的度数也占圆周角的 。
冀教版小学六年级数学上册教案圆和扇形_教案3

三、自主尝试。
1.鼓励学生自己画出第2个图案,给学生充分的画图时间。
2.展示学生画的图案,重点交流画图的过程和方法。
四、设计图案。
1.教师谈话,鼓励学生发挥想象,自己设计一个喜欢的图案。
2.全班交流画的图案,说一说自己的设计过程,并将有创意的图案贴在黑板上展示。
师:同学们很富有想象力。下面自己画出课本中的图。并涂上自己喜欢的颜色。
学生画完后,全班交流画的步骤。
师:练一练第2题,给我们提供了一个漂亮的图案,请同学们自己读书,并按照下面的步骤画一画,看你是否能画出这个漂亮的图案。
学生画完后,展示学生的作品。
师:这节课我们学会了用圆来设计图案。回家后,自己设计一个更漂亮的图案,请家人一起欣赏。
展示学生作品,让两三名同学介绍自己画图的步骤。
生:第一步:用圆规先画一个圆。第二步:用直尺在圆中画两条直径,两条直径要相互垂直。第三步:以左边半径的中心点为圆心,大圆半径的一半为半径,向上画一个半圆。第四步:绕大圆圆心顺时针旋转90度、180度、270度,以同样的方法,在另外三条半径画半圆,最后涂上颜色,第二个图案就完成了。
师:怎样画这个小半圆?以什么为半径画这个小圆?
学生可能会说:
以大圆直径的1/4为半径画出一个小圆。
以大圆半径的1/2为半径画出一个小圆。
师:对,以大圆半径的1/2为半径,那么,怎样确定小圆的圆心呢?
生:以左边半径的中心点为圆心。
师:很好。第三步以左边半径的中心点为圆心,大圆半径的一半为半径,向上画一个小半圆。
师:那么,这个图案到底是怎样画出来的呢?下面我们一起来画这个图案。大家说一说画这个图案第一步应该先画什么?
2023六年级数学上册一圆和扇形单元概述和课时安排教案冀教版

3. 随堂测试:学生在随堂测试中能够正确回答圆和扇形的相关问题,包括圆的周长和面积的计算、扇形的面积计算以及圆锥的体积计算等。他们能够应用所学知识解决实际问题,显示出对知识的掌握和应用能力。
4. 课后作业完成情况:学生在课后作业中能够认真完成相关任务,包括撰写关于圆和扇形的短文或报告。他们的作业质量高,能够清晰地表达自己的观点和想法,显示出对知识的理解和应用能力。
过程:
简要回顾本节课的学习内容,包括圆和扇形的基本概念、组成部分、案例分析等。
强调圆和扇形在现实生活或学习中的价值和作用,鼓励学生进一步探索和应用圆和扇形。
布置课后作业:让学生设计一个与圆和扇形相关的实际问题,并撰写一篇关于解决问题的短文或报告,以巩固学习效果。
六、知识点梳理
本节课主要涉及以下知识点:
过程:
讲解圆的定义,包括其主要组成元素(半径、直径等)。
详细介绍圆和扇形的组成部分或功能,使用图表或示意图帮助学生理解。
3. 圆和扇形案例分析(20分钟)
目标: 通过具体案例,让学生深入了解圆和扇形的特性和重要性。
过程:
选择几个典型的圆和扇形案例进行分析。
详细介绍每个案例的背景、特点和意义,让学生全面了解圆和扇形的多样性或复杂性。
九.教学评价与反馈
1. 课堂表现:学生能够积极参与课堂讨论,提出问题并回答问题,表现出良好的学习态度和兴趣。他们在小组活动中能够积极合作,共同完成任务,展现出良好的团队精神和沟通能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学六年级奥数教案—11圆与扇形
本教程共30讲
圆与扇形
五年级已经学习过三角形、矩形、平行四边形、梯形以及由它们形成的组合图形的相关问题,这一讲学习与圆有关的周长、面积等问题。
圆的面积=πr2,
圆的周长=2πr,
本书中如无特殊说明,圆周率都取π=3.14。
例1如下图所示,200米赛跑的起点和终点都在直跑道上,中间的弯道是一个半圆。
已知每条跑道宽1.22米,那么外道的起点在内道起点前面多少米?(精确到0.01米)
分析与解:半径越大,周长越长,所以外道的弯道比内道的弯道长,要保证内、外道的人跑的距离相等,外道的起点就要向前移,移的距离等于外道弯道与内道弯道的长度差。
虽然弯道的各个半径都不知道,然而两条弯道的中心线的半径之差等于一条跑道之宽。
设外弯道中心线的半径为R,内弯道中心线的半径为r,则两个弯道的长度之差为
πR-πr=π(R-r)
=3.14×1.22≈3.83(米)。
即外道的起点在内道起点前面3.83米。
例2有七根直径5厘米的塑料管,用一根橡皮筋把它们勒紧成一捆(如左下图),此时橡皮筋的长度是多少厘米?
分析与解:由右上图知,绳长等于6个线段AB与6个BC弧长之和。
将图中与BC弧类似的6个弧所对的圆心角平移拼补,得到6个角的和是360°,所以BC弧所对的圆心角是60°,6个BC弧等于直径5厘米的圆的周长。
而线段AB等于塑料管的直径,由此知绳长=5×6+5×3.14=45.7(厘米)。
例3左下图中四个圆的半径都是5厘米,求阴影部分的面积。
分析与解:直接套用公式,正方形中间的阴影部分的面积不太好计算。
容易看出,正方形中的空白部分是4个四分之一圆,利用五年级学过的割补法,可以得到右上图。
右上图的阴影部分的面积与原图相同,等于一个正方形与4个半圆(即2个圆)的面积之和,为(2r)2+πr2×2=102+3.14×50≈257(厘米2)。
例4 草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见左下图)。
问:这只羊能够活动的范围有多大?
分析与解:如右上图所示,羊活动的范围可以分为A,B,C三部分,
所以羊活动的范围是
例5 右图中阴影部分的面积是2.28厘米2,求扇形的半径。
分析与解:阴影部分是扇形与等腰直角三角形相差的部分。
所以,扇形的半径是4厘米。
例6 右图中的圆是以O为圆心、径是10厘米的圆,求阴影部分的面积。
分析与解:解此题的基本思路是:
从这个基本思路可以看出:要想得到阴影部分S1的面积,就必须想办法求出S2和S3的面积。
S3的面积又要用下图的基本思路求:
现在就可以求出S3的面积,进而求出阴影部分的面积了。
S3=S4-S5=50π-100(厘米2),
S1=S2-S3=50π-(50π-100)=100(厘米2)。
练习11
1.直角三角形ABC放在一条直线上,斜边AC长20厘米,直角边BC 长10厘米。
如下图所示,三角形由位置Ⅰ绕A点转动,到达位置Ⅱ,此时B,C点分别到达B1,C1点;再绕B1点转动,到达位置Ⅲ,此时A,C1点分别到达A2,C2点。
求C点经C1到C2走过的路径的长。
2.下页左上图中每个小圆的半径是1厘米,阴影部分的周长是多少厘米?
3.一只狗被拴在一个边长为3米的等边三角形建筑物的墙角上(见右上图),绳长是4米,求狗所能到的地方的总面积。
5.右上图是一个400米的跑道,两头是两个半圆,每一半圆的弧长是100米,中间是一个长方形,长为100米。
求两个半圆的面积之和与跑道所围成的面积之比。
6.左下图中,正方形周长是圆环周长的2倍,当圆环绕正方形无滑动地滚动一周又回到原来位置时,这个圆环转了几圈?
7.右上图中,圆的半径是4厘米,阴影部分的面积是14π厘米2,求图中三角形的面积。
答案与提示练习11
1.68厘米。
2.62.8厘米。
解:大圆直径是6厘米,小圆直径是2厘米。
阴影部分周长是6π+2π×7=62.8(厘米)。
3.43.96米2。
解:如下页右上图所示,可分为半径为4米、圆心角为300°的扇形与两个半径为1米、圆心角为120°的扇形。
面积为
4.60°。
解:设∠CAB为n度,半圆ADB的半径为r。
由题意有
解得n=60。
5.1∶3。
6.3圈。
7.8厘米2。
解:圆的面积是42π=16π(厘米2),空白扇形面积占圆面积的1-
的等腰直角三角形,面积为4×4÷2=8(厘米2)。
