项目三 轴向拉压杆习题
轴向拉(压)杆强度校核(例题)

问题解析问题1、什么是强度?什么是强度条件?强度是指构件抵抗破坏的能力。
房屋结构的每一个构件承受荷载后都不允许发生破坏。
如屋架、立柱、吊车梁、基础梁、承重墙等都不允许发生断裂。
这就要求每一个构件应具有足够的抵抗破坏的能力,这种能力称为强度。
强度条件公式为:[]max N A σσ=≤,要注意式中的max σ与[]σ的区别。
max N A σ=表示的是在荷载作用下构件的工作应力,这个值只与内力(由外力引起的)和截面尺寸有关,与材料无关。
[]N Aσ≤是强度条件,是构件能安全承载的依据。
式中的[]σ,表示的是所用材料本身的性质,是由实验测定的,不是工作时外力引起的内力。
问题2、2. 图示砖柱。
24=a cm ,37=b cm ,31=l m ,42=l m ,501=P kN ,902=P kN 。
略去砖柱自重。
求砖柱各段的轴力及应力,并绘制轴力图。
解:砖柱受轴向荷载作用,是轴向压缩。
(1)计算柱各段轴力AB 段: kN P N 5011-=-=(压力)BC 段: 212P P N --=1409050-=--=kN (压力)(2)画柱的轴力图(b )。
(3)计算柱各段的应力AB 段:1-1横截面上的轴力为压力,501-=N kN , 横截面面积241mm 1076.5240240⨯=⨯=A , 则 MPa A N 868.01076.5105043111-=⨯⨯-==σ (压应力) BC 段:2-2横截面上的轴力为压力 1402-=N kN 横截面面积421069.13370370⨯=⨯=A mm 2 则 MPa A N 02.11069.131014043222-=⨯⨯-==σ(压应力)。
项目三 轴向拉伸与压缩试题

【开始】单选题(分值=2分;答案=C;难度=基本题)在其他条件不变时,若受轴向拉伸的杆件横截面面积增加一倍,则杆件横截面上的正应力()。
A、4倍B、2倍C、1/2倍D、1/4倍【结束】【开始】单选题(分值=2分;答案=C;难度=水平题)在其他条件不变时,若受轴向拉伸的杆件杆长增加一倍,则杆件纵向线应变()。
A、增大B、减小C、不变D、不能确定【结束】【开始】单选题(分值=2分;答案=B;难度=基本题)弹性模量E与()有关。
A、应力和应变B、杆件的材料C、外力大小D、泊松比μ【结束】【开始】单选题(分值=2分;答案=B;难度=水平题)横截面面积不同的两根杆件,受到大小相同的轴向外力作用时,则()。
A、轴力相同,应力也相同B、轴力相同,应力不同C、轴力不同,应力也不同D、轴力不同,应力不同【结束】【开始】单选题(分值=2分;答案=A;难度=基本题)材料在轴向拉伸时,在比例极限内,线应变与()成正比。
A、正应力B、弹性模量EC、泊松比μD、都切应力【结束】【开始】单选题(分值=2分;答案=D;难度=基本题)危险截面的确定,对于杆件对象的工程设计是非常重要的,若杆件的材料相同,轴向拉伸杆件危险截面发生在()的截面上。
A、轴力最大、横截面面积最大B、轴力最小、横截面面积最小C、轴力最小、横截面面积最大D、轴力最大、横截面面积最小【结束】【开始】单选题(分值=2分;答案=D;难度=基本题)下列关于内力的说法中错误的是()。
A、由外力引起的杆件内各部分间的相互作用力B、内力随外力的改变而改变C、内力可由截面法求得D、内力不仅与外力有关,还与杆件的截面形状和尺寸有关【结束】【开始】单选题(分值=2分;答案=B;难度=基本题)对于塑性材料取()作为材料的极限应力。
A、弹性极限B、屈服极限C、比例极限D、强度极限【结束】【开始】单选题(分值=2分;答案=B;难度=基本题)轴向拉压杆的应力与杆件的()有关。
A、外力B、外力、截面面积和形状C、外力、截面面积和形状、材料D、外力、截面面积和形状、材料、杆长【结束】【开始】单选题(分值=2分;答案=D;难度=基本题)轴向拉压杆的纵向线应变与杆件的()有关。
项目三 轴向拉压杆习题

项目三轴向拉伸与压缩一、填空题:1、内力是由引起的杆件内个部分间的。
2、求内力的基本方法是。
3、直杆的作用内力称。
其正负号规定为:当杆件受拉而伸长时为正,其方向截面。
4、截面法就轴力的步骤为:、、。
5、轴力图用来表达,画轴力图时用的坐标表示横截面位置,坐标表示横截面上的轴力。
6、轴力图中,正轴力表示拉力,画在轴的。
7、轴力的大小与外力有关。
与杆件截面尺寸、材料(有关、无关)。
8、应力是,反应了内力的分布集度。
单位,简称。
9、1pa= N/mm2 = N/m2。
1Mpa= pa。
10、直杆受轴力作用时的变形满足假设,根据这个假设,应力在横截面上分布,计算公式为。
11、正应力是指。
12、在荷载作用下生产的应力叫。
发生破坏是的应力叫。
许用应力是工作应力的;三者分别用符号、、表示。
13、当保证杆件轴向拉压时的安全,工作应力与许用应力应满足关系式:。
14、等截面直杆,受轴向拉压力作用时,危险截面发生在处。
而变截面杆,强度计算应分别进行检验。
15、轴向拉压杆的破坏往往从开始。
16、杆件在轴向力作用下长度的改变量叫,用表示。
17、胡克定律表明在范围内,杆件的纵向变形与及,与杆件的成正比。
18、材料的抗拉、压弹性模量用表示,反映材料的能力。
19、EA称作材料的,它反映了材料制成一定截面尺寸后的杆件的抗拉、压能力。
EA越大,变形越。
20、ε叫作,指单位长度的变形。
21、泊松比又叫,ν= ,应用范围为弹性受力范围。
二、计算题:1、试计算轴向拉压杆指定截面的轴力。
2、绘制图示杆件的轴力图。
3、求图示结构中各杆的轴力。
4、用绳索起吊管子如图所示。
若构件重W=10KN ,绳索的直径d=40mm ,许用应力[30 20KNB 45C 455、图示支架中,荷载P=100KN。
杆1为圆形截面钢杆,其许用应力[σ]=150MPa,拉=4MPa。
试确定钢杆的直径d和木杆杆2位正方形截面木杆,其许用应力[σ]压截面的边长c。
C6、钢杆长l=2m,截面面积A=200 mm2,受到拉力P=32KN的作用,钢杆的弹性模量E=2.0×105MPa,试计算此钢杆的伸长量Δl。
材料力学轴向拉压题目+答案详解
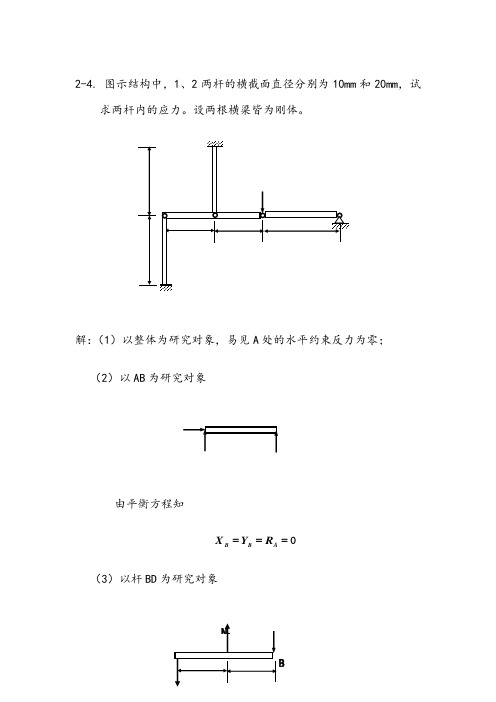
2-4. 图示结构中,1、2两杆的横截面直径分别为10mm 和20mm ,试求两杆内的应力。
设两根横梁皆为刚体。
解:(1)以整体为研究对象,易见A 处的水平约束反力为零; (2)以AB 为研究对象由平衡方程知0===A B B R Y X(3)以杆BD 为研究对象由平衡方程求得KNN N NY KNN N mC20010 01001101 021211==--===⨯-⨯=∑∑(4)杆内的应力为MPa A N MPa A N 7.63204102012710410102322223111=⨯⨯⨯===⨯⨯⨯==πσπσ2-19. 在图示结构中,设AB 和CD 为刚杆,重量不计。
铝杆EF 的l 1=1m ,A 1=500mm 2,E 1=70GPa 。
钢杆AC 的l 2=,A 2=300mm 2,E 2=200GPa 。
若载荷作用点G 的垂直位移不得超过。
试求P 的数值。
解:(1)由平衡条件求出EF 和AC 杆的内力P N N N P N N AC EF AC4332 2112=====(2)求G 处的位移22221111212243)ΔΔ23(21)ΔΔ(21Δ21ΔA E l N A E l N l l l l l l A C G +=+=+== (3)由题意kNP P P A E Pl A E Pl mml G 1125.2300102001500500107010009212143435.233222111≤∴≤⨯⨯⨯+⨯⨯⨯⨯=⨯⨯+⨯⨯≤ 2-27. 在图示简单杆系中,设AB 和AC 分别是直径 为20mm 和24mm的圆截面杆,E=200GPa ,P=5kN ,试求A 点的垂直位移。
解:(1)以铰A 为研究对象,计算杆AB 和杆AC 的受力kN N kN N AC AB 66.3 48.4==(2)两杆的变形为()伸长mm πEA l N l ABAB AB AB201.04201020045cos 20001048.42303=⨯⨯⨯⨯⨯==Δ ()缩短mm πEA l N l ACAC AC AC 0934.04241020030cos 20001066.32303=⨯⨯⨯⨯⨯==Δ (3)如图,A 点受力后将位移至A ’,所以A 点的垂直位移为AA ’’mmctg A A l A A AA A A mmA A ctg A A ctg A A A mm AA AA AA AA A A A A l l AB A AB AC 249.00355.0284.0 4545sin /Δ 035.0 4530A 0972.030sin /45sin /AΔΔAA ΔAA 00330043010243434321=-='''-=''-=''=∴='''∴'''+'''==-=-='==δ 又中在图中2-36. 在图示结构中,设AC 梁为刚杆,杆件1、2、3的横截面面积相等,材料相同。
轴向拉压习题答案2

第2章 轴向拉伸和压缩主要知识点:(1)轴向拉伸(压缩)时杆的内力和应力;(2)轴向拉伸(压缩)时杆的变形;(3)材料在轴向拉伸和压缩时的力学性能;(4)轴向拉压杆的强度计算;(5)简单拉压超静定问题。
轴向拉伸(压缩)时杆的变形4. 一钢制阶梯杆如图所示。
已知沿轴线方向外力F 1=50kN ,F 2=20kN ,各段杆长l 1=100mm ,l 2=l 3=80mm ,横截面面积A 1=A 2=400mm 2,A 3=250mm 2,钢的弹性模量E=200GP a ,试求各段杆的纵向变形、杆的总变形量及各段杆的线应变。
解:(1)首先作出轴力图如图4-11所示,由图知kN F N 301-=,kN F F N N 2032==。
(2)计算各段杆的纵向变形m m EA l F l N 5693311111075.31040010200101001030---⨯-=⨯⨯⨯⨯⨯⨯-==∆ m m EA l F l N 569332222100.2104001020010801020---⨯=⨯⨯⨯⨯⨯⨯==∆(3)杆的总变形量m l l l l 53211045.1-⨯=∆+∆+∆=∆。
(4)计算各段杆的线应变 451111075.310.01075.3--⨯-=⨯-=∆=l l ε 45222105.208.0100.2--⨯=⨯=∆=l l ε 45333100.408.0102.3--⨯=⨯=∆=l l ε材料在轴向拉伸和压缩时的力学性能5. 试述低碳钢拉伸试验中的四个阶段,其应力—应变图上四个特征点的物理意义是什么?答:低碳钢拉伸试验中的四个阶段为弹性阶段、屈服阶段、强化阶段和颈缩阶段。
在弹性阶段,当应力小于比例极限σp 时,材料服从虎克定律;当应力小于弹性极限σe 时,材料的变形仍是弹性变形。
屈服阶段的最低点对应的应力称为屈服极限,以σs 表示。
强化阶段最高点所对应的应力称为材料的强度极限,以σb 表示,它是材料所能承受的最大应力。
轴向拉伸与压缩练习题

第二章轴向拉伸与压缩练习题一.单项选择题1、在轴向拉伸或压缩杆件上正应力为零的截面是()A、横截面B、与轴线成必定交角的斜截面C、沿轴线的截面D、不存在的2、一圆杆受拉,在其弹性变形范围内,将直径增添一倍,则杆的相对变形将变为原来的()倍。
11A、4;B、2;C、1;D、23、由两杆铰接而成的三角架(如下图),杆的横截面面积为 A,弹性模量为E,当在节点 C 处遇到铅垂载荷 P 作用时,铅垂杆 AC 和斜杆 BC的变形应分别为()Pl4Pl Pl Pl Pl PlA、EA,3EA;B、0,EA;C、2EA,3EA D、EA,04、几何尺寸同样的两根杆件,其弹性模量分别为 E1=180Gpa,E2=60 Gpa,在弹性1变形的范围内二者的轴力同样,这时产生的应变的比值 2 应力为()1A、3B、 1;C、 2;D、 35、全部脆性资料,它与塑性资料对比,其拉伸力学性能的最大特色是()。
A、强度低,对应力集中不敏感;B、同样拉力作用下变形小;C、断裂前几乎没有塑性变形;D、应力 -应变关系严格按照胡克定律6、构件拥有足够的抵挡损坏的能力,我们就说构件拥有足够的()A、刚度,B、稳固性,C、硬度,D、强度。
7、构件拥有足够的抵挡变形的能力,我们就说构件拥有足够的()A、强度,B、稳固性,C、刚度,D、硬度。
8、单位面积上的内力称之为()A、正应力,B、应力,C、拉应力,D、压应力。
9、与截面垂直的应力称之为()A、正应力,B、拉应力,C、压应力,D、切应力。
10、轴向拉伸和压缩时,杆件横截面上产生的应力为()A、正应力,B、拉应力,C、压应力,D、切应力。
二、填空题1、杆件轴向拉伸或压缩时,其受力特色是:作用于杆件外力的协力的作用线与杆件轴线相 ________。
2、轴向拉伸或压缩杆件的轴力垂直于杆件横截面,并经过截面________。
3、杆件轴向拉伸或压缩时 ,其横截面上的正应力是________散布的。
轴向拉伸与压缩习题及解答

轴向拉伸与压缩习题及解答轴向拉伸与压缩习题及解答⼀、判断改错1、构件内⼒的⼤⼩不但与外⼒⼤⼩有关,还与材料的截⾯形状有关。
答:错。
静定构件内⼒的⼤⼩之与外⼒的⼤⼩有关,与材料的截⾯⽆关。
2、杆件的某横截⾯上,若各点的正应⼒均为零,则该截⾯上的轴⼒为零。
答:对。
3、两根材料、长度都相同的等直柱⼦,⼀根的横截⾯积为1A ,另⼀根为2A ,且21A A >。
如图所⽰。
两杆都受⾃重作⽤。
则两杆最⼤压应⼒相等,最⼤压缩量也相等。
答:对。
⾃重作⽤时,最⼤压应⼒在两杆底端,即max max N All A Aνσν=== 也就是说,最⼤应⼒与⾯积⽆关,只与杆长有关。
所以两者的最⼤压应⼒相等。
最⼤压缩量为 2max max22N Al l l l A EA Eνν??===即最⼤压缩量与⾯积⽆关,只与杆长有关。
所以两杆的最⼤压缩量也相等。
4、受集中⼒轴向拉伸的等直杆,在变形中任意两个横截⾯⼀定保持平⾏。
所以宗乡纤维的伸长量都相等,从⽽在横截⾯上的内⼒是均匀分布的。
答:错。
在变形中,离开荷载作⽤处较远的两个横截⾯才保持平⾏,在荷载作⽤处,横截⾯不再保持平⾯,纵向纤维伸长不相等,应⼒分布复杂,不是均匀分布的。
5、若受⼒物体内某电测得x 和y ⽅向都有线应变x ε和y ε,则x 和y ⽅向肯定有正应⼒x σ和y σ。
答:错,不⼀定。
由于横向效应作⽤,轴在x ⽅向受拉(压),则有x σ;y ⽅向不受⼒,但横向效应使y ⽅向产⽣线应变,y x εενε'==-。
A 1(a) (b)⼆、填空题1、轴向拉伸的等直杆,杆内的任⼀点处最⼤剪应⼒的⽅向与轴线成(45o)2、受轴向拉伸的等直杆,在变形后其体积将(增⼤)3、低碳钢经过冷做硬化处理后,它的(⽐例)极限得到了明显的提⾼。
4、⼯程上通常把延伸率δ>(5%)的材料成为塑性材料。
5、⼀空⼼圆截⾯直杆,其内、外径之⽐为0.8,两端承受⼒⼒作⽤,如将内外径增加⼀倍,则其抗拉刚度将是原来的(4)倍。
3--轴向拉压杆的变形

第三章练习之三轴向拉、压的变形
班级姓名学号2009-9-15
一、填空
1、杆件在外力作用下发生变形,随外力取消即随之消失的变形叫。
2、杆件在轴向力作用下杆的长度发生变化,杆件长度的改变量叫。
3、胡克定理表明在弹性范围内,杆件的纵向变形与成正比,与成反比。
4、E被称为是材料的。
它反映了某种材料的
能力,它常用的单位是。
5、EA被称为是,它反映了某种材料制成的杆件
抵抗的能力。
6、胡克定理的表达式为。
应用胡克定理计算变形的前提条件
是,。
7、单位长度的变形叫。
8、胡克定理(应力与应变)的表达式可写成,它表明在弹性范围内。
二、名词解释
1、塑性变形
2、横向变形
三、计算
1、杆件的长为4m,截面积为250mm2 ,受到拉力32KN,杆件的弹性模
量E=2.0×105Mpa,试计算杆件的伸长量
2、已知杆件的线应变为0.001,试计算当杆长为5米时杆件的变形量
3、试计算A、B、C三点的位移,A1=120×120 mm2 A2=240×240mm2
A3=370×370mm2,材料的弹性模量为E=1.5×104Mpa
3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
项目三轴向拉伸与压缩
一、填空题:
1、内力是由引起的杆件内个部分间的。
2、求内力的基本方法是。
3、直杆的作用内力称。
其正负号规定为:当杆件受拉而伸长时为正,其方向截面。
4、截面法就轴力的步骤为:、、。
5、轴力图用来表达,画轴力图时用的坐标表示横截面位置,坐标表示横截面上的轴力。
6、轴力图中,正轴力表示拉力,画在轴的。
7、轴力的大小与外力有关。
与杆件截面尺寸、材料(有关、无关)。
8、应力是,反应了内力的分布集度。
单位,简称。
9、1pa= N/mm2 = N/m2。
1Mpa= pa。
10、直杆受轴力作用时的变形满足假设,根据这个假设,应力在横截面上分布,计算公式为。
11、正应力是指。
12、在荷载作用下生产的应力叫。
发生破坏是的应力叫。
许用应力是工作应力的;三者分别用符号、、表示。
13、当保证杆件轴向拉压时的安全,工作应力与许用应力应满足关系式:。
14、等截面直杆,受轴向拉压力作用时,危险截面发生在处。
而变截面杆,强度计算应分别进行检验。
15、轴向拉压杆的破坏往往从开始。
16、杆件在轴向力作用下长度的改变量叫,用表示。
17、胡克定律表明在范围内,杆件的纵向变形与及,与杆件的成正比。
18、材料的抗拉、压弹性模量用表示,反映材料的能力。
19、EA称作材料的,它反映了材料制成一定截面尺寸后的杆件的抗拉、压能力。
EA越大,变形越。
20、ε叫作,指单位长度的变形。
21、泊松比又叫,ν= ,应用范围为弹性受力范围。
二、计算题:
1、试计算轴向拉压杆指定截面的轴力。
2、绘制图示杆件的轴力图。
3、求图示结构中各杆的轴力。
4、用绳索起吊管子如图所示。
若构件重W=10KN ,绳索的直径d=40mm ,许用
30 20KN
B 45
C 45
5、图示支架中,荷载P=100KN。
杆1为圆形截面钢杆,其许用应力[σ]拉=150MPa,杆2位正方形截面木杆,其许用应力[σ]压=4MPa。
试确定钢杆的直径d和木杆截面的边长c。
C
6、钢杆长l=2m,截面面积A=200 mm2,受到拉力P=32KN的作用,钢杆的弹性模量E=2.0×105MPa,试计算此钢杆的伸长量Δl。
7、若已知钢丝的应变ε=0.00055,问钢丝在10m,20m,长度内的绝对伸长量各是多少?。
