第35届全国部分地区大学生物理竞赛考题和答案
物理竞赛1-35届真题分类04刚体力学（无答案）
物理竞赛1-35届真题分类04刚体⼒学（⽆答案）真题分类—刚体⼒学（21届复赛）六、(20分)如图所⽰，三个质量都是m 的刚性⼩球A 、B 、C 位于光滑的⽔平桌⾯上（图中纸⾯），A 、B 之间，B 、C 之间分别⽤刚性轻杆相连，杆与A 、B 、C 的各连接处皆为“铰链式”的（不能对⼩球产⽣垂直于杆⽅向的作⽤⼒）．已知杆AB 与BC 的夹⾓为，< /2．DE 为固定在桌⾯上⼀块挡板，它与AB 连线⽅向垂直．现令A 、B 、C ⼀起以共同的速度v 沿平⾏于AB 连线⽅向向DE 运动，已知在C 与挡板碰撞过程中C 与挡板之间⽆摩擦⼒作⽤，求碰撞时当C 沿垂直于DE ⽅向的速度由v 变为0这⼀极短时间内挡板对C 的冲量的⼤⼩．⼆、（23届复赛）（25分）如图所⽰，⼀根质量可以忽略的细杆，长2L ，两端和中⼼处分别固连着质量为m 的⼩球B 、D 和C ，开始时静⽌在光滑的⽔平桌⾯上。
桌⾯上另有⼀质量为M 的⼩球A ，以⼀给定的速度Vo 沿垂直于杆DB 的⽅向与右端⼩球B 作弹性碰撞求刚碰后⼩球A 、B 、C 、D 的速度，并详细讨论以后可能发⽣的运动情况。
由杆的刚性条件有 D C C B ''''-=-v v v v （21）（19）式的⾓动量参考点设在刚要发⽣第⼆次碰撞时与D 球重合的空间点．把（18）、（19）、（20）、（21）式与（1）、（2）、（3）、（4）式对⽐，可以看到它们除了⼩球B 和D 互换之外是完全相同的．因此它们也有两个解 C 0'=v （22）和 C 0456M M m'=+v v （23）C（27届复赛）三、（ 22 分）如图，⼀质量均匀分布的刚性螺旋环质量为m ，半径为 R ，螺距H =πR ，可绕竖直的对称轴OO ′，⽆摩擦地转动，连接螺旋环与转轴的两⽀撑杆的质量可忽略不计．⼀质量也为 m 的⼩球穿在螺旋环上并可沿螺旋环⽆摩擦地滑动,⾸先扶住⼩球使其静⽌于螺旋环上的某⼀点 A ，这时螺旋环也处于静⽌状态．然后放开⼩球，让⼩球沿螺旋环下滑，螺旋环便绕转轴 OO ′，转动．求当⼩球下滑到离其初始位置沿竖直⽅向的距离为 h 时，螺旋环转动的⾓速度和⼩球对螺旋环作⽤⼒的⼤⼩．（29届复赛）三、（25分）如图所⽰，两根刚性轻杆AB 和BC 在B 段牢固粘接在⼀起，AB 延长线与BC 的夹⾓α为锐⾓，杆BC 长为l ，杆AB 长为αcos l 。
第35届全国中学生物理竞赛决赛训练试题第01套-解答v1
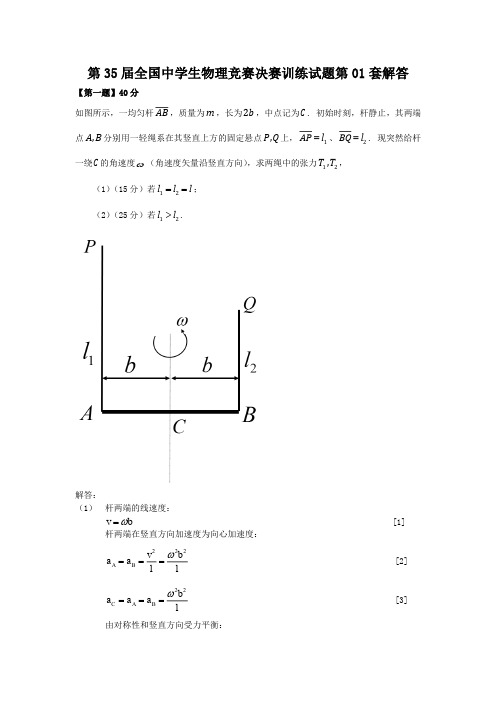
第35届全国中学生物理竞赛决赛训练试题第01套解答【第一题】40分如图所示，一均匀杆AB ，质量为m ，长为2b ，中点记为C . 初始时刻，杆静止，其两端点,A B 分别用一轻绳系在其竖直上方的固定悬点,P Q 上，=1AP l 、=2BQ l . 现突然给杆一绕C 的角速度ω（角速度矢量沿竖直方向），求两绳中的张力12,T T ， （1）（15分）若==12l l l ；（2）（25分）若>12l l .解答：（1） 杆两端的线速度：v b ω= [1] 杆两端在竖直方向加速度为向心加速度：222A B v b a a l l ω=== [2]22C A B b a a a lω===[3]由对称性和竖直方向受力平衡：12T T = [4] 12C T T mg ma +-= [5]解得：22121()2b T T m g lω==+ [6][1][2][4][5]各2分 [3]3分 [6]4分（2） 同（1）的第一步：22211A v b a l l ω== [7]22222B v b a l l ω== [8]设：A C a a b β=- [9]BC a a b β=+[10]可解得：2212122C l l a b l l ω+=[11]212122l l b l l βω-=[12]平衡和牛顿第二定律：21T b T b I β-=[13] 2211(2)123I m b mb ==[14] 12C T T mg ma +-=[15]解得：221211221(b )23l l T m g l l ω+=+[16]221221221(b )23l l T m g l l ω+=+[17][7][8][11][12][13][15]各2分[9][10][14]各1分 [16][17]各5分【第二题】40分如图，这时是一种三角打孔机的结构。
其中持钻架A被限制平行运动，A中间有一个正三角形的内孔，边长为l。
第35届全国中学生物理竞赛决赛训练试题第07套-解答v2
第35届全国中学生物理竞赛决赛训练试题第07套解答【第一题】40分如图所示，有一长为2l的轻质细杆，两端各固连一个质量为m的小球（A和B），中点处有一原长为0，劲度系数为k的轻质弹簧，弹簧一端与杆的中点相连，另一端与一个套在杆上质量也是m的小球C相连，这个小球可以沿杆无摩擦滑动. 初始时系统静止在光滑水平桌面上，一个质量也是m的小球D以速度v0与小球B发生弹性正碰，v0垂直于杆.(1)求碰后瞬间四个小球的速度.(2)在碰后的运动中，如果小球C稍稍偏离杆的中点，为了在中点附近相对于杆做简谐振动，弹簧的劲度系数k至少多大？(3)在(2)的条件下，求出振动的周期.答案(1)选择杆中点为转轴，ABC系统的转动惯量I0=2ml2[1]设碰后ABC系统质心速度（即C的速度）为v C，角速度为ω0，小球D的速度为v D，则有动量守恒mv0=3mv C+mv D[2]角动量守恒mv0l=mv D l+I0ω0[3]机械能守恒1 2mv02=123mv C2+12mv D2+12I0ω02[4]联立解得v C=4v011v D=−v011ω0=6v011l[5] 则有v A=v C−ω0l=−2v011v B=v C+ω0l=10v011[6] (18分，每式2分)(2)在ABC系统质心系研究此问题. 假设杆中点到质心的距离为x，则小球C到质心的距离为2x，C偏离杆中点共3x. 此时系统绕质心的转动惯量I=m(l+x)2+m(l−x)2+m(2x)2=2ml2+6mx2[7] 角动量守恒，有Iω=I0ω0[8] 所以转动动能为T1=12Iω2=L22I=L24m(l2+3x2)[9]其中L=I0ω0=12mv0l/11表示系统的角动量. 研究径向运动时，转动动能化为有效势能的一部分. 有效势能V eff=12k(3x)2+T1=12k(3x)2+L24m(l2+3x2)[10]利用小量展开1/(1+α)≈1−α，有V eff≈92kx2−3L24ml4x2+L24ml2[11]要形成简谐振动，x=0处V eff应极小，即要求9 2k−3L24ml4>0[12]所以k min=L26ml4=24mv02121l2[13](14分，每式2分)(3)由(14)式，等效劲度系数K=9k−3L22ml4=9k−216mv02121l2[14]径向运动的动能T2=12(2m)ẋ2+12(2ẋ)2=3mẋ2[15]等效质量M=6m[16] 所以周期T=2π√MK =2π√2m3k−72mv02121l2[17](8分，每式2分)【第二题】40分如图所示，在水平地面上放着一个物体，其由两个全同的刚体在O点光滑铰接组成。
届全国部分地区大学生物理竞赛试卷及答案
，
v|| ＝
。
２.如图所示，由三根相同的均匀细杆连成的等边
三角形刚体框架每边长a,总质量M。将框架相对于过框边上任意一点
P且垂直于框架平面的转轴的转动惯量记为 IP ，所有 IP 中最小者
I min 所对应的P点必定在
,所有 IP 中最大者
I max 与 I min 之间的差值为
。
准考证号
姓名
考场
1
附注：（1）如果你在 S 系中直接运用费马原理 求解，本题最高得分为 20 分； （2）如果你运用相对论知识结合静态抛物线光 学聚焦知识求解，本题最高得分只能为 6 分。
10
第 28 届全国部分地区大学生物理竞赛试卷
参考答案
1. v v0 ,
v|| 2v0 cot ;
2.各边中点，
1 Ma 2 ；
3.
k
,
ma0 ;
4
mk
4. n0e mgh kT , p0emgh kT ;
5. 1 , 13
1; 12
6. mv0 sin , 2mv0 cos ;
qB
qB
7.
0 IR2
2( R 2
x2
3
)2
,
0r 2 R 2
2(R2
x
2
)
3 2
;
8.
1.22 .
d
3.36 104 ;
线，它的旋转半径（注意：并非螺旋线的曲率半径） R
，
螺距 H
。
7.半径 R ，电流 I 的大圆环，在其中央轴距环心 x 处的
磁感应强度大小为 B(x)
。
有一半径为 r R 的小圆环，环心位于 x 点，环平面与
大学物理竞赛选拔试卷及答案
A BDl 0v大学物理竞赛选拔试卷1.（本题6分）一长度为l的轻质细杆，两端各固结一个小球A、B（见图），它们平放在光滑水平面上。
另有一小球D，以垂直于杆身的初速度v0与杆端的Α球作弹性碰撞．设三球质量同为m，求：碰后（球Α和Β）以及D球的运动情况．2.（本题6分）质量m=10kg、长l=40cm的链条，放在光滑的水平桌面上，其一端系一细绳，通过滑轮悬挂着质量为m1=10kg的物体，如图所示．t=0时,系统从静止开始运动,这时l1=l2=20cm<l3．设绳不伸长，轮、绳的质量和轮轴及桌沿的摩擦不计，求当链条刚刚全部滑到桌面上时，物体m1速度和加速度的大小．3.（本题6分）长为l的匀质细杆，可绕过杆的一端O点的水平光滑固定轴转动，开始时静止于竖直位置．紧挨O点悬一单摆，轻质摆线的长度也是l，摆球质量为m．若单摆从水平位置由静止开始自由摆下，且摆球与细杆作完全弹性碰撞，碰撞后摆球正好静止．求：(1)细杆的质量．(2)细杆摆起的最大角度?．4.（本题6分）质量和材料都相同的两个固态物体，其热容量为C．开始时两物体的温度分别为T1和T2（T1>T2）．今有一热机以这两个物体为高温和低温热源，经若干次循环后，两个物体达到相同的温度，求热机能输出的最大功A max．5.（本题6分）如图所示，为某种一定量的理想气体进行的一个循环过程，它是由一个卡诺正循环12341和一个卡诺逆循环15641组成．已知等温线温度比T1/T2=4，卡诺正逆循环曲线所包围面积大小之比为S1/S2=2．求循环的效率?．6.（本题6分）将热机与热泵组合在一起的暖气设备称为动力暖气设备，其中带动热泵的动力由热机燃烧燃料对外界做功来提供.热泵从天然蓄水池或从地下水取出热量，向温度较高的暖气系统的水供热.同时，暖气系统的水又作为热机的冷却水.若燃烧1kg燃料，锅炉能获得的热量为H，锅炉、地下水、暖气系统的水的温度分别为210℃，15℃，60℃.设热机及热泵均是可逆卡诺机.试问每燃烧1kg燃料，暖气系统所获得热量的理想数值（不考虑各种实际损失）是多少？7.（本题5分）如图所示，原点O是波源，振动方向垂直于纸面，波长是?．AB为波的反射平面，反射时无相位突变?．O点位于A点的正上方，hAO=．Ox轴平行于AB．求Ox轴上干涉加强点的坐标（限于x≥0）．8.（本题6分）一弦线的左端系于音叉的一臂的A点上，右端固定在B点，并用T=7.20N的水平拉力将弦线拉直，音叉在垂直于弦线长度的方向上作每秒50次的简谐振动（如图）．这样，在弦线上产生了入射波和反射波，并形成了驻波．弦的线密度?=2.0g/m，弦线上的质点离开其平衡位置的最大位移为4cm．在t=0时，O点处的质点经过其平衡位置向下运动，O、B之间的距离为L=2.1m．试求：(1)入射波和反射波的表达式；(2)驻波的表达式．9.（本题6分）用每毫米300条刻痕的衍射光栅来检验仅含有属于红和蓝的两种单色成分的光谱．已知红谱线波长?R在0.63─0.76?m范围内，蓝谱线波长?B在0.43─0.49?m范围内．当光垂直入射到光栅时，发现在衍射角为24.46°处，红蓝两谱线同时出现．(1)在什么角度下红蓝两谱线还会同时出现？(2)在什么角度下只有红谱线出现？10.（本题6分）如图所示，用波长为?=632.8nm(1nm=10-9m)的单色点光源S照射厚度为e=1.00×10-5m、折射率为n2=1.50、半径为R=10.0cm的圆形薄膜F，点光源S与薄膜F的垂直距离为d=10.0cm，薄膜放在空气（折射率n1=1.00）中，观察透射光的等倾干涉条纹．问最多能看到几个亮纹？（注：亮斑和亮环都是亮纹）．11.（本题6分）507⨯双筒望远镜的放大倍数为7，物镜直径为50mm.据瑞利判据，这种望远镜的角分辨率多大？设入射光波长为nm550.眼睛瞳孔的最大直径为7.0mm.求出眼睛对上述入射光的分辨率.用得数除以7，和望远镜的角分辨率对比，然后判断用这种望远镜观ha察时实际起分辨作用的是眼睛还是望远镜.12.（本题6分）一种利用电容器控制绝缘油液面的装置示意如图.平行板电容器的极板插入油中，极板与电源以及测量用电子仪器相连，当液面高度变化时，电容器的电容值发生改变，使电容器产生充放电，从而控制电路工作.已知极板的高度为a ，油的相对电容率为εr ，试求此电容器等效相对电容率与液面高度h 的关系.13.（本题6分）在平面螺旋线中，流过一强度为I 的电流，求在螺旋线中点的磁感强度的大小．螺旋线被限制在半径为R 1和R 2的两圆之间，共n 圈．[提示：螺旋线的极坐标方程为b a r +=θ，其中a ，b 为待定系数]14.（本题6分）一边长为a 的正方形线圈，在t =0时正好从如图所示的均匀磁场的区域上方由静止开始下落，设磁场的磁感强度为B(如图)，线圈的自感为L ，质量为m ，电阻可忽略．求线圈的上边进入磁场前，线圈的速度与时间的关系．15.（本题6分）如图所示，有一圆形平行板空气电容器，板间距为b ，极板间放一与板绝缘的矩形线圈．线圈高为h ，长为l ，线圈平面与极板垂直，一边与极板中心轴重合，另一边沿极板半径放置．若电容器极板电压为U 12=U m cos ?t ，求线圈电压U 的大小．16.（本题6分）在实验室中测得电子的速度是0.8c ，c 为真空中的光速．假设一观察者相对实验室以0.6c 的速率运动，其方向与电子运动方向相同，试求该观察者测出的电子的动能和动量是多少？（电子的静止质量m e ＝9.11×10?31kg ）17.（本题6分）已知垂直射到地球表面每单位面积的日光功率（称太阳常数）等于1.37×103W/m 2． (1)求太阳辐射的总功率．(2)把太阳看作黑体，试计算太阳表面的温度．（地球与太阳的平均距离为1.5×108km ，太阳的半径为6.76×105km ，?=5.67×10-8W/(m 2·K 4)） 18.（本题6分））已知氢原子的核外电子在1s 态时其定态波函数为a r a /3100e π1-=ψ，式中220em h a e π=ε．试求沿径向找到电子的概率为最大时的位置坐标值．(?0=8.85×10-12C 2·N -1·m -2，h =6.626×10-34J ·s ，m e =9.11×10-31kg ，e =1.6×10-19C)参考答案1.（本题6分）解：设碰后刚体质心的速度为v C ，刚体绕通过质心的轴的转动的角速度为?，球D 碰后的速度为v ?，设它们的方向如图所示．因水平无外力，系统动量守恒：C m m m v v v )2(0+'=得：(1)20C v v v ='-1分 弹性碰撞，没有能量损耗，系统动能不变；222220])2(2[21)2(212121ωl m m m m C ++'=v v v ，得(2)22222220l C ω+='-v v v 2分 系统对任一定点的角动量守恒,选择与A 球位置重合的定点计算．A 和D 碰撞前后角动量均为零，B 球只有碰后有角动量，有])2([0C B l ml ml v v -==ω，得(3)2lC ω=v 2分(1)、(2)、(3)各式联立解出lC 00;2;0vv v v ==='ω。
大学生物理竞赛试题及解答
其中 ^i 代表 x 轴正方向上的单位矢量. 你能否举出理由说明此结果并不正确. 31 ( 6 分) 用牛顿环测定透镜曲率半径实 验中, 为什么有时圆环条纹的中心并非暗斑, 甚至出现亮班 ( 理论上应是暗斑) ? 用什么数 据处理方法能消除它对曲率半径测量的影 响? 四、 在下面两题中任选一题作答. ( 10 分)
(D ) 此问题中谈 a 点、 b 点的电势无意
义 .
71 ( 3 分) 如图示, S 、 S 1、 S 2 为狭缝, P 1、 为线偏振片 (P 及 P ′ 可以撤去) , 其 P 2、 P、 P′
率, ∃ v 为一固定的速率间隔, 则速率在 v ± ∃ v 范围内的分子的百分率随着温度的增加 将 , 速率在 v p 到 v 之间的分子 的百分率随着温度的增加将 . 31 ( 2 分) 从单一热源吸取热量并将其完 全用来对外作功, 是不违反热力学第二定律 的, 例如 过程就是这种情况 . 41 ( 5 分) 如图示, 截面积为 A 、 单位长度 上匝数为 n 的螺绕环上套一边长为 l 的方形 线 圈, 今 在 方 形 线 圈 中 通 以 交 流 电 流 I = I 0 sin Ξt, 螺绕环两端为开端, 则其间电动势的 大小为
中 P 1 和 P 2 的偏振化方向互相垂直, P 和 P ′ 的偏振化方向互相平行, 且与 P 1、 P 2 的偏振 化方向皆成 45° 角. 在下列四种情况下, 屏上 有无干涉条纹. ( 四种情况全部填对才能得 分).
① 撤 掉 P 、P ′ , 保 留 P 1、P 2 , 屏 上 干涉条纹; ② 撤掉 P ′ 保留 P 、 P 1、 P 2 , 屏上 干涉条纹; ③ 撤 掉 P , 保 留 P 1、P 2、P ′ , 屏上 干涉条纹; ④ P 1、P 2、P 、P ′ 同 时 存 在, 屏 上 干涉条纹; ( 81 2 分) 卢瑟福 Α粒子散射实验证实了 , 斯 特 恩—盖 拉 赫 实 验 证 实 了
2018年第35届全国物理竞赛复赛试题与解答
L mv0 R h
该物体能绕地球做周期运动，其能量应 E0 由此条件以及 E 的表达式，得
2GM 2GM ，即 v0 ① Rh Rh 物体能绕地球做持续的周期运动，不能坠落到地球表面。当物体初始速度 v0 降低到某 个值 v0min 时，物体运动的椭圆轨道将与地球表面相切，设这种情况下物体在与地球表面相
-4-
第 35 届全国中学生物理竞赛复赛理论考试试题解答
2018 年 9 月 22 日 一、 （40 分） 假设地球是一个质量分布各向同性的球体， 地球自转及地球大气的影响可忽略。 从地球上空离地面高度为 h 的空间站发射一个小物体，该物体相对于地球以某一初速度运 动，初速度方向与其到地心的连线垂直。已知地球半径为 R ，质量为 M ，引力常量为 G 。 （1）若该物体能绕地球做周期运动，其初速度的大小应满足什么条件？ （2）若该物体的初速度大小为 v0 ，且能落到地面，求其落地时速度的大小和方向（即 速度与其水平分量之间的夹角） 、以及它从开始发射直至落地所需的时间。 已知：对于 c 0 ， b 2 4ac 0 ，有
-26
kg ，普朗克常量 h 6.6 1034 J s ，真空中的光速 c 3.0 108 m s1 。
（1）忽略激发态的能级宽度，求反冲能，以及在考虑核反冲和不考虑核反冲的情形下，57Fe 从第一激发态跃迁到基态发出的光子的频率之差； （2）忽略激发态的能级宽度，求反冲能，以及在考虑核反冲和不考虑核反冲的情形下，57Fe 从基态跃迁到激发态吸收的光子的频率之差； （3）考虑激发态的能级宽度，处于第一激发态的静止原子核 57 Fe* 跃迁到基态时发出的光子 能否被另一个静止的基态原子核 57 Fe 吸收而跃迁到第一激发态 57 Fe* （如发生则称为共振吸 收）？并说明理由。 （4）现将 57Fe 原子核置于晶体中，该原子核在跃迁过程中不发生反冲。现有两块这样的晶 体，其中一块静止晶体中处于第一激发态的原子核 57 Fe* 发射光子，另一块以速度 V 运动的 晶体中处于基态的原子核 57Fe 吸收光子。当速度 V 的大小处于什么范围时，会发生共振吸 收？如果由于某种原因，到达吸收晶体处的光子频率发生了微小变化，其相对变化为 1010 ， 试设想如何测量这个变化（给出原理和相关计算）？
第35届全国中学生物理竞赛决赛试题(word版)
第35届全国中学生物理竞赛决赛试题(word版)35届全国中学生物理竞赛决赛理论考试试题（XXX）1、（35分）如图，半径为R、质量为M的半球静置于光滑水平桌面上，在半球顶点上有一质量为m、半径为r的匀质小球。
某时刻，小球收到微扰由静止开始沿半球表面运动。
在运动过程中，小球相对半球的位置由角位置$\theta$描述，$\theta$为两球心连线与竖直线的夹角。
已知小球绕其对称轴的转动惯量为$\frac{2}{5}mr^2$，小球与半球间的动摩擦因数为$\mu$，假定最大静摩擦力等于滑动摩擦力。
重力加速度大小为g。
1）（15分）小球开始运动后在一段时间内做纯滚动，求在此过程中，当小球的角位置为$\theta_1$时，半球运动的速度大小$V_M(\theta_1)$和加速度大小$a_M(\theta_1)$；2）（15分）当小球纯滚动到角位置$\theta_2$时开始相对于半球滑动，求$\theta_2$所满足的方程（用半球速度大小$V_M(\theta_2)$和加速度大小$a_M(\theta_2)$以及题给条件表示）；3）（5分）当小球刚好运动到角位置$\theta_3$时脱离半球，求此时小球质心相对于半球运动速度的大小$v_m(\theta_3)$。
2、（35分）平行板电极板1和2的面积均为S，水平固定放置，它们之间的距离为d，接入如图所示的电路中，电源的电动势记为U。
不带电的导体薄平板3（厚度忽略不计）的质量为m、尺寸与电极板相同。
平板3平放在极板2的正上方，且与极板2有良好的电接触。
整个系统置于真空室内，真空的介电常量为$\epsilon$。
合电键K后，平板3与极板1和2相继碰撞，上下往复运动。
假设导体板间的电场均可视为匀强电场；导线电阻和电源内阻足够小，充放电时间可忽略不计；平板3与极板1或2碰撞后立即在极短时间内达到静电干衡；所有碰撞都是完全非弹性的。
重力加速度大小为g。
1）（17分）电源电动势U至少为多大？2）（18分）求平板3运动的周期（用U和题给条件表示）。
第35届全国中学生物理竞赛决赛训练试题第03套-解答
第35届全国中学生物理竞赛决赛训练试题第03套解答【第一题】40分如图所示，一个质量为m ，半径为R 的匀质圆环静止竖立在地面上，二者间的摩擦系数为μ.图中A 点所在直径与竖直方向夹角为()0/2θθπ<<，现在在A 点瞬间给予圆环一个冲量I ，与竖直方向夹角为()0/2φφπ<<.假设收到冲击后圆环竖直方向上速度为零。
(1) 参数μ,θ,ϕ满足何种条件时，圆环最低点（M 处）将与地面发生滑动？ (2) 分别在发生滑动与不发生滑动的条件下求出末态圆环的质心速度和转动角速度. (3) 在一定条件下，圆环可能在一段时间之后滚回初始位置. 这要求参数μ,θ,ϕ满足何种条件？解答：(1) 由于冲量是瞬间作用的，可以不考虑重力的作用. 考虑到圆环竖直方向没有运动，地面支持力的冲量为cos I ϕ.设摩擦力冲量为i .先确定冲量i 的方向，如果地面光滑，则容易看出sin C v I ϕ=,()sin //C I mR v R ωϕθ=-<，故最低点速度向右，由此判断摩擦力向左. 水平方向动量定理：sin C mv I i ϕ=- [1]对质心C 的角动量定理：()2sin mR IR iRωϕθ=-+ [2]假设底部没有滑动，则C v R ω= [3]联立以上三式可解得()sin sin 2I i ϕϕθ--⎡⎤⎣⎦= [4]而摩擦力可提供的冲量最大为max cos i I μϕ=,故发生滑动摩擦的条件是()sin sin cos 2ϕϕθμϕ--⎡⎤⎣⎦<[5](16分，判断摩擦力方向2分，[3]式2分，其他四式各3分)（2）不发生滑动摩擦的情况下，联立[1]-[3]式可解得()sin sin 2C I v mϕϕθ+-⎡⎤⎣⎦=,()sin sin 2I mRϕϕθω+-⎡⎤⎣⎦=[6] 发生滑动得情况下，联立[1]、[2]式以及cos i I μϕ=可解得sin cos c I I v mϕμϕ-=, ()cos sin I I mR μϕϕθω+-=[7](12分，两种情况各6分)（3）要滚离初始位置再滚回，首先要求I 作用完成后圆环底部与地面有相对滑动（否则将一直匀速纯滚动，不可能滚回来），即要满足[5]式.在这个前提下，就有可能质心速度向右，但逆时针转动，在地面摩擦力作用下达到纯滚动时向左运动，最终回到初始位置. 以地面上的固定点M 为参考点，I 作用完成后的运动中，重力与支持力的力矩相互抵消，摩擦力过M 点不产生力矩，故圆环角动量守恒. 圆环能滚回来要求初始时角动量向纸面外（逆时针转动）.由于冲量I 作用过程中支持力和摩擦力对M 点也没有力矩，故这就要求M 在I 的延长线上方，即/2ϕθ<.所以参数应满足的条件为()cos sin sin /2/2μϕϕϕθϕθ⎧<--⎡⎤⎪⎣⎦⎨<⎪⎩ [8](12分，利用上一问解得的速度和角速度计算纯滚动速度时得到结果也可，其他方法也可)【第二题】40分在数轴的原点有一只球形猪，每过0t 时间，猪就会随机向左或者向右走单位长度1。
第35届全国部分地区大学生物理竞赛试卷及答案(2018年12月)
������
杆静止，后因微小扰动，细杆开始运动，设系统处处无
������
摩擦。假设 ������ 端可以沿地面朝右滑动，但因受约束，不
会离开地面；������ 端可以沿着墙面朝下滑动，但不受相应
������
的约束，故可以离开墙面。试问在 ������ 端未达墙的底端 ������
������
之前，������ 端会否离开墙面？若会，再问 ������ 达何值时 ������ 端
如图 2 所示，每边长为 ������ 的均匀正方形电阻薄平板，已测得 ������、������ 两端间电阻 ������������������ = 5Ω 。若将每边长都增为 2������ ，质材不变， 试分析地判定相应的电阻 ���������∗��������� = ？
������ ������1
考场
准考证号
三、限做题（根据考生类别选做）
15.（20 分）相对论中，质点在惯性系 ������ 中静止时，它的质量 ������0 称为静质量，质点内在的能
量称为静能 ������0 ，且有
������0 = ������0������2
质点在 ������ 系中运动时，速度记为 ���⃑��� ，质点质量 ������ 和内含的能量 ������ 分别为
大学生物理竞赛试题大全
13.（15 分）如图所示，轻的细杆 ������������������ 的 ������ 端靠在竖直
墙上，������ 端落在水平地面上，������ 端、������ 端和杆的中点 ������
������
处各有质量相同的固定小球。开始时图中角 ������ = 0 ，细
������ = ������0 , ������ = ������������2
第35届全国中学生物理竞赛决赛训练试题第05套解答v4
第35届全国中学生物理竞赛决赛训练试题 第05套解答【第一题】40分疯狂的科学家想制造一条太空锁链.在地球赤道上两处，立起等长的足够坚固、长度可调的两根柱子，忽略地球自转，地球半径为R ，地表重力加速度为g .在两根柱子的顶端之间连接一根质量线密度为λ的链条，链条处于平衡状态. 锁链所能承受的最大张力为max T .若要求锁链最低点距离地心为0r 、有张力2002gR T r λ=，已知2max 00gR T T r λ<+，求在锁链恰好不断裂时：（1） 端点处链条切线与柱子的夹角C α； （2） 锁链的形状()r θ； （3） 两根柱子之间的夹角C φ；解答：易知引力势能为：2P R E mg r=-[1]由虚功原理，可以得到r 处张力T 的大小：()20011T T ds dsgR r r λ⎛⎫-=- ⎪⎝⎭()20011T T ds dsgR r r λ⎛⎫-=-⎪⎝⎭20011T T gR r r λ⎛⎫=+- ⎪⎝⎭[2]由于对称性，取一半锁链对地心有力矩平衡：00sin Tr T r α=[3]极坐标下有几何关系：sin α==[4]联立以上方程可得：22000011T gR T r r r λ⎡⎤⎛⎫+-=⎢ ⎪⎝⎭⎣ [5]作换元1u r=：()200011gR u u T u λ⎡⎤+-=⎢⎣进一步整理：()20000gR u u u u T λ⎡⎤+-=⎢⎥⎣⎦[6]由于θ↑r ↑u ↓，于是：d θ= [7]代入2002T gR u λ=及00r r θ==可以得到:()1arcsin1022rrπθθ⎡⎤⎛⎫=-+>⎪⎢⎥⎝⎭⎣⎦[8]()0rθ=>[9]()()()0r rθθθ=-<[10] 由[2]可知：11max0max220013CT T Trr gR r gRλλ--⎛⎫⎛⎫-=-=-⎪ ⎪⎝⎭⎝⎭[11]代入[3]有Cα：()2max00max02max max02arcsin1arcsin3CT TT T rgRT g T r gRλαλλ-⎡⎤⎡⎤=-=-⎢⎥⎢⎥⎣⎦⎣⎦[12]代入[8]有：max0212arcsin422C CT rgRπφθλ⎡⎤⎛⎫==--⎢⎥⎪⎝⎭⎦[13][1-5]共10分[8][9]共10分[12]10分[13]10分【第二题】40分记太阳质量为sM、地球质量为eM、火星质量为MM、地球半径为er、火星半径为mr.认为地球和火星在同一平面内绕太阳圆周运动，轨道半径分别为eR和mR. 现通过某种机制使火星突然获得一指向太阳的速度v.（1）（15分）若火星此后的轨道可以与地球轨道相交，求v的最小值.（2）（25分）在（1）的条件下，设火星在到达地球轨道附近时地球恰在轨道上该位置，在地球与火星的间距d满足,,e m e mr r d R R<<<<时，火星相对地球的速度的矢量线与地球球心的距离为b（如图）. 若火星和地球可以发生碰撞，求b的最大值.解答：（1） 202m s mm m mv GM M M R R = [1]0m m m m t e M v R M v R =[2]()()22221122s m s m m m m m t m eGM M GM M M v v M v v R R +-=+-[3]由t v =22212m ms e m e R v GM v R R R ⎛⎫=--++ ⎪⎝⎭[4]则可知v ≥[5][1]-[4]共10分[5]5分（2） ()2220rel t e m v v v v =-+[6]由0e v =2231rels em v GM v R R ⎛=--+ ⎝[7]质心系角动量守恒()rel rel m e v b v r r μμ'=+[8]能量守恒221122e m rel relm eGM M v v r r μμ'=-+ [9]其中约化质量e me mM M M M μ=+可解得)max m e b r r =+[10][6]-[9]共15分[10]10分【第三题】（40分）如图所示, 一个粗糙的, 半径为b 的半球固定在水平面上, 其顶部有一个半径a 的匀质薄球壳. 重力加速度为g .1两球球心的连线与地面夹角为0θ。
2022大学物理竞赛题标准版(含答案)
2022大学物理竞赛题标准版（含答案）理论竞赛卷考试形式：闭卷，允许带无存储功能的计算器入场考试时间：2022年12月10日上午8:30~11:30姓名准考证号__________所在高校__________专业___________________________密_________________封_____________线_____________密封线内不要答题题得序选分择填空计1～2计3～4计5～6计7～8总分附加题分-1-123评卷人气体摩尔常量R8.31JmolK真空介电常数0=8.8510-12C2/(Nm2)普朗克常数h=6.6310-34J真空介电常数0=8.8510-12C2/(Nm2)真空磁导率0=410-7H/m里德伯常数R1.09710m氢原子质量m=1.6710-27kg斯忒恩-波尔兹曼常数σ=5.67某10-8W/m2K4R1.09710m7-17-1玻尔兹曼常量k1.3810真空中光速c=3108m/基本电荷e=1.610-19C电子质量me=9.110-31kg真空中光速c=3108m/JK-1电子伏特1eV=1.610-19J维恩位移定律常数b=2.898某10-3mK-1-123这三项是公式编的，字号偏大。
字号改小后：R8.31JmolK，k1.3810JK，-1一、选择题：（单选题，每题3分，共30分）1．质量为m的质点在外力作用下，其运动方程为rAcotiBintj，式中A、B、都是正的常量．由此可知外力在t=0到t=/(2)这段时间内所作的功为（）1m2(A2B2)B．m2(A2B2)211222222C．m(AB)D．m(BA)22A．2．一座塔高24m，一质量为75kg的人从塔底走到塔顶.已知地球的质量为61024kg，从日心参考系观察，地球移动的距离为？（）（不考虑地球的转动）24A．12mB．24mC．4.0mD．3.022m3．边长为l的正方形薄板，其质量为m．通过薄板中心并与板面垂直的轴的转动惯量为（）A．12111mlB．ml2C．ml2D．ml23612244．子的平均寿命为2.2106．由于宇宙射线与大气的作用，在105m的高空产生了相对地面速度为0.998c（c为光速）的子，则这些子的（）A．寿命将大于平均寿命十倍以上，能够到达地面B．寿命将大于平均寿命十倍以上，但仍不能到达地面C．寿命虽不大于平均寿命十倍以上，但能够到达地面D．寿命将不大于平均寿命十倍以上，不能到达地面5．乐器二胡上能振动部分的弦长为0.3m，质量线密度为4104kg/m，调音时调节弦的理论竞赛卷第1页（共15页）张力F，使弦所发出的声音为C大调，其基频为262Hz.已知波速uF，则弦中的张力为（）A．1.0NB．4.2NC．7.0ND．9.9N6．一固定的超声波探测器在海水中发出频率为30000Hz的超声波，被迎面驶来的潜艇反射回来，测得反射波频率与原来的波频率之差（拍频）为241Hz．已知超声波在海水中的波速为1500m/，则潜艇的速率为()m/A．1B．2C．6D．107．如图所示，两个相同的平板电容器1和2并联，极板平面水平放置．充电后与电源断开，此时在电容器1中一带电微粒P恰好静止悬浮着。
第35届全国中学生物理竞赛决赛理论考试试题参考答案;
mg
0SU 2 d3
x
由此得，平板3在图b所示位置的加速度
a
Ftotal m
3 0 SU 2md 2
2
g
0SU 2 md 3
x
⑰
因为
0SU 2 2md 2
g
0 ，则 a
0
，平板3能一直向下加速运动。令
a a0 B(d x)
U
电键 K 后，平板 3 与极板 1 和 2 相继碰撞，上下往复运动。假设导体板之间的电场均可视为
匀强电场；导线电阻和电源内阻足够小，充放电时间可忽略不计；平板 3 与极板 1 或 2 碰撞
后立即在极短时间内达到静电平衡；所有碰撞都是完全非弹性的。重力加速度大小为 g 。
（1）电源电动势U 至少为多大？ （2）求平板3运动的周期（用U 和题给条件表示）。 已知积分公式
①
设小球转动角速度大小为，小球做纯滚动，故有
r (R r)
②
无耗散力做功，系统的机械能守恒
mg(R r)(1 cos )
1 2
MVM2
1 2m
R r cos VM 2 R r sin 2
1 2
I
2
③
式中
代入上式得
t2
d U
md 0S
ln
(3
0
SU
2
2mgd 2 ) 2U 0SU 2
0S(20SU 2 2mgd 2
mgd 2 )
⑲
平板 3 从极板 1 运动到极板 2 后，与极板 2 发生完全非弹性碰撞，速度变为零。其下表面所 带的负电荷与极板 2 所带正电荷交换后相互抵消，上表面所带电荷为
第35届全国中学生物理竞赛决赛训练试题第06套-解答v2
第35届全国中学生物理竞赛决赛训练试题 第06套【第一题】40分根据伯努利定律，流体沿着一条稳定、不可压缩的流线移动时，根据能量守恒，其动能、势能总保持为常数，也就是212v gh P const ρρ++= （1）由于圆柱比较简单，我们先计算一个质心cx v 水平运动，角速度ω（方向为图示中y 方向），半径为R ，高度为h （对称轴为y 轴，>>h R ）的圆柱受到的合力。
假设其表面的空气和圆柱保持同样的速度，并且假设圆柱转动比较快以至于其表面流体的流动可以看做沿着表面的流管进行流动，并且不同位置的高度差可以忽略，如图请先用对称性分析受到的合力方向再计算出其大小。
（13分）（2）假如圆柱质心以cz v 竖直运动，其他条件和（1）中一样，求受到的气体压力的大小和方向。
（5分）（3）作为一个简单的假设，只考虑流体对圆柱平动的影响而不考虑对其转动的影响，圆柱以初速度00ˆˆ(0)c y z v v y v z =+，角速度ˆy ωω=，求速度与时间的关系。
（12分）解答：（1）关于x-z 平面对称，合力无y 分量，速度大小关于y-z 平面对称，合力无x 分量，故合力应该延z 方向。
以柱为系，认为系统为定常理想流体。
则流体的定常流动如图所示，可以认为如图情形在y 方向是无限延伸的。
流体流场为u v +，其中u 为向x 轴负方向常量，v 为环流场，在R 处速度为R ω，随着距离圆柱的距离增大衰减。
对于环路12,C C ，分别是无限靠近圆柱和远离圆柱的两个环路，它们之间用两个从上和从下无限靠近x 轴的路径连接起来。
考察体积内流体动量变化为零()()()()120C C pds u v u v ds ρ-+++⋅=⎰【1】则有()()()()()()()()12--C C Fpds u v u v ds h pds u v u v ds ρρ=+++⋅=+++⋅⎰⎰【2】对于稳定流体()()2011=22P u v u v P u ρρ++++()()()()2201---2C F P v u v ds u u v ds v u ds v v ds h ρρρρρ⎛⎫⎛⎫=⋅++⋅+⋅+⋅ ⎪ ⎪⎝⎭⎝⎭⎰考虑到在环路2C 上<<v u ，()u v ds +⋅为环路内流体流量，则净流量为零，上式化简为()()()()()22=--=-C C Fu v ds v u ds h u v ds ρρ⋅+⋅⨯⨯⎰⎰可知合力为y 方向，其大小为()()2----x y y x C x y Fuv ds v uds h u v dx v dy ρρ=+=⎰⎰ 【3】由茹可夫斯基定理，以及将u 代换成cx v22cx F hR v πρω=【1】【2】各3分，结果方向2分，大小2分（2）在计算F 时，x 轴与z 轴是等地位的，所以圆柱延z 轴方向运动时所受到的力为22cz F hR v πρω=- 【4】负号代表方向沿x 轴负方向。
全国大学生物理竞赛历年考试习题(含答案)
全国大学生物理竞赛历年考试习题(含答案)一、选择题1. 下列哪个物理量是标量？A. 速度B. 加速度C. 力D. 质量答案：D解析：质量是标量，因为它只有大小，没有方向。
而速度、加速度和力都是矢量，它们既有大小，又有方向。
2. 下列哪个物理现象可以用牛顿第一定律解释？A. 摩擦力B. 重力C. 弹力D. 惯性答案：D解析：牛顿第一定律也被称为惯性定律，它指出一个物体如果不受外力作用，它将保持静止状态或匀速直线运动状态。
惯性是物体保持其运动状态的性质。
3. 下列哪个物理量是功的单位？A. 焦耳B. 牛顿C. 瓦特D. 库仑答案：A解析：焦耳是功和能量的单位，1焦耳等于1牛顿的力作用在物体上，使物体在力的方向上移动1米的距离所做的功。
4. 下列哪个物理现象可以用安培环路定理解释？A. 电流B. 电阻C. 磁场D. 电压答案：C解析：安培环路定理是电磁学中的一个重要定理，它描述了磁场与电流之间的关系。
该定理指出，通过一个闭合路径的磁场线积分等于该路径所包围的电流总和。
5. 下列哪个物理现象可以用波尔兹曼分布律解释？A. 热力学B. 统计力学C. 量子力学D. 相对论答案：B解析：波尔兹曼分布律是统计力学中的一个重要定律，它描述了在热力学平衡状态下，不同能量状态的粒子数目的分布。
该定律是统计力学的基础之一。
6. 下列哪个物理现象可以用薛定谔方程解释？A. 光的干涉B. 量子隧穿C. 原子光谱D. 相对论效应答案：B解析：薛定谔方程是量子力学中的一个基本方程，它描述了微观粒子在量子态下的行为。
量子隧穿是量子力学中的一个重要现象，它可以用薛定谔方程来解释。
7. 下列哪个物理现象可以用广义相对论解释？A. 光的折射B. 引力透镜C. 狭义相对论效应D. 光的干涉答案：B解析：广义相对论是爱因斯坦提出的一种引力理论，它描述了引力的本质和作用。
引力透镜是广义相对论的一个重要预言，它可以用广义相对论来解释。
8. 下列哪个物理现象可以用电磁感应定律解释？A. 法拉第电磁感应定律B. 安培环路定理C. 楞次定律D. 电磁感应答案：A解析：法拉第电磁感应定律是电磁学中的一个基本定律，它描述了磁场变化产生的感应电动势。
全国部分地区大学生物理竞赛电磁学部分
法拉第电磁感应定律
i
d
dt
楞次定律
闭合回路中感应电流的方向，总是使它所 激发的磁场来阻止引起感应电流的磁通量 的变化。
2
例：
3
4
5
一、动生电动势
整个导体回路或其中一部分，以及一段孤立导体 在稳恒磁场中运动时，所产生的感应电动势。
Blv
b
均
l
v
匀 磁
场
a
B
典型装置
b
a
1 v0B2l
P0
12
二、感生电动势
根据法拉第电磁感应定律，感应电动势的一般表
示式为：
d d
B dS
dt dt S
如果回L E路kL及d其l 包围 的 面 积S 保Bt持 d不S变，则
感生电动势：
动生电动势:
由于磁场随时
导体在稳恒磁场
dl B
d
L
Bldl
1BL2
O
l
0
2
o
负号表示电动势方向与积分方向相反，即
A O UO UA
A
9
半径为 R 的铜盘，在均匀磁场中以角速度 转动
，求盘上沿半径方向产生的感应电动势。
解： di (v B) dl
A
××××××
vBd l lBd l
E感生
2
dt
E感生
R2 2r
dB dt
L ××L××
B ××××r××
×××××
dB dt 0, E感 0
dB dt 0, E感 0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
夹角为
。
9.设想将地球挤压成半径为 ������0 的小球体，光子在小球体的万有引力作用下，恰好能沿着球 体表面作匀速圆周运动，地球便成为一个“黑洞”。已知地球真实半径 ������ = 6.4 × 106 m ，地
面重力加速度 ������ = 9.8 m/s2，真空光速 ������ = 3.0 × 108 m⁄s 。地球成为“黑洞”的半径 ������0 =
线，其中 ������ 的单位取为 ������������������ 。
（2）计算循环效率 ������ 。
������
������ ������
������
������
������
4 / 10
*****************************密******************封*******************线*********************************
������
������0
=
√3 4
������0
������(������) = ������������0√1���6������20���2 + 5
������
其中 ������0 为 ������ = ������0 处介质的折射率，试 求 ������ 值和在 ������ > 0 区域内的光线方程 ������~������ 。
������
摩擦。假设 ������ 端可以沿地面朝右滑动，但因受约束，不
会离开地面；������ 端可以沿着墙面朝下滑动，但不受相应
������
的约束，故可以离开墙面。试问在 ������ 端未达墙的底端 ������
������
之前，������ 端会否离开墙面？若会，再问 ������ 达何值时 ������ 端
。
水平地面
������2 2
������
������
������1
3
������
������
1
������3
3.热力学系统处于某一宏观态时，将它的熵记为 ������ ，该宏观态包含的微观态数记为 ������ ，玻尔
兹曼假设两者的关系为
。一个系统从平衡态 ������ 绝热过程到达平衡态
������ ，状态 ������ 的熵 ������������ 与状态 ������ 的熵 ������������ 之间大小关系必为
二、计算题（必做，共 4 题，每题 15 分，共 60 分）
11.（15 分）如图 1 所示，三条边长各为 ������1 、 ������2 �� 均匀流到右侧表面 ������ ，已测得
其电阻为 ������������������ = 10 Ω 。若将其各边长都增大一倍，质材不变， 试分析地判定相应的电阻 ���������∗��������� = ？
离开墙面？
考场
准考证号
姓名
学校
5 / 10
14.（15 分）如图所示，在 ������ − ������������ 平面
内，光线从
������0
=
������0
>
0
、������0
=
√3 4
������0
点
右 上 方 入 射 ， 入 射 方 向 与 ������ 轴 夹 角
������0 = 60°。假设在讨论的区域内，平面 上介质折射率 ������ 随 ������ 的分布函数为
������������ = ������ ⋅ ������������ = ������(������������2) = ������������ ：质点功能关系的微分式
������ = ∆������ ：质点功能关系的积分式
因
又可得
������������ = ������(������������ + ������0) = ������������������ + ������������0 = ������������������
*****************************密******************封*******************线*********************************
考场
考生类别
第 35 届全国部分地区大学生物理竞赛试卷
北京物理学会编印
2018 年 12 月 9 日
仍为亮斑，则平面镜移动的距离为
nm 。若开始时中心亮斑的干涉级次
为 ������，则最后中心亮斑的干涉级次为
。
8.两块理想的偏振片������1和 ������2平行放置，光强为 ������0的自然光正入射到 ������1，出射光束的光强
为
。若此光束再经 ������2 后透光全消失，则 ������1 透光轴与 ������2 透光轴之间的
13.（15 分）如图所示，轻的细杆 ������������������ 的 ������ 端靠在竖直
墙上，������ 端落在水平地面上，������ 端、������ 端和杆的中点 ������
������
处各有质量相同的固定小球。开始时图中角 ������ = 0 ，细
������
杆静止，后因微小扰动，细杆开始运动，设系统处处无
������
������
������2
������
������3
图1
������ ������ ������
������ ������ ������
������ ������
图2
考场
准考证号
姓名
学校
3 / 10
12.（15 分）某种双原子分子理想气体，其振动自由度
在温度 ������ < 2������0 时未被激发，在 ������ = 2������0 时即被激发。
������������ = ������������������：质点动能定理的微分式 ������ = ∆������������：质点动能定理的积分式 质量动量定理：
������������ = ������ ⋅ ������������ = ���������⃑��� = ������(���������⃑���) 微分式
������
������ 摩尔的此种气体经历的矩形循环过程 ������������������������������ 如图
所示，其中 ������ 、������ 、������ 处温度分别为 ������0 、2������0 、3������0 。 （1）画出循环过程中气体内能 ������ 随温度 ������ 的变化曲
如图 2 所示，每边长为 ������ 的均匀正方形电阻薄平板，已测得 ������、������ 两端间电阻 ������������������ = 5Ω 。若将每边长都增为 2������ ，质材不变， 试分析地判定相应的电阻 ���������∗��������� = ？
������ ������1
到达尾
到
������系
达尾部 ������ 。（速率 ������ 的大小可与真空光速 ������ 比拟。）
������ ������
2 / 10
*****************************密******************封*******************线*********************************
������0 ������0 = ������0 ������
6 / 10
*****************************密******************封*******************线*********************************
三、限做题（根据考生类别选做）
������
为
。
������
准考证号
姓名
学校
1 / 10
5. 据 稳 恒 电 流 磁 场 的 毕 奥 — 沙 伐 尔 定 律
������
���������⃑��� =
，可以求得图中两个互相垂直的
圆环电流公共中心处的磁感应强度大小为
������
������ =
。
������
������
6.直流电路如图所示，各支路电流方向已在图中设定。据此，节点
������ = ������0 , ������ = ������������2
√1
−
������2 ������2
称
������������
=
������
−
������0
=
������������2
−
������0������2
=
������0������2
√1
−
������2 ������2
−
m ，此时地球“表面”重力加速度 ������0 =
m⁄s2 。（如
上解答请保留两位有效数字，仅考虑经典引力的情形。）
10.静长为 ������0 的火箭以恒定速度 ������ 相对某惯性系 ������
������
运动，如图所示。从火箭头部 ������ 发出一个光讯号，
火箭上观察者认为需要经时间 ������′ = 部 ������ 。������ 系观察者认为需经时间 ������ =
椭圆轨道运动，如图所示。其中位置 1 为近太阳点，3 为
远太阳点，2 为椭圆短轴顶点。将太阳的质量记为 ������ ，
椭圆半长轴、半短轴分别记为 ������ 、������ 。������ 在位置 2 处速
度 ������2 =