分式复习(精品公开课)名师制作优质教学资料
合集下载
分式复习教学课件
9、约分
(1) x2 1 2
(2)
x2 m9
2x m3m
1
2
10、计算：
( y 1)3 (1 2 y y 2
y2 1
)
(xy
x2)
x2
2xy xy
y2
·
xy x2
x2 y
2
·
y2 x
3
y x
4
C
1、若分式
x 1
有意义，则应满足
x 1 x 2
的条件是x≠－2且x≠1
x a12
a2
ab b2 ab
3
(a
3 b)
7、不改变分式
1 2
x
0.2y
的值，把的分子和分母中各项的系数都化为整数。
0.5y
1 4
x
8、把分子分母中的多项式按x（或y）降幂排列，然后不改变分式
的值，使分子和分母中的最高次项的系数都是正数。
（1）
x
1 2x x2
；（2）
3y 7y2 57y y
2
2x y 4.若把分式 3x y
的x
和y
都扩大两倍,则分式的值(
)
ꢀꢀA．扩大两倍ꢀB．不变
ꢀꢀC．缩小两倍ꢀD．缩小四倍
xy
xy
5.若的把值(分式
x ).
y
中的
和
都扩大3倍,那么分式
ꢀꢀA．扩大3倍ꢀ B．扩大9倍 ꢀꢀC．扩大4倍 ꢀD．不变
6、 填空：
x(x y) (
)
x 2 xy x y
2、在代数式 3
、
、
x
、
y
x
中，分式共有
(A)1个 (B)2个 (C)3个 (D)4个
《分式总复习》课件
也较为复杂，学生容易出错。
经典例题解析
例题一
计算 $frac{x}{x + y} + frac{y}{x - y} frac{2xy}{x^2 - y^2}$。
解析
首先将所有项的分母统一 为 $(x + y)(x - y)$，然后 进行约分和加减运算。
解析
根据已知条件，通过等式 的性质和分式的加减法进 行证明。
特点
通常形式为 ax/b = c (其中 a、b、c 是已知数，b ≠ 0)。
复杂分式方程
定义
复杂分式方程是含有多个分式的 方程。
特点
通常形式为 f(x)/g(x) = h(x)/i(x) ( 其中 f(x)、g(x)、h(x)、i(x) 是多项 式函数)。
解法
通过消去分母，将方程转化为整式 方程或使用其他数学方法求解。
约分和通分是分式中的重要概念 ，但学生常常难以理解和掌握。 约分是将分子和分母中的公因式 约去，通分则是将两个或多个分
式化为同分母。
分式的加法与减法
在进行分式的加法和减法时，需 要寻找分母的公倍数，将分母统 一后再进行计算。这一过程对学
生来说较为复杂，容易出错。
分式的乘法与除法
在进行分式的乘法和除法时，需 要寻找分子和分母的公因式，进 行约分后再进行计算。这一过程
分式的性质
总结词
分式具有一些重要的性质，这些性质包括基本性质、等价变换性质和运算性质。
详细描述
分式的基本性质是分式的分子和分母可以同时乘以或除以同一个非零整式；等价 变换性质是分式的等价变换不改变分式的值；运算性质是分式的加、减、乘、除 等运算应先进行括号内的运算，再进行乘除运算，最后进行加减运算。
分式的约分与通分
经典例题解析
例题一
计算 $frac{x}{x + y} + frac{y}{x - y} frac{2xy}{x^2 - y^2}$。
解析
首先将所有项的分母统一 为 $(x + y)(x - y)$，然后 进行约分和加减运算。
解析
根据已知条件，通过等式 的性质和分式的加减法进 行证明。
特点
通常形式为 ax/b = c (其中 a、b、c 是已知数，b ≠ 0)。
复杂分式方程
定义
复杂分式方程是含有多个分式的 方程。
特点
通常形式为 f(x)/g(x) = h(x)/i(x) ( 其中 f(x)、g(x)、h(x)、i(x) 是多项 式函数)。
解法
通过消去分母，将方程转化为整式 方程或使用其他数学方法求解。
约分和通分是分式中的重要概念 ，但学生常常难以理解和掌握。 约分是将分子和分母中的公因式 约去，通分则是将两个或多个分
式化为同分母。
分式的加法与减法
在进行分式的加法和减法时，需 要寻找分母的公倍数，将分母统 一后再进行计算。这一过程对学
生来说较为复杂，容易出错。
分式的乘法与除法
在进行分式的乘法和除法时，需 要寻找分子和分母的公因式，进 行约分后再进行计算。这一过程
分式的性质
总结词
分式具有一些重要的性质，这些性质包括基本性质、等价变换性质和运算性质。
详细描述
分式的基本性质是分式的分子和分母可以同时乘以或除以同一个非零整式；等价 变换性质是分式的等价变换不改变分式的值；运算性质是分式的加、减、乘、除 等运算应先进行括号内的运算，再进行乘除运算，最后进行加减运算。
分式的约分与通分
初中数学八下第16章分式的复习示范课市公开课一等奖课件名师大赛获奖课件
分式复习三
复习回想一:
1.解分式方程的思路是：
分式 方程
去分母
整式 方程
2.解分式方程的普通环节
1、 在方程的两边都乘以最简公分母，约去分母， 化成整式方程.
2、解这个整式方程.
3、 把整式方程的根代入最简公分母，当作果是不 是为零，使最简公分母为零的根是原方程的增根，必 须舍去.
4、写出原方程的根.
倍，求他第二次加工时每小时加 工多少零件?
7.某人骑自行车比步行每小时 多 走 8 千 米 ， 如 果 他 步 行 12 千米所用时间与骑车行36千
米所用的时间相等，求他步 行40千米用多少小时?
例3 甲乙两人分别从相距36千米的A、B两地相向而行
甲从A出发到1千米时发现有东西遗忘在A地，立刻返回
请完毕下面的过程
学以致用
1.水池装有两个进水管，单独开甲管需a小时注满空池, 单独开乙管需b小时注满空池，若同时打开两管，那么注 满空池的时间是（ ）小时
A、 1 B、 ab C、
ab
ab
1 D1、
ab
1 ab
2.A地在河的上游，B地在河的下游，若船从A地开往B地 的速度为V1，从B地返回A地的速度为V2，则A、B两地间往 返一次的平均速度为____
大：18千米/时 小：45千米/时
5.已知轮船在静水中每小时行 20千米，如果此船在某江中 顺流航行72千米所用的时间 与逆流航行48千米所用的时
间相似，那么此江水每小时 的流速是多少千米?
6.某工人师傅先后两次加工零件各 1500个，当第二次加工时，他革
新了工具，改善了操作办法，成 果比第一次少用了18个小时.已知 他第二次加工效率是第一次的2.5
解:设江水每小时的流速是x千米，根据 题意列方程
复习回想一:
1.解分式方程的思路是：
分式 方程
去分母
整式 方程
2.解分式方程的普通环节
1、 在方程的两边都乘以最简公分母，约去分母， 化成整式方程.
2、解这个整式方程.
3、 把整式方程的根代入最简公分母，当作果是不 是为零，使最简公分母为零的根是原方程的增根，必 须舍去.
4、写出原方程的根.
倍，求他第二次加工时每小时加 工多少零件?
7.某人骑自行车比步行每小时 多 走 8 千 米 ， 如 果 他 步 行 12 千米所用时间与骑车行36千
米所用的时间相等，求他步 行40千米用多少小时?
例3 甲乙两人分别从相距36千米的A、B两地相向而行
甲从A出发到1千米时发现有东西遗忘在A地，立刻返回
请完毕下面的过程
学以致用
1.水池装有两个进水管，单独开甲管需a小时注满空池, 单独开乙管需b小时注满空池，若同时打开两管，那么注 满空池的时间是（ ）小时
A、 1 B、 ab C、
ab
ab
1 D1、
ab
1 ab
2.A地在河的上游，B地在河的下游，若船从A地开往B地 的速度为V1，从B地返回A地的速度为V2，则A、B两地间往 返一次的平均速度为____
大：18千米/时 小：45千米/时
5.已知轮船在静水中每小时行 20千米，如果此船在某江中 顺流航行72千米所用的时间 与逆流航行48千米所用的时
间相似，那么此江水每小时 的流速是多少千米?
6.某工人师傅先后两次加工零件各 1500个，当第二次加工时，他革
新了工具，改善了操作办法，成 果比第一次少用了18个小时.已知 他第二次加工效率是第一次的2.5
解:设江水每小时的流速是x千米，根据 题意列方程
分式复习课优秀课件
A.3 B.3或-3 C.-3 D.0
3.(2004年·杭州)甲、乙两人分别从两地同时出发，
若相向而行，则a小时相遇；若同向而行，则b小时
甲追上乙，那么甲的速度是乙速度的
()
C
ab
A.
b
2020/12/14
b
B. a b
ba
C. b - a
ba
D. b a
9．化简： 2 a ＝
a2 4a 4
分式 去分母 整式
方程
方程
2020/12/14
验根
【例7】 第二环节 做一做
解下列分式方程：
2020/12/14
2020/12/14
例8、若关于 x 的方程 x 8 k 8 有增根， x7 7 x
则 k 的值是多少？
练、1若关于x的方程
x
2
5
1
m x5
有增根，
则m的值等于（ ）
m 2、若方程 x 3 m 无解,则
10．计算：a
a
b
b
b
a
＝
． ．
11.计算:
x2 4y2 3xy3
x
xy 2y
＝
．
12.分式
2, a1
1 a2 2a 1 ,
1 a 1
的最简公分
母是_______________
13、1 ( 1 1)
2020/12/14
a
b
例
12、若
1 x
-
1 y
=3,则
2x+3xy-2y x-2xy-y
复习课
2020/12/14
A
分式有意义
B≠0
的形式
分式复习优质课市公开课一等奖省优质课获奖课件
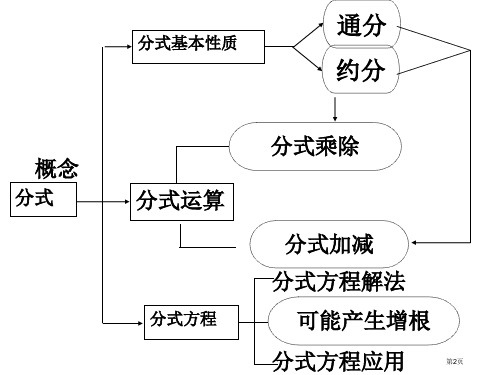
1 x2 2x 1
3
x 2x2
2 1
2 x2 1 4x 4
x2
4 (π
x)2
第4页
2.分式基本性质:
分式分子和分母都乘以（或除以）同一个不等 于0整式，分式值不变.
A AM A AM
,
(其中M是不等于0整式)
B BM B BM
第5页
1.以下式子
（1） a x a （1 2）
b x b1
n ；na ,a 0
b ； a 1
ab
（3） x y x； y（4）
xy xy
ba ab ca ac
中正确是
（）
A 、1个 B 、2 个 C、 3 个 D、 4 个
第9页
4b、值若分将别分扩式大为a原ab来b (2a倍、，b均则为分正式数值）为中（字）母a、
A．扩大为原来2倍 B．缩小为原来 1
C．不变
D．缩小为原来 2
x2 y2
B、 x y2
y2 x2 C、 x y
x2 y2 D、 x 2 y xy 2
第13页
1.计算：
第14页
第15页
5. a2 b2 (1 a2 b2 )
a2b ab2
2ab
6. x 3 (x 2 5 )
x2
x2
第16页
3.化简并求值：
x2
x2
2x
x2
x 1 4x 4
x y z
4.分式
,
,
5b2c 10a 2b 2ac
最简公分母是
；
3
y
x 2 y y 3 , xy x 2
最简公分母是
.
第11页
4.什么是最简分式？ 一个分式分子和分母没有公因式时叫做最
分式复习公开课教案(定稿)
胶州市公开课 教学案 授课时间 2016-5-27胶州市第二十五中学八年级数学下册主备人_ _ 复备人_ 审核_张其 授课班级 八年级_ 课型 复习课_ 课题：第五章 分式复习一 一、【教学目标】知识与技能： （1）使学生进一步熟悉分式的意义及分式的运算；（2）提高学生分式的基本运算技能．数学能力：（1）提高学生的运算能力，发展学生的合情推理能力；二、【教学重点和难点 】学习重点：1.分式的基本性质 2.分式的运算学习难点 分式的四则运算----它是整式运算、因式分解和分式运算的综合三、基础知识复习：★知识点一： 分式的概念：整式A 除以整式B ，可以表示成 的形式，如果除式B 中含有 ，那么称 为分式．其中A 称为分式的分子，B 称为分式的分母。
★知识点二：分式有关的条件：①若 ，则分式有意义；②若 ，则分式无意义；③若 ，则分式的值 ＝0.◆小练习一：1.在代数式中，分式共有_____个 213124, , , (), , 32232m x x a b x y x π---+-2、当x 时，分式x-13有意义。
3、分式)3)(1(12---x x x 有意义的条件是____ _____。
值为零的条件是4.当x 时，分式 242--x x 无意义。
5、若分式1-x x 无意义，则x= 。
★知识点三：分式的基本性质：分式的分子与分母都乘以（或除以）分式的 ．用式子表示为 .★知识点四：1.约分：把一个分式的分子和分母的 约去，这种变形称为分式的约分．约分的依据是2.约分的结果是：_________ ___3.约分时要注意：（1）要找出分子分母的公因式；（2）分子、分母是多项式的要先分解因式再约分； （3）约分要彻底。
★知识点五：最简分式 ：分子与分母中不含___ ___的分式◆小练习二：1、下列分式中是最简分式的是（ ）12.2+x x A x B 24. 11.2--x x C 11.--x x D2.化简下列分式：abd bca 81412）（ 164)2(22--x x x 22164)3(m m m --想一想：如何进行约分？约分的技巧：1.如果分式的分子、分母都是单项式，先找出分子和分母的__ ______，然后直接约去。
分式复习二市公开课一等奖省优质课获奖课件
((12))1xx 2
1yy3,z求, 求5 34
x xxy x2
xy xyyz y2
5yyzzx的2 的值值7 2；；
(2)
x 2
y 3
z ,求 4
xy x2
yz y2
zx 的值； z2
26
29
第12页
8. 已知x2 3x 1 0, 求x2
1 的值. x2
已知
x3 (x 2)2
A x2
3、2(a
a b)(b
2)
,
3(b
b a)(2
b)
，
c 4(b
2)
最简公分母是
第3页
4、 计算：
(1) 4 3 • aa
(2) x 1 2x 1 x 1 1 x
第4页
(3) x 1 2x 1
x 1 x 2
x x
1x 1x
2 2
2x 1x 1 x 2x 1
x2 3x
x 1x
2
2
2x2 x
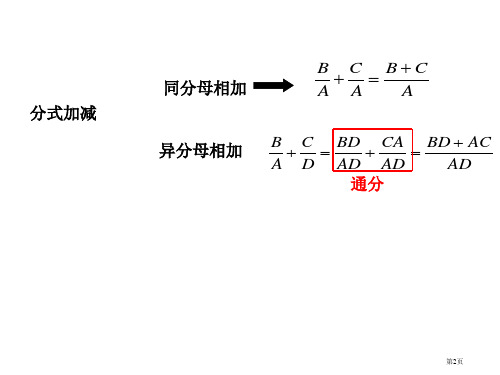
分式加减
同分母相加
B C BC AA A
异分母相加
B C BD CA BD AC
A D AD AD
AD
通分
第2页
1、通分：
5 · 2 7c 2a 9a 2b3 12a 4b2
2
1
3 x
x2 6x 8 , x2 x 6 , 12 x x2
2、 2 、 1 3x 最简公分母是 x 1 2 2x
B (x 2)2
求A、B
第13页
0
第8页
（7）当 x = 200 时，求
x x6 1 x 3 x2 3x x
解:
x x6 1 x 3 x2 3x x
分式总复习市公开课一等奖省赛课微课金奖课件
IImmaaggee x2 3x2 0 解得 x1 1, x2 2
检验：x=1是原方程根，x=2是增根
∴原方程根是x=1
第26页
例2
已知
x3 (x 2)2
A B x 2 (x 2)2
求A、B
A 1; B 5
第27页
解方程：
1. x 5 x 1 0 x3 x1
x2
第28页
2.
x x
21 2
x2 y2 x2 y2
x2 xy
0
第20页
（7）当 x = 200 时，求 x x 6 1
值.
x 3 x2 3x x
解:
x
x
3
x6 x2 3x
1 x
x2
x6 x3
x( x 3) x( x 3) x( x 3)
x2 9 ( x 3)( x 3) x 3
x( x 3) x( x 3)
第10页
x 7．假如把分式 x＋y 中x和y值都扩大３倍， 则分式值（ B ） Ａ 扩大３倍 Ｂ不变 Ｃ缩小１／３ Ｄ缩小１／６
xy 8．假如把分式 x＋y 中x和y值都扩大３倍， 则分式值（ A ） Ａ 扩大３倍 Ｂ不变 Ｃ缩小１／３ Ｄ缩小１／６
第11页
9．若x，y值均变为原来１／３ ，则分式 （ C ）．
用符号语言表示： a c ac b d bd
两个分式相除，把除式分子和分母颠倒位置后
再与被除式相乘。
a 用符号语言表示： c a d ad b d b c bc 第17页
（7）
9 6x x2 x2 16
x3 4x
x2 4x 4 x2
4
解：
9 6x x2 x2 16
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
b d bd 1 a c ac
分式的加减
例3、计算：
x y x y 2 x x y x xy x y x y2 2 解： x x y x xy
2
( x y )( x y ) x2 y2 x( x y ) x( x y ) x( x y ) 2 2 2 2 x y x y 0 2 x xy
数学·人教版（RJ）
分式的定义
1.在下列式子中，分式的个数是（ A ）
1 2 xy 5 x y 10 x 2 3 , , 4a b c, , , 9x , a 6 x 7 8 y x
A. 5 B.4 C. ３ D. ２
2
分式有意义的条件 1.当x为任意实数时,下列分式一定有意义的是( C ) x 1 x1 x1 x1 A. 2 B. 2 C. 2 D. x x 1 x 1 x 分式值为零的条件
ab ab D c c
第十六章 |过关测试（一） ►考点三 分式的约分与通分
下列运算正确的是 － x－ y x－ y A. ＝ － x＋ y x＋ y a2－ b2 a＋ b C. 2＝ a－ b a－ b
[解析]
( C )
a2－ b2 a－ b B. 2＝ a－ b a＋ b x－ 1 1 D. 2＝ 1－ x x＋ 1
－ x＋ y x＋ y a2－ b2 a＋ b A中 ＝ ， 故选项 A 不对； B 中 ＝ ， － x－ y x－ y a－ b2 a－ b
x－ 1 x－ 1 1 故选项 B 不对； C 正确； D中 ＝－ ， 故选项 D 不对． 1－ x2－ x＋ 1x－ 1 x＋ 1
数学·人教版（RJ）
1、形如 含有字母。对于任意一个分式，分母都不能为零。 2、分式的加减法则：
A B的式子叫做分式，其中A、B是整式，B中必须
a b ab 1 c c c
3、分式的乘除法则：
a c ad bc 2 b d bd b d b c bc 2 a c a d ad
知识结构 分式的基本概念 分 式
分式的运算
分式的定义 分式有意义的条件 分式值为零的条件 分式的基本性质 约分、通分 分式的乘除、加减运算 整数指数幂 分式方程 分式方程的应用
分式方程及应用
第十六章 |过关测试（一）
知识归纳
1．分式的概念 A 分式：形如 (A、 B 是 ________ 整式 ，且 B 中含有______) 字母 B 的式子叫做分式． [辨析] (1)分式有意义的条件：分母不为 0. (2)分式的值为 0 的条件：分子为 0，但分母不为 0.
2
若值为0，则x应满足（ B ）
A、x=2 C、x=-1 B、x =-2 D、x =-1或x =2
第十六章 |过关测试（一）
2．分式的基本性质 A A× M A÷ M 基本性质： ＝ ＝ (M≠ 0 的整式)，其中 A，B， B B× M B÷ M C 为整式． 公因式 约去，叫做分式 约分：把分式的分子与分母中的 _______ 的约分． 基本性质 通分：利用分式的 _______，使分子和分母同时乘适当的 整式，不改变分式的值，把 ______ 同 分母的分 异 分母化成 _______ 式，这样的分式变形叫做分式的通分．
求Ａ与Ｂ的值。
典型题型
x y z x yz 1.若 = = 且z≠0，则 3x 2 y 5 4 3 12 的值为 。 7
x 2 +1 4 2．若 x
, 则
2
1 x 2 x
2
__________ 14
1 1 2 1 x 4 x 16 x 2 2 16 x x x
零 简公分母中，使公分母为_______ 的解，不是原分式方程的解．
6．列分式方程解应用题 [易错点] 列分式方程解应用题要检验两次，第一次检验求出来的解是 否为原方程的解，第二次检验是否符合题意．
数学·人教版（RJ）
4.解方程:
x 1 4 (1) 1 2 1- x x 1
x 2 (2) 1 x 2 2x
x 9 =3 时,分式 2. 当x_____ 的值为零. x3 3 2或0 3.已知 的值是正整数，则整数a=_______. a3
2
一、练习：
1. 若分式
A、x≠-1 C、x≠2
若有意义，则x应满足（ B ）
B、x ≠-1且x ≠2 D、x ≠-1或x ≠2
x 4 ( x 1)( x 2)
数学·人教版（RJ）
分式的基本性质 1.把分式 x (x≠0)中的分子分母的x、y都同时
扩大为原来的2倍，那么分式的值将是原分式的值
（ C） A.2倍
x2 y 2
B.4倍
C.一半
）
ab ab B c c
D.不变
2.下列各式正确的是（ D
ab ab A c c ab ab C c c
5 .若关于x的分式方程
x m2 2 x3 x3
有增根，则m的值为__________。
1、如果下列关于x的方程有正数解，
x4 m 求m的取值范围； 3 x5 x5
3 2 x 2 kx 1 x3 x3
2、如果关于x的方程无解，求k的值，
例2.如果整数Ａ、Ｂ满足等式
x －4x＋4 x －2x 例3 [2013· 江西]先化简，再求值： ÷ 2 ＋1 ，
在0，1，2三个数中选一个合适的，代入求值．
2
2
2x
x
第十六章 |过关测试（一）
5．分式方程的概念和解法 分式方程：分母里含有_______ 未知数 的方程叫做分式方程． 解分式方程的基本思想：把分式方程转化为整式方程，即分式方程 去分母 ――→ 换元 整式方程． 解分式方程的具体方法：方程两边同乘各分式的____________ 最简公分母 ，约去 分母，化为整式方程，再求根验根． 验根原因和方法：在方程的变形时，有时可能产生不适合原方程的 根，使方程中的分母为_______ 零 ，因此解分式方程要验根，其方法是代入最