MATLAB作业
matlab1-8章课后作业

MATLAB基础教程1~8章作业Matlab第一章1.阐述Matlab的功能Matlab作为一种高级计算软件,是进行算法开发、数据可视化、数据分析以及数值计算的交互式应用开发环境,已被广泛应用于不同领域。
Matlab的基本功能包括:数学计算功能、图形化显示功能、M语言编程功能、编译功能、图形用户界面开发功能、Simulink建模仿真功能、自动代码生成功能。
Matlab第二章1.创建double的变量,并进行计算。
(1)a=87,b=190,计算a+b、a-b、a*b。
(2)创建uint8 类型的变量,数值与(1)中相同,进行相同的计算。
>> a=87,b=190a =87b =190>> a+bans =277>> a-bans =-103>> a*bans =16530>> c=uint8(87), d=uint8(190)c =87d =190>> c+dans =255>> c-dans =>> c*dans =2552.计算(1)sin(60)(2)e^3(3)cos(3π/4)>> sind(60)ans =0.8660>> exp(3)ans =20.0855>> cos(3*pi/4)ans =-0.70713.设u=2,v=3,计算:(1)(2)(3)>> u=2;>> v=3;>> 4*u*v/log(v)ans =21.8457>> (exp(u)+v)^2/(v^2-u)ans =15.4189>> sqrt(u-3*v)/(u*v)ans =0 + 0.4410i4.计算如下表达式:(1)(2)>> (3-5*i)*(4+2*i)ans =22.0000 -14.0000i>> sin(2-8*i)ans =1.3553e+003 +6.2026e+002i5.判断下面语句的运算结果。
MATLAB作业

MATLAB作业⼀、必答题:1. MATLAB系统由那些部分组成?答:MATLAB系统主要由开发环境、MATLAB语⾔、MATLAB数学函数库、图形功能和应⽤程序接⼝五个部分组成。
2. 如何启动M⽂件编辑/调试器?答:在操作界⾯上选择“建⽴新⽂件”或“打开⽂件”操作时,M⽂件编辑/调试器将被启动。
在命令窗⼝中键⼊“edit”命令也可以启动M⽂件编辑/调试器。
3. 存储在⼯作空间中的数组能编辑吗?如何操作?答:存储在⼯作空间的数组可以通过数组编辑器进⾏编辑:在⼯作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输⼊修改内容即可。
4. 在MATLAB中有⼏种获得帮助的途径?答:在MATLAB中有多种获得帮助的途径:(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器;(2)help命令:在命令窗⼝键⼊“help” 命令可以列出帮助主题,键⼊“help 函数名”可以得到指定函数的在线帮助信息;(3)lookfor命令:在命令窗⼝键⼊“lookfor 关键词”可以搜索出⼀系列与给定关键词相关的命令和函数(4)模糊查询:输⼊命令的前⼏个字母,然后按Tab键,就可以列出所有以这⼏个字母开始的命令和函数。
5. 有⼏种建⽴矩阵的⽅法?各有什么优点?答:(1)以直接列出元素的形式输⼊;(2)通过语句和函数产⽣;(3).在m⽂件中创建矩阵;(4)从外部的数据⽂件中装⼊。
6. 命令⽂件与函数⽂件的主要区别是什么?答:命令⽂件: M⽂件中最简单的⼀种,不需输出输⼊参数,⽤M ⽂件可以控制⼯作空间的所有数据。
运⾏过程中产⽣的变量都是全局变量。
运⾏⼀个命令⽂件等价于从命令窗⼝中顺序运⾏⽂件⾥的命令,程序不需要预先定义,只要依次将命令编辑在命令⽂件中即可。
函数⽂件:如果M⽂件的第⼀个可执⾏⾏以function开始,便是函数⽂件,每⼀个函数⽂件定义⼀个函数。
MATLAB实验练习题(计算机)-南邮-MATLAB-数学实验大作业答案
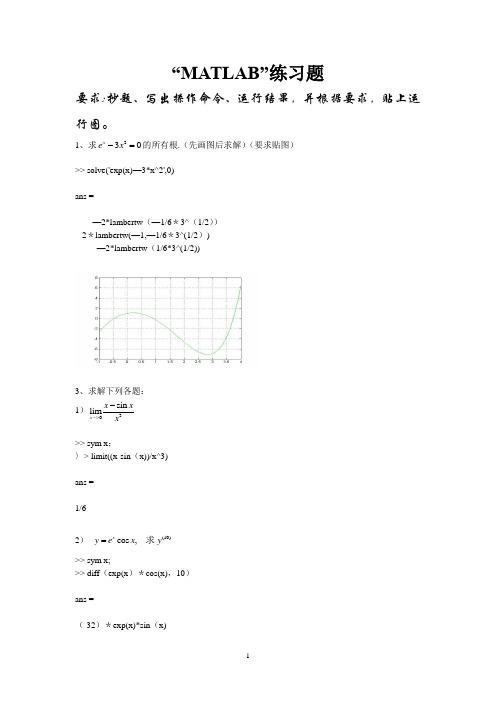
“MATLAB”练习题要求:抄题、写出操作命令、运行结果,并根据要求,贴上运行图。
1、求230x e x -=的所有根.(先画图后求解)(要求贴图)>> solve('exp(x)—3*x^2',0)ans =—2*lambertw (—1/6*3^(1/2))-2*lambertw(—1,—1/6*3^(1/2))—2*lambertw (1/6*3^(1/2))3、求解下列各题:1)30sin lim x x x x ->->> sym x ;〉> limit((x-sin (x))/x^3)ans =1/62) (10)cos ,x y e x y =求>> sym x;>> diff (exp(x )*cos(x),10)ans =(-32)*exp(x)*sin (x)3)21/20(17x e dx ⎰精确到位有效数字)〉〉 sym x;〉〉 vpa((int(exp(x^2),x,0,1/2)),17)ans =0.544987104183622224)42254x dx x+⎰〉> sym x ;>〉 int (x^4/(25+x^2),x)ans =125*atan (x/5) - 25*x + x^3/35)求由参数方程arctan x y t⎧⎪=⎨=⎪⎩dy dx 与二阶导数22d y dx 。
〉> sym t;>> x=log(sqrt (1+t^2));y=atan(t);〉> diff (y ,t )/diff (x ,t)ans =1/t6)设函数y =f (x )由方程xy +e y = e 所确定,求y ′(x ).>> syms x y ;f=x *y+exp(y )—exp (1);〉> -diff(f,x )/diff (f,y)ans =-y/(x + exp (y))7)0sin 2x e xdx +∞-⎰>〉 syms x ;>〉 y=exp(-x)*sin(2*x );〉> int(y ,0,inf )ans =2/58) 08x =展开(最高次幂为)〉> syms xf=sqrt(1+x);taylor(f,0,9)ans =— (429*x^8)/32768 + (33*x^7)/2048 — (21*x^6)/1024 +(7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + x/2 + 19) 1sin (3)(2)x y e y =求〉> syms x y ;>〉 y=exp(sin (1/x));>〉 dy=subs (diff(y,3),x ,2)dy =—0.582610)求变上限函数2x x ⎰对变量x 的导数.>> syms a t ;>〉 diff (int(sqrt(a+t),t,x ,x^2))Warning: Explicit integral could not be found 。
MATLB实验作业

实验一MATLAB运算基础1、用逻辑表达式求下列分段函数的值。
t=0:0.5:2.5y=t.^2.*((t>=0)&(t<1))+(t.^2-1).*(( t>=1)&(t<2))+(t.^2-2*t+1).*((t>=2 )&(t<3))2、求[100,999]之间能被21整除的数的个数。
p=rem([100:999],21)==0;sum(p)3、建立一个字符串向量,删除其中的大写字母。
ch='KdDdfKaWdsfCI',k=find(ch>=' A'&ch<='Z'),ch(k)=[]4、输入矩阵,并找出A中大于或等于5的元素。
A=[1 2 3;4 5 6;7 8 9],[m,n]=find(A>=5),for j=1:length(m)x(j)=A(m(j),n(j))xend5、求矩阵的行列式值、逆和特征根。
a11=input('a11='),a12=input('a12 ='),a21=input('a21='),a22=input('a22 ='),A=[a11,a12;a21,a22],DA=det(A),IA=inv(A),EA=eig(A) 6、不采用循环的形式求出和式的数值解。
sum(2.^[0:63])实验二1、1行100列的Fibonacc数组a,a(1)=a(2)=1,a(i)=a(i-1)+a(i-2),用for循环指令来寻求该数组中第一个大于10000的元素,并指出其位置i。
n=100;a=ones(1,n);for i=3:na(i)=a(i-1)+a(i-2);if a(i)>10000a(i),break;end;end,i2、编写M脚本文件,定义下列分段函数,并分别求出当()、()和()时的函数值。
MATLAB与控制系统仿真大作业

>> G1=tf(num,den);
>> G1=zpk(G1)
G1 =
5 (s+0.6) ----------------(s+3) (s+2) (s+1)
>> num=[2 1]; den=[1 2.9 1]; G2=tf(num,den); >> G2=zpk(G2)
G2 =
2 (s+0.5)
>> xlabel('x') ylabel('exp(-2.*x)')
三、simulink 建模(每题 10 分,共 20 分)
1、已知单位负反馈的开环传递函数为 G(s) =
2 s2 + 4s
,试利用
simulink
建立系在单位阶跃输入作用下的模型。
要求答案包括:(1)simulink 建模结构图;
(2)在同一个坐标中的阶跃信号和响应曲线图。
2、已知系统的开环传递函数为
G1(s)
=
2s2 + 5s + 6 s2 + 2s + 3
、G2 (s)
=
s2
s+6 + 7s +1
,H
(s)
=
5(s + 2) s +10
求:建立 Simulink 仿真模型,并求出其系统在单位阶跃响应;
要求答案包括:(1)simulink 建模结构图;
x=
-2.9709
0.5491
3.6000
0.0509
2. 已知下列矩阵
2 3 1
−1 3 5
A
=
MATLAB平时作业(图文版)

MATLAB 平时作业第一章 习题16. 以下两种说法对吗?(1)“MATLAB 的数值表达精度与其指令窗中的数据显示精度相同。
”答:此种说法错误。
MATLAB 提供了控制数据显示格式的控制指format ,该指令并不改变MATLAB 内存中变量的精度,只是改变其显示精度。
(2)“MATLAB 指令窗中显示的数值有效位数不超过7位。
”答:此种说法错误。
当变量小于1000时,使用format 或format short 后,或者默认情况下,变量的显示精度最多不超过7位,但显示精度不等于变量的精度。
7. 想要在MATLAB 中产生二维数组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321S ,下面哪些指令能实现目的? S=[1,2,3;4,5,6;7,8;9]S=[1 2 3;4 5 6;7 8 9]S=[1,2,3;4,5,6;7,8,9] %整个指令在中文状态下输入 答:操作如图:第1、2条指令可以实现,第3条指令不可实现。
第三章 习题31.在MATLAB 中,先运行指令A=magic(3), B=[1,2,1;3,4,3;5,6,7], C=reshape(1:6,3,2)生成阵列33⨯A ,23⨯B ,23⨯C ,然后根据运行结果回答以下问题:运行结果如图:(1)计算A*B, B*A ,这两个乘积相同吗? 计算结果如图:答:不同。
(2)计算A\B, B/A ,左除、右除结果相同吗?计算结果如图:答:不同。
(3)计算B( : ,[1,2]).*C和C.*B( : , [1,2]),这两个乘积相同吗?计算结果如图答:相同。
(4)计算A\A和A.\A,这两个计算结果相同吗?计算结果如图:答:相同。
(5)计算A\eye(3)和inv(A),这两个计算结果相同吗?计算结果如图:答:不同。
(提示:根据对计算结果的目测回答问题)2.在MATLAB中,先运行A=[1, 2; 3, 4],b=0.5,C=[4, 2; 1, 0.5], 然后根据计算结果回答以下问题:创建数据步骤略(1)计算A^b和A.^b, 这两个计算结果相同吗?答:不同。
matlab作业3参考答案

matlab作业3参考答案Matlab作业3参考答案Matlab作业3是一个综合性的编程任务,要求学生运用Matlab的各种功能和工具来解决实际问题。
本文将提供Matlab作业3的参考答案,并对其中的关键步骤和思路进行详细解释。
一、问题描述在本次作业中,学生需要解决一个关于图像处理的问题。
具体来说,给定一张彩色图像,学生需要编写Matlab代码来实现以下功能:1. 将彩色图像转换为灰度图像;2. 对灰度图像进行高斯滤波;3. 对滤波后的图像进行边缘检测;4. 对边缘图像进行二值化处理。
二、解决方案1. 将彩色图像转换为灰度图像首先,我们需要读取彩色图像。
可以使用Matlab的imread函数来实现。
然后,使用rgb2gray函数将彩色图像转换为灰度图像。
代码如下:```matlabrgbImage = imread('image.jpg');grayImage = rgb2gray(rgbImage);```2. 对灰度图像进行高斯滤波接下来,我们需要对灰度图像进行高斯滤波。
高斯滤波是一种常用的图像平滑方法,可以有效地去除图像中的噪声。
Matlab提供了fspecial函数来生成高斯滤波器。
代码如下:```matlabh = fspecial('gaussian', [3 3], 1);filteredImage = imfilter(grayImage, h);```3. 对滤波后的图像进行边缘检测在这一步中,我们需要对滤波后的图像进行边缘检测。
边缘检测可以帮助我们找到图像中的边缘和轮廓。
Matlab提供了多种边缘检测算法,如Sobel算子和Canny算子。
代码如下:```matlabedgeImage = edge(filteredImage, 'canny');```4. 对边缘图像进行二值化处理最后,我们需要对边缘图像进行二值化处理,将图像中的边缘转换为黑白两种颜色。
Matlab习题及答案
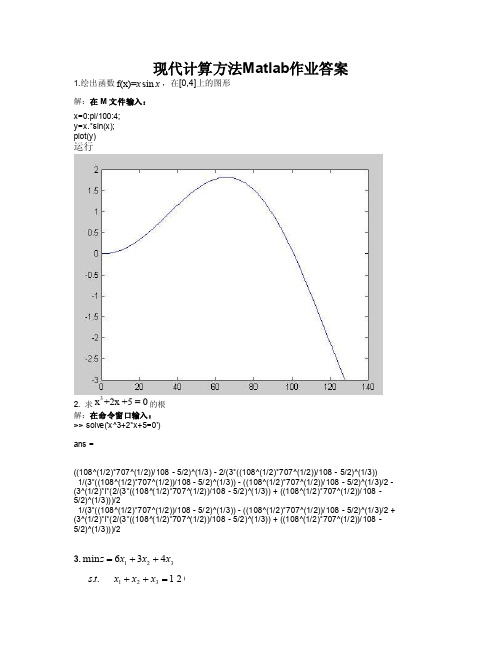
现代计算方法Matlab 作业答案1.绘出函数f(x)=sin x x ,在[0,4]上的图形解:在M 文件输入:x=0:pi/100:4;y=x.*sin(x);plot(y)运行2. 求3x +2x +5 = 0的根解:在命令窗口输入:>> solve('x^3+2*x+5=0')ans =((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3) - 2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3))1/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 -(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/21/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 +(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/23.321436min x x x z ++=120..321=++x x x t s301≥x5002≤≤x203≥x解:运用单纯形法计算此题,首先把约束条件化成标准形式:,,,,,205030120654321635241321≥=-=+=-=++x x x x x x x x x x x x x x x(1)在M 文件输入SimpleMthd 函数:function [x,minf] = SimpleMthd(A,c,b,baseVector)sz = size(A);nVia = sz(2);n = sz(1);xx = 1:nVia;nobase = zeros(1,1);m = 1;for i=1:nViaif (isempty(find(baseVector == xx(i),1)))nobase(m) = i;m = m + 1;else;endendbCon = 1;M = 0;while bConnB = A(:,nobase);ncb = c(nobase);B = A(:,baseVector);cb = c(baseVector);xb = inv(B)*b;f = cb*xb;w = cb*inv(B);for i=1:length(nobase)sigma(i) = w*nB(:,i)-ncb(i);end[maxs,ind] = max(sigma);if maxs <= 0minf = cb*xb;vr = find(c~=0 ,1,'last');for l=1:vrele = find(baseVector == l,1);if (isempty(ele))x(l) = 0;elsex(l)=xb(ele);endendbCon = 0;elsey = inv(B)*A(:,nobase(ind));if y <= 0disp('不存在最优解!');x = NaN;minf = NaN;return;elseminb = inf;chagB = 0;for j=1:length(y)if y(j)>0bz = xb(j)/y(j);if bz<minbminb = bz;chagB = j;endendendtmp = baseVector(chagB);baseVector(chagB) = nobase(ind);nobase(ind) = tmp;endendM = M + 1;if (M == 1000000)disp('找不到最优解!');x = NaN;minf = NaN;return;endend(2)在命令窗口输入:clear allA=[1 1 1 0 0 0;1 0 0 -1 0 0;0 1 0 0 1 0;0 0 1 0 0 -1];c=[6 3 4 0 0 0];b=[120;30;50;20];[xm,mf]=SimpleMthd(A,c,b,[3 4 5 6])xm =0 50 70mf =4304.计算下面函数在区间(0,1)内的最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB作业一一.编写一个脚本,判断输入字符串中每个单词的首字母是否为大写,若不是则将其修改为大写,其他字母为小写。
程序:string=input('Please enter a string:');if (string(1)>='a'&&string(1)<='z')string(1)=char(string(1)-32);endm=length(string);for i=2:mif (isspace(string(i-1))&&string(i)>='a'&&string(i)<='z')string(i)=char(string(i)-32);endenddisplay(string);结果:Please enter a string: 'gsGsdg gwg ghge'string =GsGsdg Gwg Ghge二.创建一个结构体,用于统计学生的情况,包括学生的姓名、学号、各科成绩等。
程序:student=struct('name',{'lichao'},'number',{'5262'},'subject',[1 2],...'score',[98 95])结果:student =包含以下字段的struct:name: 'lichao'number: '5262'subject: [1 2]score: [98 95]三.创建 2×2 单元数组,第 1、2 个元素为字符串,第三个元素为整型常量,第四个元素为双精度(double)类型,并将其用图形表示程序:string1=input('Please enter the first string:');string2=input('Please enter the second string:');number1=input('Please enter a numeber');number2=input('Please enter a rand number:');s={string1,string2,int8(number1),number2}cellplot(s);结果:Please enter the first string:'gsd'Please enter the second string:'sdgd'Please enter a numeber8Please enter a rand number:9s =1×4 cell 数组附:函数名功能描述函数名功能描述deal 把输入处理成输出fieldnames 获取结构的字段名getfield 获取结构中指定字段的值rmfield 删除结构的字段(不是字段内容) setfield 设置结构数组中指定的字段的值struct 创建结构数组struct2cell 结构数组转化成元胞数组isfield 判断是否存在该字段isstruct 判断某变量是否是结构类型MATLAB作业二1、找出所有这样的4 位正整数,其各位数字的4次方的和等于该数本身,例如:1634 = 14 + 64 + 34 + 44输出所有的满足条件的数至一行数组,这样的数共有多少个?程序:M=[];for t=1000:9999;a=fix(t/1000);b=fix(t/100)-a*10;c=fix(t/10)-a*100-b*10;d=rem(t,10);if t==a^4+b^4+c^4+d^4M=[M;t];endenddisp(M’);disp(numel(M));结果:1634 8208 947432、猴子吃桃问题:有一堆桃子不知数目,猴子第一天吃掉一半,觉得不过瘾,又多吃了一个,第二天照此办理,吃掉剩下桃子的一半另加一个,天天如此,到第十天早上,猴子发现只剩一只桃子了,问这堆桃子原来有多少个?程序:s=1;for i=1:9;s=2*(s+1);enddisp(s);结果:15343、求Fibonacci 数组中第一个大于10000的元素。
1,1,2,3,5,8,13,21,34,55,89,…程序:f1=1;f2=1;f=0;while(f<=10000)f=f1+f2;f1=f2;f2=f;endfprintf('Fibonacci数组中第一个大于10000的元素是%d',f);结果:Fibonacci数组中第一个大于10000的元素是10946MATLAB作业三(函数练习)函数文件:myfirstfun.mfunction y=myfirstfun(x)%一个分段函数的计算[m,n]=size(x);y=zeros(m,n);for i=1:m;for j=1:n;if x(i,j)<0&&x(i,j)~=-4a=x(i,j)*x(i,j)+x(i,j)-6;else if x(i,j)>=0&&x(i,j)<10&&x(i,j)~=2&&x(i,j)~=3a=x(i,j)*x(i,j)-5*x(i,j)+6;elsea=x(i,j)*x(i,j)-x(i,j)-1;end;end;y(i,j)=a;end;end;主程序:x=-10:0.1:10;y=myfirstfun(x);hold on;for k =1:length(x)-1plot(x([k,k+1]),y([k,k+1]));End结果:2、Matlab没有专门的函数执行多项式加法(减法)如果两个多项式的阶次相同,其系数向量的长度相等,多项式的加法就是将两个多项式向量直接相加(相减)。
当两个多项式的阶次不同时,其系数向量的长度也不同,这时需要先将低阶多项式的系数向量前边补上足够的0,以便使它和高阶多项式具有相同的长度,然后再执行加法(减法)运算。
请编写一个函数p = polyadd(p1,p2)实现不同阶次多项式的加法,并利用该函数完成下面的练习。
函数文件:ployadd.mfunction p=ployadd(p1,p2)%多项式的加法运算p1=p1(:).';p2=p2(:).';np1=length(p1);np2=length(p2);p=[zeros(1,np2-np1) p1]+[zeros(1,np1-np2) p2];主程序:p1=[0.69552 0.436 0.668 1.35];p2=[2.342 0 0.453 0];f=ployadd(p1,p2)结果:f =3.0375 0.4360 1.1210 1.3500函数文件:mysecondfun.mfunction y=mysecondfun(m,T,v)%理想气体的麦克斯韦速率分布函数y=[];k=1.381*10^(-23);for i=1:length(v)a=4*pi*((m/(2*pi*k*T))^(3/2))*exp((-m*v(i)^2)/(2*k*T))*v(i)^2;y=[y,a];end主程序:mNe=20.18*1.66*10^(-27); %前期的数值(常数)赋值mAr=39.94*1.66*10^(-27);v=0:2000;T1=273; T2=500;yNe1=mysecondfun(mNe,T1,v); %调用麦克斯韦速率分布函数yNe2=mysecondfun(mNe,T2,v);yAr1=mysecondfun(mAr,T1,v);yAr2=mysecondfun(mAr,T2,v);subplot(2,2,1); %绘制Ne气在t1,t2下的麦克斯韦速率分布曲线plot(yNe1,v,'--r');hold on;plot(yNe2,v,'-b');subplot(2,2,2); %绘制Ar气在t1,t2,下的麦克斯韦速率分布曲线plot(yAr1,v,'--r');hold on;plot(yAr2,v,'-b');subplot(2,2,3); %绘制Ne和Ar气在t1下的麦克斯韦速率分布曲线plot(yNe1,v,'--r');hold on;plot(yAr1,v,'-b');subplot(2,2,4); %绘制Ne和Ar气在t2下的麦克斯韦速率分布曲线plot(yNe2,v,'--r');hold on;plot(yAr2,v,'-b');结果:MATLAB作业四(绘图作业)1、请用三种不同的方法将三条曲线同时绘制在一个figure窗口(提示:其中有一种是用subplot),并在每一条曲线的旁边加上曲线的公式,这三条曲线的公式、颜色和线形均由你们定,但是,横轴,也就是x轴都是[-10,10],间隔为0.5。
①方法一程序:x=-10:0.5:10;y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);subplot(2,2,1);plot(x,y1,'-r');text(0,0,'y1=sin(x)');subplot(2,2,2);plot(x,y2,'--g');text(0,0,'y2=cos(x)');subplot(2,1,2);plot(x,y3,'-.b');text(0,0,'y3=sin(x)+cos(x)');结果:②方法二程序:x=-10:0.5:10;y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);hold onplot(x,y1,'-r');plot(x,y2,'--g');plot(x,y3,'-.b');legend('sin(x)','cos(x)','sin(x)+cos(x)');结果:③方法三程序:x=-10:0.5:10;y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);plot(x,y1,'-r',x,y2,'--g',x,y3,'-.b');legend('sin(x)','cos(x)','sin(x)+cos(x)','location','northwest'); 结果:2、还是这道题,不使用subplot方法将三条曲线绘制在同一个figure窗口中,然后为它们增加标注、标题、横坐标、纵坐标的名称(随便你们想),再加上网格。
